Molecular dynamics simulations of protein folding from the transition state

Abstract

Putative transition-state ensemble (TSE) conformations of src SH3 were identified by monitoring the deviation from the experimental φ values along molecular dynamics (MD) simulations of unfolding. Sixty MD trajectories (for a total of about 7 μs) were then started from the putative TSE. About one-half of the 60 runs reached the folded state while unfolding was observed in the remaining half of the runs. This result validates φ-value analysis as an approach to obtain structural information on the transition state. It also demonstrates that an atomic resolution description of the TSE can be extracted from MD simulations. All conformations in the TSE have the central three-stranded β-sheet formed in agreement with experimental data. An elongation of strand β2 as well as nonnative side-chain interactions between the diverging turn and the distal hairpin are observed. The simulation results indicate that the tight packing of the side chains between the diverging turn and the distal hairpin is a necessary condition for rapid folding. Contacts between residues in the most structured element of the TSE, the central β-sheet, are kinetically more important than those between the N- and C-terminal strands.

A better understanding of folding requires an accurate description of the transition state, in particular for single-domain, two-state proteins (1). Unfortunately, it is difficult to determine and analyze the transition-state ensemble (TSE) with conventional experimental techniques, because it corresponds to an unstable high-energy region on the free-energy surface. The protein-engineering method, pioneered by Fersht and coworkers (2), can provide structural information about the rate-limiting step of folding. It investigates the formation of side-chain interactions in the TSE by deleting parts of individual residues and assessing the effect on folding kinetics. The φ value is defined as the ratio ΔΔG^‡/ΔΔG_U−N, where ΔΔG^‡ is the change in free energy between the TSE and the unfolded state induced by a mutation of residue i, and ΔΔG_U−N is the change in free energy between the native state and the unfolded state. φ values are usually regarded as an indicator of the nativeness of residue i in the TSE. A φ value of 1 means that residue i has a native-like structure in the TSE, whereas a value of 0 indicates that in the TSE residue i is as unfolded as in the denatured state.

Molecular dynamics (MD) simulations of protein unfolding at high temperature with explicit water molecules have been used to characterize the TSE of chymotrypsin inhibitor 2 (CI2) by Li and Daggett (3, 4). The transition-state structures identified in their simulations were consistent with the available experimental data and were used for interpreting φ values at atomic level of detail (5). The synergistic combination of experimental data and MD simulations allowed for the description of the TSE of CI2 as a state close to the native structure with an almost intact α-helix and a quite disrupted β-sheet. Furthermore, a folding nucleus consisting of Ala-16 in the α-helix and Leu-49 and Ile-57 in the β-sheet was identified (5).

The TSE has also been investigated by Monte Carlo (MC) simulations of lattice models (6, 7). Their efficiency allows for the validation of putative transition-state conformations by calculating the transmission coefficient, which is the probability of a given structure to fold before it unfolds. The transmission coefficient should be close to 0.5 for conformations in the TSE. Recently, lattice MC models have led to the interpretation of nonclassical φ values (negative or larger than 1.0) as nonnative interactions in the folding nucleus (8) or as arising from multiple folding routes (9). The main drawback of lattice models is the coarse description of the protein structure and interactions. Off-lattice MC simulations of a C_α model with a Go potential have allowed for the construction of the TSE of acylphosphatase from published φ values (10). By using the same technique and an all-atom description of CI2, Li and Shakhnovich (11) have shown that the constructed TSE has a transmission coefficient of about 0.5. In contrast, MC simulations of a two-dimensional lattice model by Ozkan et al. (9) showed that φ values do not necessarily correlate with the degree of nativeness of the TSE. To clarify further the significance of φ values, it is useful to ask the following question. If φ values describe the nativeness of the transition state, do they allow for the distinction of transition-state structures from other conformations on the folding pathway? In other words, can transition-state structures be identified from an ensemble of conformations with different degrees of nativeness by the use of φ values?

MD simulations of atomic models of proteins with an implicit representation of the solvent can be used to answer these questions. Recently, they have allowed for the analysis, in a statistically relevant way, of the reversible folding of structured peptides (12, 13) and the unfolding of small proteins (14, 15). In the latter study, a detailed analysis of the high temperature (375 K) unfolding of src SH3 and a comparison with α-spectrin SH3 was performed (15). SH3 is an all-β-domain with a β-hairpin (formed by the terminal segments) packed orthogonally on top of a three-stranded antiparallel β-sheet (Fig. 1a). Putative members of the TSE were identified along the unfolding simulations at 375 K by monitoring the fraction of native contacts Q.

Figure 1.

Different conformational states of src SH3. (a) Stereoview (wall eyes) of the ribbon representation of the crystal structure (27). (b) Stereoview (wall eyes) of six transition-state conformations superimposed to the central β-sheet of the crystal structure. β1 and the RT loop are colored in cyan, the diverging turn and central β-sheet (β2-β4) are in yellow, and the 3₁₀ helix and β5 are in magenta. The N and C termini are indicated by a blue and red sphere, respectively. The native structure is shown in green (thick line). (c) β1-β5-disrupted. (d) β3-β4-disrupted. All figures were prepared with MOLMOL (28).

In this article, the identification of putative TSE structures from the MD trajectories of src SH3 is based on experimental data. Following previous works by Li and Daggett (3, 4), φ values are interpreted in terms of native-like side-chain contacts and compared with the values calculated for conformations saved during the unfolding simulations (φ). Structures with a small mean deviation between φ and φ are selected as putative members of the TSE. The main difference between the present approach and the one of Li and Daggett (3, 4) is that the latter uses a conformational cluster analysis to identify TSE structures along unfolding trajectories whereas the former makes explicit use of the φ values. Another difference is the use of an implicit model of the solvent (explicit water molecules were used in refs. 3 and 4) whose efficiency allows for the evaluation of the transmission coefficient for 6 conformations of the putative TSE by 60 MD runs at 315 K. The simulations yield a transmission coefficient of about 0.5 which validates the present approach.

Materials and Methods

Model.

The MD simulations and part of the analysis of the trajectories were performed with the charmm program (16). The protein was modeled by explicitly considering all heavy atoms and the hydrogen atoms bound to nitrogen or oxygen atoms (16). An implicit model based on the solvent-accessible surface was used to describe the main effects of the aqueous solvent on the solute (17). The model is not biased toward any particular secondary structure type. In fact, exactly the same force field and implicit solvation model have been used recently in MD simulations of folding to the correct conformation of several structured peptides (α-helices and β-sheets) ranging in size from 15 to 31 residues (12, 13, 18), and to simulate the unfolding of two SH3 domains (15).

Determination of the TSE.

The definition of φ is similar to the one used in previous MD and MC simulations (4, 10):

1

where N is the number of native contacts of residue i in a given conformation, and N is the number of native contacts of residue i that are present for more than two-thirds of the simulation time of the control run at 300 K (15). Contacts are considered to exist when the side chain heavy atoms of two nonadjacent residues (pairs i, i ± 1 are omitted) are closer than 6 Å.

To monitor the average distance from the experimentally determined TSE, the rms deviation (rmsd) between φ and φ was calculated along the unfolding trajectories at 375 K (15):

2

where M_φ is the number of φ values available for mainly hydrophobic residues (M_φ = 18; F10, V11, A12, L13, L24, F26, L32, V35, W42, W43, L44, A45, L48, T53, Y55, I56, V61, and A62) (19). Mainly nonpolar residues were selected because it was shown that for hydrophobic deletion mutation φ reflects well the ratio of contacts residue i makes with the rest of the protein in the transition state relative to the native one (2, 20). Trajectories with a well defined minimum of φ-rmsd (below 0.20) were selected. From each of these selected runs, only one conformation was picked out as a putative member of the TSE, namely the one with the lowest φ-rmsd.

Native Contacts and Progress Variable Q.

The conformations sampled at 300 K were used to define a list of 72 C_α native contacts (see table 3 of ref. 15). In contrast to previous works by others (21, 22) and us (15), Q is not used in this study to identify the transition-state conformations, but only to monitor folding and unfolding (see below). A contact was considered present if the distance between the C_α atoms was shorter than 7 Å.

Transmission Coefficient.

The TSE can be defined as the set of structures that have the same probability of folding or unfolding. For each putative TSE conformation, the probability to fold before unfolding, i.e., the transmission coefficient, was calculated by 10 simulations at 315 K. This temperature was chosen for consistency with the temperature used in the experimental studies. The midpoint of thermal denaturation of src SH3 is 333 K at pH 3.5 (23), whereas the protein-engineering experiments were performed at 295 K and pH 6 (19). The only difference among the 10 runs was the seed for the random-number generator used for the initial assignment of the atomic velocities. A trajectory was considered to lead to the native state if the C_α rmsd reached values ≤2.5 Å and Q ≥ 0.875 (63 contacts). C_α rmsd values ≥7.0 Å and Q values ≤0.375 (27 contacts) were used as the unfolding criteria. Simulations reaching the unfolding criteria before 100 ns were stopped, whereas trajectories that did not satisfy either the folding or the unfolding criteria were restarted and run for an additional 100 ns. A 100-ns run requires ≈9 days on a 1-GHz Pentium III processor.

Results and Discussion

Identification of TSE Conformations.

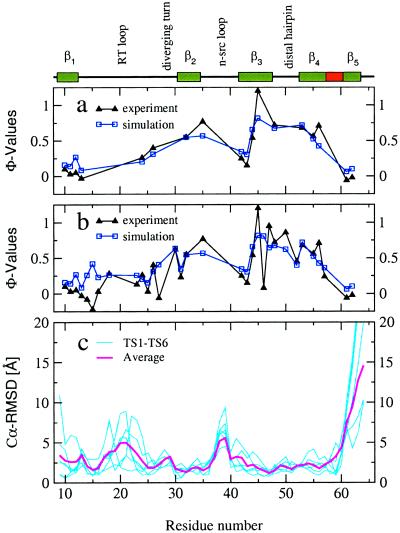
Several unfolding simulations at 375 K (15) show a distinct minimum in the time series of the φ-rmsd (based on 18 hydrophobic residues; see Materials and Methods). This observation allowed us to isolate 12 putative members of the TSE from 12 different unfolding runs. The Pearson linear correlation coefficient (ρ) between the 18 φ values and those obtained by averaging φ over the 12 putative TSE conformations is 0.93 (Fig. 2a). A ρ value of 0.74 is found by using 32 φ values (Fig. 2b), 18 for hydrophobic and 14 for hydrophilic residues, where the 14 values for hydrophilic residues were not used to identify the TSE by the φ-rmsd criterion. The crossvalidated coefficient (ρ_cv), which is based on the 14 residues not used to identify the TSE conformations, is 0.54. Only the φ values of the residues Asp-15, Lys-27, and His-46 show major deviations from the φ values. These three residues are solvent-exposed in the x-ray structure of src SH3. Leaving out the three outliers yields a ρ of 0.92 for 29 residues, and a ρ of 0.94 for 11 hydrophilic residues. These results indicate that simulation-based prediction of φ values is possible, in agreement with a recent MC study of a C_α model of acylphosphatase (10).

Figure 2.

Properties of the TSE. (a and b) Comparison of φ with φ. (a) The 18 φ used to identify the TSE by the φ-rmsd criterion. (b) Thirty-two residues with well defined φ. (c) C_α rmsd from the native state as a function of residue number. The native secondary structural elements are indicated above the diagram.

Because the calculation of the transmission coefficient for folding is computationally expensive, only half of the 12 putative TSE conformations were used for further MD runs. Table 1 lists the C_α rmsds from the x-ray structure and the number of native contacts for the 6 conformations (TS1-TS6) that were selected at random out of the 12 putative TSE structures for the calculation of the transmission coefficient. The C_α rmsd from the native structure averaged over the 6 TS1-TS6 conformations is 4.7 Å (3.6 Å if one neglects two residues at each of the termini). The 12 putative TSE conformations have an average C_α rmsd of 4.3 Å (3.5 Å without termini). Furthermore, the fraction of native contacts is similar if the average is calculated over 6 or 12 conformations, 0.74 and 0.72, respectively. This observation justifies the use of only 6 conformations.

Table 1.

Properties of the transition state (TS) and the disrupted conformations

Conformation	ρ*	Cαrmsd†	Native Cα contacts‡	Pfold§
TS1	0.79	3.7 (3.5)	50 (0.69)	0.5
TS2	0.89	5.8 (4.0)	60 (0.83)	0.5
TS3	0.86	3.6 (3.3)	45 (0.63)	0.4
TS4	0.91	5.8 (3.9)	51 (0.71)	0.5
TS5	0.85	5.1 (3.2)	57 (0.79)	0.5
TS6	0.90	4.6 (3.4)	57 (0.79)	0.6
Mean values	0.87	4.7 (3.6)	53 (0.74)	0.5
β1–β5-disrupted	0.13	4.6 (3.6)	52 (0.72)	0.0
β3–β4-disrupted	−0.49	3.8 (3.8)	51 (0.71)	0.0

^*Pearson correlation coefficient between the φ and φ values. 

^† C_α rmsd from the native structure. For the values in parentheses, two N-terminal and two C-terminal residues were excluded, because they displayed high deviations in the control run at 300 K (15). 

^‡ The fraction of native contacts, Q, is indicated in parentheses. 

^§ Transmission coefficient calculated by 10 MD runs at 315 K. 

From each of the 6 putative TSE structures, 10 315 K simulations of 100 ns each were started with different initial atomic velocities. Sixteen of the 60 runs had to be elongated for an additional 100 ns because they did not fold or unfold within the first 100 ns (for criteria, see Materials and Methods). Finally, 30 simulations reached the folded state while 24 unfolded. Of the remaining six simulations, four are closer to the unfolding thresholds than the folding ones and two vice versa. Time series for four trajectories started from TS4 are shown in Fig. 3, and snapshots of one of them are shown in Fig. 4. Folding from the TSE is characterized by the formation of native contacts between the N- and C-terminal strands, which precedes the stabilization of the RT loop, n-src loop, and the 3₁₀ helix. Overall, four TSE conformations have a transmission coefficient of 0.5 whereas the remaining two have values of 0.4 and 0.6 (Table 1).

Figure 3.

Evolution of the C_α rmsd and Q as a function of time in two folding and two unfolding simulations at 315 K started from the same transition-state structure. The dotted lines indicate the threshold values of folding and unfolding.

Figure 4.

Folding from the TSE. Snapshots from one of the TS4 folding trajectories at (from left to right and top to bottom) 0, 0.6, 1.0, 2.0, 7.7, and 15.4 ns. The first (Top Left) and last (Bottom Right) conformations have a C_α rmsd from the native structure of 5.8 and 1.9 Å, respectively. In all frames, segments of the polypeptide chain that correspond to the native β-strands and 3₁₀ helix are colored in cyan and red, respectively, whereas loops and segments with nonnative regular secondary structure are in gray.

The transmission coefficient values close to 0.5 validate the TSE conformations obtained by combining φ-value analysis and MD unfolding simulations. This result justifies, at least for src SH3, the main assumption of φ-value analysis, i.e., transition-state theory. Furthermore, the selected structures allow an atomic level description of the structural and folding/unfolding properties of the TSE. In particular, they permit us to investigate the presence of nonnative interactions that are expected to stabilize the TSE of src SH3 (19). Hence, the present approach, which is based on a standard all-atom force field and MD simulations, seems most suited to identify TSE conformations of src SH3 than the use of a Go potential, which neglects or penalizes nonnative contacts.

Analysis of the TSE.

The C_α rmsd between members of the TSE ranges between 2.7 Å and 5.9 Å, with an average value of 4.2 Å (Fig. 1b). The rmsd from the native structure as a function of residue number is shown in Fig. 2c. As suggested by experimental studies, the transition state is characterized by a pronounced structural polarization (19, 24). The termini and the RT loop present large deviations from the native state, whereas the three-stranded antiparallel β-sheet (β2-β4) is folded. The dissociated N- and C-terminal strands (β1,β5) have lost all native backbone and most side-chain interactions. In the RT loop, significant deviations are seen in some TSE conformations because of a rotation of its tip away from the central β-sheet as well as an opening of the tip itself. Although only about one-half of the native C_α contacts are broken in the RT loop, most of the side-chain interactions are absent in agreement with φ values uniformly close to 0 throughout its N-terminal strand and tip. Interestingly, backbone contacts between β1 and β2 at the base of the RT loop are present in some of the TSE conformations. These results suggest that the RT loop is primarily stabilized by backbone and not side-chain interactions in the transition state. Similar conclusions were recently drawn from kinetic studies of src SH3 domains with a crosslinked RT loop (24).

Although most native backbone interactions of the central β-sheet are present in the TSE, residues Asn-37-Trp-42 in the n-src loop deviate up to 9 Å from the x-ray structure. This deviation is related to the presence of nonnative contacts that result in a tight hairpin connecting an elongated strand β2 with β3 in 9 of 12 TSE conformations (Fig. 4). These nine members of the TSE have very similar structures of the central three-stranded β-sheet with less than 2.0 Å in C_α rmsd from each other (Fig. 1b). As reported in our previous study, the elongation of β2 in the transition state is consistent with φ values greater than 1 in the n-src loop (15). To investigate the elongation of β2 and the formation of nonnative contacts, the TSE was searched for specific side-chain interactions (contacts present in all TSE conformations) that were not present in the native state. Only about one-half of the residues yield such specific nonnative interactions; they are within or close to the diverging turn, the n-src loop, and the adjacent distal hairpin. In the n-src loop, Ile-34 and Asn-37 are closer to Trp-43 in the TSE than in the native state. More than half of the side-chain interactions between these residues are nonnative in agreement with deletion mutations resulting in φ values larger than 1 or negative (19). A tighter packing of the side chains in the diverging turn (Glu-30 and Arg-31) and the distal hairpin (Ser-47, Leu-48, Ser-49, and Thr-50) is associated with the formation of nonnative contacts between these residues. Results from mutagenesis experiments on src SH3 indicate that a network of native hydrogen bonds connecting the diverging turn and the distal hairpin might be formed in the transition state (25). The simulation results indicate that the nonlocal interactions between these structural elements are stabilized further by nonnative side-chain contacts.

Although 12 is a small fraction of the actual number of configurations making up the TSE, the important structural characteristics of the ensemble are likely to be reflected in this sample. The MD description of the transition state is in very good agreement with the experimental data on src SH3 (24). Crosslinking and glycine-insertion experiments indicate that the distal hairpin and the diverging turn are ordered in the TSE and interact with each other, whereas the variability is confined to the RT loop and the termini. The simulation results confirm theoretical and experimental studies that indicate that φ values greater than 1 refer to interactions that stabilize the transition state more than the native structure (8, 26).

Analysis of Non-TSE Conformations.

To validate the TSE obtained by MD, two additional conformations with a number of native C_α contacts and an rmsd from the native structure similar to the 12 TSE structures were used to calculate the transmission coefficient. They were both identified along the 375 K unfolding runs and have similar structural properties as the 12 TSE structures except for a low or negative correlation between φ and φ (Table 1). In both conformations, residues with high φ values miss most of their native side-chain interactions. In particular, the hydrophobic core residues Phe-26, Leu-32, Ala-45, and Ile-56, which form a network of nonlocal interactions between the distal hairpin and the diverging turn, have less than 50% of the contacts present in the transition state. One of the two conformations (henceforth called β1-β5-disrupted; Fig. 1c) has similar backbone contacts as the TSE. β1 and β5 as well as the tip of the RT loop are disrupted whereas the central three-stranded β-sheet is folded. In the other conformation, the backbone contacts between β3 and β4 are absent (β3-β4-disrupted; Fig. 1d). The central β-sheet has an rmsd of 3.1 Å from the native state. Interestingly, β3-β4-disrupted has more native contacts between the termini than the TSE, which explains the negative value of the correlation coefficient. The transmission coefficient of the two conformations was calculated as for the six TSE structures, i.e., by performing 10 315 K MD simulations of 100 ns each.

All runs started from β1-β5-disrupted and β3-β4-disrupted reached the unfolding criteria within 100 ns. In β1-β5-disrupted, no folding was observed although the distribution of backbone contacts is similar to the one in the transition state, in particular in the central β-sheet. In β3-β4-disrupted, additional long-range interactions between residues with low φ values in the termini could not compensate the loss of interactions in the central β-sheet and the hydrophobic core. Taken together with the folding simulations from the six members of the TSE, this finding suggests that the correct packing of the side chains that connect the distal hairpin with the diverging turn is necessary for fast folding. Theses results are consistent with recent glycine insertion and crosslinking experiments (24). The elongation of the n-src loop (connecting the distal hairpin with the diverging turn) with a 10-glycine insertion decreases the rate of folding by a factor of 4. In contrast, the oxidized form of a double-cysteine mutant covalently crosslinking the distal hairpin folds about 30 times faster than the reduced one, which indicates that the distal hairpin is structured at the transition state.

The results presented here complement recent all-atom MC simulations with a Go model by Li and Shakhnovich (11), who have shown that a disruption of mostly nonlocal contacts between β-strands 3 and 4 in CI2, an α/β protein of 64 residues, significantly reduces the tendency to rapidly reach the native state. The reduction of nonlocal contacts between the distal hairpin and the diverging turn of SH3 had a similar negative effect. However, the simulations of CI2 indicate that the α-helix is kinetically less important than β-strands 3 and 4, even though the φ values suggest that the α-helix is the most structured element in the TSE. The simulation results presented here show a different behavior for the all-β-domain src SH3, where residues in the most structured element of the TSE, the central β-sheet, are kinetically the most important. The absence of side-chain contacts in the central β-sheet (β1-β5-disrupted) prevented fast folding and this could not be compensated by native high contact-order interactions between the termini (β3-β4-disrupted). Hence, contacts between residues closer in sequence (strands β2-β3-β4) can be kinetically more important than contacts further apart in the sequence (strands β1-β5).

Conclusions

By monitoring the deviation of φ from the corresponding experimental values, 12 putative TSE structures of src SH3 were extracted from high-temperature MD unfolding simulations. Their transmission coefficient values close to 0.5 confirm that the conformations belong to the TSE. This finding is consistent with the interpretation of φ values as an indicator of the degree of nativeness of the transition state. In agreement with experimental results, the MD transition state of src SH3 has strong structural polarization. The central three-stranded β-sheet is formed whereas the RT loop is partially opened and the termini dissociated. Moreover, there are nonnative side-chain contacts between residues in the diverging turn and the distal hairpin, and a nonnative elongation of strand β2. Two conformations with disrupted side-chain contacts between residues with high φ values have also been isolated from high-temperature MD trajectories. Simulations started from these structures indicate that the correct packing of the side chains between the diverging turn and the distal hairpin is necessary for fast folding, and that the most structured element in the TSE, the central β-sheet, is kinetically more important than the contacts between the N- and C-terminal strands.

Abbreviations

TSE

transition-state ensemble

MD

molecular dynamics

rmsd

rms deviation

CI2

chymotrypsin inhibitor 2

MC

Monte Carlo