Abstract
The three-dimensional structure of the chemotactic peptide N-formyl-l-Met-l-Leu-l-Phe-OH was determined by using solid-state NMR (SSNMR). The set of SSNMR data consisted of 16 13C–15N distances and 18 torsion angle constraints (on 10 angles), recorded from uniformly 13C,15N- and 15N-labeled samples. The peptide's structure was calculated by means of simulated annealing and a newly developed protocol that ensures that all of conformational space, consistent with the structural constraints, is searched completely. The result is a high-quality structure of a molecule that has thus far not been amenable to single-crystal diffraction studies. The extensions of the SSNMR techniques and computational methods to larger systems appear promising.
Over the last two decades, multidimensional nuclear magnetic resonance (NMR) methods have been developed which permit determinations of globular protein structures in solution (1). To date most structures addressed with these techniques involve proteins with molecular weights ≤20,000, but the continued development of new methodology shows promise for studies of larger systems (2–6). Despite the success of these approaches, there remain fundamental limits on the size and physical state of molecules amenable to study with solution-state NMR. In contrast, high-resolution solid-state NMR (SSNMR) methods have no inherent molecular weight limit, and have for many years been used to determine details of molecular structure for high molecular weight systems. For example, specific structural features of intact membrane proteins such as bacteriorhodopsin (effective molecular weight ≈85,000) (7, 8) and large enzyme complexes such as 5-enolpyruvylshikimate-3-phosphate synthase (46,000) (9) and tryptophan synthase (143,000) (10) have been reported. SSNMR methods have also been used to examine surface-bound peptides (11) and to determine a low-resolution structure [1.9-Å backbone root-mean-square deviation (rmsd)] of an insoluble peptide fragment from β-amyloid (12) under experimental conditions inaccessible to both solution-state NMR and crystallography.
To date, essentially all structural NMR studies of solid peptides and proteins have relied on site-specific incorporation of a pair of spin-½ nuclei, such as 13C–13C and 13C–15N. This approach has been very successful and will likely continue to be important in experiments that address detailed mechanistic questions in large biomolecular systems. However, recent advances in solid-state NMR methodology, most notably the development of approaches to perform dipolar recoupling during magic-angle spinning (MAS) (13, 14), in principle permit multiple distance and torsion angle measurements on molecules that are uniformly 13C and 15N labeled (15–18). The development of these approaches considerably simplifies preparation of samples for SSNMR experiments and concurrently opens the possibility of complete structural determinations with solid-state MAS NMR. In this paper we describe the realization of this goal with a complete structure determination of the chemotactic tripeptide N-formyl-l-Met-l-Leu-l-Phe-OH (f-MLF-OH) (19). The structure of the peptide is based on sets of NMR data that constrain 16 13C–15N distances and 10 torsion angles derived from a series of MAS NMR experiments performed on uniformly 13C,15N- and 15N-labeled samples. Finally, we discuss extensions of the solid-state MAS NMR techniques and computational methods used here to larger systems.
Experimental Procedures
f-MLF-OH samples were synthesized by standard solid-phase methods and HPLC purification (American Peptide Company, Sunnyvale, CA). One sample, synthesized from U-13C,15N-labeled amino acids (Cambridge Isotope Laboratories, Andover, MA), was used for all resonance assignment experiments and the majority of the three-dimensional (3D) torsion angle experiments (1H–15N–13C–1H, 1H–13C–13C–1H, 15N–13C–13C–15N). A second sample was prepared by dilution of the U-13C,15N-labeled f-MLF-OH peptide in natural abundance material in the ratio of 1:9 and was used for the frequency-selective rotational-echo double-resonance (REDOR) experiments. A third sample, synthesized from 15N-labeled amino acids, was used for the 1H–15N–15N–1H torsion angle experiments. In all cases, microcrystals of the f-MLF-OH peptides were grown by overnight evaporation from 2-propanol, and ≈15–20 mg of each polycrystalline material was packed into a 4-mm zirconia NMR rotor (Varian-Chemagnetics, Fort Collins, CO). Attempts to grow single crystals suitable for diffraction studies were not successful. The structures of the f-MLF methyl ester (f-MLF-OMe) and other analogs of f-MLF have been determined by diffraction methods (20), but that of the f-MLF-OH acid form has not. Presumably the acid form does not form large single crystals because of small differences in crystal packing forces, relative to the methyl ester. We note that the previously published structure of f-MLF-OH includes a d-Phe residue (21), which is not present in the chemotactically active form (19).
MAS NMR experiments were performed on Cambridge Instruments spectrometers operating at 400 and 500 MHz (courtesy of D. J. Ruben), together with custom-designed 400- and 500-MHz multiple-resonance transmission line probes, or a Varian-Chemagnetics (Fort Collins, CO) 500-MHz triple-resonance probe. All of the probes were equipped with 4-mm MAS spinner modules. The resonance assignment (22) and REDOR experiments (16) were performed at 500 MHz, as were most of the torsion angle experiments (1H–15N–13C–1H, 1H–13C–13C–1H, and 15N–13C–13C–15N), with the exception of 1H–15N–15N–1H (400 MHz) (23). Typical radiofrequency field strengths were ≈100–120 kHz on 1H during recoupling periods, ≈80-kHz two-pulse phase modulation (TPPM) during chemical shift evolution periods (using TPPM decoupling; ref. 24), and ≈60 kHz during cross-polarization. Fields of ≈50 kHz or less were used on the 13C and 15N recoupling channels. Additional details regarding the pulse sequences and data acquisition periods are available in prior publications (16, 18, 22, 23). Experiments were performed at room temperature. Tensor magnitudes along the entire backbone [1H–15N and 1H–13Cα dipolar couplings and 13C′ chemical shift tensors] are consistent with rigid lattice values. Further, the spectra and internuclear distances did not change when the temperature was lowered to −30°C. Likewise the Leu side chain is rigid, based on local dipolar field measurements. Signals from the Phe aromatic ring show evidence of two-site conformational exchange, and the observed Met side-chain dipolar couplings (13Cβ–1Hβ, 13Cγ–1Hγ, 13Cα–13Cβ) are ≈25% less than the rigid lattice values, consistent with small librations of the side chain. Thus, apart from the Phe and Met side chains, we believe that the structure shown below reflects little in the way of dynamic behavior.
Resonance Assignments
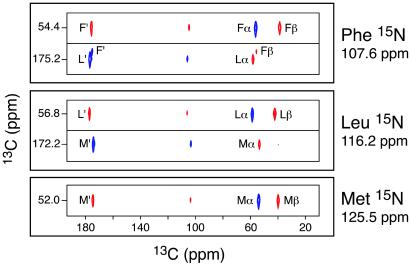
The initial step in a structural study by NMR involves the sequence-specific assignment of the chemical shifts. Several multidimensional chemical shift correlation methods for resolving and assigning peptide 13C and 15N resonances have been developed (22, 25, 26). Experiments for 13C–13C assignments generally employ either a homonuclear zero-quantum recoupling sequence such as RFDR (27) or a double-quantum sequence (28–30) such as SPC-5 (31). Heteronuclear assignments are accomplished with frequency-selective 15N–13C double cross-polarization methods (32, 33) refined with adiabatic passage techniques (34). Slices from 13C–13C planes extracted from a 3D 15N–13C–13C experiment are shown in Fig. 1 and serve to illustrate this point (22). The slices correspond to the three 15N resonances, and the 13C connected to each amide 15N appears in the 13C–13C plane. Thus, the Leu 15N slice (116.2 ppm) shows positive cross-peaks (blue) to the Met C′ and Leu Cα. Because the 13C–13C correlations were established by using double-quantum recoupling, the cross-peaks to Leu C′ and Met Cα are negative absorption (indicated by red cross-peaks). 2D 13C–13C experiments and the 2D 13C–13C planes from 15N–13C–13C experiments also permit the resolution and assignment of the side-chain resonances. These methods have already been used at high magnetic fields (750- to 800-MHz 1H frequency) in studies of larger proteins, yielding partial assignments in the bovine pancreatic trypsin inhibitor (BPTI) (35) and LH2 light-harvesting membrane protein complex (36) and a complete de novo assignment of a 62-residue α-spectrin SH3 domain (37).
Fig 1.
Strip cross sections through the 15N planes of the 3D 15N–13C–13C chemical shift correlation spectrum of f-MLF-OH, showing the backbone resonance assignments. The Met 15N plane (125.5 ppm) shows only 13C cross-peaks from the Met residue. In contrast, the Leu 15N plane (116.2 ppm) shows Met and Leu 13C cross-peaks, and the Phe 15N plane (107.6 ppm) displays Leu and Phe 13C cross-peaks. Since 13C–13C correlations were established by using the SPC-5 double-quantum recoupling pulse sequence (31) the cross-peaks corresponding to subsequent 13C–13C dipolar transfers alternate in sign (28) (blue and red for positive and negative absorption, respectively). Details of the pulse sequence and experimental parameters used to record this spectrum can be found in ref. 22.
Torsion Angle Measurements
When spectral assignments are complete, multidimensional experiments can be used to obtain two types of structural constraints: torsion angles and internuclear distances. Measurements of backbone and side-chain torsion angles (φ, ψ, and χ) provide constraints on the local structure and usually involve experiments that employ one or two chemical shift dimensions, and an additional dimension to record the evolution under the local dipolar interactions. Thus, the angular information is determined by the measurement of the relative orientation of two dipolar tensors. For example, we recently described a 3D experiment for constraining the torsion angles φi, ψi−1, and χ by 1H–15N–13C–1H spectroscopy (18). Similar 3D 15N–13Cα–13C′–15N (38, 39) and 1H–13Cα–13C′–15N experiments (40) can be used to constrain ψi, and 1H–13C–13C–1H experiments (41) constrain the side-chain χi angles. Finally, the projection angle θi,i+1 measured in a 1Hi–15Ni–15Ni+1–1Hi+1 experiment (23) further constrains φi and ψi. We combined data from four 3D experiments in f-MLF-OH: 1H–15N–13C–1H, 1H–13C–13C–1H, 15N–13C–13C–15N, and 1Hi–15Ni–15Ni+1–1Hi+1. Each of the torsion angle measurements is most precise when the correlated dipole tensors are approximately collinear. Therefore, the 15N–13C–13C–15N experiment is very precise for 140° < |ψ| < 180°, and the 1H–15N–13Cα–1H experiment for −150° < φ < −90°. The dephasing of the Met C′–Cα double-quantum coherence under C′–N and Cα–N dipolar couplings during the NCCN experiment in f-MLF-OH is illustrated in Fig. 2. For this particular measurement, the best-fit simulation gives the torsion angle |ψMet| = 157°. The precision (±1 σ) of this experiment is ±1°, due to the high signal-to-noise ratio of the NMR data (>1,000:1 in first data point of the dephasing trajectory), and the fact that this result falls within the most sensitive angular region of the experiment. For other torsion angle constraints (Table 1), the precision ranges from ±2° to ±18°, and in all cases at least two (and sometimes four or six) solutions are consistent with the experimental data, because of mirror-plane degeneracies. Determining multiple NMR constraints on each torsion angle removes many of the degeneracies. For this reason we have combined the results from multiple 3D torsion angle experiments to provide a total of 18 constraints on 10 torsion angles in f-MLF-OH. All torsion angle solutions consistent with the NMR data (based on ≈10,000 iterations of Monte Carlo simulations) are allowed for purposes of searching the conformational space (see below).
by 1H–15N–13C–1H spectroscopy (18). Similar 3D 15N–13Cα–13C′–15N (38, 39) and 1H–13Cα–13C′–15N experiments (40) can be used to constrain ψi, and 1H–13C–13C–1H experiments (41) constrain the side-chain χi angles. Finally, the projection angle θi,i+1 measured in a 1Hi–15Ni–15Ni+1–1Hi+1 experiment (23) further constrains φi and ψi. We combined data from four 3D experiments in f-MLF-OH: 1H–15N–13C–1H, 1H–13C–13C–1H, 15N–13C–13C–15N, and 1Hi–15Ni–15Ni+1–1Hi+1. Each of the torsion angle measurements is most precise when the correlated dipole tensors are approximately collinear. Therefore, the 15N–13C–13C–15N experiment is very precise for 140° < |ψ| < 180°, and the 1H–15N–13Cα–1H experiment for −150° < φ < −90°. The dephasing of the Met C′–Cα double-quantum coherence under C′–N and Cα–N dipolar couplings during the NCCN experiment in f-MLF-OH is illustrated in Fig. 2. For this particular measurement, the best-fit simulation gives the torsion angle |ψMet| = 157°. The precision (±1 σ) of this experiment is ±1°, due to the high signal-to-noise ratio of the NMR data (>1,000:1 in first data point of the dephasing trajectory), and the fact that this result falls within the most sensitive angular region of the experiment. For other torsion angle constraints (Table 1), the precision ranges from ±2° to ±18°, and in all cases at least two (and sometimes four or six) solutions are consistent with the experimental data, because of mirror-plane degeneracies. Determining multiple NMR constraints on each torsion angle removes many of the degeneracies. For this reason we have combined the results from multiple 3D torsion angle experiments to provide a total of 18 constraints on 10 torsion angles in f-MLF-OH. All torsion angle solutions consistent with the NMR data (based on ≈10,000 iterations of Monte Carlo simulations) are allowed for purposes of searching the conformational space (see below).
Fig 2.
Measurement of ψMet in f-MLF-OH by the double-quantum 15N–13C–13C–15N experiment (38). (a) Experimental and simulated dephasing of the Met C′–Cα double-quantum coherence under the C′–N and Cα–N dipolar couplings. The best simulation yields a torsion angle of ±157° ± 1°. (b) rmsd between the NCCN simulation and experiment for the Met residue, calculated as a function of ψ.
Table 1.
Torsion angle structural constraints in f-MLF-OH determined by 3D MAS dipolar-chemical shift experiments
| Residue | Angle | Data type | Most likely solutions, ° | Less likely solutions, ° |
|---|---|---|---|---|
| Met | φ | H-Ni–C –H –H |
−150 ± 2 | −6 ± 2 |
| −90 ± 2 | ||||
| ψ | N–C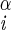 –C′i–N –C′i–N |
±157 ± 1 | NA | |
| 108 ± 18 | ||||
| −151 ± 10 | ||||
H–Ni+1–C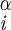 –H –H |
161 ± 4 | 78 ± 5 | ||
| −10 ± 8 | ||||
| 24 ± 11 | ||||
| χ1 | H–C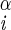 –C –C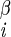 –H2 –H2
|
−163 ± 3 | 163 ± 3 | |
| −77 ± 3 | −43 ± 3 | |||
| χ2 | H2–C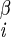 –C –C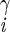 –H2 –H2
|
±169 ± 2 | NA | |
| Leu | φ | H–Ni–C –H –H |
−94 ± 2 | NA |
| −146 ± 2 | ||||
| ψ | N–C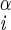 –C′i–N –C′i–N |
±91 ± 4 | ±45 ± 4 | |
| ±120 ± 4 | ±65 ± 5 | |||
H–Ni+1–C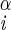 –H –H |
−69 ± 4 | −178 ± 7 | ||
| −51 ± 4 | −59 ± 10 | |||
| ±177 ± 3 | ||||
| χ1 | H–C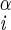 –C –C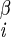 –H2 –H2
|
−57 ± 3 | NA | |
| −64 ± 3 | ||||
| ±173 ± 3 | ||||
| χ2 | H2–C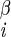 –C –C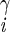 –H –H |
−65 ± 4 | NA | |
| −56 ± 4 | ||||
| Phe | φ | H–Ni–C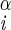 –H –H |
−163 ± 2 | −45 ± 6 |
| −77 ± 2 | 162 ± 2 | |||
| χ1 | H–C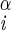 –C –C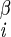 –H2 –H2
|
68 ± 4 | NA | |
| 52 ± 4 |
Four types of 3D experiments were performed, involving sets of nuclei A–B–C–D: 1H–15N–13C–1H (18), 1H–13C–13C–1H (41), 15N–13C–13C–15N (38, 39), and 1H–15N–15N–1H (23). In each experiment, B–C 2D chemical shift planes were recorded as a function of the dipolar mixing time between nuclei A–B and C–D. The modulation of the B–C cross–peak intensity reported on the relative orientation of the A–B and C–D dipole vectors, and therefore the A–B–C–D torsion angle (assuming invariant bond lengths and angles). Each experiment yielded several types of data, as listed in column three. Because of mirror plane symmetry, multiple solutions are possible in each experiment. Monte Carlo simulations (18) were performed, with a minimum of 10,000 iterations, to determine all possible solutions. Solutions were grouped within local minima; those that occurred in more than 20% of Monte Carlo simulations are listed as most likely solutions (with ±1 σ precision), whereas those that occurred less often are indicated as less likely solutions. [The results in cases where the B and C nuclei were not directly bonded (e.g., H–Ni–C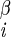 –H) depended on two intervening torsion angles (e.g., φ and χ1) in a coupled manner; several such 2D solution spaces were included in the final calculations, but are not shown here. The determinations of ψi by means of H–Ni+1–C
–H) depended on two intervening torsion angles (e.g., φ and χ1) in a coupled manner; several such 2D solution spaces were included in the final calculations, but are not shown here. The determinations of ψi by means of H–Ni+1–C –H data presumed a trans peptide bond (ω = 180°).] NA, not applicable.
–H data presumed a trans peptide bond (ω = 180°).] NA, not applicable.
Internuclear Distance Measurements
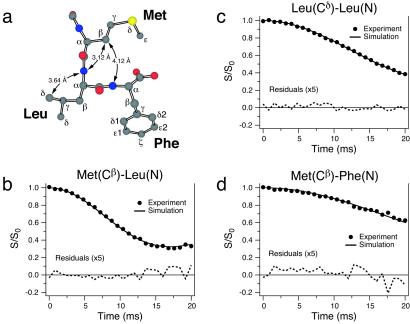
Long-range internuclear distances (3–6 Å) provide highly useful complementary constraints for the peptide structure. Determination of these distances is particularly important because small errors in the local torsion angle measurements can propagate over multiple bonds, resulting in an increased uncertainty in the global fold of the peptide. Furthermore, distance measurements can provide constraints on the position of nuclei, which are inaccessible to dihedral angle measurements (e.g., Met Cɛ). Individual 13C–13C and 13C–15N distances can be measured in site-specifically labeled samples by using techniques such as rotational resonance (R2) (42) or its variants [e.g., R2 tickling (43)] and REDOR (44), respectively. Recently techniques have been developed for accurate measurements of multiple 13C–13C (15) and 13C–15N (16) distances in uniformly 13C,15N-labeled molecules. For 13C–15N dipolar interactions, selective recoupling is possible by combining the REDOR technique (44) with selective Gaussian inversion pulses (16). Using this approach, we have measured a total of 16 13C–15N distances in f-MLF-OH (14 distances >3 Å), which are assembled in Table 2. Several representative distance measurements are illustrated in Fig. 3 and clearly demonstrate the strong dependence of the decay of 13C magnetization on the dipolar coupling to the selected 15N. The 3.12-Å Met(Cβ)–Leu(N) distance further constrains ψMet. The Met(Cβ)–Phe(N) and Leu(Cδ)–Leu(N) distances depend on multiple torsion angles and are important in determining the shape of the turn in the f-MLF-OH backbone, and the conformation of the Leu side chain, respectively. With 95% statistical confidence, 15 of the 16 measured distances have precision of ±0.3 Å or better.
Table 2.
Comparison of the internuclear 15N–13C distance constraints in f-MLF-OH, determined by using frequency-selective (FS)-REDOR (16) and the distances in f-MLF-OMe determined with x-ray diffraction (20)
| Atoms
|
rC–N, Å | ||||
|---|---|---|---|---|---|
| f-MLF-OH FS-REDOR | f-MLF-OMe x-ray | f-MLF-OH full structure | f-MLF-OH CNS | ||
| Met(N) | Met(Cβ) | 2.52 ± 0.02 | 2.50 | 2.47 | 2.47 |
| Met(Cγ) | 3.20 ± 0.03 | 3.04 | 3.25 | 3.23 | |
| Met(Cɛ) | 5.4 ± 0.3 | 5.71 | 5.85 | 5.63 | |
| Leu(Cβ) | 5.7 ± 0.7 | 6.03 | 5.97 | 5.92 | |
| Leu(Cδ) | 5.5 ± 0.3 | 6.28 | 5.92 | 5.80 | |
| Leu(N) | Met(Cβ) | 3.12 ± 0.03 | 3.20 | 3.07 | 3.02 |
| Met(Cγ) | 4.17 ± 0.10 | 4.56 | 4.19 | 4.16 | |
| Met(Cɛ) | 5.5 ± 0.3 | 5.93 | 5.52 | 5.56 | |
| Leu(Cβ) | 2.46 ± 0.01 | 2.50 | 2.46 | 2.45 | |
| Leu(Cδ) | 3.64 ± 0.09 | 3.63 | 3.53 | 3.52 | |
| Phe(N) | Met(C′) | 3.4 ± 0.2 | 3.41 | 3.54 | 3.59 |
| Met(Cβ) | 4.12 ± 0.15 | 4.06 | 4.11 | 4.13 | |
| Met(Cγ) | 4.8 ± 0.2 | 5.43 | 5.11 | 5.11 | |
| Met(Cɛ) | 5.2 ± 0.3 | 5.62 | 5.03 | 5.08 | |
| Leu(Cβ) | 3.24 ± 0.12 | 3.12 | 3.15 | 3.11 | |
| Leu(Cδ) | 5.4 ± 0.3 | 5.38 | 5.34 | 5.32 | |
In columns three and four are the average distances determined from the 56,975 structures generated by the full search procedure developed here and the cns calculation. Note that most of the experimental distance constraints are more precise than is customarily observed in solution NMR experiments. The excellent agreement between the experimental and calculated distances lends credence to the structural model illustrated in Fig. 5.
Leu(Cδ) resonance frequency is 19.6 ppm (22).
Fig 3.
Measurement of carbon–nitrogen internuclear distances in [U-13C,15N]f-MLF-OH by frequency-selective REDOR (16). (a) Structural model of f-MLF-OH displaying the distances measured in b–d. Experimental REDOR S/S0 curves (S0 and S represent the reference and dipolar dephasing experiments, respectively) and simulations are shown for Met(Cβ)–Leu(N) (b), Leu(Cδ)–Leu(N) (c), and Met(Cβ)–Phe(N) (d), and they correspond to internuclear distances of 3.12 ± 0.03 Å (b), 3.64 ± 0.09 Å (c), and 4.12 ± 0.15 Å (d). A total of 16 distances between 2.5 and 6 Å were measured in f-MLF-OH. Distance measurements were performed in a sample prepared by cocrystallizing [U-13C,15N]f-MLF-OH with natural-abundance f-MLF-OH in a 1:9 ratio, to minimize the interference from intermolecular 13C–15N couplings. Details of the pulse sequence and experimental parameters can be found in ref. 16.
Computational Procedures
Since this is the initial determination of a molecular structure by MAS dipolar recoupling techniques, it required us to develop new approaches to calculating molecular structures from the collection of experimental distance and torsion angle constraints. Accordingly, we have explored two approaches to this problem, both of which are described below. The first is based on simulated annealing and incorporates molecular potentials configured to permit transitions among the multiple conformations consistent with the structural constraints. Thus, during the annealing protocol the structures are biased toward the closest minima in the experimental rmsd plots at each time step. This prerequisite requires that the force constants for these potentials be sufficiently low to allow transitions among these minima. In a second approach we have addressed a problem that is often ignored in NMR structure calculations that sample the conformational space stochastically. In particular, these approaches do not necessarily guarantee that all regions of conformational space are examined and therefore they may lead to structures where the uncertainty in the final ensemble is anomalously low. Here we address this issue by dividing the search space into discrete nonoverlapping volumes and assign each volume as allowed or disallowed, based on whether or not it contains viable structures. Ordinarily a search through such a space would be intractable for all but the smallest molecular systems. To circumvent this problem, we developed a divide-and-conquer strategy that allows us to eliminate voxels that contain conformations that violate the structural constraints. The approach condenses the search space sufficiently so that significantly larger problems may be computationally tractable with this procedure.
Simulated Annealing
An ensemble of 24 f-MLF-OH structures was calculated by using the SSNMR constraints collected above incorporated into the simulated annealing protocol of Nilges et al. (45) and the program cns (46). The program was modified to accommodate the structural constraints generated by the SSNMR distance and torsion angle experiments described above. The internuclear distances were incorporated by using a standard distance potential and the 95% confidence limits. For the experimental torsion angle data sets, the simulations based on each experimental measurement were pooled according to the constrained angles, and the resulting joint probability distributions enclosing the 75% confidence limits were used. For example, the 15N–13C–13C–15N, 1H–15N–13Cα–1H, 1H–15Ni+1–13Cα–1H and 1H–15N–15N–1H experiments were joined to define a constraint on the Met φ and ψ torsion angles. Harmonic square wells, with the square wells enclosing the 75% confidence limits, were incorporated directly into the source code for each pair of angles. For many of these constraints, there are several distinct minima. In these cases, the potential is written to permit switching so that during the simulated annealing the structures are biased toward the closest minima at each time step. Because of this requirement, the force constants for these potentials had to be sufficiently low to allow transitions between minima.
The results from the simulated annealing calculation are summarized and compared in Table 2 with the experimental distance constraints from the frequency-selective REDOR experiments. In Table 3 we summarize and compare the torsion angles from the known x-ray crystal structure of f-MLF-OMe with the torsion angles calculated with cns. Note that in both cases there is excellent agreement between the calculations and the experimental data.
Table 3.
Comparison of the 14 torsion angles derived from the SSNMR structures in f-MLF-OH with the corresponding angles from the x-ray structure of f-MLF-OMe (20)
| Residue
|
Angle
|
Angle, ° | ||
|---|---|---|---|---|
| f-MLF-OMe x-ray | f-MLF-OH full structure | f-MLF-OH cns | ||
| Met | φ | −146.0 ± 0.7 | −145.5 | −150.6 |
| Met | ψ | 151.3 ± 0.6 | 158.5 | 158.0 |
| Met | χ1 | −61.2 ± 0.9 | −85 | −82.3 |
| Met | χ2 | 172.9 ± 0.6 | 171.4 | 157.8 |
| Met | χ3 | 77.5 ± 0.8 | 87.1 | 71.3 |
| Leu | ω | 169.6 ± 0.6 | 175 | −177.2 |
| Leu | φ | −67.7 ± 0.8 | −89.5 | −92.1 |
| Leu | ψ | −49.1 ± 0.8 | −39.5 | −44.0 |
| Leu | χ1 | −59.9 ± 0.8 | −58.7 | −59.4 |
| Leu | χ2 | −178.5 ± 0.8 | −178.3 | −176.5 |
| Phe | ω | 175.7 ± 0.6 | 176.1 | 180.0 |
| Phe | φ | −155.4 ± 0.6 | −166.5 | −162.9 |
| Phe | χ1 | 64.4 ± 0.8 | 55.7 | 53.1 |
| Phe | χ2 | −78.4 ± 0.9 | −76.2 | −89.2 |
The average rmsd error in the calculated torsion angles was 3.5° for the full structure calculation and 1.0° for the cns calculation.
Full Structure Search
In addition we developed a systematic computational procedure to analyze the distance and torsion angle constraints. The simulating annealing procedure used above typically samples the space of allowed conformations stochastically, a procedure that does not ensure that all regions of conformational space are sampled and thus may underestimate the uncertainty in the final structural ensemble. An alternative that overcomes this difficulty is to subdivide the search space into discrete voxels (small nonoverlapping volumes that together entirely fill the conformational space) and to assign each voxel as allowed or disallowed, based on whether or not it contains structures that satisfy the constraints. If each voxel were searched explicitly, the search space would be intractable for all but the smallest problems. We have adopted divide-and-conquer strategies to allow relatively large regions of the search space to be eliminated if they contain a substructure that violates the constraints. Such approaches can effectively prune the search tree to make even large problems computationally tractable (47).
The search space was constructed from 16 torsion angles, 10 of which were constrained directly by the SSNMR data. Three additional angles were peptide bonds and constrained to be within 5° of planar (either cis or trans), and the remaining three angles had no direct torsion constraints (ψPhe, χ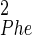 , and χ
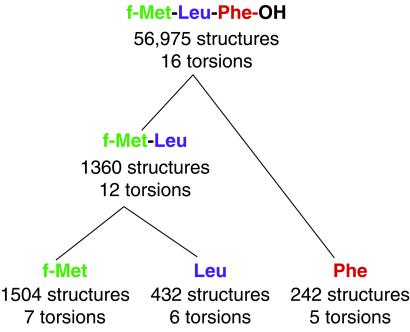
, and χ ). Fixed bond lengths and angles were used to simplify the space, the values of which were determined in trial calculations involving energy minimization from an extended conformation with full freedom in the presence of intramolecular constraints alternating with the systematic search described below. Excluded volume (van der Waals) constraints were enforced, using 90% of the radius values (σ/2) from the all-hydrogen protein parameters in cns version 4.02 (46). Divide-and-conquer was implemented through initial searches systematically performed for each residue independently at a voxel grid resolution of 5° for all but the free torsion angles, which were enumerated in 30° steps. In this initial search, each “residue” included one additional atom along the backbone chain from its neighbors to allow the join in the subsequent step. Each substructure voxel was searched by first checking the center of the voxel to determine whether this substructure satisfied the subset of constraints involving only the atoms in the substructure (“active constraints”). If so, the substructure was retained. Otherwise, the substructure was minimized subject to the active constraints and the additional constraint that the substructure remains within the voxel boundary [using CFSQP, a constrained nonlinear programming method (48), and an objective function that included only NMR constraints and excluded volume]. For the search of each voxel, up to three minimizations were performed. The midpoint of every voxel was always used as one of the starting points for minimization, and additional starting conformations were created by assigning each torsion angle either to the midpoint of its range in the voxel or to other values in the voxel that had previously been found, during the searches of other partial structures, to satisfy local constraints. If any minimization resulted in a structure that satisfied the active constraints, the structure and voxel was retained and no further minimizations were performed. If no satisfying substructure was found, the voxel was eliminated. This procedure yielded 1,504 substructures for f-Met, 432 for Leu, and 242 for Phe. In the second phase of the divide-and-conquer strategy, these successful substructure voxels were systematically joined without regard to constraints, resulting in ≈650,000 structures for the f-Met-Leu “dipeptide.” Of these possibilities all but 1,360 were eliminated because they violated either NMR or excluded volume constraints (see Fig. 4). Similarly, joining the f-Met-Leu “dipeptide” structures with the 242 Phe structures and applying the constraints yielded the 56,975 allowed structures for the tripeptide.
). Fixed bond lengths and angles were used to simplify the space, the values of which were determined in trial calculations involving energy minimization from an extended conformation with full freedom in the presence of intramolecular constraints alternating with the systematic search described below. Excluded volume (van der Waals) constraints were enforced, using 90% of the radius values (σ/2) from the all-hydrogen protein parameters in cns version 4.02 (46). Divide-and-conquer was implemented through initial searches systematically performed for each residue independently at a voxel grid resolution of 5° for all but the free torsion angles, which were enumerated in 30° steps. In this initial search, each “residue” included one additional atom along the backbone chain from its neighbors to allow the join in the subsequent step. Each substructure voxel was searched by first checking the center of the voxel to determine whether this substructure satisfied the subset of constraints involving only the atoms in the substructure (“active constraints”). If so, the substructure was retained. Otherwise, the substructure was minimized subject to the active constraints and the additional constraint that the substructure remains within the voxel boundary [using CFSQP, a constrained nonlinear programming method (48), and an objective function that included only NMR constraints and excluded volume]. For the search of each voxel, up to three minimizations were performed. The midpoint of every voxel was always used as one of the starting points for minimization, and additional starting conformations were created by assigning each torsion angle either to the midpoint of its range in the voxel or to other values in the voxel that had previously been found, during the searches of other partial structures, to satisfy local constraints. If any minimization resulted in a structure that satisfied the active constraints, the structure and voxel was retained and no further minimizations were performed. If no satisfying substructure was found, the voxel was eliminated. This procedure yielded 1,504 substructures for f-Met, 432 for Leu, and 242 for Phe. In the second phase of the divide-and-conquer strategy, these successful substructure voxels were systematically joined without regard to constraints, resulting in ≈650,000 structures for the f-Met-Leu “dipeptide.” Of these possibilities all but 1,360 were eliminated because they violated either NMR or excluded volume constraints (see Fig. 4). Similarly, joining the f-Met-Leu “dipeptide” structures with the 242 Phe structures and applying the constraints yielded the 56,975 allowed structures for the tripeptide.
Fig 4.
An illustration of the divide-and-conquer strategy used to search conformational space. Starting from the individual residues (bottom) and progressing to the tripeptide, the number of substructures satisfying the SSNMR and excluded-volume constraints and the number of searchable torsions are indicated.
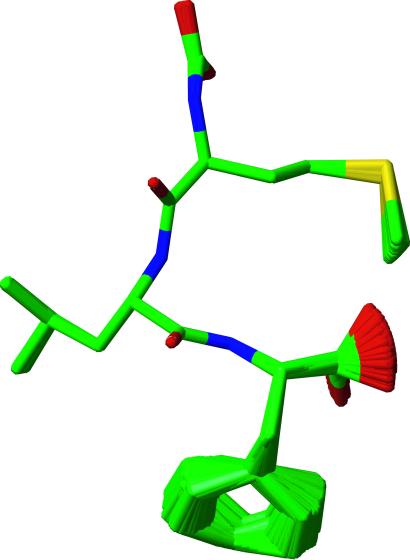
In Fig. 5 we illustrate the family of ≈57,000 f-MLF-OH structures consistent with the SSNMR torsion angle and 13C–15N distance data and excluded-volume constraints. We can conclude that the experimental data defined most of the structure almost uniquely, but that some ambiguity remains for the Phe ring and the chain termini. By one of the usual criteria, the quality of the f-MLF-OH structure is especially high (0.02 Å rmsd for the peptide backbone and 0.38 Å rmsd for all heavy atoms). However, it should be noted that because this peptide is small, the rmsd values are not directly comparable with values computed for proteins. Nevertheless, the backbone is fully constrained with the exception of the formyl group, which is not isotopically labeled in our samples. Note that the formyl group was allowed to assume either cis or trans conformation with low (≈5°) angular fluctuations. It therefore appears in the figure as a carboxyl-like group. The carboxyl-terminal carboxyl group, for which no SSNMR torsion angle technique currently exists, is not constrained. Similarly, we presently do not have a method to constrain χ2 and therefore the orientation of the Phe aromatic ring. However, our experiments indicate scaled Cδ–Hδ and Cɛ–Hɛ dipolar interactions for the Phe ring, which are consistent with twofold flipping observed in a number of cases (48, 49). The side-chain conformations of Met have slightly greater uncertainty than the backbone, largely because of the paucity of constraints on the Met S and Cɛ.
Fig 5.
An illustration of a family of nearly identical structures that were filtered from the total of 56,975 f-MLF-OH structures for ease of display. The set shown is representative of the entire ensemble and is consistent with the SSNMR torsion angle measurements, 13C–15N distances, and excluded-volume constraints. The structure of the backbone is of especially high quality (0.02 Å rmsd). Since the formyl group was not labeled, it was permitted to assume both the cis and trans conformations in the calculation, and it exhibits the appearance of a carboxyl group in the figure. The carboxyl terminus and the Phe ring appear disordered because no torsion angle methods currently exist to constrain the terminal ψ or χ2 angle. The ring conformation is largely determined by excluded volume constraints, and it is likely undergoing twofold flips (see text). The Met and Leu side-chain conformations are also relatively well defined.
More extensive data are presented in Tables 4–6, which are published as supporting information on the PNAS web site, www.pnas.org. The single structure used for Tables 2–6 is a representative selected from the full structure search.
Conclusions
We have determined the 3D structure of the chemotactic tripeptide f-MLF-OH, based on solid-state MAS NMR constraints (torsion angles and 13C–15N distances) derived from uniformly 13C,15N- and 15N-enriched samples. Simulated annealing procedures and computational methods that systematically search the entire conformational space were used to define a set of structures consistent with the NMR measurements. The prospects for extension of this work to larger systems are very promising. We note that complete 13C and 15N chemical shift assignments for a U-13C,15N-labeled 62-residue SH3 domain from α-spectrin have been performed by using solid-state NMR data alone (37), representing significant experimental progress. Because the methods used to obtain the torsion angle constraints are already 3D, they are directly applicable to these larger systems; one structural constraint can be extracted from each resolved cross-peak in the 2D 13C–13C and 13C–15N spectra, and the most critical constraints (φ, ψ, χ1) are derived from the well-resolved 13Cα, 13Cβ, and 13CO signals. These approaches are being applied to α-spectrin (37), bacteriorhodopsin (M.T.M., J. Herzfeld, and R.G.G., unpublished work), and ubiquitin (C.M.R. and A. E. McDermott, unpublished work). In proteins, distance measurements are crucial for determining the global fold, and improved multidimensional SSNMR methods for distance measurements in U-13C,15N-labeled proteins are beginning to appear and will be used to measure multiple distances in a single 3D experiment (17).
Supplementary Material
Acknowledgments
We thank L. J. Mueller, B. A. Tounge, M. Hong, and D. J. Ruben for many helpful discussions during the course of this work. C.M.R. acknowledges the support of a National Institutes of Health National Research Service Award (GM-20134); C.P.J., the support of a National Science Foundation Graduate Research Fellowship; M.H., the support of a Danish Natural Science Council Postdoctoral Fellowship and a postdoctoral fellowship from the European Human Frontier Science Program; and M.T.M., the support of a National Institutes of Health National Research Service Award (GM-20818). This research was supported by grants from the National Institutes of Health (AG-14366, GM-23403, and RR-00995).
Abbreviations
SSNMR, solid-state NMR
rmsd, root-mean-square deviation
MAS, magic-angle spinning
f-MLF-OH, N-formyl-l-Met-l-Leu-l-Phe-OH
f-MLF-OMe, f-MLF-OH methyl ester
2D and 3D, two- and three-dimensional
REDOR, rotational-echo double-resonance
References
- 1.Wüthrich K., (1986) NMR of Proteins and Nucleic Acids (Wiley, New York).
- 2.Gayathri C., Bothner-By, A. A., van Zijl, P. C. M. & MacLean, C. (1982) Chem. Phys. Lett. 87, 192-196. [Google Scholar]
- 3.Tolman J. R., Flanagan, J. M., Kennedy, M. A. & Prestegard, J. H. (1995) Proc. Natl. Acad. Sci. USA 92, 9279-9283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Tjandra N. & Bax, A. (1997) Science 278, 1111-1114. [DOI] [PubMed] [Google Scholar]
- 5.Pervushin K., Riek, R., Wider, G. & Wüthrich, K. (1997) Proc. Natl. Acad. Sci. USA 94, 12366-12371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yamazaki T., Lee, W., Arrowsmith, C. H., Muhandiram, D. R. & Kay, L. E. (1994) J. Am. Chem. Soc. 116, 11655-11666. [Google Scholar]
- 7.Creuzet F., McDermott, A. E., Gebhard, R., van der Hoef, K., Spijker-Assink, M. B., Herzfeld, J., Lugtenburg, J., Levitt, M. H. & Griffin, R. G. (1991) Science 251, 783-786. [DOI] [PubMed] [Google Scholar]
- 8.Thompson L. K., McDermott, A. E., Raap, J., van der Wielen, C. M., Lugtenberg, J., Herzfeld, J. & Griffin, R. G. (1992) Biochemistry 31, 7931-7938. [DOI] [PubMed] [Google Scholar]
- 9.McDowell L. M., Klug, C. A., Beusen, D. D. & Schaefer, J. (1996) Biochemistry 35, 5395-5403. [DOI] [PubMed] [Google Scholar]
- 10.McDowell L. M., Lee, M. S., McKay, R. A., Anderson, K. S. & Schaefer, J. (1996) Biochemistry 35, 3328-3334. [DOI] [PubMed] [Google Scholar]
- 11.Long J. R., Dindot, J. L., Zebrowski, H., Kiihne, S., Clark, R. H., Campbell, A. A., Stayton, P. S. & Drobny, G. P. (1998) Proc. Nat. Acad. Sci. USA 95, 12083-12087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lansbury P. T., Costa, P. R., Griffiths, J. M., Simon, E. J., Auger, M., Halverson, K. J., Kocisko, D. A., Hendsch, Z. S., Ashburn, T. T., Spencer, R. G. S., et al. (1995) Nat. Struct. Biol. 2, 990-998. [DOI] [PubMed] [Google Scholar]
- 13.Griffin R. G. (1998) Nat. Struct. Biol. 5, 508-512. [DOI] [PubMed] [Google Scholar]
- 14.Dusold S. & Sebald, A. (2000) Annu. Rep. NMR Spectros. 41, 185-264. [Google Scholar]
- 15.Nomura K., Takegoshi, K., Terao, T., Uchida, K. & Kainosho, M. (2000) J. Biomol. NMR 17, 111-123. [DOI] [PubMed] [Google Scholar]
- 16.Jaroniec C. P., Tounge, B. A., Herzfeld, J. & Griffin, R. G. (2001) J. Am. Chem. Soc. 123, 3507-3519. [DOI] [PubMed] [Google Scholar]
- 17.Jaroniec, C. P., Filip, C. & Griffin, R. G. (2002) J Am. Chem. Soc. 124, in press. [DOI] [PubMed]
- 18.Rienstra, C. M., Hohwy, M., Mueller, L. J., Jaroniec, C. P., Reif, B. & Griffin, R. G. (2002) J. Am. Chem. Soc. 124, in press. [DOI] [PubMed]
- 19.Showell H. J., Freer, R. J., Zigmond, S. H., Schiffman, E., Aswanikumar, S., Corcoran, B. & Becker, E. L. (1976) J. Exp. Med. 143, 1154-1169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gavuzzo E., Mazza, F., Pochetti, G. & Scatturin, A. (1989) Int. J. Peptide Protein Res. 34, 409-415. [DOI] [PubMed] [Google Scholar]
- 21.Morfew A. J. & Tickle, I. (1981) Cryst. Struct. Commun. 10, 781-788. [Google Scholar]
- 22.Rienstra C. M., Hohwy, M., Hong, M. & Griffin, R. G. (2000) J. Am. Chem. Soc. 122, 10979-10990. [Google Scholar]
- 23.Reif B., Hohwy, M., Jaroniec, C. P., Rienstra, C. M. & Griffin, R. G. (2000) J. Magn. Reson. 145, 132-141. [DOI] [PubMed] [Google Scholar]
- 24.Bennett A. E., Rienstra, C. M., Auger, M., Lakshmi, K. V. & Griffin, R. G. (1995) J. Chem. Phys. 103, 6951-6958. [Google Scholar]
- 25.Sun B. Q., Rienstra, C. M., Costa, P. R., Williamson, J. R. & Griffin, R. G. (1997) J. Am. Chem. Soc. 119, 8540-8546. [Google Scholar]
- 26.Detken A., Hardy, E. H., Ernst, M., Kainosho, M., Kawakami, T., Aimoto, S. & Meier, B. H. (2001) J. Biomol. NMR 20, 203-221. [DOI] [PubMed] [Google Scholar]
- 27.Bennett A. E., Ok, J. H., Griffin, R. G. & Vega, S. (1992) J. Chem. Phys. 96, 8624-8627. [Google Scholar]
- 28.Sun B. Q., Costa, P. R., Kocisko, D. A., Lansbury, P. T., Jr. & Griffin, R. G. (1995) J. Chem. Phys. 102, 702-707. [Google Scholar]
- 29.Nielsen N. C., Bildsøe, H., Jakobsen, H. J. & Levitt, M. H. (1994) J. Chem. Phys. 101, 1805-1812. [Google Scholar]
- 30.Lee Y. K., Kurur, N. D., Helmle, M., Johannessen, O. G., Nielsen, N. C. & Levitt, M. H. (1995) Chem. Phys. Lett. 242, 304-309. [Google Scholar]
- 31.Hohwy M., Rienstra, C. M., Jaroniec, C. P. & Griffin, R. G. (1999) J. Chem. Phys. 110, 7983-7992. [Google Scholar]
- 32.Schaefer J. & Stejskal, E. O. (1979) J. Magn. Reson. 34, 443-447. [Google Scholar]
- 33.Baldus M. A., Petkova, A. T., Herzfeld, J. H. & Griffin, R. G. (1998) Mol. Phys. 95, 1197-1207. [Google Scholar]
- 34.Hediger S., Meier, B. H. & Ernst, R. R. (1995) Chem. Phys. Lett. 240, 449-456. [Google Scholar]
- 35.McDermott A., Polenova, T., Bockmann, A., Zilm, K. W., Paulsen, E. K., Martin, R. W. & Montelione, G. T. (2000) J. Biomol. NMR 16, 209-219. [DOI] [PubMed] [Google Scholar]
- 36.Egorova-Zachernyuk T. A., Hollander, J., Fraser, N., Gast, P., Hoff, A. J., Cogdell, R., de Groot, H. J. & Baldus, M. (2001) J. Biomol. NMR 19, 243-253. [DOI] [PubMed] [Google Scholar]
- 37.Pauli J., Baldus, M., van Rossum, B., de Groot, H. & Oschkinat, H. (2001) Chembiochem. 2, 272-281. [DOI] [PubMed] [Google Scholar]
- 38.Costa P. R., Gross, J. D., Hong, M. & Griffin, R. G. (1997) Chem. Phys. Lett. 280, 95-103. [Google Scholar]
- 39.Feng X., Eden, M., Brinkmann, A., Luthman, H., Eriksson, L., Graslund, A., Antzutkin, O. N. & Levitt, M. H. (1997) J. Am. Chem. Soc. 119, 12006-12007. [Google Scholar]
- 40.Ladizhansky V., Veshtort, M. & Griffin, R. G. (2002) J. Magn. Reson. 154, 317-324. [DOI] [PubMed] [Google Scholar]
- 41.Feng X., Lee, Y. K., Sandström, D., Edén, M., Maisel, H., Sebald, A. & Levitt, M. H. (1996) Chem. Phys. Lett. 257, 314-320. [Google Scholar]
- 42.Raleigh D. P., Levitt, M. H. & Griffin, R. G. (1988) Chem. Phys. Lett. 146, 71-76. [Google Scholar]
- 43.Costa P. R., Sun, B. Q. & Griffin, R. G. (1997) J. Am. Chem. Soc. 119, 10821-10830. [Google Scholar]
- 44.Gullion T. & Schaefer, J. (1989) J. Magn. Reson. 81, 196-200. [Google Scholar]
- 45.Nilges M., Clore, G. M. & Groenborn, A. M. (1988) FEBS Lett. 229, 317-324. [DOI] [PubMed] [Google Scholar]
- 46.Brunger A. T., Adams, P. D., Clore, G. M., DeLano, W. L., Gros, P., Grosse-Kunstleve, R. W., Jiang, J. S., Kuszewski, J., Nilges, M., Pannu, N. S., et al. (1998) Acta Cryst. D 54, 905-921. [DOI] [PubMed] [Google Scholar]
- 47.Tucker-Kellogg L., (2002) Ph.D. thesis (Massachusetts Institute of Technology, Cambridge).
- 48.Lawrence C. T., Zhou, J. L. & Tits, A. L., (1997) Technical Report TR-94-16r1 (Institute for Systems Research, Univ. of Maryland, College Park).
- 49.Rice D. M., Meinwald, Y. C., Scheraga, H. A. & Griffin, R. G. (1987) J. Am. Chem. Soc. 109, 1636-1640. [Google Scholar]
- 50.Rice D. M., Wittebort, R. J., Griffin, R. G., Meirovitch, E., Stimson, E. R., Meinwald, Y. C., Freed, J. H. & Scheraga, H. A. (1981) J. Am. Chem. Soc. 103, 7707-7710. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.