An atomically detailed study of the folding pathways of protein A with the stochastic difference equation

Abstract

An algorithm is applied here to compute folding pathways of staphylococcal protein A, fragment B. Emphasis is on studies of the complete process, starting from an ensemble of fully denatured conformations and ending at the folded state. The stochastic difference equation algorithm is based on optimization of an action that makes it possible to use a large integration step. Motions with typical displacements that change rapidly on the size scale of the step are filtered out, providing numerically stable and approximate solutions. The present approach is unique in maintaining an atomically detailed picture while providing a systematic, controlled approximation to the classical equations of motion. Analysis of 130 trajectories suggests the following folding mechanism for protein A: At an early precollapse phase of the process, a few native hydrogen bonds form near the C terminus of the protein. The hydrogen bonds are formed mostly within the third helix. The next step is chain collapse that occurs in parallel to additional growth of secondary structure seeds. Therefore, the present study does not support a pure hydrophobic collapse, or substantial early formation of secondary structure. At the last step, native tertiary contacts are formed at the same time as the completion of the secondary structure elements. To a large extent, the process is parallel and not sequential. The early formation of the third helix of protein A, fragment B (in the calculation), is consistent with experimental data.

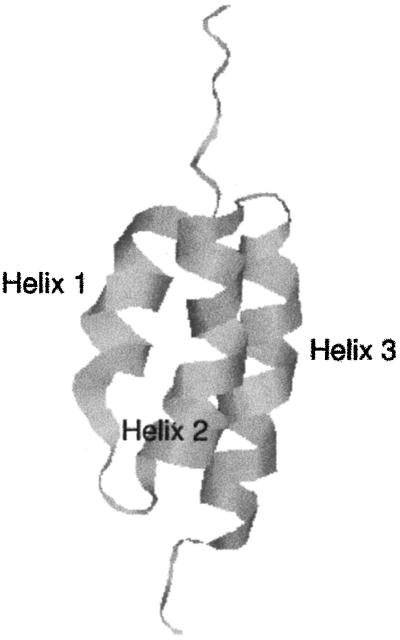
Mechanisms of protein folding are topics of intensive theoretical and experimental investigations. For recent books on folding see refs. 1 and 2. The present paper focuses on the folding pathways of a protein that has received considerable attention in the past: protein A (3–7). Fragment B from staphylococcal protein A is a small, 60-residue, three-helix bundle, making it a good target for theoretical investigations (Fig. 1). Theoretical studies of this class of proteins are more advanced than those for β or α/β folds. Nevertheless, even this small model system presents significant challenges for long-time atomically detailed computations, which so far have been attempted only once in the most straightforward fashion (8).

Fig 1.

Ribbon model of the 60-residue fragment B of staphylococcal protein A.

Because of the complexity of the protein-folding problem, past simulations used approximations within the framework of the atomically detailed molecular dynamics approach. The pioneering studies of Boczko and Brooks (9) of a 46-residue fragment of the full 60-residue protein, and follow-up works (10, 11), focused on the equilibrium of the folding process, estimating free energy profiles along an assumed progress variable (like a reaction coordinate), the radius of gyration. While the calculations lead to considerable insight into folding mechanisms, it is not obvious whether they can be effectively viewed as a quasi-equilibrium process along one or a few reaction coordinates. Alonso and Daggett (12) used high-temperature unfolding trajectories to characterize plausible folding pathways. No equilibrium assumption was made, but the effects of the high temperatures and limited sampling are not obvious, although these effects were suggested to be small by further studies (13, 14).

The two calculations, employing different approximations, varied significantly in their conclusions. Alonso and Daggett (12) concluded from their study that helix 3 unfolds last (folds first) in accord with equilibrium measurements of the relative stability of the helices (3, 4). Boczko and Brooks (9) came to the conclusion that helix 3 is the least stable thermodynamically and folds last. In light of the disagreement between the theoretical calculations, it is desirable to carry out more calculations that (at the least) use a different set of approximations and a different physical approach.

The Algorithm

Here we describe yet another calculation of the folding kinetics of protein A by using an atomically detailed model. The present study is based, however, on a different approach for calculations of trajectories (15). Instead of solving Newton's equations in small time steps (initial value formulation), we solve a boundary value problem in which the initial coordinates of an unfolded conformation, Y_u, and the coordinates of the final conformation, Y_f, are specified. Instead of solving for the (mass-weighted) coordinates, Y, as a function of time, we compute them as a function of the trajectory length, l. We search for a trajectory that makes the action, S = ∫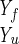 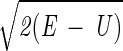dl, stationary (16). E is the total energy, U is the potential energy, and dl is an element of length.

A discrete approximation for the action, S ≅ ∑_i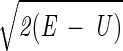Δl_i,i+1, is used to define a discrete approximation of the classical trajectory. Since the condition on the classical action is only that a stationary point exists (the action need not be a minimum), the trajectory is computed by minimization of the gradient norm, or of the following target function:

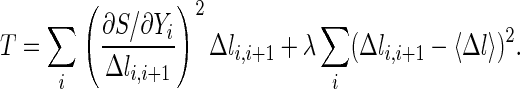For sufficiently small steps, Δl_i,i+1, an exact classical trajectory is obtained. The parameter λ is the strength of a penalty function that keeps all of the length elements, Δl_i,i+1, equal to the average length, 〈Δl〉 = (1/N)∑_i Δl_i,i+1, and (of course) equal to each other.

The minimization of T is carried out with the additional constraint on the path that any overall center of mass rotations and translations are subtracted out at each step, thereby keeping the overall system rotations and translations stationary. Let Δy_ij be a mass-weighted displacement vector of one of the j atoms in the ith structure along the reaction path. For all i and j, we impose the linear constraints: {∑_j Δy_ji}_i = 0 and {∑_j y_ji × Δy_ji}_i = 0 during the minimization. This is similar to the constraints that we used in calculations of the reaction coordinates (17). It should be noted that, although the function T can be used to sample trajectories stochastically (17), here we restrict ourselves to optimization.

No assumption of equilibrium conditions or of a reaction coordinate is made, and the energy that is used corresponds to room temperature, estimated as described below in Computational Procedure. Two other approximations, however, are used in the algorithm, making our calculations complementary to past atomically detailed studies. The first is the use of the generalized Born model (18) (with the generalized Born code provided by D. A. Case) to describe solvation effects implicitly. We did not add friction to account for kinetic effects of solvation, because the formulation is one of constant energy. However, some frictional effects are included in the model as described below because of the filtering out of high-frequency motions (19). The filtering of high-frequency motions is the second approximation used in the algorithm. It can be shown (19) that the use of a large step eliminates high-frequency modes from the system. This is similar to the use of a frequency-dependent friction that affects only high-frequency modes. It is also possible to show (R.E., unpublished results) that, in the limit of maximum filtering, the observed trajectory becomes the steepest descent path. Hence, the trajectory obtained as a function of the size of the length element changes from an exact classical trajectory (a very small step size) to a “highly viscous” path when the step size is large. Clearly, the approximations (and the method) used here are very different from those used in the past. We, therefore, expect the application of the present protocol to provide new insight into the kinetics of folding.

Computational Procedure

Preparation of Folded and Unfolded State.

For the folded state, the experimental coordinates of Protein Data Bank ID code (20) were used. These are the same experimental coordinates that were used by Shea et al. (11) and Alonso and Daggett (12). In the procedure used here, which is based on boundary conditions, the coordinates of the starting and ending conformations need to be specified. The nature of the unfolded state, which cannot be represented by a single structure, is under debate (21). It is clearly a function of the experimental conditions. It is possible to use relatively gentle unfolding conditions in which significant native structure remains. On the other hand, it is of interest to examine extreme unfolding conditions in which no trace of the native state remains in the unfolded conformation. More moderate unfolding processes could be found along the pathway starting at later positions. Moreover, we suggest that experiments that push the unfolded conformations of protein A further from the folded state, exploring larger portions of the energy surface and earlier events of the folding process, are possible and worthy of theoretical investigation.

Ten molecular dynamics simulations of 5 ns each at 1000 K, starting from the native conformation, prepared unfolded conformations. One thousand structures, separated by 50 ps in time, were selected, and their energies were minimized. The conformations were clustered, and only shapes that were different from each other by at least 8.5 Å were kept. The final set of highly diverse unfolded structures includes 130 shapes with no native contacts remaining.

Calculations of Trajectories.

For each of the 130 unfolded shapes described above, a classical folding trajectory to the single correct fold is computed. The computer code seeking a stationary solution of the action was implemented in our program moil (22), and versions for the LINUX and Windows operating systems were run in parallel with the Message Passing Interface library. All trajectories were computed on the Computational Biology Service Unit cluster of the Cornell Theory Center, using 20 central processing units for 6 hr to compute a single trajectory. Overall, the communication overhead when optimizing trajectories is minimal (23), making it possible to use more nodes as they become available.

The force field of moil used here is a united-atom version (with explicit polar hydrogens) from a combination of amber (24) and opls (25) with addition of the “pair-wise” generalized Born model of Hawkins et al. (18) from the laboratory of D. A. Case. We have tested the force field by running ten 1-ns simulations of protein A at room temperature, verifying that the protein remains near the native fold with an rms deviation of about 3 Å. The total energy of the system, E, was estimated from initial-value molecular dynamics simulations that were equilibrated at room temperature. The folded and the unfolded states from 50-ps trajectories were considered in the estimation of the total energy E. With the estimate of the equilibrium folded and unfolded state total energy available and the prespecified folded and unfolded conformations, the target function T (and the path) were optimized by using five cycles of 2,000 simulated annealing steps. The typical value of the gradient of the target function, T, normalized to the number of degrees of freedom, was 3 kcal/Å. The simulated annealing temperature varied linearly from 300 K to 2 K during each cycle.

By the end of the simulated annealing runs, we had 130 folding trajectories of protein A, spanning considerable diversity of the initial unfolded structures, and sampled from the approximate microcanonical ensemble (our method being strictly one of classical mechanics). These trajectories are used in the analysis described in the next section.

Results

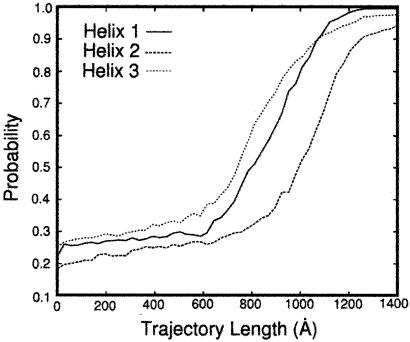
The progression of helix probability as a function of the trajectory length is shown in Fig. 2. At each length slice, the probability of having particular secondary structure was averaged over all of the 130 trajectories. Helix 3 formed earlier in the process, but the temporal difference of formation from other helices was not profound. It should be noted that, according to classical mechanics, there is a one-to-one correspondence between time and length t=∫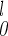 dl/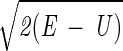. In principle, we could make reference to the sequence of events by using the length, even without making explicit use of time. The actual calculation of the time scale is difficult because (i) the filtering of high-frequency modes makes the path and, therefore, the time scale considerably shorter than the exact result, and (ii) the constant-energy trajectories with the generalized Born model do not include the frictional slow-down caused by water, leading (again) to trajectories that are too fast.

Fig 2.

The fractions of amino acids in the helical conformation (probability) for each of the three helices of protein A, defined as a sequence of 3 residues with dihedral angles φ and ψ within 30° of (−60°, −60°). The fraction is followed as a function of the trajectory length measured in ångstroms. The length of the path, l, is defined by the line integral, l ≡ ∫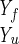 dl. The integral is evaluated between the two fixed end points, Y_u and Y_f, and dl is a length element along the path. Since we approximate the continuous path by a set of discrete points, we have l ≅ ∑_i Δl_i,i+1 and Δl_i,i+1 ≡ |Y_i − Y_i+1|. The results are averaged over 130 folding trajectories. Helix 3 forms somewhat earlier than helices 1 and 2 in accordance with suggestive conclusions from experiments (3, 4). However, the difference between the rates of formation of helices 1 and 2 on the one hand, and helix 3 on the other, is not large. In another estimate of the rate of formation of different helices, we counted the number of trajectories that fold first to helix 1 (45), helix 2 (30), and helix 3 (55) structures. This independent analysis is a confirmation of the above calculation of the fractions.

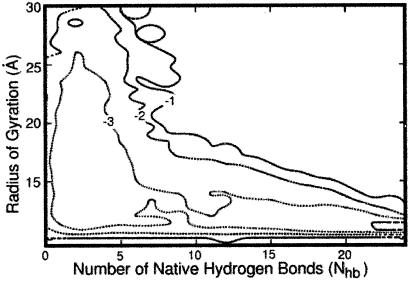
Fig. 3 shows a contour plot examining the process as a function of two degrees of freedom: the radius of gyration, R_gyr, and the number of hydrogen bonds, N_hb. The probability, P(R_gyr, N_hb), that a reactive trajectory (one that starts at the unfolded and ends at the folded state) will correspond to a given radius of gyration and number of hydrogen bonds was computed. The probability was estimated by using all 130 trajectories and all length slices. For convenience, a “free energy,” F = −RT × ln[P(R_gyr, N_hb)], in kcal/mol, is presented in Fig. 3. It should be noted that the computed distribution is not an equilibrium quantity because only reactive trajectories were taken into account.

Fig 3.

A “free energy” plot (−RT ln[P(R_gyr, N_hb)]) as a function of the radius of gyration, R_gyr, and the number of hydrogen bonds, N_hb. P(R_gyr, N_hb) is the joint probability of the radius of gyration and the number of native hydrogen bonds averaged over 130 reactive trajectories. Sequential contour lines are separated by 1 kcal/mol. The picture, averaged over all of the trajectory slices, suggests earlier hydrophobic collapse and later formation of secondary structure. It is difficult to appreciate from the average picture the details of the mechanism that are revealed when individual length slices (Fig. 4) are considered.

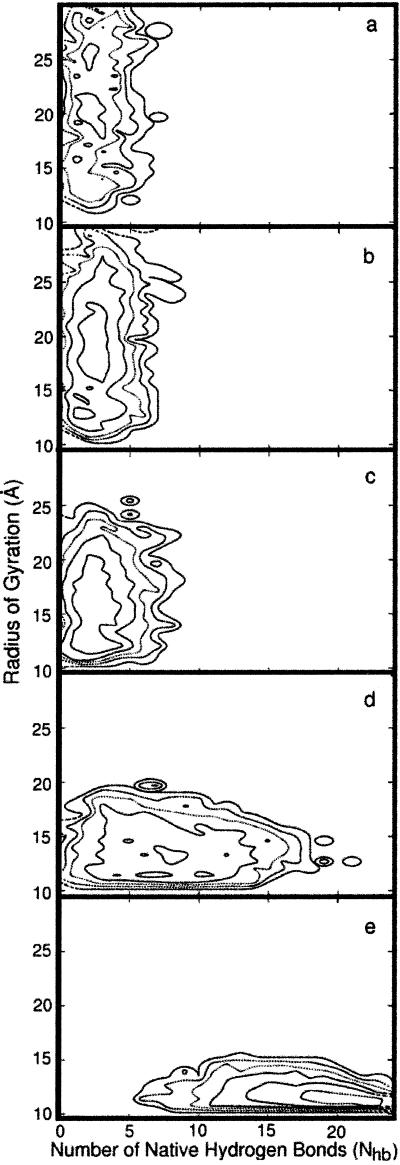
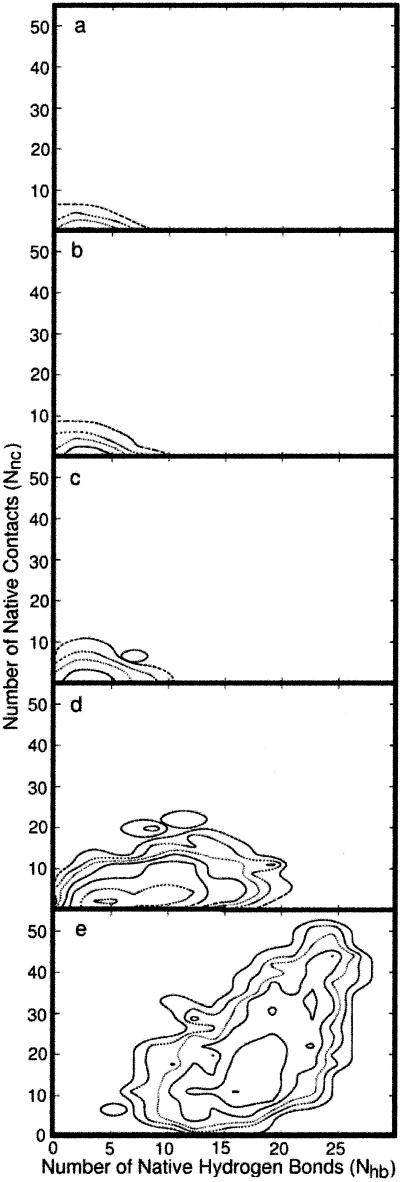
In contrast to equilibrium investigations, the trajectories computed here make it possible to study the sequence of events determined by (potentially) nonequilibrium effects. In Fig. 4, two-dimensional (R_gyr, N_hb), path-length dependent, “free energy” surfaces are presented. In Figs. 4 a–e, “free energies” averaged over sequential fractions of the trajectories are shown. Fig. 4a is an average over the first fifth (in length) of the 130 folding trajectories; Fig. 4b is an average over the second fifth, and so on.

Fig 4.

Two-dimensional “free energy profiles” are shown as a function of the radius of gyration, R_gyr, and the number of hydrogen bonds, N_hb, at different sequential length slice (a–e) of the trajectory. The five snapshots in length are averaged over 130 trajectories and over the corresponding fifth of the trajectory length (e.g., the quantities in b are averaged over the second fifth). Sequential contour lines are separated by 1 kcal/mol. See text for more details.

Fig. 4a (the earliest events) shows a wide distribution of the radius of gyration while only a few hydrogen bonds are formed. In Fig. 4b, the radius of gyration remains roughly the same as in Fig. 4a, suggesting little progress along that reaction coordinate. The driving force leading to structure at the length slice in Fig. 4 a and b is the significant formation of new hydrogen bonds. The hydrogen bonding probability in Fig. 4a is bounded by five native hydrogen bonds—i.e., there is no probability of forming more than five native hydrogen bonds at this point. However, in Fig. 4b, the probability exceeds five hydrogen bonds slightly and includes a few more bonds not included in the earlier structures.

In Fig. 4c, simultaneous increase in the number of native hydrogen bonds and collapse of the structure to a more compact shape are observed. In Fig. 4d, a significant reduction in the radius of gyration (collapse) is seen, which is coupled to a continuous growth in the number of hydrogen bonds. In the final phase of the folding process (Fig. 4e), secondary structure elements build up further while the radius of gyration maintains the same value (approximately) as in the fourth slice of the trajectory. Hence, there is only one phase of the folding pathway in which the radius of gyration changes significantly (Fig. 4d). At the very early beginning and at the end of the folding pathways, the process seems to be dominated by hydrogen-bond formation rather than by changes in the radius of gyration.

It is also of interest to compare the relative rates of formation of tertiary contacts versus secondary structure elements. In Fig. 5, the rates of folding projected on two dimensions [the number of hydrogen bonds (as before) and the number of native contacts] are compared. A native contact is defined by two amino acids that are separated by at least four residues along the chain and by a spatial distance between the centers of mass of the side chains below 6.5 Å. It is evident that there are about the same number of hydrogen bonds as the number of tertiary contacts in the earliest phase (Fig. 5 a and b). However, the total number of hydrogen bonds in the native state is roughly 30, whereas the number of native contacts is about 50. Comparisons of the fractions of contacts or hydrogen bonds that form (compared with those in the native state), are therefore more meaningful. The fraction of native contacts as a function of path length is consistently lower than the fraction of native hydrogen bonds. Although tertiary structure is formed together, in parallel, with secondary structure, it seems that the secondary structure forms first. Hence, comparison of the three plausible reaction coordinates—radius of gyration, hydrogen-bond formation, and tertiary-contact formation—suggests that nuclei of secondary structure are the earliest to form. Of course, our conclusion is limited to the present small helical protein.

Fig 5.

Two-dimensional “free energy profiles” are shown as a function of the number of hydrogen bonds and the number of native contacts for different length slices of the trajectory. The averages are over 130 trajectories and over the corresponding fifth of the trajectory length. Sequential contour lines are separated by 1 kcal/mol. The relatively slow progress of the folding process along two reaction coordinates at the early phases and the significant pick-up in speed at the last length segment should be noted. Whereas the secondary structure seeds occur before the hydrophobic collapse (as shown in Fig. 4), the majority of the structural changes, early in the folding process, are connected with collapse of the radius of gyration.

Discussion

We present here an approach for computing long-time dynamics that is used to calculate the folding pathways of protein A. This approach is complementary to other atomically detailed simulation techniques to compute protein dynamics. Not only are different approximations used, but also a view of early events in protein folding is possible. Such a view is difficult to obtain by other techniques: The study of Guo et al. (10) examined compact conformations, whereas the high-temperature unfolding simulations by Alonso and Daggett (12) consist of trajectories that are too short for comprehensive sampling of late events in folding. We emphasize that the early segments of the folding process, unique to the present investigation, are of significant general interest. It has been the focus of theory (26–28) and experiments [see, for example, experiments on cytochrome c (29–31)].

The present calculations suggest a two-step picture of protein folding. In the first step of the folding of protein A, small nuclei with native hydrogen bonds form at the C terminus of the protein, mostly in the third helix; at the second step, the chain collapses into a more compact “molten-globule” state. This early folding does not conform to a pure hydrophobic collapse (ignoring hydrogen bonds) or to a model in which substantial secondary structure is assumed to form first. The results are also consistent with those of the simplified model of Zhou and Karplus (32).

The steps that follow the collapse were studied by other methods as well, and a few comparisons can be made. One feature of the simulation reported here, which is in qualitative agreement with the limited equilibrium experimental data, is the relative stability (that may imply early formation) of the third helix (3, 4, 33, 34). This observation is also in qualitative agreement with the unfolding simulations of Alonso and Daggett (12).

We also make a prediction about the relative rates of hydrogen-bond and tertiary-contact formation: The simultaneous formation of both, with the somewhat earlier appearance of secondary structure elements, is not contradictory with earlier work (9–12) and in fact provides further support for the strong coupling between alternative folding coordinates.

Final Remarks

We have provided a comprehensive view of the folding process of protein A, starting from extreme unfolded conditions and continuing all of the way to the unique shape of the folded state. The calculations pertain to room-temperature energies, using an atomically detailed model, and are direct (although approximate) solutions of the equations of motion. The most significant approximations made here are (i) the use of a large step size, leading to filtering of high-frequency modes and (ii) the use of effective solvation, employing the generalized Born model (18). The complex process of protein folding can benefit from alternative computational techniques and different views as a way to test different approximations and to focus on consensus results of alternative approaches. The boundary-value protocol used here provides a fundamentally different technique compared with the solution of initial-value problems, and is, therefore, likely to provide the desired alternative outlook.