Protein-solvent preferential interactions, protein hydration, and the modulation of biochemical reactions by solvent components

Abstract

Solvent additives (cosolvents, osmolytes) modulate biochemical reactions if, during the course of the reaction, there is a change in preferential interactions of solvent components with the reacting system. Preferential interactions can be expressed in terms of preferential binding of the cosolvent or its preferential exclusion (preferential hydration). The driving force is the perturbation by the protein of the chemical potential of the cosolvent. It is shown that the measured change of the amount of water in contact with protein during the course of the reaction modulated by an osmolyte is a change in preferential hydration that is strictly a measure of the cosolvent chemical potential perturbation by the protein in the ternary water–protein–cosolvent system. It is not equal to the change in water of hydration, because water of hydration is a reflection strictly of protein–water forces in a binary system. There is no direct relation between water of preferential hydration and water of hydration.

For the better part of a century, it has been common practice to modulate biochemical (biological) reactions by the addition to the aqueous solvent (dilute buffer) of compounds that were required at high concentration (∼0.5 M or higher) to exert their effect. For example, sucrose and glycerol were used to stabilize biological systems, whereas urea and guanidine hydrochloride were used to solubilize coagulated systems and to unfold (denature) proteins. The aim in the use of these additives, referred to as cosolvents, was to displace to the right or left the chemical equilibrium, Reactant ⇌ Product. Although this practice was widespread, a theoretical underpinning was lacking until the discovery by Wyman in 1948 of the phenomenon of linked functions (1) and his development of the linkage relationship equations (2, 3), which showed the necessary thermodynamic interdependence between the displacement of a chemical equilibrium and the change in binding of a ligand to the system during the course of the reaction. Complete understanding of the action of cosolvents in such modulation required the combination of the Wyman linkage relations with the multicomponent solution thermodynamics theory developed by Kirkwood and Goldberg (4), Stockmayer (5), and Scatchard (6).

The basic Wyman linkage equation states that, at any ligand concentration, m_L, the gradient of the equilibrium constant with respect to ligand activity is equal to the change in the binding of the ligand to the biological system during the course of the reaction (at constant temperature and pressure that will be maintained throughout):

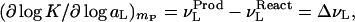1

where K is the equilibrium constant of the reaction, a_L is the activity of the ligand (a_L = m_Lγ_L), ν and ν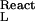 are the bindings of the ligand to the two end states of the reaction, and m_L and γ_L are the molal concentration and activity coefficient of the ligand. [In our notation, the subscripts W, L, and P refer to water, ligand (cosolvent), and protein (macromolecule), respectively.] Tanford, in 1969 (7), showed that the binding parameters, ν 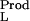and ν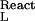, are actually balances between ligand and water molecules that interact with the biological system, e.g., a protein molecule. Let us examine now the basic thermodynamics of binding that define the nature of the chemical processes involved and the significance of the measured parameters. We will treat an isolated protein molecule, which, experimentally, can be achieved by proper extrapolation to zero protein concentration.

Interaction of Solvent Components with Protein Loci; Exchange

In solution, any locus on the surface of a protein molecule must be in contact with a solvent component, because a vacuum cannot be tolerated in an aqueous medium. The reference state is the protein dissolved in water, in which it is fully hydrated. Therefore, in a binary solvent, the binding of the nonaqueous solvent component to any locus must displace water, i.e., binding is an exchange reaction (8):

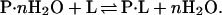2

Let us consider thermodynamically a protein molecule in its fully hydrated reference state. It is possible to define formally a free energy of hydration, ΔG°_W, as the sum of the free energies of interaction of all water molecules with all the interacting loci, ∑ δg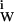. We define an interacting locus as any volume element about the protein molecule that is thermodynamically affected by the protein, ranging from immobilization of water molecules on the protein to momentary perturbation of the translational or rotational motions of a water molecule by the protein, to their repulsion (δg 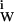may be both negative and positive). Physically, the consequence of these interactions can be described as the mass of water that, at any instant, travels nonrandomly in the same direction as the protein in a transport process. Division by the molecular weight of water gives the effective number of water molecules that hydrate the protein, W_H. This is the definition of water of hydration. Therefore, W_H does not have the physical meaning of an integral number of whole water molecules that interact with the protein. Formally, it can be described by a hypothetical equilibrium in aqueous medium between empty (dry) protein loci and the same loci in a hydrated state: P (dry) + H₂O ⇌ P⋅H₂O; (ΔG°_W; K_W).

The exchange of Eq. 2 requires the departure of water molecules with a free energy change, −G°_W (which can be zero if the particular water molecule was not affected by the protein) and the occupancy of the vacated sites by ligand molecules with a free energy change, ΔG°_L, for the hypothetical equilibrium between empty (dry) protein loci in an aqueous medium and loci occupied by ligand: P (dry) + L ⇌ P⋅L; (ΔG°_L; K_L). The net free energy change, measured experimentally as the free energy of binding, ΔG°_b, is, therefore, an exchange free energy, ΔG°_ex (9, 10):

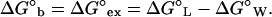3

When ΔG°_L and ΔG°_W are of similar magnitude, i.e., the affinity is similar for water and ligand, the exchange with water must be taken into consideration explicitly.‡ The concept of exchange has been treated by Schellman in a set of classical papers (11–16) in which he examined the interaction of proteins with weakly interacting ligands. Schellman (11–13) has treated the exchange reaction (Eq. 2) in terms of the binding equilibrium constant, K_b, which, for an exchange reaction, is the exchange constant, K_ex:

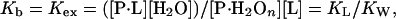4

where K_W and K_L are the hypothetical equilibrium constants for the binding of water and ligand to a dry site on the protein. As a simple example, which is helpful in thinking about the exchange process, Schellman treated the case of a single isolated site in which one ligand molecule replaces one water molecule. At any ligand concentration, m_L or X_L (in mol fraction units), the extent of binding at a site is (11, 12):

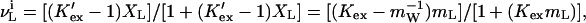5

where the first equality refers to mol fraction concentration units and the second to molality. Cursory examination of Eq. 5 shows that, if K′_ex < 1 or K_ex <0.018 (m_W = 55.56), the measured binding stoichiometry of the ligand must be negative.

The weakly interacting ligands used to modulate reactions are used at high concentrations, ∼0.2 − 10 M, and may occupy as much as 40% of the solvent volume. This renders the two solvent components equivalent (13). Hence, these ligands are referred to as cosolvents. The requirement of high concentration means that the interactions of the cosolvents with the protein proceed with low free energy changes (K′_ex ∼1 in mol fraction units). As a consequence, the measured binding and the change in binding defined by the Wyman linkage equation (Eq. 1) are a preferential binding (19). The epithet “preferential” refers to the relative affinities of the interacting loci on the protein for ligand and water. If the affinity is greater for ligand than for water, there is an excess of ligand in the protein domain§ relative to bulk solvent composition. This defines preferential binding of ligand. If there is a deficiency of ligand, i.e., a greater affinity for water, K′_ex <1, the measured binding is negative, and there is preferential exclusion of the ligand and an excess of water in the protein domain. This defines preferential hydration. Therefore, binding and exclusion are symmetrical phenomena on the two sides of a point of neutrality, defined by whether for the ligand ΔG°_L > ΔG°_W or ΔG°_L < ΔG°_W. At the point of neutrality, ΔG°_L = ΔG°_W, the protein is thermodynamically indifferent to contact with water or cosolvent, and the solvent composition in the domain§ of the protein is equal to that of bulk solvent (11, 12). Total inertness of the cosolvent toward the protein requires that ΔG°_L = ΔG°_W at all solvent compositions (20, 21).

Thermodynamic Binding; Preferential Hydration

Now, let us consider the thermodynamic events that occur when a cosolvent is added to an aqueous protein solution. There are two consequences: one general, the other specific to the given protein–cosolvent pair. The first consequence is the colligative decrease in water activity, which is identical for the addition of all solutes at identical osmolality and is the same whether in pure water or in a protein solution. At our standard state constant temperature and pressure, the activity of pure water is a_W = 1, and its chemical potential is μ_W = μ°. Addition of any solute (cosolvent) lowers the water activity to a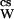, where

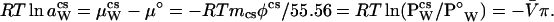6

The magnitude of the lowering of a_W is defined by the product m_csφ^cs, the osmolality, where m_cs is the cosolvent molal concentration and φ^cs is its osmotic coefficient, which is a measure of its departure from ideality. Lowering of the water activity has as a consequence the lowering of the vapor pressure to P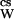 from that of pure water, P°_W. This gives rise to the generation of osmotic pressure (π) across a semipermeable membrane and to the lowering of the freezing point and the increase of the boiling point. [V̄ is the partial molar volume of water, R is the universal gas constant, and T is the thermodynamic (Kelvin) temperature.]

The second consequence will be examined by carrying out the equivalent operation of introducing a hydrated protein molecule into the aqueous cosolvent solution. The immediate effect is a perturbation of the chemical potential of the cosolvent by the protein, (∂μ_L/∂m_P)_mL = (∂μ_P/∂m_L)_mP. This perturbs the chemical equilibrium in the domain§ of the protein. To restore the chemical equilibrium, the chemical potential of the cosolvent in the protein domain must be changed by an identical amount but with a sign opposite to that of the perturbation. This can be accomplished by adjusting the concentration of the cosolvent, m_L, in the domain of the protein (μ_L = μ°_L + RT ln m_Lγ_L) by the increment (4, 19):

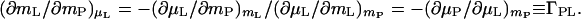7

The quantity (∂m_L/∂m_P)_μL, which is the preferential binding defined above, is the binding measured experimentally in dialysis equilibrium (19) or vapor pressure osmometry (22) and which appears in the Wyman linkage equation (Eq. 1). It is expressed as ν in Scatchard notation (6) and as Γ₂₃ in Casassa and Eisenberg (19) and Schellman (12) notation and designated by Γ_PL in the present discussion. Eq. 7 shows that preferential binding, (∂m_L/∂m_P)_μL, is a purely thermodynamic quantity: it is the mutual perturbation of the chemical potentials of cosolvent and protein, hence its identification as thermodynamic binding (13). This also means that a molecule does not have to be in contact with protein to be bound to it (12). The adjustment of the solvent composition can be accomplished by an increase (or decrease) in the number of cosolvent molecules in the domain‡ of the protein, a decrease (or increase) in the number of water molecules, or both (14). Therefore, molecularly, (∂m_L/∂m_P)_μL has contributions of both cosolvent and water molecules. It is not the actual number of cosolvent molecules that are in physical contact with the protein (12).

The perturbation of the chemical potential, (∂μ_L/∂m_P)_mL, can be positive if the interaction between the cosolvent and the protein is unfavorable (most osmolytes, e.g., sugars, polyols, or methylamines), or it can be negative if the interaction is favorable (urea, ethylene glycol, guanidine hydrochloride) (8). Therefore, by Eq. 7, the thermodynamic binding, (∂m_L/∂m_P)_μL = Γ_PL, can also be positive or negative. Negative Γ_PL means preferential exclusion of cosolvent, which means preferential hydration, Γ_PW, which is related to preferential binding by (23):

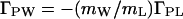8

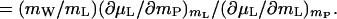Eq. 8 shows that, like preferential binding, preferential hydration is a measure of the perturbation of the chemical potential of the cosolvent by the protein. The two binding parameters, Γ_PL and Γ_PW, are equivalent (m_WΓ_PL = −m_LΓ_PW), just as the two solvent components are equivalent (14), and the quantity Γ_PW contains contributions of both water and cosolvent molecules.¶ From Eqs. 7 and 8, it is evident that, for any given protein, the value and sign of preferential hydration may be different for various cosolvents at identical concentration [e.g., positive for trehalose (24) and negative for urea (25)]. Similarly, for any water–cosolvent system, the values of Γ_PL and Γ_PW will be defined by the protein added [e.g., urea is preferentially bound to native β-lactoglobulin (25) and excluded from myoglobin (26)]. However, at identical osmolality of cosolvents, the lowering of water activity is identical for all water–cosolvent–protein systems. Furthermore, protein hydration, being a manifestation of protein–water interaction only, whether in the binary protein–water system or in a ternary system with a cosolvent, varies little with solvent systems: W_H is defined solely by ΔG°_W. Preferential binding (and preferential hydration), being a function of ΔG°_ex in Eq. 3, is defined by the magnitude of ΔG°_L for each particular cosolvent, which, at any locus, may be positive, negative, or zero. Therefore, the two quantities refer to independent chemical processes that are defined by independent thermodynamic parameters. In fact, preferential hydration, Γ_PW, may be smaller than, equal to, or greater than protein hydration, W_H; measurements of preferential hydration can give no direct information on the hydration of a protein, nor can changes in preferential hydration be equated with changes in protein hydration.

Site Occupancy

The thermodynamic binding, whether expressed as preferential binding, Γ_PL, or preferential hydration, Γ_PW, is a net measure of preference by the protein for water or cosolvent (12). Because all sites must be in contact with either water or cosolvent molecules, is it possible to deduce their numbers from equilibrium binding measurements? A relation has been derived by various intuitive approaches (7, 17, 27–29):

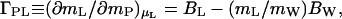9

where B_L and B_W are the effective numbers of molecules of cosolvent and water, respectively, that interact with the protein at a given value of thermodynamic binding, Γ_PL. The parameters B_L and B_W are not thermodynamic quantities (14), nor do they correspond to real physical numbers of whole cosolvent and water molecules (7, 8). They are useful descriptive quantities that sum up all the perturbations by the protein of cosolvent and water molecules, each of which may make only a fractional contribution to B_L or B_W. This is determined by the strength of the interaction with the protein, which may vary from strong immobilization to weak momentary perturbations, to repulsion, that cause these molecules to fluctuate to different degrees with the protein in Brownian motion. B_L and B_W are not independent quantities. They are immutably linked by the exchange of Eq. 2, and their combination is defined by the real measurable thermodynamic quantity, Γ_PL, so that, by Eq. 9, assignment of a value to one fixes that of the other. A given value of Γ_PL does not correspond to a unique pair of B_L and B_W, because the difference on the right-hand side of Eq. 9 can be generated by an infinite number of B_L and B_W pairs (7) with B_W always equal to (B_L − Γ_PL) (m_W/m_L). For any given protein, the values of B_L and B_W sets of pairs are particular for each cosolvent added. Therefore, by definition, B_W is not identical with the water of hydration, and it cannot be equated with W_H or a change in W_H during the course of a reaction. In practice, values of B_W and B_L are frequently assigned on the basis of assumptions, e.g., that water occupancy of the protein surface, W_H, in pure water gives the maximal value of B_W. Yet, measured Γ_PW and, hence, B_W can attain values superior to the expected W_H (8). Nevertheless, such practices are useful in probing the molecular state of the protein environment and its changes during the course of protein unfolding and have permitted mechanistic insight into details of interactions within the local-bulk domain model of Record and coworkers (17, 18, 22, 30).

Modulation of Protein Reactions by Cosolvents

In the case of reactions, the Wyman linkage relation, Eq. 1, gives the change in the preferential thermodynamic, binding, Δ(∂m_L/∂m_P)_μL = ΔΓ_PL, of the cosolvent to the protein that accompanies the reaction at a given cosolvent concentration, m_L. This can be positive, negative, or zero. If ΔΓ_PL is zero, the ligand has no effect on the reaction at that solvent concentration and Δ(∂μ_L/∂m_P)_mL = 0. A negative value of ΔΓ_PL means an increase in preferential hydration, ΔΓ_PW (Eq. 8), which can be measured directly by expressing the Wyman relation in terms of water activity (8):

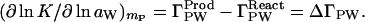10

Comparison of Eqs. 8 and 10 shows that ΔΓ_PW is the expression in terms of water molecules of the change in the perturbation of the chemical potential of cosolvent by the protein during the course of the reaction.

Expansion of Eqs. 1 and 10 in terms of Eq. 9 gives the changes during the course of the reaction of the effective numbers of cosolvent, ΔB_L, and water, ΔB_W, molecules that interact with the protein (7, 8):

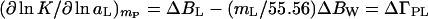11

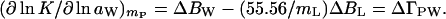12

All the limitations that apply to B_L and B_W also apply to ΔB_L and ΔB_W. Therefore, the gradients of Eqs. 11 and 12 correspond to an indeterminate set of pairs of ΔB_W and ΔB_L, because the addition of each ligand molecules can compensate for the addition of (m_W/m_L) effective water molecules, ΔB_W = (ΔB_L − ΔΓ_PL)(m_W/m_L).

Early applications of the Wyman linkage relation and its extension by Tanford (Eqs. 1 and 11) to the modulation of protein reactions by cosolvents go back a quarter of a century to the analysis of the guanidine hydrochloride denaturation of lysozyme by Aune and Tanford (31), the modulation of tubulin self-assembly into microtubules (32, 33), and the stabilization of proteins by sucrose (34).

Starting a decade ago, a number of papers in which the same approach was used refer to it by the term “osmotic stress” (35–40). The stated aim of these later studies was the determination of the number of stoichiometric water molecules, n, involved in the reaction (35)

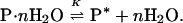13

In these studies, the equilibrium was perturbed by addition of a cosolvent, which was stipulated as being an inert excluded osmolyte (35–38). The equilibrium constant measured as a function of cosolvent concentration was plotted in the form of the Wyman relation (Eq. 10), i.e., ln K (or ΔG°) vs. ln a_W (or π), and the slope, ΔΓ_PW, was identified as the number of stoichiometric water molecules, n, involved in the reaction, i.e., the change in the water of hydration during the course of the reaction, ΔW_H. In “osmotic stress,” it was stated that the only role of the preferentially excluded cosolvent in modulating the reaction was its effect on the activity of water, a_W (35–38).

In a critique of “osmotic stress” (41), certain thermodynamic inconsistencies and misconceptions inherent to this treatment were pointed out. These were: first, that a cosolvent (solute in “osmotic stress” nomenclature) cannot be both inert (or neutral) and excluded, because this implies that the perturbation of the chemical potential of the cosolvent by the protein that generates the preferential exclusion is equal to zero. Second, that the restriction of the driving force in the modulation of the reaction solely to the effect of the excluded cosolvent on water activity is, in general, incorrect, because, at equilibrium, the activities both of water and cosolvent in the domain of the protein must be equal to those in the bulk solvent. In the seminal papers on “osmotic stress,” exclusion was attributed to a hydration shell‖ (36–38) around the protein that is inaccessible to a “neutral” solute. Its boundary was apparently considered equivalent to a semipermeable membrane. Third, the identification of the slope of the Wyman plot (Eq. 10) as the stoichiometric number of water molecules involved in the reaction was incorrect, because this implies that water of hydration is identical to preferential hydration.

More recently, proponents of “osmotic stress” have published a reply (43). It is gratifying that, subsequent to the publication of my critique, they seem to have modified their position somewhat. There appears to be a suggestion that “osmotic stress” may be restricted to water molecules located in compartments physically inaccessible to the larger cosolvent molecules, although the concept of the impenetrable hydration shell has not been repudiated, and there is allusion to a “hydrated molecule being surrounded by its own effective membrane” (43). We will deal briefly with this reply and address certain misconceptions that still remain.

To counter our criticism that a cosolvent cannot be both inert and excluded, Parsegian et al. (43) state that my critique was based on “a particular ad hoc definition of inert that we imposed,” namely that “an inert cosolvent in aqueous medium is one that interacts as strongly (or weakly) as water with the macromolecule,” i.e., that the measured thermodynamic binding (∂m_L/∂m_P)_μL must be zero at all solvent concentrations.** In the reply (43), it is stated, “For us, an inert solute is one that does not act directly on the macromolecule; there is no reaction nor binding that causes a change in the conformation of macromolecules.” We all agree with the criterion that all cosolvents used to modulate biochemical equilibria must not damage the biological macromolecules. The discussion, however, is concerned with weakly interacting cosolvents. The Parsegian et al. definition of inert leads to an asymmetric definition of thermodynamic interaction, which is restricted to preferential binding, (∂m_L/∂m_P)_μL = +, i.e., a negative free energy change. This omits from the definition of interaction those cosolvents that are preferentially excluded, (∂m_L/∂m_P)_μL = −, i.e., a positive free energy change. This position is already found in an earlier publication (35), in which the authors discuss the effect of some osmolytes on the oxygen affinity of hemoglobin (Hb): “One may think of different amounts of cosolvent bound to … Hb or view the action of a cosolvent primarily through its effect on water activity.” There is no mention of preferential exclusion. The relegation of preferentially excluded cosolvents to the class of inert is stated clearly (43): “One wide class of such inert molecules is that of the naturally occurring osmoprotectants such as betaine and glycerol.” The fact is that these preferentially excluded stabilizing osmolytes interact with proteins just as strongly as, say, urea or propyleneglycol, albeit with an opposite sign of free energy change (8, 22). For the stabilizing osmolytes, (∂μ_L/∂m_P)_mL is positive and real (8), just as it is negative and real for denaturants (8, 25). For an inert cosolvent, (∂μ_L/∂m_P)_mL = 0. As shown above, thermodynamic binding is a symmetrical function about the point of indifference, (neutrality, inertness):

The thermodynamic effects of the addition of preferentially excluded and preferentially bound cosolvents on a reaction can be of equal magnitude but will drive the reaction in opposite directions, as has been strikingly demonstrated by Qu et al. (44) for the effects of urea and naturally protecting osmolytes on the Stokes radius of reduced and carboxymethylated ribonuclease A:

It is this asymmetric definition of “interacting” and, as a consequence, of “inert” that appears to have led Parsegian et al. to neglect the free energy of the change in preferential exclusion during the course of a reaction as the driving force in the modulation and to restrict the role of the preferentially excluded molecules solely to the lowering of the water activity, a_W, by the colligative effect. Scrutiny of the “Symbol Translation Table” drawn up by Parsegian et al. (43), as useful as it may be, reveals a substantive flaw: it is the absence of the terms (∂m_L/∂m_P)_μL = Γ_PL and (∂μ_L/∂m_P)_mL, nor are they ever referred to in their articles. Yet these terms are the key to the meaning of the observations and to the understanding of the interactions that drive them. It is their neglect that has led to the conceptual errors discussed here. Parsegian et al. have chosen to work solely in terms of effective site occupancy by cosolvent and water, N_S and N_W in their notation (43) (B_L and B_W of Eq. 9), which become ΔN_S and ΔN_W in the case of a reaction. As explained above, these numbers have no real physical meaning. They are useful parameters in the description of the data in terms of what the changes in cosolvent and water binding might be if these were true stoichiometric quantities. Furthermore, these parameters are indeterminate in value; they are strictly coupled, and the value of each (N_S or N_W) is determined by the value assigned to the other, because their combination (Eq. 9) must conform to the only measurable parameter, (∂m_L/∂m_P)_μL for binding, or Δ(∂m_L/∂m_P)_μL for a reaction (Eqs. 11 and 12). The last quantities are intrinsic properties of the interacting protein–cosolvent pair, being generated by the mutual perturbations of their chemical potentials. It is the change in this perturbation, Δ(∂μ_L/∂m_P)_mL, which drives (modulates) a reaction, whereas the effect of the cosolvent on the activity of water cannot do this (8, 41), except in some highly restricted situations (41) that will be discussed in what follows. The invocation of a hypothetical effective membrane (43) or of a boundary around an impenetrable shell of water (36) is not equivalent to a semipermeable membrane required for the generation of osmotic pressure.

The lack of realization by the proponents of “osmotic stress” of the key role of Δ(∂μ_L/∂m_P)_mL must be the source of their identification of the Wyman slopes (Eq. 10) as changes in stoichiometric water (water of hydration), i.e., their setting ΔΓ_PW = ΔB_W = ΔW_H = n (35, 37). The situation, however, is more complicated. As explained above, Γ_PW expresses a redistribution of both water and cosolvent molecules in the domain§ of the protein molecule due to the perturbation of the cosolvent chemical potential by the protein, and ΔΓ_PW is a change in this redistribution during the course of a reaction. Setting ΔΓ_PW as equal to the stoichiometric water, n = ΔW_H of Eq. 13, implies (i) that only water molecules are involved, i.e., ΔB_L = 0 in Eq. 12; and (ii) that ΔB_W represents an integral number of whole water molecules and not an effective number. Both of these assumptions are fraught with hazard. The second assumption has been handled above in the discussion of the meaning of B_W and B_L. The first assumption has been treated by Courtenay et al. (22) in their thoughtful analysis of what is being measured in “osmotic stress.” It is clear that, unless there is proof that the osmolyte used is fully excluded from the protein surface, the value of ΔΓ_PW (the slope of Eq. 12) will be smaller than ΔB_W, n, or ΔW_H. Furthermore, Courtenay et al. (22) propose the identification of the water of preferential hydration, B_W, with the water of biopolymer hydration only as a working hypothesis even when the numerical values of the two parameters are essentially identical.

The departure of solvent molecules from a protein surface during the course of a reaction is a complicated event. As depicted in Fig. 1, departing molecules encompass waters of hydration (stoichiometric water), additional water molecules of preferential hydration, and cosolvent molecules. All make a contribution to ΔΓ_PW (Eq. 12). The argument that linearity of the plot of Eq. 10 with log a_W (or π) establishes that only water molecules are involved (35, 37, 38, 43), i.e., ΔB_L = 0, is unconvincing. For very weak interactions, the extent of binding increases close to linearly with ligand concentration up to 1 M; e.g., several such sites for which the sum of occupancies is equal to one at m_L = 1 (ΔB_L = 1), can give an almost constant value of (m_W/m_L)ΔB_L at lower concentrations. In this situation, each effective molecule of ΔB_L will reduce the value ΔΓ_PW by 55.56 molecules of water from the total number of effective water molecules involved, ΔB_W, but the plot as a function of log a_W (or π) will remain linear. This introduces a major uncertainty in ΔB_W for measured slopes that have typically values of, say, 200. The same applies to the comment that linearity means that there is very little difference in cosolvent binding to the two end states (43). The minimal difference, one cosolvent molecule, will introduce an error of 55.56/m_L in the number of water molecules interpreted as stoichiometric (n) in the reaction of Eq. 13.

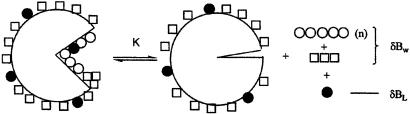
Figure 1.

Meaning of the slope, ΔΓ_PW, of Eq. 10. The departing species consists of the n stoichiometric waters of hydration (○), additional preferential hydration water (□), and cosolvent molecules (●). Note that the pattern of distribution of water and cosolvent molecules over the rest of the protein surface remains unchanged during the course of the reaction.

Let us illustrate this with the example of the glycerol enhancement of assembly of microtubules (32) from tubulin. The slope of the Wyman plot (Eq. 10) for the reaction Mt + TB ⇌ Mt⋅TB, ΔΓ_PW = −13.5 ± 1.5, indicates that the reaction is accompanied by the net departure of 13.5 water molecules per protomer added. Detailed analysis (32) showed that this cannot be equated with stoichiometrically departing water of hydration, ΔW_H. A packing of 9 Ų per water molecule (22) gives a change in surface area per protomer added of 122 Ų. This obviously underestimates the contacts formed in the assembly reaction. Hence, the measured slope must contain contributions also of departing glycerol molecules, each of which would mask (55.56/m_glyc) departing waters. Such considerations apply to the interpretation of all the Wyman plot slopes reported in the various “osmotic stress” studies (e.g., 35, 37–40). This has been discussed by Courtenay et al. (22), who state that when a cosolvent that is not completely excluded from the protein domain “is used as a probe of changes in macromolecular hydration, applying the ‘osmotic stress’ analysis will underestimate the total number of water molecules released in a process, as well as the change in the water accessible protein surface. Any interaction between macromolecular surfaces that involves release of water of hydration will also release any small solute molecules present in the water of hydration, and must be analyzed using preferential interaction coefficients.”

The final question is: Can the driving force in the modulation of a reaction ever be the change in water activity due to the presence of the cosolvent? In all situations in which the protein reacting surface is in contact with solvent, this colligative effect, measured by osmotic pressure, cannot affect the reaction because, at equilibrium, the activities of water and cosolvent in the domain§ of the protein must be equal to their activities in the bulk solvent.

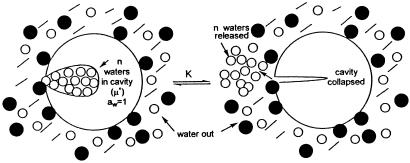
Nevertheless, there is one situation, depicted in Fig. 2, in which the lowering of the activity of water by addition of a cosolvent can modulate a reaction. This, necessarily, involves a change in water of hydration, ΔW_H. As stated previously (41), this situation exists when the reacting cavity is totally impenetrable to cosolvent (osmolyte) molecules. This would be true of a narrow channel, a narrow interstice, or a pocket internal to the protein molecule with an opening that permits only water molecules to cross it, dynamic motions of the protein notwithstanding. These situations are akin to a semipermeable membrane or an osmotic pressure cell.‡‡ The number of water molecules measured in this situation will be the n stoichiometric molecules of Eq. 13 if and only if the pattern of protein–solvent interaction over the rest of the macromolecule remains totally identical in the two end states.†† Because, in this restricted case, the only action of the cosolvent is to reduce the activity of water, it is immaterial whether it is preferentially excluded, preferentially bound, or neutral. To ascertain that one is, indeed, dealing with such a cavity, it seems imperative to perform the measurements in the presence of several osmolytes of the various classes, e.g., sucrose, trimethylamine N-oxide (TMAO), glycerol, urea, DMSO, methyl urea, and propylene glycol. If all give identical values of ΔΓ_PW (Eq. 10), then the probability is high that the driving force is the lowering of the water activity that causes water molecules to flow from the internal pocket to the external medium, because a_W(in) > a_W(out). Such a test has never been performed. If this criterion is satisfied, we have for the reaction of Eq. 13: ΔG° (in cosolvent) = ΔG° (water) − RT n ln (a_W(out)/a_W(in)). In such a case of descending along a water activity gradient, it is possible to speak descriptively of the relief of vapor pressure stress or of osmotic stress. It must be noted, however, that, in equilibrium measurements, this physical situation is fully governed by the binding equations of three-component thermodynamics, and that the n water molecules situated within the cavity of Fig. 2 will be recognized thermodynamically as departing waters of preferential exclusion, ΔΓ_PW. This leads to the conclusion that, as stated previously (41), “osmotic stress” is a restricted case of preferential interactions.

Figure 2.

Release of water molecules from a cavity impenetrable to all cosolvents: a_W(in) > a_W(out). ○, water; ●, cosolvent.