Cerebral energetics and spiking frequency: The neurophysiological basis of fMRI

Abstract

Functional MRI (fMRI) is widely assumed to measure neuronal activity, but no satisfactory mechanism for this linkage has been identified. Here we derived the changes in the energetic component from the blood oxygenation level-dependent (BOLD) fMRI signal and related it to changes in the neuronal spiking frequency in the activated voxels. Extracellular recordings were used to measure changes in cerebral spiking frequency (Δν/ν) of a neuronal ensemble during forepaw stimulation in the α-chloralose anesthetized rat. Under the same conditions localized changes in brain energy metabolism (ΔCMR_O2/CMR_O2) were obtained from BOLD fMRI data in conjunction with measured changes in cerebral blood flow (ΔCBF/CBF), cerebral blood volume (ΔCBV/CBV), and transverse relaxation rates of tissue water (T and T₂) by MRI methods at 7T. On stimulation from two different depths of anesthesia ΔCMR_O2/CMR_O2 ≈ Δν/ν. Previous ¹³C magnetic resonance spectroscopy studies, under similar conditions, had shown that ΔCMR_O2/CMR_O2 was proportional to changes in glutamatergic neurotransmitter flux (ΔV_cyc/V_cyc). These combined results show that ΔCMR_O2/CMR_O2 ≈ ΔV_cyc/V_cyc ≈ Δν/ν, thereby relating the energetic basis of brain activity to neuronal spiking frequency and neurotransmitter flux. Because ΔCMR_O2/CMR_O2 had the same high spatial and temporal resolutions of the fMRI signal, these results show how BOLD imaging, when converted to ΔCMR_O2/CMR_O2, responds to localized changes in neuronal spike frequency.

Relations between cerebral energy consumption and neuronal activity have been intensely studied since such a coupling was suggested by Roy and Sherrington (1). Sokoloff and coworkers (2) showed that in peripheral neurons increases in energy consumption associated with electrical activity are localized to the neuropil and are approximately proportional to spiking frequency. This proportionality suggested that quantitation of regional brain energy metabolism may provide a direct measure of cortical activity. Nearly all cerebral energy consumption is derived from glucose oxidation (3). ¹³C magnetic resonance spectroscopy (MRS) studies have measured the oxidative rate of [1-¹³C]glucose use by the flow of the ¹³C label into neuronal glutamate pools (4). The subsequent flow of the ¹³C label into astrocytic glutamine pools showed that the rates of neuronal oxidative metabolism (CMR_O2) and glutamate neurotransmitter release/cycling (V_cyc) are stoichiometrically related (5). The model of glutamate neurotransmitter cycling (6) supported by the ¹³C MRS data provides the hypothesis that V_cyc, and consequently CMR_O2, should be proportional to spiking frequency of glutamatergic neurons.

In this paper we have measured the relationship between energy metabolism and the neuronal spiking frequency in the α-chloralose anesthetized rat during forepaw stimulation (7, 8). First, ΔCMR_O2/CMR_O2 values were derived from multimodal MRI measurements based on the blood oxygenation level-dependent (BOLD) image-contrast as described (9–12). Second, relative spiking frequency (ν) of a neuronal ensemble in the same region was determined from extracellular recordings (13–15). The measured value of Δν/ν was approximately equal to ΔCMR_O2/CMR_O2 over a wide range of neuronal activity. Because ΔCMR_O2/CMR_O2 was derived from calibrated BOLD (10, 12), the results establish a neuronal basis of functional MRI (fMRI).

Materials and Methods

Animal Preparation.

Artificially ventilated (70%N₂O/30%O₂) Sprague–Dawley rats (adult, male, 150–210 g) were anesthetized (α-chloralose i.p.; see below) and paralyzed (d-tubocurarine chloride i.p., 0.5 mg/kg/h). A femoral artery was cannulated for continuous mean arterial blood pressure monitoring and periodic sampling for measurement of blood gases (pO₂ and pCO₂) and pH. These parameters were maintained within physiological limits throughout the experiment. A femoral vein was cannulated for i.v. infusion of iron oxide contrast agent (AMI-227, Advanced Magnetics, Cambridge, MA) for blood volume measurements. The anesthesia was initially maintained at a low dose (36 ± 2 mg/kg/h; condition I) followed by a higher dose (46 ± 4 mg/kg/h; condition II). No data were collected during a 1-hour stabilization period between conditions I and II. The sensory stimulation was provided by electrical stimulation of the forepaw (2 mA, 0.3 ms, 3 Hz; block design of 2–5 min OFF, ON, OFF; ≈10 min resting period between stimulations) with two copper electrodes (7, 8). The baseline and stimulated activities (reflected by changes in ν and CMR_O2) were recorded at each level of anesthesia.

CMR_O2 Measurements.

All in vivo fMRI data were collected on a 7T Bruker (Billerica, MA) horizontal-bore spectrometer with a homogeneous transmit and local receive ¹H radio-frequency coil (10, 16). Changes in CMR_O2 were calculated from the BOLD signal (9, 10, 12)

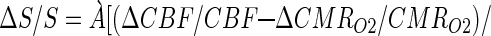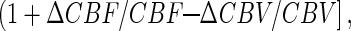which required multimodal MRI measurements of changes in cerebral blood flow (ΔCBF/CBF), cerebral blood volume (ΔCBV/CBV), and BOLD signal (ΔS/S) as described (10, 12). ΔCBF/CBF (spin labeling) and ΔS/S (gradient and spin echo) were measured in an interleaved manner (17) in both conditions I and II. ΔCBV/CBV in condition II was measured by introducing an MRI contrast agent (18), whereas in condition I ΔCBV/CBV was established from its relation with ΔCBF/CBF (10, 12, 19). The value of Á (0.4 ± 0.1) was determined from a prior calibration obtained by comparison of measured (by ¹³C MRS) and predicted (from Eq. 1) values of ΔCMR_O2/CMR_O2 over a wide range of activity (10, 12). A localized region of 2 × 2 voxels in the somatosensory forepaw region of the rat cortex (20) was interrogated for ΔCMR_O2/CMR_O2. Basic acquisition parameters were (gradient and spin echo data): excitation flip-angle, 90°; inversion flip-angle, 180°; recycle time, 5,000 ms per slice; echo-time, 20 and 40 ms; inversion recovery time, 200 and 700 ms; image matrix (x, y), 32 × 32; slice thickness, 1,000 μm; slice inversion thickness, 5,000 μm; in-plane resolution (x, y), 430 × 430 μm.

Extraceullar Recordings.

The rat was placed in a stereotaxic holder (Kopf Instruments, Tujunga, CA) on a vibration-free table inside a Faraday cage. Tiny burr holes above the contralateral and ipsilateral somatosensory regions [4.4 mm lateral and 1.0 mm anterior to bregma (20)] were thinned and tungsten-iridium microelectrodes (FHC, Bowdoinham, ME) were inserted at a depth of 1 mm from the pial surface (layer 4) with stereotaxic manipulators (Kopf). All electrophysiological studies were guided by prior fMRI coordinates. Each microelectrode (tip <1 μm) had an impedance of 2–4 MΩ (measured with a 1-kHz, 100 nA sine wave current). Before digitization, the raw extracellular signals were filtered (low and high cut-offs at 100 and 20 kHz, respectively) and amplified (×1,000) with an A-M Systems amplifier (Carlsborg, WA). The signal was then digitized (>20 kHz) with a μ-1401 interface using SPIKE-2 software (Cambridge Electronic Design, Cambridge, U.K.). Spiking activity of the neuronal ensemble was extracted from the extracellular recordings by shape recognition of high signal-to-noise ratio spikes with the SPIKE-2 software, which utilizes a procedure similar to that described by Zouridakis and Tam (15). For data obtained in the baseline period of condition I, off-line spike analysis was used to assign particular neurons (maximum of two neurons per electrode), which were then followed to create a temporal history for each experimental run. The individual neurons in the template created in condition I were used to assign data in condition II. This approach assured that the spiking data extracted from the extracellular recordings were from the same ensemble of neurons in both conditions (per rat). The extracted data were then converted to reflect the relative spiking frequency (ν) of the neuronal ensemble by analyzing consecutive 10-s bins. Because ν was measured in both conditions for each rat, the changes in spiking frequency (Δν/ν) reflected the behavior of the neuronal ensemble on stimulation from both baseline levels.

Results

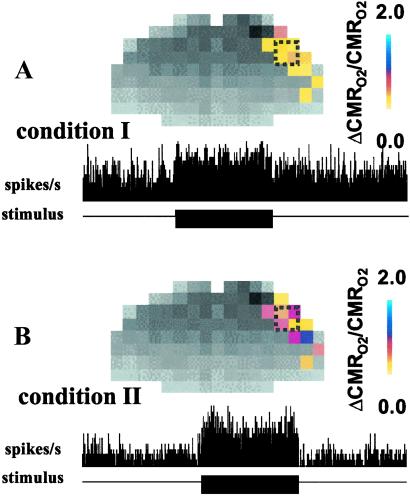
Fig. 1 shows the localized changes in energy metabolism and spiking activity in contralateral rat cortex during forepaw stimulation as measured by calibrated-BOLD and extracellular recordings, respectively. In each case, the fMRI and electrophysiology measurements (i.e., resting and stimulated signals) were made under high basal activity (Fig. 1A, condition I) then under low basal activity (Fig. 1B, condition II), using two different anesthetic doses in each rat. The ΔCMR_O2/CMR_O2 maps were determined by calibrating BOLD signal changes (ΔS/S) from multimodal MRI maps of changes in blood flow (ΔCBF/CBF) and blood volume (ΔCBV/CBV). The values of each parameter for conditions I and II are shown in Table 1. Approximately 92% of all microelectrode penetrations (in layer 4) yielded at least two discrete waveforms (i.e., neurons) from the spike analysis (see Table 2) with a minimum signal-to-noise ratio of 5, which is sufficient to differentiate spike shapes in vivo (13–15). The mean values of ν obtained from all measurements for conditions I and II are shown in Table 2. No significant stimulation-induced changes in ν and CMR_O2 were observed in the ipsilateral side (data not shown).

Fig 1.

Calibrated BOLD maps (Upper) of ΔCMR_O2/CMR_O2 (Table 1) and changes in spiking activity (Lower) extracted from extracellular recordings in cortical layer 4 (Table 2) during contralateral forepaw stimulation. The resting and stimulated signals were made under high basal activity (A, condition I) followed by low basal activity (B, condition II) in the same rats. For the fMRI measurements, the colored bar shows the scale for ΔCMR_O2/CMR_O2 from the respective baselines. For the electrophysiology measurements, the black bar shows the stimulation period where the horizontal axis represents 900 s of data acquisition and the vertical axis (same range in A and B) represents number of spikes per second (1-s bins). The magnitudes of changes in CMR_O2 and spiking activity were greater from baseline of condition II.

Table 1.

Summary of multimodal MRI data for calculation of ΔCMR_O2/CMR_O2 maps

	ΔCBF/CBF	ΔCBV/CBV	ΔS/S	ΔCMRO2/CMRO2
Stimulation increment (I)	0.55  ± 0.15	0.04  ± 0.02	0.02  ± 0.01	0.40  ± 0.13
Baseline decrement (I to II)	−0.39  ± 0.13	−0.05  ± 0.02	−0.03  ± 0.01	−0.32  ± 0.08
Stimulation increment (II)	1.56  ± 0.34	0.09  ± 0.03	0.05  ± 0.02	1.02  ± 0.22

Data (mean ± SD) averaged across all rats from 2 × 2 voxels in contralateral forepaw region of rat cortex (20), as shown in Fig. 1. Student's t test with two samples assuming unequal variances (one-tail) was used for comparing mean values (n = 6).

^*Significantly different values in condition I vs. condition II (consecutively) for all increments: P < 0.02, P < 0.03, P < 0.06, P < 0.02).

^† Significantly different basal CBF (P < 0.05; estimated from 0.9 ± 0.2 ml/g/min in baseline of condition I vs. 0.6 ± 0.2 ml/g/min in baseline of condition II) were measured by spin labeling MRI (16, 17). On forepaw stimulation from baseline of conditions I and II the final CBF values were 1.4 ± 0.2 and 1.5 ± 0.3 ml/g/min, respectively, which were insignificantly different (P < 0.32).

^‡ ΔCBV/CBV was calculated from (1ΔCBF/CBF)^ϕ − 1, as described in the literature (10, 12, 19), where the value of ϕ has been determined to be ≈0.1 in the same rat brain model (12).

^§ ΔCBV/CBV was measured using the MRI contrast agent (AMI-227; see Materials and Methods) as described (10, 12, 18).

^¶ ΔS/S measured from spin echo (echo time, 40 ms) contrast (12, 17) with sequentially sampled echo-planar data (21).

^∥ ΔCMR_O2/CMR_O2 was calculated from rearrangement of Eq. 1, where the value of Á has been determined to be ≈0.4 in the same rat brain model (12).

Table 2.

Summary of electrophysiology data reflecting the ν of a neuronal ensemble

	Baseline ν, Hz	Stimulation ν, Hz	Δν/ν
Condition I	9.5  ± 2.4†	12.3  ± 4.0†	0.29  ± 0.13
Condition II	6.7  ± 1.8‡	13.7  ± 3.2‡	1.04  ± 0.32

Data (mean ± SD) averaged across all rats (Fig. 3) from all extracellular recordings in the contralateral side, where ≈60% of the spiking data showd an increase in ν, ≈10% of the spiking data showed a decrease in ν, and ≈30% of the spiking data showed no change in ν (Fig. 2). Student's t test with two samples assuming unequal variances (one-tail) was used for comparing mean values of ν in baseline and stimulation periods in both conditions (n = 36). Spike analysis of extracellular data from 33 electrode penetrations generated two recognizable neurons each (i.e., 33 × 2 = 66). Since data from three penetrations generated either one (two data sets) or three (on data set) recognizable neurons, the spiking frequency from each data set was normalized to reflect two neurons (i.e., 3 × 2 = 6). Therefore, the ensemble represented a total of 72 recognizable neurons (i.e., 36 × 2). The correlation coefficients (22) of the stimulation-induced changes in ν for different experimental runs from all rats were high (0.7–0.9; data not shown) for both conditions. Spiking activity in the ipsilateral side did not show any significant changes during stimulation (data not shown).

^*The baseline values for ν in conditions I and II were significantly different (P < 0.01), where baseline in condition II was lowered by 0.29 ± 0.11 from baseline in condition I. The stimulation values for ν in conditions I and II were not significantly different (P > 0.25). The incremental changes in ν from respective baselines (Δν/ν) were also significantly different (P < 0.05).

^† Significantly different baseline and stimulation values for ν in condition I (P < 0.05).

^‡Condition II (P < 0.01).

In condition II, statistically significant increases and decreases in ν were observed on stimulation in ≈60% and ≈10% of the recordings, respectively, whereas there were no statistically significant changes in ≈30% of the recordings (Fig. 2A). Similar behaviors of neuronal populations in cortical columns have been reported (23, 24). The histograms of ν for condition I (Fig. 2B) and condition II (Fig. 2C) for the baseline and stimulation periods reveal that during stimulation the distributions of ν became similar.

Fig 2.

(A) Experimental variations across electrophysiological measurements (shown for condition II only) from the contralateral forepaw region. Significant increases and decreases in ν were observed in ≈60% and ≈10% of the recordings, respectively (Top and Middle), whereas in ≈30% of the recordings the stimulation did not induce any significant changes in ν (Bottom). The vertical and horizontal bars represent the scales for ν and time, respectively (see text and Table 2 for details). The thick black horizontal bar represents the stimulus duration. (B and C) The comparison in a small neuronal ensemble (72 neurons; see Table 2) between basal activity achieved with two dosages of α-chloralose shows significantly different spiking frequencies at rest (P < 0.01), whereas on stimulation the spiking frequencies became similar (P > 0.25).

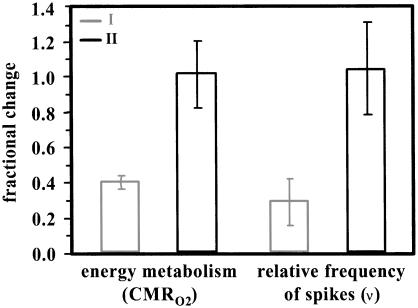
Fig. 3 shows that the fractional changes in CMR_O2 were 0.40 ± 0.13 and 1.02 ± 0.22 from the respective baseline values in conditions I and II (Table 1). Similarly, the changes in ν were 0.29 ± 0.13 and 1.04 ± 0.32 from their baseline values in conditions I and II (Table 2). Comparison of mean values of ν (Table 2) from baseline to stimulation periods reveal that whereas the baseline distributions were different (P > 0.01), the distributions reached during stimulation in both conditions were similar (P < 0.25).

Fig 3.

Relative changes in CMR_O2 (from black dotted regions in Fig. 1) and ν (guided by fMRI) during stimulation obtained from baseline conditions I and II are shown in gray and black, respectively. The baseline condition II was lowered by ≈30% from baseline condition I because of higher dosage of α-chloralose; however, the incremental change on stimulation from condition II was larger (see Tables 1 and 2). In each modality, on stimulation approximately the same levels of activation are reached from both starting baseline levels. The larger incremental change from condition II reflects the lowered starting baseline value, but the same stimulated final value.

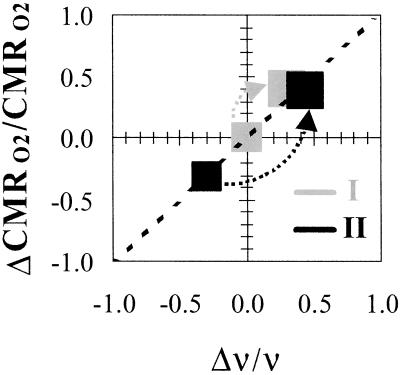
The changes in CMR_O2 and ν on forepaw stimulation were greater for condition II, which, when added to its lowered baseline values, brought each parameter to approximately the same absolute value during stimulation (Fig. 4). The baseline values for condition II compared with condition I were lower by 0.32 ± 0.08 and 0.29 ± 0.11, respectively, for CMR_O2 and ν (Tables 1 and 2). This agreed with previous [¹⁴C]2-deoxyglucose autoradiography observations of α-chloralose dose-dependency (25). However, the changes in condition I on stimulation were smaller than in condition II so that the stimulated values of both parameters in both conditions were approximately equal. The current results show that ΔCMR_O2/CMR_O2 ≈ Δν/ν (Fig. 4). Furthermore, the increments of CMR_O2 and ν on forepaw stimulation elevated each signal to the same final values in both conditions (26).

Fig 4.

Relationship between ΔCMR_O2/CMR_O2 and Δν/ν in α-chloralose-anesthetized rats. The sizes of boxes represent the mean ± the largest standard deviation from all rats studied. The data from conditions I and II are shown in gray and black, respectively, where the arrows show the increment on stimulation from the respective baseline levels. The final level reached on stimulation from both baseline conditions are similar within experimental errors. The dotted line represents the best linear regression (R² = 0.98) of the pooled data. The overall changes in CMR_O2 and ν from all rats studied are plotted to show a relationship of ≈1:1 between ΔCMR_O2/CMR_O2 and Δν/ν.

Discussion

In the present study, both CMR_O2 and ν were measured (Fig. 1) under high (condition I) and low (condition II) basal activity levels to determine the fractional increases of each parameter on stimulation (Figs. 2 and 3). ΔCMR_O2/CMR_O2 approximately equaled Δν/ν for stimulation from both high and low basal activity levels (Fig. 4). Present results agree with and extend previous ¹³C MRS studies of rat brain (4, 5), in which ΔCMR_O2/CMR_O2 ≈ ΔV_cyc/V_cyc under moderate anesthetized levels (as in present study). The combined results show that ΔCMR_O2/CMR_O2 ≈ ΔV_cyc/V_cyc ≈ Δν/ν, relating both electrical and transmitter responses to energetics of glutamatergic neurons.

Relationship Between Cortical Energy Metabolism and Spiking Frequency.

The present study correlated the changes of ν in layer 4 with similarly localized CMR_O2 changes. Layer 4 was chosen because previous studies using [¹⁴C]2-deoxyglucose autoradiography (7, 23) demonstrated that the largest increment in glucose metabolism with sensory stimulation is in this layer. In the adult mammalian brain, glutamate is the primary excitatory neurotransmitter (27) and the majority of synapses in layer 4 are glutamatergic (28). Because a majority of the synapses in the cerebral cortex are local (29), most glutamate-initiated electrical activity across nerve terminals (excitatory or inhibitory) originate in nearby cells (30).

The present results extend reports by Sokoloff and coworkers (2) that glucose utilization in peripheral neurons increases proportionately with stimulation frequency. The rate of action potentials (generated by either afferent or efferent stimuli) resulted in the same magnitude of metabolic demand on specific nuclei of the nervous system. Until now, no quantitative studies between electrical activity of neurons and energy metabolism have been performed in the intact mammalian brain. The approximately equal relationship found between ΔCMR_O2/CMR_O2 and Δν/ν (Fig. 4) might appear paradoxical given the variety of energy consuming processes associated with neuronal activity.

The term “neuronal activity” has been applied to a host of energy-requiring processes (30), including action potential generation and propagation, maintenance of resting membrane potentials, neurotransmitter release and uptake, vesicular recycling, and presynaptic Ca²⁺ currents. All of these processes are involved in short- and long-term information encoding. In the glutamatergic synapse of the mammalian brain, an “excited” neuron generates short-lived (1–2 ms) action potentials (i.e., spikes), which propagate (scale of μm) down the axon to initiate Ca²⁺-triggered glutamate neurotransmitter release via exocytosis of vesicles from the presynaptic neuron. The release of glutamate into the extracellular space produces dendritic field potentials that can integrate over time (10–20 ms) and space (scale of mm) to generate new trains of spikes in nearby postsynaptic neurons (30). These processes in glutamatergic neurons, as well as associated ion conductivity in glia and GABAergic neurons (4, 5), all require energy because active Na⁺–K⁺ pumps use ATP to restore Na⁺ and K⁺ concentrations across the cell membrane. The astrocytic uptake of glutamate and its recycling to the neuron is another critical energy-consuming step in neurotransmission (6).

The apparent paradox of a range of energy-consuming processes being proportional to a single electrical activity may be resolved if these processes are all coupled to the averaged rate of the electrical activity (30), which in this case is the firing of an ensemble of pyramidal neurons. This coupling has been proposed by Attwell and Laughlin (31), who calculated the distribution of energy amongst these different processes. Their results suggested that almost all of the energy associated with cortical signaling is coupled to the ensemble firing frequency of pyramidal cells. Furthermore, they calculated that at a resting spiking frequency of 4 Hz per neuron, more than 80% of the total ATP is used for functional processes coupled to glutamate release. The highly efficient use of energy at rest is in good agreement with previous ¹³C MRS measurements (4, 5). These energy budget estimations by Attwell and Laughlin (31), relying on morphologic and functional data of rat brain, stand in contrast to previous estimates by Creutzfeldt (32), which were based on data obtained from the giant squid axon inappropriately extended to the mammalian brain.

Assessment of Ensemble Average Firing Frequency.

The courser spatial scale of fMRI (≈0.2 μl) relative to the electrical recordings necessitated comparison of ΔCMR_O2/CMR_O2 (derived from BOLD fMRI) with the average ensemble firing frequency of the activated region. Extracellular recordings respond to the activity of a small group of neurons in the vicinity of the electrode (30). Action potentials are easily identifiable signals in vivo because they are short-lived and have relatively high signal-to-noise ratio, and their different spike shapes can be assigned to individual neurons (13–15, 30). Thus spike sorting from extracellular data have regional specificity (≈0.05 μl per electrode) to spiking neurons near the microelectrode tip.

The spiking frequency did not always increase with stimulation. Fig. 2 shows that ≈60% of the population showed an increase in ν, ≈10% of the population showed a decrease in ν, and ≈30% of the population showed no change (Table 2; Results). This result is similar to electrophysiological measurements under a variety of conditions (23, 24). It suggests that collaboration among a large number of neurons (some of which are firing faster and others slower but all requiring energy) is crucial for encoding information. A larger number of multichannel electrodes (33) could provide a more quantitative correlation.

fMRI and Electrophysiological Measurements.

The current study and prior studies (34–38) have shown in different ways that the stimulation-induced neuronal activity (as measured by electroencephalogram, local field potentials, or spiking activity) is spatially colocalized with the BOLD response. However, the existence of a quantitative relationship has been controversial, with findings in primates supporting a relationship between BOLD signal and average spike frequency (37) or with local field potentials (38).

Logothetis and coworkers (38) compared these parameters simultaneously in the anesthetized monkey brain at 4.7 T. Because the insertion of microelectrodes in rat brain during high-resolution fMRI studies at 7 T modifies the BOLD response over a significant fraction of a typical voxel size (F.H., unpublished results; see also figure 1 a and b in ref. 38), we conducted sequential fMRI and electrophysiological measurements. Logothetis et al. (38) concluded that changes in the BOLD signal represent the neuronal input because they observed a high correlation between similar time courses of BOLD signal (several seconds delayed) and local field potentials. The time course of local field potentials is believed to reflect mainly the neuronal input because they represent the weighted sum of the changing membrane potentials in the dendritic branches and the soma as a consequence of spiking from neighboring neurons. Because the input and output signals are not entirely distinct in a neuronal ensemble (29, 30), it seems premature to link the fMRI signal to either the input or output of the system simply because of a better correlation with the BOLD time course over several seconds. In contrast, the rate of action potentials generated from an ensemble directly reflects the degree of electrical activity quantitatively (30).

Rees et al. (37) attempted to relate the stimulation-induced BOLD signal in humans with the spiking frequency in non-human primates. They suggested that an ≈1% change in the BOLD signal at 1.5 T in humans corresponds to an ≈9 Hz change in the spiking frequency per neuron in region V5 of the non-human primate visual cortex, but reported [as have other groups (39)] large differences in this proportionality constant in other brain regions. These variations may largely reflect regional variations in the biophysical determinants of BOLD contrast (9, 40, 41), rather than fundamental differences in the coupling between energy metabolism and electrical activity.

The relationship found in the present study between changes in CMR_O2 and ν has the advantage over previous studies of not depending on the complex biophysical and technical fMRI parameters (e.g., field strength or pulse sequence) and statistical determinants of BOLD contrast. These factors are effectively normalized by the BOLD calibration and validation procedure (10–12), and by using the same stimulation for both baseline conditions (in the same rats). In our study, the BOLD signal changes (ΔS/S), when calibrated to yield values of ΔCMR_O2/CMR_O2, provides a quantitative relationship between energy consumption and the frequency of neuronal spiking activity (Fig. 4). This provides a biophysical relation between the neuroimaging signal and a basic measurement of neuronal activity, which agrees with the relationship between ΔCMR_O2/CMR_O2 and ΔV_cyc/V_cyc obtained from ¹³C MRS studies (4, 5). These results extend the relationship between these parameters so as to support the earlier conclusion (42) that in the absence of stimulation a large majority of cerebral energy consumption is devoted to supporting resting brain activity.

In summary, the present findings suggest that functional neuroenergetics in the somatosensory cortex support proportionately the ensemble firing frequency of pyramidal neurons in layer 4. Cellular models and in vivo ¹³C MRS studies show this coupling to be largely through the metabolic sequelae of neurotransmitter glutamate release (6, 31). The results imply that signal transmission in the mammalian cerebral cortex is an expensive process that has energetic demands tightly coupled to the information encoding by the neuronal ensemble. A consequence of these findings is that the signal from BOLD fMRI studies, when calibrated to obtain values of CMR_O2 (10, 12), can be used to map pyramidal cell electrical activity in the somatosensory cortex. However, future animal studies dealing with other neurotransmitter systems in the cerebral cortex, as well as specific nuclei, will be necessary to extend these results to other brain regions and to humans.

Abbreviations

• fMRI, functional MRI

• BOLD, blood oxygenation level-dependent

• MRS, magnetic resonance spectroscopy

• CBF, cerebral blood flow

• CBV, cerebral blood volume

• CMR_O2, cerebral metabolic rate of oxygen consumption

• ν, relative spiking frequency