A unified model of NMDA receptor-dependent bidirectional synaptic plasticity

Abstract

Synapses in the brain are bidirectionally modifiable, but the routes of induction are diverse. In various experimental paradigms, N-methyl-d-aspartate receptor-dependent long-term depression and long-term potentiation have been induced selectively by varying the membrane potential of the postsynaptic neurons during presynaptic stimulation of a constant frequency, the rate of presynaptic stimulation, and the timing of pre- and postsynaptic action potentials. In this paper, we present a mathematical embodiment of bidirectional synaptic plasticity that is able to explain diverse induction protocols with a fixed set of parameters. The key assumptions and consequences of the model can be tested experimentally; further, the model provides the foundation for a unified theory of N-methyl-d-aspartate receptor-dependent synaptic plasticity.

Synapses throughout the brain are bidirectionally modifiable. This property, postulated in almost every theoretical description of synaptic plasticity, has been most clearly demonstrated at the Schaffer collateral-CA1 synapse in the hippocampus. Here, it was shown that a low-frequency tetanus induces long-term depression (LTD), whereas high-frequency stimulation produces long-term potentiation (LTP) of the stimulated synapses, and that LTD and LTP are inversely related (1–4). Similar results have been obtained at excitatory synapses throughout the brain.

A considerable body of evidence indicates that the important variable is actually the amount of integrated postsynaptic N-methyl-d-aspartate (NMDA) receptor (NMDAR) activation during conditioning (1, 2, 4–6). Modest NMDAR activation induces LTD, whereas strong activation produces LTP. Because of their voltage dependence, the contribution of NMDARs to synaptic transmission during conditioning stimulation varies with the level of postsynaptic depolarization. Thus, it is possible to induce LTD or LTP with a constant stimulation frequency by clamping the postsynaptic membrane potential at different values (approximately −50 mV for LTD and −20 mV for LTP).

Recently, it has been demonstrated that synaptic modification also can depend on the precise timing of pre- and postsynaptic action potentials (7–11). If a presynaptic action potential occurs in a window of several tens of milliseconds before a back-propagating postsynaptic action potential, LTP is induced. In contrast, if a presynaptic action potential occurs after the postsynaptic spike, LTD is induced.

Ideally, one would like to develop a unified description of bidirectional synaptic plasticity that can account for all routes of induction. One approach is to look beyond the various induction protocols to the critical role of calcium influx through NMDARs. One attractive idea is that modest increases in postsynaptic calcium trigger LTD, whereas large increases trigger LTP (12–14). This hypothesis is consistent with the classical rate-based induction protocols if it is assumed that high-frequency stimulation triggers a larger rise in postsynaptic calcium than does low-frequency stimulation. Indeed, recent experiments have shown that a moderate elevation of calcium correlates with induction of LTD, whereas a larger elevation of intracellular calcium correlates with LTP (15, 16). Further, it has been shown that calcium elevation alone, without presynaptic activity, can cause bidirectional synaptic plasticity (17). Thus, there is significant evidence that postsynaptic calcium is a fundamental factor determining the sign and magnitude of synaptic plasticity.

Spike timing-dependent plasticity (STDP) is also NMDAR-dependent (7, 8), suggesting utilization of the same Ca²⁺-dependent mechanisms. However, on the surface, it seems that mechanisms in addition to NMDAR-mediated Ca²⁺ flux must be invoked to account for STDP. The brief voltage change caused by a postsynaptic spike during an excitatory postsynaptic potential (EPSP) should produce only a modest increase in Ca²⁺ flux through NMDARs over what would occur with the EPSP alone. This situation is very different from pairing protocols used to induce LTP, where the postsynaptic voltage is clamped at depolarized potentials for the duration of the EPSPs. Even more perplexing is the situation where LTD is induced with STDP: the postsynaptic spike comes and goes before the onset of the EPSP. How can the postsynaptic spike leave a trace that significantly alters the Ca²⁺ flux through NMDARs during the subsequent EPSP?

The goal of the current study is to develop the consequences of a single underlying Ca²⁺-dependent mechanism that leads to the observed bidirectional plasticity under diverse induction protocols. The mathematical embodiment of these ideas results in a theoretical structure that can provide the foundation for a unified theory of NMDAR-dependent synaptic plasticity.

Methods

Our aim here is to construct a model based on a minimal number of assumptions. We assume (i) that calcium is the primary signal for synaptic plasticity, (ii) that the dominant source of calcium influx to the postsynaptic cell is through NMDARs, and (iii) that dendritic back-propagating action potentials (BPAPs) contributing to STDP have a slow “after-depolarizing” tail component. Of course, there might be other signals that trigger synaptic plasticity, and there are other sources of calcium in the postsynaptic cell. However, our study shows that our minimal assumptions are sufficient to qualitatively (quantitatively when parameter values are specified) account for the different induction protocols; further, they imply previously uncharacterized consequences that can be tested experimentally. Later, we discuss a fourth assumption that metaplasticity, possibly implemented by activity-dependent regulation of NMDAR properties, contributes to the stabilization of plasticity.

Assumption 1: The Calcium Control Hypothesis.

The hypothesis that different calcium levels trigger different forms of synaptic plasticity (12, 13, 18) can be formulated mathematically as:

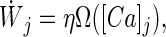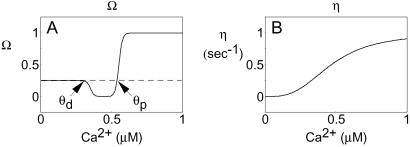
where W_j represents the synaptic strength of synapse j, η is the learning rate, and the calcium level at synapse j is denoted by [Ca]_j. When the calcium level is below a lower threshold θ_d, no modification occurs. If θ_d < [Ca]_j < θ_p, W_j is depressed, and for [Ca]_j > θ_p, the synaptic strength is potentiated (Fig. 1A).

Fig 1.

The calcium control hypothesis. (A) The Ω function: when [Ca]_I < θ_d, the synaptic weight vector stays at the basal level; when θ_d < [Ca]_i < θ_p, the synaptic weight is reduced (LTD); for [Ca]_i > θ_p, the synaptic weight is increased (LTP). (B) The learning rate η as a function of intracellular calcium.

According to Eq. 1, for a sustained elevated level of calcium, the synaptic weight would either increase or decrease indefinitely—a problem that might be solved, for example, by adding upper and lower bounds to synaptic weight strength. Alternatively, a weight decay term can be added. This term helps stabilize synaptic growth without imposing a saturation limit, and results in the following equation:

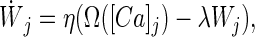where λ represents a decay constant. In contrast to Eq. 1, Eq. 2 has a fixed point for a given calcium level and does not usually converge to the upper or lower saturation bounds.

An unwanted consequence of the decay term, however, is that the synaptic weights rapidly converge back to their initial values when calcium returns to the basal level. In addition, equal learning rates for potentiation and depression can lead to unwanted oscillations in synaptic weight. Both problems can be avoided if the learning rate, η, is assumed to be calcium dependent and to increase monotonically with calcium levels (Fig. 1B). Thus we write:

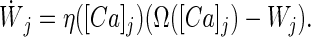The learning rate η is inversely proportional to the learning time constant τ. In Eq. 3, we set λ = 1 without loss of generality.

Eq. 3 contains a dependence on the total level of calcium through the Ω function (Fig. 1A) as well as on the temporal pattern of calcium through a variable learning rate (Fig. 1B). This equation also can be derived from a biophysical model that accounts for phosphorylation and dephosphorylation of the α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid receptors in response to NMDAR activation (19, 44). For such a biochemical process, a natural consequence is that η is calcium dependent. We designate the principles embodied by Eq. 3 the calcium control hypothesis.

Assumption 2: NMDARs Are the Primary Source of Calcium.

It has been shown recently that NMDARs are the major source of calcium influx into postsynaptic dendritic spines when presynaptic activity is paired with postsynaptic depolarization (21). This finding is consistent with the large body of evidence showing that NMDAR activation is crucial for synaptic induction of many forms of calcium-dependent LTP and LTD (22).

To calculate the change in postsynaptic calcium concentration caused by NMDAR activation in our model, we use a standard set of assumptions about NMDAR voltage dependence, ligand-binding kinetics, and calcium dynamics. The calcium current through NMDAR is assumed to have the form:

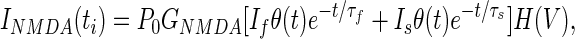where H(V) summarizes the voltage dependence as described by Jahr and Stevens (23), P₀ = 0.5 is the fraction of NMDARs in the closed state that shift to the open state after each presynaptic spike (see Simulation Details and Methods, which is published as supporting information on the PNAS web site, www.pnas.org), and θ(t) is the zero if t < 0 and one if t ≥ 0. The temporal dynamics are assumed to be the sum of a fast (τ_f = 50 ms) and a slow (τ_s = 200 ms) exponential (24). Unless stated otherwise, we assume an equal magnitude for the fast and slow components. Calcium dynamics are described by a first-order linear differential equation of the form:

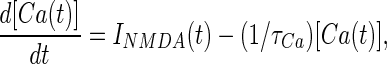with a time constant τ_ca = 50 ms, chosen as an intermediate value between different published results (21, 25).

We assume throughout this paper that the primary source of Ca²⁺ is the NMDAR. Although the NMDAR is a major source of Ca²⁺ influx (21), other calcium sources, such as voltage-dependent Ca²⁺ and release from intercellular stores, would add details to our model.

Assumption 3: Back-Propagating Spikes That Contribute to STDP Have a Slow After-Depolarizing Tail.

STDP produces LTP if a postsynaptic spike occurs within a certain time window after a presynaptic spike (we define this condition as pre-post) and produces LTD if a postsynaptic spike comes before a presynaptic spike (post-pre; refs. 7 and 8). If we accept the calcium control hypothesis (assumption 1), then the post-pre stimulation must produce a modest elevation in calcium (above θ_d), and pre-post stimulation must produce a larger elevation of the calcium level (above θ_p). One way in which information about spiking of the postsynaptic cell can be conveyed back to the synapse is through a BPAP. If we accept assumption 2 above, then the only way the BPAP can influence the sign of synaptic plasticity is by altering the Ca²⁺ flux through the NMDAR, and this must be accomplished by changing the postsynaptic voltage when glutamate is bound to the receptor.

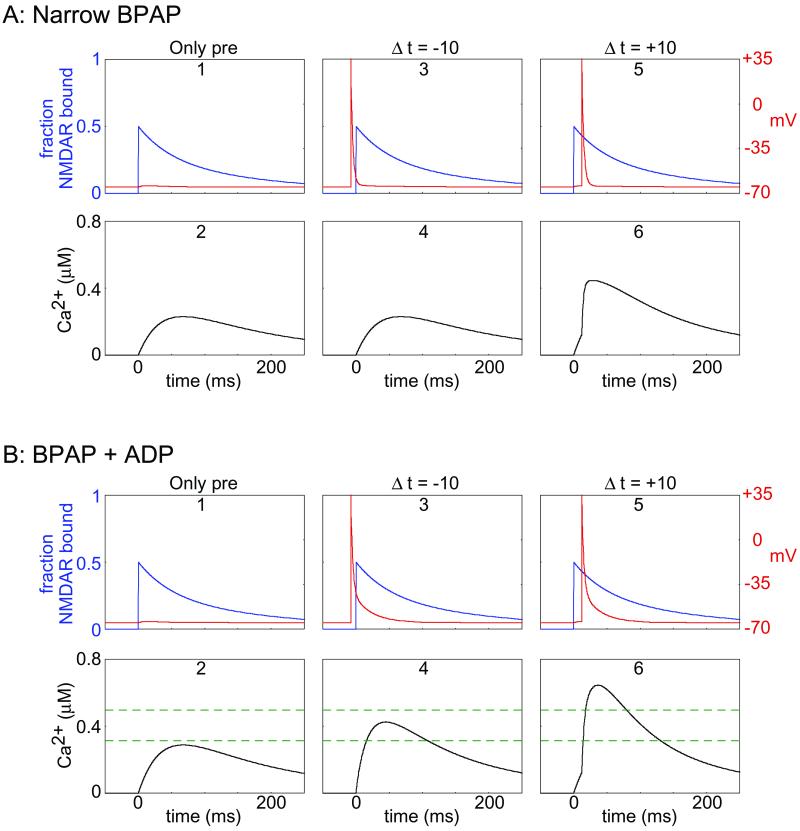
If the BPAP duration is short (say 3 ms; ref. 26), the pre-post procedure would elevate calcium levels over those obtained with presynaptic stimulation alone (Fig. 2A 5 and 6); however, the effect would be small because the short duration of the spike only briefly relieves the Mg²⁺ block of the NMDAR. Worse, the post-pre stimulation procedure (Fig. 2A 3 and 4) would produce calcium levels that are essentially identical to those produced by presynaptic stimulation alone (Fig. 2A 1 and 2).

Fig 2.

Consequences of changing the duration of the BPAP. (A) Narrow BPAP. Presynaptic stimulation alone (A1) results in the binding of glutamate to NMDAR (blue) and a small postsynaptic depolarization (red; not visible at this scale), which produces moderate calcium influx (A2). Post-pre stimulation (Δt = −10 ms) (A3) results in a large but brief postsynaptic depolarization that is nearly over before the opening of the NMDARs, which produces calcium influx (A4) nearly identical to that produced by pre alone (A2). Pre-post stimulation (Δt = −10 ms) (A5) results in a strong but brief depolarization shortly after NMDAR open, which results in slightly larger calcium transients (A6). (B) Consequences of a BPAP with a long repolarization tail. Presynaptic stimulation alone (B1, B2) is identical to the previous case described above with narrow BPAP (A1, A2). Post-pre stimulation (Δt = −10 ms) (B3) results in a strong postsynaptic depolarization that partially overlaps the onset of glutamate binding to NMDAR. Therefore, the calcium influx in this case (B4) is significantly larger than for pre alone (B2). Pre-post stimulation (Δt = −10 ms) (B5) results in a strong depolarization (red) shortly after NMDARs open (blue). This stimulation protocol results in calcium transients (B6) that are larger than the calcium transients in the pre-post condition. Therefore, with the wider back spike, two thresholds (dashed green lines) can be set for LTD and LTP.

These problems can be overcome by assuming that the BPAP has a wide after-depolarizing tail in the dendrites. Therefore, we propose a BPAP composed of two components: a fast spike (with time constant τ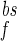 = 3 ms) followed by a slower (and much smaller) after-depolarizing potential (ADP; with a time constant τ 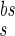= 25 ms). We have chosen the simple functional form:

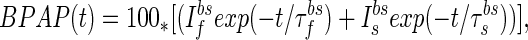where 100 is the maximal depolarization due to the BPAP, an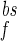d I and I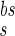 are the relative magnitudes of the fast and slow component of the back spike, respectively, that sum to one. The width and relative magnitude of the ADP component we have assumed is consistent with measurements in dendrites (27, 28). In comparing this assumption with experimental measurement, it should be noted that measurements of half-width at half-height of the full BPAP are nearly independent of the ADP, provided it has a small enough magnitude.

Under this assumption, a post-pre stimulus (Fig. 2B 3 and 4) results in a significantly elevated calcium level when compared with presynaptic stimulation alone (Fig. 2B 1 and 2). Further, the pre-post stimulation results in a much larger calcium increase (Fig. 2B 5 and 6). Notice that because of the form of the calcium transient in the pre-post stimulation sequence (Fig. 2B 6), as much time is spent between θ_d and θ_p as is spent above θ_p. If learning rates were uniform, all synaptic enhancement above θ_p would be canceled by synaptic depression between θ_d and θ_p. This problem is overcome by our proposal that the learning rates increase with increasing calcium levels (Fig. 1B).

A detailed description of the methods and equations used can be found in Simulation Details and Methods.

Results

We now show that the various induction protocols can be simulated with our model by using a single set of parameters. These parameters were chosen to yield STDP consistent with what was reported by Bi and Poo (8); however, quantitatively different results can be obtained with different parameter choices.

Induction of Synaptic Plasticity by Pairing Presynaptic Stimulation with Postsynaptic Voltage Clamp.

The calcium control hypothesis is formulated with the aid of a thought experiment in which the calcium level is controlled directly for a sustained period. This experiment, although conceptually simple, is practically difficult to implement (17). A more common approach is the induction of plasticity by “pairing,” in which the postsynaptic voltage is clamped to a fixed value and low-frequency pulses are delivered to the presynaptic pathway (5, 29–31).

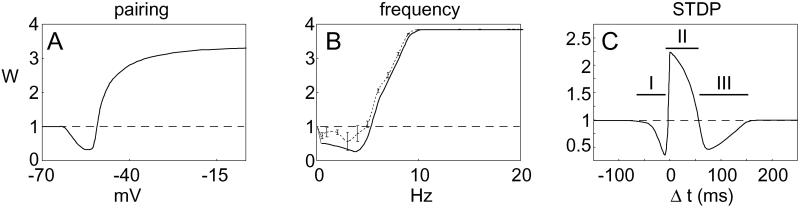
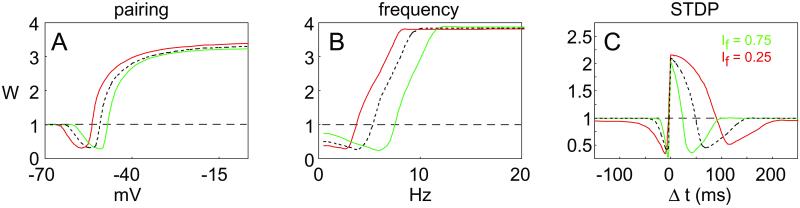
Pairing was simulated with 100 presynaptic pulses at low frequency (1 Hz), whereas the postsynaptic cell was held at a constant voltage. The fixed point of the synaptic weight, W, varied continuously with the level of the postsynaptic potential during pairing (Fig. 3A). No plasticity was induced below −65 mV, LTD was induced between −60 mV and −52.5 mV, and LTP was induced at higher postsynaptic potentials. This result is reminiscent of the Φ function of the Bienenstock, Cooper, Munro (BCM) theory (32), and is a direct consequence of the form of Ω in assumption 1.

Fig 3.

Synaptic modification functions derived from model. The y axis represents normalized (final/initial) synaptic weights at the end of the induction protocol. (A) Pairing-induced plasticity. Below 62.5 mV, no change is induced; between 62.5 and 52.5 mV, LTD is induced; and above 50 mV, LTP is induced. (B) Presynaptic rate-induced synaptic plasticity, with (dashed) and without (solid) postsynaptic spikes. A similar LTP/LTD curve is obtained in both cases. The degree of similarity depends on the parameters. In the presence of postsynaptic spikes, the magnitude of LTD is decreased because postsynaptic spikes occurring at low frequency tend to fall in the LTP window. In addition, the crossover threshold between LTD and LTP is slightly lower in the presence of postsynaptic spikes. Calcium transients in the presence of postsynaptic spikes are more variable than in the absence of spikes because of the stochastic nature of spike generation. As a result, the induction of LTP and LTD is more variable (error bars on solid curve based on five runs). (C) STDP. For post-pre conditions (region I: −30 < Δt < −5 ms), LTD is induced. For pre-post conditions (region II: 0 < Δt < 45 ms), LTP is induced. Surprisingly, for larger pre-post intervals (region III: 45 < Δt < 100 ms), LTD is induced.

Because of the calcium-dependent learning rate, induction of LTP is more rapid than the induction of LTD, and because of the decay term, the rate of plasticity depends on the initial synaptic strength. Both of these results are consistent with experimental observations, and are described further in Figs. 6 and 7, which are published as supporting information on the PNAS web site.

Induction of Synaptic Plasticity by Varying the Rate of Presynaptic Stimulation.

Most synaptic plasticity experiments have been performed by using extracellular field potential recording. Such procedures do not allow as much control of postsynaptic depolarization and action potentials as does the induction paradigm described above. When using extracellular methods, LTP is attained by high-frequency stimulation of presynaptic afferents, and LTD is attained by low-frequency stimulation (1, 3). The frequency and intensity of the stimulus is used to indirectly control the postsynaptic depolarization and magnitude of intracellular calcium.

Applying the calcium control hypothesis to rate-based induction paradigms requires a mathematical description of a cortical cell. Neuronal responses to tetanic stimulation are complex and depend on physiological properties of cells and synapses that can vary substantially. As a first approximation, we implemented a simple statistical model of the postsynaptic neuron for generating postsynaptic spikes (see Simulation Details and Methods); in addition, to simplify the analysis further, we also simulated synaptic plasticity in the absence of postsynaptic action potentials. The latter situation is easier to simulate and requires fewer additional assumptions about neuronal excitability. Such simulations are further justified by the fact that most LTD (and many LTP) experiments are carried out in the low-intensity regime where few postsynaptic spikes are generated. In the absence of spikes, we assume that local temporal and spatial integration of excitatory postsynaptic potentials are the sole source for the postsynaptic depolarization, which we take into account by using a spatial integration parameter (see Simulation Details and Methods).

To induce frequency-dependent synaptic plasticity, we simulate an induction paradigm composed of 900 extracellular stimuli at different frequencies from 0.5–20 Hz. Simulations of rate-induced plasticity with and without postsynaptic spikes result in a complete LTP/LTD curve similar to those observed experimentally (Fig. 3B). We also find that the generation of spikes during low-frequency stimulation reduces the magnitude of LTD and lowers the LTP threshold.

Induction of Synaptic Plasticity by Varying Spike Timing.

To simulate STDP, we evoke pre- and postsynaptic action potentials with different time lags between them. We denote by Δt = t_post − t_pre the time lag between the post- and presynaptic action potentials; negative numbers imply that the postsynaptic action potential preceded the presynaptic action potential. Pairs of presynaptic and postsynaptic stimuli were repeated 100 times at 1 Hz. In Fig. 3C, we display the full STDP plot as a function of Δt. The y axis represents the value of the synaptic weight after 100 pairs of pre- and postsynaptic stimulation. For −30 ms < Δt < −5 ms, we obtain LTD; for 0 < Δt < 45 ms, we obtain LTP. This finding is consistent with experimental results (7, 8).

Pre-Post LTD.

In addition to the expected results displayed in Fig. 3C, however, we also obtain an unexpected LTD region at values of Δt > 50 ms. This LTD occurs because the fraction of NMDARs in the open state decays continuously (although in a stochastic manner) after the initial binding of glutamate, and the concentration of calcium that produces LTD, according to Eq. 3, is at an intermediate value between the concentration that produces no change and the concentration that produces LTP. If a postsynaptic spike arriving at a short time interval (Δt₁) after a presynaptic event causes LTP, and if a postsynaptic spike arriving at a very long interval (Δt₃) after the presynaptic spike elicits no change, then there must be an intermediate time (Δt₂, such that Δt₁ > Δt₂ > Δt₃) which, on average, produces LTD. Although the existence of this LTD region is a robust prediction of our model, we show below (Figs. 4 and 5 and Figs. 8 and 9, which are published as supporting information on the PNAS web site) that the width of this region depends on the model parameters and, primarily, on the NMDAR time constants. In addition, we expect considerable variability in producing LTD at any single delay because of large fluctuations in the relative number of NMDAR in the open state in this time window.

Fig 4.

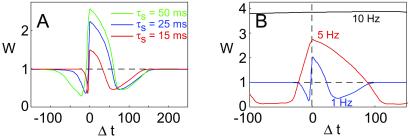
Predicted effect of BPAP duration and stimulation rate on STDP. (A) Changing the time constant of the slow component of the BPAP alters the form of the STDP curve. A narrower BPAP (τ_s = 15 ms, red) results in reduced magnitude of the STDP curve, and a significant reduction in the time window for inducing the post-pre form of LTD. A slower slow component (τ_s = 50 ms, green) results in an STDP curve of larger magnitude and in a wider post-pre LTD window (blue for τ_s = 25, as in Fig. 3). (B) Changing the frequency of the pre-post pairs changes the form of the STDP curve. At 5 Hz (red), the STDP curve has larger magnitude, and the LTP and LTD windows are broader than at 1Hz (blue). At 10 Hz (black), every value of Δt results in LTP.

Fig 5.

Predicted effects of changing NMDAR kinetics. Assuming faster (I_f = 0.75, green) or slower kinetics (I_f = 0.25, red) alters the form of the synaptic plasticity functions in comparison to previous results obtained for an intermediate value (I_f = 0.5, black dots). In both pairing (A) and presynaptic rate (B) induction protocols, faster kinetics (green) result in higher thresholds, and slower kinetics (red) result in lower LTP thresholds. For STDP (C), faster kinetics (green) result in narrower LTD and LTP induction windows, whereas slower kinetics (red) result in wider induction windows.

If experiments show that the pre-post form of LTD does not exist, they would necessitate the alteration of one of our key assumptions. Because it likely that calcium levels vary continuously as a function of Δt, whether their primary source is NMDAR (assumption 2) or another calcium source, a failure to find pre-post LTD would indicate that the calcium control hypothesis must be altered.

Existing data are relatively sparse at pre-post delays greater than 20 ms (7, 8, 10), and we hope our model will encourage greater scrutiny of longer Δt. However, Nishiyama et al. (ref. 33; Fig. 2) reported LTD at pre-post delays greater than those effective for LTP, consistent with the prediction of our model.

Necessary Properties of the BPAP.

To account for STDP under the assumption that NMDARs are the primary source of calcium, we additionally assume that the BPAP has a slow after-depolarizing tail (Fig. 2A). It is not surprising, therefore, that the shape of the STDP curve has a strong dependence on the form of the BPAP. Changing the width of the ADP from 25 ms to 15 and 50 ms, for example, significantly alters the STDP function, particularly the width of the post-pre LTD window (Fig. 4A). A strong prediction of our model is that in the absence of a broad BPAP there will be no post-pre form of LTD. We also predict that regulation of this property, e.g., by those in modulation of dendritic potassium conductances, will have a profound effect on the properties of synaptic plasticity.

Rate Dependence of STDP.

Another fundamental consequence of our model is that the STDP function varies with the frequency of stimulation (Fig. 4B). The form of the STDP curve changes at 5 Hz, and LTP is induced at all values of Δt at 10 Hz. This result is because of temporal integration of calcium transients. It is important to stress that the detailed frequency dependence will depend on the choice of parameters. However, regardless of the specific parameters used, there is a frequency at which potentiation is induced at all Δt. We note that the qualitative form of the frequency dependence of STDP, which is a consequence of our theoretical model, has very recently received some initial experimental support (34).

Unlike hippocampal neurons in culture (8), pre-post LTP in some neocortical slices have been shown to require high rates of stimulation (7), yielding a frequency dependence different from that displayed in Fig. 4B. These findings can be reproduced by varying some of the parameters of the model (see Fig. 10, which is published as supporting information on the PNAS web site). In other neocortical preparations, STDP has been induced with low-frequency stimulation (10, 34) but requires more robust extracellular stimulation. It is important to emphasize that, just as the properties of neurons vary significantly from one preparation to another, it is to be expected that parameter values also vary. Such variation can reproduce different manifestations of STDP.

Stability in previous models of STDP has required the assumption that LTD predominates over LTP (35). Thus, the saturation of STDP at higher frequencies poses a potential problem for our theory. Therefore, an additional mechanism for stabilizing plasticity should be assumed. Possible mechanisms that have experimental support are changes in NMDAR excitatory postsynaptic potential amplitude and duration that occur as a function of the history of cortical activity (24, 36–38). In the next section we describe the effect changing the temporal dynamics of the NMDAR.

Effect of Varying NMDAR-Binding Kinetics.

The magnitude and the kinetics of the calcium influx through NMDARs affect the functional form of synaptic plasticity in all of the induction protocols we have simulated. Both properties are modifiable, changing during development and as a function of the history of cortical activity (24, 36, 37, 39, 40). Therefore, we also examine the consequences of altering NMDAR kinetics. In previous simulations, we assume the magnitude of the fast component of the NMDAR is I_f = 0.5. However, by changing the NMDAR kinetics to I_f = 0.25 and I_f = 0.75, we find that the functional form of synaptic plasticity is altered for all routes of induction.

In Fig. 5A, we show the effect of changing the NMDAR kinetics on pairing induced plasticity. We see that slower NMDAR kinetics shifts the LTP/LTD curve to the left and faster kinetics shifts the curve to the right. Similar results are shown in Fig. 5B for presynaptic rate-based plasticity. These results show how different NMDAR kinetics can affect the form of the plasticity curves. However, there is indication that the NMDAR kinetics are themselves activity-dependent (24, 36, 37). Therefore, our results are consistent with a form of metaplasticity (41) in which the LTP/LTD curve and the modification threshold (the crossover point from LTP to LTP) are shown to depend on the history of cortical activity. These results also show that modification of NMDAR kinetics can serve as a physiological mechanism for the sliding modification threshold proposed in the BCM theory (12, 32, 36, 42, 43).

The effect of NMDAR kinetics on STDP is also significant (Fig. 5C). Slower NMDAR kinetics result not only in larger LTP magnitude and a broader range of spike timings in which LTP is produced but also in an increase in the magnitude and range of both forms of LTD. Faster NMDA kinetics reduces the magnitudes of LTP and LTD and the widths of the LTP and LTD regions. In Fig. 10, we show that changes in the magnitude of NMDAR conductance also alter the properties of synaptic plasticity.

The effect of changing the NMDAR kinetics and the width of the BPAP are, to first order, independent. Therefore, if we assume fast NMDAR kinetics and a wide, slow component of the BPAP, we obtain an STDP curve with narrower LTP and pre-post LTD time windows and a wider post-pre LTD time window (Fig. 9). This STDP curve is more similar to some of the STDP curves that have been obtained in neocortex (10, 34).

Discussion

We have presented a unified model of NMDAR-dependent synaptic plasticity based on three key assumptions: (i) postsynaptic Ca²⁺ controls the rate and sign of synaptic plasticity, according to the calcium control hypothesis; (ii) NMDARs are the relevant sources of Ca²⁺; and (iii) the BPAP has a long-lasting depolarization tail. This model accounts for forms of synaptic plasticity induction as diverse as STDP, pairing-induced plasticity, and rate-dependent plasticity. It also accounts for the frequency dependence of STDP. However, a model based solely on these three assumptions is likely to be unstable—like many other Hebbian models. Therefore, we propose an additional assumption (iv), that metaplasticity, through activity-dependent regulation of NMDAR properties, is required for stability. In this paper, we show that metaplasticity can be achieved by plasticity of NMDAR but do not show that it is required for stability or specify a dynamic equation governing the plasticity of NMDAR. In another paper (44), we propose a specific dynamical equation. Further investigation of the implications of these coupled dynamical equations for receptive field plasticity is needed.

In the past, a common description of synaptic plasticity was based on the rates of pre- and postsynaptic firing (45). Recent results have shown that plasticity can also depend on the precise timing of pre- and postsynaptic spikes. These new findings have led to the suggestions that rate- and pairing-based induction protocols are artificial, whereas spike-time induction protocols are more similar to those occurring naturally, and that naturally occurring forms of plasticity can be accounted for on the basis of STDP. Indeed, some theoretical studies have shown how rate-based plasticity can be derived from STDP (45–47). However, in vitro (5, 29) and in vivo (48, 49) plasticity can occur in the absence of postsynaptic spikes. Moreover, naturally occurring plasticity, even when postsynaptic spikes are present, cannot be accounted for solely by linearly superimposing STDP curves obtained at a single frequency, because this will not account for the frequency dependence of STDP.

Other models that attempt to account theoretically for various forms of induction on the basis of a common mechanism have been put forward (20, 50, 51). Although these attempts are conceptually similar to ours, they differ in the specific mechanisms assumed, as well as in the resulting consequences, and therefore can be distinguished experimentally from our proposal.

Our model of NMDAR-dependent synaptic plasticity is based on a common, low-level, physiological mechanism that can account both for the various induction protocols and naturally occurring plasticity. The structure we have presented here, with its clear connections between assumptions and consequences (expected as well as previously uncharacterized), can and should be tested experimentally. If it passes the experimental test, it can serve as a basis for a unified theory of synaptic plasticity.

Abbreviations

• LTD, long-term depression

• LTP, long-term potentiation

• NMDA, N-methyl-d-aspartate

• NMDAR, NMDA receptor

• STDP, spike timing-dependent plasticity

• EPSP, excitatory postsynaptic potential

• BPAP, back-propagating action potentials