Characterization of the folding landscape of monomeric lactose repressor: Quantitative comparison of theory and experiment

Abstract

Recent theoretical/computational studies based on simplified protein models and experimental investigation have suggested that the native structure of a protein plays a primary role in determining the folding rate and mechanism of relatively small single-domain proteins. Here, we extend the study of the relationship between protein topology and folding mechanism to a larger protein with complex topology, by analyzing the folding process of monomeric lactose repressor (MLAc) computationally by using a Gō-like C^α model. Next, we combine simulation and experimental results (see companion article in this issue) to achieve a comprehensive assessment of the folding landscape of this protein. Remarkably, simulated kinetic and equilibrium analyses show an excellent quantitative agreement with the experimental folding data of this study. The results of this comparison show that a simplified, completely unfrustrated C^α model correctly reproduces the complex folding features of a large multidomain protein with complex topology. The success of this effort underlines the importance of synergistic experimental/theoretical approaches to achieve a broader understanding of the folding landscape.

Understanding protein folding dynamics at the detailed molecular level continues to challenge both theory and experiment. From a physicochemical point of view, protein-folding mechanisms are governed by the search for the best “compromise” in the delicate tradeoff between the many contributions to the protein's free energy. The overwhelmingly large number of degrees of freedom, combined with the broad range of time and length scales involved in the folding process, make the investigation of the overall folding landscape of large proteins and protein complexes at the atomic level computationally unfeasible. For this reason, coarse-grained (minimalist) protein models, where several atoms are grouped into one “average” degree of freedom and an effective energy function is defined, are oftentimes used to explore the general folding landscape topography (1-4). In this context, one of the prominent theoretical challenges is presented by the definition of a reduced protein representation and average variables amenable to modeling and simulation but at the same time retaining the essential physicochemical ingredients of the folding reaction. The main assumption at the base of coarse-grained protein modeling is that the essential features of the protein free energy can be reproduced even using a strongly reduced number of degrees of freedom. This working hypothesis is based on the evidence that the folding transition involves the high cooperation of a large number of interacting constituents, and each one singly is not of special importance by itself. This view encourages the use of statistical mechanics to simplify the complex scenario created by the large number of interacting degrees of freedom and the intricate network of molecular interaction by organizing the multitude of the protein's microstates in terms of a minimal number of collective parameters. This approach is generally referred to as the free energy landscape perspective of protein folding (5-9).

Recent theoretical/computational studies of folding rates and mechanisms based on minimalist models have achieved noticeable success in reproducing, at least qualitatively, various features of the folding mechanisms of relatively small fast-folding proteins (see, e.g., refs. 10-21). Most of these studies are based on the so-called Gō-like (22) model Hamiltonian that is generally defined by completely neglecting interactions not present in the native state. The Gō-like approximation is based on both theoretical and experimental evidence. From the theoretical point of view, the commonly accepted minimal frustration principle of protein folding (5, 23, 24) implicitly invites one to disregard nonnative interactions between residues as a zeroth-order level of approximation. Moreover, members of homologous protein families generally show a conservation of the folding mechanism, even when they have little sequence identity (25-28). Simple empirical parameters that summarize the characteristics of a protein topology also are generally able to correctly order protein-folding rates of single-domain proteins (13, 29-38).

Despite the success and popularity of Gō-models, recent work has shown that the complete removal of frustration can significantly distort the representation of the folding landscape, even if its overall topography is qualitatively preserved (39-42). Moreover, the relationship between protein topology and folding mechanisms may not hold for larger proteins with more complex folding mechanisms. From one perspective, single atomic details may become even less important in the overall balance of the cooperative folding transition of larger system, where many more degrees of freedom orchestrate together. Conversely, nonnative interactions and sequence dependence may more strongly modulate the free energy landscape associated with complex folding reactions, and their contributions can accumulate to produce larger distortions in the approximated landscape obtained from unfrustrated minimalist models. Understanding the interplay of configurational entropy (i.e., topological factors) and energetic details in the dynamics of large protein systems is an important issue. The possibility to use simplified models to quantitatively characterize large and complex systems is even more crucial than for small proteins, because the study of the protein dynamics over the folding time scale becomes more unapproachable by all-atom computations as the system sizes increases. Previous work on large protein systems has already provided evidence that simple coarse-grained models are able to describe the short time-scale fluctuation dynamics of large proteins (43, 44).

We present here a first step in assessing the applicability of a simplified model to study the folding of a large protein. We show that a completely unfrustrated C^α model reproduces remarkably well the complex folding process of a monomeric variant of the lactose repressor protein (MLAc). The analysis of the simulated folding process is carried out by means of kinetics and equilibrium studies and quantitatively compared with the experimental measurements of MLAc folding behavior [see companion article by Wilson et al. (45) in this issue].

Model and Methods

Coarse-Grained Protein Model. MLAc was modeled by using an off-lattice simplified representation of the protein, where each amino acid is described by a single bead on a polymer chain located on the C^α position. The energy of a protein configuration is approximated by a homogeneous Gō-like Hamiltonian that takes into account native interactions only and considers each interaction contributing with the same weight

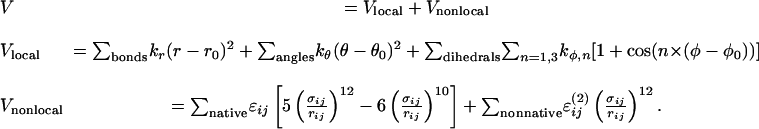[1]

Local interactions V_local comprise standard bond, angle, and dihedral terms (see ref. 46 for details). Nonlocal terms represent noncovalent attractive native interactions and repulsive nonnative interactions, respectively. The energy parameters are set as ε_ij = constant > 0 and 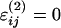if the residue pair (i, j) forms a native contact, whereas ε_ij = 0 and 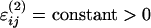if it forms a nonnative contact. The interaction distance σ_ij between two C^α atoms is set equal to their distance in the native state if (i, j) is a native residue pair or to a hard-core repulsive radius σ_ij = 3.8 Å if (i, j) form a nonnative pair. A pair of residues (i, j) is considered native if a heavy atom of residue i is found <5 Å from a heavy atom of residue j in the protein crystal structure (Protein Data Bank ID code 1EFA). Similar energy functions have been used in previous studies (2, 15, 18, 42, 46, 47). Details on the choice of the parameters used can be found in ref. 46.

The model greatly simplifies the folding free energy landscape of the protein by completely removing energetic frustration. Folding/unfolding molecular dynamics simulations of a large protein such as MLAc then become possible on the artificially smoothed landscape. We used the sander module (properly adapted to deal with the minimalist protein representation) of the simulation package amber (Version 6) (48) for all molecular dynamics simulations presented in this work. Thermodynamic (equilibrium) quantities are obtained from the analysis of folding and unfolding constant-temperature molecular dynamics simulations around the folding temperature, T_f. Simulations at different temperatures are combined by using the WHAM algorithm (49, 50) to obtain the heat capacity as a function of temperature and a free energy profile as a function of two different reaction coordinates. The folding temperature T_f is estimated as the temperature corresponding to the peak in the heat capacity curve.

Fit of Kinetic Data. The kinetic analysis was performed on a large (>200) set of folding simulations for each considered temperature, each starting from a different unfolded configuration. Unfolded configurations with Q < 0.1 and rms deviation, rmsd, >30.0 were created by running short molecular dynamics simulations at very high temperature T (≳2T_f). To create independent initial conditions, the total simulation time of each initial unfolding simulation was set to be larger than the average unfolding time (1/k_unf) at the corresponding temperature.

The average signal 〈X(t)〉 (defined as the helical content or the fraction of contacts formed with Trp residues as described in Eqs. 9 and 10) obtained from kinetic simulation (see Kinetic Analysis of MLAc Folding: Quantitative Connection Between Theory and Experiment) was fit both to a two-phase and a three-phase kinetic model, as described below.

Two-phase kinetic. We assume the following sequential kinetic mechanism:

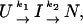[2]

where U, I, and N indicate the unfolded, intermediate, and folded states, respectively, and k₁, k₂ are the rate constants for the processes U → I and I → N. The solution of the system of differential equations associated with this kinetic model for the relative population of the different states as a function of time {[U](t), [I](t), and [N](t)} is in the form (using the initial condition [U](0) = 1) (51)

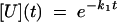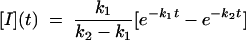[3]

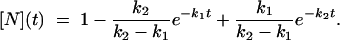Normalizing the signal such that X(t = 0) = X_U = 0 and X(t → ∞) = X_N = 1, and letting A indicate the percentage of signal corresponding to the state I (with X_U < A < X_N), the time evolution of the observed signal for this kinetic model can be written in the form

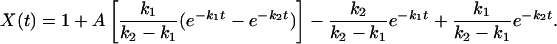[4]

Simulation data are fit to Eq. 4 with the three independent parameters k₁, k₂, and A, by using a least-squares fit algorithm to a nonlinear function (52, 53).

Three-phase kinetic. A three-phase mechanism is modeled as

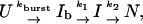[5]

where I_b to I proceeds by way of U [see companion article (45)]. The associated system of differential equations yields the following solution (51):

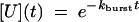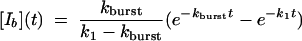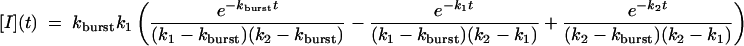[6]

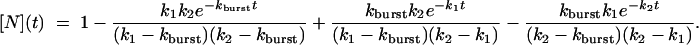Normalizing the signal such that X(t = 0) = X_U = 0 and X(t → ∞) = X_N = 1, and using the parameters A, B to indicate the percentage of signal in I_b and I, respectively (0 < A < 1, 0 < B < 1), the observed signal as a function of time for this model is given by the following expression:

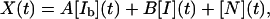[7]

where [I_b](t), [I](t), and [N](t) are given by Eq. 6. Simulation data are fit to Eq. 7 with the five independent parameters k_burst, k₁, k₂, A, and B, by using a least-squares fit algorithm to a nonlinear function (52, 53).

Folding Free Energy Landscape of MLAc Model

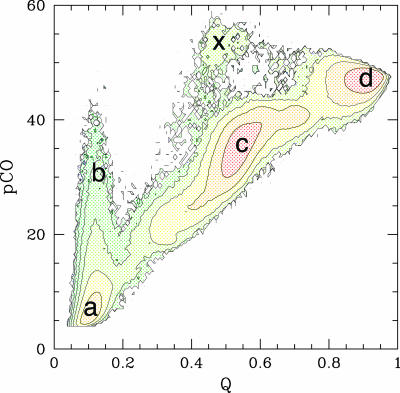
Fig. 1 represents the folding free energy of the simplified MLAc model as a function of two reaction coordinates: the fraction of native contacts formed, Q, and the partial contact order, pCO. The partial contact order is defined as the average loop length over all of the formed native contacts in a partially folded structure Γ (see also ref. 54)

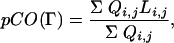[8]

where the sum runs over all of the native contacts, L_i,j is the sequence separation (loop length) between residues (i, j), and Q_i,j = 1 (or 0) if the native pair (i, j) forms (or does not form) a contact in the configuration Γ.

Fig. 1.

Folding free energy landscape of the MLAc model as a function of two reaction coordinates: the fraction of native contacts formed, Q, and the partial contact order, pCO (54). An intermediate state (c) appears as a local minimum in the free energy at Q ≃ 0.5. The fluctuations toward high values of the pCO coordinate (b) from the unfolded minimum (a) indicates that structures with very long-range contacts are temporarily formed in the early stages of the folding process. The native state is labeled as d. Each contour line in the plot marks an increase in free energy of 2k_BTf, where T_f is the folding temperature. A very small number of folding events (<1%) populated a different pathway, involving the formation of an intermediate where the N terminus is formed and the C terminus is unfolded (x). This alternative pathway can be an artifact of the Gō model, but in any case this state is not significantly populated and would not be experimentally detected.

The free energy minimum corresponding to the folded state is identified in the region (Q ∼ 0.9-0.95; pCO ∼ 45-50), whereas the minimum at (Q ≲ 0.2, pCO ≲ 10) corresponds to the unfolded state. An intermediate state appears as a local minimum in the free energy at Q ≃ 0.5. The broad range of values spanned by the pCO coordinate in the unfolded state (Q < 0.2) indicates that some of the unfolded structures may have very long-range contacts formed, although the overall shape of the landscape indicates that the folding reaction proceeds to later stages mainly from configurations with a relatively low value of pCO (i.e., only with local contacts formed). This interpretation is fully consistent with time-resolved experimental data suggesting the initial formation of long-range interactions in the burst phase of folding, which need to unform for the folding to proceed [see companion article (45)]. The results shown in Fig. 2 a-c confirm this idea. The probability of finding any given native contact formed is shown for four different regions of the folding landscape: (a) the local free energy minimum corresponding to the unfolded state, (b) the high pCO region accessible from the unfolded state (pCO > 25; Q < 0.25), (c) the local free energy minimum corresponding to the intermediate state, and (d) the folded state. It is clear from Fig. 2 that the unfolded minimum is mainly populated by protein configurations lacking tertiary interactions but with secondary structures locally formed. The fluctuations to higher pCO values on the free energy landscape correspond to a transient formation of structures with a few contacts between residues far apart along the chain, as, for instance, the native contacts in the N subdomain and/or the contacts between N and C subdomains. Because the model considered here does not include nonnative interactions, the temporary formation of structures that need to partially unfold for the folding to proceed does not necessarily signal the formation of a misfolded species. However, the tendency of the protein to temporarily populate a partially misfolded state can be further investigated by considering the effect of a relatively weak amount of nonnative energy that can be introduced as a perturbation to the model Hamiltonian. The introduction of a random Gaussian distribution of energy per nonnative interaction (see ref. 42 for details) produces a significant increase in the probability of visiting the high pCO region from the unfolded state (pCO > 25, Q < 0.25): at a temperature T = 0.9T_f the percentage 𝒫 of folding trajectories (starting from a completely open configuration, generated by a short high temperature unfolding, see Fit of Kinetic Data) visiting this region of the landscape before proceeding toward the folded state increases from 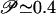for the plain Gō-model to 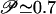upon introduction of random Gaussianly distributed nonnative interactions with an energy variance δε_nonnat = 0.25, and to 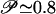for δε_nonmat = 0.5. These results are in excellent agreement with the experimental data [see companion article by Wilson et al. (45)] that suggest the formation of temporarily populated misfolded intermediates in the very early stage of the folding reaction. Consistent with experimental data, the misfolded structures have ≈40-50% of the secondary structure formed, on average. The kinetic study presented in the next section further quantifies this point and provides a robust framework for the interpretation of the experimental data.

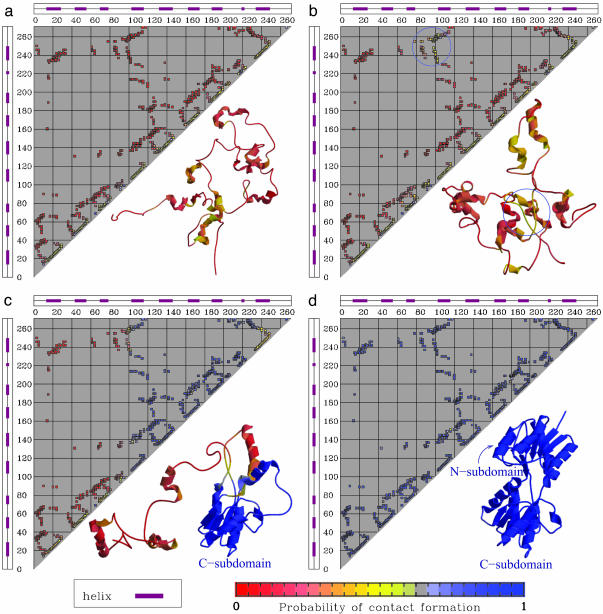
Fig. 2.

The probability of native contact formations in different regions of the folding landscape. (a) The local free energy minimum corresponding to the unfolded state. (b) The high pCO region accessible from the unfolded state (pCO > 25; Q < 0.25). The blue circle highlights the long-range native interactions that are temporarily formed in the high-pCO region. (c) The local free energy minimum corresponding to the intermediate state. (d) The folded state. A representative configuration is shown for each state. Corresponding states in Fig. 1 are labeled with the same letters as in this figure.

Kinetic Analysis of MLAc Folding: Quantitative Connection Between Theory and Experiment

The stopped-flow analysis of the kinetic folding process of MLAc suggests a three-phase folding mechanism for this protein. The experimental study [see companion article (45)] indicates a mechanism consisting of a burst phase intermediate (with ≈40-50% secondary structure formed and involving the formation of partially misfolded structures) populated in the dead time of the experiment, followed by the population of an on-pathway intermediate (with about the same amount of secondary structure formed) before the native state is reached. To quantitatively compare the folding of MLAc as obtained in simulations with the results from the experimental kinetic study, it is necessary to define average quantities that can be computed in simulations and can be closely compared with the ones that are experimentally monitored. Because the experimental kinetic analysis is based on the time relaxation of far-UV CD and Trp fluorescence signals, we define the following two quantities:

• Helicity content as a function of time, H(t)

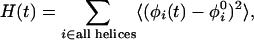[9]

where φ_i(t) is the value at time t of the dihedral angle centered at residue i in a helical structure, and φ⁰_i is the value of φ_i(t) in the native state.

• Fraction of contacts formed by the Trp residues as a function of time, Q_trp(t)

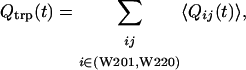[10]

where Q_ij(t) = 1 if the residue pair (i, j) forms a native contact at time t, and Q_ij(t) = 0 otherwise.

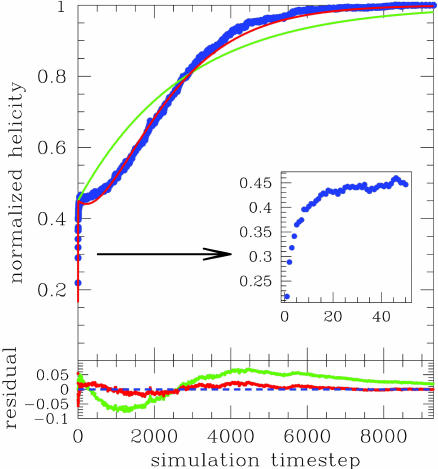
The kinetic signals H(t) and Q_trp(t) are computed as averages over a large number (>200) of folding trajectories at a fixed temperature T < T_f, each starting from a completely unfolded configuration (with Q < 0.1 and rmsd > 30.0; see Fit of Kinetic Data). The initial configurations are obtained from independent, short high-temperature simulations, T >> T_f (see Fit of Kinetic Data for details). The relaxation of both H(t) and Q_trp(t) to their equilibrium value (corresponding to the folded state) exhibits distinct three-phase behavior for all values of temperature considered (0.8 < T/T_f < 0.9). Fig. 3 shows the relaxation to equilibrium of H(t) (normalized such that H (0) = 0 and H(t → ∞) = 1), as obtained from kinetic simulations at T = 0.9T_f. A burst phase is clearly detected as a sudden increase of the signal up to ≈45% of its final value, within the first 0.1% of the total relaxation time. Both the fit to a two-phase (Eq. 4) and to a three-phase (Eq. 7) kinetic model are shown in Fig. 3: Whereas the agreement with a two-phase kinetic model is poor, the simulation data are fully consistent with a three-phase kinetic model. The parameters A and B extracted from the fit (see Fit of Kinetic Data) estimate that, on average, the helicity signal is ≈40-45% in I_b, with a minimal increase to 50% in I, whereas the signal Q_trp is only ≈10% in I_b and increases to 40-50% in I. Experimental analysis confirms that the folding kinetics of MLAc conform to a three-phase model [see companion article (45)]. Moreover, the parameters A and B obtained in the fit of the far-UV CD and fluorescence signals in the experiments are in remarkable agreement with the values obtained from the theoretical analysis here. Taken together, both experiment and simulation suggest a folding mechanism for MLAc (at least for refolding from completely denaturated condition) consisting of two intermediates, the first of which is populated in the burst phase and involves partially misfolded structures.

Fig. 3.

Relaxation to equilibrium of helicity content H(t) as obtained from kinetic simulations at T = 0.9T_f. The signal is normalized such that H(0) = 0 and H(t → ∞) = 1. A burst phase is clearly detected as a sudden increase of the signal up to ≈45% of its final value, within the first 0.1% of the total relaxation time. Both the fit to a two-phase kinetic model (green curve) and to a three-phase kinetic model (red curve) are overlapped to the actual simulation data (blue points). Inset zooms in on the evolution of the signal in the burst phase. The residuals from the fit are plotted in the bottom part of the figure, with colors matching the corresponding fit.

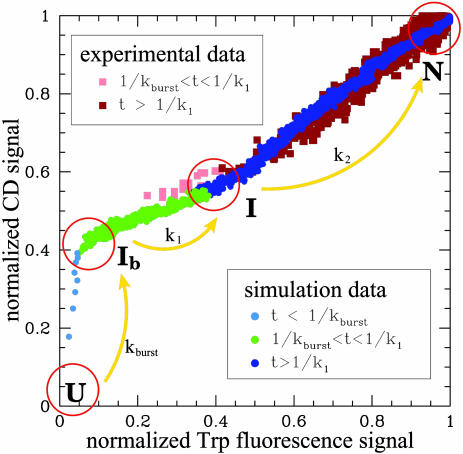
An overall folding rate for MLAc can be estimated from equilibrium simulations (at the folding temperature, T_f) by using the correlation observed between experimentally measured folding rates and folding rates obtained by simulating a large set of proteins with a similar coarse-grained model (53). The folding rate so obtained is log(k_f) = -1.6 ± 0.4 [or log(k_f) = -1.3 ± 0.3 if also the correction on the energy scale as discussed in ref. 54 is taken into account]. These values are in excellent agreement with the experimental value of log(k_f) = -1.5 ± 0.2 in water [see companion article (45)]. The detailed kinetic analysis becomes prohibitively slow for simulations close to the folding temperature, and the rate constants k₁ and k₂ cannot be reliably estimated at the transition midpoint, as needed for a direct comparison with experimental values. However, a more quantitative comparison of the detailed folding mechanism as obtained in simulation and experiment can be obtained by monitoring the increase of the two kinetic signals [H(t) and Q_trp(t) in simulation, or CD and fluorescence signals in experiment] relative to each other. This analysis is based on the observation that when the normalized value of H(t) at a given time is plotted against the corresponding value of Q_trp(t) at the same time, data corresponding to simulations at different temperatures collapse into the same curve (shown in Fig. 4). Similarly, the plot of far-UV CD vs. fluorescence signal recorded in the experiments is found to be essentially independent of denaturant concentration (data not shown). These curves obtained from simulation and experimental data can be used to quantitatively compare the folding mechanisms. The remarkable agreement illustrated in Fig. 4 provides a strong evidence that, despite the simplicity of the model, the folding mechanism predicted by simulation is fully consistent with the mechanism emerging from experiment.

Fig. 4.

Normalized helicity as obtained in kinetic simulation is plotted as a function of the Q_trp(t) signal detected at the same time. Blue dots correspond to the signal measured in the burst-phase time scale (t < 1/k_burst); green dots correspond to the signal detected in the time scale of the accumulation of the intermediate state, after the burst phase (1/k_burst < t < 1/k_burst + 1/k₁ ≃ 1/k₁); and dark blue dots correspond to the final folding phase (1/k₁ < t). The folding constants k_burst and k₁ are obtained by fitting simulation data to a three-phase kinetic model (see text for details). The far-UV CD signals measured in the kinetic experiments also are plotted as a function of the Trp fluorescence signal. Analogously, different colors highlight different phases of the folding process: light pink squares correspond to events detected within the time scale associated with the formation of an intermediate state (1/k_burst < t < 1/k₁), and dark brown squares correspond to the relaxation to the completely folded state (1/k₁ < t). Rate constant k₁ is measured from fits to the experimental data [see companion article (45)], whereas the time 1/k_burst falls within the stopped-flow mixing dead time. Simulation data were obtained at a temperature T = 0.9T_f, and experimental data correspond to a concentration of [Urea] ∼ 1 M (pH 7, 20°C).

Conclusion

The complex folding process of MLAc was investigated by means of a minimalist unfrustrated model. The results of kinetic and equilibrium analysis are in excellent quantitative agreement with the experimental counterpart of this study [see the companion article by Wilson et al. (45)]. The compounding of simulation and experimental results allows a synoptic understanding of the folding mechanism of MLAc at a level of detail that could not be achieved solely by experiments and could not be a priori considered sufficiently accurate/realistic if obtained solely by simulation. The lactose repressor protein is a paradigmatic system for studies of gene regulation and allosteric response. The results presented here provide a solid starting point for studies of direct biomedical relevance, including the characterization of the assembly of lactose repressor into the functional homotetramer form and the folding/binding/function relationship in its protein-DNA complex.