Abstract
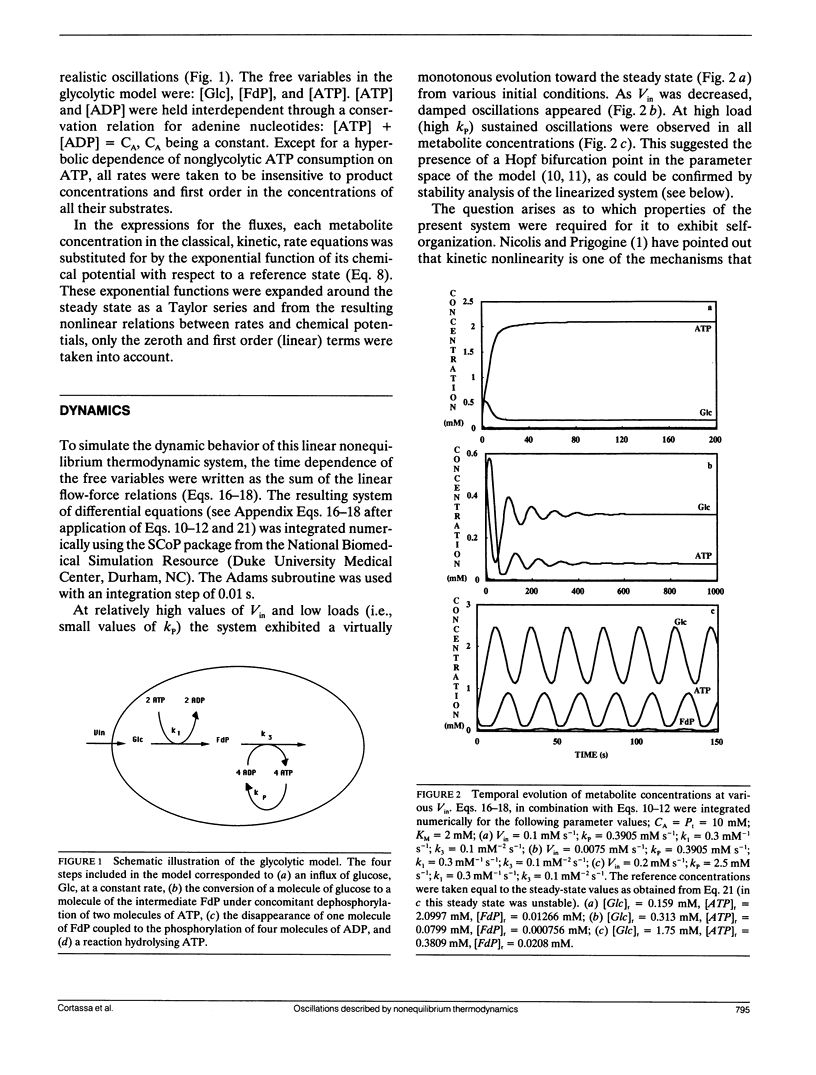
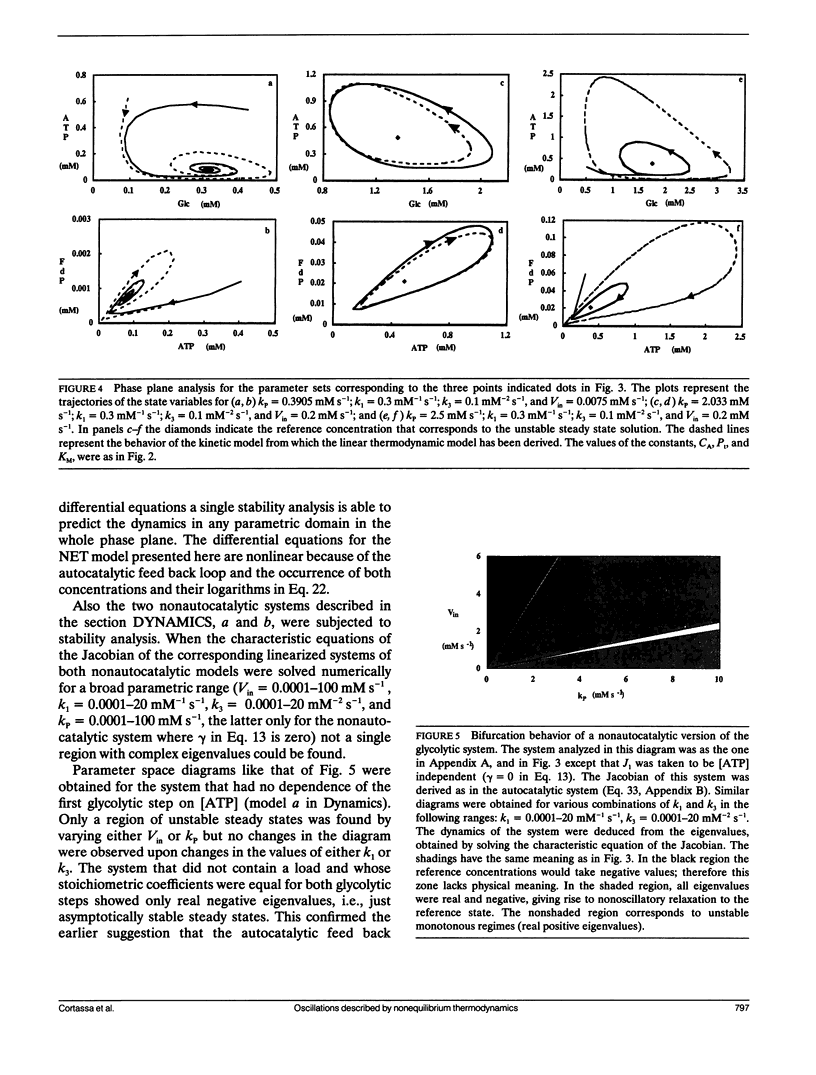
A model simulating oscillations in glycolysis was formulated in terms of nonequilibrium thermodynamics. In the kinetic rate equations every metabolite concentration was replaced with an exponential function of its chemical potential. This led to nonlinear relations between rates and chemical potentials. Each chemical potential was then expanded around its steady-state value as a Taylor series. The linear (first order) term of the Taylor series sufficed to simulate the dynamic behavior of the system, including the damped and even sustained oscillations at low substrate input or high free-energy load. The glycolytic system is autocatalytic in the first half. Because oscillations were obtained only in the presence of that autocatalytic feed-back loop we conclude that this type of kinetic nonlinearity was sufficient to account for the oscillatory behavior. The matrix of phenomenological coefficients of the system is nonsymmetric. Our results indicate that this is the symmetry property and not the linearity of the flow-force relations in the near equilibrium domain that precludes oscillations. Given autocatalytic properties, a system exhibiting liner flow-force relations and being outside the near equilibrium domain may show bifurcations, leading to self-organized behavior.
Full text
PDF







Images in this article
Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Astumian RD, Chock PB, Tsong TY, Westerhoff HV. Effects of oscillations and energy-driven fluctuations on the dynamics of enzyme catalysis and free-energy transduction. Phys Rev A Gen Phys. 1989 Jun 15;39(12):6416–6435. doi: 10.1103/physreva.39.6416. [DOI] [PubMed] [Google Scholar]
- Goldbeter A., Caplan S. R. Oscillatory enzymes. Annu Rev Biophys Bioeng. 1976;5:449–476. doi: 10.1146/annurev.bb.05.060176.002313. [DOI] [PubMed] [Google Scholar]
- Hyver C. Impossibility of existence of undamped oscillations in linear chemical systems. J Theor Biol. 1972 Jul;36(1):133–138. doi: 10.1016/0022-5193(72)90182-8. [DOI] [PubMed] [Google Scholar]
- Juretić D., Westerhoff H. V. Variation of efficiency with free-energy dissipation in models of biological energy transduction. Biophys Chem. 1987 Oct;28(1):21–34. doi: 10.1016/0301-4622(87)80072-8. [DOI] [PubMed] [Google Scholar]
- Rothschild K. J., Ellias S. A., Essig A., Stanley H. E. Nonequilibrium linear behavior of biological systems. Existence of enzyme-mediated multidimensional inflection points. Biophys J. 1980 May;30(2):209–230. doi: 10.1016/S0006-3495(80)85090-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rottenberg H. The thermodynamic description of enzyme-catalyzed reactions. The linear relation between the reaction rate and the affinity. Biophys J. 1973 Jun;13(6):503–511. doi: 10.1016/S0006-3495(73)86004-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stucki J. W., Compiani M., Caplan S. R. Efficiency of energy conversion in model biological pumps. Optimization by linear nonequilibrium thermodynamic relations. Biophys Chem. 1983 Sep;18(2):101–109. doi: 10.1016/0301-4622(83)85003-0. [DOI] [PubMed] [Google Scholar]
- Stucki J. W. The optimal efficiency and the economic degrees of coupling of oxidative phosphorylation. Eur J Biochem. 1980 Aug;109(1):269–283. doi: 10.1111/j.1432-1033.1980.tb04792.x. [DOI] [PubMed] [Google Scholar]
- Van Dam K., Westerhoff H. V., Krab K., van der Meer R., Arents J. C. Relationship between chemiosomotic flows and thermodynamic forces in oxidative phosphorylation. Biochim Biophys Acta. 1980 Jul 8;591(2):240–250. doi: 10.1016/0005-2728(80)90156-5. [DOI] [PubMed] [Google Scholar]
- Van der Meer R., Westeroff H. V., Van Dam K. Linear relation between rate and thermodynamic force in enzyme-catalyzed reactions. Biochim Biophys Acta. 1980 Jul 8;591(2):488–493. doi: 10.1016/0005-2728(80)90179-6. [DOI] [PubMed] [Google Scholar]
- Wanders R. J., Westerhoff H. V. Sigmoidal relation between mitochondrial respiration and log ([ATP]/[ADP])out under conditions of extramitochondrial ATP utilization. Implications for the control and thermodynamics of oxidative phosphorylation. Biochemistry. 1988 Oct 4;27(20):7832–7840. doi: 10.1021/bi00420a037. [DOI] [PubMed] [Google Scholar]
- Westerhoff H. V., Lolkema J. S., Otto R., Hellingwerf K. J. Thermodynamics of growth. Non-equilibrium thermodynamics of bacterial growth. The phenomenological and the mosaic approach. Biochim Biophys Acta. 1982 Dec 31;683(3-4):181–220. doi: 10.1016/0304-4173(82)90001-5. [DOI] [PubMed] [Google Scholar]



