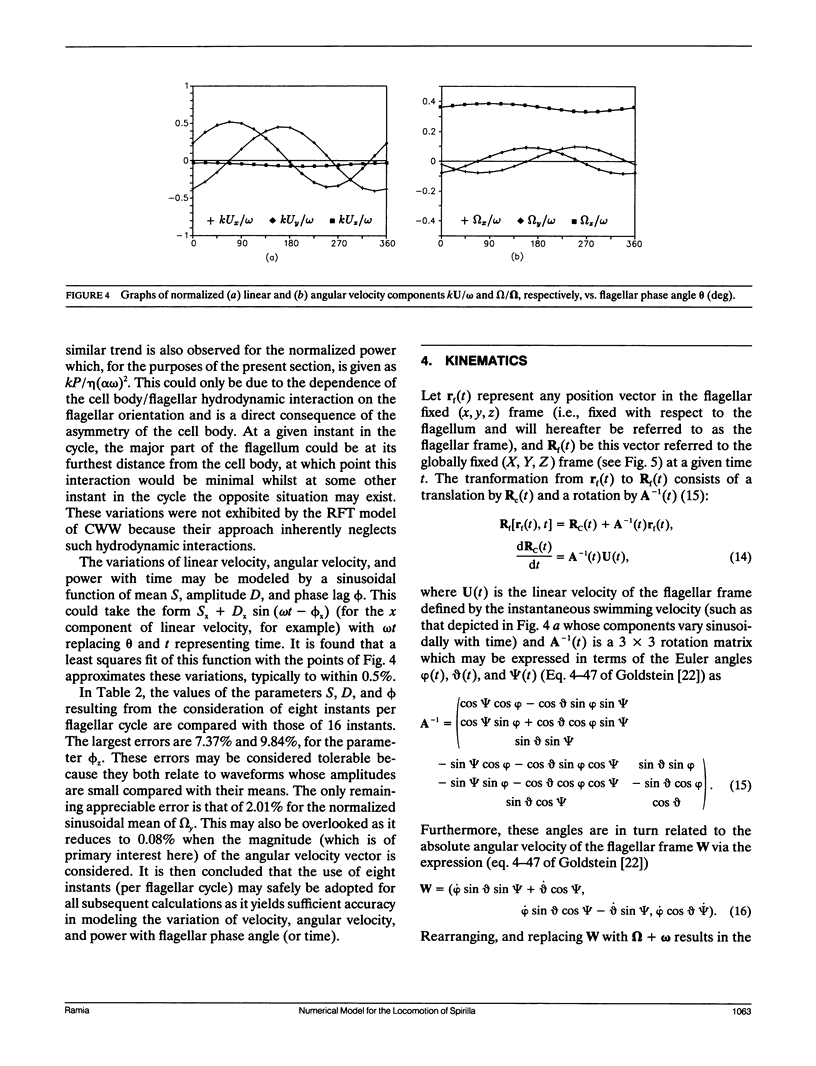
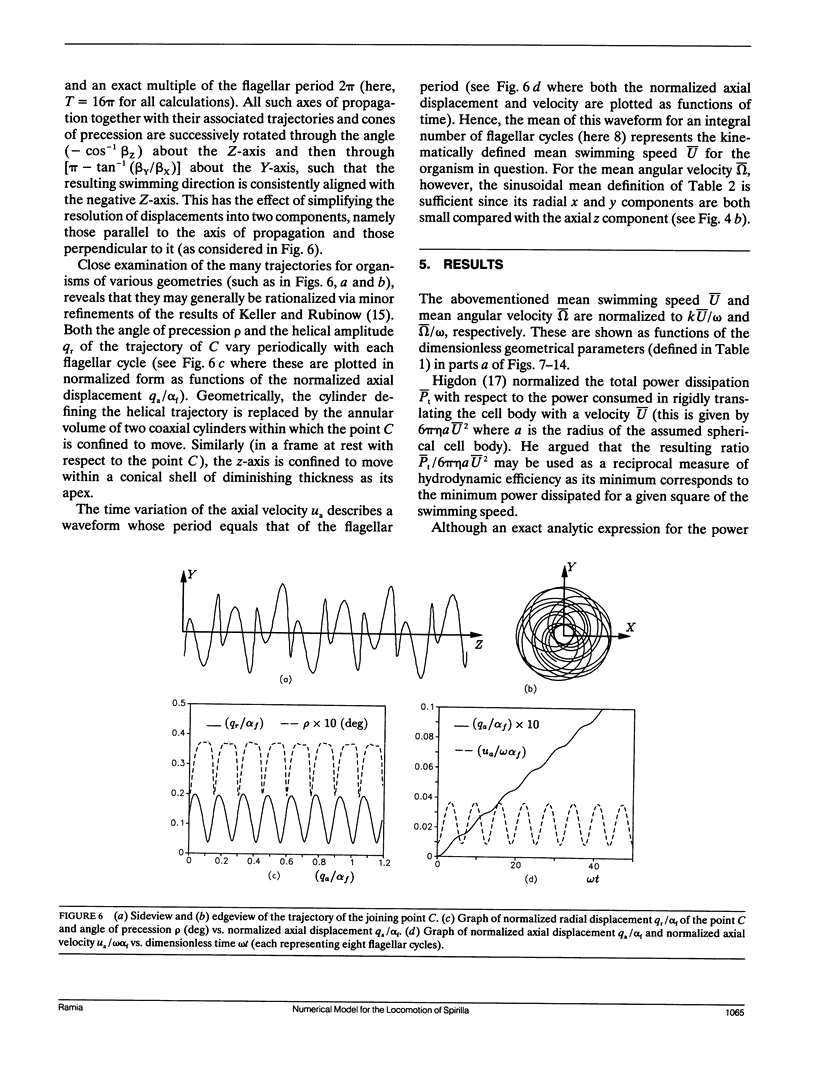
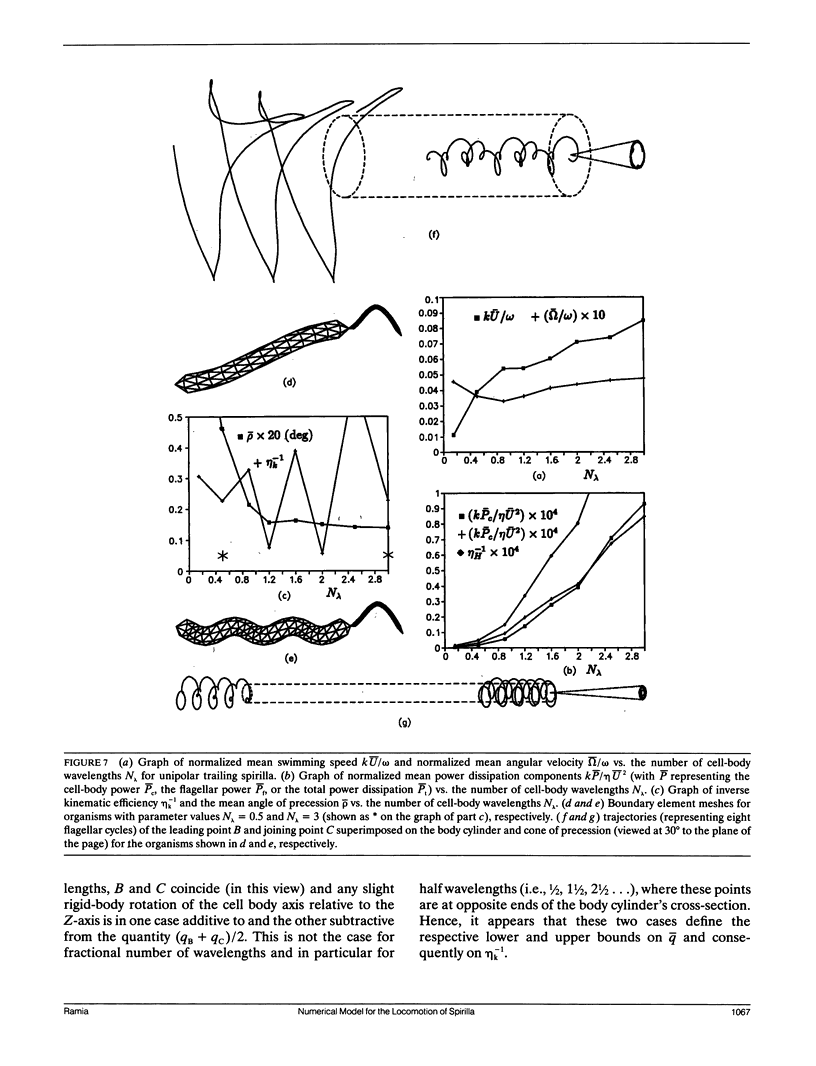
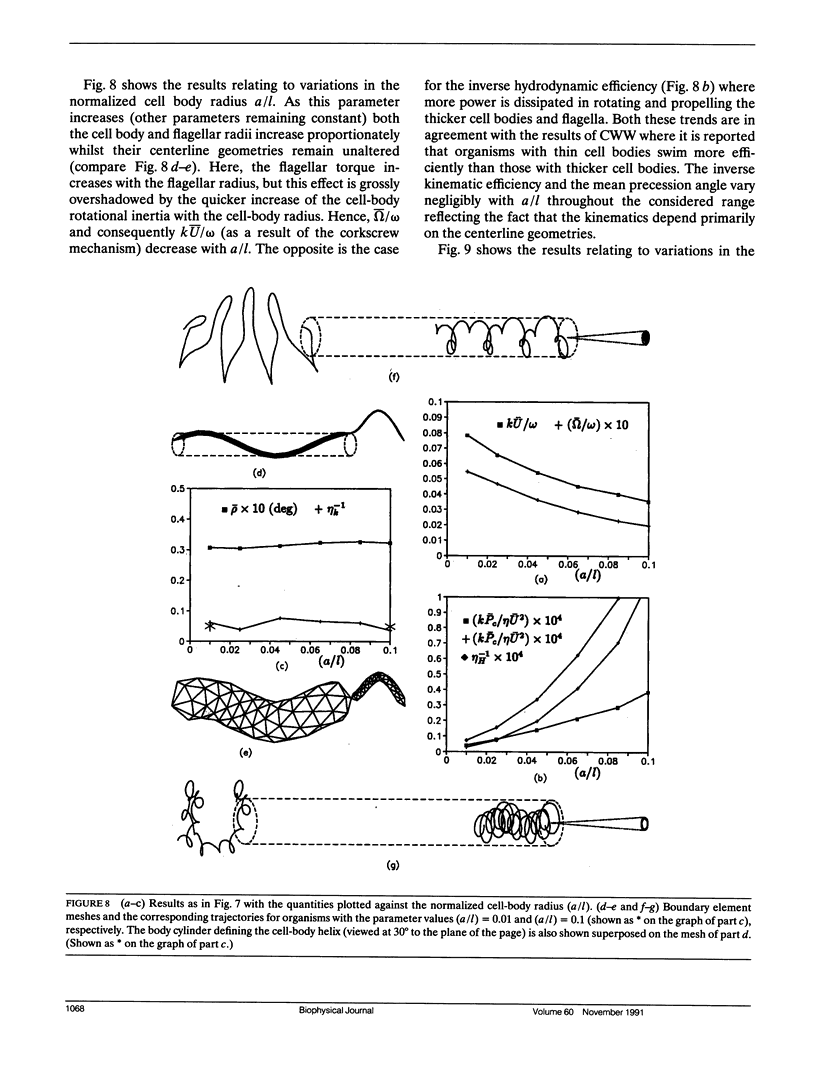
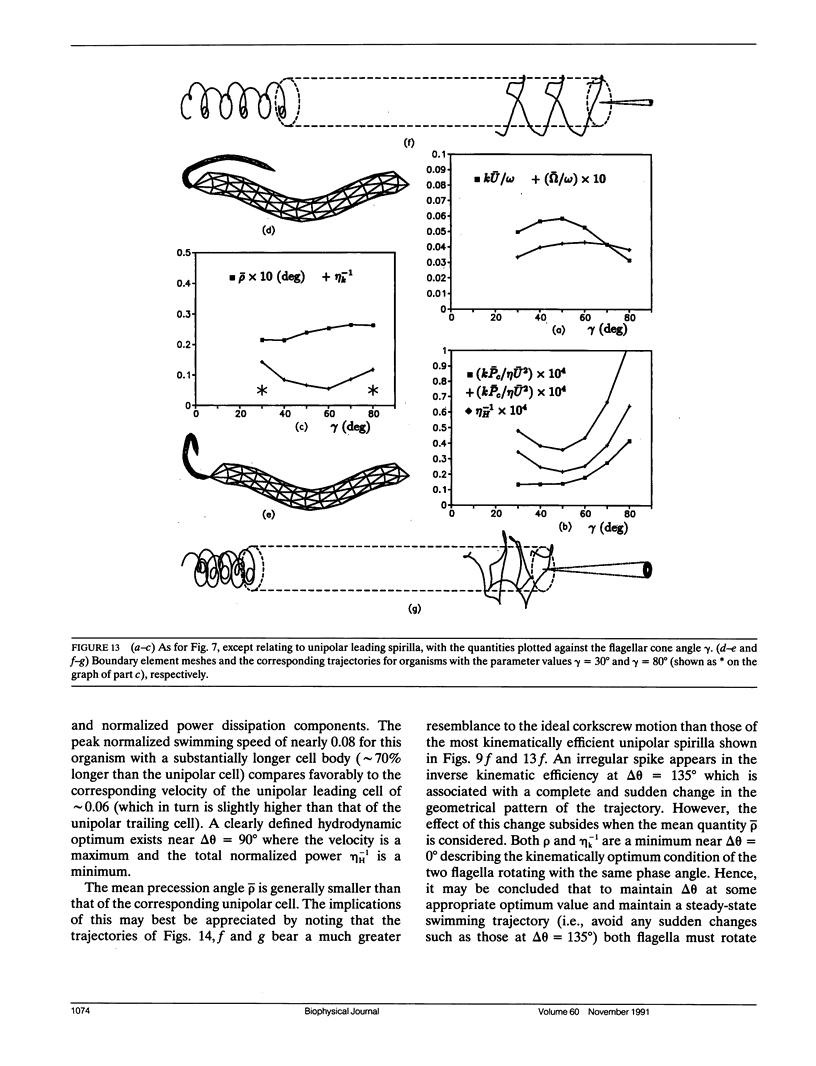
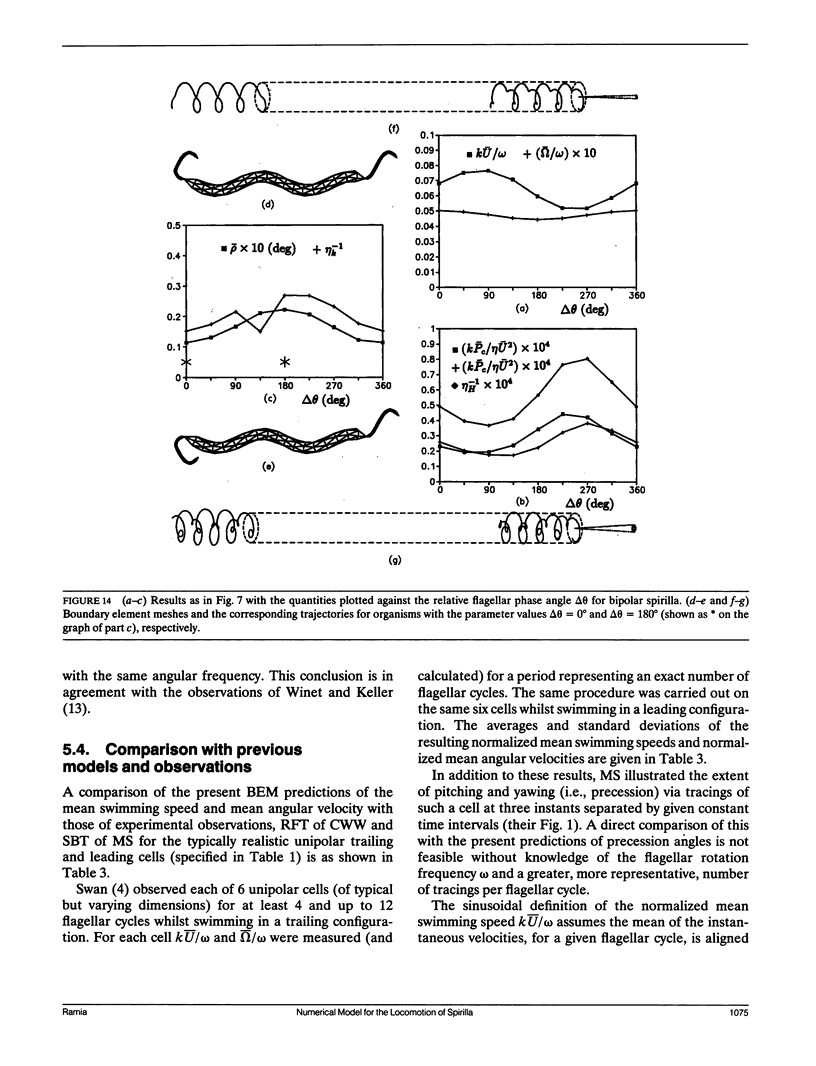
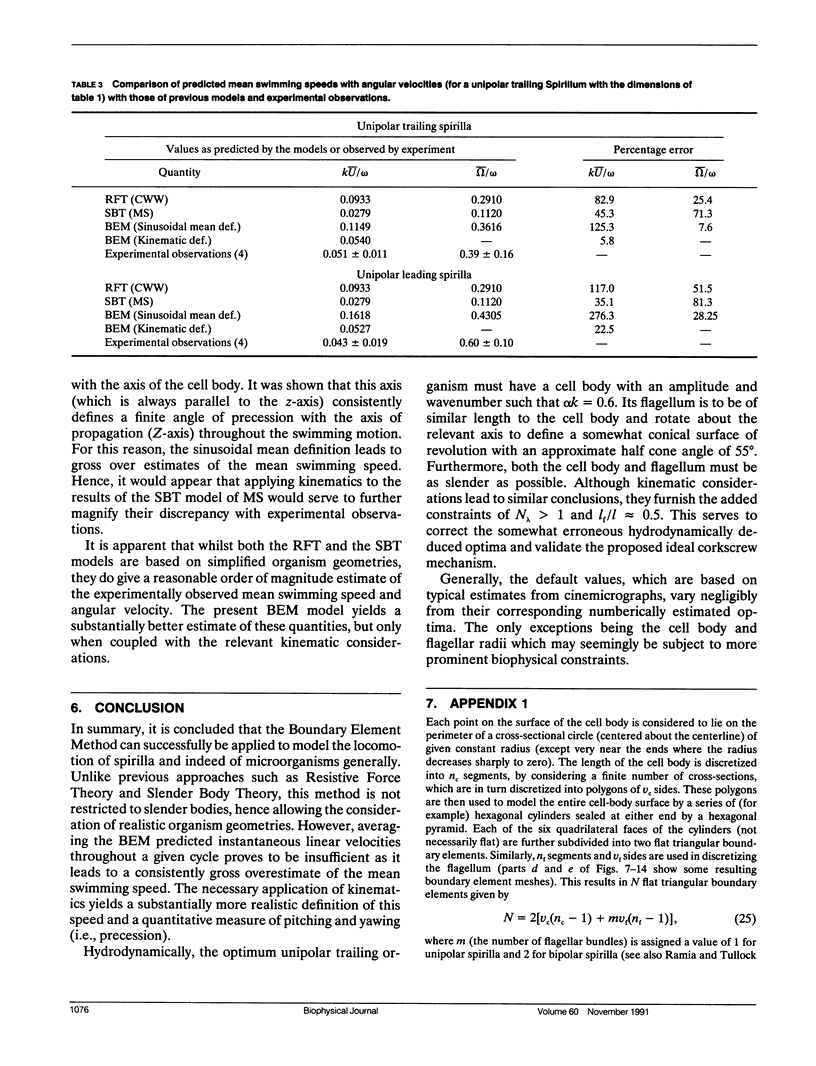
Abstract
The swimming of trailing, leading, and bipolar spirilla (with realistic flagellar centerline geometries) is considered. A boundary element method is used to predict the instantaneous swimming velocity, counter-rotation angular velocity, and power dissipation of a given organism as functions of time and the geometry of the organism. Based on such velocities, swimming trajectories have been deduced enabling a realistic definition of mean swimming speeds. The power dissipation normalized in terms of the square of the mean swimming speed is considered to be a measure of hydrodynamic efficiency. In addition, kinematic efficiency is defined as the extent of deviation of the swimming motion from that of a previously proposed ideal corkscrew mechanism. The dependence of these efficiencies on the organism's geometry is examined giving estimates of its optimum dimensions. It is concluded that appreciable correlation exists between the two alternative definitions for many of the geometrical parameters considered. Furthermore, the organism having the deduced optimum dimensions closely resembles the real organism as experimentally observed.
Full text
PDF










Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Chwang A. T., Wu T. Y. A note on the helical movement of micro-organisms. Proc R Soc Lond B Biol Sci. 1971 Aug 3;178(1052):327–346. doi: 10.1098/rspb.1971.0068. [DOI] [PubMed] [Google Scholar]
- Chwang A. T., Wu T. Y., Winet H. Locomotion of Spirilla. Biophys J. 1972 Nov;12(11):1549–1561. doi: 10.1016/S0006-3495(72)86181-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keller J. B., Rubinow S. I. Swimming of flagellated microorganisms. Biophys J. 1976 Feb;16(2 Pt 1):151–170. doi: 10.1016/s0006-3495(76)85672-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myerscough M. R., Swan M. A. A model for swimming unipolar spirilla. J Theor Biol. 1989 Jul 21;139(2):201–218. doi: 10.1016/s0022-5193(89)80100-6. [DOI] [PubMed] [Google Scholar]
- Swan M. A. Electron microscopic observations of structures associated with the flagella of Spirillum volutans. J Bacteriol. 1985 Mar;161(3):1137–1145. doi: 10.1128/jb.161.3.1137-1145.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swan M. A. Trailing flagella rotate faster than leading flagella in unipolar cells of Spirillum volutans. J Bacteriol. 1982 Apr;150(1):377–380. doi: 10.1128/jb.150.1.377-380.1982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winet H., Keller S. R. Spirillum swimming: theory and observations of propulsion by the flagellar bundle. J Exp Biol. 1976 Dec;65(3):577–602. doi: 10.1242/jeb.65.3.577. [DOI] [PubMed] [Google Scholar]


