Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 1991 Dec;60(6):1411–1423. doi: 10.1016/S0006-3495(91)82178-6

Propagation of action potentials along complex axonal trees. Model and implementation.

Y Manor 1, J Gonczarowski 1, I Segev 1
PMCID: PMC1260201  PMID: 1777566

Abstract

Axonal trees are typically morphologically and physiologically complicated structures. Because of this complexity, axonal trees show a large repertoire of behavior: from transmission lines with delay, to frequency filtering devices in both temporal and spatial domains. Detailed theoretical exploration of the electrical behavior of realistically complex axonal trees is notably lacking, mainly because of the absence of a simple modeling tool. AXONTREE is an attempt to provide such a simulator. It is written in C for the SUN workstation and implements both a detailed compartmental modeling of Hodgkin and Huxley-like kinetics, and a more abstract, event-driven, modeling approach. The computing module of AXONTREE is introduced together with its input/output features. These features allow graphical construction of arbitrary trees directly on the computer screen, and superimposition of the results on the simulated structure. Several numerical improvements that increase the computational efficiency by a factor of 5-10 are presented; most notable is a novel method of dynamic lumping of the modeled tree into simpler representations ("equivalent cables"). AXONTREE's performance is examined using a reconstructed terminal of an axon from a Y cell in cat visual cortex. It is demonstrated that realistically complicated axonal trees can be handled efficiently. The application of AXONTREE for the study of propagation delays along axonal trees is presented in the companion paper (Manor et al., 1991).

Full text

PDF
1418

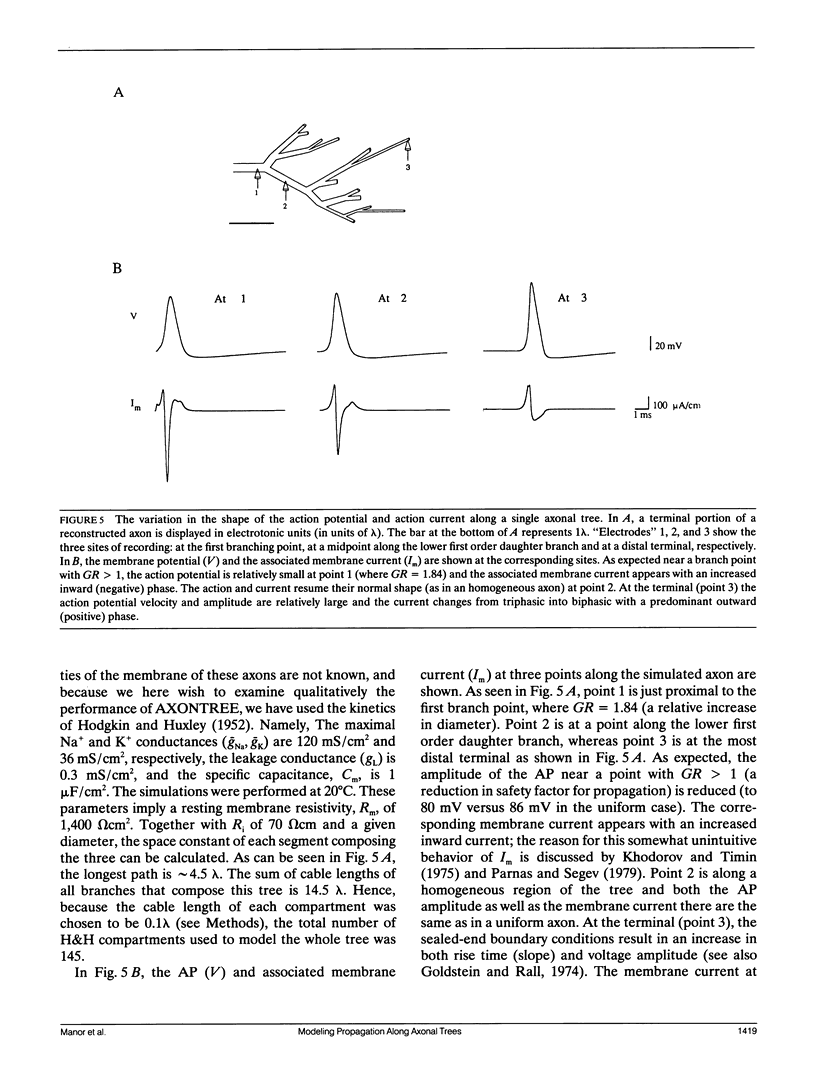
Images in this article

1418FIGURE 4
on p.1418

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Barron D. H., Matthews B. H. Intermittent conduction in the spinal cord. J Physiol. 1935 Aug 22;85(1):73–103. doi: 10.1113/jphysiol.1935.sp003303. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bittner G. D. Differentiation of nerve terminals in the crayfish opener muscle and its functional significance. J Gen Physiol. 1968 Jun;51(6):731–758. doi: 10.1085/jgp.51.6.731. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Braitenberg V. Is the cerebellar cortex a biological clock in the millisecond range? Prog Brain Res. 1967;25:334–346. doi: 10.1016/S0079-6123(08)60971-1. [DOI] [PubMed] [Google Scholar]
  4. Carnevale N. T., Lebeda F. J. Numerical analysis of electrotonus in multicompartmental neuron models. J Neurosci Methods. 1987 Jan;19(1):69–87. doi: 10.1016/0165-0270(87)90022-7. [DOI] [PubMed] [Google Scholar]
  5. Carnevale N. T., Woolf T. B., Shepherd G. M. Neuron simulations with SABER. J Neurosci Methods. 1990 Aug;33(2-3):135–148. doi: 10.1016/0165-0270(90)90017-a. [DOI] [PubMed] [Google Scholar]
  6. Carr C. E., Konishi M. Axonal delay lines for time measurement in the owl's brainstem. Proc Natl Acad Sci U S A. 1988 Nov;85(21):8311–8315. doi: 10.1073/pnas.85.21.8311. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Chung S. H., Raymond S. A., Lettvin J. Y. Multiple meaning in single visual units. Brain Behav Evol. 1970;3(1):72–101. doi: 10.1159/000125464. [DOI] [PubMed] [Google Scholar]
  8. Clements J. D., Redman S. J. Cable properties of cat spinal motoneurones measured by combining voltage clamp, current clamp and intracellular staining. J Physiol. 1989 Feb;409:63–87. doi: 10.1113/jphysiol.1989.sp017485. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Cooley J. W., Dodge F. A., Jr Digital computer solutions for excitation and propagation of the nerve impulse. Biophys J. 1966 Sep;6(5):583–599. doi: 10.1016/S0006-3495(66)86679-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. De Schutter E. Computer software for development and simulation of compartmental models of neurons. Comput Biol Med. 1989;19(2):71–81. doi: 10.1016/0010-4825(89)90001-2. [DOI] [PubMed] [Google Scholar]
  11. Fleshman J. W., Segev I., Burke R. B. Electrotonic architecture of type-identified alpha-motoneurons in the cat spinal cord. J Neurophysiol. 1988 Jul;60(1):60–85. doi: 10.1152/jn.1988.60.1.60. [DOI] [PubMed] [Google Scholar]
  12. Fyffe R. E., Light A. R. The ultrastructure of group Ia afferent fiber synapses in the lumbosacral spinal cord of the cat. Brain Res. 1984 May 23;300(2):201–209. doi: 10.1016/0006-8993(84)90831-x. [DOI] [PubMed] [Google Scholar]
  13. Goldstein S. S., Rall W. Changes of action potential shape and velocity for changing core conductor geometry. Biophys J. 1974 Oct;14(10):731–757. doi: 10.1016/S0006-3495(74)85947-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Grossman Y., Parnas I., Spira M. E. Differential conduction block in branches of a bifurcating axon. J Physiol. 1979 Oct;295:283–305. doi: 10.1113/jphysiol.1979.sp012969. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Hines M. A program for simulation of nerve equations with branching geometries. Int J Biomed Comput. 1989 Mar;24(1):55–68. doi: 10.1016/0020-7101(89)90007-x. [DOI] [PubMed] [Google Scholar]
  16. Hines M. Efficient computation of branched nerve equations. Int J Biomed Comput. 1984 Jan-Feb;15(1):69–76. doi: 10.1016/0020-7101(84)90008-4. [DOI] [PubMed] [Google Scholar]
  17. Hopfield J. J. Neural networks and physical systems with emergent collective computational abilities. Proc Natl Acad Sci U S A. 1982 Apr;79(8):2554–2558. doi: 10.1073/pnas.79.8.2554. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Humphrey A. L., Sur M., Uhlrich D. J., Sherman S. M. Projection patterns of individual X- and Y-cell axons from the lateral geniculate nucleus to cortical area 17 in the cat. J Comp Neurol. 1985 Mar 8;233(2):159–189. doi: 10.1002/cne.902330203. [DOI] [PubMed] [Google Scholar]
  19. Jahromi S. S., Atwood H. L. Three-dimensional ultrastructure of the crayfish neuromuscular apparatus. J Cell Biol. 1974 Nov;63(2 Pt 1):599–613. doi: 10.1083/jcb.63.2.599. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Joyner R. W., Westerfield M., Moore J. W., Stockbridge N. A numerical method to model excitable cells. Biophys J. 1978 May;22(2):155–170. doi: 10.1016/S0006-3495(78)85481-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. KATZ B., MILEDI R. PROPAGATION OF ELECTRIC ACTIVITY IN MOTOR NERVE TERMINALS. Proc R Soc Lond B Biol Sci. 1965 Feb 16;161:453–482. doi: 10.1098/rspb.1965.0015. [DOI] [PubMed] [Google Scholar]
  22. Khodorov B. I., Timin E. N. Nerve impulse propagation along nonuniform fibres. Prog Biophys Mol Biol. 1975;30(2-3):145–184. doi: 10.1016/0079-6107(76)90008-0. [DOI] [PubMed] [Google Scholar]
  23. Kisvarday Z. F., Martin K. A., Friedlander M. J., Somogyi P. Evidence for interlaminar inhibitory circuits in the striate cortex of the cat. J Comp Neurol. 1987 Jun 1;260(1):1–19. doi: 10.1002/cne.902600102. [DOI] [PubMed] [Google Scholar]
  24. Lüscher H. R., Shiner J. S. Computation of action potential propagation and presynaptic bouton activation in terminal arborizations of different geometries. Biophys J. 1990 Dec;58(6):1377–1388. doi: 10.1016/S0006-3495(90)82484-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Lüscher H. R., Shiner J. S. Simulation of action potential propagation in complex terminal arborizations. Biophys J. 1990 Dec;58(6):1389–1399. doi: 10.1016/S0006-3495(90)82485-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Manor Y., Koch C., Segev I. Effect of geometrical irregularities on propagation delay in axonal trees. Biophys J. 1991 Dec;60(6):1424–1437. doi: 10.1016/S0006-3495(91)82179-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Moore J. W., Ramon F. On numerical integration of the Hodgkin and Huxley equations for a membrane action potential. J Theor Biol. 1974 May;45(1):249–273. doi: 10.1016/0022-5193(74)90054-x. [DOI] [PubMed] [Google Scholar]
  28. Parnas I. Differential block at high frequency of branches of a single axon innervating two muscles. J Neurophysiol. 1972 Nov;35(6):903–914. doi: 10.1152/jn.1972.35.6.903. [DOI] [PubMed] [Google Scholar]
  29. Parnas I., Hochstein S., Parnas H. Theoretical analysis of parameters leading to frequency modulation along an inhomogeneous axon. J Neurophysiol. 1976 Jul;39(4):909–923. doi: 10.1152/jn.1976.39.4.909. [DOI] [PubMed] [Google Scholar]
  30. Parnas I., Segev I. A mathematical model for conduction of action potentials along bifurcating axons. J Physiol. 1979 Oct;295:323–343. doi: 10.1113/jphysiol.1979.sp012971. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Rockland K. S. Bistratified distribution of terminal arbors of individual axons projecting from area V1 to middle temporal area (MT) in the macaque monkey. Vis Neurosci. 1989 Aug;3(2):155–170. doi: 10.1017/s0952523800004466. [DOI] [PubMed] [Google Scholar]
  32. Schüz A., Münster A. Synaptic density on the axonal tree of a pyramidal cell in the cortex of the mouse. Neuroscience. 1985 May;15(1):33–39. doi: 10.1016/0306-4522(85)90120-4. [DOI] [PubMed] [Google Scholar]
  33. Segev I. Computer study of presynaptic inhibition controlling the spread of action potentials into axonal terminals. J Neurophysiol. 1990 May;63(5):987–998. doi: 10.1152/jn.1990.63.5.987. [DOI] [PubMed] [Google Scholar]
  34. Sereno M. I., Ulinski P. S. Caudal topographic nucleus isthmi and the rostral nontopographic nucleus isthmi in the turtle, Pseudemys scripta. J Comp Neurol. 1987 Jul 15;261(3):319–346. doi: 10.1002/cne.902610302. [DOI] [PubMed] [Google Scholar]
  35. Shepherd G. M., Brayton R. K. Computer simulation of a dendrodendritic synaptic circuit for self- and lateral-inhibition in the olfactory bulb. Brain Res. 1979 Oct 19;175(2):377–382. doi: 10.1016/0006-8993(79)91020-5. [DOI] [PubMed] [Google Scholar]
  36. Stockbridge N. Solution of the Hodgkin-Huxley and cable equations on an array processor. Ann Biomed Eng. 1989;17(3):253–268. doi: 10.1007/BF02368045. [DOI] [PubMed] [Google Scholar]
  37. Stockbridge N. Theoretical response of a bifurcating axon with a locally altered axial resistivity. J Theor Biol. 1989 Apr 6;137(3):339–354. doi: 10.1016/s0022-5193(89)80076-1. [DOI] [PubMed] [Google Scholar]
  38. Swadlow H. A., Kocsis J. D., Waxman S. G. Modulation of impulse conduction along the axonal tree. Annu Rev Biophys Bioeng. 1980;9:143–179. doi: 10.1146/annurev.bb.09.060180.001043. [DOI] [PubMed] [Google Scholar]
  39. Traub R. D., Wong R. K. Synchronized burst discharge in disinhibited hippocampal slice. II. Model of cellular mechanism. J Neurophysiol. 1983 Feb;49(2):459–471. doi: 10.1152/jn.1983.49.2.459. [DOI] [PubMed] [Google Scholar]
  40. Waxman S. G. Integrative properties and design principles of axons. Int Rev Neurobiol. 1975;18:1–40. doi: 10.1016/s0074-7742(08)60032-x. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES