Essential equilibria

Abstract

The connected uniformly hyperstable sets of a finite game are shown to be precisely the essential components of Nash equilibria.

The concept of equilibrium proposed by Nash (1, 2) is a cornerstone of game theory. He defined an equilibrium as a profile of players' strategies such that each is an optimal reply to others' strategies. Most games have multiple equilibria so his definition is not a complete theory of rational play. Hillas and Kohlberg (3) survey refinements that impose additional decision-theoretic criteria. Nash also showed that a game's equilibria are the fixed points of an associated map (i.e. a continuous function) from the space of strategies into itself, and in algebraic topology, too, refinements select fixed points with stronger properties.

Here, we establish for finite games an exact equivalence between a game-theoretic refinement and a topological refinement. The game-theoretic refinement is the uniform variant of Kohlberg and Mertens' (4) definition of a hyperstable component of equilibria of a game (this and other technical terms are defined below). The topological refinement is O'Neill's (5) definition of an essential component of fixed points of a map. Basically, Theorem 1 below shows that the space of perturbed games considered in the definition of hyperstability is as rich as the class of perturbed maps considered in the definition of essentiality.

Any map whose fixed points are the equilibria is called a Nash map for the game. We (6) prove for two-player games that within the set of Nash maps that are continuous in payoffs as well as strategies, between every two Nash maps there is a homotopy that preserves fixed points; our extension to N-player games has not been published. Similarly, Demichelis and Germano (7) show that the topological index, and thus also the topological essentiality, of an equilibrium component is independent of the map used. Here, in Formulation and Appendix A we show that, in fact, the index depends only on the local degree of the projection map from the equilibrium graph to the space of games. Therefore, hereafter we say that an equilibrium component is essential if it is an essential component of the fixed points of some Nash map, and thus all Nash maps. The restriction to components of equilibria is immaterial for extensive-form games with perfect recall and generic payoffs since for such games all equilibria in a component induce the same probability distribution over outcomes [Kreps and Wilson (8); Govindan and Wilson (9)]. The following paragraphs review definitions of the two refinements.

Essential Components of Fixed Points

Let 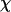be the space of maps f: X → X from/into a topological space X, where 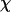is endowed with the compact-open topology. Given f ∈ 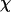, a component is a maximal connected set of its fixed points. A component K is topologically essential if for each neighborhood U of K there is a neighborhood V of f such that each map in V has a fixed point in U. In this article the focus is on the case that X is the space of profiles of players' mixed strategies and f is a Nash map of a game. (In Formulation the space X is denoted Σ and it is a compact convex subset of 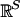with the 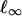norm.)

Uniformly Hyperstable Components of Equilibria

Hyperstability invokes two principles. “Hyper” refers to the axiom of invariance, which requires that a refinement should be immune to treating a mixed strategy as an additional pure strategy. This excludes presentation effects by ensuring that equivalent equilibria are selected in equivalent games. Stability requires that every nearby game has a nearby equilibrium. Here, a nearby game is one with players' payoffs in a neighborhood of those of the given game, represented as a point in Euclidean space with the 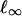norm (we use the 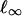norm throughout). Invariance and stability are applied as follows.

Equivalence of Games and Strategies. Two strategies of one player are equivalent if they yield every player the same expected payoff for each profile of others' strategies. A pure strategy is redundant if the player has another strategy that is equivalent. From a game G one obtains its reduction G_* by deleting redundant pure strategies until none remain; the reduction is unique (apart from names of pure strategies). Two games are equivalent if their reductions are the same. If σ is a profile of players' strategies in G then its reduction σ_* is the profile of equivalent strategies of G_*. For each set C of strategy profiles for game G the corresponding set C′ for an equivalent game G′ consists of the profiles of equivalent strategies.

Hyperstability and Uniform Hyperstability. A closed set C of equilibria of game G is hyperstable if for every neighborhood U′ of the equivalent set C′ of equilibria for any equivalent game G′ there exists a neighborhood V′ of G′ such that every game in V′ has an equilibrium in U′. A stronger variant is: A closed set C of equilibria of G is uniformly hyperstable if for every neighborhood U of C there exists δ > 0 such that every δ-perturbation of every equivalent game G′ has an equilibrium equivalent to some strategy profile in U.

Formulation establishes notation, and then Proof of the Theorem proves the following.

Theorem 1. The connected uniformly hyperstable sets are the essential components of any Nash map of the game.

As mentioned above, essential for some Nash map implies essential for every Nash map of the game.¶

Theorem 1 is proved in two parts: an essential component is uniformly hyperstable, Theorem 2; a connected uniformly hyperstable set is an essential component, Theorem 3. An implication of Theorem 1 is that a component is uniformly hyperstable iff its topological index is nonzero. Independently, von Schemde (10) establishes this result for two-player outside-option games. Appendices A and B provide technical tools.

Formulation

We consider games with a finite set N of players, |N| ≥ 2. Each player n ∈ N has a finite set S_n of pure strategies. Interpret a pure strategy s_n as a vertex of player n's simplex Σ_n = Δ(S_n) of mixed strategies. The sets of profiles of pure and mixed strategies are S = Π_n S_n and Σ = Π_n Σ_n. For player n, S_–n = Π_m≠n S_m and Σ_–n = Π_m≠n Σ_m denote the sets of profiles of others' pure and mixed strategies. Given N and S, each game G is described by its payoff function 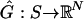from profiles of pure strategies to players' payoffs. Thus a game is specified by a point in 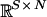. Let Gⁿ and G_n be the extensions of Ĝ_n from profiles of mixed strategies to player n's expected payoffs from pure and mixed strategies; namely, player n's expected payoffs from his pure strategies are given by 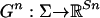, where 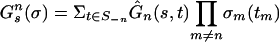, and 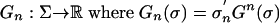. Note that Gⁿ(σ) does not depend on σ_n but G_n(σ) does.

A profile σ ∈ Σ is an equilibrium of G if each player's strategy σ_n is an optimal reply to others' strategies; that is, [τ_n – σ_n]′Gⁿ(σ) ≤ 0 for all τ_n ∈ Σ_n. Equilibria are characterized as fixed points of a map as follows [Gül, Pearce, and Stacchetti (11)]. Let 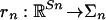be the piecewise-affine map that retracts each point in 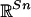to the point of Σ_n nearest in Euclidean distance; i.e., r_n(z_n) is the unique solution r ∈ Σ_n to the variational inequality [τ_n – r]′[z_n – r] ≤ 0 for all τ_n ∈ Σ_n. Let 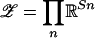and define 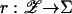via r(z)_n = r_n(z_n) for each player n, and 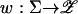via w_n(σ) = σ_n + Gⁿ(σ). Then σ is an equilibrium iff 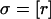(σ). Hence the equilibria are the fixed points of the map 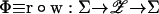. An equilibrium component is a maximal connected set of equilibria and thus compact. Each component of fixed points of the permuted map 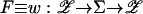is homeomorphic to a corresponding component of the fixed points of Φ and their indices agree [Dold (12)]. In particular, the index is the local degree of the displacement map f ≡ Id – F used below.

A restricted class of perturbations perturbs a player's payoffs from his pure strategies independently of others' behaviors. For each g ∈ 𝒵 define the perturbed game G ⊕ g by (G ⊕ g)ⁿ(σ) = Gⁿ(σ) + g_n and thus 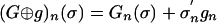. Let 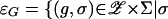is an equilibrium of G ⊕ g} be the graph of equilibria over this class of perturbations. Define 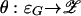by θ_n(g, σ) = σ_n + Gⁿ (σ) + g_n, and let 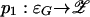be the natural projection. Then θ is a homeomorphism; in particular, θ^–1(z) = (f(z), r(z)). Consequently, 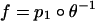. Moreover Appendix A shows that map f has degree +1. There exists an orientation of 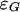such that the local degree of f is the same as the local degree of the projection map p₁. Hence the local degree of f and thus also the index of a component C of G is the same as the degree of the projection map p₁ on any sufficiently small neighborhood of (0, C) in the graph 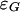. Appendix A presents an alternative definition of the index that depends only on the best-reply correspondence, which is intrinsic to a game independently of the map characterizing equilibria as fixed points.

As described in the Introduction, a profile σ ∈ Σ for game G induces an equivalent profile σ_* ∈ Σ_* of G's reduction G_*. Let A_n be the matrix whose columns are the pure strategies in S_n represented as mixed strategies in Σ_*n. Then σ_*n = A_nσ_n and 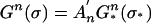. A profile σ ∈ Σ is an equilibrium of G if and only if the equivalent profile σ_* = (A_nσ_n)_n∈N is an equilibrium of G_*.

Proof of the Theorem

We now prove the two parts of Theorem 1. Theorem 2 extends to the entire class of equivalent games the implication of nonzero index established by Ritzberger (13).

Theorem 2. An equilibrium component is uniformly hyperstable if it is essential.

Proof: Let C be an equilibrium component of game G that is an essential component of a Nash map. Then its index is nonzero [O'Neill (5), McLennan (14)], say d ≠ 0. As shown in Appendix A, the index is invariant to addition of redundant strategies, so we can assume that G is reduced. Let U be an open neighborhood of C in Σ. We show that there exists δ > 0 such that for each equivalent game G* and each game G̃* within δ of G* there exists an equilibrium of G̃* equivalent to some profile in U. If necessary by replacing U with a smaller neighborhood, we can assume that the only equilibria in the closure of U are in C. Because no strategy in its boundary ∂U is an equilibrium, 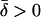, where 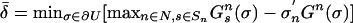. Fix 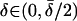. Let G* be a game whose reduction is G, and let C* be the equilibrium component of G* whose reduction is C. Let 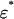be the graph of the equilibrium correspondence over the space of games with the same set of strategies as in G*. Let 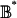be the open ball around G* with radius δ. Let U* ⊃ C* be the set of profiles of G* that reduce to profiles in U; note that a profile in ∂U* reduces to a profile in ∂U. Then 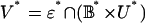is an open neighborhood of (G*, C*) in the graph. Suppose σ* ∈ ∂U* and let σ be the corresponding profile in ∂U. Then there exists a pure strategy s for some player n whose payoff Gⁿ_s(σ) in G from s against σ is greater than the payoff G_n(σ) from the reduction σ_n of σ*_n by at least 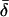. For a game G̃* ∈ 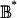, the payoff from s against σ* is strictly greater than 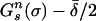while the payoff from σ*_n against σ* is strictly less than 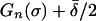. Thus, σ* cannot be an equilibrium of G̃*. Therefore, G̃* has no equilibrium in ∂U*. Consequently, the projection map P*: V* → 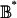is proper: the inverse image of every compact subset of 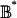under P* is compact. Appendix A shows that the index of C and C* agree. Therefore, by Appendix A, the local degree of G* under P* is d. Because P* is a proper map, this implies that the local degree of each game G̃* ∈ 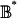is d [Dold (12)]. Therefore the sum of the indices of equilibrium components of G̃* in U* is d. Since d ≠ 0, G̃* has an equilibrium in U*. Since G* could be any game whose reduction is G and every game G̃* in its neighborhood 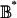has an equilibrium in U*, C is uniformly hyperstable.

Thus those components with nonzero indices are uniformly hyperstable, and such components exist because the sum of the indices of all components is +1. Now we prove necessity.

Theorem 3. A connected uniformly hyperstable set is an essential component.

Proof: Let C be a closed connected set of equilibria of G and let K be the component containing it. Suppose that Ind(K) = 0 or C ≠ K; we show that C is not uniformly hyperstable. Fix a neighborhood U as in the corollary of Appendix A and let δ > 0. We construct an equivalent game G̃ and a perturbation G̃_δ of G̃ such that ∥ G̃ – G̃_δ∥ ≤ δ and the perturbed game G̃_δ has no equilibrium equivalent to a strategy profile in U. The construction of G̃ is done in three steps (we are indebted to a reviewer for suggesting a simplification of Step 2).

The best-reply correspondence for game G is 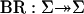, where 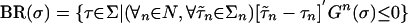. More generally, for β ≥ 0 say that a strategy τ_n of player n is a β-reply against σ ∈ Σ if τ′_nGⁿ(σ) ≥ Gⁿ_s(σ) – β, where s ∈ S_n is any optimal reply of player n against σ. A profile τ is a β-reply against σ if for each n the strategy τ_n is a β-reply for player n against σ.

Step 1: First, we show that without loss of generality we can assume that G satisfies the following property (*): for every neighborhood W of Graph(BR) there exists a map h: Σ → Σ such that:

1. Graph(h) ⊂ W.

2. For each player n the n-th coordinate map h_n of h depends only on Σ_–n.

3. h has no fixed points in U.

It suffices to show existence of an equivalent game G* satisfying (*).

Define G* as follows. Player n's pure strategy set is S*_n = S_n × S_n+1, where n + 1 is taken modulo N. For each n, and m ∈ {n, n + 1}, denote by p_nm the natural projection from S*_n to S_m. Then the payoff function from pure strategies for player n is given by G*_n(s*) = G_n(s), where for each m, s_m = p_m,m(s*_m). In other words, n's choice of a strategy for n + 1 is payoff irrelevant. Clearly G* is equivalent to G. Let Σ*_n be player n's set of mixed strategies in the game G*. We continue to use p_nm to denote the map from Σ*_n to Σ_m that computes for each mixed strategy σ*_n the induced marginal distribution over S_m. Let p: Σ* → Σ be the map p(σ*) = (p_1,1(σ*₁),..., p_N,N(σ*_N)); i.e., p computes the payoff-relevant coordinates of σ*. Finally, let P: Σ* × Σ* → Σ × Σ be the map for which P(σ*, τ*) = (p(σ*), p(τ*)). Use BR* to denote the best-reply correspondence for the game G*. Similarly, C* denotes the component of equilibria of G* equivalent to equilibria in C, and U* denotes the neighborhood corresponding to U.

Fix a neighborhood W* of Graph(BR*). For each μ > 0, let W(μ) be the set of those (σ, τ) ∈ Σ × Σ for which τ is a μ-reply to σ in G. Then the collection {W(μ) | μ > 0} is a basis of neighborhoods of the graph of BR. Choose μ > 0 such that P^–1(W(μ)) ⊆ W*. By the corollary in Appendix A, there exists a map h: Σ → Σ such that Graph(h) ⊂ W(μ) and h has no fixed points in U. Now define the map h*: Σ* → Σ* as follows: for each n, h*_n(σ*) is the product distribution τ_n(σ*) × p_n+1,n+1(σ*_n+1), where τ_n(σ*) = h_n(p_1,1(σ*₁),..., p_n–1,n–1(σ*_n–1), p_n–1,n(σ*_n–1), p_n+1,n+1(σ*_n+1),..., p_N,N(σ*_N)). By construction, each coordinate map h*_n depends only on Σ*_–n. We claim that the graph of h* is contained in W*. To see this, observe first that τ_n(σ*) is player n's component of the image of (p_–n(σ*), p_n–1,n(σ*_n–1)) under h. Since Graph(h) ⊂ W(μ), τ_n(σ*) is a μ-reply to p_–n(σ*). Therefore, (p(σ*), τ(σ*)) belongs to W(μ). Hence (σ*, h*(σ*)) ∈ P^–1(W(μ)) ⊆ W*.

We finish the proof by showing that h* has no fixed point in U*. Suppose σ* is a fixed point of h*. Then each σ*_n is a product distribution with p_n,n+1(σ*_n) = p_n+1,n+1(σ*_n+1) for all n. Therefore p_nn(σ*_n) = p_nn(h*_n(σ*)) = h_n(p_–n(σ*), p_n–1,n(σ*_n–1)) = h_n(p(σ*)) for each player n, which implies that p(σ*) is a fixed point of h. Since h has no fixed point in U, σ* ∉ U*.

Step 2: Let I be the interval [0, δ]. We now show that without loss of generality we can assume that G satisfies the following property (**): there exists a map g: Σ → I^R, where R = Σ_n |S_n|, such that:

1. For each player n, g_n depends only on Σ_–n.

2. No profile σ ∈ U is an equilibrium of the game G ⊕ g(σ).

As in Step 1 we prove this by constructing an equivalent game with the property (**). Since the payoff functions are multilinear on the compact set Σ, there exists a Lipschitz constant M > 0 such that ∥G_n(σ) – G_n(τ)∥ ≤ M∥σ – τ∥ for all n and σ, τ ∈ Σ. We begin with a preliminary lemma.

Lemma. If τ_n is a β₁-reply against σ, ∥τ′_n – τ_n∥ ≤ β₂, ∥σ′ – σ∥ ≤ β₃ then τ′_n is a (β₁ + Mβ₂)-reply to σ and τ_n is a (2Mβ₃ + β₁)-reply to σ′.

Proof of the Lemma: The first result follows directly from the Lipschitz inequality. Let s be an optimal reply for player n to σ′. Then the second result follows by using the Lipschitz inequality along with the inequality: G_n(s, σ′_–n) – G_n(τ_n, σ′_–n) ≤ |G_n(s, σ′_–n) – G_n(s, σ_–n)| + G_n(s, σ_–n) – G_n(τ_n, σ_–n) + |G_n(τ_n, σ_–n) – G_n(τ_n, σ′_–n)|.

Fix η = δ/6M. For each σ ∈ Σ there exists an open ball B(σ) around σ of radius < η such that for each σ′ ∈ B(σ) the set of pure best replies against σ′ is a subset of those that are best replies to σ. Since the set of best replies for each player n to a strategy profile is the face of Σ_n spanned by his pure best replies, BR(σ′) ⊆ BR(σ) for each σ′ ∈ B(σ). The balls B(σ) define an open covering of Σ. Hence there exists a finite set of points σ¹,..., σ^k whose corresponding balls form a subcover. For each σⁱ, let W(σⁱ) be the η-neighborhood of BR(σⁱ). Let W = ∪_i (B(σⁱ) × W(σⁱ)). Then W is a neighborhood of the graph of BR. From Step 1 there exists a map h: Σ → Σ such that (i) Graph(h) ⊂ W; (ii) for each n, h_n depends only on Σ_–n; and (iii) h has no fixed point in U. If τ = h(σ) then there exist σ ⁱ, τⁱ such that σ ∈ B(σ ⁱ), τⁱ is a best reply to σ ⁱ, and τ is within η of τⁱ. Therefore, the Lemma implies that τⁱ is a 2Mη-reply against σ and therefore that τ is a 3Mη-reply against σ.

Fix α > 0 such that if σ ∈ U then ∥σ – h(σ)∥ > α. For each n, let 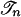be the simplicial complex obtained by taking a sufficiently fine subdivision of Σ_n such that the diameter of each simplex is less than both η and α, and let T_n be the set of vertices of this simplicial complex. Define T = Π_n T_n. We now define a game Ḡ that is equivalent to G, as follows. For each player n the set of pure strategies is T_n. The pure strategy t_n ∈ T_n is a duplicate of the mixed strategy in Σ_n corresponding to the vertex t_n of 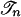. Since the vertices of Σ_n belong to T_n, Ḡ is equivalent to G. Let 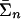be the set of mixed strategies of player n in Ḡ and let 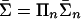. Denote by C̄ and Ū the sets in 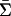that are equivalent to C and U, respectively.

For t_n ∈ T_n, define X(t_n) ⊆ Σ_–n as the projection on to Σ_–n of the inverse image of the closed star (cf. Appendix B) of t_n under the map h_n. And let Y(t_n) be the set of σ_–n ∈ Σ_–n such that ∥t_n – h_n(σ)∥ ≥ 2η [recall that h_n(σ) does not depend on σ_n]. Since the diameter of each simplex of is < η, X(t_n) ∩ Y(t_n) = [null]. Now use Urysohn's lemma to define a function π _tn: Σ_–n → [0, 1] such that .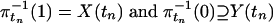

Let R′ = Σ_n |T_n|. We now construct a map 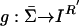with the requisite properties by first defining g on Σ and then extending it to the whole of 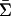by letting g(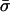) be g(σ), where σ is the equivalent profile in G. For each n, let 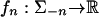be the map defined by f(σ_–n) = max_s∈Sn G_n(s, σ_–n). For each n, t_n ∈ T_n, σ ∈ Σ, let g_tn(σ) = π _tn(σ_–n)[f_n(σ_–n) – G_n(t_n, σ_–n) + Mη]. We first show that g is well defined, i.e. g maps each σ to a point in I^R′. Fix n, t_n, and σ. If σ_–n ∈ Y(t_n), then g_tn(σ) = 0. If σ_–n ∉ Y(t_n), then ∥t_n – h_n(σ)∥ ≤ 2η. Since h_n(σ) is a 3Mη-reply to σ_–n, the Lemma implies that t_n is a 5Mη-reply to σ_–n, i.e., 0 ≤ f_n(σ_–n) – G_n(t_n, σ_–n) ≤ 5Mη. Hence, 0 ≤ g_tn (σ) ≤ 6Mη = δ. Thus, g is a well defined map from Σ into I^R′. Obviously the extension of g to the whole of 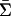also has norm at most δ. Also, by construction for each n, g_n depends only on .

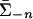To finish the proof of this step we show that if 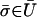then 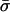is not an equilibrium of . Suppose to the contrary that 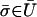is such an equilibrium and let σ be the corresponding strategy in Σ. In the game 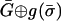, consider the payoff that player n gets when he plays a pure strategy t_n while the others play according to 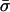. If σ_–n ∈ X(t_n), then his payoff is f_n(σ_–n) + Mη; if σ ∉ X(t_n) then his payoff is G_n(t_n, σ_–n) + π _tn(σ_–n)[f_n(σ_–n) – G_n(t_n, σ_–n) + Mη], which is strictly smaller than f_n(σ_–n) + Mη since π _tn (σ_–n) < 1. Obviously there exists at least one t_n such that σ_–n ∈ X(t_n), for instance, any vertex of the simplex of 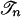that contains h_n(σ) in its interior. Thus, the set of optimal replies to 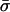for player n, call it T′_n, is the set of t_n's such that σ_–n ∈ X(t_n). For each t_n ∈ T′_n, there exists a simplex of 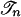that contains t_n and h_n(σ). Hence, the distance between h_n(σ) and t_n is < α. The support of 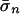being a subset of T′_n, we then have ∥σ_n – h_n(σ)∥ ≤ α. Since we are using the l_∞-distance, ∥σ – h(σ)∥ ≤ α, which is impossible. Thus, there does not exist 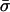in Ū that is an equilibrium of .

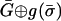Step 3: Suppose g: Σ → I^R has the property (**) described in Step 2. For each σ ∈ U there exists ζ(σ) > 0 and an open ball B(σ) around σ such that for each σ′ ∈ B(σ) and each g′ such that ∥g′–g(σ′)∥ ≤ ζ(σ), σ′ is not an equilibrium of G ⊕ g′. The balls B(σ) form an open covering of U. Hence, there exists a finite set of points σ¹,..., σ^k such that their corresponding balls cover Σ. Let ζ = min_i ζ(σ ⁱ). Construct a simplicial subdivision ℐ of the interval I such that the diameter of each simplex (i.e., a subinterval) is at most ζ. Using the multisimplicial approximation theorem from Appendix B, there exists a simplicial subdivision 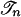of each Σ_n, and for each s ∈ S_n a multisimplicial approximation 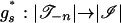of g_s that is multilinear on each multisimplex of 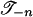. 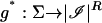Let be the corresponding multisimplicial map defined by the coordinate maps g*_s. By construction, no σ ∈ U is an equilibrium of G ⊕ g*(σ).

As in Appendix B let 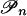be the polyhedral complex generated by 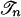, and let γ_n: Σ_n → [0, 1] be the associated convex map. For each n let P_n be the set of vertices of 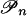. Given a polyhedron P_–n in 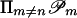, there exists a multisimplex T_–n of 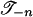that contains it. Since g* is multilinear on each multisimplex, g* is multilinear on each polyhedron.

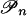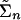Consider now the equivalent game G̃ where the strategy set of each player n is the set P_n of vertices of the polyhedral complex . Let be the set of mixed strategies of player n in the game G̃. For each player n, let A_n be the |S_n| × |P_n| matrix, where column p is the mixed strategy vector that corresponds to the vertex p of 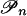. Then the payoff to player n from a strategy vector 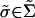is his payoff in G from the profile σ, where 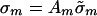for each m. For each n, let B_n: P_–n → I^Pn be the map defined by B_n(p_–n) = A′_ng*_n(p_–n). Consider now the game G̃′ obtained by modifying the payoff functions to the following: for each player n, his payoff from the pure-strategy profile p is G̃_n(p) + B_n,pn(p_–n). By construction G̃′ is a δ-perturbation of G̃. Let c_n be the vector in 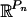where the coordinate p of c_n is γ_n(p). For each δ′ ≤ δ let G̃_δ′ be the game G̃′ ⊕ [–δ′c]. Then G̃_δ′ is a δ-perturbation of G̃.

We claim now that for sufficiently small δ′ the game Ĝ_δ′ has no equilibrium in the set Ũ that is the neighborhood equivalent to U of the equilibrium component C̃ for G̃ equivalent to C. Indeed, suppose to the contrary that there is a sequence δ^k converging to zero and a corresponding sequence of equilibria of G̃_δk that lie in Ũ. For each k let σ ^k be the equivalent profile in Σ. For each k and each player n, if 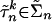is a mixed strategy such that 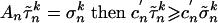. Thus 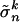solves the linear programming problem 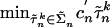subject to 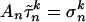. Let 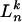be the unique polyhedron of 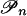that contains 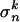in its interior. Since γ_n is a convex function, 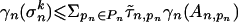for all 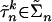such that 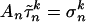, where A_n,p is the p_nth column of A_n and 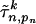is the probability that 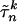assigns to the pure strategy p_n. Moreover, the construction of γ_n ensures that this inequality is strict unless the support of 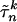is included in 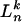. Therefore, the equilibrium strategy 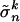assigns positive probability only to points in .

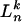Now let 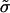be a limit of 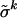as δ^k ↓ 0 and let σ be the equivalent mixed strategy. Then 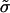is an equilibrium of the game G̃′. Therefore, σ is an equilibrium of the game G ⊕ b, where 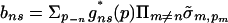for each n and s ∈ S_n. By the arguments in the previous paragraph, there exists for each n a polyhedron 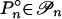such that 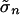assigns positive probability only to points in . Since each 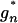is multilinear on the multisimplex T_–n that contains 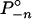, 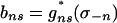. Thus σ is an equilibrium of G ⊕ g*(σ), which is a contradiction. Thus, for all sufficiently small δ′ the game G̃_δ′ has no equilibrium in Ũ.

Thus the connected uniformly hyperstable sets are precisely the essential components as stated in Theorem 1.

Appendix A: Index Theory

An Index Derived from the Best-Reply Correspondence. We define an index for equilibrium components by using the best-reply correspondence and show that this index coincides with the standard index constructed from a Nash map.

Let 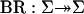be the best-reply correspondence for the game G, i.e. BR(σ) = {τ ∈ Σ | (∀n) τ_n ∈ arg 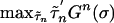}. The set E of equilibria of G is the set of fixed points of BR; i.e. those for which σ ∈ BR(σ). Let C be a component of the equilibria of G. We follow McLennan (14) in defining an index for C. Let U be an open neighborhood of C such that its closure Ū satisfies Ū ∩ E = C. Let W be a neighborhood of Graph(BR) such that W ∩ {(σ, σ) ∈ Σ × Σ | σ ∈ Ū – U} = [null]. By corollary 2 in ref. 14 there exists a neighborhood V ⊆ W of Graph(BR) such that if f₀ and f₁ are any two maps from Σ to Σ whose graphs are contained in V, then there is a homotopy F: [0, 1] × Σ → Σ from f₀ to f₁ such that Graph(F) ⊂ [0, 1] × V. By the proposition in ref. 14 there exists a map f: Σ → Σ for which Graph(f) ⊂ V. Define the index Ind_BR(C) to be the standard index of the restricted map f: U → Σ. The choice of the neighborhood V and the homotopy axiom for index ensure that this index does not depend on the particular map f chosen to compute the index.

The index of the component C can also be defined by using the index obtained from the Nash map Φ: Σ → Σ defined in Formulation, which has the equilibria as its fixed points. Define the Gül-Pearce-Stacchetti (11) index Ind_GPS(C) to be the standard index of the component C computed from the restriction of Φ to the map g: U → Σ.

Theorem 4. Ind_BR(C) = Ind_GPS(C).

Proof: For each λ > 0 define the game G^λ as the game where the payoff functions of all players in G are multiplied by λ; i.e., G^λ = λG. Clearly, all games G^λ have the same equilibria. For G^λ let w^λ be the map corresponding to w in the game G, and let 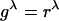be the corresponding GPS map. Then for each λ > 0 the homotopy H: [0, 1] × Σ → Σ, H(t, σ) = g^1+t(λ–1), from g to g^λ preserves the set of fixed points. Hence, the index of C under g^λ is the same for all λ. To prove Theorem 4 it is sufficient to show that there exists λ > 0 such that the graph of g^λ is contained in V, the neighborhood specified in the definition of Ind_BR(C). For each λ > 0 and σ ∈ Σ, w^λ(σ) ≡ z^λ is such that 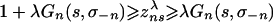for all n, s. Choose c(σ) > 0 such that if s is not a best reply to σ_–n for player n, then G_n(s′, σ_–n) – G_n(s, σ_–n) ≥ c(σ), where s′ is a best reply for player n against σ. Then 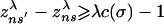if s is not a best reply and s′ is. In particular, if λ ≥ 2/c(σ), then this difference is at least 1. Therefore, for each such λ, z^λ is retracted by r to a point in BR(σ). Now choose an open ball B(σ) around σ in Σ such that (i) B(σ) × BR(σ) ⊂ V; and (ii) for each n and each s ∈ S_n that is not a best reply to σ, there is an s′ such that G_n(s′, σ′_–n) – G_n(s, σ′_–n) ≥ c(σ)/2 for all σ′ ∈ B(σ). Then as before, g^λ(σ′) ∈ BR(σ) for each λ ≥ 4/c(σ) and σ′ ∈ B(σ). The balls B(σ) for σ ∈ Σ form an open cover of Σ. Since Σ is compact there exists a finite set σ¹,..., σ^K ∈ Σ such that ∪ B(σ^k) ⊃ Σ. Let λ* = max_k 4/c(σ^k). For each λ ≥ λ* the graph of g^λ belongs to V, as required.

A corollary follows from results of A. McLennan (personal communication).

Corollary. If C is a closed subset of a component K of equilibria, with C = K only if Ind(K) = 0, then there exists a closed neighborhood U of C for which, for each neighborhood W of Graph(BR), there exists a map h such that Graph(h) ⊂ W and h has no fixed point in U.

Equivalence of Index and Degree. Let 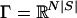be the space of all finite N-player games with a fixed strategy set S_n for each player, and S = Π_n S_n. Let 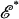be the graph of the Nash equilibrium correspondence over Γ and let 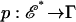be the natural projection. Each game G can be decomposed uniquely as G = G̃ ⊕ g, where for each player n and each pure strategy s ∈ S_n, Σ_s–nG̃_n(s, s_–n) = 0. Thus, Γ is the product space 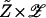of all pairs (G̃, g). Define 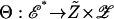by Θ(G̃, g, σ) = (G̃, z) where for each player n and each s ∈ S_n, z_ns = σ_ns + G̃_n(s, σ_–n) + g_ns. Theorem 1 of ref. 4 shows that Θ is a homeomorphism. The inverse Θ^–1 is defined by Θ^–1(G̃, z) = (G̃, g, r(z)), where r(z) = σ is the retraction of z to Σ and g_ns = z_ns – σ_ns – G̃_n(s, σ_–n) for all n and s ∈ S_n. 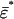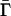Furthermore, Θ extends to a homeomorphism between the one-point compactifications, call them and , of 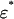and Γ, respectively; and 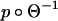is homotopic to the identity map on 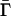. Thus, the map 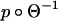has degree +1. We can therefore orient 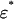such that the projection map p: 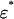→ Γ has degree 1. Given a game G and a component C of the game, choose a neighborhood U of {(G̃, g)} × C in the graph that is disjoint from the other components of equilibria of G (viewed as a subset of 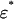). The degree of C, denoted deg(C), is the local degree of (G̃, g) under the restriction of p to U. Since Θ is the identity on the 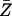factor, we can also define the degree of C by using 𝒵 as the space of games. Indeed given the game G = (G̃, g), let 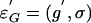such that ((G̃, g′), σ) belongs to 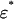. 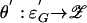Let be the map θ′(g′, σ) = z, where z is such that Θ((G̃, g′), σ) = (Ĝ, z). Then θ′ is a homeomorphism between 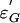and 𝒵 and as before we can define the degree of C as the local degree of the projection map from a neighborhood of {g} × C in 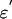whose closure does not contain any other equilibria of the game G. Obviously, these two definitions are equivalent. If we use θ′ then the degree of C is just the degree of g under the map 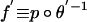from a neighborhood V of θ′({g} × C) in 𝒵, where p is the natural projection from 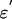to 𝒵. Letting θ and f be the maps defined in Formulation, we have θ′({g} × C) = θ({0} × C), and f = f′ – g. Therefore, the degree of zero under the map f over V is the same as the degree of g under the map f′ over V. As in Formulation, the degree of zero under the map f over V is the index of the component w(C) of the fixed point set of F, which is the same as the index of C under the GPS map Φ.

Invariance of Index and Degree. We provide a simple proof by using the index defined by the best-reply correspondence.

Theorem 5. The index of a component of equilibria is invariant under the addition or deletion of redundant strategies.

Proof: Let C be an equilibrium component of game G. It suffices to show that the index of C is invariant under the addition of redundant strategies. Accordingly, for each player n let T_n be a finite collection of mixed strategies. Let G* be the game obtained by adding the strategies in T_n as pure strategies for n; i.e., n's pure strategy set in G* is S_n ∪ T_n. Let Σ*_n be his set of mixed strategies. Let BR* be the best-reply correspondence in Σ*. Let p*: Σ* → Σ be the function that maps each mixed strategy in G* to the equivalent mixed strategy in G. Let ι: Σ → Σ* be the inclusion map that sends a point in Σ to the corresponding point on the face of Σ*; precisely, ι(σ) = σ*, where σ*_ns = σ_ns for s ∈ S_n and σ_nt = 0 for t ∈ T_n. Obviously, ι(σ) ⊂ p^–1(σ) for each σ ∈ Σ.

Let C* ≡ p^–1(C) be the equilibrium component of G* corresponding to C. Let U be an open neighborhood of C whose closure is disjoint from other equilibrium components of G. Let U* = p^–1(U). Choose a neighborhood W* of the graph of BR* such that the index of C* can be computed as the sum of the indices of the fixed points in U* of any map h* whose graph is contained in W*.

Let W be a neighborhood of the graph of BR such that (σ, τ) ∈ W implies p^–1(σ) × p^–1(τ) ⊂ W*. By ref. 14, every neighborhood of the graph of BR contains the graph of a function. Therefore, by the definition of Ind_BR(C), there exists a map h: Σ → Σ such that (i) the graph of h is contained in W; (ii) h has no fixed points on the boundary of U; and (iii) Ind_BR(C) is the index of the map h over U. Define now a map h*: Σ* → Σ* by 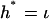. Then, by construction the graph of h* is contained in W*.

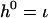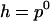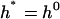Moreover, h and h* have homeomorphic sets of fixed points. In fact, the fixed points of h* are the image of the fixed points of h under the injective map ι. Letting , we have that and . Therefore, by the commutativity property of the index [Dold (12)], the index of the map h: U → Σ is the same as that of h*: U* → Σ*. Hence Ind_BR*(C*) = Ind_BR(C).

Appendix B: Multisimplicial Complexes

A Multisimplicial Approximation Theorem. We establish a multilinear version of the simplicial approximation theorem. This result may be known but we found no reference. We begin with some definitions; see Spanier (15) for details.

A set of points {v₀,..., v_n} in 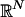is affinely independent if the equations 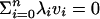and Σ_i λ_i = 0 imply that λ₀ = ··· = λ_n = 0. An n-simplex K in 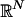is the convex hull of an affinely independent set {v₀,..., v_n}. Each v_i is a vertex of K and the collection of vertices is called the vertex set of K. Each σ ∈ K is expressible as a unique convex combination Σ_i λ_iv_i; and for each i, σ(v_i) ≡ λ_i is the v_ith barycentric coordinate of σ. The interior of K is the set of σ such that σ(v_i) > 0 for all i. A face of K is the convex hull of a nonempty subset of the vertex set of K.

A (finite) simplicial complex 𝒦 is a finite collection of simplices such that the face of each simplex in 𝒦 belongs to 𝒦, and the intersection of two simplices is either empty or a face of each. The set V of 0-dimensional simplices is called the vertex set of 𝒦. The set given by the union of the simplices in 𝒦 is called the space of the simplicial complex and is denoted 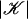. For each 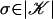, there exists a unique simplex K of 𝒦 containing σ in its interior; define the barycentric coordinate function σ: V → [0, 1] by letting σ(v) = 0 if v is not a vertex of K and otherwise by letting σ(v) be the corresponding barycentric coordinate of σ in the simplex K. For each vertex v ∈ V, the star of v, denoted St(v), is the set of 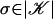such that σ(v) > 0. The closed star of v, denoted ClSt(v), is the closure of St(v).

A subdivision of a simplicial complex 𝒦 is a simplicial complex 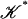such that each simplex of 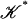is contained in a simplex of 𝒦 and each simplex of 𝒦 is the union of simplices in 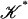. Obviously 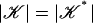. We need the following theorem on simplicial subdivisions for our approximation theorem below (15).

Theorem 5. For every simplicial complex 𝒦 and every positive number λ > 0 there exists a simplicial subdivision 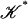such that the diameter of each simplex of 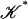is at most λ.

A multisimplex is a set of the form K₁ × ··· × K_m, where for each i, K_i is a simplex. A multisimplicial complex 𝒦 is a product 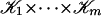, where for each i, 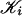is a simplicial complex. The vertex set V of a multisimplicial complex 𝒦 is the set of all (v₁,..., v_m) for which each v_i is a vertex of 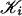. The space of the multisimplicial complex is 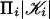and is denoted 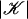. For each vertex v of 𝒦, the star of v, St(v), is the set of all 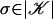such that for each i, σ_i ∈ St(v_i). The closure of this set is Cl St(v). A subdivision of a multisimplicial complex 𝒦 is a multisimplicial complex 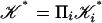where for each i, 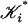is a subdivision of 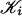. In the following, 𝒦 is a fixed multisimplicial complex and ℒ is a fixed simplicial complex.

Definition 1: A map 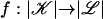is called multisimplicial if for each multisimplex K of 𝒦 there exists a simplex L in ℒ such that:

1. f maps each vertex of K to a vertex of L;

2. f is multilinear on |K|; i.e. for each σ ∈ |K|, f(σ) = Σ_v∈V f(v)·Π_i σ_i(v_i).

By property (i) vertices of K are mapped to vertices of L. Therefore, for each σ ∈ |K|, f(σ) is an average of the values at the vertices of K. Since the simplex L is a convex set, the image of the multisimplex K is contained in L. If 𝒦 is a simplicial complex then Definition 1 coincides with the usual definition of a simplicial map. In this special case the image of a (multi)simplex K under f is a simplex of ℒ, which is not necessarily true in general.

Definition 2: Let 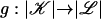be a continuous map. A multisimplicial map 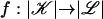is a multisimplicial approximation to f if for each 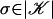, f(σ) is in the unique simplex of ℒ that contains g(σ) in its interior.

We could equivalently define a multisimplicial approximation by requiring that for each σ and each simplex L of ℒ, if g(σ) ∈ L then also f(σ) ∈ L. We now prove a multisimplicial approximation theorem.

Theorem 6. Suppose that 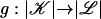is a continuous map. Then there exists a subdivision 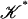of 𝒦 and a multisimplicial approximation 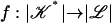of g.

Proof: The collection {g^–1(St(w)) | w is a vertex of ℒ} is an open covering of 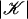. Let λ > 0 be a Lebesgue number of this covering; i.e., every subset of 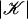whose diameter is < λ is included in some set of the collection. By Theorem 5, there exists for each i a simplicial subdivision 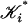of 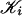such that the diameter of each simplex is < λ/2. Then for each vertex v of K*, St(v) has diameter < λ (recall that we use the 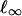norm). We first define a function f ⁰ from the vertex set of 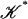to the vertex set of ℒ as follows. For each vertex v of 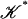, since the diameter of St(v) is < λ, there exists a vertex w of ℒ such that g(St(v)) ⊂ St(w). Let f ⁰(v) = w. Suppose v¹,..., v^k are vertices of a multisimplex K. We claim that their images under f ⁰ span a simplex in ℒ. Indeed, since the v^j's are vertices of a multisimplex, we have that ∩_jSt(v^j) is nonempty. Therefore,

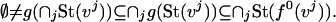Therefore, the vertices f ⁰(v^j) span a simplex in ℒ. Since f ⁰ maps vertices of a multisimplex to vertices of a simplex, there exists a well defined unique multilinear extension of f ⁰, call it f. To finish the proof we show that f is a multisimplicial approximation of g. Let σ be an interior point of a multisimplex K and let L be the simplex containing g(σ) in its interior. For every vertex v of K, g(St(v)) ⊆ St(f(v)) by construction. Thus g(σ) ∈ St(f(v)) for each vertex v of K. In particular, the set of vertices {f(v) | v is a vertex of K} span a subsimplex L′ of L. Since f(σ) ∈ L′, f is a multisimplicial approximation of g.

The proof of Theorem 6 shows a slightly stronger result. Let η = λ/2, where λ is as defined in the proof. If each 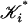is subdivision of 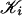such that the diameter of each simplex is at most η then g admits a multisimplicial approximation 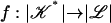. Thus, we obtain:

Corollary 2. There exists η > 0 such that, for each subdivision 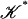of 𝒦 with the property that the diameter of each multisimplex is at most η, there exists a multisimplicial approximation 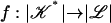of g.

Construction of a Convex Map on a Polyhedral Subdivision. We describe the construction of a convex map associated with a polyhedral refinement of a simplicial subdivision.

Let 𝒯 be a simplicial complex obtained from a simplicial subdivision of the d-dimensional unit simplex Σ in 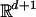. The polyhedral complex 𝒫 is derived from 𝒯 as follows [Eaves and Lemke (16)]. For each simplex τ ∈ 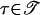whose dimension is d – 1, let 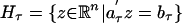be the hyperplane that includes τ and is orthogonal to Σ. Then each closed d-dimensional admissible polyhedron of 𝒫 has the form 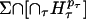, where each p_τ ∈ {+, –} and H⁺_τ and H^–_τ are the two closed half-spaces whose intersection is H_τ. Enlarge 𝒫 by applying the rule that each lower-dimensional polyhedral face of an admissible polyhedron is also admissible. By construction, the closure of each simplex in 𝒯 is partitioned by admissible polyhedra of 𝒫, any two nondisjoint admissible polyhedra meet in a common face that is also an admissible polyhedron, and each admissible polyhedron is convex. Associate with 𝒫 the map γ: Σ → [0, 1] for which γ(σ) = α Σ_τ |a′_τσ – b_τ|, where the scaling factor α > 0 is sufficiently small that γ(Σ) ⊆ [0, 1]. Then γ is convex and piecewise affine. In particular for any finite collection σ¹,..., σ^k of points in Σ and nonnegative scalars λ¹,..., λ^k such that Σ_i λⁱ = 1, we have that γ(Σ_i λⁱσⁱ) ≤ Σ_i λⁱγ(σⁱ), with the inequality being strict if and only if there does not exist an admissible polyhedron of 𝒫 that contains all of the σⁱs.