Mechanisms of classical crystal growth theory explain quartz and silicate dissolution behavior

Abstract

The central control of mineral weathering rates on biogeochemical systems has motivated studies of dissolution for more than 50 years. A complete physical picture that explains widely observed variations in dissolution behavior is lacking, and some data show apparent serious inconsistencies that cannot be explained by the largely empirical kinetic “laws.” Here, we show that mineral dissolution can, in fact, be understood through the same mechanistic theory of nucleation developed for mineral growth. In principle, this theory should describe dissolution but has never been tested. By generalizing nucleation rate equations to include dissolution, we arrive at a model that predicts how quartz dissolution processes change with undersaturation from step retreat, to defect-driven and homogeneous etch pit formation. This finding reveals that the “salt effect,” recognized almost 100 years ago, arises from a crossover in dominant nucleation mechanism to greatly increase step density. The theory also explains the dissolution kinetics of major weathering aluminosilicates, kaolinite and K-feldspar. In doing so, it provides a sensible origin of discrepancies reported for the dependence of kaolinite dissolution and growth rates on saturation state by invoking a temperature-activated transition in the nucleation process. Although dissolution by nucleation processes was previously unknown for oxides or silicates, our mechanism-based findings are consistent with recent observations of dissolution (i.e., demineralization) in biological minerals. Nucleation theory may be the missing link to unifying mineral growth and dissolution into a mechanistic and quantitative framework across the continuum of driving force.

Over long time scales, the geochemistry of earth systems is, in large part, controlled by the kinetics of silicate mineral dissolution. Because waters contain a wide variety of solute types and concentrations, including significant levels of aqueous silica, there is considerable need to understand the dependence of silicate mineral dissolution rates on chemical driving force, as measured by the extent of undersaturation. This need has motivated intense investigations of both mineral weathering and the corrosion behavior of silica-based glasses.

Basic thermodynamic principles predict that mineral dissolution rates should increase with increasing driving force or chemical potential; however, experimental studies of major silicate minerals show that this dependence is complex. A further complication is the so-called “salt effect” reported for quartz, SiO₂, whereby the dissolution rate of this oxide end-member to all silicates is increased up to 100 times in the presence of the major cationic solutes found in natural waters (Na⁺, K⁺, Ca²⁺, Mg²⁺) (1–3). In contrast, dissolution rates of silicate minerals have only a weak sensitivity to the introduction of electrolytes (4). To explain these behaviors, many of the widely used rate models are based on variants of transition state theory and assume microscopic reversibility (5–7). Their shortcomings raise the question of whether or not the mechanistic models developed in the last few decades to so successfully explain crystallization can be used to resolve the confusion surrounding mineral dissolution.

Twenty years ago, a mechanistic model of nucleation-driven crystal growth was introduced that described growth kinetics in terms of four primary parameters: temperature T, supersaturation σ, step edge energy α, and step kinetic coefficient β (8, 9). By examining energy barriers to growth, the theory considered the probability of growth at dislocation defects vs. growth by nucleation of two-dimensional (2D) adatom islands either at impurity defects or homogeneously across the surface, as illustrated in Scheme 1.

Scheme 1.

This same theory also should apply to dissolution by analogous processes that also assume rates are controlled through T, σ, α, and β, but this hypothesis has never been tested. Application of this formalism to dissolution assumes that, in analogy to growth, it may occur by activating “corrosion” either at dislocation defects or by nucleation of 2D vacancy islands at impurities or homogeneous sites, as illustrated in Scheme 2.

Scheme 2.

Indeed, by using this approach, we can quantitatively explain the dissolution kinetics of quartz and of the major silicate weathering minerals, feldspar (KAlSi₃O₈) and kaolinite [Al₂Si₂O₅(OH)₄]. We also show that the principle of detailed balancing (5) is only applicable to quartz dissolution at very near to equilibrium conditions where corrosion occurs by simple step edge retreat.

Methods

Dissolution Experiments. Dissolution-rate experiments used the 300- to 425-μm fraction of pure quartz sand (Destin, FL). The material was pretreated with 30% H₂O₂ for 24 h, then alternately washed with 10% HNO₃ and distilled deionized water. Specific surface area of the final material was determined in triplicate (Micromeritics, Norcross, GA). Mixed flow-through reactors constructed of commercially pure titanium were used to measure the rate of silica production at 200°C for the overall reaction

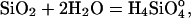[1]

at steady-state conditions using established methods (3). The solutions were prepared to specific values of undersaturation by adding carefully characterized levels of the monomeric silicic acid, H₄SiO₄. Some silica solutions also contained reagent-grade salts (Aldrich) using 0.05 M NaCl or 0.0167 M CaCl₂·2H₂O such that total ionic strength was constant at 0.05 M. All input solutions had circumneutral pH and calculated in situ pH (pH_T) of ≈5.7. The degree of undersaturation, σ, is defined by

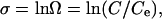[2]

where C and C_e are the measured and equilibrium concentrations of 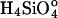. We use concentrations instead of activities because H₂O and 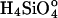have activity coefficients very near unity for the conditions of our experiments. A value of C_e = 10^-2.4 M SiO₂ (236 ppm SiO₂), obtained from our dissolution experiments, is used to calculate undersaturation, σ.

Atomic Force Microscopy (AFM) Imaging. In parallel experiments, natural (100) prismatic surfaces of euhedral quartz crystals (Herkimer, NY) were exposed to the solution conditions provided in Table 1. The rationale for these choices will become clear later.

Table 1. Treatment conditions for (100) quartz surfaces.

Number	Solution	Ω	σ
	No electrolyte	0.10	—2.3
	0.0167 M CaCl2	0.10	—2.3
	0.0167 M CaCl2	0.65	—0.4
	0.0167 M CaCl2	0.90	—0.1

The surfaces were prepared as thin slices taken from the natural crystal surface and restrained in a hydrothermal mixed flow-through reactor using titanium screen. Durations of each treatment were determined by using measured dissolution rates to calculate the amount of reaction time necessary to give equal silica production (0.010 mol·m^-2) for each treatment. Thus, etching times ranged from 28 days to 4 h. Resulting surface morphologies were examined by AFM under a drop of water at ambient conditions.

Results

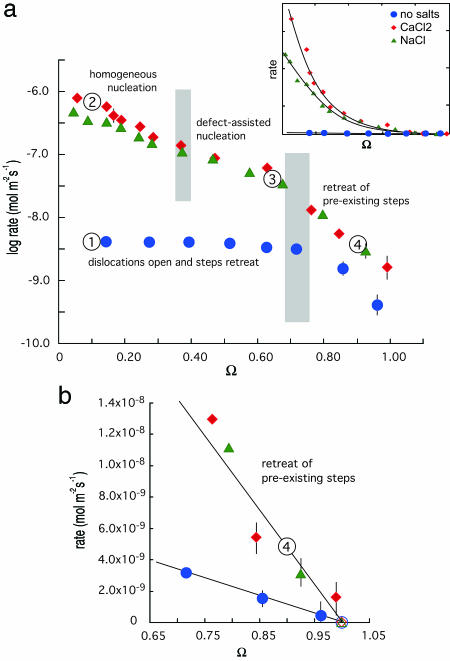
Kinetic measurements of quartz dissolution show a complex dependence on saturation state (Fig. 1a). At the low driving force of near-equilibrium conditions, dissolution rates are inversely correlated with Ω and the rate-enhancing effect of electrolytes is small (1–4×, Fig. 1b). This result indicates that salts have relatively little effect on quartz dissolution at the near-equilibrium conditions commonly found in geothermal systems with large rock/water ratios or long contact times. When the driving force to reaction is higher (Ω < 0.70) rates acquire a nonlinear dependence on undersaturation. In the absence of electrolytes, quartz exhibits the characteristic “dissolution plateau” also reported for gibbsite and kaolinite (6, 10) (Fig. 1a). In contrast, rates measured in solutions that also contain 0.05 M NaCl or 0.0167 M CaCl₂ become up to 100 times faster with decreasing Ω. This salt-promoted rate enhancement at low Ω, the so-called salt effect, is unique to quartz (3), and Fig. 1a Inset shows that this effect is highly dependent on Ω.

Fig. 1.

Measured rates of quartz dissolution vs. saturation state (Ω) show the dependence on driving force and the presence or absence of simple electrolyte salts. Calculated experimental errors indicate 1SD of the mean estimate and are illustrated for values larger than the symbol diameter. (a) Logarithm of rate vs. saturation state in water (blue circles), 0.0167 M CaCl₂ (red diamonds), and 0.05 M NaCl (green triangles). Numbers correspond to conditions that produced the surface structures in Fig. 2, and gray zones show undersaturation range where transitions occur in the dominant dissolution mechanism. Inset uses a linear ordinate to better illustrate the exponential dependence of rate on driving force when salts are introduced. (b) Expanded view of rate dependence on Ω shows the linear dependence on saturation at near-equilibrium conditions. This region is where the widely accepted first-order rate dependence such as Eq. 8 applies. Eq. 8 is fit to the data by forcing rate to zero at Ω = 1.0 as denoted by open symbols.

Discussion

A mechanism-based explanation for the kinetic behavior in Fig. 1a is found in the dislocation and 2D nucleation theories developed for crystal growth (8, 9, 11). A brief description of our application to dissolution is as follows. The rate at which a crystal dissolves is controlled by the density of steps on the surface. These steps can be preexisting on the initial crystal surface or at the crystal edges, emerge from dislocation sources, or be created by nucleating new vacancy islands. Whichever source creates the greatest step density will dominate the dissolution process. Vacancy islands are initiated by removal of molecules from the otherwise perfect crystal surface. These pits will, on average, grow provided they exceed a critical size determined by the Gibbs–Thomson effect, a well-known thermodynamic principle. At this critical size, the free energy change goes through a maximum that defines an energy barrier to island formation. The height of the free energy barrier decreases with increasing undersaturation and increases with increasing interfacial energy of the newly created surface (i.e., the edge of the island).

At sufficiently low undersaturation, the free energy barrier becomes too high for vacancy island nucleation to occur on a time scale that is competitive with the other processes. Dislocations, although few in number, then provide the dominant source of steps. The step density of etch pits at dislocations also depends on interfacial energy and undersaturation. At very low undersaturations, step density drops below the natural roughness of the crystal surface including the crystal edges, which are always a source of steps because they are rounded due to free energy minimization. Dissolution then is dominated by retreat of these preexisting steps.

To test these models for the dissolution of minerals, we generalize the original growth equations so that they describe both growth and dissolution for a wide range of saturations.

Dissolution at Dislocation. Regardless of the step source, the surface normal growth or retreat rate R of a crystal can be expressed as

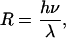[3]

where h = step height, λ = step spacing, and ν = speed of a moving step. Both R and v are negative for dissolution. Similarly, regardless of the step source, the ν in Eq. 3 depends on solution concentration according to the relation (8, 12)

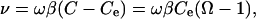[4]

where β is the step kinetic coefficient (cm·s^-1). Because β depends only on step direction and not the source of the steps, the determining factor for which step source dominates is the step spacing, λ.

Classical crystal growth theory states that there is a critical negatively free energy, ΔG_Crit, beyond which the line defects would expand continuously and become an etch pit (13–16). This relation is given by

[5]

where α is the interfacial free energy, ω is the molecular volume of a molecule in the crystal, μ is the bulk shear modulus, and b is a Burgers vector. This critical value represents the activation energy barrier for the formation of an etch pit at a dislocation. The height of the activation energy barrier depends on the nature of the crystal (e.g., interfacial free energy and its Burgers vector) and is independent of solution undersaturation. Note that for an edge dislocation in quartz, the equation still applies because Poisson's ratio for quartz is small (0.077) (15).

When dissolution occurs at a dislocation, λ is related to the critical size r_c and the perimeter of the dislocation source P by

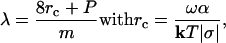[6]

where m = number of elementary steps, k = Boltzmann constant, T = temperature, and α = interfacial free energy associated with the step edge created at a pit, henceforth called “step edge energy.” By substituting Eqs. 4 and 6 into Eq. 3 and rewriting in the form of log|-R| vs. Ω to conform to the conventional method of presenting mineral dissolution data (as in Fig. 1a), we obtain the surface normal dissolution rate at a dislocation R_d as a function of undersaturation

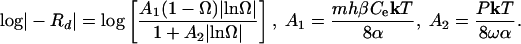[7]

Eq. 7 has properties that show the physical basis of the dissolution plateau and also shows the link to macroscopic rate laws. This function diverges negatively as Ω approaches 1, rises rapidly as Ω decreases, transitions to a plateau region of low slope near Ω = exp(-1/A₂), and reaches a finite value as Ω goes to zero (note that plotting the data in this form accentuates the plateau). This result is qualitatively in agreement with quartz dissolution rates in pure H₂O. There are two additional effects that need to be considered. First, at very small Ω, step spacing becomes so close that the relationship in Eq. 4 is no longer valid because overlap in the diffusion fields for adjacent steps weakens the dependence on Ω (17). This effect accentuates the dissolution plateau by further reducing the slope. The second effect becomes important as Ω approaches 1 where step spacing at dislocation sources, which varies as 1/Ω, becomes larger than the average step spacing of the initial crystal surface and/or the steps retreating from the crystal's edges, λ₀. In addition, there is a critical energy barrier to etch pit formation. In this case, the step spacing also is given by λ₀. Combining Eqs. 3 and 4, the dissolution rate becomes

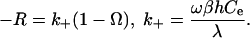[8]

This equation is of the form used to describe macroscopic dissolution rate data within standard transition state theory (5, 7) for the kinetics of a pseudo-first-order reaction. Here, we have related the macroscopic rate coefficient k₊ to the microscopic kinetic coefficient β of elementary step motion. As Fig. 1b shows, the near-equilibrium dissolution data do indeed exhibit a linear dependence on Ω. As a result, the electrolyte effect on relative dissolution rate becomes constant, whereas the absolute differences diminish to zero as the two curves converge to equilibrium (Ω = 1). From a fit to the data we estimate k₊ to be 1.1 ± 0.2 × 10^-8 and 5.1 ± 1.2 × 10^-8 mol·m^-2·s^-1 for dissolution in the absence and presence of electrolytes, respectively.

Independent evidence for a transition from step retreat to dislocation-controlled dissolution at these conditions is found in the AFM images of the (100) quartz surfaces. Samples treated in solutions without salts at high driving force (Ω = 0.1) reveal irregularly spaced etch pits having large dimensions of ≈4,000 × 10,000 nm (Fig. 2, ). The sloping sides of these features merge with pointed bottoms, thus indicating that they arise from dislocation defects in the mineral (18). The prevalence of these etch structures concurs with earlier studies citing the importance of dislocation defects in controlling silicate dissolution at small values of Ω (15).

Fig. 2.

AFM images of representative (100) surfaces of quartz exposed to four different solution chemistries for equivalent extents of reaction show the different dissolution processes across driving force and solution chemistry. (Scale bar: 1 μm in all images.) When Ω = 0.10 in H₂O, surfaces are dominated by large etch pits with sloping sides that converge at dislocation sources. Pits are separated by relatively flat regions on the surface. For conditions where Ω = 0.10 and the solution contains 0.0167 M CaCl₂, the surface is covered with a high density of small pits with flat bottoms and with flanks that are 25% steeper than those measured for pits in . At the intermediate driving force of Ω = 0.65 in a salt solution of 0.0167 M CaCl₂, a mixture of larger and smaller flat bottom pits form across the surface. At a low driving force of Ω = 0.90 in 0.0167 M CaCl₂, the surface shows only straight-edged steps with no evidence of pitting.

The complementary AFM images of quartz surfaces exposed to very near-equilibrium conditions (Ω = 0.90) in CaCl₂ solutions confirm that dissolution occurs through a simple step retreat process by showing surfaces comprised of multiple straight-edged steps without evidence of etch pits (Fig. 2, ). Note that these experiments purposefully used CaCl₂ solutions, which, as we show below, increase rates and probabilities of pit formation. We infer, therefore, that dissolution in solutions without electrolytes in these near-equilibrium solutions also proceeds by simple step retreat. At conditions where the driving force needed to initiate dissolution at dislocation defects is exceeded, our AFM observations reinforce the conclusion that total rate is governed by density of step edges.

Dissolution by Nucleation of Vacancy Islands. To explain the differences in the data obtained with and without salts in Fig. 1a, we now consider dissolution by etch pit nucleation at vacancy islands. The general expression for dissolution or growth by nucleation processes is based on the assumption that the free energy barrier to initiating a vacancy or adatom island, respectively, from a perfect surface, ΔGⁿ_Crit, is given by (9)

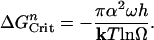[9]

Eq. 9 shows that the barrier to formation of vacancy islands by 2D nucleation depends on solution undersaturation, in contrast to the energy barrier for etch pits formed at dislocations (Eq. 5). Hence, as the undersaturation increases, the energy barrier to nucleation must decrease.

When growth or dissolution occurs at a smooth face through 2D nucleation, the normal growth or dissolution rate (R_n) of the face due to formation of 2D nuclei at a rate of J is expressed as (8, 18)

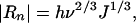[10]

where the steady-state nucleation rate, J, is given by (9)

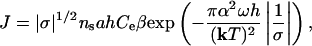[11]

where a is the lattice spacing and n_s is the density of nucleation sites, which in turn is proportional to exp(-E_b/kT) where E_b is the kinetic barrier to etch pit formation associated with removal of atoms from the surface layer. Note that Eq. 11 shows that the nucleation process takes over because of the strong exponential dependence of rate on saturation state in contrast to the weak dependence that comes from Eq. 4. By substituting Eqs. 4 and 11 into Eq. 10, we rewrite Eq. 10 into a form that is linear in 1/σ

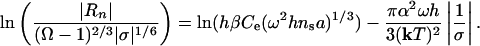[12a]

To derive an equivalent expression for dissolution at dislocations we rewrite Eq. 7

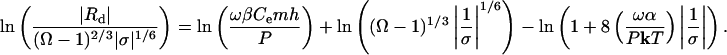[12b]

Although this expression is no longer linear in 1/σ, it allows us to make a direct comparison with Eq. 12a. The slopes of Eqs. 12a and 12b yield the step edge free energy, α, that corresponds to dissolution or growth by nucleation and dislocation processes, respectively. However, these energies are not those of the perfect crystal surface. Rather they are associated with the region of the crystal in the vicinity of the dislocation and/or impurity. Consequently, they are expected to be far less than that of the perfect crystal surface.

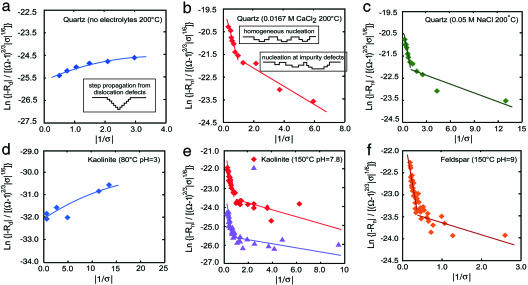
Applying Eq. 12a to the dissolution rate measurements collected in CaCl₂ and NaCl solutions results in two linear trends (Fig. 3 b and c). A similar result also was documented for the dependence of growth on supersaturation in both inorganic and macromolecular systems (9, 19, 20). The region of steep slope found for growth at far-from-equilibrium conditions was postulated to correspond to the homogenous nucleation of adatom islands, whereas the region of shallow slope corresponds to islands nucleated at defects such as impurity atoms (9, 19, 20). Images and in Fig. 2 confirm that dissolution features show the analogous nucleation of vacancy islands, and comparison with image in Fig. 2 shows that these structures contrast sharply with those produced in the absence of electrolytes; instead of exhibiting large, widely spaced, pointed-bottom pits, the (100) surfaces treated with solutions at Ω= 0.1 that also contained CaCl₂ display a very high density of small etch pits with typical sizes of 250 × 600 nm.

Fig. 3.

Mechanistic models describe the dependence of dissolution rate on the driving force of undersaturation for measured rates of quartz and previously reported rates of aluminosilicate dissolution. (a) Dislocation model (Eq. 12b) predicts the behavior of quartz dissolution rate in the absence of electrolytes. (b) In contrast, dependence of quartz dissolution rate on undersaturation in 0.0167 M CaCl₂ solutions is predicted by the nucleation model (Eq. 12a). (c) Again, nucleation model fits quartz dissolution behavior in 0.05 M NaCl. (d) The lower temperature measurements of kaolinite dissolution rate at 80°C show a dependence on driving force that is predicted by the dislocation model. (e) In contrast, the markedly different dependence of kaolinite dissolution rate on driving force at 150°C is predicted by the nucleation model. The nucleation model describes data reported at acidic and circumneutral pH. (f) Reported rates of K-feldspar dissolution measured at 150°C and pH 9 also exhibit a dependence on undersaturation that is predicted by the nucleation model.

On surfaces etched under conditions corresponding to the region of steeper slope in Fig. 3b, the small, uniform size and distribution of pits across the surface indicate that they are the result of homogeneous 2D nucleation of vacancy islands (Fig. 2, ). As such, they are continuously regenerated as the surface retreats. Comparisons of images and 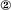in Fig. 2 show that the physical basis for the salt effect arises through a transition from dissolution controlled by the population of dislocation defects to 2D nucleation of vacancy islands. As shown in Eqs. 11 and 12a, the data do not allow us to determine whether the source of this transition is from a reduction in the step edge free energy associated with the free energy barrier to stabilizing a pit or a reduction in the kinetic barrier, E_b, to removing atoms from the surface to initiate a pit, which manifests itself in n_s. Moreover, this physical model provides no information about the chemical source of either reduction. The calculated free energy barriers to dissolution by the 2D process are 61 ± 6 and 79 ± 14 mJ/m² for NaCl and CaCl₂ solutions, respectively (see Table 2, which is published as supporting information on the PNAS web site).

The nucleation model also fits rates measured at the intermediate driving force to exhibit a linear trend of lower slope (Fig. 3 b and c). This result corresponds to the growth regime in which Malkin and others (9, 19, 20) postulated that nucleation occurred preferentially at impurity defects. In this “defect-assisted” model, impurities induce localized strain to give lower free energy barriers than for 2D nucleation at a perfect surface. This explanation for growth is consistent with our dissolution data. The surface morphology, as seen in image 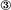in Fig. 2 at Ω = 0.65, shows the dominance of widely spaced, larger etch pits (≈400 × 1,300 nm) surrounded by smaller etch pits. The former are the pits that nucleate at defect sites. The latter are the homogenously nucleating pits that grow in number until they completely dominate at high undersaturation (Fig. 2, 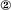). Fitting rates measured in CaCl₂ and NaCl solutions for conditions of region 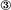with Eq. 12a indeed leads to a linear dependence and lower step edge energies. Our estimates of step edge energy for the CaCl₂ and NaCl solutions give values of 32 ± 10 and 18 ± 8 mJ/m², respectively, for region .

To extract the step edge energy for dislocation sources, Eq. 12b is fitted to the rate measurements obtained for solutions with Ω < 0.85 in solutions without electrolytes (region of Fig. 1a). The fit to the data (Fig. 3a) yields β values of ≈1 × 10^-6 cm/s and α = 16.2 ± 5 mJ·m^-2. These estimates are specific to quartz at 200°C without electrolytes where the chemical potential conditions favor dissolution at dislocation defects. As one expects from the theory, this direct estimate of quartz step edge energy is quite low compared with the macroscopic interfacial free energy estimated as 120 mJ·m^-2 for 25°C (21) and 280 mJ·m^-2 at 300°C (15). More significantly, it is also substantially lower than that for nucleation of vacancy islands either at homogenous or impurity sites. However, once these latter barriers are overcome, the measured rates are faster because the total number of pits, and therefore the total amount of step edge, or roughness, is far greater.

Nucleation Theory also Explains Silicate Dissolution Kinetics. Our success in applying nucleation rate theory to quartz dissolution leads us to test dissolution-rate data for silicate minerals. The complex rate data reported for the major rock-forming silicate, K-feldspar (22), appears to also obey nucleation rate theory (Fig. 3f) through the same processes that govern quartz dissolution in salt solutions (compare Fig. 3 b and c). The evidence suggests that, for decreasing driving force, the dominant dissolution process for this aluminosilicate also undergoes a transition from the homogeneous nucleation of vacancy islands to nucleation at impurity sites with step edge energies of 30 ± 4 and 8 ± 4, respectively, for the conditions of the experiments.

We also find that nucleation theory reconciles the origin of different dependencies of kaolinite dissolution rates on driving force. To conduct this analysis, we use published experimental dissolution rates for kaolinite dissolution and growth measured at 80°C and 150°C (6, 23). By fitting these two data sets to the nucleation rate model, we show that the 150°C data fit the rate model for dissolution by 2D nucleation homogeneously and at impurity defects to give surface energies of 23 ± 2 and 4 ± 2 mJ/m² at high and low driving force, respectively (Fig. 3e). In contrast, the rates measured at 80°C exhibit behavior predicted by the dislocation defect model (Fig. 3d). For this lower-temperature condition, we estimate α = 2.6 ± 0.4 mJ/m² and β = ≈2 × 10^-8 cm/s. Comparisons of these values show that the lower interfacial energy measured for the dislocation-driven dissolution is consistent with the theoretical model, but these differences alone do not account for the dramatic difference in behavior at these two temperatures. The true source of this difference is easy to understand from Eqs. 7 and 12a. R_d is weaker than linear in T, whereas R_n has an exponential dependence. At low T, R_d dominates, but as T increases, R_n quickly becomes greater. We conclude, therefore, that these kaolinite data sets are not at all inconsistent; rather, they exhibit a predictable thermally activated transition in the dominant dissolution mechanism.

Several insights to kinetic controls on mineral dissolution arise from our analyses of these aluminosilicates. First, the silicate minerals we tested are able to undergo dissolution by 2D nucleation at hydrothermal temperatures in pure solutions at moderate values of Ω, whereas quartz requires the presence of salts and far-from-equilibrium conditions to induce dissolution by this process. This difference can be understood from the lower value of α for silicate minerals, which allows dissolution by 2D nucleation without salts: no further change in mechanism occurs when salts are added. This finding explains why rates of silicate dissolution are not enhanced (4) when electrolytes are introduced. Second, the three mineral systems that we tested indicate that 2D nucleation dominates rates measured at higher temperatures of 150–200°C. In contrast, the 80°C data for kaolinite is predicted by the dislocation defect model. This sharp temperature-dependent change in mechanism suggests that the practice of extrapolating high temperature data to the ambient temperatures of earth surface environments may greatly overpredict rates of dissolution under circumstances where the extrapolation comes from rates driven by 2D nucleation. The lesson from this analysis is that one needs to know the boundaries between the various dissolution regimes before extrapolating measured kinetics to different temperatures. Third, we show that pH, which has a strong control on silicate dissolution rate, does not alter this behavior. Data reported for kaolinite at both pH 2 and 7.8 show that temperature drives the dependence of rate on saturation state.

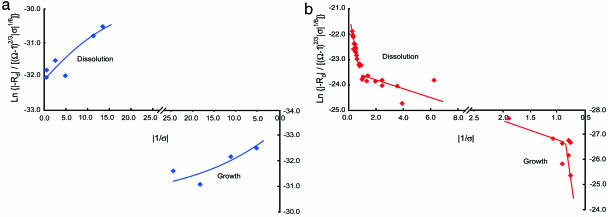
Finally, we test the ability of the general forms of this theory given by Eqs. 12a and 12b to predict the dependence of kaolinite dissolution and growth on saturation state and temperature. By using reported rates for kaolinite at 80°C (6), Fig. 4a shows that dissolution and growth obey Eq. 12b. However, rates of growth and dissolution at 150°C (23) appear to be dominated by 2D and impurity-assisted nucleation processes at large and small excursions from equilibrium, respectively (Fig. 4b), according to Eq. 12a. Application of these relations again shows that, although the values of the material-dependent parameters α, β, and E_b will differ, the surface processes that hold for growth are directly analogous to those active during dissolution.

Fig. 4.

Published kinetic data for kaolinite dissolution and growth give a test of the mechanistic models for both growth and dissolution. The theories predict the distinct differences in the dependence of dissolution and growth rates on undersaturation and supersaturation, respectively, that are reported. (a) The dislocation model, Eq. 12b, describes the dependence of reaction rates of growth and dissolution on positive and negative driving force, respectively, at 80°C. (b) Because of the exponential dependence of nucleation rate, J, on temperature, Eq. 11, a transition to dissolution and growth rates by surface nucleation processes occurs to give rate behavior described by the 2D nucleation model, Eq. 12a.

Broad Implications for Other Families of Crystalline Materials. Recent observations reported in the literature suggest that the nucleation model presented in this work also may predict the dissolution rates of the sparingly soluble salts. This finding hints at the possibility that the mechanistic model also will predict the rapid dissolution or “demineralization” of biological materials under some conditions. For example, brushite (CaHPO₄·2H₂O) demineralization results in “polypit” formation on the surface (24, 25). Similarly, a study of barite (BaSO₄) dissolution at high ionic strength showed 2D nucleation features (26). More recently, nanoscale observations of calcite (CaCO₃) dissolution across driving force found that surfaces undergo the same transitions in “dissolution modes” that change from retreat of steps, to opening and dissolution on dislocation etch pits, to the formation of 2D and defect-assisted nuclei (27). Although qualitative, the observations in these studies suggest that, as would be explained by the model, dissolution of sparingly soluble salts can be controlled by nucleation processes. This result is predicted with the mechanistic model because the relatively lower energy barriers to dissolution of these salts would allow a transition by 2D nucleation without the thermal activation required by the covalently bonded quartz and silicates.

The successes of classical growth theory in explaining the dissolution kinetics of minerals with properties spanning the covalent to ionic chemistries suggest it may become possible to predict the dependence of dissolution and corrosion on undersaturation and temperature for a large variety of minerals and crystalline materials. However, a number of questions are still unanswered. First, during dissolution, step splitting and retreat from crystal edges leads to the rounding of facet edges, but it is unclear what the contribution of this process is to the overall dissolution rate. Given sufficient time, it seems that these steps must retreat across the full diameter of a crystallite, but no evidence for these steps is seen in Fig. 2. Second, the step density and step speed will always determine the dissolution rate. Yet comparison of step densities for dislocation pits and etch pits in images and of Fig. 2, respectively, does not show an increase of the magnitude expected from the rate measurements. Moreover, the flat areas between dissolution pits in both cases show that, even at steady state, step retreat near the top of the pits must exceed that within the pits (28). Finally, although the model can be used to predict the dependence of rates on saturation state and temperature, without independent knowledge of materials parameters such as α, it cannot predict absolute dissolution rates. Moreover these parameters are likely to be largely unknown in natural systems. Consequently, despite the unifying and intuitive view of growth and dissolution provided by this model, there is much to be done to develop and test its concepts.