Dynamical model of long-term synaptic plasticity

Abstract

Long-term synaptic plasticity leading to enhancement in synaptic efficacy (long-term potentiation, LTP) or decrease in synaptic efficacy (long-term depression, LTD) is widely regarded as underlying learning and memory in nervous systems. LTP and LTD at excitatory neuronal synapses are observed to be induced by precise timing of pre- and postsynaptic events. Modification of synaptic transmission in long-term plasticity is a complex process involving many pathways; for example, it is also known that both forms of synaptic plasticity can be induced by various time courses of Ca²⁺ introduction into the postsynaptic cell. We present a phenomenological description of a two-component process for synaptic plasticity. Our dynamical model reproduces the spike time-dependent plasticity of excitatory synapses as a function of relative timing between pre- and postsynaptic events, as observed in recent experiments. The model accounts for LTP and LTD when the postsynaptic cell is voltage clamped and depolarized (LTP) or hyperpolarized (LTD) and no postsynaptic action potentials are evoked. We are also able to connect our model with the Bienenstock, Cooper, and Munro rule. We give model predictions for changes in synaptic strength when periodic spike trains of varying frequency and Poisson distributed spike trains with varying average frequency are presented pre- and postsynaptically. When the frequency of spike presentation exceeds ≈30–40 Hz, only LTP is induced.

Investigations of long-term synaptic plasticity have revealed many striking results over the past two decades. The intense interest in this feature of nervous systems comes in part from the fact that these phenomena are widely held to underlie learning and memory. It is known from recent experiments that the precise timing of pre- and postsynaptic activity is important for long-term potentiation (LTP) and long-term depression (LTD) (1–4). Spikes initiate a sequence of complex biochemical processes during a short time window after synaptic activation at the postsynaptic side. Identifying the detailed molecular processes underlying LTP and LTD remains a complex and challenging problem. It is widely accepted that N-methyl-d-aspartate (NMDA) receptors are crucial for the development of LTP or LTD. NMDA-dependent activity determines Ca²⁺ concentrations in the postsynaptic cell. The Bienenstock, Cooper, and Munro rule (5) describes the synaptic plasticity process as a function of postsynaptic activity presumed to be connected to Ca²⁺ concentration (6). Modest activity induces LTD, whereas strong activation produces LTP. On the basis of this idea, models of calcium-dependent synaptic plasticity that describe the experimental data with a fixed set of parameters have been proposed (7, 8). Different theoretical hypotheses are also suggested by the authors of refs. 9 and 10. Senn et al. (9), for example, formulate a learning algorithm for regulating neurotransmitter release probability.

These models are very interesting and promising. Building on these results, we propose here a fully dynamical model of synaptic plasticity. The model is phenomenological because we introduce dynamical variables P(t) and D(t) that do not have a direct relationship with the concentration of any biochemical component.

The resulting model of an activity-dependent modifiable synapse is on the same footing as familiar phenomenological models describing the generation of action potentials. In the latter case, despite the huge number of ionic channels and their complex voltage dependence, as well as the complex activity of cellular pumps maintaining a dynamic balance in a neuron, it has been possible to build phenomenological models such as conduction-based Hodgkin–Huxley models or even more simplified models such as the Hindmarsh–Rose and the Morris–Lecar models (for a discussion of many models, see ref. 11). These models have been successful in replicating observations and in understanding unknown features of neuron activity.

A set of observations over many years has shown that temporally correlated action potentials from a pre- and a postsynaptic neuron in culture can lead to incremental strengthening or weakening of the strength of excitatory synapses connecting them. In their clear recent review of these experiments, Bi and Poo (3) present a quantitative description of dependence on spike timing for the modification of the synapses connecting two excitatory neurons as a function of τ = t_post − t_pre when a single presynaptic and a single postsynaptic spike is evoked at times t_pre and t_post, respectively. The biophysical description of LTP and LTD actions associates them with augmented or reduced Ca²⁺ release into a postsynaptic cell as voltage-gated Mg⁺ blockers on NMDA receptors are removed by depolarization (12). Our approach here is not at this cellular level. Instead, we identify a phenomenological action with each part of the two-component process.

In their experiments on synaptic modification at excitatory synapses between hippocampal glutamatergic neurons in culture, Bi and Poo (2, 3) indicate that if a presynaptic spike arrives at time t_pre and a postsynaptic spike is observed or induced at t_post, then when τ = t_post − t_pre is positive, the incremental percentage increase in synaptic strength behaves as

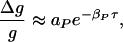1

with β_P ≈ (1/16.8 ms). When τ < 0, the percentage decrease in synaptic strength behaves as

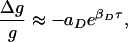2

with β_D ≈ (1/33.7 ms). a_P and a_D are constants.

Others have shown that LTP and LTD can be induced without postsynaptic action potentials. For example, one can depolarize the postsynaptic cell and then, by presenting presynaptic action potentials, induce LTP. Interestingly, introducing various time courses of Ca²⁺ concentration in the postsynaptic cell, either LTP or LTD can be induced. LTP is associated with rapidly induced high concentrations of Ca²⁺, whereas LTD is induced with lower concentrations presented at lower frequencies (13, 14). These experiments suggest the cooperation of two processes in the postsynaptic cell that have different time constants. A two-component postsynaptic model for LTP/LTD processes is also suggested in the review of Malenka and Nicoll (15).

Two-Component Model for Synaptic Plasticity

The data in figure 1 of Bi and Poo (3) also may indicate that two processes are at work in synaptic plasticity. Each has its own time constant and strength. We suggest that these two processes are possibly both postsynaptic and related to NMDA receptors, and that each satisfies a phenomenological kinetic equation. The resultant LTP or LTD from the joint action of these two processes depends on the relative timing between them. We describe the processes by the variables P(t) and D(t). Our model takes P(t) to be activated by presynaptic voltages V_pre(t), whereas D(t) is activated by postsynaptic actions V_post(t). Our two macroscopic variables embody two cellular events that compete with each other to achieve plasticity. This view does not contradict well-accepted descriptions such as the BCM rule (5).

We refer the reader to the discussion of Bi and Poo (3) on biochemical mechanisms that may underlie the two observed time scales. It is argued that postsynaptic spiking after EPSPs induced by presynaptic action leads to opening NMDA receptors accompanied by a high flux of Ca²⁺, whereas the opposite order may permit low concentrations of Ca²⁺ through voltage-gated channels for Ca²⁺ followed by a further small influx associated with NMDA receptors. At the level of phenomenological formulation presented here, we do not propose a specific identification of the underlying cellular dynamics with either dynamical variable D(t) or P(t).

Whether or not these are the correct identifications of the biophysical and biochemical processes associated with Biand Poo's and others' observations, we attempt to capture those processes in a kind of “spatial average” of underlying dynamics that must be described by appropriate kinetic and nonlinear reaction–diffusion equations. Performing the required averages on a set of equations describing the basic processes goes well beyond the scope of the present paper. Instead, we wish to determine whether a quantitative expression of the observations is possible in a quite simplified two-component/two-timescale model. As we discuss here, our model quantitatively realizes the experiments of Bi and Poo (3) and appears in qualitative agreement with many other features of LTP and LTD observations. A derivation of the proposed model or equivalent models from more a fundamental point of view would thus seem quite attractive.

We take the activities D(t) and P(t) to satisfy the simple first-order kinetic equations

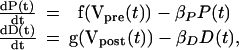3

where the functions f(V) and g(V) are typical logistic or sigmoidal functions that rise from zero to order unity when their argument exceeds some threshold. These driving or input functions are a simplification of the detailed way in which each dynamical process is forced. The P(t) process is associated with one time constant (1/β_P), whereas the D(t) process is associated with a different time constant (1/β_D). Experiment shows that β_P ≠ β_D, and this is the primary embodiment of the two different time scales seen in many observations. The two time constants are a coarse-grained representation of the diffusion and leakage processes that damp and terminate the activities. Presynaptic voltage activity serves to release the neurotransmitter in the usual manner, and this in turn induces the postsynaptic actions of P(t), which has a time course determined by the time constant β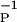. Similarly, we associate the postsynaptic voltage, constant or time varying, with induction of the D(t) process.

The driving functions f(V) and g(V) could also depend on Ca²⁺ concentrations in the postsynaptic cell as suggested by refs. 13–15, but we do not propose any specific mechanism for this. If there are no changes in pre- or postsynaptic potentials, a representation of this Ca²⁺ dependence would permit our phenomenological modeling to be extended to the experiments discussed in refs. 13–15.

We attribute the change in synaptic strength to the nonlinear joint action of these pre- and postsynaptic processes. This is an embodiment of the ideas of many authors whose work is reviewed in refs. 3, 14, and 16, and we build on their work. Calling the percentage change in synaptic strength Δg(t), we write the time variation of this due to P(t) and D(t) processes as

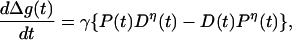4

where η > 1. γ > 0 is proportional to the strength of the synaptic connection; as that remains nearly constant, we take γ to be a constant; we have also investigated the case where γ is proportional to g(t). This rule incorporates a kind of competition between the two processes that seems to be implicated by the results in refs. 13–15. Further, this requires both P(t) and D(t) processes to be operating to alter synaptic strengths. Isolated P(t) activity, perhaps followed long afterward or preceded long before by D(t) activity, will not produce synaptic strength change. “Long” is determined by the time scales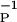 β and β.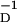

We can interpret the combination of P(t) and D(t) appearing in the dynamical equation for Δg(t) as saying that if t_pre, the nominal time at which an action potential from the presynaptic cell invades the synapse occurs before t_post, the nominal time of postsynaptic backpropagation activity, then when t = t_post, P(t) has been on for a time τ = t_post − t_pre and the term P(t)D^η(t) dominates D(t)P^η(t) for η > 1 leading to overall enhancement of Δg. This is because both P(t) and D(t) start at zero and rise only when the pre- or postsynaptic action, respectively, arrives at the synapse, so each is small in magnitude. This leads to positive changes in the synaptic strength g. The opposite effect occurs if τ = t_post − t_pre < 0.

The net change Δg due to D(t) and P(t) activity is

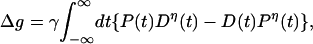5

where at long times in the past, we have Δg = 0; namely, we start with the baseline synaptic strength, and the actual upper limit on the integral is set by the extinction of either D(t) or P(t) activity.

The general solutions of the kinetic equations for P(t) or D(t) activation are

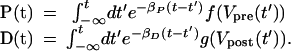6

If the action potentials V_pre(t) and V_post(t) are localized around t = t_pre and t = t_post, respectively, then the approximate value of these integrals becomes

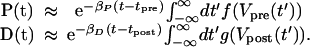7

We first consider the simplest case of an isolated very narrow presynaptic spike occurring at t = t_pre and an isolated narrow postsynaptic spike occurring at t = t_post. For this setup, the equations for P(t) and D(t) become

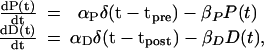8

where α_P and α_D are the strengths of the spikes represented as δ functions at t = t_pre and t = t_post, respectively.

The solutions to these equations are then

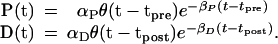9

θ(t) = 0, t < 0 and θ(t) = 1, t > 0.

The integral for Δg(τ), with τ = t_post − t_pre, is for τ ≥ 0

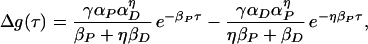10

whereas for τ ≤ 0, we have

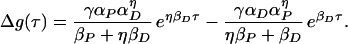11

The idea that the LTP/LTD rule seen by Bi and Poo and others could provide a balance between LTD events and LTP events (17, 18) is automatically embodied in these two formulae. If we integrate Δg(τ) over all possible τ, we find

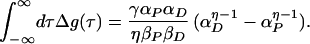12

When the strengths of the pre- and postsynaptic spikes are equal, this integral is 0. Because evoked action potentials are very similar, with only interspike intervals carrying neural information, the idea that α_P = α_D is quite natural. That the integral is zero for whatever β_P and β_D means that a neuron receiving random spikes from the environment will, on average, produce Δg = 0, and that only information bearing spike trains will affect synaptic strengths.

Determination of Model Parameters

For our solution using δ functions, we first note that for large positive τ we have

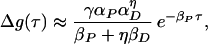13

as in figure 1 of Bi and Poo (2), and for large negative τ, we have

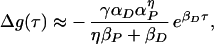14

also as in ref. 2.

The value of Δg(τ) at τ = 0 is continuous for any pre- or postsynaptic spike strength and is a positive constant times (η − 1)(β_P − β_D) for α_P = α_D. Using the values indicated by Bi and Poo (2) β_P ≈ 2β_D, we see Δg(τ = 0) > 0, which is consistent with figure 1 of ref. 3.

If the strengths of the P(t) and D(t) spikes are equal α_P = α_D, then the large τ LTP and large (negative) τ LTD amplitudes determine η when we know β_P and β_D. This relation is

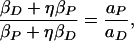15

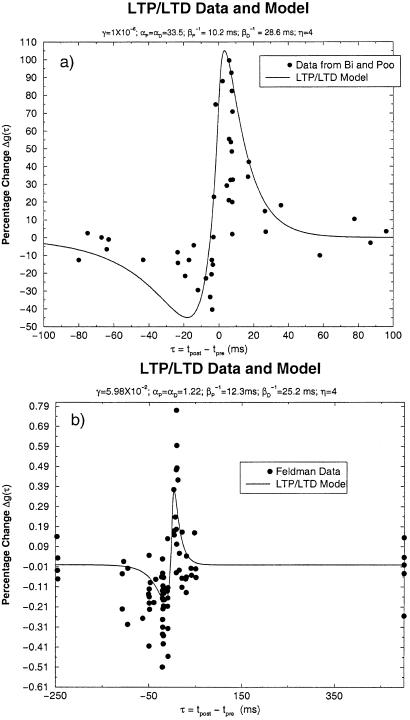
where a_P and a_D are the constants from ref. 2. From their paper, we find (a_P/a_D) = 1.8. Using the data of Bi and Poo (2), we have made a fit to formulae 10 and 11, which is displayed in Fig. 1a. The parameters from this fit are

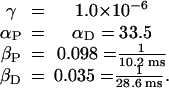16

From Eq. 15, we determine that η = 4. These time constants are slightly different from those reported by Bi and Poo, who fit only the exponential tails of the distributions. They report β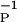 ≈ 16.8 ms and β 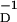≈ 33.7 ms. All these numbers are well within the scope of the errors associated with the measurements reported in refs. 2 and 3. For example, in ref. 17 it is noted that the errors in time constants seen in ref. 2 were β 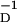= 34 ± 13 ms and β 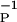= 17 ± 9 ms. Our values are well within these error limits.

Figure 1.

(a) Δg(τ) for the data of Bi and Poo (2) and for the two-component LTP/LTD model. (b) Δg(τ) for the data of ref. 4 and the two-component model.

We have looked at a “best” fit to the data of Bi and Poo and found that as a function of η there is a broad minimum in the least-squares error associated with our formula. From the existing data, we cannot confidently select a value of η from the range 3 ≤ η ≤ 20. We have chosen η = 4 as representative. The qualitative look of the fits to the data with values of η in the range given is excellent, and the least-squares error differs by only a few percent in this range. For all values of η in this range, we find α_P ≈ α_D, indicating that equal strength pre- and postsynaptic pulses were used, and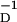 β ≈ 3β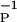 for all η. The overall strength γ varied quite substantially with η. The main uncertainty in selecting better values for these parameters comes from measurements near τ = 0.

We have also examined the data from Feldman (4) on LTP/LTD induced in the Barrel Cortex of rat by using protocols similar to those of Bi and Poo. Again with η = 4 and α_P = α_D, we find, as shown in Fig. 1b, α_P = 1.22, γ = 5.98 × 10⁻², β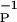 = 12.3 ms, and β 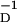= 25.2 ms. Again, note that the major uncertainty in these estimated parameters comes from the region τ ≈ 0.

Predictions Using the Model

Our simple formulae 10 and 11 provide a way to unify a variety of observations over many preparations. They also provide a means for predicting the outcome from presenting different spike trains or other waveforms to the pre- and postsynaptic cells. As an illustration of the prediction abilities of the model, we examined finite sequences of periodic and random spike trains.

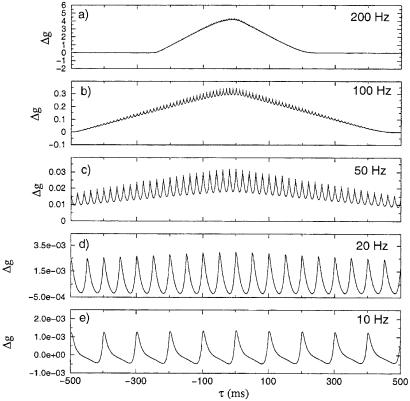
We have investigated the LTP/LTD effect arising from a finite length periodic train of pre- and postsynaptic spikes by using our basic dynamical equations. We introduced two periodic spike trains with paired pre- and postsynaptic spikes at relative times t_post − t_pre and each with spikes separated by interspike intervals T. Fifty pairs of spikes were presented to the synapse with frequencies T⁻¹ varying between 10 Hz, T = 100 ms, and 200 Hz, so T = 5 ms. The results are shown in Fig. 2 for a selection of T. When T is large, T = 100 ms, or T⁻¹ = 10 Hz, the actions of the pre- and postsynaptic pairs are independent, and we see 50 repetitions of the basic process displayed in Fig. 1. At 20 Hz, we see substantial interaction between the effects of paired spikes, and at 50 Hz and above, we see LTD disappear and only potentiation is observed. This result is strikingly consistent with the experimental results observed in neurons in the rat visual cortex (19). The oscillations present at all T are due to the selection of strictly periodic pairs of pre- and postsynaptic spikes. At 200 Hz, we see that before the spike trains arrive at the synapse, no effect is seen, and this is true after they no longer are affecting the synapse. During the time when they overlap, only LTP is seen. If we increase the number of spike pairs, we see the temporal region of potentiation increase as well. It is interesting to note that in these simulations, if we choose a time shift τ between spikes that leads to LTD for individual pairs, then when we increase the frequency over a threshold, only LTP is observed. This result is again consistent with the experiments reported in ref. 19.

Figure 2.

Prediction of Δg(τ) when two periodic spike trains with the same frequency and number of spikes are generated in the pre- and postsynaptic neurons. We plot Δg(τ) as a function of the time shift τ between the pre- and postsynaptic spike trains. The frequency of the spike trains are (a) 200, (b) 100, (c) 50, (d) 20, and (e) 10 Hz. In all cases, spike trains with 50 pre- and 50 postsynaptic spikes were used. Note that at spike pair frequencies above 50 Hz, only LTP is seen. This is a result of the asymmetry in the single spike pair response.

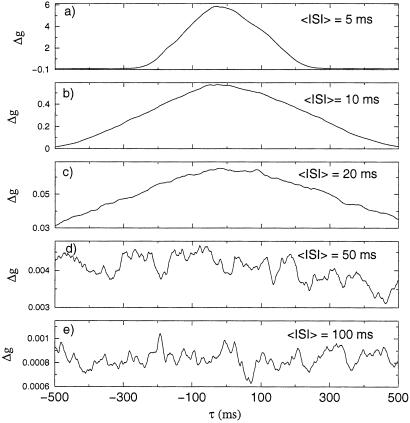
We also investigated the model prediction when we presented spike trains with a Poisson distribution of interspike intervals (ISIs) with varying mean ISI. In Fig. 3, we show the result of an average over 500 trials with 50 pre- and 50 postsynaptic spikes with Poisson distributions of ISIs. The mean ISI interval ranges from 100 to 5 ms. In the simulations for the parameters obtained from the experimental data, only LTP is observed.

Figure 3.

Prediction of Δg(τ) when two spike trains with interspike intervals generated by a Poisson process are generated in the pre- and postsynaptic neurons. The mean ISI values, denoted as 〈ISI〉, are: (a) 5, (b) 10, (c) 20, (d) 50, and (e) 100 ms. The time lag τ between the pre- and postsynaptic spike trains is calculated by the time difference between the first two spikes of both spike trains. These figures are averaged over 500 realizations of the Poisson distributed spike train with 50 spikes in each set.

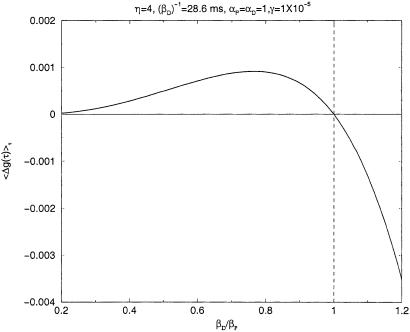
Another remaining issue is the dependence of LTP and LTD on the decay constants. To illustrate this point, we fixed β_D and varied the ratio (β_D/β_P) to determine whether there is a separation between regions of LTP and LTD. In Fig. 4, we show the synaptic strength change Δg as a function of (β_D/β_P) plotting the average 〈Δg(τ)〉_τ over the window [−100 ms, 100 ms]

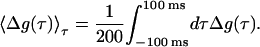17

We can see that near β_P ≈ β_D, LTP, on average, and LTD, on average, switch roles. This result comes from a simulation using our proposed LTP/LTD rule with periodic spike trains presented to the pre- and postsynaptic neurons at 50 Hz. We expect the same result for other presentation frequencies and other dynamical parameters, as the crossover at β_P ≈ β_D is a kinematic result associated with the different time scales of LTP or LTD.

Figure 4.

Prediction of 〈Δg(τ)〉_τ, Δg(τ) averaged over a window [−100 ms; 100 ms], for periodic spike trains of 50 periodic spikes with a firing frequency of 50 Hz. We plot average synaptic change as a function of (β_D/β_P) for fixed β = 28.6 ms. Two well defined regions of LTP and LTD are seen, with β_P ≈ β_D as the separation point.

Possible Connection with the BCM Rule

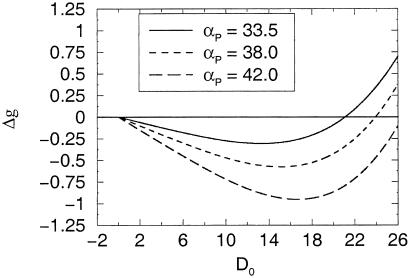
There is a very interesting solution to our equations, based on protocols to produce LTP or LTD by using a steady depolarization of the postsynaptic neuron (20, 21). If the postsynaptic cell is voltage clamped, then D(t) rapidly approaches a constant value D₀ that will depend on the voltage clamp level. If the driving function g(•) in the equation for D(t) depends on other cellular parameters, such as the concentration of Ca²⁺, then D₀ also depends on them. In qualitative terms, we refer to D₀ as indicative of postsynaptic neural activity.

If the presynaptic voltage is a spike as above and the postsynaptic cell is still activity clamped, then we find for times (t − t_pre)β_P ≫ 1

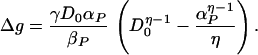18

In Fig. 5, we plot Δg as a function of the clamped activity D₀ for three different values of α_P. These show the characteristic form of the BCM rule with a region of depression followed by a regime of potentiation separated by a sliding threshold.

Figure 5.

Clamped postsynaptic activity. Dependence of Δg as a function of D₀, which represents the level of postsynaptic activity. This is shown for three different setting of α_P; see Eq. 18. The qualitative connection to the BCM rule is clear. The parameter values for the process are γ = 1 × 10⁻⁶, η = 4, and β = 10.2 ms.

The case of voltage clamping both the post- and presynaptic cells also gives a simple result for Δg. These two cases have been examined experimentally by Wigström et al. (22), Kelso et al. (23), and Malinow and Miller (24). Their results are in agreement with the patterns of plasticity predicted by the two-component model.

Discussion

The discovery of spike time-dependent plasticity has important implications for our understanding of information processing, learning, and memory in the brain. One of the most important aspects is in the coding of neural information by exact spike timing and not just spike rates. Recent experiments on excitatory synapses in hippocampal and neocortical slices (1, 25) and in cultured neurons (2, 3) have shown that the specific timing of pre- and postsynaptic action potentials plays a crucial role in synaptic modification. To investigate this possibility in a simulation of neural networks with such synapses, one needs a convenient dynamical model of learning processes. In this paper, we have proposed and investigated a model of synaptic plasticity that is able to reproduce the experimental evidence associated with spike time-dependent plasticity and predict new dynamical features.

Because molecular events in synaptic firing have many different time scales, at first sight it seems necessary to build a many-dimensional model for the description of the temporal variation of any synaptic efficacy, depending on pre- and postsynaptic activity. However, the experimental data display a comparatively simple dependence of changes in the synaptic efficiency on the relative timing of pre- and postsynaptic events. This means that a macroscopic dynamical model of this synaptic plasticity can be low dimensional. Some experiments on LTP/LTD are suggestive of oscillations in Δg(τ), and if these are present, a straightforward modification of the first-order kinetics for P(t) and D(t) can account for such additional degrees of freedom.

We also performed a simulation of the response of excitatory synapses with model parameters determined by the data of Bi and Poo to presentations of periodic pre- and postsynaptic spike trains with periods ranging from 5 to 100 ms and to pre- and postsynaptic spikes trains with Poisson ISI distributions of different mean ISIs. Our modeling predicts that long-term plasticity for an excitatory synapse presented with periodic fast repetition of pre- and postsynaptic spikes exhibits only LTP. Again we note this is consistent with the experiments reported in ref. 19. Poisson spike trains for the parameters obtained from the experimental data always produce LTP.

It seems reasonable that the direction and magnitude of synaptic modifications depend not only on the relative spike timing between neurons but also on the intrinsic features of each neuron. This idea is supported by the experimental results of refs. 26 and 27. The first result (26) is related to activity-induced synaptic modification between excitatory and inhibitory neurons. The authors have observed the “anti-hebbian” synaptic modification: LTD for positive τ and LTP for negative values in these synapses. Such spike timing dynamics is described in our model by changing the sign of γ. “Anti-hebbian” learning is also observed by Holmgren and Zilberter (28) on LTP and LTD in inhibitory synapses with pyramidal cells from neocortex. We can use our formula with γ < 0 to evaluate the expected result from their combination of pre- and postsynaptic stimuli.

The experiments of Froemke and Dan (27) investigate two presynaptic spikes and one postsynaptic spike, or vice versa. Their results indicate that the contribution of each pre/post-spike pair may depend not only on its temporal separation but also on the presence of other spikes in both neurons. In particular, a preceding spike in the presynaptic neuron can suppress the contribution of a pre/post-spike pair in synaptic modification. Our model gives an analytic formula, generalizing 10 and 11, for this kind of experiment. The number of data presented in these experiments does not permit a quantitative comparison here.

Our model is also in qualitative agreement with experiments on voltage-clamped postsynaptic cells. In a situation where the activity of the postsynaptic cell is “clamped,” leading to constant D(t) = D₀, we have suggested a connection with the BCM rule for synaptic plasticity. In this circumstance, we have Δg as a function of D₀, which resembles the BCM rule in many details and has an activity-dependent sliding threshold.

Because spike time-dependent modification of synaptic strengths certainly has important implications for the function of real neural circuits, we anticipate that our suggested model will prove useful for the simulation of such dynamics and for inquiries into their ability to process information.

Abbreviations

LTP

long-term potentiation

LTD

long-term depression

N-methyl-d-aspartate

ISI, interspike interval