Dynamic force spectroscopy of parallel individual Mucin1–antibody bonds

Abstract

We used atomic force microscopy to measure the binding forces between Mucin1 (MUC1) peptide and a single-chain variable fragment (scFv) antibody selected from a scFv library screened against MUC1. This binding interaction is central to the design of molecules used for targeted delivery of radioimmunotherapeutic agents for prostate and breast cancer treatment. Our experiments separated the specific binding interaction from nonspecific interactions by tethering the antibody and MUC1 molecules to the atomic force microscope tip and sample surface with flexible polymer spacers. Rupture force magnitude and elastic characteristics of the spacers allowed identification of the rupture events corresponding to different numbers of interacting proteins. We used dynamic force spectroscopy to estimate the intermolecular potential widths and equivalent thermodynamic off rates for monovalent, bivalent, and trivalent interactions. Measured interaction potential parameters agree with the results of molecular docking simulation. Our results demonstrate that an increase of the interaction valency leads to a precipitous decline in the dissociation rate. Binding forces measured for monovalent and multivalent interactions match the predictions of a Markovian model for the strength of multiple uncorrelated bonds in a parallel configuration. Our approach is promising for comparison of the specific effects of molecular modifications as well as for determination of the best configuration of antibody-based multivalent targeting agents.

Interactions between biological molecules drive a vast variety of cellular processes and span a wide range of strength and complexity. Multivalent interactions where several binding units combine to produce superior binding strength play an important role in adaptive immune response (1) and intercellular adhesion (2), as well as in the mechanism of action of many pharmaceuticals (3). Clinical researchers have used multivalency as an affinity-enhancing approach (4, 5) in a variety of immunotherapies and imaging techniques to target specific tissues (6, 7).

Linking several molecules into a large multivalent binding construct also creates bulky agents that exhibit reduced tissue penetration and have a higher probability of accumulation in liver (8). Therefore, a better understanding of the multivalent binding is necessary for the creation of optimized agents that balance binding efficiency and molecular size. Quantitative characterization of multivalent interactions is also important for understanding the basic biophysics of complex molecular systems.

The last decade saw an explosion of interaction force measurement techniques that allowed researchers to measure and apply molecular level stresses (9–11). Atomic force microscopy (AFM) probes ligand–receptor interactions by simply pulling off the ligand from the receptor using external force (12). Kinetic approaches to the binding force measurements, such as dynamic force spectroscopy (DFS), can quantify kinetic off-rates and the distances to the transition states (13).

We have used DFS to characterize binding of several individual single-chain variable fragments (scFv) antibody (Ab) to the Mucin1 (MUC1) peptide. This interaction is the main targeting mechanism for a family of experimental radioimmunotherapeutics for cancer treatment (14). These agents consist of several Ab fragments on a poly(ethylene glycol) (PEG) scaffold that preloads onto the cancer cells and then catches a subsequently administered radioactive Y⁹⁰ payload (Fig. 1A). MUC1 is a large transmembrane glycoprotein that is commonly expressed in a variety of epithelial tissues in the human body (15, 16) where it hydrates the epithelia, enhances adhesion to neighboring cells, and provides a barrier to pathogenic invasion. Overexpression of MUC1 with reduced glycosylation is characteristic for prostate, breast, colon, lung, gastric, and pancreatic cancers (17, 18), and clinical trials targeting the MUC1 marker in solid tumors with multivalent Ab-based drugs have produced promising results for metastatic breast and prostate cancers (19, 20).

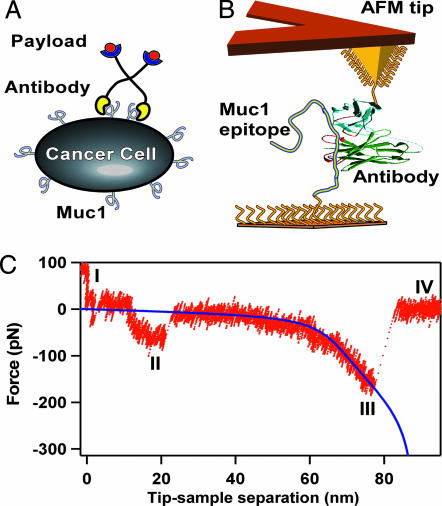
Fig. 1.

Measurement overview. (A) Schematic of a multivalent radioimmunotherapeutic agent interacting with the target receptor on the surface of a cancer cell. Flexible tethers link the targeting Abs to the radioactive payload. (B) Schematic of the force spectroscopy measurement showing the AFM tip connected to an Ab and a sample surface connected to the target MUC1 peptide with flexible PEG tethers. (C) A representative force vs. separation trace showing different interaction regions (see the main text for explanation of the regions). The blue line indicates an extended freely jointed chain model fit for the tether stretching region.

Our experiments recreated the targeting unit of the drug by tethering scFv Abs to the AFM tip. We have obtained the force spectra for the Ab interactions with the MUC1 peptide immobilized on the sample surface and determined kinetic off-rates and interaction potential widths for monovalent, divalent, and trivalent interactions. We found that increase in the interaction valency leads to the precipitous drop in the kinetic off-rate of complex dissociation. Moreover, the experimental data show remarkable agreement with a Markovian model for uncorrelated rupture of individual parallel molecular bonds.

Materials and Methods

Further details are given in Supporting Materials and Methods, which is published as supporting information on the PNAS web site.

Preparation of the scFv Ab and MUC1 Peptide. The scFvs used for the measurements as well as for in vivo targeting (21) were screened against the synthesized MUC1 peptide core, which consists of the 20-amino acid (aa) tandem repeat sequence, PDTRPAPGSTAPPAHGVTSA (22). Five repeats of this sequence, for a total of 100 aa, were obtained from the Peptide Synthesis Facility at the University of Pittsburgh (Pittsburgh). The scFvs for this experiment were produced in the Escherichia coli HB2151 strain. scFv clones selected from an anti-MUC1 phage display library (21) were expressed with an additional cysteine tag at the C terminus, which does not interfere with the binding domain (14).

Functionalization of AFM Tips and Substrates. The anti-MUC1 scFvs were covalently linked to the surface of the cantilever tip with bifunctional PEG linkers (Nektar Therapeutics, Huntsville, AL) as shown schematically in Fig. 1B. Commercial model NP silicon nitride AFM cantilevers (Veeco, Santa Barbara, CA) were coated with a thin layer of gold (750 Å with 50 Å chromium adhesion underlayer), cleaned with a piranha etch (70% concentrated sulfuric acid and 30% hydrogen peroxide solution), rinsed, and then incubated in 1 mM cystamine solution for 30 min to form an amine-terminated self-assembled monolayer.

The amine surface then was treated with two types of bifunctional PEG linkers, capped with either N-hydroxysuccinimyl (NHS) and methoxy (OMe) groups or NHS and maleimide (Mal) groups. We used a 50:1 molar ratio of 10 mM NHS–PEG 2000–OMe and 0.2 mM NHS–PEG 3400–Mal in dry chloroform to create low surface density of Mal groups. Finally, we incubated the tips of the cantilevers in 20 μl of scFv solution (2.5 mg/ml concentration, pH 7) for 30 min to link the free thiol group on the Ab to the AFM tip. To increase the frequency of multivalent interactions, several measurements were made by using the dilution ratio of –OMe to –Mal functionalities of 30:1.

Gold surfaces prepared by evaporation of gold onto silicon substrates were functionalized with the MUC1 peptide by using the same tethering scheme used for the AFM tips. Because the only free amine group on the MUC1 peptide is at the N terminus, we used this group to link the peptide to the tether.

Force Spectroscopy. All force measurements used a Nanoscope IIIa AFM (Veeco) in force calibration mode. Measurements were performed at 0.5- to 3-Hz frequencies. A relative trigger of 7 nm was used on all force–distance curves to limit the potential for probe damage. In addition, upon activation of the trigger, the tip was held at the sample surface for 0.4 s to allow the tethered scFvs to form bonds with tethered MUC1 peptide. All measurements were carried out in 20 mM PBS and 100 mM NaCl.

Cantilever spring constants were calibrated with the Fast Fourier Transform spectrum analyzer (SR760, Stanford Research Systems, Sunnyvale, CA) by using the thermal noise method (23) and ranged from 40 to 180 pN/nm. Rupture traces were collected at 14 kHz acquisition rate and were analyzed by using igor pro 5.0 (WaveMetrics, Lake Oswego, OR) and a custom-written set of procedures. Laser optical interference at 635 nm was filtered by removing its spectral component from the force signal. Before the rupture force determination, rms force noise was reduced by low-pass filtering the force signal immediately before and after rupture.

For quantitative analysis of the tether stretching, all single-bond rupture events were fit by an extended freely jointed chain model with parameters determined by Oesterhelt et al. (24), with the only fitting parameter being the tether contour length. For multiple bond ruptures, we assumed that we were stretching multiple parallel identical tethers and that the total force was equal to the sum of the contributions from individual traces.

Homology Modeling of CD5 scFv and Docking of MUC1. The sequence alignment between the CD5 Ab, which is 75% identical, and the single chain Fv Ab molecule MFE-23 (Protein Data Bank ID code 1QOK) (25) was performed by using clustalw (26). Three-dimensional models were generated automatically from the alignment with modeller (27). The linker joining the V_H and V_L regions of the Ab was not present in the crystal structure and was not generated for the homology models of CD5. The quality of the models was evaluated by using prosaii (28), and the model with the lowest score was used for docking studies.

The MUC1 peptide region containing the epitope (SAPDTR-PAP) of breast-tumor-specific Ab SM3 defined by crystal structure analysis (Protein Data Bank ID code 1SM3) (29) was docked onto the surface of the CD5 model by using the program autodock 3.05 (30). The procedures used for the docking can be found in Supporting Materials and Methods. Although the epitope recognized by the CD5 Ab has not been determined, the modeled MUC1 peptide fragment contains the highly immunogenic core peptide sequence PDTRP that is the epitope for many MUC1-specific Abs (31).

Results and Discussion

Binding System Architecture. We have designed our experimental system to minimize the impact of nonspecific interactions and to maximize the probability of detecting specific peptide–Ab interactions. An effective approach for discriminating between specific and nonspecific forces involves attaching the interacting molecules to flexible polymer tethers (32, 33). The tethers spatially isolate nonspecific probe–sample interactions from the specific interactions of the tethered molecules and allow researchers to discriminate between rupture events using both the rupture location and binding force values.

For our experiments we chose to use 30 ± 10-nm-long PEG tethers (Fig. 1B) to mimic the architecture of the MUC1-targeting immunotherapy drugs (compare Fig. 1 A and B), as well as to simplify the assignment of the specific rupture events. Note that the length of our tethers was much larger than the PEG persistence length (34); therefore, these tethers remain truly flexible, allowing the necessary conformational freedom to maximize the efficiency of the MUC1–Ab interactions. To maximize the probability of observing discrete individual interactions, we diluted the active tethers on the AFM probe with the inactive spacer, while keeping high surface density of the MUC1 target. This strategy resulted in ≈10% probability of specific interaction detection in our experiments.

Binding Force Measurements. A typical force vs. separation trace obtained in our measurements showed complicated structure (Fig. 1C). As the cantilever pulled away from the surface it passed through several interaction regions. After the probe left the tip-sample repulsive contact region (I), it entered the first of the attractive interaction regions (II). This region in the 10–25 nm range corresponds to nonspecific tip–sample interaction. A second attractive interaction region distinguished by a characteristic tether stretching shape (region III) corresponds to the interactions of the tethered molecules with the sample surface or with each other. This region is where we expected to observe the specific interaction of the tethered Abs and MUC1 peptide, which should be clustered at around two-tether-length rupture distance. In region IV the cantilever completely separated from the sample surface and returned to its equilibrium deflection.

To identify specific MUC1–Ab interactions, we compiled histograms of the rupture forces that occur at one and two tether lengths (Fig. 2A). Distributions of the rupture forces of <125 pN were very similar for both tether lengths. In contrast, the force distribution observed at two-tether-lengths separation showed a distinct peak centered at 150 pN, which was absent in the force distribution observed for one-tether-length separation. This peak corresponds to the specific MUC1–Ab interactions, whereas the forces of <125 pN at both one and two tether lengths likely originate from different nonspecific interactions between the proteins and the PEG tethers.

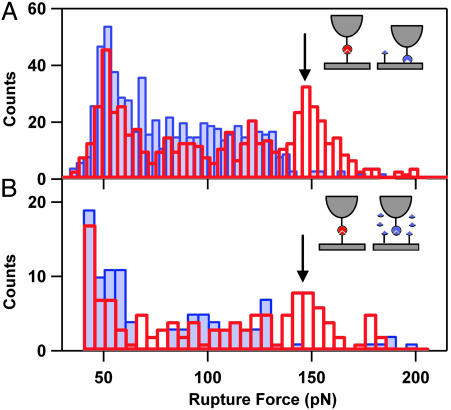
Fig. 2.

Detection of specific MUC1–Ab interactions. (A) Histograms of the rupture forces measured in the one-linker-length (blue filled bars) and two-linker-lengths (red unfilled bars) rupture regions. An arrow indicates the peak corresponding to the specific MUC1–Ab interactions. (B) Histograms of the rupture forces obtained in the two-tether-lengths region in absence (red unfilled bars) and presence (blue filled bars) of excess of MUC1 in solution.

Blocking of Specific Interactions in a Competition Assay. To verify that the observed peak at 150 pN is due to specific MUC1–Ab binding, we blocked the specific MUC1–Ab interactions by adding excess of free MUC1 antigen to the buffer solution. Histograms of the rupture forces measured at two tether lengths for blocked and unblocked interactions (Fig. 2B) showed that addition of the excess free MUC1 suppressed only the interactions that occur at two tether lengths and >125 pN, which confirms our assignment of the specific interactions peak.

DFS of Tethered Systems. Despite the conceptual simplicity of force spectroscopy measurements, their quantitative interpretation is not straightforward. The relationship between the experimentally measured bond rupture forces and the interaction potential is described by a kinetic model first proposed by Bell (35) and then developed by Evans and coworkers (13, 36). Exponential amplification of the bond dissociation rate by an external loading force produces a characteristic proportionality of the rupture force, f, to the logarithm of the loading rate, r

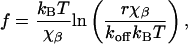[1]

where k_BT is the Boltzmann thermal energy, χ_β is the distance to the transition state, and k_off is the kinetic off-rate for the bond in absence of applied load. Flexible tethers introduce an additional complication to this picture, because they form highly nonlinear springs connected in series with the Hookean cantilever spring; fortunately, Gaub and coworkers (37) showed that Eq. 1 is still valid for tethered systems if we replace the nominal loading rate with the instantaneous loading rate provided by the slope of the tether extension curve close to the rupture event. This approximation, which is valid at fast loading rates, is applicable to our experiments because the nominal loading rates were >2 orders of magnitude above the thermal velocity that defines the threshold for fast loading (38).

DFS of Single MUC1–scFv Bonds. To determine the interaction parameters for the single MUC1–scFv bond, we used the stretching region of the force vs. extension traces preceding rupture (Figs. 1C and 3A) with the PEG chain elasticity model (24). Close fit of the model to the experimental data indicates that the observed traces indeed correspond to the rupture of a single pair of interacting molecules connected to the surfaces of tip and sample by single PEG tethers. When we plotted the measured rupture forces as a function of the logarithm of the instantaneous loading rate determined from the PEG elasticity fits, we obtained the dynamic force spectrum (Fig. 4A, red squares) showing the typical linear behavior predicted by Eq. 1. This dynamic force spectrum indicates that the unbinding events observed in our experiments correspond to a potential energy barrier located at 2.8 ± 0.2 Å (as determined from the fit of the experimental data to Eq. 1). The kinetic off-rate of 2.6 × 10^–3 s^–1 determined from the dynamic force spectrum is faster than the 0.4 × 10^–3 s^–1 off-rate determined from bulk surface plasmon resonance (SPR) measurements (data not shown). However, the SPR measurement included some contribution from scFv dimers; therefore, a higher off-rate value measured by force spectroscopy is not surprising. An alternative explanation is that the lower off-rates measured in the SPR experiments may indicate the existence of an additional energy barrier situated further out on the potential energy surface. The limited range of the loading rates used in our experiments did not permit us to investigate this possibility. We believe that other techniques, such as Biomembrane Force Probe (36), which could achieve the very slow loading rates necessary for probing such barriers, are better suited for that study.

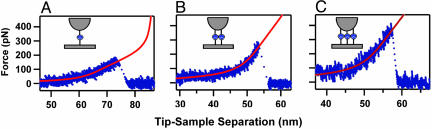
Fig. 3.

Individual tether stretch traces before specific bond rupture events showing rupture of one (A), two (B), and three (C) MUC1–Ab bonds. Red lines indicate extended freely jointed chain model fits for the corresponding number of traces. Tether contour length was the only fitting parameter.

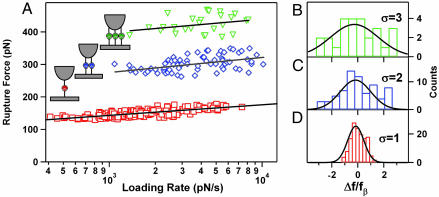
Fig. 4.

Dynamic force spectra. (A) Dynamic force spectra for the rupture of one (□), two (⋄), and three (▿) MUC1–Ab bonds. The loading rates for the multibond rupture events were normalized by the number of bonds. Solid lines represent the best fits of each spectrum to Eq. 1. (B–D) Histograms of normalized residuals from A for one (B), two (C), and three (D) bonds. The residuals were normalized by the corresponding value of the force scale f_β. Solid lines are Gaussian fits with the width of one, two, and three, respectively.

We ruled out heavy and light domain unfolding in our experiments because of the larger forces that this process requires. Kinetic off-rates for scFv unfolding measured by bulk spectroscopy techniques (39) are 2 orders of magnitude slower than the off-rates measured in our experiments. In addition, Hinterdorfer and colleagues (40) showed that forces required for breaking scFv–antigen interactions are much weaker than those required for scFv unfolding.

Rupture of Multiple MUC1–Ab Bonds. Approximately 10% of all specific rupture events occurred at much higher forces than the typical forces for single bond rupture. We have found consistently that tether-stretching traces preceding these events were fit best by a freely jointed chain model describing stretching of multiple PEG tethers in parallel (Fig. 3 B and C). These fits provided an additional means to determine the number of the individual protein–Ab pair for each rupture. When a cantilever stretches several identical tethers connected in parallel, the load is shared among all bonds (41). Therefore, the effective loading rate applied to each of the n bonds will be 1/n of the nominal loading rate. When we used this assumption to normalize the loading rates we produced the dynamic force spectra for two- and three-tether ruptures shown in Fig. 4A. Remarkably, a comparison of the force spectra for rupture of one, two, and three bonds shows that they exhibit very similar slopes (Fig. 4A and Table 1), which correspond to a similar distance to the transition state. We also have determined the effective kinetic off-rates for monovalent and multivalent MUC1–Ab interactions by fitting the spectra to Eq. 1 (Table 1). As expected, the off-rates drop precipitously with an increase in the number of bonds. These data clearly illustrate that the main benefit of multivalent interactions is the reduction on the kinetic off-rate and the corresponding increase in the bond lifetime. The half-life for the common radioactive payload Y⁹⁰ is 65 h, and an ideal multivalent targeting molecule should remain bound to the tumor site for at least this amount of time. Therefore, these results suggest that an effective MUC1-targeting immunotherapeutic should link three scFv units to achieve the necessary binding efficiency.

Table 1. The distances to the transitions state, χ_β, kinetic off-rates, k_off, and the average bond lifetime, τ_off = 1/k_off.

No. of bonds	χβ, Å	Koff, s-1	τoff
1	2.8 ± 0.2	2.6 × 10-3	284 s
2	2.0 ± 0.4	7.2 × 10-5	3.8 h
3	2.4 ± 1.5	3.6 × 10-8	320 days

Values were determined from the fits of the data in Fig. 4 to Eq. 1.

It is also useful to compare the experimentally measured spread in the rupture force values with the model predictions. Numerical simulations showed that deviations in the normalized rupture force F at high loading rates scale as the number of bonds N (42). Indeed, the histograms of experimental data residuals from the best fits for one, two, and three bonds fit well to the Gaussian distributions with the width N·σ, where σ is the residual standard deviation from the one-bond case (Fig. 4 B–D). This comparison provides an additional validation for the parallel uncorrelated bond rupture model predictions.

Theoretical Description of Failure of Multiple Parallel Bonds Under Load. Our experimental system represents one of the three basic configurations for multiple-bond attachments (43), parallel attachment where the load is shared between all of the bonds. The other two configurations are the serial connection, where all bonds experience the same load (44–46), and a “zipper” connection, where only one of the bonds experiences the loading force at any given time. In addition to the connection architecture, rupture dynamics of the multiple bonds also depends on the failure mode. In the correlated mode all bonds are closely coupled, and failure of one bond implies failure of the rest of the bonds. In the uncorrelated system all attachments can fail independently and the load force is redistributed among the surviving bonds. Quantitative analysis under a correlated bond failure assumption shows that our measured kinetic off-rates would result in an unreasonably low value of the energy barrier of 6.5k_BT. This result is not surprising, because correlated rupture requires close mechanical coupling between individual bonds (43) that long tethers used in our study cannot provide.

The uncorrelated failure mode implies no particular mechanical coupling between individual bonds. Williams (42) showed that the force-induced rupture of the multiple uncorrelated bonds could be described as a Markovian sequence and used numerical simulations as well as analytical approximations to predict the dynamic force spectra for this process. He also showed that although the kinetic equations for the uncorrelated parallel bond rupture cannot be solved analytically, a numerical solution and a useful analytical approximation exist. To simplify the description, we will use the normalization for force and loading rate suggested by Evans and Williams in a later publication (43):

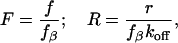[2]

where f_β is the thermal force scale defined as k_BT/χ_β. The equivalent single-bond approximation (42, 43) then produces the following expression relating the normalized loading rate, R, to the most probable rupture force, F*, and the number of bonds, N:

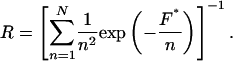[3]

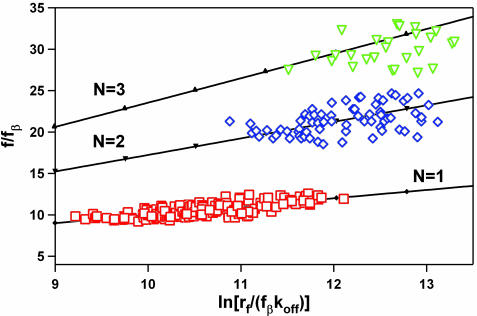
To test the model predictions, we compared our experimental data normalized according to Eq. 2 with the most probable rupture forces calculated using Eq. 3 [we did not use the full set of master equations for the multibond system (42) because we found that Eq. 3 produces very close results for our loading regime]. The calculated rupture forces fit our experimental data extremely well (Fig. 5). We stress that we did not use any fitting parameters to generate the theoretical curves on the Fig. 5; therefore, the Markovian model (42) provides an accurate description of the dynamics of the failure of multiple uncorrelated parallel connections. This work presents a direct experimental verification of this model in a parallel bond system. We believe that this description will apply to other multivalent systems comprising uncorrelated parallel bonds.

Fig. 5.

Comparison of the normalized dynamic force spectra for the rupture of one (□), two (⋄), and three (▿) MUC1–Ab bonds with the prediction of the uncorrelated multiple bond rupture model. The experimental data were normalized according to Eq. 2. Note that for this plot the loading rate was not normalized by the number of bonds (unlike the data in Fig. 4A). Solid lines represent the results of the numerical solutions of the Eq. 3 for n = 1(–♦–), 2 (–▾–), and 3 (–▴–). χ² values for the correlation between the experimental data and the model correspond to the probability of null hypothesis of P < 10^–6 for one and two bonds and P < 2 × 10^–6 for three bonds.

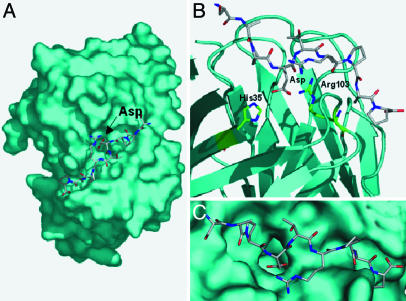
MUC1 Docking Simulations. For an additional validation of the force spectroscopy results, we compared the measured distance to the transition state with the results of molecular docking of the MUC1 fragment onto the hypervariable loops (antigen binding region) of the homology model of our Ab. The docking simulation shows that the dominant contribution to the bond formed between the MUC1 fragment and the Ab is a slightly buried salt bridge between the residues Arg-103 in the scFv and Asp in MUC1 (Fig. 6A). In the docked conformation, the Asp residue of the MUC1 peptide is 2.6 Å away from the NH group of the Arg-103 residue on the Ab (Fig. 6 B and C). Although only one carboxylate oxygen (OD2) of Asp from MUC1 is interacting with Arg-103, a slight rearrangement of the Arg side chain or a change in the MUC1 backbone would likely allow the second carboxylate oxygen (OD1) of Asp to interact with Arg-103. An alternative interaction between the imidazole nitrogen (NE2) of His-35 and OD1 of the Asp (2.7 Å separation) is also possible. In either case, two strong interactions dominated by a buried salt bridge can form between the Asp residue of MUC1 and the Ab. Potential mean force calculations for similar salt bridges show bond widths that range from 2.2 to 3.0 Å (47, 48), which compare well with the characteristic rupture distance of 2.8 Å measured in the force spectroscopy experiments.

Fig. 6.

Homology model simulation results. (A) The lowest-energy docked MUC1 fragment onto the surface of the CD5 homology model. The Asp of MUC1 is oriented into a pocket on the surface of CD5. (B) A close-up of the interaction between Asp of MUC1 and residues within the Ab. (C) Close-up of the MUC1 fragment bound on the scFv surface.

Conclusions

We have used AFM to characterize interactions of MUC1 peptide with the scFv Ab in both monovalent and multivalent configurations. Long flexible tethers used for attaching the interacting molecules to the AFM tip and samples surfaces allowed us to identify specific binding interactions and separate them from the nonspecific interactions. We used instantaneous loading rate values obtained from the fits of the tether elasticity curves to construct accurate dynamic force spectra for the rupture of monovalent and multivalent MUC1–Ab interactions and to quantify the advantages of the multivalent binding. Each additional MUC1–Ab interaction preserves the force scale for a single interaction and leads to a precipitous drop in the effective kinetic off-rate. Moreover, measured dynamic force spectra show excellent agreement with the Markovian model for the rupture of multiple uncorrelated molecular bonds, providing a solid experimental corroboration for the theoretical predictions.

We believe that these results open up significant opportunities for researchers in areas ranging from biophysics to drug design. Tethered ligand systems can serve as a flexible and versatile model for studying fundamental dynamics of individual bond rupture in biological systems. Multivalent binding is a common tool for molecular targeting that enables extended and more accurate delivery of drugs and molecular labels to specific tissues. We showed that DFS can provide an accurate measurement of the kinetic off-rates in molecular systems. These off-rates are the main determinant of the drug efficiency and quantification of the advantages of multivalent binding can provide a valuable input into the design efforts. Our technique will be especially useful for characterization of very strong interactions that could be difficult to observe on reasonable experimental time scales by other methods. Finally, researchers can use force spectroscopy experiments similar to what we described to determine the binding efficiency of different configurations of multivalent binders, which should help to establish optimal configurations for such agents. These results could guide the efforts to design the next generation of superior multivalent drugs and molecular labels.