Abstract
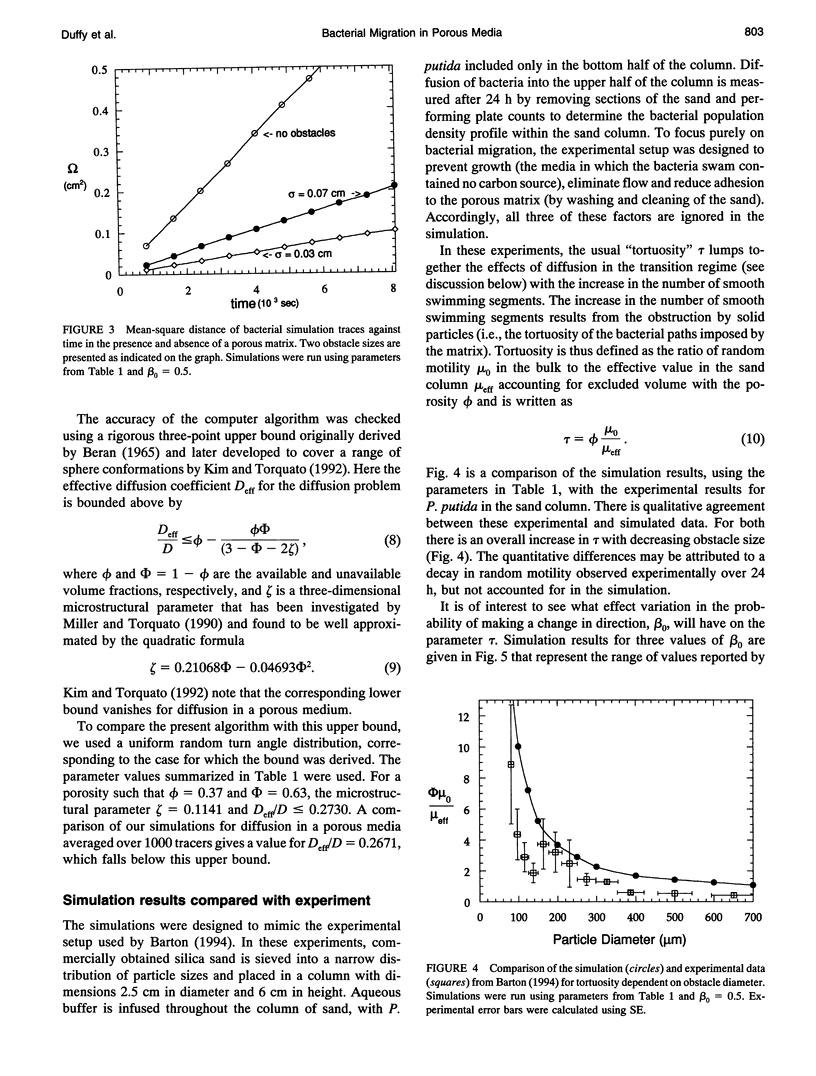
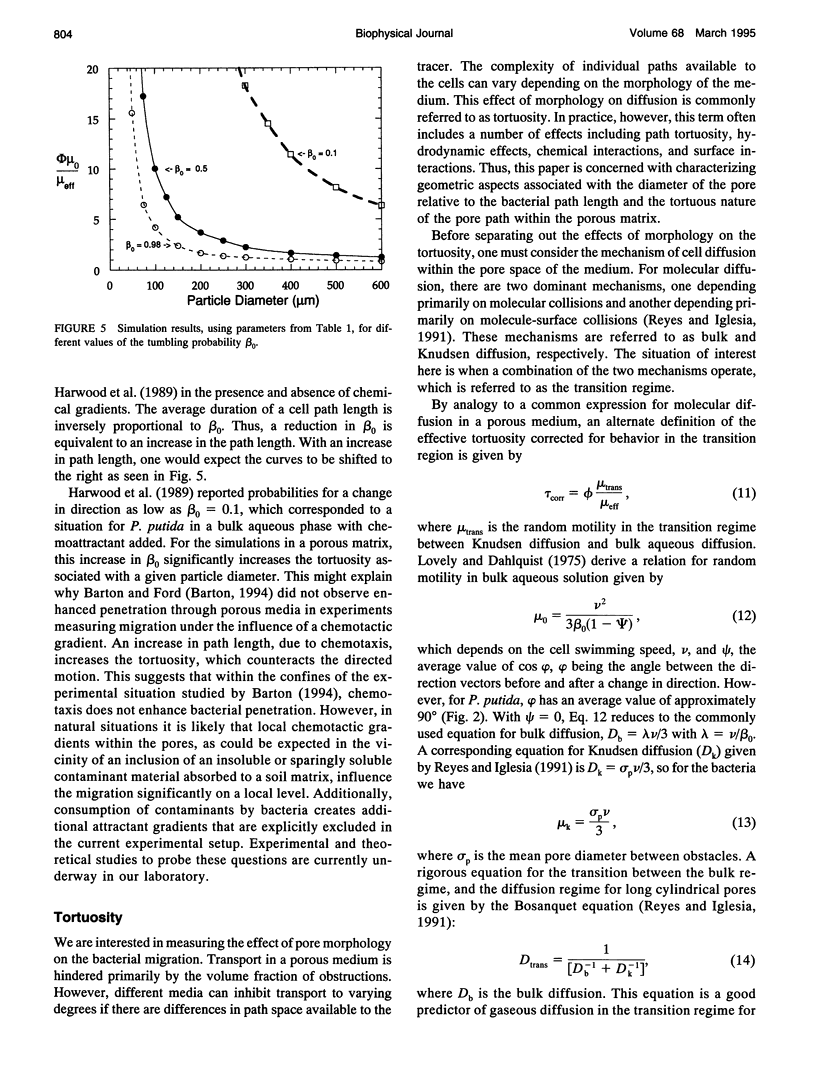
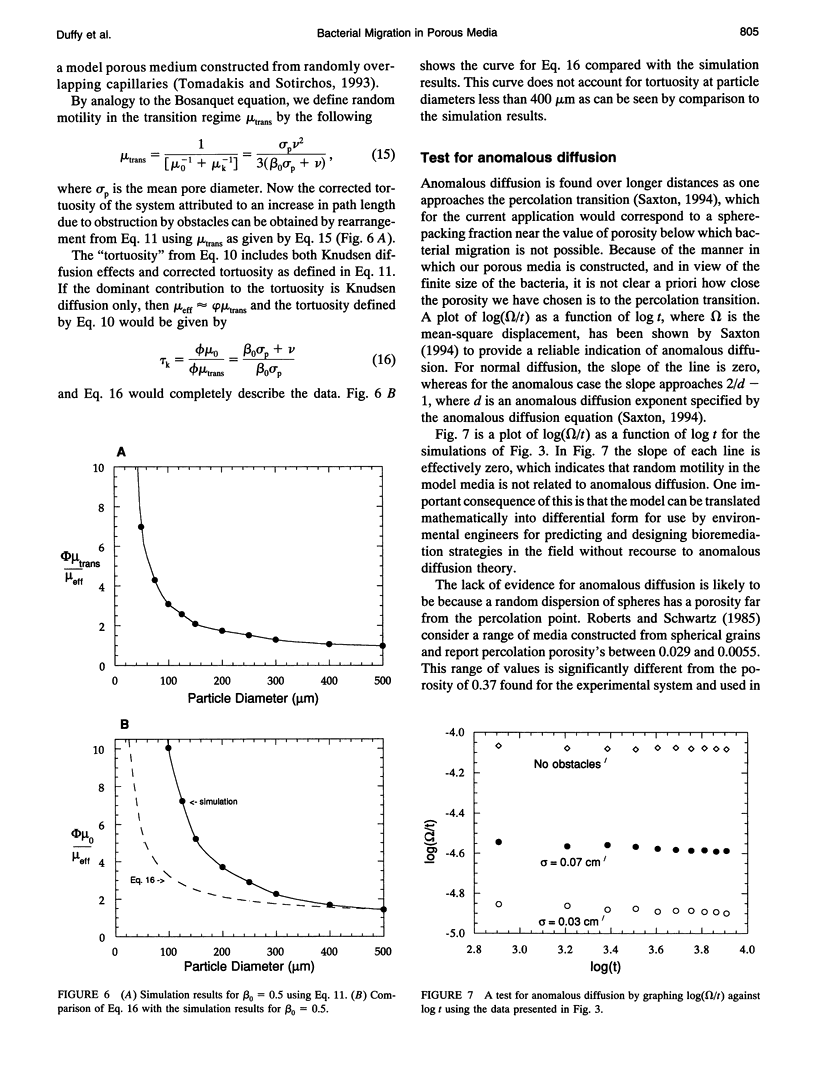
Bacterial migration is important in understanding many practical problems ranging from disease pathogenesis to the bioremediation of hazardous waste in the environment. Our laboratory has been successful in quantifying bacterial migration in fluid media through experiment and the use of population balance equations and cellular level simulations that incorporate parameters based on a fundamental description of the microscopic motion of bacteria. The present work is part of an effort to extend these results to bacterial migration in porous media. Random walk algorithms have been used successfully to date in nonbiological contexts to obtain the diffusion coefficient for disordered continuum problems. This approach has been used here to describe bacterial motility. We have generated model porous media using molecular dynamics simulations applied to a fluid with equal sized spheres. The porosity is varied by allowing different degrees of sphere overlap. A random walk algorithm is applied to simulate bacterial migration, and the Einstein relation is used to calculate the effective bacterial diffusion coefficient. The tortuosity as a function of particle size is calculated and compared with available experimental results of migration of Pseudomonas putida in sand columns. Tortuosity increases with decreasing obstacle diameter, which is in agreement with the experimental results.
Full text
PDF



Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Berg H. C., Brown D. A. Chemotaxis in Escherichia coli analysed by three-dimensional tracking. Nature. 1972 Oct 27;239(5374):500–504. doi: 10.1038/239500a0. [DOI] [PubMed] [Google Scholar]
- Harwood C. S., Fosnaugh K., Dispensa M. Flagellation of Pseudomonas putida and analysis of its motile behavior. J Bacteriol. 1989 Jul;171(7):4063–4066. doi: 10.1128/jb.171.7.4063-4066.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lovely P. S., Dahlquist F. W. Statistical measures of bacterial motility and chemotaxis. J Theor Biol. 1975 Apr;50(2):477–496. doi: 10.1016/0022-5193(75)90094-6. [DOI] [PubMed] [Google Scholar]
- Roberts JN, Schwartz LM. Grain consolidation and electrical conductivity in porous media. Phys Rev B Condens Matter. 1985 May 1;31(9):5990–5997. doi: 10.1103/physrevb.31.5990. [DOI] [PubMed] [Google Scholar]
- Sahimi M, Jue VL. Diffusion of large molecules in porous media. Phys Rev Lett. 1989 Feb 6;62(6):629–632. doi: 10.1103/PhysRevLett.62.629. [DOI] [PubMed] [Google Scholar]
- Saxton M. J. Anomalous diffusion due to obstacles: a Monte Carlo study. Biophys J. 1994 Feb;66(2 Pt 1):394–401. doi: 10.1016/s0006-3495(94)80789-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz LM, Banavar JR. Transport properties of disordered continuum systems. Phys Rev B Condens Matter. 1989 Jun 1;39(16):11965–11970. doi: 10.1103/physrevb.39.11965. [DOI] [PubMed] [Google Scholar]


