“Waves” vs. “particles” in the atmosphere's phase space: A pathway to long-range forecasting?

Abstract

Thirty years ago, E. N. Lorenz provided some approximate limits to atmospheric predictability. The details—in space and time—of atmospheric flow fields are lost after about 10 days. Certain gross flow features recur, however, after times of the order of 10–50 days, giving hope for their prediction. Over the last two decades, numerous attempts have been made to predict these recurrent features. The attempts have involved, on the one hand, systematic improvements in numerical weather prediction by increasing the spatial resolution and physical faithfulness in the detailed models used for this prediction. On the other hand, theoretical attempts motivated by the same goal have involved the study of the large-scale atmospheric motions' phase space and the inhomogeneities therein. These “coarse-graining” studies have addressed observed as well as simulated atmospheric data sets. Two distinct approaches have been used in these studies: the episodic or intermittent and the oscillatory or periodic. The intermittency approach describes multiple-flow (or weather) regimes, their persistence and recurrence, and the Markov chain of transitions among them. The periodicity approach studies intraseasonal oscillations, with periods of 15–70 days, and their predictability. We review these two approaches, “particles” vs. “waves,” in the quantum physics analogy alluded to in the title of this article, discuss their complementarity, and outline unsolved problems.

The atmosphere is one of the most complex physical systems known to humanity. In fact, we have about 10⁵ observations of the atmosphere every day, which makes it probably the best-observed macroscopic physical system there is (1). Despite—or because of?—this detailed knowledge, our ability to predict even large-scale atmospheric motions, as seen on a global weather map or a hemispheric satellite picture, is limited to a few days (2–4). The purpose of studying low-frequency, or intraseasonal, atmospheric variability is to find out which features of this variability are predictable for longer time spans, of weeks to months.

Intraseasonal time scales range from the deterministic limit of atmospheric predictability, of about 10 days, up to a season, say 100 days. These time scales occupy a window of overlap between low-frequency variability intrinsic to the atmosphere and short climatic time scales that also involve the upper ocean and land-surface features. These time scales are of particular importance to extended-range weather prediction. There are two complementary ways of describing low-frequency atmospheric variability: (i) episodic, by means of multiple weather (5) or flow (6) regimes, and (ii) oscillatory, by means of broad-peak slowly modulated oscillations (ref. 7 and references therein).

The overall features of atmospheric low-frequency variability (LFV) are described in Observational Characteristics of LFV. Planetary flow regimes are characterized by their persistence, recurrence, and the geographically fixed character of the flow features. The duration of a flow pattern's persistence and the intervals from one occurrence of that pattern to another are fairly irregular. The regimes' observed characteristics and some theories that attempt to explain them are reviewed in Planetary Flow Regimes. In the very loose analogy of the title, these regimes are the “particles” in the large-scale atmosphere's phase space. Extended-range prediction can benefit from a description and explanation of the regimes by using the Markov chain of transitions between them.

Intraseasonal oscillations refer to changes in the large-scale flow that have a more or less repetitive, nearly periodic character. Such cyclic changes were reported first in the intensity and the latitudinal position of the mid-latitude westerly (i.e., eastward) jet (8, 9). More recently, Madden and Julian (10, 11) reported changes in tropical winds and cloudiness with a period of 40–50 days. The efforts spent over the last two decades in describing the latter tropical oscillations are reviewed in ref. 12, and a brief review of theories to explain them is provided in ref. 13. We concentrate here on the mid-latitude oscillations that exhibit shorter periods, of 15–30 days (14), and longer ones, of 60–70 days (15), as well as of 40–50 days.

The observed characteristics of these extratropical oscillations, some theories that attempt to explain them, and the results of simulating them by using general circulation models (GCMs) are reviewed in Intraseasonal Oscillations: Their Theory and Simulation. In the very loose analogy of the title, these are the “waves” that share the atmosphere's phase space with the “particles,” i.e., with the regimes. The total fraction of large-scale atmospheric variance that is captured by the relatively regular oscillations is fairly small, of the order of 20–30%. Still, this fraction is rather predictable and can thus help extended-range forecasting.

How can these two apparently contradictory descriptions of LFV be reconciled? The regimes are points in phase space, i.e., multiple equilibria (16, 17) or, more precisely, relatively small “blotches” in phase space where the probability density function (pdf) of finding an atmospheric map is fairly high. The oscillations are closed trajectories in phase space, i.e., limit cycles or, more precisely, doubly or multiply connected strips in hyperspace where the pdf is comparatively high. Are the regimes merely slow phases of the intraseasonal oscillations or do the oscillations arise as instabilities of certain regimes? We discuss these still wide-open questions and their implications for practical predictability computations (e.g., refs. 15 and 18) in Complementarity of the Two Approaches and Implications for Predictability.

Observational Characteristics of LFV

Atmospheric variability is highly irregular, as anybody who follows the daily weather in mid-latitudes cannot fail to notice. Nonetheless, on time scales between a week and a season there are certain large-scale flow patterns that appear repeatedly at fixed geographical locations and persist beyond the lifetimes of individual weather disturbances, i.e., beyond about a week.

It is central to long-range forecasting to understand these time scales of variability, because 10–15 days also coincide with the theoretical limit of atmospheric deterministic predictability. Furthermore, the large horizontal scales of many thousands of kilometers that characterize LFV exert an organizing influence on weather-bringing disturbances. The underlying circulation regimes play, therefore, a fundamental role in the study of climate variability and predictability on interannual and even longer time scales. Climatic variability may thus be closely connected with changes in the prevalence of the atmosphere's intrinsic circulation regimes (see section 6.5 of ref. 4; ref. 19).

LFV represents, in fact, a very substantial fraction of the entire atmospheric variability, as seen from Fig. 6, which is published as supporting information on the PNAS web site, www.pnas.org. Fig. 6a shows the total Northern Hemisphere (NH) rms variance during the winter season; Fig. 6b shows LFV, obtained here by low-pass filtering the record with a mid-power point at 10 days; and Fig. 6c shows the synoptic-scale rms variance that captures the major weather phenomena, concentrated in the 2.5–6-day band. It is clear that the band-pass SD, which is plotted in Fig. 6c, is smaller by a factor of roughly 3 than the one associated with the LFV (as plotted in Fig. 6b), and hence the weather variance is smaller by an order of magnitude than the LFV variance.

There are three NH maxima in LFV (Fig. 6b); they are almost equal in amplitude to those in total variance (Fig. 6a) and almost precisely collocated with them. Two of these winter maxima occur over the northeastern part of the two NH ocean basins, Pacific and Atlantic, the third over the Siberian Arctic. The maxima in the “weather band” occur slightly upstream of the LFV maxima, mainly over the storm tracks off the east coasts of North America and Asia.

By using increasingly extensive surface- and upper-air data sets, the temporal and spatial characteristics of extratropical LFV have been described in further detail. To do so, correlation and regression analysis of atmospheric fields has concentrated on sea-level pressures and on the field that best describes upper-air behavior, the geopotential height of the 500-hPa (same as 500-mb) pressure surface. Wallace and Gutzler (20) have thus identified coherent variations between widely separated regions of the globe. Following Bjerknes (21), these are called “teleconnection patterns” and are most easily described in terms of anomalies, i.e., differences between the instantaneous or mean-monthly map and the climatological value of the field at a given location.

Some of these teleconnections, such as the Pacific–North-American (PNA) pattern or the North-Atlantic Oscillation (NAO) are now well known as dominant modes of LFV. Their horizontal structures resemble wave trains with alternating high and low values of height anomalies (e.g., the PNA) or are characterized by north-south seesaws in sea-level pressure (e.g., the NAO). Their vertical structure tends to be “equivalent barotropic” throughout the troposphere, with the same horizontal pattern on all pressure surfaces, and amplitude that increases with height to a maximum near the tropopause.

The three centers of high-amplitude LFV (Fig. 6b) have been known since the 1950s to be regions of frequent “blocking” of the zonal flow (22), characterized by strong and long-lived anticyclones near the surface. In the upper troposphere, a strong ridge accompanies blocking, with the westerly jet displaced far toward the pole. The intensity of NH LFV is much weaker in the summertime (23). In the Southern Hemisphere (SH), which is largely covered by oceans, there are much smaller geographical and seasonal variations in LFV.

Persistent anomalies of LFV, in which the flow patterns differ significantly from the normal climatological circulation and remain stationary for more than a week, have been objectively identified over the North Pacific and North Atlantic in the 1980s (24, 25). Their onsets and breaks, on the other hand, are rather abrupt. Within the last decade it has been demonstrated that these persistent anomalies or “Grosswetterlagen” of synoptic experience can be identified by examining the pdf distribution in the atmosphere's phase space (26–29). The resulting patterns resemble those found previously by using correlation analysis.

In the following section, we present these planetary flow regimes as they have been derived from atmospheric data. We discuss them in terms of previous observational results, and interpret them by using basic theoretical concepts of geophysical fluid dynamics.

Planetary Flow Regimes

Classification of Weather Maps.

Data sets.

Long upper-air data sets with daily resolution are required to obtain statistically significant results on the coarse-graining of the atmosphere's phase space in LFV. Until recently, many studies have used the NH 700-hPa observations compiled at the National Oceanic and Atmospheric Administration (NOAA) Climate Analysis Center, for the time interval since 1949. The “reanalysis” projects at the U.S. National Centers for Environmental Prediction (NCEP; ref. 30) and the European Center for Medium-range Weather Forecasts (ECMWF) have now produced global data sets that are 40-years-long or longer, available at a large number of vertical levels, and have higher horizontal resolutions. They use the numerical forecast models' dynamical consistency to supply any missing data and thus provide objectively smoothed fields. To isolate LFV, the seasonal cycle is usually removed by constructing a filtered data set that is averaged over many decades. The anomalies so obtained are usually low-pass filtered (as in Fig. 6) to remove variability with time scales that are shorter than 10 days.

Methodology.

A variety of methods that have been used to classify weather maps are summarized in Table 1. In such a classification, an individual atmospheric map is thought of as a point in phase space. To achieve a reliable, statistically significant classification, it is necessary to consider a low-dimensional subspace of this phase space that still captures most of the variance. The usual choice is to compute the analyzed record's empirical orthogonal functions, i.e., the eigenvectors of the covariance (or correlation) matrix. The subspace chosen is spanned by a few leading eigenvectors (25–29).

Table 1.

Classification methods for weather maps

Approach	Method	Data sets	Refs.	Comments
Classification into regimes by position
Cluster analysis	Categorical	NH	25	Fuzzy
		NH + sectorial	33	Hard (K − means)
	Hierarchical	NH + sectorial	26	3 NH clusters
PDF estimation	Univariate	NH	48 and 49	Bimodality
	Multivariate	NH	27 and 31	3 modes
		NH + sectorial	28	Multimodal
			29	3 NH clusters
Classification into regimes by persistence
Pattern correlations		NH	81
		SH	82	3 regimes
Minima of tendencies		Models Atl.–Eur. sector	6, 34, and 83 35	4 regimes
Transition probabilities
Counts	Model & NH		25	Elementary
Monte Carlo	NH & SH		54	Advanced
	NH + sectorial		28	Advanced

Many of the classification methods define the regimes as classes of distinct atmospheric states that have a high probability of occurrence—the blotches discussed in the introduction—and are separated by regions of lower probability. Some of these methods seek maxima of the pdf by using kernel density estimation (19, 28) or more ad hoc methods (31). Each regime is then formed by the points, or maps, that exceed a given probability threshold in the neighborhood of a pdf maximum. The number of pdf peaks depends on the kernel smoothing parameter used, which can be determined objectively by using a least-squares crossvalidation procedure (32).

Smyth et al. (29) have used a mixture model that approximates the pdf by the sum of a small number of multivariate Gaussians. In this case, the regimes are “fuzzy” in the sense that they overlap, and that each particular daily weather map can be assigned a probability of belonging to one or another regime.

Cluster analysis is a less ambitious approach that localizes high concentrations of points, called clusters, but does not pretend to estimate the pdf. There are two main types of clustering algorithm: hierarchical and partitioning. In hierarchical algorithms, one builds a classification tree iteratively, starting from single data points and merging them into clusters according to a similarity criterion. Cheng and Wallace (26) used Ward's method to do this. In partitioning algorithms, a prescribed number of clusters is chosen, and data points are agglomerated around kernels initially chosen from random seeds. The kernels are iteratively modified so as to globally minimize the data scatter about the kernels (33).

Some measure of persistence is usually built into the above methods, which are based on frequency of occurrence, by using low-pass filtered data. A second broad class of methods uses quasi-stationarity explicitly. Here, the regimes are defined as comprising states for which large-scale motion is slow in the statistical sense. More precisely, one seeks the large-scale patterns that have, on average over many realizations, a small time derivative (6). This phase-space speed can be computed for maps that do include synoptic-scale motions by a nonlinear equilibration technique (33–35).

The large number of different methods that have been used to identify LFV regimes makes it possible to assess whether a consensus has been reached on the existence, robustness, and characteristics of these regimes. It is still somewhat controversial to discuss LFV in terms of multiple regimes, but the studies cited above over the past decade or so do provide a tentative consensus.

To discuss the regimes themselves, it is important to make the distinction between hemispheric and regional classifications. The former assume that circulation patterns with hemispheric coherence do exist or that regionally confined ones can be identified from hemispheric data. The regional classifications are motivated by evidence that the strongest patterns of NH LFV are confined to either the Pacific–North-American or the Atlantic-Eurasian sectors.

Hemispheric regimes.

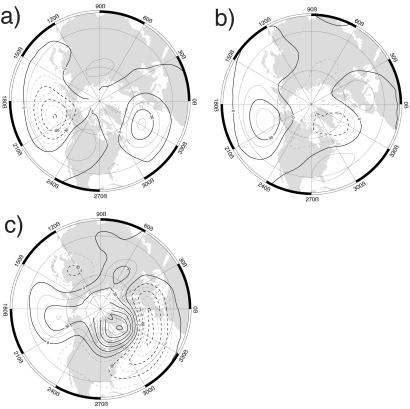
The most striking agreement between the numerous classifications obtained so far is that between the three hemispheric regimes of Cheng and Wallace (26), using hierarchical clustering, and of Smyth et al. (29), based on their Gaussian mixture model. Fig. 1 shows the centroids of the three NH wintertime circulation regimes derived by using the latter method: they are the PNA, an approximate inverse of this often called the reverse PNA or RNA, and the blocked phase of the NAO. This set seems therewith to be the minimal set of NH regimes that is unequivocally supported by the data, such as they are. The 500-hPa maps associated with the centroids of the classification in (26) (not shown) are very similar to those in Fig. 1.

Fig 1.

Hemispheric regimes: anomaly maps of 700-hPa heights for the three cluster centroids identified by a Gaussian mixture model. (a) PNA. (b) Reverse PNA (RNA). (c) Blocked-NAO. Contour interval: 15 m. [Reproduced with permission from ref. 29 (Copyright 1999, American Meteorological Society).]

All three circulation patterns in Fig. 1 are hemispheric in extent, with features over both the Pacific and Atlantic sectors. A zonally symmetric component is visible in Fig. 1 b and c; in atmospheric and oceanic dynamics, one refers to axial symmetry as zonal. This component has height anomalies of one sign in high latitudes and predominantly of the opposite sign in mid-latitudes. It is not clear at present whether this zonal symmetry reflects a fundamental dynamical mode of the atmosphere—the so-called “Arctic Oscillation” (refs. 36 and 37; see also the North-South seesaw of ref. 25)—or a mere coincidence of two separate sectorial patterns. One of these patterns involves, largely but not exclusively, a seesaw between the Aleutian Low and the ridge over western North America, the other between the Icelandic Low and the Azores High (see also the discussion in GCM Simulations and Their Validation about lack of synchroneity between the blocked and zonal phases of the 40-day oscillation for the two NH ocean basins).

In the SH, the zonally symmetric component of flow variability is much stronger, because of the absence of large landmasses and major mountain ranges. The two main regimes identified in all seasons consist of an amplification and reduction, respectively, of the strength of the westerly winds in mid-latitudes. This change in intensity is also associated with a meridional displacement of the jet (18, 38).

Regional classifications.

Many of the circulation features typified by Fig. 1 have a strongly regional nature. This fact has lead several investigators to focus on the Pacific–North-American and North-Atlantic–European sectors separately. When applying the Gaussian mixture model of Smyth et al. (29), as well as the hierarchical clustering of Cheng and Wallace (26), to each sector in turn two regimes are found: they consist of opposing polarities of the PNA and NAO patterns, respectively (cf. Fig. 1 a and c).

These sectorial analyses reinforce the notion of a single dominant mode of variability in each sector. The Gaussian mixture model, however, is probably overly conservative in this respect. Studies based on detecting inhomogeneities in the pdf have identified up to six or seven regimes in each sector (28, 33). This finer structure in the atmosphere's phase space has been identified only at the cost of lower statistical confidence. Nonetheless, it may be crucial to understanding climate anomalies on longer time scales. El Niño events in the Tropical Pacific tend to be associated with a circulation pattern that bears some similarity with the PNA, but is quite distinct from it—the so-called Tropical Northern-Hemisphere pattern (TNH; ref. 23). La Niña events, however, tend to be accompanied by an increased frequency of occurrence of patterns that are quite different from the opposite polarity of the TNH (39). This lack of mirror symmetry in the mid-latitude response to tropical heating indicates the presence of substantial nonlinearities in LFV.

Interpretation of the Regimes.

Rossby wave propagation and interference.

The slowly traveling, large-scale wave patterns that were first associated with weather phenomena in the 1930s are solutions of the partial differential equation for the conservation of potential vorticity q along a particle trajectory (40, 41). For the purposes of this expository review, q can be defined as the vorticity ζ of a column of fluid divided by its height h, i.e., q = ζ/h. Conservation of q thus means, for instance, that a column of fluid's anti-clockwise rotation (defined as ζ > 0) will slow down (i.e., ζ decreases to smaller positive values) as the column moves over a mountain range (i.e., h > 0 decreases). This type of vorticity balance leads to slow Rossby waves (8, 42) that propagate westward with respect to the mean westerly jet.

One view of persistent anomalies in mid-latitude atmospheric flows is that they result simply from the coincidental slowing down or linear interference of such Rossby waves (43, 44). Another view is that a standing wave induced by topography can lead to a resonant interaction with two separate Rossby waves of distinct wavenumbers and thus produce a long-lived resonant wave triad (section 6.2 of ref. 4; ref. 45). Neither one of these views provides an explanation of the observed clustering of persistent anomalies into distinct flow regimes. But the second one does suggest the more radically nonlinear theory described in the next subsection.

Multiple equilibria.

It was Rossby (16) who first mentioned multiple equilibria as a possible explanation of preferred planetary flow patterns in the atmosphere. Rossby (46) then drew an analogy between such equilibria and hydraulic jumps and formulated some simple models in which similar transitions between faster and slower atmospheric flows could occur.

Charney and colleagues (17, 47) took a major step in formulating a self-consistent atmospheric model for multiple equilibria and connecting it to observations of blocked and zonal flow. They used a highly idealized barotropic, i.e., single-layer, model to study the interaction between a zonal flow and simple topography with zonal wavenumber 2. Their model exhibits two stable equilibria for the same strength of the prescribed zonal forcing, which represents the strength of the pole to equator temperature contrast.

Fig. 2a shows the model's bifurcation diagram, with the strength ψ_A of the zonal jet in the model's steady-state solutions plotted against the corresponding strength ψ_A* of the forcing. The two stable equilibria—marked Z and R₋—are associated with “zonal” and “blocked” flow, respectively, as illustrated in Fig. 2b. The near-zonal solution is close in amplitude and spatial pattern to the forcing jet and is influenced very little by the topography, whereas the blocked solution is strongly affected by it. In the blocked-flow solution, a high-amplitude ridge is located upstream of the “mountains,” similar to the situation during typical observed blocks over the North Pacific and the western U.S. This configuration, with a negative zonal pressure gradient on the windward slope of the mountains, corresponds to a negative mountain torque on the atmosphere.

Fig 2.

Multiple equilibria of a three-mode quasi-geostrophic model with simplified forcing and topography. (a) Bifurcation diagram showing model response to changes in forcing; see text for the explanation of abscissa and ordinate. The “S”-shaped bifurcation curve is typical of two back to back saddle-node bifurcations that give rise to two stable solution branches (solid) separated by an unstable one (dashed). (b) Flow patterns of the zonal (Upper) and blocked (Lower) equilibria, corresponding to the two stable equilibria Z and R₋ (after Charney and DeVore, 1979). [Reproduced with permission from ref. 4 (Copyright 1987, Springer, New York).]

Benzi et al. (48) and Hansen and Sutera (49) found evidence of bimodality in a composite index of wave amplitude in the NH mid-latitude flow. Although the statistical significance and robustness of their findings have been subject to criticism (50), direct confrontation of theoretical bimodality with observations has clearly stimulated LFV research during the 1980s.

Multiple regimes and “ghost equilibria.”

The main contribution of Charney and associates (17, 47) to explaining the existence and persistence of blocked flows was to move away from dynamic meteorology's prevailing paradigm throughout the 1950s and 1960s. In this paradigm, all atmospheric motions were explained as linear perturbations of purely zonal flow, seen as the unique equilibrium of the governing equations. The observations, as summarized in Observational Characteristics of LFV and the present section, show, however, that the atmosphere does not reside in two equilibria, zonal and blocked, any more than in just one (see also section 6.3 of ref. 4).

The next step on the road to a satisfactory explanation of the three or more NH regimes and several sectorial regimes is to show how fuzzy clusters might arise from the equations of motion, along with the transitions between them. Such a step was taken, independently, in the Ph.D. theses of B. Legras at the Univ. of Paris VI and B. Reinhold at the Massachusetts Institute of Technology (Cambridge, MA). By using a two-layer atmospheric model with Cartesian channel geometry, Reinhold and Pierrehumbert (5) showed that two weather regimes with persistent anomalies of varying duration did arise.

Legras and Ghil (6) used a single-layer model on the sphere in which they connected two zonal and one blocked regime to the model's bifurcation diagram. They showed that the flow simulations obtained for realistic parameter values were quite irregular but exhibited persistent sequences. The flow patterns of these sequences resembled those of the model equilibria, although these three equilibria were no longer stable at the parameter values of interest. Because of their role in generating such regime-like persistent flow patterns, these unstable fixed points were called “ghost” equilibria: they are dimly visible through the observed, irregular flow (section 6.4 of ref. 4).

Among the instabilities that lead in this model from stable equilibria to irregular flow, the oscillatory instability of the blocked equilibrium plays a special role. We shall return to it in Extratropical Oscillations: Observations and Theory.

Markov Chains.

Transition matrices.

A reasonable classification of low-pass filtered flow maps into discrete regimes provides only a static view of LFV. The next step is to study the transitions between these regimes over time. A matrix of probabilities for transitions from regime i to regime j is constructed by simply counting the transitions occurring in the data set. This yields an estimated set of conditional probabilities, in line with long-range forecasting experience (51, 52) and the physical intuition that certain pathways of transition are more probable than others.

One kinematic approach to LFV is based on the Markov chain of these transitions. In this approach, knowledge of the system's present state is put to use to make a forecast, rather than using only unconditional probabilities. The Markov-chain view of LFV and, hence, long-range forecasting, is based on the existence of multiple regimes, the expected time of residence in each regime, and the probabilities of transition from one regime to another (Fig. 3).

Fig 3.

Schematic Markov chain with three regimes, B, C, and Z. (a) Some preferential paths between pairs of regimes are shown, along with the corresponding transition probabilities, for instance p_ZB. (b and c) The distribution of residence times in log–linear coordinates differs from the straight line associated with a red-noise process; the mean residence time for each regime is denoted by τ (after Ghil, ref. 75).

Statistical significance.

Once a transition matrix has been constructed, it is crucial to properly assess the statistical significance of its entries. Asymptotic methods to do so, based on parameter-dependent probability models, have been known for some time (53). To be applied reliably, however, these methods require a much larger number of data points than those available in observed data sets. To circumvent this difficulty, Vautard et al. (54) designed a nonparametric method based on Monte Carlo simulation. In it, the integer-valued time series of regime occurrences is tested against a large number of surrogate series with random transitions. To account approximately for the number of events in each regime and their average duration, the sequence of observed events is paired with their succeeding transition intervals and shuffled 1,000 times. The 95th percentile is then easily computed from this shuffle (see again Table 1).

Kimoto and Ghil (28) used this method to identify a chain of highly significant regime transitions over the Pacific. This chain involves a vacillation between zonal and strongly meandering configurations of the Pacific westerly jet.

Starting with the Markov chain for NH hemispheric regimes by Mo and Ghil (25), it was consistently found that transitions between regimes tend to avoid, rather than favor, passages through the climatological mean (see Fig. 3). This “kinematic” result is more consistent with nonlinear explanations of the regimes (see Multiple Equilibria) than with the simple phase reversal suggested by linear theories (see Rossby Wave Propagation and Interference). The connection between the Markov-chain kinematics of LFV and the oscillatory view will be discussed in Complementarity of the Two Approaches and Implications for Predictability.

Intraseasonal Oscillations: Their Theory and Simulation

Extratropical Oscillations: Observations and Theory.

Oscillations in atmospheric angular momentum (AAM).

Variations in global AAM and in the length of day are highly correlated with each other on intraseasonal time scales. Both quantities exhibit spectral peaks with periods near 40 and 50 days (55), among others. Essentially, the Earth-atmosphere system is closed with respect to angular momentum exchanges on this time scale, except for the well known tidal effects of the Sun and Moon, which can be easily computed and eliminated. Once this is done, what remains is the following: when the mid-latitude westerly winds pick up or the tropical trade winds slow down, the solid earth slows down in its rotation, and the length of day increases; hence, the high positive correlation between the latter and AAM.

Power spectra of observed AAM variance are shown in Fig. 7, split into three latitude bands [(i) NH extratropics (26°N–90°N); (ii) Tropics (20°S–20°N); and (iii) SH extratropics (90°S–26°N)], which is published as supporting information on the PNAS web site. It is clear from the figure that the 50-day peak is largely associated with AAM fluctuations in the tropics, which dominate the global AAM. The 40-day peak, however, seems to be associated primarily with variations in the strength of the mid-latitude westerlies, particularly in the NH. Indeed, the amplitude of the 40-day oscillation in zonal winds is known to be largest during boreal winter, when the winds are strongest in the NH (56–59), and we shall thus concentrate here on the longer data sets and more detailed modeling studies for the NH.

The extent to which the tropical and NH oscillations are independent phenomena or influence each other is still the subject of active debate. Madden and Julian (10, 11) discovered the tropical oscillation in zonal winds and tropical convection over the equatorial Pacific, although its origins are still not well understood (13). Extratropical oscillations have been found in observed NH planetary-scale circulation anomalies with periods of 20–70 days (15, 57, 60, 61). There is some evidence that the mid-latitude circulation over the North Pacific is correlated to convective anomalies associated with the tropical oscillation (56, 62, 63). On the other hand, Dickey et al. (55) and Ghil and Mo (57) found the extratropical mode to be often independent of, and sometimes to lead, the tropical one. Upper-level potential vorticity anomalies are known to propagate from the mid-latitudes into the tropics; this propagation is associated with NW–SE tilting troughs (64). They are accompanied by cold surges and can cause episodes of intense tropical convection that seem to be related to the intraseasonal oscillation in the tropics (65, 66).

Basic theoretical results.

We outline here how a hierarchy of models can be used to formulate and test the hypothesis that the 40-day oscillation is an intrinsic mode of the NH extratropics, associated with the interaction between the jet stream and mid-latitude mountain ranges. The rudiments of this hypothesis originate in the highly idealized barotropic model of Charney and DeVore (17), which we discussed in Interpretation of the Regimes.

More complex models—both barotropic (i.e., single-layer) and baroclinic (i.e., multilayer), with more spatial degrees of freedom than the Charney and DeVore (17) model—exhibit multiple flow patterns that are similar to those found in Fig. 2b above, for realistic values of the forcing. The crucial difference is that the equilibria found in the more complex models are no longer stable, and the system oscillates around the blocked solution or fluctuates between the zonal and blocked solutions in an irregular way (4, 6).

A sample bifurcation diagram from such a model is shown in Fig. 8, which is published as supporting information on the PNAS web site (see also the discussion in sections 6.4 and 6.5 of ref. 4). In this diagram, the branch of blocked equilibria is destabilized by a Hopf bifurcation as the intensity of the forcing jet increases. The limit cycle that arises from this bifurcation has a period of roughly 40 days.

Jin and Ghil (67) showed that, when a sufficiently realistic meridional structure of the solutions' zonal jet is allowed, the back to back saddle-node bifurcations of Fig. 2a are indeed replaced by a Hopf bifurcation and thus transition to finite-amplitude periodic solutions can occur. Eigenanalyses of the unstable equilibria in a barotropic model with higher horizontal resolution, as well as its time-dependent solutions, indicate oscillatory instabilities with intraseasonal (35–50 days) and biweekly (10–15 days) time scales (58). Floquet analysis of this model's limit cycles (59) confirms that the 40-day oscillations that arise in it by oscillatory topographic instability are stronger in winter than in summer, like the NH observed oscillations (57, 68).

GCM Simulations and Their Validation.

Atmospheric GCMs provide a powerful tool for testing the theory of NH extratropical oscillations developed in simpler models. Marcus et al. (69, 70) made a 3-year perpetual-January simulation with a version of the Univ. of California, Los Angeles, GCM that produces no self-sustained Madden–Julian oscillation in the tropics. A robust 40-day oscillation in AAM is found to arise in the model's NH extratropics when standard topography is present. Three shorter runs with no topography produced no intraseasonal oscillation; this result is consistent with a topographic origin for the NH extratropical oscillation in the standard model. The spatial structure of the circulation anomalies associated with the model's extratropical oscillation is shown in Fig. 4, in terms of 500-mb geopotential height composites during the peak (a) and quadrature (b) phase of the AAM cycle.

Fig 4.

Intraseasonal oscillations in a GCM: composite 500-mb maps from the perpetual-January GCM experiment of Marcus et al. (70). (a) For days on which the 36–60 day NH extratropical AAM exceeded 1.5 times its rms value; maps for days with a negative (positive) anomaly were added with a positive (negative) sign. (b) Constructed from maps taken 12 days earlier than those included in a. Contour interval is 20 m, and negative contours are dashed. [Reproduced with permission from ref. 70 (Copyright 1996, American Meteorological Society).]

The oscillation is dominated by a standing wavenumber-2 pattern, which undergoes tilted-trough vacillation. High values of AAM are associated with low 500-mb heights over the northeast Pacific and the North Atlantic oceans (Fig. 4a), and vice versa. These flow patterns resemble the configurations seen in the Charney and DeVore (17) simple model (see Fig. 2b here). The NE–SW tilting phase in Fig. 4a and NW–SE tilting phase in Fig. 4b of the GCM are strongly reminiscent of the extremes and intermediate phases of the 40-day oscillation that arises by Hopf bifurcation from the blocked equilibrium in the Legras and Ghil (6) model (see Fig. 8 here for the bifurcation; spatio-temporal patterns of the limit cycle in that model were analyzed by M. Kimoto, personal communication).

The successive phases of the 28–72-day band-passed fluctuations in 250-mb streamfunction anomalies analyzed by Weickmann et al. (ref. 56; see figures 7 and 9 a–d there) also exhibit good agreement with the evolution of the 40-day oscillation in the work of Marcus and colleagues (71) with the Univ. of California, Los Angeles, atmospheric GCM [see ref. 71 for a video clip of the evolution of 500-mb heights, 250-mb streamfunction fields, and sea-level pressures during the atmospheric 40-day oscillation of the GCM (available also from M.G. upon request)]. The height pattern in Fig. 4a is very similar, furthermore, to the extreme-phase patterns obtained from observed data by correlating the 10-day low-pass filtered wintertime 500-mb height fields with the sum of the mountain torques computed over the Rockies, Himalayas, and Greenland (14).

In the GCM, the two centers of action, over the North Pacific and North Atlantic oceans, have slightly different frequencies; this gives rise to a long-period modulation (of about 300 days) in the amplitude of the intraseasonal oscillation, similar to that observed by Penland et al. (72) in globally averaged AAM time series. Global correlations with the leading empirical orthogonal functions of the NH extratropical 500-mb height field show NE–SW teleconnection patterns extending into the tropics, in particular into the Indian Ocean, similar to those found in observational studies (56, 73).

The model's zonally averaged latent heating in the tropics exhibits no intraseasonal periodicity, but a nearly 40-day oscillation is found in cumulus precipitation over the western Indian Ocean, which suggests an extratropical trigger of the 50-day oscillation in the tropics. Madden and Speth (see figure 10 of ref. 74) find that (mostly extratropical) mountain torques do lead (mostly tropical) friction torques and eastward-moving convective systems during the 1987–1988 winter singled out already by Dickey et al. (see figure 16 of ref. 55) for the striking intensity of its episodes of intraseasonal variability.

The careful analysis of perpetual-January runs with an atmospheric GCM thus confirms, on the one hand, the topographic origin of the NH 40-day oscillation, originally suggested by simple- and intermediate-model studies (6, 58, 59, 67, 75). On the other, it provides greater realism and spatio-temporal detail, permitting therewith a much better confrontation of the theory with the existing observations (55, 57).

Complementarity of the Two Approaches and Implications for Predictability

We have seen that there is considerable progress in describing and explaining the coarse-grained structure of the large-scale atmosphere's phase space. The existence of multiple flow, or weather, regimes is observationally well established (see Classification of Weather Maps). The preferential paths between these regimes are less firmly documented, but are also starting to gain credence and detail (see Markov Chains). The explanation of the regimes (see Interpretation of the Regimes) and of the Markov chains between them requires further study across a hierarchy of models and confrontation with the observations.

Among the various intraseasonal oscillations, the 40-day oscillation in mid-latitude NH flows has been used in Intraseasonal Oscillations: Their Theory and Simulation here for illustration purposes. A fairly complete set of observational studies, as well as research across a hierarchy of models—from the simplest analytical models (67), through intermediate models of increasing resolution (6, 58, 59, 75, 76), all of the way to GCMs (69, 70)—has produced a consistent view of the decisive role of topography in this oscillation.

Still, we have not reached a convincing answer to the question asked at the end of the introduction: Are the regimes merely slow phases of the intraseasonal oscillations or do the oscillations arise as instabilities of certain regimes? There is theoretical evidence that points to the 40-day oscillation as arising from a Hopf bifurcation off the blocking flow (6, 75). On the other hand, observational studies have produced closed paths within a Markov chain whose states resemble well known phases of certain intraseasonal oscillations (28). Multiple regimes and intraseasonal oscillations can coexist in a two-layer model on the sphere within the scenario of “chaotic itinerancy” (77, 78).

There is, in fact, mounting evidence that the time evolution of intraseasonal oscillations is related to regime occurrence. Plaut and Vautard (15) showed that the occurrence of an Atlantic blocked-flow regime is strongly favored, although not systematically caused, by particular phases of the 30–35-day oscillation they described over the Atlantic. Koo (18) found analogous results for the zonal-flow regimes of the SH.

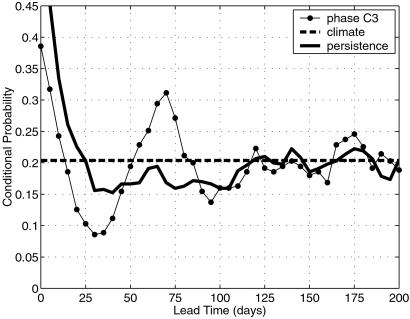
These relationships imply potential predictability of the weather regimes by taking the current phase of the corresponding oscillation as a predictor. This idea is illustrated in Fig. 5 for the SH 70-day oscillation as a predictor of the low-latitude regime, in which the SH westerly jet is displaced equatorward. Given that the current phase of the 70-day oscillation is in phase-category 3 (of 8), the figure shows that the probability of occurrence of the low-latitude regime 70 days later is more than 50% higher than the unconditional climatological forecast. Similar curves can be constructed for each initial-phase category in turn (see also ref. 15).

Fig 5.

Enhanced regime predictability: conditional probability of occurrence of the SH low-latitude regime events, taking the phase category of the SH 70-day oscillation as a predictor (thin solid curve with filled circles), as a function of lead time. The heavy horizontal dashed line indicates climatological probability, and the heavy solid curve denotes the persistence forecast. [Reproduced with permission from ref. 18 (Copyright 2001).]

We conclude that an in-depth answer to the basic question about waves and particles in the atmosphere's phase space can greatly help increase the accuracy and reliability of extended-range forecasts. Studies aimed at answering this question can thus usefully complement the approach of improving numerical weather prediction models by increasing their accuracy and the details of the physical processes they include (79, 80).

Abbreviations

• LFV, low-frequency variability

• GCM, general circulation model

• pdf, probability density function

• NH, Northern Hemisphere

• PNA, Pacific–North-American

• NAO, North-Atlantic Oscillation

• SH, Southern Hemisphere

• AAM, atmospheric angular momentum