Complexity and robustness

Abstract

Highly optimized tolerance (HOT) was recently introduced as a conceptual framework to study fundamental aspects of complexity. HOT is motivated primarily by systems from biology and engineering and emphasizes, (i) highly structured, nongeneric, self-dissimilar internal configurations, and (ii) robust yet fragile external behavior. HOT claims these are the most important features of complexity and not accidents of evolution or artifices of engineering design but are inevitably intertwined and mutually reinforcing. In the spirit of this collection, our paper contrasts HOT with alternative perspectives on complexity, drawing on real-world examples and also model systems, particularly those from self-organized criticality.

A vision shared by most researchers in complex systems is that certain intrinsic, perhaps even universal, features capture fundamental aspects of complexity in a manner that transcends specific domains. It is in identifying these features that sharp differences arise. In disciplines such as biology, engineering, sociology, economics, and ecology, individual complex systems are necessarily the objects of study, but there often appears to be little common ground between their models, abstractions, and methods. Highly optimized tolerance (HOT) (1–6) is one recent attempt, in a long history of efforts, to develop a general framework for studying complexity. The HOT view is motivated by examples from biology and engineering. Theoretically, it builds on mathematics and abstractions from control, communications, and computing. In this paper, we retain the motivating examples but avoid theories and mathematics that may be unfamiliar to a nonengineering audience. Instead, we aim to make contact with the models, concepts, and abstractions that have been loosely collected under the rubric of a “new science of complexity” (NSOC) (7) or “complex adaptive systems” (CAS), and particularly the concept of self-organized criticality (SOC) (8, 9). SOC is only one element of NSOC/CAS but is a useful representative, because it has a well-developed theory and broad range of claimed applications.

In Table 1, we contrast HOT's emphasis on design and rare configurations with the perspective provided by NSOC/CAS/SOC, which emphasizes structural complexity as “emerging between order and disorder,” (i) at a bifurcation or phase transition in an interconnection of components that is (ii) otherwise largely random. Advocates of NSOC/CAS/SOC are inspired by critical phenomena, fractals, self-similarity, pattern formation, and self-organization in statistical physics, and bifurcations and deterministic chaos from dynamical systems. Motivating examples vary from equilibrium statistical mechanics of interacting spins on a lattice to the spontaneous formation of spatial patterns in systems far from equilibrium. This approach suggests a unity from apparently wildly different examples, because details of component behavior and their interconnection are seen as largely irrelevant to system-wide behavior.

Table 1.

Characteristics of SOC, HOT, and data

	Property	SOC	HOT and Data
1	Internal configuration	Generic, homogeneous, self-similar	Structured, heterogeneous, self-dissimilar
2	Robustness	Generic	Robust, yet fragile
3	Density and yield	Low	High
4	Max event size	Infinitesimal	Large
5	Large event shape	Fractal	Compact
6	Mechanism for power laws	Critical internal fluctuations	Robust performance
7	Exponent α	Small	Large
8	α vs. dimension d	α ≈ (d − 1)/10	α ≈ 1/d
9	DDOFs	Small (1)	Large (∞)
10	Increase model resolution	No change	New structures, new sensitivities
11	Response to forcing	Homogeneous	Variable

Table 1 shows that SOC and HOT predict not just different but exactly opposite features of complex systems. HOT suggests that random interconnections of components say little about the complexity of real systems, that the details can matter enormously, and that generic (e.g., low codimension) bifurcations and phase transitions play a peripheral role. In principle, Table 1 could have a separate column for Data, by which we mean the observable features of real systems. Because HOT and Data turn out to be identical for these features, we can collapse the table as shown. This is a strong claim, and the remainder of this paper is devoted to justifying it in as much detail as space permits.

What Do We Mean By Complexity?

To motivate the theoretical discussion of complex systems, we briefly discuss concrete and hopefully reasonably familiar examples and begin to fill in the “Data” part of Table 1. We start with biological cells and their modern technological counterparts such as very large-scale integrated central processing unit (CPU) chips. Each is a complex system, composed of many components, but is also itself a component in a larger system of organs or laptop or desktop personal computers or embedded in control systems of vehicles such as automobiles or commercial jet aircraft like the Boeing 777. These are again components of the even larger networks that make up organisms and ecosystems, computer networks, and air and ground transportation. Although extremely complex, these systems have available reasonably complete descriptions and thus make good starting examples. Engineering systems are obviously better understood than biological systems, but the gap is closing. Engineers now build systems of almost bewildering levels of complexity, and biologists are beginning to move beyond the components to characterizing the networks they create. Although no one person understands in complete detail how all these systems work, there is now a rich variety of accessible introductory material in each area that gives additional details well beyond what is discussed here. In each of the following paragraphs, we consider a critical question about complexity and the answers that these example systems suggest.

What Distinguishes the Internal Configurations of Systems as Complex?

It is not the mere number of component parts. Any macroscopic material has a huge number of molecules. It is the extreme heterogeneity of the parts and their organization into intricate and highly structured networks, with hierarchies and multiple scales (Table 1.1). (Some researchers have suggested that “complicated” be used to describe this feature.) Even bacterial cells have thousands of genes, most coding for proteins that form elaborate regulatory networks. A modern CPU has millions of transistors and millions of supporting circuit elements; many computers have billions of transistors, and the Internet will soon have billions of nodes. The 777 is fully “fly-by-wire,” with 150,000 different subsystems, many of them quite complex, including roughly 1,000 CPUs that operate and automate all vehicle functions. Even automobiles have dozens of CPUs performing a variety of control functions. If self-similarity describes multiscale systems with similar structure at different scales, then these systems could be described as highly self-dissimilar, that is, extremely different at different scales and levels of abstraction. Just the design and manufacture of the 777 involved a global software and computing infrastructure with roughly 10,000 work stations, terabytes of data, and a one billion dollar price tag.

What Does This Complexity Achieve?

In each example, it is possible to build similar systems with orders of magnitude fewer components and much less internal complexity. The simplest bacteria have hundreds of genes. Much simpler CPUs, computers, networks, jets, and cars can be and have been built. What is lost in these simpler systems is not their basic functionality but their robustness. By robustness, we mean the maintenance of some desired system characteristics despite fluctuations in the behavior of its component parts or its environment. Although we can loosely speak of robustness without reference to particular systems characteristics, or particular component or environmental uncertainties, this can often be misleading, as we will see. All of our motivating examples illustrate this tradeoff between robustness and internal simplicity. Although it has become a cliche that greater complexity creates unreliability, the actual story is more complicated.

What Robustness Would Be Lost in Simpler Systems?

Simple bacteria with several hundred genes, like mycoplasma, require carefully controlled environments, whereas Escherichia coli, with almost 10 times the number of genes, can survive in highly fluctuating environments. Large internetworks do not change the basic capabilities of computers but instead improve their responsiveness to variations in a user's needs and failures of individual computers. A jet with many fewer components and no very large-scale integrated chips or CPUs could be built with the same speed and payload as a 777, but it would be much less robust to component variations, failures, or fluctuations such as payload size and distribution or atmospheric conditions. Whereas older automobiles were simpler, new vehicles have elaborate control systems for air bags, ride control, antilock braking, antiskid turning, cruise control, satellite navigation, emergency notification, cabin temperature regulation, and automatic tuning of radios. At the same size and efficiency, they are safer, more robust, and require less maintenance. Thus robustness drives internal complexity and is the most striking feature of these complex systems.

What Is the Price Paid for These Highly Structured Internal Configurations and the Resulting Robustness?

Although there is the expense of additional components, this is usually more than made up for by increased efficiency, manufacturability, evolvability of the system, and the ability to use sloppier and hence cheaper components. It is far more serious that these systems can be catastrophically disabled by cascading failures initiated by tiny perturbations. They are “robust, yet fragile,” that is, robust to what is common or anticipated but potentially fragile to what is rare or unanticipated and also to flaws in design, manufacturing, or maintenance (Table 1.2). Because robustness is achieved by very specific internal structures, when any of these systems is disassembled, there is very little latitude in reassembly if a working system is expected. Although large variations or even failures in components can be tolerated if they are designed for through redundancy and feedback regulation, what is rarely tolerated, because it is rarely a design requirement, is nontrivial rearrangements of the interconnection of internal parts. The fraction of all possible amino acid sequences or complementary metal oxide semiconductor circuits that yield functioning proteins or chips is vanishingly small. Portions of macromolecular networks as well as whole cells of advanced organisms can function in vitro, but we do not yet know how to reassemble them into fully functional cells and organisms. In contrast, when arbitrary interconnection is a specific design requirement, such as in routers in an internet protocol network, then this can be robustly designed for but with some added expense in resources.

How Does “Robust, Yet Fragile” Manifest Itself in the Example Systems?

Biological organisms are highly robust to uncertainty in their environments and component parts yet can be catastrophically disabled by tiny perturbations to genes or the presence of microscopic pathogens or trace amounts of toxins that disrupt structural elements or regulatory control networks. The 777 is robust to large-scale atmospheric disturbances, variations in cargo loads and fuels, turbulent boundary layers, and inhomogeneities and aging of materials, but could be catastrophically disabled by microscopic alterations in a handful of very large-scale integrated chips or by software failures. (Such a vulnerability is completely absent from a hypothetical simpler vehicle.) This scenario fortunately is vanishingly unlikely but illustrates the issue that this complexity can amplify small perturbations, and the design engineer must ensure that such perturbations are extremely rare. The 777 is merely a component in a large, highly efficient, and inexpensive air traffic network, but also one that can have huge cascading delays. Processor chips are similarly robust to large variations in the analog behavior of their CMOS circuit elements and can perform a literally “universal” array of computations but can fail completely if an element is removed or the circuit rearranged. Processor, memory, and other chips can be organized into highly fault-tolerant computers and networks, creating platforms for complex software systems with their own hierarchies of components. These software systems can perform a broad range of functions primarily limited only by the programmer's imagination but can crash from a single line of faulty code.

How Does NSOC/CAS Differ from HOT with Respect to the Complexity of the Example Systems?

As a specific, if somewhat whimsical, example, note that a 777 is sufficiently automated that it can fly without pilots, so we could quite fairly describe the mechanism by which it can transport people and material through the air across long distances as an adaptive, emergent, self-organizing, far-from-equilibrium, nonlinear phenomenon. What is both an attraction and a potential weakness of this perspective is that it could be applied to a tornado as well. The HOT view is quite different. Our examples all have high performances and yields and high densities of interconnection (Table 1.3), as well as robustness and reliability. We want to sharpen the distinction not only between the likely short and fatal ride of a tornado with the much faster but relatively boring 777 experience but, more importantly between the 777 design and alternatives that might have worse, or even better, performance, robustness, and reliability.

Are All These Features of Complexity Necessary?

That is, must systems be broadly robust if they are to successfully function and persist, must this robustness entail highly structured internal complexity, and is fragility a necessary risk? In this sense, is complexity in engineering and biological systems qualitatively the same? We believe that the answer to these questions is largely affirmative, and the examples briefly examined in this section support this, as do numerous other studies of this issue (e.g., see ref. 10). The remainder of this paper offers a thin slice through the HOT theoretical framework that is emerging to systematically address these questions. The concept of HOT was introduced to focus attention on exactly these issues. Tolerance emphasizes that robustness in complex systems is a constrained and limited quantity that must be carefully managed and protected. Highly optimized emphasizes that this is achieved by highly structured, rare, nongeneric configurations that are products either of deliberate design or evolution. The characteristics of HOT systems are high performance, highly structured internal complexity, and apparently simple and robust external behavior, with the risk of hopefully rare but potentially catastrophic cascading failure events initiated by possibly quite small perturbations.

Power Laws and Complexity

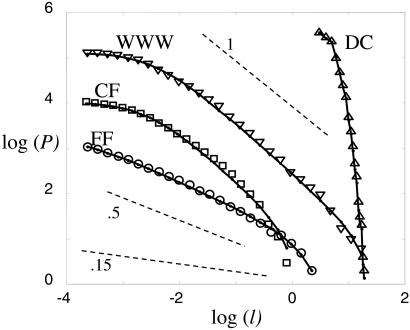
Recently a great deal of attention has been given to the fact that statistics of events in many complex interconnected systems share a common attribute: the distributions of sizes are described by power laws. Several examples are illustrated in Fig. 1, where we plot the cumulative probability 𝒫(l≥l_i) of events greater than or equal to a given size l_i. Power laws 𝒫(l ≥ l_i) ∼ {l_i}^−α are associated with straight lines of slope −α in a log(𝒫) vs. log(l) plot, and describe all of the data sets reasonably well, with the exception of data compression (DC), which is exponential. Whether the other distributions are power laws exactly we will not attempt to resolve, because this is not important for HOT. What is clear is that these distributions have heavy tails and are far from exponential or Gaussian.

Fig 1.

Log–log (base 10) comparison of DC, WWW, CF, and FF data (symbols) with PLR models (solid lines) (for β = 0, 0.9, 0.9, 1.85, or α = 1/β = ∞, 1.1,1.1, 0.054, respectively) and the SOC FF model (α = 0.15, dashed). Reference lines of α = 0.5, 1 (dashed) are included. The cumulative distributions of frequencies 𝒫(l ≥ l_i) vs. l_i describe the areas burned in the largest 4,284 fires from 1986 to 1995 on all of the U.S. Fish and Wildlife Service Lands (FF) (17), the >10,000 largest California brushfires from 1878 to 1999 (CF) (18), 130,000 web file transfers at Boston University during 1994 and 1995 (WWW) (19), and code words from DC. The size units [1,000 km² (FF and CF), megabytes (WWW), and bytes (DC)] and the logarithmic decimation of the data are chosen for visualization.

In this regard, the 777 has boring but fortunate statistics, as there have been no crashes or fatalities so far. More generally, the deaths and dollars lost in all disasters from either technological or natural causes is a power law with α ≈ 1. Forest fires and power outages have among the most striking and well-kept statistics, but similar, although less heavy tailed, plots can be made for species extinction, social conflict, automotive traffic jams, air traffic delays, and financial market volatility. Other examples that are not event sizes per se involve Web and Internet traffic and various bibliometric statistics.

Although power law statistics is one of many characteristics we might consider, our focus on this property provides a meaningful quantitative point of departure for contrasting HOT with SOC. Of course, SOC and HOT are two of many possible mechanisms for power laws. Statistics alone can be responsible (11). What differentiates SOC and HOT from statistical mechanisms are their broader claims suggesting links between power laws and internal structure, as summarized in Table 1. If SOC were the underlying mechanism leading to complexity in a given system, power laws would be one signature of an internal self-sustaining critical state. The details associated with the initiation of events would be a statistically inconsequential factor in determining their size. Large events would be the result of chance random internal fluctuations characteristic of the self-similar onset of systemwide connectivity at the critical state. In contrast, for HOT power law, statistics are just one symptom of “robust, yet fragile,” which we suggest is central to complexity. Heavy tails reflect tradeoffs in systems characterized by high densities and throughputs, where many internal variables have been tuned to favor small losses in common events, at the expense of large losses when subject to rare or unexpected perturbations, even if the perturbations are infinitesimal.

The Forest Fire Models

In this section, we review the lattice models that have served as the primary template for introducing SOC and HOT. Our story begins with percolation (12), the simplest model in statistical mechanics, which exhibits a critical phase transition. We focus on site percolation on a two-dimensional N × N square lattice. Individual sites are independently occupied with probability ρ and vacant with probability (1 − ρ). Properties of the system are determined by ensemble averages in which all configurations at density ρ are equally likely. Contiguous sets of nearest-neighbor occupied sites define connected clusters. The percolation forest fire model includes a coupling to external disturbances represented by “sparks” that impact individual sites on the lattice. Sparks initiate “fires” when they hit an occupied site, burning through the associated connected cluster. Fires are the rapid cascading failure events analogous to individual events, which comprise the statistical distributions in the previous section.

Sparks are all of equal size (one lattice site) but may initiate fires of a wide range of sizes, depending on the configuration and the site that is hit. The impact site (i, j) is drawn from a probability distribution P(i, j). The most realistic cases involve variable risk, where ignitions are common in some regions and rare in others and are represented by P(i, j)s that are skewed. In the thermodynamic limit, translational invariance of the ensemble renders the choice of P(i, j) irrelevant (Table 1.11), and the density ρ is a priori the only tunable parameter (Table 1.9). Site percolation exhibits a continuous phase transition at density ρ_c ≈ 0.592, associated with the emergence of an infinite connected cluster. The probability that any given site is on the infinite cluster defines the percolation probability 𝒫_∞(ρ), which is zero for ρ < ρ_c and increases continuously and monotonically to one for ρ ≥ ρ_c. At the critical density, the infinite cluster is fractal and an infinitesimal fraction of the total density.

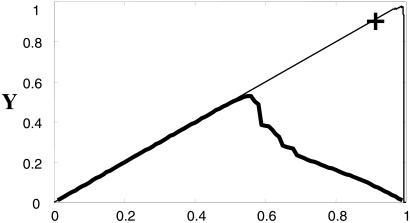
We define yield, Y, to be the remaining density after one spark:Y = ρ − <l>. Here ρ is the density before the spark, and <l> is the average loss in density because of the fire, computed over the distribution of sparks P(i, j) as well the configurations in the ensemble. For a given strategy (i.e., configuration or ensemble of configurations), yield is a measure of the mean survival, which may be viewed as profit or biological fitness. Optimization of yield can occur through deliberate design, or via evolutionary selection pressure, for a given distribution of sparks P(i, j).

The only time a spark leads to macroscopic loss is when ρ > ρ_c and the infinite cluster is hit, in which case the loss is given by the density fraction associated with the infinite cluster:

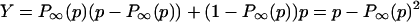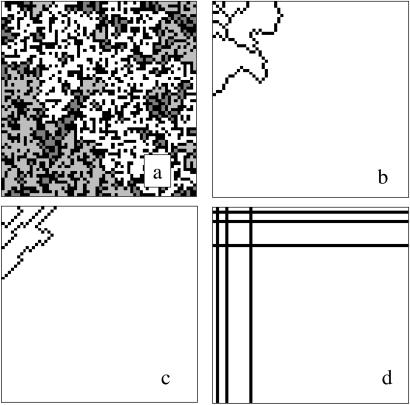
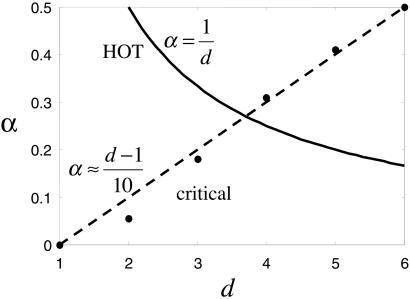
The maximum yield corresponds to the critical density ρ_c (see Fig. 2), which is the maximum density for which <l> = 0. At ρ_c the distribution of cluster sizes is a power law, reflecting the fractal self-similarity of the critical state (Table 1.5 and 1.6). A sample configuration at the critical density is illustrated in Fig. 3a. The power law in the cluster size distribution leads to a power law in the fire size distribution, which written cumulatively takes the form: 𝒫(l) ∼ l^−α. For site percolation on a two-dimensional square lattice, the exponent α ≈0.05, which is significantly smaller than the power laws in Fig. 1. As the dimension increases toward the upper critical dimension, the power laws become increasingly steep (see Fig. 4 and Table 1.8), reflecting the fact that large fluctuations that arise through chance aggregation in random systems become increasingly unlikely with increased dimension.

Fig 2.

Yield vs. density curves for 64 × 64 random and HOT lattices. Here and in Fig. 3, we take P(i,j) = exp(−η(i + j)/N) with η = 24. The heavy solid line illustrates the percolation forest fire model, with maximum yield at ρ_c. The light solid line illustrates the results generated by the local incremental algorithm, where the maximum yield point corresponds to Fig. 3c. The + marks the result for grid design (Fig. 3d).

Fig 3.

Sample lattices contrasting criticality and HOT: (a) The percolation forest fire model at ρ_c and HOT configurations obtained by (b) Darwinian evolution, (c) local incremental algorithm, and (d) grid design. Empty sites are black, and occupied clusters are grayscale (percolation) or white (HOT). Simulation parameters are as in Fig. 2.

Fig 4.

Exponent α versus dimension d for percolation and HOT. The results for percolation (dots) are taken from ref. 11, and the fit α ≈(d−1)/10 is approximate.

In equilibrium statistical mechanics, criticality is a necessary and sufficient condition for power laws and universality. There are two quite different ways that this can be and has been interpreted. Physicists see complexity emerging between order and disorder at the critical point. When physicists find power laws in the statistics of some phenomena and say that this is “suggestive of criticality,” they are implicitly (i) referring to the necessity results, (ii) assuming that some appropriate model system is relevant, and (iii) assuming that some mechanism has tuned the density to the critical point. SOC addresses the third issue, replacing tuning with feedback dynamics that creates a stable equilibrium at a critical point.

Engineers and many mathematicians would tend to have an opposite interpretation of the same theoretical results about criticality. They would tend to approach the problem in terms of tuning rather than phase transitions, and power laws would be viewed as arising from tuning and optimization, with criticality a rare and extreme special case when only one parameter—density—is used. Introducing feedback dynamics as in SOC to replace tuning would be one design alternative among many that would lead to the critical state. Most importantly, they would tend to view the standard necessity result as a special case and look for generalizations of the sufficiency part. The natural question then would be, what happens if we tune more parameters to optimize yield? Do we still get power laws? What is the nature of the optimal state? This is the HOT alternative to criticality and SOC and leads to a radically different picture, even with identical starting points. To illustrate this contrast, we next describe modifications of the percolation forest fire model, which produce lattice models exhibiting SOC and HOT.

The SOC forest fire model (13, 14) adds dynamics to the basic percolation model described above, so that the density is no longer a free variable, and the configurations that contribute to the ensemble and their corresponding statistical weight are determined over time through iteration of the rules. Trees grow (vacant sites randomly become occupied) at a fixed rate, which is large compared with the rate of ignition but infinitesimal compared with the rate at which fires propagate through connected clusters. SOC assumes this separation of time scales is preserved, so that losses associated with the infinitesimal rate of ignitions are balanced by the slow but steady regrowth of trees.

The key defining feature that makes this model an example of SOC is that it converges to a critical point, which shares the characteristic features of criticality discussed above (see Table 1). Again the macroscopic loss is zero even in the largest events (Table 1.4), so that the density remains stationary at ρ_c = 0.39 (13, 14) (slightly less than that of percolation) in the thermodynamic limit (Table 1.3). At this stationary point, the system exhibits a power law distribution of self-similar fractal events (Table 1.5), characterized by the exponent α = 0.15 (Table 1.7), which is slightly steeper than percolation but still very flat compared with the data in Fig. 1.

Alternatively, the extension of the percolation forest fire model toward the highly designed limit leads to specialized high-yield configurations, which we refer to as HOT states. HOT states are optimized for yield given P(i, j) and reach unit densities and unit yields in the limit of large system sizes (Table 1.3). Several examples of HOT configurations are illustrated in Fig. 3. In each case, the configuration breaks up into a set of compact cellular regions of unit density, separated by linear barriers, or fire breaks, which prevent fires from spreading into neighboring cells (Table 1.1, 1.3–1.5). The fire breaks are not put in by hand but rather arise from optimization as discussed below and are concentrated in regions where sparks are likely and sparse in regions where sparks are rare. HOT configurations are extremely robust to fires compared with random configurations at a similar density. However, they have also developed sensitivities not present in the random percolation forest fire model. In particular, the robustness and high yields associated with designed configurations come at a cost of introducing fragility to changes in the distribution of sparks P(i, j) and flaws in the design (i.e., a defect in a fire break) (Table 1.2).

Power laws statistics in the distribution of events is an outcome of optimization for yield when P(i, j) is skewed. Compared with the power law statistics associated with criticality, the distributions tend to be steeper, have opposite trends with dimensionality, and involve macroscopic loss in density—all in better agreement with the example systems we have discussed (Table 1.3–1.8). At a cost of decreased yield, heavy tails can be eliminated by increasing the number of barriers, which decreases the sensitivity to changes in P(i, j). Redundant barriers reduce the risks associated with possible design flaws, which mimic common engineering strategies for increasing robustness.

HOT states naturally emerge from an initial ensemble of random percolation configurations in a simulation that mimics Darwinian evolution (6). Although the SOC forest fire model includes a primitive feedback that selects a critical density, mechanisms associated with biological heredity preserve much more detailed structure from one generation to the next. In a community of bounded size, we represent individual organisms by percolation lattices. The initial configurations are generated randomly. Each parent gives rise to two offspring, with a certain probability of mutation per site. The offspring lattices are subject to sparks drawn from P(i, j). We define fitness in terms of yield and, if fitness is low, the organism dies. For those that live, selection for space in the community is based on fitness. Fig. 3b illustrates a configuration obtained after a large number of generations leads to the evolution of high fitness individuals, characterized by cellular barrier patterns that prevent large losses in common disturbances.

Over time, evolution refines the configuration, site by site, subject to stochastic effects associated with random mutation and sampling of the sparks. One way to describe the spatial patterns that distinguish HOT from SOC is by the number of design degrees of freedom (DDOFs), which is a count of the parameters that are deliberately tuned or evolved. Random percolation has only one DDOF, the density ρ, and SOC also has one, the ratio of spark frequency to site growth (Table 1.9). HOT represents the opposite extreme. If we specifically choose whether each site individually is occupied or vacant on an N × N lattice, then we have N² DDOFs, which diverges in the limit N→ ∞. This is the limit probed stochastically and locally by the evolutionary model. A brute force global (deterministic) optimization of yield for an N × N lattice involves a search through 2^N2 configurations and quickly becomes intractable for increasing N. However, a wide range of constraints on the search space for optimal configurations (as in the Darwinian evolution model), or limiting the number of DDOFs, or both, leads to HOT states with qualitatively similar features. We briefly discuss a few additional examples below, referring the reader to more detailed expositions that appear elsewhere. Here the specific algorithms for constrained optimizations are less important than the shared features that emerge from almost any sensible heuristic.

Fig. 3c illustrates the optimal configuration obtained by using a deterministic local incremental algorithm for increasing the density, always choosing the next occupied site to maximize yield, as described in ref. 2. Here there are of order N² DDOFs, but far fewer configurations (<N⁴) are considered to determine a maximum compared with the global search. The search picks a measure zero set of configurations that define a yield curve, Y (ρ), with a maximum at some ρ = ρ_max (see Fig. 2). Fig. 3c illustrates the maximum yield point for a 64 × 64 lattice.

Fig. 3d illustrates a HOT configuration that results from global optimization in a subset of configuration space comprised of grid designs. The lattice is fully occupied, except for vertical and horizontal cuts composed of vacancies. In ref. 1, a recursive formula for the positions of the cuts was derived and shown asymptotically to lead to a power law distribution of events for a wide range of P(i, j). In this case, there are 2N DDOFs, the choices whether to place a cut in each row or column.

The beauty of the lattice models is that they show how highly specialized structures, in particular barriers separating compact regions, arise naturally and necessarily when yield is optimized. Recalling the discussion of What Do We Mean by Complexity?, we note that HOT has all of the essential features we were looking for at the beginning: “highly structured, nongeneric, self-dissimilar configurations and robust, yet fragile behavior.” Although we clearly get heavy-tailed distributions that are roughly power laws, it is hard to get definitive exponents. The problem is that it is hard to optimize on lattices large enough to escape finite size limitations. We can and do solve some one-dimensional problems analytically that yield power laws with α = 1 (3).§ For higher-dimensional problems, we have no corresponding results, and computationally accessible lattices are too small to obtain conclusive statistics. Thus we are motivated to seek even simpler models that are more tractable analytically.

Generalized Coding Theory

In this section, we summarize the probability-loss-resource (PLR) problem, the simplest framework illustrating HOT (3). The PLR problem is a generalization of Shannon source coding theory for DC, which is among the simplest most elegant design theories in engineering. Solutions can be obtained analytically and are somewhat reminiscent of mean-field theories in statistical physics, because the geometric constraints inherent in the lattice models are substantially relaxed. The PLR objective is to allocate resources in a manner that minimizes the expected cost J:

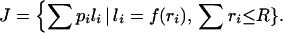Here i, 1≤ I ≤ N, indexes a set of events of sizes l_i, which in Fig. 1 corresponds to the area burned in a forest fire [California brushfires (CF), U.S. Fish and Wildlife Service Land Fires (FF)], or the length of a web file [World Wide Web (WWW)] or code word (DC) to be transmitted on the Internet. Each event is assumed to be independent and initiated with probability p_i during some time interval of observation. Note that in the lattice models, the P(i, j) were probabilities of sparks, whereas here the probabilities are associated with the resulting aggregate events. Minimizing the expected cost involves determining the optimal allocation of resources r_i to suppress the sizes of events. Resources correspond to barriers, and their relationship to the event size l_i = f(r_i) is the one geometric feature we retain. The resource cost is the length or size of the barrier. In the lattice models, this cost is simply loss of density, but now it can be motivated more generally by dimensional arguments relevant to specific applications.

We define a general one-parameter function l_i = f_β(r_i):

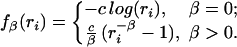Resources are normalized so that 0≤ r_i ≤ 1 and f_β (1) = 0. Although the constants c and R are adjustable parameters determined by the small size cutoff and overall rate of events, the value of β is fixed by the dimensional relationships between resource allocations and losses. The values of β that characterize DC, WWW, CF, and FF (β = 0,1,1,2, respectively) are discussed in more detail below and in ref. 3.

The strongest assumptions are that the p_i are independent of the resource r_i, which is not true in the lattice models, and that the events are independent. Both are exactly true in Shannon DC, but will be assumed throughout for simplicity. The optimal solution minimizes J (Eqs. 2 and 3) and yields optimal sizes

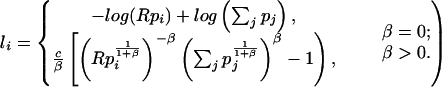The first formula (which applies to DC) leads to an exponential distribution, whereas the second leads to a power laws relating event probabilities and the corresponding sizes: p_i(l_i) ∼ l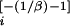, or in cumulative form P_i(l_i) ∼ l 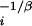= l_i^−α with α = 1/β (Table 1.8). We compare this to data for the examples considered in Fig. 1 after motivating our choices of β.

We begin with DC, where the objective is to compress long source messages into short coded messages for more efficient storage or transmission (15). The standard DC formulation due to Shannon (16) is exactly the PLR problem with β = 0, although with different notation (3). The resource constraint is equivalent to unique decodability and can be interpreted as building barriers in a zero-dimensional discrete tree. The optimal barriers assign short and long codewords to frequent and rare source words, respectively, yielding an optimal compression algorithm that has the fragilities that we associate with HOT. Specifically, if the probabilities change, the algorithm can actually expand source code streams rather than compress them. If a single bit is lost in the compressed file, the entire file can be unreadable. Both fragilities can be addressed by using universal and error-correcting codes, at the expense of longer compressed files.

Inspired by DC, we next cast efficient web site design as a PLR problem. Suppose a long document must be divided into files, which are linked together in a linear chain or tree of hyperlinks on a web site. The user enters the document beginning with the first file and proceeds by clicking through consecutive files, stopping at some point. If the typical user's interest is high in the initial portion of the document but fades as she progresses, what partitioning minimizes the cost, taken to be the average length of accessed files? Here the essential WWW PLR abstraction is that web layout is dominated by the tradeoff between short files for fast download and few clicks for ease of navigability. This abstraction of the web site design problem leads to optimizing the placement of a bounded number of “cuts” denoting the endpoints of files. The first files are more frequently accessed and smaller than the larger and less frequently accessed later files. In this simple formulation, the document is one-dimensional, and the barriers are zero-dimensional. In footnote §, the PLR formulation is extended to more complete models for web site layout and management, which allow for the dependence p_i(r_i) and more complex web topologies.

In FF, we associate design with the subdivision of a two-dimensional forest by one-dimensional engineered firebreaks and fire-fighting suppressors. In FF, the l_i are burned areas. The p_i are the probabilities of sparks occurring in different regions and initiating fires. The cost J is the average timber lost, which would tend to be minimized by deliberate design in managed forests. The resource r_i is the density of firebreaks and suppressors used to stop the spread of fires. The tradeoff between use of land for trees or firebreaks sets the constraint on the total resources available.

For WWW and FF, parallel dimensional arguments lead to appropriate choices for β in Eq. 3. A physical model for which these heuristic arguments become exact is defined in ref. 3. Suppose the loss or cost of an event associated with a d-dimensional volume scales like l_i = ξ^d, where ξ is a characteristic length of the file accessed or the region burned. The event size is limited by the resources, which can be thought of as (d − 1)-dimensional cuts that isolate the event from the rest of the system. In WWW, dividing a one-dimensional document or tree of documents into a chain or tree of linked files corresponds to d = 1, whereas in FF, dividing a two-dimensional forest into areas corresponds to d = 2. Although loss scales like a d-dimensional volume, the resource density allocation limiting loss scales like surface/volume r_i = ξ^d−1/l_i = ξ⁻¹, leading to l_i ∝ r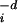, consistent with our interpretation that β = d, the dimension of the design problem, in the PLR formulation.

In general, β is determined by a resource/loss relationship, which may or may not be directly related to physical dimensions. For example, power system outages in customers (not shown in Fig. 1) have α ≈ 1, corresponding to β = d = 1 in the PLR problem. Power grids are roughly trees of one-dimensional lines connecting generators with loads, with some crosslinks, all of which are embedded in an essentially two-dimensional surface. The embedding dimension is largely irrelevant to the dynamics of cascading failures, and power outages propagate along one-dimensional lines and are primarily stopped by throttling generation or opening breakers to shed load, which occur at (zero-dimensional) points in the grid, consistent with the PLR abstraction d = β = 1.

Next we compare the results of the PLR problem with the data for DC, WWW, CF, and FF in Fig. 1. The data sets in Fig. 1 consist of pairs (l_i,P_i) with cumulative frequencies P_i of events of size l ≥ l_i. In the standard “forward engineering” PLR design problem, the noncumulative p_is are given, and optimizing the r_i produces the l_i in Eq. 4. “Reverse engineering” starts with the l_i data as given and generates model predictions by using the PLR solution, with β given by dimensional arguments and the two parameters c and R fit to the small-scale cutoff and the overall rate of events. Details are given in ref. 3. For β>0, this leads to roughly power law distributions (P_i ∝ l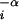) with α ≈ 1/β.

As shown in Fig. 1, when we compare the raw cumulative data for DC, WWW, and FF with the results of the PLR model, the agreement is excellent. The qualitative dependence on dimension is most striking. Although the systems are intrinsically extremely different, the event statistics are all captured by this simple PLR model. The percolation and SOC forest fire models have much smaller exponents that do not fit the data sets. The agreement between the PLR model and DC follows immediately from Shannon Theory because it was used to forward engineer the compressed file. For WWW, high-traffic web sites are designed to minimize congestion, so it is not surprising to find that the aggregate statistics are consistent with optimal design. On the other hand, the role of optimization for FF is more complex and subtle, and thus our conclusions are necessarily most speculative for this case. We considered the three additional FF data sets from ref. 16, which yield similar excellent correspondence with the PLR predictions with β = 2. The crucial fact may be that most mechanisms for fire spreading lead to expanding fronts. The fire terminates when the energy is absorbed by a resource, whether it be a firebreak (no fuel to burn) or some alternative engineered or natural means of suppression. This much more general scenario still leads to β = d, with d = 2 for mesoscopically homogeneous forests. More aggressive fire prevention might shift the curve without altering the shape. Alternatively, landscapes that naturally break forests into regions of fractal dimension lower than 2 would have steeper power laws. For example, brush fires in California occur in unusually rugged terrain. Large fires run along ridges between desert valleys and mountain peaks and are further driven by highly directional Santa Ana winds. The CF data from ref. 17 is also plotted in Fig. 1, and there is an excellent match to the PLR prediction with β = 1. The one-dimensional SOC forest fire yields α ≈ 0, which is not plotted.

The percolation α(d) is plotted in Fig. 4, along with the dependence α(d) = 1/d, which is predicted by the HOT PLR model (Table 1.8). Note that they have the opposite dependence on dimension, and that the PLR dependence is consistent with the data. This contrast can be seen intuitively from the underlying models. In percolation and other examples of equilibrium critical phenomena, as well as the standard SOC forest fire (13, 14) and sand-pile (19) models, increasing the dimension d leads to steeper power laws, corresponding to a relative suppression of large collective fluctuations of microscopic degrees of freedom. On the other hand, decreasing the effective dimension in both the WWW and FF PLR formulations leads to steeper power laws, because for small β microscopic resources are more efficient in suppressing large events. For example, all other things being equal, a one-dimensional fire is easier to stop than a two-dimensional fire, which is easier to contain than a hypothetical fire burning fuel in three dimensions. Comparisons of the brush fire data (18) as well as the 1995 Web statistics (20) with more recent results (21) lead to an effectively reduced dimensionality and steeper power laws.

HOT and its application to DC, WWW, CF, and FF suggest a new type of universality might apply to complex systems in which design and evolution play a role, but with most features in sharp contrast to familiar properties found in statistical physics (1, 2). Again it is the robust, yet fragile feature that is most strikingly different. In the PLR setting, inaccurate assumptions about the p_i for a known category of disturbance can result in misallocation of the r_i, sometimes with disastrous effects. This sensitivity is particularly apparent for the small p_i, where few resources are allocated. Maximal costs associated with errors in p_i are of order the size of the largest event, so that the more tuned the design (i.e., the more nongeneric the allocation of r_i), the greater the performance, but also potentially the greater the risk.

Discussion

The lattice models were motivated by the desire to illustrate HOT by using familiar accessible models from statistical physics. In this context, adding even simple design mechanisms produces results that are strikingly different. Despite their extreme abstraction and simplicity, the models provide clear connections between microscopic mechanisms and macroscopic features. They further capture how intrinsic robust design tradeoffs interact with and constrain natural selection and engineering design to generate highly ordered structure, even from initial randomness. Indeed, simple HOT models match all of the features of our motivating examples and data, as summarized in Table 1, and aside from the existence of power laws, their properties are the opposite of SOC. In addition, what emerged was a very particular, although we believe fundamental, abstraction of biological and engineering complexity: building highly structured barriers to cascading failures.

Although there are obviously fundamental differences between biology and engineering, the design and evolution processes and the resulting system-level characteristics may differ much less than often realized. High-performance lattices must have certain highly structured features, such as high densities overall with barriers concentrated in high spark regions. This feature is largely independent of the design process, whether it be deliberate or random mutation and natural selection. Highly complex engineering systems are very new, far from optimal, and heavily constrained by both historical and nontechnical considerations. Biological “design” involves pure trial and error, but at least the “primitive” biosphere of microorganisms has had billions of years of evolution and appears to be highly optimized and extraordinarily robust. As we better understand the role of complexity and robustness, the more they appear to use the same system-level regulatory strategies as engineering systems (22).

Recalling the examples from engineering and biology, we ask how many parameters (DDOFs) need to be tuned to obtain these designs. If we accept the components as given, then the design parameters are the choice and interconnection of the components and settings of remaining design variables. For a bacterial cell with millions of base pairs in its DNA, most perturbations lead to poorer fitness but are not lethal, although many sufficiently small perturbations are neutral, and similarly for the engineering examples. Thus to zeroth order, the DDOFs are roughly the same as all the system degrees of freedom and thus very high, although this does not imply that they are at a global optimum. In What Do We Mean by Complexity?, we emphasized that in biology most genes code for sensors, actuators, and the complex regulatory networks that control them, and thus confer to the cell robustness to variations rather than the mere basic functionality required for survival in ideal circumstances. The essence of this robustness, and hence of complexity, is the elaboration of highly structured communication, computing, and control networks that also create barriers to cascading failure events, albeit in a broader sense than is represented in the lattice models.

Although some robustness barriers are obvious from an organism's external physiology or an engineering systems external configuration, most barriers are not, so this abstraction requires further justification. Indeed, most robustness barriers are far from obvious and involve complex regulatory feedback and dynamics to stop cascading failures that are themselves often cryptic and complex. There is no simple identification directly with external physiological features. Engineering theories of control, communications, and computing can be explicitly rephrased mathematically in terms of the construction and verification of barriers that separate acceptable from unacceptable system behavior, where the latter typically involves a complex cascading failure event. A detailed exposition of this mathematics is beyond the scope of this paper, but fortunately familiar robustness barriers in human engineered systems surround us.

The most obvious examples of robustness barriers in land transportation include lane dividers, vehicle bumpers, fenders, roll bars, and door braces, and occupant restraints such as seat belts, air bags, and helmets. Whereas we can think of, say, a seat belt as simply providing specific restraining forces as a function of position, the airbag is more complex. An electronic control system measures vehicle acceleration during a crash and determines whether to deploy an airbag. It is designed to deploy only when the vehicle dynamic state enters a certain regime that is dangerous to the occupant. The feedback control systems in antilock braking and antiskid turning are even more complex but have a similar objective. Feedback regulation of temperature and oxygen in airliners and mammalian bodies is also complex but effectively keeps the internal state in a safe regime. The Internet is enabled in essence by a collection of protocols specifying control strategies for managing the flow of packets. These create barriers to cascading failures because of router outages and congestion. In all these cases, the abstraction of barriers continues to hold, but now we must consider them as occurring in the state space of a system's dynamics.

In advanced systems, designed features are so dominant and pervasive that we often take them for granted. Primitive technologies often build fragile machines by using simple strategies and precision parts, but with a complexity that is readily visible. In contrast, advanced technologies and organisms, at their best, use complicated architectures with sloppy parts to create systems so robust as to create the illusion of very simple, reliable, and consistent behavior apparently unperturbed by the environment. Even the rare cascading failure event that is the fragile side of HOT complexity typically reveals only a limited glimpse of a system's internal architecture. As a consequence, it can be difficult to precisely characterize and quantify the role of design in complex technical and biological systems without going into great detail. Nevertheless, HOT illustrates that design leads to fundamental characteristics missed by theories that ignore design.

Abbreviations

• NSOC, new science of complexity

• CAS, complex adaptive systems

• SOC, self-organized criticality

• HOT, highly optimized tolerance

• CPU, central processing unit

• DC, data compression

• DDOF, design degree of freedom

• CF, California brushfires

• FF, U.S. Fish and Wildlife Service land fires

• PLR, probability-loss-resource

• WWW, World Wide Web