Adaptive shift in the domain of negative stiffness during spontaneous oscillation by hair bundles from the internal ear

Abstract

When a hair cell of the bullfrog's sacculus is maintained in vitro under native ionic conditions, its mechanosensitive hair bundle may oscillate spontaneously. This movement has been hypothesized to result from the interaction of the bundle's negative stiffness, which creates a region of mechanical instability, with a myosin-based adaptation mechanism that continually repositions the bundle there. To test this proposition, we used a flexible stimulus fiber in an analog feedback loop to measure the displacement-force relation of an oscillating hair bundle. A digital signal processor was used to monitor spontaneous oscillations in real time and trigger measurements at particular phases of the movement cycle. By comparing the displacement-force curves obtained at the two extremes of a hair bundle's motion, we demonstrated a shift in the negative-stiffness region whose direction, orientation, magnitude, and kinetics agreed with the predictions of the gating-spring theory. The results are in accordance with the idea that adaptation underlies spontaneous hair-bundle oscillation, and therefore powers the active process that also amplifies and tunes the hair cell's mechanical responsiveness.

The active process of the inner ear increases the sensitivity of hearing, sharpens frequency discrimination, and compresses an enormous range of input intensity into a far narrower gamut of response (reviewed in refs. 1 and 2). Under certain circumstances, this active process also causes intra-aural oscillations that lead to the spontaneous emission of sound from the ear. In nonmammalian tetrapods (3), and perhaps in mammals as well (4, 5), the active process stems from motility of the hair bundle, the mechanosensitive organelle of the sensory hair cell. Driven by cellular energy sources, a hair bundle can do mechanical work on an external load (6), thereby amplifying inputs and countering the dissipative effect of hydrodynamic damping. In addition to displaying frequency tuning and compressive nonlinearity (3), an individual hair bundle can produce spontaneous movements indicative of active energy production and likely to underlie otoacoustic emissions (7).

Active hair-bundle motility rests on negative hair-bundle stiffness (8). This phenomenon may be demonstrated by using a displacement-clamp system to move a hair bundle by various specified distances and measuring the forces that a flexible fiber must exert to effect these movements. The ensuing displacement-force relation reveals that the force does not increase monotonically with displacement. Instead, there is a narrow domain of bundle positions, 20-40 nm in extent, over which the force diminishes with increasing displacement, a region of negative stiffness. A hair bundle cannot reside stably within this zone, for even a small perturbation causes it to jump in one direction or the other to a stable position where its stiffness is positive.

Active hair-bundle motility has been proposed to occur when a hair bundle is driven into its region of negative stiffness by molecular motors of two types (8, 9). On a time scale of a few tens of milliseconds, the motors involved in adaptation of the mechanoelectrical transduction process (reviewed in refs. 10-12) regulate the force applied to the mechanosensitive ion channels. Myosin-1c is the predominant constituent of these motors (13, 14). The second motor process, which operates on a millisecond time scale, involves the Ca²⁺-dependent reclosure of transduction channels (15). Although the details remain uncertain, it is known that Ca²⁺ entering through open transduction channels acts to shut them. The chemical energy of Ca²⁺ binding may close the channels directly; alternatively, Ca²⁺ may reduce the tension that holds them open, for example, by relaxing the myosin molecules (16-18).

If myosin-based adaptation fosters active hair-bundle motility by the hypothesized mechanism, then the region of negative stiffness in the displacement-force relation should shift during bundle oscillation (8). In the present study, we have used real-time computer analysis of spontaneous hair-bundle oscillations to detect the extremes of bundle motion, and then applied dynamic displacement-clamping to capture “snapshots” of the displacement-force relation there. This approach permits a direct test of the hypothesized role of adaptation in active hair-bundle motility.

Materials and Methods

Experimental Preparation. Each experiment was performed on a saccular macula excised from the inner ear of an adult bullfrog (Rana catesbeiana). After the otolithic membrane had been removed by exposure of the preparation for 30 min at room temperature to 67 μg·ml^-1 protease (type XXIV, Sigma), the macula was maintained at room temperature in a two-compartment experimental chamber (3, 6, 17). To mimic native physiological conditions as closely as possible, the apical and basolateral surfaces of the sensory epithelium were bathed in distinct oxygenated saline solutions. The apical surface was exposed to artificial endolymph containing 117.5 mM K⁺, 2 mM Na⁺, 0.25 mM Ca²⁺, 118 mM Cl^-, 3 mM d-glucose, and 5 mM Hepes at pH 7.3. The lower compartment was filled with artificial perilymph consisting of 110 mM Na⁺, 2 mM K⁺, 1.5 mM Ca²⁺, 118 mM Cl^-, 3 mM d-glucose, 1 mM sodium pyruvate, 1 mM creatine, and 5 mM Hepes at pH 7.3.

Stimulation and Measurement of Hair-Bundle Movement. We measured the movements of individual hair bundles with standard techniques (3, 6, 17). Each bundle was imaged in an upright microscope with a ×40 water-immersion objective lens of numerical aperture 0.8. To enhance optical contrast, we attached to the kinociliary bulb the tip of a sputter-coated glass fiber ≈100 μm in length and ≈0.5 μm in diameter. This fiber had a stiffness ranging from 100 to 700 μN·m^-1 and a drag coefficient of 50-140 nN·s·m^-1. A piezoelectric actuator was used to displace the fiber's base to deliver mechanical stimuli to the attached hair bundle. The bundle's motion was measured by magnifying the image of the fiber's tip 1,000 times and projecting it onto a dual photodiode. The movement was calibrated by offsetting the photodiode by 20 μm before each measurement.

Dynamic Displacement-Clamping and Data Acquisition. We used a dynamic displacement-clamp system to displace the hair bundle to a fixed position and measure the requisite force exerted by the stimulus fiber. The piezoelectric stimulator was connected to a negative-feedback amplifier (19, 20) with proportional and derivative gains (8). The error signal was based on the difference between the command signal and the movement of the bundle's tip, as measured by the dual photodiode. The output of the circuit was passed through a voltage multiplier that allowed an external signal to modulate the strength of clamping.

The external control signal was provided by a digital signal processor (M67, Innovative Integration, Westlake Village, CA) that combines a dedicated microprocessor with a fast input-output module and can be programmed in the c language. To lock the stimuli to the sudden opening and closing of the channels, we used this processor to detect abrupt movement steps during hair-bundle oscillations. We estimated the temporal derivative of the hair-bundle position X(t) by calculating the difference X(t) - X(t - τ). The processor operated with an update rate of 10 kHz; the time interval τ was typically 1 ms. By visual inspection of the derivative record before the measurements, we chose a threshold value that would detect the fast steps in the oscillations while disregarding noisy fluctuations. Whenever the derivative reached this threshold, the digital signal processor sent both a triggering signal and a position command to the displacement-clamp circuit for a duration of 30 ms. For experiments designed to probe the intermediate states of an oscillating bundle, we added delays of varying duration between the detection of the steps and the onset of stimulation.

The displacement commands were corrected for slow drifts by high-pass filtering with a cutoff frequency of 2 Hz. This correction ensured that the origin for the displacement axis (abscissa) in each displacement-force curve represented the center of the oscillation. Although the correction prevented minor distortions of the displacement-force relations, it was not necessary to observe the reported shifts. The origin for the force axis (ordinate) was determined before each set of measurements by offsetting the stimulus fiber until the hair-bundle oscillations reached their greatest magnitude.

Measurements of the commanded displacements and hair-bundle movements were low-pass-filtered at 2 kHz with an eight-pole Bessel filter and sampled at 200-μs intervals. Data were acquired with labview (version 7.0, National Instruments, Austin, TX). The displacement-force curves presented in this article represent the averages of 8-20 measurements for each point.

Theoretical Shift of Displacement-Force Relations. In the recording environment used in these experiments, the open probability P_O of transduction channels as a function of hair-bundle displacement X fits the Boltzmann relation

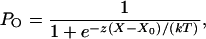[1]

in which z is the single-channel gating force, k the Boltzmann constant, and T the temperature (reviewed in ref. 21). X₀, the position at which the open probability is one half, is defined by

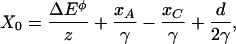[2]

in which ΔE^ø is the intrinsic energy difference on opening a channel, x_A the bundle's extent of adaptation, x_C the gating-spring extension of a closed channel at rest, d the gating distance of a channel, and γ the geometrical gain relating gating-spring extension to hair-bundle displacement. The single-channel gating force z = γκd.

During the slow phases of oscillatory hair-bundle motion (8), when inertial and drag forces are negligible, the force F_SF exerted by the stimulus fiber is equal and opposite to the force F_HB produced by the bundle; it follows that

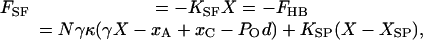[3]

in which K_SF is the fiber's stiffness, N the number of gating springs, κ the stiffness of each, K_SP the stiffness of the ensemble of stereociliary pivots, and X_SP their equilibrium position.

Rearranging and differentiating Eq. 3 with the substitution of Eq. 1 for the open probability yields an expression for the total stiffness K_T of a hair bundle and the attached stimulus fiber:

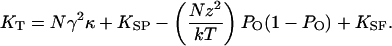[4]

An oscillating hair bundle enters its region of instability when the force on the bundle and attached stimulus fiber reaches zero at a local maximum or minimum in the displacement-force relation, a position corresponding to zero total stiffness. Equating the expression above to zero, and designating the open probabilities at the two extrema with a caret, we obtain

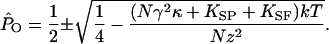[5]

From Eqs. 3 and 5, we can derive an expression for the maximal shift ΔX₀ in the midpoint of the displacement-force relation:

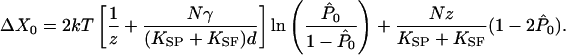[6]

Note that the conditions specified above for the spontaneous oscillation of a hair bundle necessarily take into account the stiffness of the load imposed by the stimulus fiber. Under displacement-clamp conditions, however, only the hair bundle's properties are measured. It is convenient to fit displacement-clamp data to a simplified form of Eq. 3,

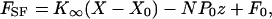[7]

in which K_∞ represents the hair bundle's limiting stiffness for large displacements and F₀ subsumes all of the constant-force terms (8). The average results of these fits, as well as other average experimental values reported, are reported here as means ± standard deviations for the indicated numbers of observations.

Results

Experimental Paradigm. In a suitable ionic environment, a hair bundle from the frog's sacculus oscillates spontaneously (Fig. 1A) at a frequency of 5-50 Hz and with a peak-to-peak excursion of up to ≈150 nm. The myosin-based adaptation motors in the bundle are thought to power these movements by continually situating the bundle in its unstable region of negative stiffness (8). More specifically, the motors are hypothesized to slide down the stereociliary actin cores after each rapid step of the bundle in the positive direction and to reascend after each negative step. If this model is correct, the relation between a hair bundle's position and the external force required for holding it there should vary with time. Immediately before or after a positive bundle step, when the motors have ascended maximally, the negative-stiffness region in a hair bundle's displacement-force curve should shift in the negative direction along both the displacement and the force axes. Conversely, around the time of an excursion in the negative direction, the range of negative stiffness should be shifted positively.

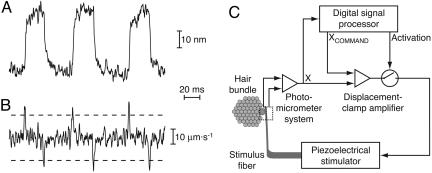
Fig. 1.

Principle of the experiment. (A) The spontaneous oscillation of a hair bundle typically consists of a rapid step in the positive or negative direction, followed by a slower movement of the same polarity; thereafter, the sequence recurs in the opposite direction. (B) The temporal derivative of the foregoing trace demonstrates positive and negative spikes corresponding to the rapid movement steps. The user-defined thresholds for the detection of fast steps (dashed lines) lie well outside the range of noise. (C) In the experimental apparatus, a digital signal processor monitors the spontaneous oscillation of a hair bundle (A) and continuously computes its temporal derivative (B). When the derivative signal crosses the threshold, the processor activates the displacement-clamp amplifier and commands a specific displacement of the hair bundle (X_COMMAND). The clamp circuit then compares this command signal with the bundle's actual position (X), as measured by the photomicrometer system, and produces a feedback signal proportional to the difference. By displacing the base of the stimulus fiber, the piezoelectrical stimulator brings the fiber's tip, and the top of the hair bundle, to the commanded position.

Because a hair bundle cannot remain within its domain of negative stiffness, a displacement-clamp system with negative feedback must be used to hold the bundle in this region (8, 19, 20). Continuous displacement-clamping, however, suppresses hair-bundle oscillations. We therefore used an experimental paradigm in which a bundle was permitted to oscillate freely for a period of a few hundreds of milliseconds and was then subjected to a brief period of displacement-clamping to determine its state. We used a digital signal processor to rapidly and continuously compute the temporal derivative of the bundle's position, thereby producing a record of abrupt positive and negative transients corresponding to bundle steps in the corresponding directions (Fig. 1B). At a specified interval after the bundle stepped in a particular direction, the processor activated the displacement-clamp circuit and commanded a specific displacement of the bundle (Fig. 1C). After a stimulus period of 30 ms, displacement-clamping was discontinued and the hair bundle resumed its spontaneous oscillation. The force measurements were accomplished during the first few milliseconds of the 30-ms stimulus, before adaptation had progressed substantially.

At each instant during the imposition of a displacement, we determined the force necessary to hold the hair bundle in the commanded position from the flexion of the fiber, the difference in the positions of the fiber's tip and base, and its calibrated stiffness (Fig. 2 A and B). We measured the force after hydrodynamic transients had subsided, ordinarily 4 ms after the onset of displacement-clamping. Because adaptation meanwhile began to blur the effect of gating by restoring positive stiffness, measurements were usually concluded 9 ms after the onset of stimulation. By repeating the procedure with a range of displacement commands, we were able to produce a displacement-force relation demonstrating the hair bundle's region of negative stiffness (Fig. 2C). In every instance, this curve was fitted well by the relation derived from the gating-spring theory (Eq. 7).

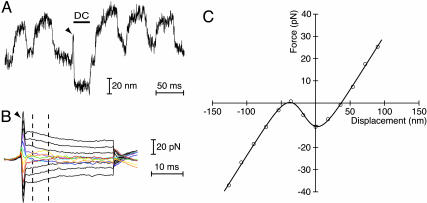
Fig. 2.

Measurement of the displacement-force relation. (A) This hair bundle oscillated spontaneously at 20 Hz with a peak-to-peak magnitude averaging 60 nm. Activated by a rapid step in the positive direction (arrowhead), the displacement-clamp (DC) system moved the hair bundle to the commanded position of -70 nm and held it there for 30 ms (horizontal bar). During this period, the force necessary to position the bundle was computed from the measured flexion of the stimulus fiber. This paradigm was then repeated for a range of displacements of both polarities. (B) The average force produced by the stimulus fiber for 13 levels of hair-bundle displacement showed three regimes. First, immediately after the displacement command, the hydrodynamic transient (arrowhead) dominated the response. During the second period, the presence of negative stiffness was signaled by the crossover of the responses for the smaller stimuli in both directions. Measurements were averaged during this period, over the interval 4-9 ms after the command (dashed lines). Finally, as adaptation concluded, the negative stiffness vanished. (C) The displacement-force curve produced from the data in B is representative of those measured just after rapid positive steps. The relation demonstrates a region of negative stiffness encompassing 40 nm. The continuous curve through the data points is a fit to Eq. 7 for the parameter values K_∞ = 490 μN·m^-1, n = 120, and z = 0.37 pN. The stiffness of the stimulus fiber was K_SF = 273 μN·m^-1.

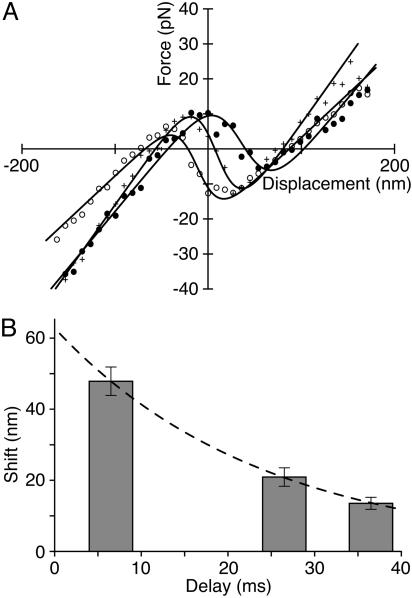
Shift at Extremes of Oscillation. We used the experimental procedures described above to capture displacement-force relations immediately after fast positive and negative steps by a spontaneously oscillating hair bundle (Fig. 3). Shortly after a positive step, the region of negative stiffness was consistently found to be offset in the negative direction. Conversely, the “snapshot” measurement taken just after closing of the channels revealed an offset in the positive direction.

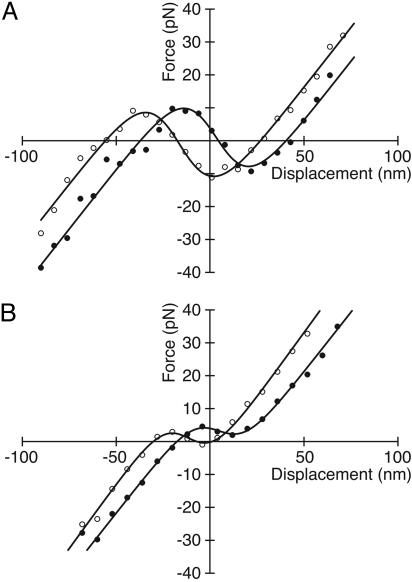
Fig. 3.

Shifting of displacement-force curves during oscillation. (A) The relation obtained just after rapid steps in the positive direction (○) is offset 20 nm in the negative direction with respect to the curve measured immediately after rapid negative steps (•). This hair bundle underwent a 10-Hz spontaneous oscillation 56 nm in peak-to-peak magnitude. The average values of the fitting parameters were K_∞ = 127 μN·m^-1, n = 123, and z = 0.46 pN; the stimulus fiber's stiffness was K_SF = 685 μN·m^-1. (B) Another hair bundle oscillated spontaneously at 17 Hz with a magnitude of 50 nm. In this instance, the displacement-force curve after rapid positive steps (○) lies 16 nm to the left of that for negative steps (•). Here, the average values of the fitting parameters were K_∞ = 750 μN·m^-1, n = 57, and z = 0.54 pN; the stimulus fiber's stiffness was K_SF = 305 μN·m^-1.

For the six spontaneously oscillating hair bundles from which we obtained complete data sets, we measured shifts in the displacement-force curves ranging from 7 to 48 nm, with an average of 22 ± 13 nm. The curves moved not only along the displacement axis, but along the force axis as well; the average slope along which the shift occurred was 279 ± 250 μN·m^-1. For each hair bundle, the overall shape of the negative-stiffness region and the asymptotic stiffness were similar at each of the extreme phases of oscillation. The average parameter values for the displacement-force relations (Eq. 7) were K_∞ = 680 ± 450 μN·m^-1, n = 100 ± 50, and z = 0.47 ± 0.17 pN, all of which agree with previously published results (8, 15, 17, 22).

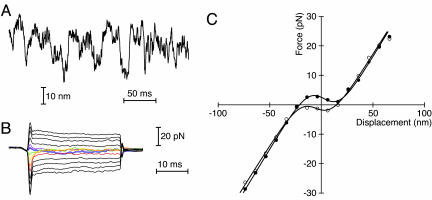
Because of the noise inherent in the measurement of hair-bundle movements, we focused our efforts on bundles with relatively large, regular oscillations. One hair cell whose behavior differed markedly provided us with a control experiment. Although this hair bundle oscillated (Fig. 4A), it displayed little adaptation (Fig. 4B). If oscillation is powered by adaptation motors, then such a cell could oscillate only if its displacement-force curve was so shallow that a very small movement of the adaptation motors sufficed to drive the bundle into its region of negative stiffness. Displacement-clamp measurements confirmed this inference. The maximum negative stiffness for this hair bundle, 130 μN·m^-1, was below the range of 290-840 μN·m^-1 observed for the remaining bundles. Had this hair bundle presented a steep negative-stiffness region, its weak adaptation motors would not have been able to force a jump across the unstable region and thus drive the oscillation. The shallowness of the displacement-force relation for this hair bundle also explains why its oscillation was significantly noisier, and the observed shift of 7 nm was much smaller, than for the other cells. This bundle was intermediate between the robust oscillators that we usually studied and a passive, bistable hair bundle exhibiting excursions between the closed and open states activated by thermal motion, the substrate for stochastic resonance (23).

Fig. 4.

Response of a weakly adapting cell. (A) The hair bundle produced relatively small, erratic oscillations of poorly defined frequency. (B) The force records reveal negative stiffness, as manifested by the crossover of the responses for the smallest displacements in each direction, that persisted for >25 ms. (C) As a result of weak adaptation, the displacement-force curve after rapid positive steps of the hair bundle (○) is shifted only 7 nm in the negative direction with respect to that for rapid negative steps (•). The average values of the fitting parameters were K_∞ = 568 μN·m^-1, n = 54, and z = 0.47 pN; the stimulus fiber's stiffness was K_SF = 215 μN·m^-1.

Shift at Intermediate Phases of Oscillation. If the proposed model for the oscillation is correct, the displacement-force curves at intermediate phases of the movement cycle should lie between the extremes measured just after the fast steps. To test this prediction, we made measurements in which the onset of displacement clamping was delayed by an additional 20 or 30 ms after the detection of a rapid step. As anticipated, the displacement-force curves for the delayed measurements were centered at intermediate positions between the two extreme curves (Fig. 5A). A plot of the curves' shift as a function of time after a rapid negative step could be fitted by an exponential function with a time constant of 24 ms (Fig. 5B).

Fig. 5.

Rate of shift of the displacement-force curve. (A) For a hair bundle that oscillated spontaneously through 160 nm at 15 Hz, displacement-force curves were measured shortly after rapid positive steps (○), just after rapid negative steps (•), or with an additional delay of 20 ms after negative steps (crosses). (B) Plotting the amplitude of the shift at three intervals after large negative steps reveals an exponential course with a time constant of 24 ms (dashed line). The positions and widths of the bars represent the intervals over which the data were analyzed. The average values of the fitting parameters were K_∞ = 280 μN·m^-1, n = 140, and z = 0.32 pN; the stimulus fiber's stiffness was K_SF = 273 μN·m^-1.

Discussion

Negative Hair-Bundle Stiffness. The measurement of a domain of negative stiffness is difficult, for a hair bundle's inherent instability in this region requires the use of a displacement clamp to hold the bundle there. The rate at which this negative-feedback system can operate is limited by the hydrodynamic damping of the stimulus fiber; as a consequence, meaningful measurements cannot be taken with the present apparatus during a period of a few milliseconds after a commanded displacement. At the same time, however, adaptation by a hair bundle ordinarily limits the period during which the bundle's stiffness remains negative. As a consequence of these two factors, we can generally observe negative stiffness only during a brief interval after a commanded displacement (8, 17). In addition, the use of excessive gain in the displacement-clamp circuit can produce mechanical oscillations that might be confused with mechanical responses of the hair bundle. These considerations might raise concerns about the validity of negative-stiffness measurements.

In the present experiments, the occurrence of one hair bundle with minimal adaptation provided a useful control for our experimental and analytical procedures (Fig. 4). This bundle displayed a stiffness that was only slightly negative. Because of the bundle's reduced adaptation, however, negative stiffness persisted for the duration of stimuli as great as ±10 nm. As a consequence, we were able to measure negative stiffness well after the mechanical transients associated with displacement stimuli had settled.

Shifting of the Displacement-Force Curve. By examining spontaneously oscillating hair bundles with a rapid displacement-clamp system, we established that each rapid phase of a bundle's oscillatory movement is preceded by a shift of the bundle's displacement-force curve. The results are consistent with the hypothesis that oscillation is driven by the mechanical activity of a hair bundle (8). More specifically, the alternate excursions of adaptation motors up and down the stereocilia suffice to explain the oscillations.

Four aspects of the observed shift in the displacement-force curve are in accordance with this hypothesis and the predictions of the gating-spring theory. First, the shift occurs in the anticipated direction. Immediately after a positive step by an oscillating hair bundle, when climbing adaptation is expected to have tensioned the gating springs maximally, the region of negative stiffness lies at its most negative position along the displacement axis. Conversely, a negative step is associated with a shift in the positive direction, as expected after slipping adaptation has relaxed the gating springs. Next, the rate of the shift agrees with that of myosin-based adaptation in saccular hair cells of the bullfrog: the time constant of 24 ms lies squarely in the range observed for adaptation to positive stimuli (18, 24). Third, the shape of the displacement-force curve alters little during the shift. This constancy is anticipated if adaptation simply tightens or loosens an ensemble of linear gating springs without affecting the intrinsic energy difference between the closed and open states of the transduction channels (25). Finally, the shift along the displacement axis is accompanied by movement along the force axis. According to the gating-spring model for transduction (25), adaptation should translate the displacement-force curve along a line whose slope represents the combined stiffnesses of the stereociliary pivots, ≈200 μN·m^-1 (15, 26). In the present experiments, the observed slope of 279 μN·m^-1 agrees satisfactorily with this expectation.

The magnitude of the displacement-force curve's shift along the displacement axis is also qualitatively consistent with the theoretical expectation. By substituting into Eq. 6 the parameter values from each of the six hair cells, we ascertained that the observed shifts were 70% ± 50% of those predicted. On three grounds, however, we expect the shifts to be smaller than the theoretical value. First, just after each rapid step by an oscillating hair bundle, adaptation reverses its direction. By the time of our measurement of negative stiffness, ordinarily 4-9 ms later, the region of negative stiffness has retreated from its peak excursion. Extrapolation of the time course of shifting (Fig. 5B) to the instant of a rapid step indicates that the peak shift is greater by at least 20%. Moreover, we have compensated here for only the slow phase of adaptation; including the effect of rapid adaptation would raise the shift still further.

The second reason that measured shifts may be smaller than the theoretical value is that, at the end of each half-cycle of oscillation, thermal noise usually drives a hair bundle into its region of instability slightly before adaptation has completed the shift of the displacement-force curve. Because this phenomenon is stochastic in nature, its quantitative effect is difficult to compute.

Finally, our analysis produced a slight overestimate of the expected shift. Whereas the dynamical system that oscillated comprised both a hair bundle and a stimulus fiber, the fiber's contribution was omitted during displacement-clamp measurements. If corrected for the ensuing systematic distortion, displacement-force curves would display less negative stiffness and shift along a steeper slope during adaptation. These corrections would therefore reduce the magnitude of the expected shift.

Conclusion. The present results support the inference (8) that spontaneous hair-bundle oscillation, a manifestation of the ear's active process, results from the adaptation process of hair cells. Modeling studies have demonstrated in principle that adaptation can also explain the other three characteristic features of the active process: amplification, frequency tuning, and compressive nonlinearity (9, 16, 17). Because both the fast and slow components of adaptation are driven principally by myosin-1c (13, 14, 18), the shifts in the displacement-force curve observed here reflect the fundamental mechanism of the active process in the ears of nonmammalian tetrapods, and perhaps in mammals as well (4, 5, 27).