Huntington's disease age-of-onset linked to polyglutamine aggregation nucleation

Abstract

In Huntington's Disease and related expanded CAG repeat diseases, a polyglutamine [poly(Gln)] sequence containing 36 repeats in the corresponding disease protein is benign, whereas a sequence with only 2–3 additional glutamines is associated with disease risk. Above this threshold range, longer repeat lengths are associated with earlier ages-of-onset. To investigate the biophysical basis of these effects, we studied the in vitro aggregation kinetics of a series of poly(Gln) peptides. We find that poly(Gln) peptides in solution at 37°C undergo a random coil to β-sheet transition with kinetics superimposable on their aggregation kinetics, suggesting the absence of soluble, β-sheet-rich intermediates in the aggregation process. Details of the time course of aggregate growth confirm that poly(Gln) aggregation occurs by nucleated growth polymerization. Surprisingly, however, and in contrast to conventional models of nucleated growth polymerization of proteins, we find that the aggregation nucleus is a monomer. That is, nucleation of poly(Gln) aggregation corresponds to an unfavorable protein folding reaction. Using parameters derived from the kinetic analysis, we estimate the difference in the free energy of nucleus formation between benign and pathological length poly(Gln)s to be less than 1 kcal/mol. We also use the kinetic parameters to calculate predicted aggregation curves for very low concentrations of poly(Gln) that might obtain in the cell. The repeat-length-dependent differences in predicted aggregation lag times are in the same range as the length-dependent age-of-onset differences in Huntington's disease, suggesting that the biophysics of poly(Gln) aggregation nucleation may play a major role in determining disease onset.

The expanded CAG repeat diseases, which include Huntington's disease (HD) and at least seven similar disorders, are associated with the expansion of polyglutamine [poly(Gln)] sequences within the corresponding disease proteins (1). In HD, poly(Gln) stretches of 36 or less are benign, whereas mutated, expanded forms with repeat lengths of 38 or more carry disease risk. For pathological-length poly(Gln) repeats, age-of-onset correlates with repeat length. Thus, whereas repeat lengths of 38–39 are associated with slow, progressive disease with onset in the 60–80 age range, repeat lengths greater than 70 lead to aggressive disease with onset in the 5–15 age range (2).

A number of lines of evidence point to the critical involvement of poly(Gln) aggregation in the disease process. Nuclear intraneuronal inclusions (NII) are often observed in or near affected brain regions in human patients (3) and in animal and cell models (4). Aggregates of poly(Gln) peptides prepared in vitro and introduced into cells in culture are benign when delivered to the cytoplasm, but highly toxic when delivered to the nucleus (5). Toxicity can be modulated by molecular chaperones (6, 7). Strong evidence has been obtained for a toxicity mechanism involving the recruitment and subsequent inactivation of critical poly(Gln)-containing proteins (8). Finally, the aggregation kinetics (9, 10) of poly(Gln)-containing polypeptides exhibit dependencies on repeat length that qualitatively mirror the repeat length dependence of disease risk. How small changes in poly(Gln) repeat length might so dramatically influence the aggregation and neurotoxicity of this peptide sequence has remained obscure.

Protein aggregation occurs in a number of human diseases (11), including the neurodegenerative diseases Alzheimer's disease, Parkinson's disease, amyotrophic lateral sclerosis, Creutzfeld–Jacob disease, and the expanded CAG repeat diseases (12). In many of these conditions, protein deposition involves amyloid fibril formation, and poly(Gln) aggregates share many of the attributes of amyloid (13, 14). Amyloid fibril growth is generally considered to be controlled by nucleated growth polymerization kinetics. Nucleated growth polymerization is a two-stage process consisting of the energetically unfavorable formation of a nucleus, followed by efficient elongation of the nucleus via sequential additions of monomer (15, 16). Previous discussions and theoretical treatments of nucleated growth aggregation of proteins feature a nucleation step involving the condensation of multiple molecular units into an unstable oligomer (15–19). This is the central premise of classical nucleation theory (20) and has been successfully used in modeling the polymerization of a number of biological systems (21), of which the most completely described is sickle hemoglobin assembly (22).

In this paper we show that poly(Gln) aggregation has all of the attributes of a nucleated growth polymerization reaction. We also find, however, that the critical nucleus—the number of monomeric units comprising the nucleus—is equal to 1. This suggests that the rate-limiting nucleation event involves folding within the monomer, rather than condensation of monomers into an oligomer. We also use parameters from the mathematical model to calculate the difference in free energy of nucleation between benign and pathological repeat lengths of poly(Gln), and to determine the concentration of aggregation-prone poly(Gln) required to generate lag times corresponding to the observed disease ages-of-onset for particular poly(Gln) repeat lengths.

Methods

Poly(Gln) Peptides.

Poly(Gln) peptides were purchased in crude form as custom-synthesized by the Keck Center at Yale University according to the general design K₂Q_nK₂. Crude peptide product was disaggregated (23) and subjected to HPLC purification on a preparative C₃ reverse-phase column (Amersham Pharmacia Biotech) to yield peptides of repeat lengths 28, 36, 42, and 47, as confirmed by mass spectrometric analysis. Before each experiment, the purified, lyophilized peptides were freshly disaggregated (23). Peptide concentrations were determined by the integrated area of an HPLC peak monitored at 215 nm, compared with that of a poly(Gln) peptide standard (10).

CD Experiments.

CD spectra were collected on an OLIS 1000 CD (OLIS, Jefferson, GA) as described (10, 14). To determine the CD spectra associated with the aggregated and nonaggregated fractions of a poly(Gln) aggregation reaction time point, we centrifuged an aliquot of the reaction mixture for 30 min at 20,400 × g in an Eppendorf centrifuge. The pellet was resuspended in an equivalent volume of Tris buffer, and CD spectra of supernatant and pellet were recorded. Molar ellipticities were calculated based on the poly(Gln) concentrations of the supernatant and pellet as determined by HPLC (see above). Because the molar ellipticities of these fractions were lower than expected based on the initial and final spectra of an aggregation reaction, we centrifuged the supernatant from the intermediate time point in an ultracentrifuge at 227,000 × g (50,000 rpm in a Beckman 50.2 Ti rotor) and redetermined the CD curve, which now gave the expected molar ellipticity for this concentration of poly(Gln) in random coil. This exercise indicated the presence of 8.3% by weight of aggregates that remain in the supernatant after centrifugation in an Eppendorf centrifuge. This 8.3% value for the amount of aggregate not pelletable after 30 min at 20,400 × g was used to correct the HPLC-determined kinetics data shown in Figs. 2a and 3.

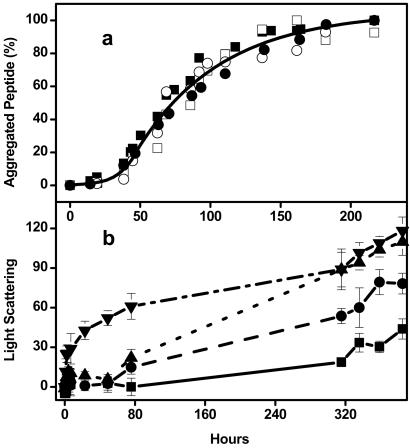
Figure 2.

(a) Aggregation progress of 66 μM K₂Q₄₂K₂ in 10 mM Tris-TFA, pH 7.0 monitoring by CD ([Θ]₂₀₀) (■), HPLC (●), light scattering (□), and thioflavin T (○) methods and a single curve fit from the four sets of data. (b) Aggregation progress of 20 μM K₂Q₂₈K₂ in PBS, pH 7.4, without seed (—) and with 0.01% (– –), 0.1% (- - -), and 1% (– ■ –) of preformed K₂Q₂₈K₂ aggregates, prepared by the −20°C method as described (14). Aggregation was monitored by Rayleigh light scattering as described (14).

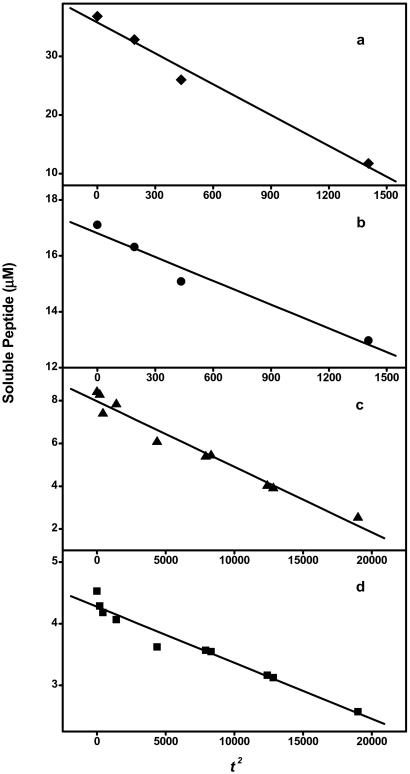
Figure 3.

t² plot of K₂Q₃₆K₂ peptide at 36.9 μM (a), 17.1 μM (b), 8.4 μM (c), and 4.5 μM (d).

Nucleation Kinetics.

The derivation of equations describing nucleation kinetics in a nucleated growth polymerization mechanism has been described (16). The integrated rate equation describing the initial phase of nucleation kinetics is Δ = ½ JJ*c*t², where Δ is the concentration of monomers that have gone into polymers, J is the elongation rate of polymers, J* is the elongation rate of the nucleus, c* is the concentration of the nucleus, and t is time. Substituting J = k₊c, where k₊ is the forward elongation rate constant and c is the bulk concentration of monomers, and substituting c* = K_n*c^n*, where n* is the critical nucleus (the number of monomers in the nucleus) and K_n* is the equilibrium constant describing the monomer–nucleus equilibrium, one obtains Δ = ½ k₊²K_n*c^(n*+2)t²; a plot of Δ vs. t² thus yields slopeA = ½ k₊²K_n*c^(n*+2). (The foregoing assumes that the monomer concentration is unchanged from its initial concentration, which is strictly true only in the limit of small Δ, but which does provide the leading term in a perturbation expansion of Δ, from which the concentration dependence and rate constants may be extracted. It also assumes that the elongation rate of the nucleus, k₊*, is identical to the elongation rate for aggregates, k₊.) Because [soluble monomer] = [soluble monomer]_t=0 − Δ, a plot of [soluble monomer] vs. t² gives the same slope as a plot of Δ vs. t². Because log (slopeA) = log (½ k₊²K_n*) + (n* + 2) log (c), a plot of log (slopeA) vs. log (c) yields a slopeB of n* + 2.

Because in this system n* was determined to be equal to 1, the above equation can be solved to yield k₊²K_n* = 2(slopeA)/c³. Simulated aggregation curves can then be constructed using the equation Δ = ½ k₊²K_n*c³ t² and k₊²K_n* values (Table 1). Lag phases were determined by fitting the first 5% of the calculated aggregation curve to a sigmoidal equation, finding the point on the sigmoidal fit where the aggregation rate is maximal, and extrapolating the tangent of the fitted curve at that point back to the x axis. For each of the three curves shown, the point of intersection corresponds to the time at which the aggregation reaction is 0.9% complete.

Table 1.

Kinetic parameters for poly(Gln) peptide aggregation nucleation

	Q28	Q36	Q47
Slope of the log–log plot (Fig. 4)	2.98	2.68	2.59
Calculated critical nucleus (n*) from slope	0.98	0.68	0.59
k+2Kn* (M−2s−2)	0.001128	0.09193	1.8304

The difference in free energies of folding, ΔΔG, corresponding to a difference between two equilibrium constants is equal to −RT ln (K₁/K₂).

Results

β-Structure Formation Is Coincident with Aggregation.

Previously we showed that poly(Gln) peptides regardless of repeat length exist in solution in a statistical coil state (10). In contrast, consistent with their suspected amyloid-like nature (14), we found that aggregates of the same poly(Gln) peptides are dominated by β-sheet structure (10). Because of the apparent importance of poly(Gln) aggregation in the disease process, we initiated studies to determine the kinetic details of aggregation, and the transition between statistical coil and β-sheet that accompanies poly(Gln) aggregation.

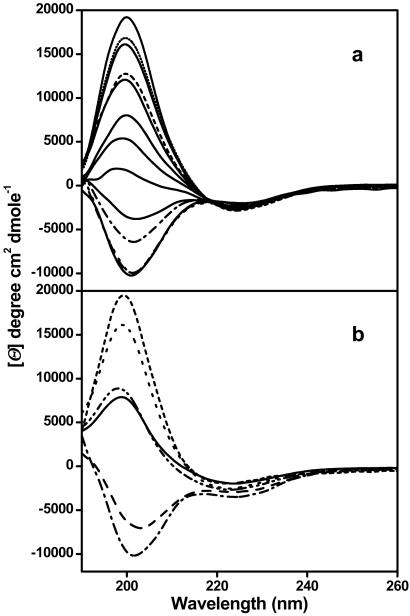
Fig. 1a shows that when a solution of purified, freshly disaggregated monomeric Q₄₂ peptide is incubated for long periods at 37°C, the CD spectrum undergoes a regular transition into a classical β-sheet CD spectrum. The tight isodichroism point at 219 nm is consistent with a simple transition between two structural types with no populated intermediates. The relative amplitude of this transition at 200 nm is plotted with respect to time in Fig. 2, along with a number of other standard measures of amyloid-like protein aggregate formation. Fig. 2a shows that the acquisition of β-sheet structure in the poly(Gln) suspension is intimately associated with the development of aggregate structure; that is, there is no evidence for a significant development of β-structure within the poly(Gln) peptide before its aggregation. This means either that individual peptide molecules aggregate rapidly after they acquire β-sheet structure, or that aggregation and β-sheet acquisition are concerted events.

Figure 1.

CD spectra of 0.39 mg/ml K₂Q₄₂K₂ during its aggregation in 10 mM Tris⋅TFA buffer, pH 7.0, 37°C. (a) From bottom to top the spectra are those of the aggregation mixture at : 0, 14.35 (— -), 19.63 (■ ■ ■), 38.35 (– ■ –), 44.68, 62.25, 68.62, 85.83, 91.97, 110.60 (– – –), 136.95, 161.60 (■ ■ ■), and 216.82 h. The spectra are in solid except lines indicated. (b) Spectra of the reaction mixture at 90 h (—), Eppendorf centrifugation supernatant (- - -) and pellet (⋅ ⋅ ⋅), sum of the supernatant and pellet (– - -), and ultracentrifugation supernatant (— ■ —) and pellet (– – –).

The intimate linkage between β-sheet formation and aggregation is further indicated by a centrifugation partitioning experiment. Fig. 1b shows that the centrifugation of a partially aggregated reaction mixture leads to its fractionation into a soluble fraction exhibiting statistical coil structure and a pellet fraction that, when resuspended, exhibits β-sheet structure.

Aggregation of Poly(Gln) Occurs by a Nucleated Growth Polymerization Mechanism.

The CD data in Fig. 1 addresses the mechanism of aggregate elongation, but not how aggregation is initiated. It has previously been pointed out (9) that poly(Gln) aggregation in vitro displays two qualities often associated with nucleated growth polymerization, a kinetic lag phase and abbreviation of the lag phase by seeding (15). Fig. 2a shows that, by all four experimental measures of the aggregation reaction time course, the kinetics of Q₄₂ aggregation consist of a lag phase of 1–2 days followed by a rapid growth phase during which aggregation proceeds rapidly to near completion. Aggregation of similar poly(Gln) peptides of other repeat lengths (10), as well as poly(Gln)-containing huntingtin (htt) fragments (9), also exhibit lag phases followed by rapid growth phases. Fig. 2b shows that the lag phase can be attenuated or entirely eliminated by the addition, at time 0, of a very small amount of previously prepared Q₂₈ poly(Gln) aggregates.

More stringent tests for a nucleated growth polymerization mechanism lie in the detailed analysis of aggregation kinetics (16). Two features of the initial phase of the aggregation kinetics are especially important: a dependence on time squared (t²), and a concentration dependence of the effective nucleation rate constants obtained from t² plots (16). To analyze these features of the nucleation kinetics of poly(Gln) aggregation, we prepared rigorously disaggregated (23) solutions of purified poly(Gln) peptides of repeat lengths 28, 36, and 47 and studied their aggregation kinetics at 37°C in PBS by determining concentrations of unpolymerized monomer at each time point with analytical HPLC (10), the most quantitative and linear means of monitoring a protein aggregation reaction. The panels of Fig. 3 show an analysis of the t² dependence of aggregation for different concentrations of the Q₃₆ peptide. In each case, an excellent linear fit of the data was obtained, confirming the t² dependence. Furthermore, a plot of the log of the slopes of the t² plots (such as those shown in Fig. 3b) versus the log of peptide concentration indicates a concentration dependence greater than one for this initial rate (Fig. 4). Thus, kinetics analysis confirms that poly(Gln) aggregation fits a nucleated growth polymerization mechanism.

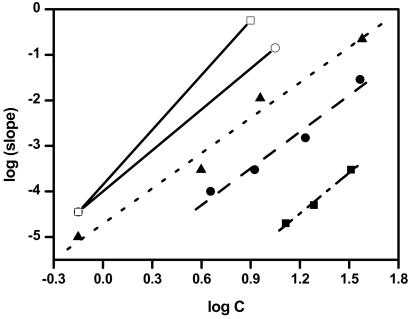
Figure 4.

Linear fits of log (½ k₊² K_n*c^(n*+2)) vs. log c for K₂Q₂₈K₂ (■), K₂Q₃₆K₂ (●), and K₂Q₄₇K₂ (▴). Reference lines with exact slopes of 3 (○) and 4 (□) are shown for comparison. The slope plotted is that from fits such as those shown in Fig. 3.

The Nucleus for Poly(Gln) Aggregation Is Monomeric.

The time-dependent decrease in the monomer concentration at the outset of a nucleated polymerization reaction contains contributions from the nucleus concentration, the rate at which nuclei undergo elongation, and the rate at which developing aggregates undergo elongation (16). One outcome of the mathematical analysis of these contributions is that the slope of a plot of log (aggregation rate) vs. log (peptide concentration), such as those shown in Fig. 4, is equal to n* + 2, where n* is the “critical nucleus,” or the number of monomers that associate together to form the nucleus (see Methods). Table 1 lists the slopes of the log–log plots from Fig. 4 describing the nucleation kinetics of Q₂₈, Q₃₆, and Q₄₇ peptides along with the calculated n* values. For all three peptides studied, the slope of the linear regression fit is between 2.5 and 3. A slope of 2 (n* = 0) has no meaning in the nucleated growth mechanism. Each of the three data series is much more consistent with a slope of 3 (n* = 1) than a slope of 4 (n* = 2) (Fig. 4). The question is whether a slope of 3 has meaning within the context of the nucleated growth mechanism, because a slope of 3 corresponds to a critical nucleus of 1—that is, a monomeric nucleus.

In the context of conventional models for nucleated growth polymerization, a monomeric nucleus seems counterintuitive. However, a monomeric nucleus is not incompatible with general nucleation theory. In fact, the fundamental requirement for producing nucleated growth kinetics is simply that the nucleus be an energetically unfavorable species within the bulk monomer pool. In the derivation of the equations describing nucleation kinetics (16), this is described by the relationship

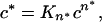where c* is the concentration of nuclei, c is the concentration of monomers, and K_n* is the constant describing the equilibrium between nuclei and bulk phase monomers. The concentration dependence of the nucleation rate is typically thought of as owing primarily to the n* exponent of c in this relationship. However, even when the exponent n* is equal to 1, it is apparent from this equation that the concentration of nuclei c*, and hence the nucleation rate, will depend on the concentration of bulk phase monomer c.

The kinetic analysis described here cannot directly inform us as to the structural nature of the nucleus. However, it is a reasonable possibility that nucleation corresponds to the conversion of a statistical coil monomer to a more ordered monomer rich in β-structure. Fig. 1 shows that, within the CD detection limit, monomers in the bulk phase remain in the random coil state until they aggregate. The hypothesized nucleation transition from random coil monomer to β-sheet monomer, as illustrated schematically in Fig. 5, is equivalent to an energetically unfavorable protein folding reaction. Our proposal for a monomeric nucleus is based on solid kinetic data, but the inference is nonetheless indirect. However, obtaining more direct detection and characterization of aggregation nuclei is, by definition, very challenging. The very low apparent percentage of monomer that exists in the nucleus state at any one time, and the speed with which it either converts to an elongating amyloid fibril, or collapses back to bulk phase monomer, means that a method for directly detecting and characterizing the nucleus will have to be both very fast and very sensitive.

Figure 5.

A model for poly(Gln) aggregate nucleation and extension. In the model, nucleation consists of an unfavorable transition (step a) from an extended, statistical coil state to a compact state corresponding to the aggregation nucleus. The elongation process consists of an initial binding (step b) of the nucleus to an extended conformation monomer, followed by a consolidation of structure (step c) that generates a new binding site for monomer. The resulting dimeric species binds another extended chain monomer (step d) to continue the process.

Poly(Gln) Folding Stability and HD Pathology.

Previous studies clearly show strong repeat-length dependence to poly(Gln) aggregation kinetics, including the length of the lag phase (9, 10). It has not been possible, however, to account for the energetic basis of this effect. Because we find that repeat length effects on lag time, at least in the Q₂₈–Q₄₇ range, cannot be accounted for by differences in n* (Table 1), they must be due to differences either in K_n* (the equilibrium constant describing the bulk phase monomer to nucleus equilibrium) and/or in k₊ and k₊* (the forward rate constants for elongation of aggregate and nucleus, respectively) (16). These terms appear as a k₊²K_n* product in the rate equations. The value of this product term can be determined from the experimental data (see Methods) and is listed in Table 1 for each peptide. It can be seen that the value of k₊²K_n* varies by 1 to 2 orders of magnitude as poly(Gln) repeat length changes in stages from 28 to 47. Unfortunately, it is not possible to formally segregate the two components of the k₊²K_n* product (16).

Nonetheless, under certain circumstances it is possible to make a reasonable estimate of the difference in the free energy of folding for nucleation between the Q₃₆ and Q₄₇ peptides. Previously we showed that the elongation rates of poly(Gln) peptides change little with respect to repeat length above a length of about Q₃₆ (10). Similarly, using aggregates of the Q₄₇ peptide as a seed, we find that the solution phase elongation of the Q₃₆ and Q₄₇ peptides occurs at identical rates, within error, when determined by the thioflavin T method (ref. 24 and data not shown). Assuming such an identity in the elongation rate constants between these two peptides, the difference between the k₊²K_n* terms for their nucleation kinetics must be attributable entirely to differences in K_n*, the constant describing the equilibrium between disordered bulk phase monomer and the folded nucleus. Thus, the ratio of the k₊²K_n* terms of Q₃₆ and Q₄₇ (i.e., 19.9) is identical to the ratio between their K_n* terms, which can be converted into a ΔΔG, describing the folding of the presumptive monomeric nucleus, of 1.84 kcal/mol. Assuming a linear variation in ΔΔG with repeat lengthening over this range, this corresponds to a difference in free energy of folding between benign Q₃₅ and pathogenic Q₃₈ of about 0.5 kcal/mol. These calculations thus suggest that the difference between a normal life and tragic illness in the CAG repeat diseases can be attributed to a very small difference in the (highly unfavorable) thermodynamics of folding of the poly(Gln) sequence into the aggregation nucleus.

Nucleation Kinetics and HD Age-of-Onset.

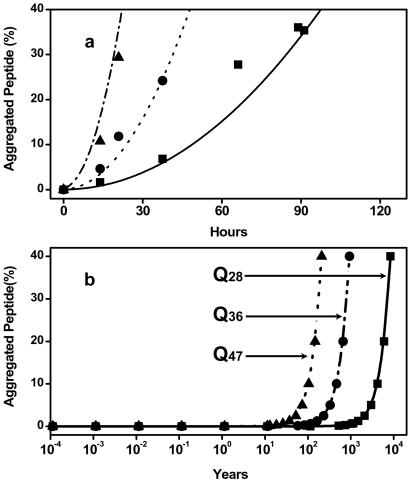
Because of constraints in both time and instrumental sensitivity, direct experimental determination of the nucleation kinetics for poly(Gln) peptides at physiological concentrations is not possible. However, assuming no change in mechanism, it should be possible to use the nucleation kinetics parameters n* and k₊²K_n*, derived from the study of the aggregation of poly(Gln) peptides at high concentrations, to calculate the nucleation kinetics for other peptide concentrations. The feasibility of this approach is illustrated in Fig. 6a, which shows the excellent fit of aggregation kinetics curves calculated, using these parameters, for different concentrations of the Q₄₇ peptide superimposed over the original experimental data.

Figure 6.

(a) Simulated aggregation progress of K₂Q₃₆K₂ at 8.4 μM (—), 17.1 μM (⋅ ⋅ ⋅), and 36.9 μM (– ■ –) and the experimental data of 8.4 μM (■), 17.1 μM (●), and 36.9 μM (▴). (b) Simulated aggregation progress of K₂Q₂₈K₂ (■, —), K₂Q₃₆K₂ (●, – ■ –), and K₂Q₄₇K₂ (▴, ⋅ ⋅ ⋅) at a concentration of 0.1 nM.

Is it possible that ages-of-onset for expanded poly(Gln) diseases might be at least partially accounted for by nucleated growth kinetics? Unfortunately, neither the molecular forms of poly(Gln) protein responsible for aggregation, nor their steady-state concentrations in neurons, are known. To test whether it is feasible that nucleation kinetics might play a role in determining age-of-onset differences, we used the parameters in Table 1 to calculate kinetics curves for the Q₄₇ peptide at several different concentrations. At a poly(Gln) concentration of 0.1 nM, we obtained a lag phase of 31 years (Fig. 6b), which is in the age-of-onset range of 30–40 years of age for HD patients with this repeat length (2). We then repeated the calculation for the Q₃₆ and Q₂₈ peptides at this same 0.1 nM concentration, and found lag times of 141 years and 1,273 years, respectively. There are no known cases of HD in a person with a repeat length of 36; individuals with repeat lengths of 38 develop HD around the age of 70. The calculation for the Q₃₆ peptide is therefore also in rough agreement with the medical genetics.

Discussion

The common underlying mutation in the expanded CAG repeat diseases is the expansion of the encoded polyglutamine sequence in the corresponding disease gene product (1). A reasonable hypothesis therefore is that there is a common mechanistic driving force for these diseases related to the properties of the shared expanded poly(Gln) sequence. In turn, the expression characteristics, cellular environments, trafficking, processing, and chemical natures of the flanking sequences of the various disease proteins would be expected to constitute secondary, modulating effects, producing the individual nuances of these diseases. Studies of the physical behavior and biological effects of simple poly(Gln) sequences and aggregates are thus expected to reveal the common process that triggers pathology this disease family. Studies on simple peptides are also technically justified, because (i) parallel experiments using either recombinant fragments of disease proteins or chemically synthesized peptides show no substantive differences concerning either the solution conformation of poly(Gln) monomers (10, 25, 26) or repeat length-dependent aggregation behavior (9, 10); and (ii) simple peptides offer advantages in facilitating elimination of aggregated impurities that might act as heterogeneous nuclei in aggregation kinetics studies (23).

In homogeneous nucleation theory, the impediment to phase transition is visualized as a large free-energy barrier that is ultimately overcome by the interplay between a finite monomer concentration and a Boltzmann relation that describes the sporadic formation of the high energy nuclei through which phase transition occurs (20). This barrier can be considered either as a free energy of activation (20) or as a free energy of formation (16). In the context of the model on which our mathematical treatment is based, the unanticipated result n* = 1 is consistent with a nucleus that is an energetically unfavorable monomeric state in equilibrium with the bulk phase poly(Gln) monomer. Consistent with the model, the pathway to oligomeric species in the aggregation pathway is energetically downhill.

The detailed mechanism by which this elongation reaction proceeds is not known. However, several lines of argument favor the mechanism illustrated in Fig. 5, involving initial binding of a disordered poly(Gln) molecule to the ordered nucleus (or aggregate), followed by structure acquisition in the newly added monomer to ultimately create a new elongation site. Evidence for such a template-assisted, or “dock-and-lock,” mechanism has been provided for Aβ fibril extension at low Aβ concentrations (27) and also may be involved in replication of the prion state of mammalian PrP in vitro (28). Recently, we observed kinetics for the extension of poly(Gln) peptides in a microtiter plate assay (29) reminiscent of Aβ dock-and-lock kinetic behavior in a similar assay format (27). Such a mechanism would be expected to give kinetics of β-sheet formation equal to the kinetics of aggregation, as observed (Fig. 1).

The nucleus illustrated in the schematic in Fig. 5 is drawn as a short antiparallel β-sheet; it could be as easily depicted as a duplex of two-stranded sheets. A poly(Gln) molecule folded into a β-helix (30) is another possible structure for the monomeric nucleus implicated here. It is reasonable to assume that the nucleus is rich in β structure and that it will resemble the repeating folding motif in the amyloid fibril. There is no consensus, however, on the nature of the basic amyloid fibril structure (31).

The recognition that nucleus formation can occur by refolding within a monomeric unit has implications beyond poly(Gln) aggregation. Although some cases of disease-related protein aggregate formation involve peptides that are relatively unstructured in the native state, other cases involve proteins normally possessing stable, folded, globular structures (15, 32). Our results suggest that even in the latter case it may be possible that fibril formation reactions meeting all of the defining characteristics of a nucleated growth polymerization pathway (see above) might depend on a nucleation event consisting of an energetically unfavorable misfolding transition starting from the native molecule. This idea may be particularly relevant to the field of mammalian prion research, where the oligomerization state of infectious and replicating prions continues to be actively addressed.

Given the complexity of the cellular environment, including (i) the presence of chaperones known to modulate poly(Gln) aggregation (33) and cellular toxicity (6, 7), (ii) degradation and transport processes capable of partitioning proteins into different molecular forms and compartments, and (iii) other molecules and assemblies that might act as stimulators or seeds for aggregation, it seems unlikely that cellular poly(Gln) aggregation and toxicity might be successfully modeled by considering only the biophysics of the poly(Gln) aggregation process as characterized in vitro. All this not withstanding, it is remarkable that the kinetic analysis reported here, coupled with a not-unreasonable estimate for the cellular concentration of aggregation-prone forms of a poly(Gln) protein, should generate predictions for the relative magnitudes of aggregation lag times consistent with ages-of-onset for patients. When experimental estimates of the cellular and compartmental concentrations of various forms of huntingtin and other expanded CAG repeat disease proteins become available, the calculated aggregation curves at these concentrations should provide clues to the degree of involvement of other molecular and cellular factors and processes, and whether their net effect is to accelerate or decelerate disease-associated aggregation.

Abbreviations

HD

Huntington's disease

poly(Gln)

polyglutamine