Abstract
A combined experimental and theoretical charge density study of the pentapeptide Boc-Gln-d-Iva-Hyp-Ala-Phol (Boc, butoxycarbonyl; Gln, glutamine; Iva, isovaline; Hyp, hydroxyproline; Ala, ethylalanine; Phol, phenylalaninol) is described. The experimental analysis, based on synchrotron x-ray data collected at 20 K, is combined with ab initio theoretical calculations. The topologies of the experimental and theoretical densities are analyzed in terms of the atoms in molecules quantum theory. Topological parameters, including atomic charges and higher moments integrated over the atomic basins, have been evaluated with the program topxd and are used to calculate the electrostatic interactions between the molecules in the crystal. The interaction energies obtained after adding dispersive and repulsive van der Waals contributions agree quite well with those based on M-B3LYP/6–31G** dimer calculations for two of the three dimers in the crystal, whereas for the third a larger stabilization is obtained than predicted by the calculation. The agreement with theory is significantly better than that obtained with multipole moments derived directly from the aspherical atom refinement. The convergence of the interaction as a function of addition of successively higher moments up to and including hexadecapoles (l = 4) is found to be within 2–3 kJ/mol. Although shortcomings of both the theoretical and experimental procedures are pointed out, the agreement obtained supports the potential of the experimental method for the evaluation of interactions in larger biologically relevant molecules.
Recent development of very low temperature diffraction techniques, area detectors, and computational methods, combined with the availability of synchrotron sources, allows the extension of x-ray charge density analysis to much larger molecules than was previously possible (1). The work of Lecomte and collaborators has demonstrated that such studies are eminently possible (2, 3) and that extension to proteins for which high-resolution data are available is within reach (4–6).§ For such studies to be productive, the interpretive methods to be applied to the experimental results must be fully tested on relevant smaller compounds. Oligopeptides are prime prototypes for such studies as they can be considered as protein fragments with typical functional groups and representative intermolecular interactions. Lecomte and coworkers (7) pioneered such studies with the charge density analysis of the pentapeptide Leu-enkaphalin trihydrate reported in 1994.
We describe here a combined experimental and theoretical charge density study of the pentapeptide Boc-Gln-d-Iva-Hyp-Ala-Phol (Boc, butoxycarbonyl; Gln, glutamine; Iva, isovaline; Hyp, hydroxyproline; Ala, ethylalanine; Phol, phenylalaninol), first analyzed by E. Ciszak, R. Miller, and G. D. Smith (personal communication). The experimental analysis is based on synchrotron x-ray data collected at 20 K and is combined with ab initio theoretical calculations. The topologies of the experimental and theoretical densities are analyzed in terms of the atoms in molecules (AIM) quantum theory (8).
Although point charge models for the evaluation of Coulombic interactions, as implemented in programs such as amber (9) and charmm (10), are often effective, they do not explicitly take into account the effect of dipoles and higher atomic electrostatic moments on the interaction energy, which can make an important contribution to the equilibrium energy in the crystal. Rather than use empirically adjusted atomic charges or charges based on theoretical calculations of isolated molecules, it would be desirable to base the electrostatic force field on experimentally determined quantities, including higher moments.
In this study, the program xdinter (11), which uses the electron charge density approach (ECDA) (12, 13), is applied to evaluate the intermolecular interactions in Boc-Gln-d-Iva-Hyp-Ala-Phol, and results are compared with those obtained with the amber force field. Two different methodologies, based on x-ray refined pseudoatom moments and atomic moments from the topological analysis of the x-ray charge density, are tested.
Experiments
Data Collection and Reduction.
Data were collected at 20(1) K with a Bruker (Madison, WI) SMART 1000 CCD area detector at the SUNY X3A1 beamline at the National Synchrotron Light Source, Brookhaven National Laboratory, Upton, NY, using a wavelength λ = 0.643 Å obtained with a sideways-reflecting curved Si(111) crystal. A 0.12 × 0.10 × 0.08-mm colorless crystal was glued to the tip of an amorphous carbon fiber, which in turn was attached to the cold finger of the two-stage close-cycle helium Displex (Advanced Research Systems, Allentown, PA) cryostat. The cryostat was mounted on a Huber (Blake Industries, Scotch Plains, NJ) D-511.1 four-circle diffractometer as described by Graafsma et al. (14). A special antiscattering device inside the chamber of the cryostat (15) was used to avoid the scattering of the direct beam by the beryllium vacuum chamber. The crystal was mounted in two orientations with respect to the ϕ rotation axis. At each orientation, three data sets at three different detector 2θ positions, 0°, 35°, and 55°, were collected by rotation of the ϕ axis with a range of 0.3° per frame. The correction for the decay of the synchrotron beam was based on the count from a beam monitor installed in front of the crystal, but behind the beam-defining slits.
The intensities were integrated by using saint software (16). Because of the small size of crystal and low absorption coefficient (μ = 0.09 mm−1), no absorption correction was made. To eliminate the effect of small instabilities of the vertical position of the cryostat, a ϕ-dependent intensity correction was applied (17), which led to a 1% improvement in the Rmerge internal agreement factor. With the program sortav (18), a total of 222,397 measurements (0.078 < sinθ/λ < 1.054 Å−1) were reduced to 33,131 independent reflections (average multiplicity of 6.7) by averaging over symmetry-equivalent and redundant measurements. Only 21,542 unique reflections with I > 3σ(I) and measured three or more times were used in subsequent analysis. Experimental details and crystal data are summarized in Table 1.
Table 1.
Crystallographic data for Boc-Gln-d-Iva-Hyp-Ala-Phol
| Formula | C32H50N6O9 |
| Formula weight | 662.78 |
| Crystal system | Orthorhombic |
| Space group | P212121 |
| A | 10.3793(4) Å |
| b | 16.0728(5) Å |
| c | 21.0938(7) Å |
| α = β = γ | 90° |
| Z | 4 |
| Volume | 3518.9(12) Å3 |
| Calculated density, g/cm3 | 1.25 |
| T | 20(1) K |
| λ | 0.643 Å |
| (sinθ/λ)max | 1.054 Å−1 |
| Reflections collected | 222,397 |
| Unique reflections | 33,131 |
| Reflections included in refinement (I > 3σ(I)) | 21,542 |
| Rint | 0.052 |
| R[F] | 0.030, 0.020 |
| Rw[F] | 0.071, 0.023 |
| Goodness of fit | 0.918, 0.593 |
First entry: spherical atom refinement; second entry: multipole refinement.
Least-Squares Refinements.
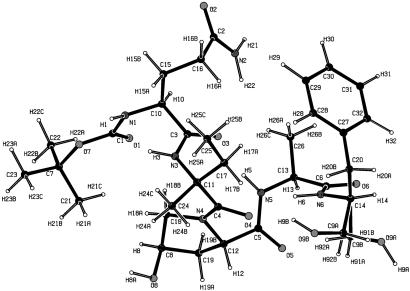
The low-temperature structure was solved and refined in the spherical-atom approximation by using the program SHELXL-97 (19). All hydrogen atoms were located by difference-Fourier synthesis before refinement. The molecular structure is shown in Fig. 1. The terminal H2COH group of the phenylalaninol segment has two different orientations, with, at 20 K, 89% and 11% occupancy, respectively, compared with equal occupancy at room temperature. In the major conformer A, the COH group is intermolecularly hydrogen-bonded with an O(9A). . . . .O(1) (1-x, y-1/2, 3/2-z) distance of 2.829(1) Å, whereas in conformer B the hydrogen bond is intramolecular with an O(9B). . . . .O(4) distance of 2.940(5) Å. Although the presence of partial disorder is not conducive to a charge density analysis, it is often unavoidable in large macromolecules and must therefore be accepted if such molecules are to be studied.
Fig 1.
Experimental molecular structure of Boc-Gln-d-Iva-Hyp-Ala-Phol, showing both the A and B conformations of the CH2OH group.
Following the conventional refinement, an aspherical-atom refinement was carried out with the xd (20) program package, which is based on the Hansen–Coppens multipole formalism (1, 21). The formalism expresses the static electron density in the crystal by a nucleus-centered multipole expansion.
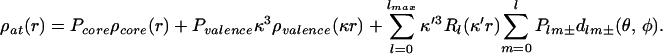 |
The first and second terms are the spherically averaged Hartree-Fock (HF) core and valence densities, normalized to one electron. The population of the core Pcore is fixed, whereas the population of the spherical valence shell Pvalence is refined together with the κ expansion-contraction parameter. The functions dlm± are real spherical harmonics describing the angular dependence, Rl are normalized Slater-type radial functions, whereas κ and κ′ are dimensionless expansion-contraction parameters, which can be refined along with the populations Pv and Plm±.
As Boc-Gln-d-Iva-Hyp-Ala-Phol is among the larger molecules that have been subjected to a charge density refinement, the details of the refinement process deserve description. To reduce the number of parameters, local symmetry constraints were imposed, and chemical constraints, linking the charge density parameters on chemically equivalent atoms, were applied to the multipole parameters.¶ Each of the hydrogen atom densities was restricted to be cylindrical along the relevant hydrogen–heavy atom bond. To reduce the interaction between the charge density and the thermal parameters, a rigid bond constraint was applied to all bonds between nonhydrogen atoms (22). As the population of higher multipoles was negligible, the multipole expansion was truncated at the octupole level (lmax = 3) for the nonhydrogen atoms, and at the dipole level (lmax = 1) for the hydrogen atoms. The κ′s of the hydrogen atoms were fixed at the recommended value of 1.17 (23). A molecular electroneutrality constraint was applied in all refinements.
Hydrogen positions were obtained by extending X-H distances to their standard neutron diffraction values (Cprimary–H = 1.092 Å, Csecondary–H = 1.099 Å, Car–H = 1.082 Å, N–H = 1.032 Å, O–H = 0.964 Å) (24). These distances were kept constant in subsequent refinements. In the next stage a κ refinement (Plm± = 0) was performed with all structural parameters, except the isotropic thermal parameters of the hydrogens, which were fixed at the previously refined values. Finally, a κ′-restricted multipole model refinement was carried out (25). In this type of refinement the κ′ parameters are fixed at recommended values derived from multipole refinements of the theoretical structure factors, obtained from periodic density functional theory (DFT) calculations at the 6–31G** level on a large series of organic compounds (25), thus avoiding charge/κ correlations that can be pronounced in larger molecules. A considerable improvement in agreement factor was obtained compared with the spherical atom refinement (Table 1), indicating the significance of the deviations from spherical atomic symmetry in this pentapeptide.
Theoretical Calculations.
Single molecule calculations were performed at the DFT level by using the GAUSSIAN94 program package (26) with the molecular geometry from the x-ray κ′-restricted multipole model refinement. The calculations were performed with the B3LYP functional, which combines Becke's three-parameter hybrid exchange functional (27) with the nonlocal correlation functional of Lee et al (28). In the isolated molecule and isolated dimer calculations, the standard molecular split valence 6–31G** basis set was used, with one exception as noted. In the following and in the tables the notation M-B3LYP is used to distinguish molecular calculations from those for the periodic crystal, which are marked as P-B3LYP.
Fully periodic DFT calculations at the experimental geometry were performed with the CRYSTAL98 program (29), using the same exchange and correlation functionals as in the single-molecule calculations and the split valence 3–21G* basis set. Static crystal structure factors were obtained through Fourier transform of the theoretical crystal charge density. Only the charge density parameters were varied in the refinement of the theoretical structure factors.
To calculate the pairwise interaction energies in the crystal, the isolated molecule option of CRYSTAL98 was used, in which the distance between the molecules, or pairs of molecules, and their neighbors is increased sufficiently to eliminate all neighbor–neighbor interactions. Experimental molecular geometries were used in the calculations, which used the 6–31G** basis set. The theoretical basis-set superposition error was corrected by the counterpoise method (30) (basis sets of all ghost atoms at a distance less than 3.15 Å from the atoms in the original molecule). The pairwise interaction energy is obtained as the difference between the energies of the dimer and the isolated molecule. The theoretical binding energy of a molecule in the crystal is derived as the difference between its energy and the energy of the isolated molecule with the crystal geometry.
Topological Analysis.
The topological properties of the charge density were calculated with the programs topxd (31) (experiment) and AIMPAC95 (32) (theory for the isolated molecule). The results of the integration of the atomic basins for the C, N, and O atoms are summarized in Table 2, while the corresponding values for the hydrogen atoms are listed in Table 6, which is published as supporting information on the PNAS web site, www.pnas.org. Determination of the interatomic surfaces and subsequent integration of the experimental density typically took 8 h per atom on a Sun (Sun Microsystems, Santa Clara, CA) Blade 1000 workstation with 750-MHz UltraSparc III dual processors and an average of 14 h per atom on a Sun Ultra5 workstation with a single 333-MHz UltraSparc IIi processor. A total of 80 processors in a cluster including both types of computers were used in parallel in the calculations.
Table 2.
Net atomic charges for C, N, and O atoms from experiment and theory
| Atoms
|
Conformer A | |||
|---|---|---|---|---|
| Experiment | P-B3LYP/3-21G* | M-B3LYP/6-31G** | ||
| q(Pv) | q(Ω) | q(Pv) | q(Ω) | |
| O1 | −0.54 (4) | −1.07 | −0.41 | −1.24 |
| O2 | −0.37 (4) | −0.99 | −0.41 | −1.20 |
| O3 | −0.45 (3) | −0.87 | −0.41 | −1.22 |
| O4 | −0.55 (4) | −1.07 | −0.41 | −1.21 |
| O5 | −0.49 (3) | −0.91 | −0.40 | −1.20 |
| O6 | −0.57 (3) | −0.89 | −0.41 | −1.21 |
| O7 | −0.54 (5) | −1.13 | −0.33 | −1.12 |
| O8 | −0.54 (5) | −1.26 | −0.45 | −1.08 |
| O9A | −0.54 (4) | −1.24 | −0.43 | −1.10 |
| N1 | −0.31 (6) | −1.04 | −0.39 | −1.20 |
| N2 | −0.63 (12) | −1.35 | −0.39 | −1.29 |
| N3 | −0.26 (6) | −0.94 | −0.36 | −1.24 |
| N4 | −0.09 (7) | −0.80 | −0.40 | −1.19 |
| N5 | −0.32 (6) | −1.05 | −0.40 | −1.28 |
| N6 | −0.24 (6) | −0.98 | −0.40 | −1.28 |
| C1 | 0.38 (5) | 1.55 | 0.41 | 2.11 |
| C2 | 0.30 (5) | 1.19 | 0.32 | 1.54 |
| C3 | 0.37 (4) | 1.10 | 0.28 | 1.49 |
| C4 | 0.24 (6) | 1.12 | 0.30 | 1.49 |
| C5 | 0.37 (4) | 1.10 | 0.29 | 1.53 |
| C6 | 0.37 (4) | 1.10 | 0.30 | 1.54 |
| C7 | 0.01 (5) | 0.21 | 0.11 | 0.44 |
| C8 | 0.07 (5) | 0.41 | 0.07 | 0.57 |
| C9A | 0.07 (5) | 0.37 | 0.00 | 0.58 |
| C10 | 0.03 (6) | 0.21 | 0.06 | 0.41 |
| C11 | −0.03 (6) | 0.20 | 0.04 | 0.38 |
| C12 | −0.07 (7) | 0.13 | 0.06 | 0.38 |
| C13 | 0.03 (6) | 0.21 | 0.06 | 0.43 |
| C14 | −0.03 (7) | 0.24 | 0.06 | 0.41 |
| C15 | 0.23 (5) | 0.18 | −0.19 | 0.09 |
| C16 | 0.23 (5) | 0.17 | −0.19 | 0.07 |
| C17 | 0.23 (5) | 0.25 | −0.19 | 0.10 |
| C18 | −0.03 (7) | 0.11 | −0.20 | 0.37 |
| C19 | 0.09 (8) | 0.06 | −0.19 | 0.09 |
| C20 | 0.23 (5) | 0.15 | −0.19 | 0.09 |
| C21 | 0.10 (7) | 0.11 | −0.30 | 0.08 |
| C22 | 0.10 (7) | 0.11 | −0.30 | 0.08 |
| C23 | 0.10 (7) | 0.12 | −0.30 | 0.09 |
| C24 | 0.10 (7) | 0.06 | −0.30 | 0.07 |
| C25 | 0.10 (7) | 0.08 | −0.30 | 0.08 |
| C26 | 0.10 (7) | 0.04 | −0.30 | 0.08 |
| C27 | 0.21 (7) | 0.13 | 0.01 | 0.01 |
| C28 | −0.18 (5) | −0.03 | −0.06 | −0.01 |
| C29 | −0.18 (5) | −0.09 | −0.10 | −0.01 |
| C30 | −0.18 (5) | −0.09 | −0.12 | 0.00 |
| C31 | −0.18 (5) | −0.10 | −0.10 | 0.01 |
| C32 | −0.18 (5) | −0.02 | −0.06 | 0.01 |
| Σq | 0.001 | 0.11 | 0.04 | |
| Σ|L| | — | 1 × 10−1 | — | 4 × 10−2 |
| Average L(Ω) per atom | — | 1 × 10−3 | — | 4 × 10−4 |
q(Pv), net atomic charge derived from monopole population; q(Ω), net atomic charge obtained from topological analysis. The prefixes P and M indicate periodic and molecular calculations, respectively.
After rescaling, the whole molecule keeps neutrality.
The Intermolecular Interaction Model.
The program xdinter (11) uses the ECDA to calculate the intermolecular interaction energy (33). The ECDA model describes electrostatic intermolecular interaction energy via summation of the interactions between the atom-centered multipoles in the traceless Cartesian tensor formulation, as formulated by Buckingham (34). Exp-6 atom-atom potentials as parameterized by Spackman (12) are used for the calculation of the van der Waals contribution to the intermolecular interaction energy. Full details of the method have been described (11). In the current study, the usual calculation based on the moments from the multipole refinement of the experimental structure factors is complemented by a calculation based on the atomic moments derived from the topological analysis of the experimental charge density.
Results and Discussion
Net Atomic Charges and the Molecular Dipole Moment.
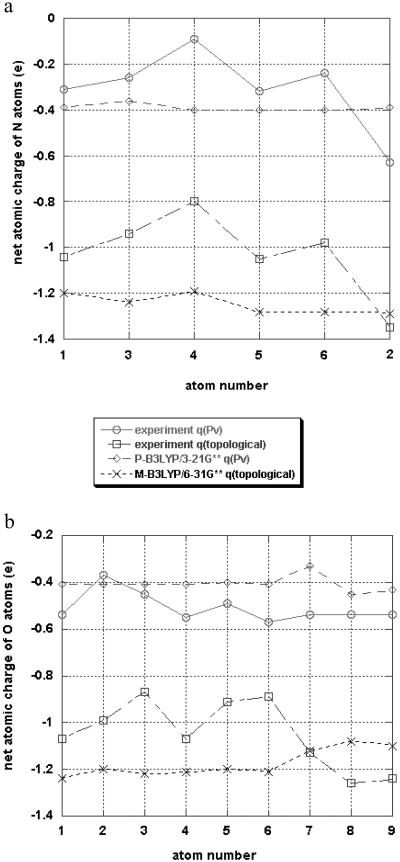
The net atomic charges from the aspherical refinements of both the experimental and theoretical structure factor are listed in Tables 2 and 6 [columns headed by q(Pv)], and graphically illustrated for the N and O atoms in Fig. 2. The agreement between theory and experiment is only qualitative. To some extent the discrepancies can be attributed to the limited 3–21G* basis set of the periodic crystal calculation, although the lack of locality of the overlapping spherical harmonic functions used in the multipole refinement is likely to be a major contributor. A local definition of the atomic properties is provided by the AIM theory (8), in which atomic basins are bounded by discrete “zero-flux” surfaces. The results of the integration with the topxd program are listed in Table 2 in the columns headed q(Ω), while the N and O atomic AIM and multipole-refinement charges are plotted in Fig. 2. Whereas general trends are well reproduced, the experimental topological charges for N and O are systematically smaller than those for the isolated molecule, except for the intermolecularly hydrogen-bonded CH2OH and glutamine NH2 groups, which tend to be larger than the theoretical isolated molecule values, indicating the effect of the intermolecular interaction.
Fig 2.
Comparison of net charges from multipole refinements and topological analysis (a) for the nitrogen atoms (lanes 1 and 3–6 are peptide nitrogen atoms, lane 2 is the N atom of the glutamine group) and (b) for the oxygen atoms (lanes 1–6 are the oxygen atoms of the peptide bonds and the glutamine group (2), lane 7 is the oxygen atom of the terminal BOC group, and lanes 8–9 are oxygen atoms of the CH2OH groups).
The molecular dipole moments from both experiment and theory are given in Table 3. The experimental dipole moments from the multipole refinement results and the topological integration of the experimental density agree well. This is as expected, as discrepancies between the individual multipole and AIM atomic charges are caused by different atomic definitions in the two methods, which are based on the same charge density. The molecular boundary, which could affect the molecular dipole moment, falls in a low density region. The experimental dipole moment in the crystal is larger than calculated for the isolated molecule with both DFT and HF methods (the latter not reported here), a manifestation of polarization of the molecular density by neighboring molecules in the crystalline environment (37).
Table 3.
Experimental and theoretical dipole moments (conformer A); components in the crystal coordinate system
|
|
Experiment, crystal | P-B3LYP/3-21G*, crystal | M-B3LYP/6-31G**, isolated molecule | |
|---|---|---|---|---|
| μ (multipole) | μ (AIM) | μ (multipole) | μ (AIM) | |
| |μ| (Debye) | 18.6 | 17.5 | 14.1 | 13.4 |
| μx | −16.0 | −14.2 | −12.8 | |
| μy | 6.8 | 5.5 | 1.2 | |
| μz | 6.7 | 8.4 | 5.8 | |
Topological Analysis of the Electron Density.
The AIM theory allows quantitative evaluation of the nature of bonding in a molecule by topological analysis of the total density. Critical point properties were calculated with xdprop, the properties evaluation routine in the xd program package for the crystal density and with the program aimpac for the theoretical isolated molecule density. The properties describing the (3,−1) bond-critical points, which characterize the bonding interactions between adjacent atoms, are summarized in Table 7, which is published as supporting information on the PNAS web site. While the critical points are close to the bond center for the homonuclear C—C bonds, they are displaced toward the less electronegative atom in the heteronuclear C—N and C—O bonds, as observed in previous studies on other molecules, including small peptides (35–38). The displacement from the center of the bond is more pronounced in the theoretical density. The distance to the less electronegative atom, averaged over equivalent bonds, is for experiment and theory, respectively, 0.45 and 0.41 Å for C O, 0.55 and 0.47 Å for C—N, 0.63 Å and 0.55 Å for Cα—N, and 0.55 and 0.47 Å for the other C—N bonds.
O, 0.55 and 0.47 Å for C—N, 0.63 Å and 0.55 Å for Cα—N, and 0.55 and 0.47 Å for the other C—N bonds.
While the electron densities at the bond critical points (ρc) are in quite reasonable agreement for the two methods, significant discrepancies between theory and experiment are observed for λ3, the curvature of the density along the bond path, the theoretical values being more positive for the C O bonds, but significantly smaller for the other bonds. As shown in the study on p-nitroaniline, discrepancies between experimental and theoretical values are at least in part caused by the nature of the multipolar functions defined by Eq. 1 (31). As λ1 and λ2 are similar for theory and experiment, the differences in λ3 are reflected in the ▿2ρ values at the bond critical points (BCP), which are the sum of the principal curvatures λ1 + λ2 + λ3. The experimental value of the Laplacian (i.e., ▿2ρ) at the BCP of the C
O bonds, but significantly smaller for the other bonds. As shown in the study on p-nitroaniline, discrepancies between experimental and theoretical values are at least in part caused by the nature of the multipolar functions defined by Eq. 1 (31). As λ1 and λ2 are similar for theory and experiment, the differences in λ3 are reflected in the ▿2ρ values at the bond critical points (BCP), which are the sum of the principal curvatures λ1 + λ2 + λ3. The experimental value of the Laplacian (i.e., ▿2ρ) at the BCP of the C O bonds ranges from −7.2 to −29.4 e/Å5, compared with −1.4 to −4.2 e/Å5 for the theoretical results. The Laplacian values for C—N bonds are quite similar to those obtained for the C—Namino bond in p-nitroaniline (39), but noticeable differences occur between the experimental and theoretical values, the latter being more negative.
O bonds ranges from −7.2 to −29.4 e/Å5, compared with −1.4 to −4.2 e/Å5 for the theoretical results. The Laplacian values for C—N bonds are quite similar to those obtained for the C—Namino bond in p-nitroaniline (39), but noticeable differences occur between the experimental and theoretical values, the latter being more negative.
The experimental ellipticities of the aromatic bonds in the phenyl ring average 0.23, compared with the theoretical value of 0.21, both in good agreement with Bader et al.'s 1983 HF value of 0.23, obtained for benzene with a 6–31G* basis set (40).
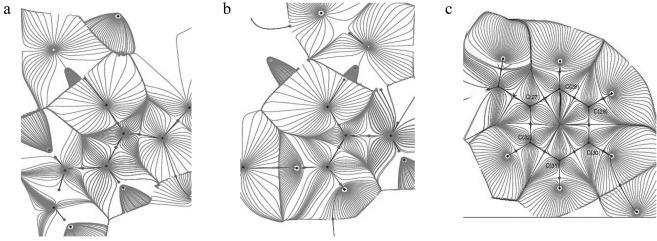
The gradient paths in the different CO—NH planes show a very similar pattern. The gradient path and the topological boundaries (zero flux surfaces) for the average density in the peptide plane are shown in Fig. 3a, while the C—O—N (glutamine) and phenyl ring planes are reproduced in Fig. 3 b and c, respectively.
Fig 3.
The gradient paths and atomic basins in average peptide bond (a), the plane through the C, O, and N atoms of the CONH2 group of the glutamine residue (b), and the plane of the phenyl group (c).
Intermolecular Interactions and Binding Energies.
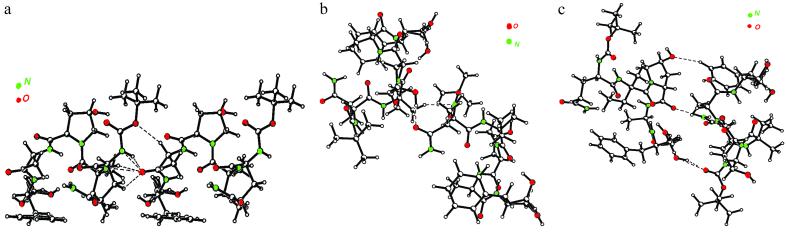
Three different molecular pairs can be distinguished in the crystal (Fig. 4). In each the molecules are linked by both strong and weak hydrogen-bonding interactions. The intermolecular interaction energies evaluated by different methods are listed in Table 4.
Fig 4.
The three dimer configurations in the crystal. Hydrogen-bonding interactions listed in Table 5 are indicated by broken lines.
Table 4.
Dimer interaction energies of conformer A, kJ/mol
| Dimer
|
Symmetry operation
|
Hydrogen bond
|
RH—A, Å
|
D—H . . . . . A
|
ECDA (crystal) multipoles
|
ECDA (crystal) AIM moments lmax = | Theory (dimer) M-B3LYP/6-31G**
|
AMBER4.0
|
|||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||||||||
| a | 1 + X, Y, Z | N(1)-H(1)—O(6) | 1.85 | 153.12 | −159 (34) | −125 | −108.4 | −111.6 | −110.0 | −60.6 | −72.1 |
| 1 + X, Y, Z | N(3)-H(3)—O(6) | 1.92 | 157.26 | ||||||||
| 1 + X, Y, Z | C(15)-H(15A)—O(6) | 2.44 | 135.07 | ||||||||
| 1 + X, Y, Z | C(23)-H(23C)—O(5) | 2.58 | 153.75 | ||||||||
| 1 + X, Y, Z | C(13)-H(13)—O(7) | 2.43 | 160.01 | ||||||||
| b | 2 − X, ½ + Y, ½ − Z | O(8)-H(8A)—O(2) | 1.78 | 171.82 | −34 (15) | −12 | −12.6 | −18.8 | −16.2 | −11.3 | −55.2 |
| 2 − X, ½ + Y, ½ − Z | C(24)-H(24B)—N(1) | 2.54 | 142.46 | ||||||||
| c | 1 − X, −½ + Y, ½ − Z | N(2)-H(21)—O(5) | 1.81 | 174.21 | −87 (11) | −64 | −53.8 | −54.6 | −54.5 | −60.7 | −81.9 |
| 1 − X, −½ + Y, ½ − Z | C(31)-H(31)—O(8) | 2.52 | 154.13 | ||||||||
| 1 − X, −½ + Y, ½ − Z | O(9A)-H(9A)—O(1) | 1.86 | 158.61 | ||||||||
As pointed out above, the atomic basins as defined by the AIM theory are bounded by the discrete zero-flux surface and are thus fully localized. The localized definition of the AIM atomic basins suggests basing the calculation of the interaction energy on the electrostatic moments of the AIM-defined atoms (41, 42). A potential disadvantage of this approach is that, because of the irregular shape of the AIM basins, the higher moments are relatively large. However, calculation of the interaction including successive higher orders of the moments, up to and including the hexadecapole (l = 4) moments, shows that a quite reasonable convergence is reached at this level. Kosov and Popelier (41) reached the same conclusion for the convergence of AIM-based multipole expansion in calculation of the electrostatic potential of a series of isolated molecules including the amino acid alanine, and for the electrostatic interaction energies between very small molecules such as HF and H2O, CO2 and NH3, using a topological “atom–atom partitioning” of the electrostatic energy between unperturbed molecules (42). The current results fully support their conclusions.
The AIM analysis results agree better with those from the theoretical dimer calculations than the energies based on the least-squares multipole moments, especially for the two lower energy interactions. Although the theoretical results may suffer from an underestimate of the dispersion contribution (11), the agreement together with the convergence of the AIM results supports the use of topological moments in the calculation of electrostatic interactions between molecules. The last column of Table 4 lists the results of AMBER 4.0 calculations as implemented in SYBYL 6.6 (43). Rather large quantitative differences with the experimental and theoretical results are evident, although the ordering of the interactions is the same with all three methods.
The intermolecular binding energy of one molecule (A) in the crystal as calculated with xdinter is given in Table 5. The ECDA-AIM result agrees well with the theoretical value, indicating the potential of accurate experimental x-ray data for the evaluation of molecular binding energies.
Table 5.
Binding energy of one molecule (conformer A), kJ/mol
| Conformer | ECDA (crystal) x-ray multipole refinement | ECDA-AIM (crystal) x-ray topology moments | P-B3LYP/3-21G* (crystal, theory) |
|---|---|---|---|
| A | −334 (50) | −209 (lmax = 1) | −227.6 |
| −226 (lmax = 2) | |||
| −248 (lmax = 3) |
The structural disorder was investigated by replacing a molecule A in the center of cluster of 27 unit cells by conformer B. The resulting change of the intermolecular interaction energy in the cluster is 23.6 kJ/mol. This energy difference, which is in accordance with the preference for the A configuration in the crystal, is in part compensated by the intramolecular energy difference of two conformers, which favors B because of its intramolecular O—H . . . . . O hydrogen bond. We have performed ab initio HF calculations on the molecule in the geometry of each of the conformers. Using 4–31G** and 6–311G** basis sets, energy differences of, respectively, 9.58 kJ/mol and 10.04 kJ/mol are obtained. These values are differences between very large total electronic energies of the conformers and should be used with caution.
Although the energy of the cluster is almost twice as small as an estimate made previously (11), the sum of the cluster and the intramolecular energy differences between A and B (≈14 kJ/mol) is still too large to account for the observed ratio of the A and B conformers in the crystal, which, assuming a Boltzmann distribution, corresponds to an energy difference of only of 0.35 kJ/mol.
Conclusions
A quantitative characterization of the bonding in the pentapeptide Boc-Gln-d-Iva-Hyp-Ala-Phol has been obtained by high-resolution x-ray diffraction and both isolated atom and periodic crystal calculations at the DFT level. Although the AIM and multipole atomic charges differ systematically as they correspond to a different partitioning of the molecular space, the dipole moments from the AIM analysis of the experimental and theoretical charge densities and those obtained directly from the multipole population parameters agree quite well. They are larger than the moments calculated for the isolated molecule, as expected from the polarizing influence of the crystal matrix.
The molecular interaction energies in the crystal have been evaluated from the experimental data. The agreement of the experimental dimer interaction energies with the theoretical values is considerably improved when the topologically defined electrostatic moments are used, especially for the lower energy interactions. The experimental and theoretical results agree with those based on the amber force field on the order of the intra-pair molecular interactions. The molecular binding energy in the crystal is well reproduced by the analysis based on the topological moments.
Although shortcomings of both theory and experiment have been pointed out, the agreement obtained supports the potential of the experimental method for the evaluation of interactions in larger biologically relevant molecules. The ultimate aim is an experiment-based Coulombic force field for use in macromolecular structure calculations.
Supplementary Material
Acknowledgments
We thank Dr. Robert Blessing of the Hauptman–Woodward Institute for stimulating interactions. Support of this work by the National Institutes of Health (Grant GM56829), the National Science Foundation (Grant CHE9981864), and the U.S. Department of Energy (Grant DE-FG02-86ER45231) is gratefully acknowledged. The Center for Computational Research at the State University of New York/Buffalo is supported by Grant DBI9871132 from the National Science Foundation. Research was carried out in part at the National Synchrotron Light Source at Brookhaven National Laboratory, which is supported by the U.S. Department of Energy, Division of Materials Sciences and Division of Chemical Sciences.
Abbreviations
AIM, atoms in molecules
HF, Hartree–Fock
DFT, density functional theory
ECDA, experimental charge density approach
Guillot, B., Jelsch, C., Muzet, N., Lecomte, C., Howard, E., Chevrier, B., Mitschler, A., Podjarny, A., Cousson, A., Sansishvili, R. & Joachimiak, A., 19th European Crystallographic Meeting, August 25–31, 2000, Nancy, France, p. 199 (abstr.).
The multipole coefficients of the nonhydrogen atoms were constrained to obey local mirror-plane symmetry (m) for all carbon, oxygen, and nitrogen atoms in CONH groups, and all carbon atoms in CH2 groups and the phenyl ring, mm2 symmetry for the NH2 group in glutamine, 3-fold symmetry in CH3 groups and C(7). No local symmetry constraints were applied to the α carbon atoms. CH2 groups (except those in Hyp) and CH3 groups, were constrained to be equivalent within each set, as were the C and H atoms of the C6H5 group, with the exception of the substituted C(27) atom. No constraints were applied to the atoms of the peptide group.
References
- 1.Coppens P., (1997) X-Ray Charge Density Analysis and Chemical Bonding (Oxford Univ. Press, Oxford).
- 2.Pichon-Pesme V., Lecomte, C., Wiest, R. & Bénard, M. (1992) J. Am. Chem. Soc. 114, 2713-2715. [Google Scholar]
- 3.Pichon-Pesme V., Lecomte, C. & Lachekar, H. (1995) J. Phys. Chem. 99, 6242-6251. [Google Scholar]
- 4.Fernandez-Serra M. V., Junquera, J., Jelsch, C., Lecomte, C. & Artacho, E. (2000) Solid State Commun. 116, 395-400. [Google Scholar]
- 5.Jelsch C., Teeter, M. M., Lamzin, V., Pichon-Pesme, V., Blessing, R. H. & Lecomte, C. (2000) Proc. Natl. Acad. Sci. USA 977, 3171-3176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Housset D., Benabicha, F., Pichon-Pesme, V., Jelsch, C., Maierhofer, A., David, S., Fontecilla-Camps, J. C. & Lecomte, C. (2000) Acta Crystallogr. D 56, 151-160. [DOI] [PubMed] [Google Scholar]
- 7.Wiest R., Pichon-Pesme, V., Bénard, M. & Lecomte, C. (1994) J. Phys. Chem. 98, 1351-1362. [Google Scholar]
- 8.Bader R. F. W., (1990) Atoms in Molecules: A Quantum Theory (Clarendon, Oxford).
- 9.Bayly C. I., Cieplak, P., Cornell, W. & Kollman, P. A. (1993) J. Phys. Chem. 97, 10269-10280. [Google Scholar]
- 10.Brooks B. R., Bruccoleri, R. E., Olafson, B. D., States, D. J., Swaminathan, S. & Karplus, M. (1983) J. Comput. Chem. 4, 187-217. [Google Scholar]
- 11.Abramov Y. A., Volkov, A., Wu, G. & Coppens, P. (2000) Acta Crystallogr. A 56, 585-591. [DOI] [PubMed] [Google Scholar]
- 12.Spackman M. A. (1986) J. Chem. Phys. 85, 6587-6601. [Google Scholar]
- 13.Spackman M. A., Weber, H. P. & Craven, B. M. (1988) J. Am. Chem. Soc. 110, 775-782. [Google Scholar]
- 14.Graafsma H., Sagerman, G. & Coppens, P. (1991) J. Appl. Crystallogr. 24, 961-962. [Google Scholar]
- 15.Darovsky A., Bolotovsky, R. & Coppens, P. (1994) J. Appl. Crystallogr. 27, 1039-1040. [Google Scholar]
- 16.Siemens, (1996) saint: Program to Integrate and Reduce Raw Crystallographic Area Detector Data (Siemens Analytical X-Ray Instruments, Madison, WI).
- 17.Volkov A., Wu, G. & Coppens, P. (1999) J. Synchrotron Rad. 6, 1007-1015. [Google Scholar]
- 18.Blessing R. H. (1997) J. Appl. Crystallogr. 30, 421-426. [Google Scholar]
- 19.Sheldrick G. M., (1997) SHELXL97: Program for Crystal Structure Refinement (University of Gottingen, Gottingen, Germany).
- 20.Koritsanzky T., Howard, S., Richter, T., Su, Z., Mallinson, P. R. & Hansen, N. K., (1997) xd: A Computer Program Package for Multipole Refinement and Analysis of Electron Densities from Diffraction Data (Free University of Berlin, Berlin).
- 21.Hansen N. K. & Coppens, P. (1978) Acta Crystallogr. A 34, 909-921. [Google Scholar]
- 22.Hirshfeld F. L. (1976) Acta Crystallogr. A 32, 239-244. [Google Scholar]
- 23.Stewart R. F., Davidson, E. R. & Simpson, W. T. (1965) J. Chem. Phys. 42, 3175-3187. [Google Scholar]
- 24.Wilson A. J. C., (1992) International Tables for Crystallography (Kluwer, Dordrecht, The Netherlands), pp. 685–706.
- 25.Volkov A., Abramov, Y. A. & Coppens, P. (2001) Acta Crystallogr. A 57, 272-282. [DOI] [PubMed] [Google Scholar]
- 26.Fisch M. J., Trucks, G. W., Schlegel, H. B., Gill, P. M., Johnson, B. G., Robb, M. A., Cheeseman, J. R., Keith, T., Petersson, G. A., Montgomery, J. A., et al., (1995) gaussian 94 (Gaussian, Pittsburgh), Revision E2.
- 27.Becke A. D. (1993) J. Chem. Phys. 98, 5648-5652. [Google Scholar]
- 28.Lee C., Yang, W. & Parr, R. G. (1988) Phys. Rev. B 37, 785-789. [DOI] [PubMed] [Google Scholar]
- 29.Saunders V. R., Dovesi, R., Roetti, C., Causà, M., Harrison, N. M., Orlando, R. & Zicovich-Wilson, C. M., (1998) crystal 98 User's Manual (University of Torino, Torino, Italy).
- 30.Boys S. F. & Bernardi, F. (1970) Mol. Phys. 19, 553-566. [Google Scholar]
- 31.Volkov A., Gatti, C., Abramov, Y. & Coppens, P. (2000) Acta Crystallogr. A 56, 252-258. [DOI] [PubMed] [Google Scholar]
- 32.Biegler-König F. W., Bader, R. F. W. & Tang, T.-H. (1982) J. Comput. Chem. 13, 317-328. [Google Scholar]
- 33.Spackman M. A. (1986) J. Chem. Phys. 85, 6579-6586. [Google Scholar]
- 34.Buckingham A. D. (1978) in Intermolecular Interactions: From Diatomics to Biopolymers, ed. Pullman, B. (Wiley, New York), pp. 1–67.
- 35.Benabicha F., Pichon-Pesme, V., Jelsch, C., Lecomte, C. & Khmou, A. (2000) Acta Crystallogr. B 56, 155-165. [DOI] [PubMed] [Google Scholar]
- 36.Dahaoui S., Jelsch, C., Howard, J. A. K. & Lecomte, C. (1999) Acta Crystallogr. B 55, 226-230. [DOI] [PubMed] [Google Scholar]
- 37.Koritsanszky T. S. & Coppens, P. (2001) Chem. Rev. 6, 1583-1628., and references therein. [DOI] [PubMed] [Google Scholar]
- 38.Pichon-Pesme V., Lachekar, H., Souhassou, M. & Lecomte, C. (2000) Acta Crystallogr. B 56, 728-737. [DOI] [PubMed] [Google Scholar]
- 39.Coppens P., Abramov, Y., Carducci, M., Korjov, B., Novozhilova, I., Alhambra, C. & Pressprich, M. R. (1999) J. Am. Chem. Soc. 121, 2585-2593. [Google Scholar]
- 40.Bader R. F. W., Slee, T. S., Cremer, D. & Kraka, E. (1983) J. Am. Chem. Soc. 105, 5061-5068. [Google Scholar]
- 41.Kosov D. S. & Popelier, P. L. A. (2000) J. Chem. Phys. 113, 3969-3974. [Google Scholar]
- 42.Popelier P. L. A., Joubert, L. & Kosov, D. S. (2001) J. Phys. Chem. 105, 8254-8261. [Google Scholar]
- 43.Tripos, (2000) sybyl 6.6.1 (Tripos, St. Louis).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.