Identifying the conserved network of cis-regulatory sites of a eukaryotic genome

Abstract

A major focus of genome research has been to decipher the cis-regulatory code that governs complex transcriptional regulation. We report a computational approach for identifying conserved regulatory motifs of an organism directly from whole genome sequences of several related species without reliance on additional information. We first construct phylogenetic profiles for each promoter, then use a blast-like algorithm to efficiently search through the entire profile space of all of the promoters in the genome to identify conserved motifs and the promoters that contain them. Statistical significance is estimated by modified Karlin–Altschul statistics. We applied this approach to the analysis of 3,524 Saccharomyces cerevisiae promoters and identified a highly organized regulatory network involving 3,315 promoters and 296 motifs. This network includes nearly all of the currently known motifs and covers >90% of known transcription factor binding sites. Most of the predicted coregulated gene clusters in the network have additional supporting evidence. Theoretical analysis suggests that our algorithm should be applicable to much larger genomes, such as the human genome, without reaching its statistical limitation.

Deciphering the cis-regulatory network of an organism is a major challenge in molecular and computational biology because regulatory elements are usually short, degenerate, and hidden in very long sequences. For over 15 years, many computational algorithms have been developed to identify sequence motifs that constitute regulatory sites. Most earlier algorithms explore a small sequence space representing a set of coregulated promoters to identify overrepresented sequence elements (1–4). A more recent complementary approach explores phylogenetic footprints in orthologous sequences to identify sequence elements under selective pressure (5). Most recently, algorithms that integrate phylogenetic and coregulation data have significantly improved the ability to discern regulatory sites from genomic sequences (6–9). These algorithms, along with experimental data culled from genome sequencing, gene ontology, expression profiling, and in vivo and in vitro protein–DNA binding assays, have become the driving force to identify key sequence motifs in the transcriptional regulatory networks of several organisms (10–12). Such a strategy of studying regulatory networks relies on finding regulatory elements for a small group of functionally related genes before assembling the entire network, with experimental evidence providing the gene sets and computational algorithms inferring with the regulatory sites. That strategy depends highly on the experiments, so limitations in experiments are propagated to the computational methods that infer motifs from the data. This limitation can be overcome by systematically analyzing sequences from multiple species at the whole-genome level without preassumption of gene coregulation (13–16). However, conventional motif-finding algorithms reach their statistical limitation for problems of such complexity. Only the most significant patterns are identified, with weak signals lost because they cannot be distinguished from random patterns (17).

We present a highly sensitive computational approach, phylonet, that systematically identifies phylogenetically conserved motifs by analyzing all of the promoter sequences of several related genomes and defines a network of regulatory sites for the organism. By comparing promoters using phylogenetic profiles (multiple sequence alignments of orthologous promoters) rather than individual sequences, together with the application of modified Karlin–Altschul statistics, we can readily distinguish biologically relevant motifs from background noise and have greatly improved the theoretical limitation for motif discovery. When applied to Saccharomyces cerevisiae promoters with Saccharomyces mikatae, Saccharomyces kudriavzevii, and Saccharomyces bayanus sequences as references (13), phylonet identified 296 statistically significant motifs with a sensitivity of >90% for known transcription factor (TF) binding sites. The specificity of the predictions appears very high because most predicted gene clusters have additional supporting evidence, such as enrichment for a specific function, in vivo binding by a known TF, and/or similar expression patterns. The predicted regulatory network overlaps significantly with our current understanding of gene regulation in yeast and predicts the existence of additional regulatory modules that await experimental tests.

Software for academic users is available from the authors upon request.

Methods

We developed a framework to identify conserved regulatory motifs and their networks from genome sequences of related species. The architecture and theoretical developments are described here, whereas some details of the algorithm components are provided in Supporting Appendix, which is published as supporting information on the PNAS web site. Briefly, the algorithm enables “motif-blast” by integrating comparative genomics information and regulatory network topology and exploring a phylogenetic profile space. Each promoter is represented by its phylogenetic profiles and queried against a database of phylogenetic profiles of all promoters in a genome. Statistical significance of motifs is determined by Karlin–Alschul statistics that are modified for profile searches. The motifs and regulatory networks discovered are evaluated with experimental evidence of gene regulation.

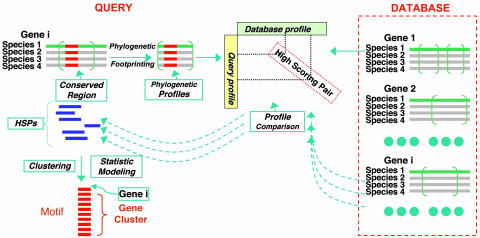
phylonet Algorithm. The goal of a motif-finding algorithm is to discover subtle similarities among sequences and align them with defined boundaries. In principle, this similarity search is no different from blast (18) but in practice is much harder because motifs are short and the signal is much weaker than the homology sought for by blast. phylonet takes advantage of two key properties of regulatory systems to increase the signal: phylogenetic conservation and network topology. The architecture of phylonet is similar to blast (Fig. 1) with sequence data divided into query (promoter of interest) and database (all promoters of a genome). Each promoter has several orthologous sequences as reference. Phylogenetic footprinting for each promoter generates multiple sequence alignments that are encoded as profiles. The choice of algorithm for phylogenetic footprinting is flexible; we use wconsensus (2) because it generates multiple ungapped suboptimal alignments from which we can extensively explore the space of phylogenetic profiles. Local alignments between the query profiles and database profiles represent potential conserved elements that are common between the query and database promoters. Because a regulatory network is predicted to have a high level topology in which each TF regulates multiple downstream targets, a functional element in the query should be found in multiple database promoters, and alignments between query profiles and different database profiles should overlap or cluster within the query promoter. Conversely, alignments that occur by chance should be sparse and not cluster. Moreover, a functional motif shared by several promoters should be identified when any of the promoters is queried, providing additional confidence for the prediction. Overlapping profile alignments are assembled into multiple profile alignments and reported as putative motifs. The cluster of promoters that contribute to the motif assembly is reported as coregulated genes. We expand the Karlin–Altschul statistics for blast to address the statistical significance of the phylogenetic profile alignments and alignment clusters.

Fig. 1.

phylonet architecture. Promoter sequences are represented as green lines, and promoters of related species are shown as gray lines. Multiple suboptimal alignments of orthologous sequences are generated and encoded as phylogenetic profiles, represented as alignments in green parentheses. The red, aligned, short bars in the query promoter alignments indicate conserved motifs. Query profiles and database profiles are compared to generate HSPs that are represented by blue bars. The HSPs are ranked by ALLR scores and clustered according to their locations relative to the query. Clustered HSPs are assembled into profile alignments, which are reported as the final motifs, and promoters form a gene cluster that contains the motif.

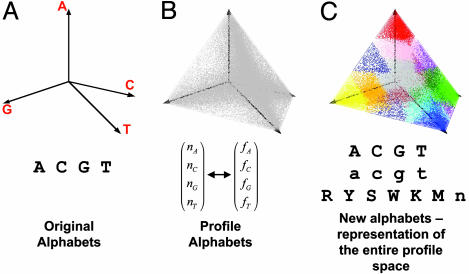
Profile Space Modeling. Whereas DNA sequences are composed of A, C, G, and T, individual positions are under functional constraints that can be captured by representing them as profiles, distributions of sequences from multiple sequence alignments. For a single position, a profile is the distribution of four nucleotides represented by frequency vectors (f_A, f_C, f_G, and f_T) or a count vector (n_A, n_C, n_G, and n_T). Much information about evolutionary conservation and nucleotide selectivity of a TF binding site can be incorporated into profiles (19). Moreover, profile search and comparison almost always guarantees better performance than sequence comparison (20). Under this framework, the alphabet of DNA becomes single position profiles: in principle, a continuous space. The difference between this alphabet and the four-letter alphabet can be conceptually viewed in Fig. 2 A and B. Fig.2A depicts a “sequence space” that contains the four disjointed points for each base. Fig. 2B depicts a “profile space” of length 1, where each point represents a profile position observed in some matrices in transfac (21). Just as two sequences can be optimally aligned by using a scoring function for aligned bases, we can optimally align two profiles by using a scoring function for aligned profile positions. We use an average log-likelihood ratio (ALLR) with a negative expected value so that we can obtain optimal alignments with a Smith–Waterman algorithm (7).

Fig. 2.

Profile space partition. A DNA profile space can be considered a four-dimensional space, with A, C, G, and T as the four axes. Here we depict such a space in three dimensions by using a hollowed tetrahedron. The four axes go from the center of the tetrahedron, which has coordinates (0, 0, 0, 0) to the four vertices of the tetrahedron, which has one of the four coordinates being 1 and the rest being 0. A profile that describes the base frequency distribution (f_A, f_C, f_G, and f_T) can be mapped to a point within the tetrahedron, with restriction Σ_{i=A.. .T} f_i = 1. (A) A, C, G, and T are mapped to the four vertices of the profile space, representing the alphabet that describes DNA sequence. (B) PWMs are obtained from the transfac database, and all positions are converted to profiles of 1 bp and mapped to the profile space. Each gray spot in the tetrahedron represents a unique profile. This space is in principle continuous, with different density at different regions. Those points represent the alphabet that describes DNA profiles. (C) The profile space is partitioned into 15 subprofile spaces according to the text. Each subprofile space is labeled with a different color. The partitions represent the reduced alphabet that describes DNA profiles.

Because phylonet performs pairwise comparisons of all promoters, an efficient search algorithm is needed. We established a partition of the profile space and developed a blast-like algorithm that has linear time and memory complexity. A proper partition of the profile space can greatly reduce the complexity of the search while maintaining the expressive power of a profile, resulting in optimal performance in motif discovery (22). Based on the similarities among all profiles, we partitioned the profile space into 15 subspaces by supervised learning (Supporting Appendix). For each subspace we elect a deputy profile and a consensus letter based on the weighted sum of all profiles in the subspace. This partition coincides with common degenerate DNA representations, but the actual boundaries are optimized based on all pairwise profile comparisons (Supporting Appendix). Two close profiles on two sides of a boundary will have a slightly reduced approximate ALLR score, but the loss in sensitivity is very small (see Results). Fig. 2C color-codes the partition of the profile space and defines the consensus letter of each subspace. The new alphabet of 15 letters (A, C, G, T, a, c, g, t, W, S, R, Y, M, K, and N) replaces the original DNA sequences with additional conservation information. Based on the weighted similarity measurements by the ALLR statistic among profiles of any two subspaces, we constructed a substitution scoring matrix (Table 1, which is published as supporting information on the PNAS web site). The ALLR matrix is a log-odds scoring system that satisfies the restrictions needed to apply Karlin–Altschul statistics (23). Therefore, we can provide precise numerical formulae for assessing the statistical significance of scores of local profile alignments.

Here we reveal two additional properties of the ALLR scoring matrix as a log-odds matrix. First, we back-calculated the target profile frequencies and estimated the optimal application range (Supporting Appendix). For primary DNA sequence, this range corresponds to ≈70–90% conservation (i.e., ≈70–90% identity in an alignment column), which coincides with the degenerate level of a typical TF motif. Second, we calculated the entropy of the matrix, which is 3.26 bits of information per aligned position (Supporting Appendix). In contrast, the blast default scoring matrix (match +5, mismatch –4) corresponds to 0.52 bits per base pair. Obtaining the 30 bits of information that are needed for a significant match among all yeast promoters requires a DNA alignment 56 bp on average, whereas it requires a profile alignment of 9 bp, making “motif blast” effective and efficient (Supporting Appendix).

Expansion of Karlin–Altschul Statistics. The distribution of ungapped local alignment scores of random profiles can be described by an extreme-value distribution (2, 24). For the comparison of random profiles of sufficient lengths M and N, the number of local alignments with score of at least S is approximately Poisson-distributed, with mean (23, 25)

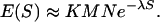[1]

λ and K can be easily calculated (Supporting Appendix). An optimal alignment score S′ approximately follows an extreme-value distribution, with

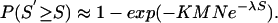[2]

Eqs. 1 and 2 follow the Karlin–Altschul method for assessing the statistical significance of molecular sequence features, except expanded for profile sequence features. This framework allows us to estimate significance of profile alignments and calculate a P value for the final motif (Supporting Appendix) (W. Gish, personal communication).

Motif blast, Clustering, and Assembly. Replacing DNA sequences with deputy profiles allows us to develop an efficient blast-like search engine. Subprofiles of a given length of the query profile serve as seeds of a designed format (Supporting Appendix). Neighborhood profiles, defined as any profile with an alignment score greater than a threshold when compared with any seed, are generated by using a branch and bound algorithm (Supporting Appendix). Seed profiles and neighborhood profiles are hashed, and the database profiles are scanned linearly to obtain word hits, i.e., subprofiles that are identical to any seed or neighborhood profile. A word hit is extended to a high-scoring pair (HSP), which is a pair of aligned subprofiles of the query and a database promoter and indicates a putative motif. A P value is calculated for each HSP based on its ALLR score. Although deputy profiles are used in the blast-like search to locate regions with a high promise of generating an HSP, the final ALLR scores are based on realigned real sequences. This design allows a profile comparison to be 1,000 times faster than a pairwise comparison of all profiles by dynamic programming, with a minimum loss of sensitivity.

A network topology predicts that most motifs regulate a number of promoters. Therefore, multiple HSPs should be identified clustering around a true regulatory element, whereas spurious HSPs should have a much lower chance of overlapping. Clustering of HSPs further increases the statistical power to distinguish a real motif from system noise. Based on the positional relationship among distinct HSPs, we identified mutually overlapping HSPs by employing a maximum clique-finding algorithm from graph theory (26). Each HSP cluster is converted to a motif whose boundaries are determined by a greedy algorithm that maximizes the total ALLR scores, obtaining the motif length automatically. The P value of the motif is estimated based on the Poisson approximation of observing a fixed number of independent events that have an upper bound P value (Supporting Appendix). Each predicted motif inherently links a group of promoters (presumably coregulated) that share this motif.

To provide an empirical estimate of statistical significance and to further validate our theory, we shuffled the profiles of the query and the database and maintained the primary sequence identity levels, lengths, and conservation blocks. This shuffling process approximates a random profile model and estimates background parameters.

Biological Function Enrichment of Predicted Gene Clusters. To determine functional enrichment, we obtained yeast gene annotation from the Gene Ontology Database. We calculated the probability of enrichment of a function within a predicted cluster by using the cumulative hypergeometric distribution (27). To determine enrichment for targets of certain TFs, we obtained genome-wide location data from Harbison et al. (10) and calculated P values for overlapping clusters. To determine the enrichment of coexpressed genes, we obtained expression data for the following conditions: cell cycle (28), meiosis (29), methyl methanesulfonate-induced damage (30), sporulation (31), stress response (32), DNA damage (33), pheromone response (34), and mitochondrial dysfunction (35). For each cluster, we calculated the expression coherence and the P value according to Cliften et al. (13). The P values are not corrected for multiple hypothesis testing.

Results

Predicting Yeast Motifs at the Whole-Genome Level. To determine the sensitivity and power of phylonet to identify regulatory motifs and build regulatory networks, we ran it on yeast sequence data. We obtained 3,524 S. cerevisiae intergenic sequences with orthologous counterparts in S. mikatae, S. kudriavzevii, and S. bayanus (13) to construct a database. Each sequence group was queried, and up to the 10 most significant motifs were further analyzed.

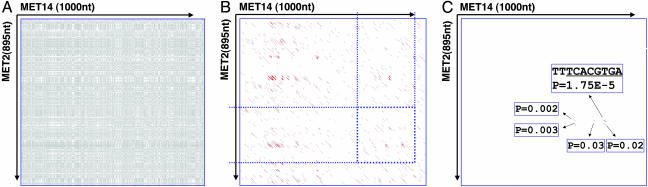
The Met-14 promoter provides an example of the advantage of using phylogenetic profiles in combination with our statistical framework. Met-14 (YKL001C) encodes adenylylsulfate kinase involved in sulfate assimilation and sulfur amino acid biosynthesis and is regulated by a protein complex of Cbf1, Met-4, and Met-28. Cbf1, a basic helix–loop–helix TF, has a documented site (NRTCACRTGA, transfac). Met-2, which encodes l-homoserine-O-acetyltransferase, is also involved in sulfur amino acid biosynthesis and is coregulated by the same complex. Met-14 and Met-2 promoters should share a regulatory motif, but no such element is immediately visible in the two sequences, as illustrated by a dot plot, with stretches of similarity between them appearing as diagonal strings of dots (Fig. 3A). Given a proper scoring scheme for match and mismatch, such diagonals or ungapped local alignments can be identified. We show local alignments of the forward strands that are >6 bp as red lines in Fig. 3B, most of which clearly occur by chance. The sheer number of alignments highlights the difficulty in distinguishing a functional motif from the background. The longest alignment of 37 bp merely represents two AT-rich regions and does not contain the correct site. Thus, ranking alignments by their length/score can be misleading, which is true even if we apply common phylogenetic shadowing procedures. In Fig. 3B, the blue dotted lines define conserved regions identified by comparing orthologous promoters from four species. The search space is reduced; but the number of alignments is still too large to accurately identify the motif.

Fig. 3.

Power of profile comparison. Compared with sequence comparisons, profile comparison greatly reduces system noise when phylogenetic data are incorporated, which is especially helpful for finding weak similarities. (A) A dot plot between the Met-14 promoter and Met-2 promoter. A gray dot indicates an identical base. (B) Short sequence similarities between the Met-14 promoter and Met-2 promoter. Each red line in the diagonal represents a local alignment between the two that is >6 bp. The region between the blue dotted lines in Met-14 and Met-2 promoters are conserved across four yeast species. (C) Comparison between phylogenetic profiles of the Met-14 promoter and Met-2 promoter. Each red line in the diagonal represents a local alignment between the two profiles that has a P value of <0.1. For the most statistically significant alignment, the corresponding site in the Met-14 promoter is shown.

Our approach gains its power by comparison of phylogenetic profiles that greatly reduces background noise and enables us to identify real signals. Fig. 3C shows the local alignments from a phylonet analysis of the profiles of Met-14 and Met-2, with P < 0.1 as red lines. Only five alignments satisfy this criterion; the best (P = 1.75 × 10^–5) represents site TTTCACGTGA of the Met-14 promoter. This site agrees with Cbf1's motif and is statistically significant.

phylonet compares the Met-14 promoter to other promoters in a similar fashion, and HSPs of profile alignments are clustered and assembled. As expected, these HSPs show a clustering pattern (Fig. 5A, which is published as supporting information on the PNAS web site), indicating a highly organized network topology, unlike scattered HSPs resulting from comparing shuffled profiles (Fig. 5B). The best motif in Met-14 exhibits the consensus CACGTGAtca, with a P value of 6.76 × 10^–49 and is similar to the Cbf1 motif. phylonet identifies 124 promoters sharing this element. This gene cluster overlaps known targets of Cbf1 (10) with a P value of 5.95 × 10^–23. The functional annotations of these genes are enriched for sulfate assimilation (P < 1.87 × 10^–9) and methionine metabolism (P < 8.85 × 10^–6). In contrast, the best motif identified by a shuffled run has a P value of 0.06, and the target genes display no significant overlap with genome-wide location data or enrichment for any specific function. Thus, using only promoter sequences phylonet can pinpoint known TF binding sites and identify a large cohort of putatively coregulated genes, many with similar functional properties.

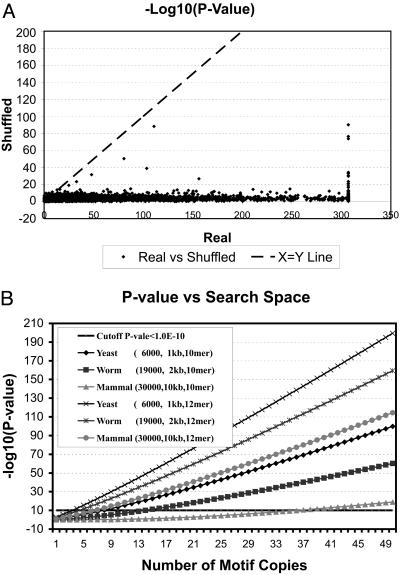
Next we summarize the result of applying phylonet to 3,524 promoters. For each query, we also ran shuffling three times to provide a background control. With the cut-off P value set at 1.0 × 10^–5, we were able to predict at least one motif for 3,315 (94%) of the 3,524 queries. The log-transformed P value of the best motif of each promoter is plotted against the log-transformed P value of the best motif among three shuffled runs (Fig. 4A). With very few exceptions, real promoters generate many more statistically significant motifs than shuffled promoters. In addition, motifs from shuffled promoters nearly always have P values close to 1. These data directly validate our statistical framework, because in random profile space without a network structure we find only what is expected by chance.

Fig. 4.

Statistical power of phylonet.(A) Comparing motifs predicted based on real promoters versus shuffled promoters. For 3,524 yeast promoters, phylonet was run once with default parameters and three times with the “shuffling” mode. The P values of the best motifs predicted based on real promoters are plotted against P values of the best motif of three independent shuffling runs. All P values are converted to –log₁₀(p). The smallest number in our programming system is 1.0 × 10^–308; therefore, any P value smaller than that is recorded as 1.0 × 10^–308. (B) A motif contains an arbitrary amount of information, such as the degeneracy level, length, and number of copies in a genome. The probability of finding a motif with a particular amount of information varies when the search space changes. The bigger the search space is, the less statistically significant a motif is. We estimated for yeast (6,000 genes, 1-kb promoter), worm (19,000 genes, 2-kb promoter), and human (30,000 genes, 10-kb promoter) the significance level of discovering a motif of 10 or 12 bp with various numbers of copies in the genome. The x axis is the number of copies, and the y axis is the significance level. The assumptions are (i) that the motifs have on average 20–30% degeneracy and (ii) that it is possible to obtain reference genomes for the genome of interest with phylogenetic branch lengths similar to the yeast genomes in this study.

Our algorithm is naturally reciprocal, because querying any promoter from a cluster of coregulated promoters usually recovers the same motif and gene cluster. Thus, we use this information to consolidate predictions and require that the same motif be predicted using every promoter from its final regulated cluster. Predicted motifs identify 296 nonredundant motifs/clusters and define a total of 32,026 motif–target relationships (Table 2, which is published as supporting information on the PNAS web site). Interestingly, the sizes of these 296 clusters closely fit the power-law distribution, which reveals the scale-free nature of the regulatory network we discovered without prior knowledge of gene coregulation (Fig. 6, which is published as supporting information on the PNAS web site) and suggests that, at least based on size distribution, the predicted network is nearly complete.

Validation of Predicted Motifs and Gene Clusters. We first determined the number of known TF motifs we had identified. We combined position-specific weight matrices (PWMs) of yeast TFs from transfac and carefully trained matrices from Harbison et al. (10) and obtained a total of 167 PWMs for 136 TFs (some TFs have multiple sources). Among the 167 PWMs, 153 (corresponding to 125 TFs) show significant similarity to one of 111 of the 296 motifs predicted by phylonet (Table 3, which is published as supporting information on the PNAS web site). Thus, we identified >90% of the known TF PWMs.

The 185 phylonet motifs that do not identify known motifs may represent TFs whose specificities have not been determined or previously uncharacterized regulatory motifs. To evaluate the biological significance of previously uncharacterized motifs, we ran the gene clusters defined by each through the following three tests. First, we asked whether the gene cluster is enriched for a biological function. Second, we determined whether our gene clusters exhibit significant overlap with targets of TFs identified by genome-wide location analysis. Third, we asked whether genes in a predicted cluster exhibit similar expression patterns. Using a P value of <1.0 × 10^–4 as a stringency cutoff, we determined that of the 185 previously uncharacterized clusters 45 are enriched for at least one biological function, 22 display significant overlap with targets of individual TFs, and 35 exhibit similar expression patterns in at least one experimental condition (Table 4, which is published as supporting information on the PNAS web site).

Taken together, this evidence supports the functional significance of 87 of the 185 motif–gene cluster relationships. We believe that this is an underestimation of the specificity, because the experimental data are limited. We calculated the specificity value by using different P value cutoffs for each type of biological information (Fig. 7A, which is published as supporting information on the PNAS web site). We also calculated similar statistics for the 296 motif–gene clusters (Fig. 7B). Interestingly, the specificities calculated with or without known motifs are very similar: ≈50% (47% for predictions and 54% for known motifs at P < 1.0 × 10^–4) of the motif–gene clusters have at least one type of support (Fig. 7C), indicating that the predicted motifs have levels of experimental support similar to the known ones (Table 4).

Although identification of the motif of a TF is difficult, the identification of physiological targets of the TF is equally challenging. The power of phylonet derives from its ability to identify motifs and from its ability to identify the most likely targets of these motifs. The following example illustrates the quality of the phylonet motif–targets prediction and its relationship to conventional computational and experimental approaches. Motif YDR097C.1 has consensus ACGCGTC, and phylonet identifies 142 promoters with this element. This motif matches the MCB box used by TF Mbp1 to regulate cell cycle. Simply taking the PWM and scanning the genome reveals 262 promoters that contain high-scoring sites. Harbison et al. (10) identified 85 promoters bound by Mbp1 in rich media. So we have three sets of potential Mbp1 targets: phylonet prediction (set A); genome-wide scan prediction, which represents a conventional computational approach (set B); and genome-wide location assay prediction, which represents an experimental approach (set C). To obtain a measure of the relative accuracy of the three approaches, we first asked how well each approach enriched for genes involved in cell cycle and DNA processing, the known function of Mbp1. In this test, all three sets are enriched for this function but to different degrees. Set A enrichment (P < 4.56 ×10^–12) is much more statistically significant than set B (P < 4.14 × 10^–9) or set C (P < 8.07 × 10^–6) (Fig. 8A, which is published as supporting information on the PNAS web site). Analysis of the expression coherence of genes in each group through the cell cycle also identified set A as the most robust prediction with an expression coherence value of 0.2311 and a P value of 3.92 × 10^–5 relative to set B (expression coherence 0.1579, P < 0.0077) and set C (expression coherence 0.1414, P < 0.022) (Fig. 8 B–D).

Another example is discussed in Supporting Appendix (see also Fig. 9, which is published as supporting information on the PNAS web site). phylonet's superior performance over the computational scan and genome-wide location analysis in finding targets of regulatory motifs holds the potential of associating functions and TFs to predicted motifs when experimental data are integrated.

Improvement Over Previous Efforts. As a final test we asked how much improvement we have achieved compared with two previous studies that identified regulatory motifs for yeast at the whole-genome level by using comparative analyses. From the analysis of four to six yeast genomes Kellis et al. (14) and Cliften et al. (13) predicted 71 and 92 regulatory motifs, respectively. Both collections identified many known TF motifs as well as many predicted motifs. However, the two collections overlap by <50%, demonstrating that neither collection reached saturation: 30 (42%) motifs in the Kellis set match a motif in the Cliften set, whereas 43 (47%) in the Cliften set match the Kellis prediction. Despite using the sequences from only four yeast species from Cliften et al., phylonet not only identified over twice as many predictions as either previous study, it also identified 86% (n = 61) of the Kellis motifs and 92% (n = 85) of the Cliften motifs, including all motifs supported by both studies. These comparisons highlight phylonet's ability to extract substantially more information from comparative analysis than previous methods (Table 5, which is published as supporting information on the PNAS web site).

Discussion

We have developed an algorithm for identifying conserved regulatory motifs of an organism based on genome sequences of related species, without additional knowledge of coregulation. When applied to yeast genomes, our algorithm predicted 296 regulatory motifs and 32,026 motif–target relationships. Our predicted motifs cover >90% of known yeast TF binding motifs and motifs predicted by other means using similar data. In addition, our data also include a large number of predicted regulatory relationships supported by experimental data to essentially the same degree as the known relationships.

Our validation tests provide strong support that the phylonet predictions contain a wealth of biologically significant information that can be used in a multitude of ways to explore distinct issues of gene regulation. First, >100 predicted motifs can be confidently assigned to known TFs, allowing us to assemble a regulatory network. Second, previously uncharacterized motifs identify gene clusters enriched for specific biological functions, providing a powerful tool to associate functions and TFs to the predicted motifs. Third, motifs and gene clusters that do not link to known functions hold the promise to provide insight into gene regulation: predicted motifs likely identify the binding sites of poorly characterized TFs, and previously unknown gene clusters may control poorly studied cellular functions or respond to poorly studied environmental perturbation. Finally, interaction between TFs is an important mode of regulation. Such data can be readily deduced from our predictions: among 43,660 possible pairs between our predicted 296 gene clusters, 2,185 pairs overlap significantly (P < 1.0 × 10^–4), each of which likely identifies a set of genes controlled by two TFs acting in concert. In support of this conclusion, gene annotation data indicate that 454 of these clusters are enriched for a specific function, whereas chromatin immunoprecipitation data identify 248 enriched for specific TF targets. In addition, expression profiling data reveal 398 clusters with coherent expression pattern.

Although the predictions clearly require experimental tests, they highlight the utility of phylonet to synergize with traditional experimental approaches to decipher gene regulatory networks on a genome-wide level. In the future, it will be exciting to see the extent to which experimental approaches use computational-based whole-genome predictions of regulatory interactions to provide definitive links into the known regulatory cascade and insight into the integration of distinct regulatory modules.

Our study also has a profound effect on the statistical limitation on solving motif-finding problems. The presented data reveal that, by exploring phylogenetic data and network topology, we can greatly reduce the system noise and strengthen the biological signals in a large sequence space. It is important to ask whether the resolving power will transfer from yeast to genomes of worm, fly, and human with their significantly greater size and regulatory complexity. Because the motif-finding process is not limited by preassumptions of gene regulation, our statistical framework allows us to estimate the power as it relates to increasing genome size. Assuming the presence of reference genomes with a similar phylogenetic relationship as the yeast genomes here (36), we estimated the amount of information a motif must contain (e.g., width, degeneracy, or number of occurrences in the genome) to be discovered at a certain statistical stringency. In Fig. 4B, we plotted such estimations for discovering motifs of 10 and 12 bp, with typical levels of degeneracy, in genomes of yeast, worm, and human. The analysis suggests that we should be able to identify a human motif of 12 bp at a significance level of P <1.0 × 10^–10 if the motif has at least eight conserved copies in the genome. Therefore, we expect that our algorithm should be applicable to much larger genomes without encountering the statistical limitations of current methods.