Oxygen isotopes indicate most intracellular water in log-phase Escherichia coli is derived from metabolism

Abstract

The transport of water into and out of unicellular organisms is a seemingly simple process in which water diffuses either through pores or directly across the membrane. Because of the rates at which water can theoretically diffuse, it is generally accepted that intracellular water is indistinguishable from extracellular water. Using stable isotope ratio mass spectrometry, we directly tested this assumption. Here we demonstrate that under active growth, up to 70% of the intracellular water in log-phase Escherichia coli cells was actually generated during metabolism and was isotopically distinct from extracellular water. The contribution of metabolism to intracellular water was substantially less in stationary-phase or quiescent cells.

Stable isotopes are commonly used as a tool for probing complex biological and environmental processes. For instance, at the cellular level, hydrogen, carbon, nitrogen, and oxygen isotopes are often used to dissect reaction mechanisms and as tracers to follow metabolic pathways. On a more global level, these same isotopes are used in ecological studies to probe the relationship among environmental nutrients, water, and organic molecules and biological tissues. Information from these studies can be used to deduce information about the growth environment of an organism or source of a sample from its isotope ratios (1–3). A common approach to environmental reconstruction by geochemists is the analysis of isotope ratios of biomarkers, resistant biogenic molecules, to infer the conditions under which the metabolites were formed (4). Because the hydrogen and oxygen isotope ratios of precipitation are strongly influenced by environmental variables, these elements are of particular utility in both paleoclimate and forensic studies.

Studies of isotopic relationships between growth water and organic components of organisms are often carried out under laboratory conditions to determine fractionation factors between organism and environment. The results from these studies are then used to infer information about the growth environment that led to the production of the same compounds isolated from environmental samples. Two implicit assumptions are nearly always made during environmental reconstruction. The first is that intracellular water is isotopically identical to extracellular water (5, 6). This idea is based on the notion that water inside of a cell should be in rapid equilibrium with water outside of the cell. The second assumption is that the isotopic fractionations determined from cellular studies performed in the laboratory will be equivalent to those ratios measured in the natural environment.

We recently questioned the validity of these two common assumptions when studying the biosynthesis of heme O. When Escherichia coli cells were grown in the laboratory in 2× LB prepared with 95% H¹⁸₂O, ≈40% of the heme O molecules contained a labeled oxygen atom in the 17-hydroxyethylfarnesyl moiety (7), despite the fact that this oxygen atom is known to be derived from water (8). Thus, the isotope ratio of the heme O metabolite did not match what would be predicted from the known isotope ratio of the growth medium water. Based on these data, we surmised that much of the water inside of the rapidly dividing E. coli cells must have been isotopically distinct from the water in the growth medium.

Here we demonstrate that ≈70% of the intracellular water in rapidly dividing E. coli cells grown in 2× LB is generated during metabolism. Furthermore, we demonstrate that the extent to which intracellular water is isotopically distinct from extracellular water is significantly influenced by the metabolic state of the cell. These results will have a profound impact on both biochemistry and environmental reconstruction data using oxygen and hydrogen isotopes, because they demonstrate that intracellular water is not necessarily isotopically identical to extracellular water, and that isotope ratios obtained from heterotrophic organisms grown under optimal conditions in the laboratory may very well be different from ratios obtained from organisms grown in natural environments.

Materials and Methods

Cultures. E. coli BL21 (DE3) cultures were grown in 2× Miller LB broth (EMD Chemicals, Gibbstown, NJ) at 37°C with shaking at 225 rpm. The culture volume was 1/10 the flask volume. The 2× LB contained 20 g of tryptone, 10 g of yeast extract, and 20 g of NaCl per liter and had an osmolality of 838 milliosmolar/kg, as measured on a Wescor (Logan, UT) 5500 vapor pressure osmometer. Batches of LB were made with isotopically varying water.

To determine the optical density readings associated with mid-log phase, we monitored growth of cultures in 2× LB, taking regular absorbance measurements at 600 nm on a Hach Odyssey (Loveland, CO) spectrophotometer. Mid-log phase was associated with OD₆₀₀ readings of 0.8–1.0 and a doubling time of ≈30 min. Stationary-phase cells were harvested ≈12 h after inoculation, when the OD₆₀₀ of a 1:10 dilution of the culture had been ≈0.7 for 3 h. Cell cakes were harvested by pouring the culture through a 0.2-μm NL 16 filter (Schleicher & Schuell) under house vacuum. As soon as the cell cake appeared dry, it was either harvested by scraping it from the membrane with a razor blade or washed with 1 ml of 2× LB made with isotopically varying water and then harvested. The cell mass was transferred immediately to a vial, sealed, and frozen. Samples of spent medium and wash solutions were collected and frozen at the same time.

Water was extracted cryogenically from the cell pellets and spent medium samples using a modification of earlier methods (9, 10). Vials containing frozen cell pellets or medium were placed inside a heavy-walled Pyrex (Fisher Scientific) test tube connected to a cold finger trap. The Pyrex tube and cold finger assembly was connected to a vacuum line but kept isolated from the vacuum pump via a valve. The test tube containing the sample vial was then submerged in liquid nitrogen for several minutes, after which the valve to the vacuum pump was opened and the assembly evacuated. The test tube and cold finger were then reisolated from the vacuum pump and checked for constant vacuum with an in-line vacuum gauge. Water was then completely distilled from the sample and collected in the cold finger under static vacuum by placing the Pyrex tube containing the sample vial into a boiling water bath for ≈1 h. Once distillation was complete, the distilled water was placed in crimp-top vials, sealed, and stored in a cold room before stable isotope ratio analysis.

Stable Isotope Ratio Measurements. Stable isotope ratios are measured relative to internationally recognized standards. We calibrate laboratory standards to the international standards and then include the laboratory standards as internal standards in every run. Stable isotope contents are expressed in “delta” notation as δ values in parts per thousand (‰), where δ‰ = (R_A/R_Std – 1)·1,000‰, and R_A and R_Std are the molar ratios of the rare to abundant isotope (e.g., ¹⁸O/¹⁶O) in the sample and the standard. The standard used for both oxygen and hydrogen is Vienna standard mean ocean water (11).

Oxygen stable isotope ratios were determined on a ThermoFinnegan-MAT Delta Plus XL isotope ratio mass spectrometer (Bremen, Germany) equipped with a Thermo Chemical Elemental Analyzer (ThermoFinnegan-MAT) and a GC-PAL autosampler (CTC Analytics, Zwingen, Switzerland) (12). Injection volume was 0.5 μl. Water samples were analyzed in duplicate, and the results were averaged. The average standard deviation of repeated measurements of water standards was 0.2‰.

Results

Cellular Water Can Be Isotopically Distinct from Growth Medium Water. Water molecules can enter a cell via diffusion from the culture medium water or be generated during metabolic reactions. If an isotopic gradient could be maintained during harvesting of a cake of cells on a filter, then water extracted from the cell cake could be modeled as a two-component mixture in which

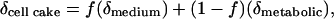[1]

where δ_cell cake, δ_medium, and δ_metabolic are the oxygen isotope ratios of the water extracted from the cell cake and the culture medium and the metabolic water, respectively, and f is the fraction of the cell cake water that is identical to the culture medium water. If δ_medium is manipulated and δ_{cell cake} measured, Eq. 1 becomes the equation of a straight line where the slope is equal to f.

We grew four cultures of E. coli to mid-log phase in 2× LB medium made with isotopically varying water and harvested the cells on filters. The cell cakes were then scraped from the filters, sealed in vials, and frozen. Samples of the spent medium were also collected. Water was extracted from both the cell cakes and the spent medium and the oxygen isotope ratios determined. This experiment was conducted five times.

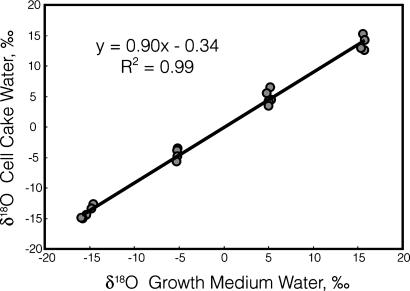
The slopes of δ_{cell cake} versus δ_medium values obtained in the five experiments were not significantly different (F = 1.03, where F_0.05 = 3.63) (13), and the data from the five experiments were therefore combined (Fig. 1). The slope of the regression line of the pooled data are 0.90 (Table 1). Thus, the water extracted from the cell cakes was isotopically distinct from the growth medium water. One way in which the cell cake water could become different from the growth medium water would be if significant evaporation occurred as the cells were being collected on the filters, because evaporation generally increases the isotope ratios of the residual water (14–16). Our data are not consistent with evaporative enrichment, however, because the cell cake water samples extracted from cells grown in media made with isotopically heavy water were depleted when compared with the medium water. This difference is unlikely to be accounted for by evaporation and is instead more consistent with the two-component mixing model of Eq. 1. The slope of 0.90 indicates that ≈10% of the oxygen atoms extracted in the cell cake water was isotopically distinct from the growth medium water.

Fig. 1.

Regression of the oxygen isotope ratio of extracted cell cake water versus that of growth medium water. Data are from five experiments in which cells were grown in 2× LB and harvested at mid-log phase. The standard errors of the slope and intercept are 0.019 and 0.21, respectively. Error bars representing the standard error of measurement for each data point are concealed within the symbols on the graph.

Table 1. Regression statistics of extracted cell cake water versus growth medium water for cells harvested under different conditions.

Temperature and growth stage at time of harvest	Slope of regression	R2 value of regression	Standard error of slope	Number of experiments (four cultures per experiment)	P value at which the slope is different from the 37°C log-phase experiments*
37°C, log phase	0.90	0.99	0.019	5	—
37°C, stationary phase	0.96	0.99	0.011	2	0.01†
6°C, log phase	0.98	0.99	0.015	1	0.05‡

^*Confidence level determined in an F test (13).

^†F = 8.38, F_0.01 = 7.88.

^‡F = 7.60, F_0.05 = 4.38.

The Presence of Isotopically Distinct Water Is Correlated with Metabolic Activity. To test whether this isotopically distinct water was generated during metabolism, two experiments were performed in which water was extracted from cells that were less metabolically active than cells harvested in log phase. Our prediction was that water from less metabolically active cells would have a lower percentage of oxygen generated from metabolism, and that the slopes of the cell cake versus medium graphs would therefore be higher than 0.90. In the first test, we harvested cells at stationary phase (after ≈12 h of growth). The slopes of the regression lines from the two experiments were each 0.96 (Table 1). A statistical comparison of the pooled stationary-phase experiments (Table 1) to the pooled data from the log-phase experiments showed that the slopes were significantly different.

In the second test, we grew cultures to mid-log phase at 37°C as before but then split each culture into two equal parts. One part was harvested immediately, whereas the second part was transferred to a chilled flask and put on a shaker at 6°C for 90 min before harvesting. The optical density of the chilled cultures only increased from 1.08 to 1.12 during this time. The slope of the regression line of water extracted from the 37°C cells versus medium water was 0.90, confirming that the relationship between intracellular water and growth water in this experiment was the same as in the five log-phase experiments described above. The slope of the regression line of the 6°C cell cake water versus medium water, however, was 0.98, significantly different from the 37°C log-phase data (Table 1). Thus, when cells are chilled before harvesting, only 2% of the oxygen atoms of the total cell cake water are isotopically distinct from the medium.

The results from both of these tests are consistent with our hypothesis that some of the water extracted from the cell cakes was a product of cellular metabolism. In both cases, slowing the metabolic rate of the culture, either by allowing the cultures to go to stationary phase or by chilling the cells, resulted in a smaller contribution of metabolic water to the total cell cake water. This reduction was reflected in the larger slopes of the cell cake water versus medium water relationships.

Approximately 70% of Intracellular Water in Log-Phase E. coli Cells Is a Product of Metabolism. What percentage of the intracellular water is derived from metabolism? Our data indicate that 10% of the total water extracted from log-phase cells was generated by metabolism, but that total pool of water was itself a mixture of extracellular and intracellular water. To determine what percentage of the intracellular water was metabolic water, we first needed to determine what percentage of the total cell cake water was intracellular.

The relationship between the isotope ratios of the total cell cake water, extracellular water, and intracellular water can be expressed as follows:

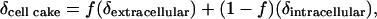[2]

where f is the fraction of the cell cake water that is extracellular water, and δ_{extracellular} and δ_{intracellular} are the oxygen isotope ratios of the extracellular and intracellular water. If δ_{extracellular} is manipulated and δ_{cell cake} measured, Eq. 2 becomes the equation of a straight line where the slope is equal to f.

We therefore grew a culture of E. coli to mid-log phase in 2× LB, split the culture into four aliquots, and immediately harvested them on separate filters. The cell cakes were then washed with fresh 2× LB made with isotopically distinct water. This washing procedure replaced the extracellular water in the cake, and the isotope ratio of the water in the 2× LB used to wash the cell cakes (δ_{wash solution}) was therefore equal to δ_{extracellular} in Eq. 2. We extracted water from the washed cell cakes and the wash solutions, measured their δ¹⁸O values, and regressed the cell cake water values onto the wash water (Table 2). This experiment was conducted four times, varying the isotopic composition of the growth medium water. An F test showed that the slopes of the regression lines were not significantly different. The average slope was 0.86 (Table 2), indicating that 14% of the total cell cake water was intracellular.

Table 2. Regression statistics of extracted cell cake water versus wash water.

δ18O of growth medium water, ‰	Slope of extracted cell water versus wash water	R2 of regression	y intercept value†	Calculated δ18O of intracellular water, ‰*†
-15.2	0.81	0.99	-1.2	-6.32
-4.9	0.85	0.99	-0.77	-5.13
5.5	0.93	0.99	-0.04	-0.55
16.1	0.86	0.99	+0.32	2.26
	Average = 0.86‡
	Standard error = 0.025

^*The δ¹⁸O value of intracellular water = (y intercept)/(1 - slope). Intracellular water is itself a combination of growth medium water and intracellular water as described by Eq. 3.

^†Average and standard error are not presented, because the y intercept values and the δ¹⁸O values of the intracellular water are expected to be different as a result of the different δ¹⁸O values of the growth medium waters.

^‡These slopes are not statistically different (F = 1.59; F_0.05 = 4.35) (13).

The fraction of intracellular water derived from metabolism is equal to the fraction of total cell cake water derived from metabolism (0.10, Fig. 1) divided by the fraction of total cell cake water that is intracellular (0.14, Table 2). Therefore, ≈71% of the oxygen atoms in intracellular water extracted from log-phase cell cakes originated from metabolism. The total error in this estimation is 19% when the standard error of the two slopes (0.019 for metabolic water and 0.025 for intracellular water) are used in a propagation of errors calculation (17). A 71% estimate of the oxygen atoms in intracellular water being derived from metabolism is consistent with and explains our previous in vivo heme O labeling results (7).

We also performed two wash experiments in which the cells were allowed to go to stationary phase before harvesting. A comparison of these data to that from the log-phase harvests showed no significant difference in slopes (F = 0.08, F_0.05 = 4.84). Therefore, the result reported above in which the water extracted from stationary-phase cell cakes had a smaller contribution from metabolic water was not a consequence of a greater contribution of extracellular water to the cell cake water.

The δ¹⁸O value of metabolic water can be estimated by two independent methods by using either the data from the growth experiments or the data from the washing experiments. According to Eq. 1, the y intercept term is equal to (1–f)δ_metabolic, where f is the slope of the line, and δ_metabolic is the oxygen isotope ratio of the metabolic water. In Fig. 1, the y intercept value from the growth experiments is –0.34 and the slope is 0.90, yielding a predicted oxygen isotope ratio for the metabolic water of –3.4‰.

Estimating the δ¹⁸O value of metabolic water from the washing experiment data requires that we first calculate the δ¹⁸O value of intracellular water. In Eq. 2, the y intercept from the washing experiments is equal to (1–f)(δ_{intracellular}), where f is the slope of the line. Thus, dividing the intercept value by (1–f) yields an estimate of the δ¹⁸O value of the intracellular water (Table 2). According to our model, the isotope ratio of the intracellular water can be represented as:

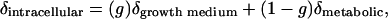[3]

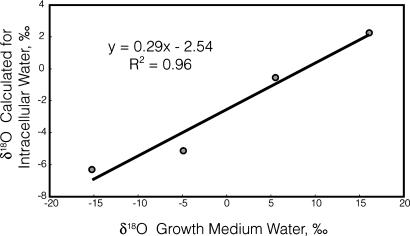
where g is the fraction of intracellular water that originated from the growth medium. A plot of the calculated δ_{intracellular} values versus the measured δ_{growth medium} values yielded a regression slope of 0.29, representing g (Fig. 2). The δ¹⁸O value of the metabolic water is equal to the y intercept value divided by (1–g). This value is –3.6‰, almost identical to the value estimated from the data in Fig. 1 but derived by using independent data.

Fig. 2.

Regression of the calculated value of the oxygen isotope ratio of intracellular water as determined from the washing experiments versus the oxygen isotope ratio of the growth medium water. The slope of 0.29 indicates that 71% of the intracellular water was generated during metabolism, in agreement with the value calculated independently using the regression in Fig. 1.

Significantly, the data from the washing experiments also support the previous estimate of the fraction of intracellular water derived from metabolism. From Eq. 3, the fraction of intracellular water generated from metabolism is equal to (1–g), or 0.71. This estimation that 71% of intracellular water is derived from metabolism is identical to that reached using the slope of the regression in Fig. 1.

Discussion

The notion that up to 70% of intracellular water in E. coli can be derived from metabolism and be isotopically distinct from extracellular water is perhaps surprising. Despite the fact that biological membranes are generally impermeable to ionic compounds, the small size of water molecules allows them to diffuse passively across cellular membranes, moving through the defects or vacancies of the bilayer as the lipids diffuse laterally through the membrane (18–20).

Until relatively recently, it was generally assumed that passive diffusion across cell membranes was the primary mechanism by which water was transported into and out of the cell (21). With the discovery of aquaporins, however, it became clear the water could also be transported through channels in the membrane (22, 23), and it now appears that these pores are critical for the rapid transport of large quantities of water during times of osmotic stress (21, 22). The gene encoding one of these channel-forming proteins, ApqZ, is known to be down-regulated considerably under high-salt conditions (22), although expression was observed under osmolarities matching those used in these experiments.

Given these two different mechanisms by which water can equilibrate across biological membranes, the implicit assumption often made during environmental reconstruction by ecologists, geochemists, and others that intracellular water is isotopically identical to extracellular water is understandable. However, rapidly dividing cells are constantly undergoing numerous metabolic processes, many of which generate water or exchangeable oxygen atoms (24). In addition, a number of studies have demonstrated that the equilibration of water in plants and animals is a time-dependent process (14, 25, 26), and there is evidence for the existence of different pools of water in plants (27, 28), one of which might be an intracellular pool. Thus, previous data exist suggesting that perhaps this assumption is not necessarily correct.

The data presented in this manuscript provide direct evidence that intracellular water in E. coli can be isotopically distinct from extracellular water. During log-phase growth in 2× LB, ≈70% of the intracellular water in E. coli is isotopically distinct from the medium water, and this intracellular water has an oxygen isotope ratio of approximately –3.5‰. Two lines of evidence support the conclusion that this isotopically distinct water is the result of metabolism. In separate experiments, the metabolic activity of the cells was slowed considerably before harvesting. In the first experiment, cells were harvested during stationary phase, whereas in the second experiment, log-phase cells were cooled to 6°C for 90 min before harvesting. In both cases, a significantly higher fraction of the intracellular water was isotopically identical to the medium water.

These results have clear implications for those engaged in determining fractionations between environmental water and organic components of cells, as in studies for environmental reconstruction. Intracellular and extracellular water are not necessarily isotopically equivalent, and the degree to which they differ appears to depend on the metabolic state of the organism. Thus, controls performed in the laboratory under ideal growth conditions may not be relevant to results obtained in the field when the organisms are in their natural environment.

Data obtained by Sessions et al. (29) provide evidence that a sizeable contribution of metabolic activity to intracellular water may not be a phenomenon confined to rapidly growing organisms such as E. coli in rich laboratory media. Using the heterotrophic methylotroph Methylococcus capsulatus, they traced the origins of hydrogen atoms in a variety of cellular lipids to either methane or water, the only two possible sources of hydrogen in their culture system. They found that ≈30% of the hydrogen atoms in a variety of lipids originated from methane. Considering the different biochemical pathways used to synthesize the lipids, the most parsimonious explanation for their observations was that the methane hydrogen atoms were first oxidized to water and then used in lipid biosynthesis. The authors (29) included a mathematical model of substrate (methane and molecular oxygen) diffusion into the cells and of diffusion of water into and out of cells to argue that this explanation was feasible. If their interpretation is correct, then fully 30% of the intracellular water in this slow-growing organism may have been derived from metabolic activity.

Our results also offer an explanation for observations of changes in the magnitude of isotopic fractionation between culture water and specific cellular products measured either at different growth stages or when the organism in question was growing at different rates. For example, Valentine et al. (30) found that the fractionation of hydrogen between source water and methane by a methanogenic bacterium was correlated with both temperature and metabolic rate. Similarly, Sessions et al. (29) reported a consistent shift of 13–26‰ in the hydrogen isotope ratios of fatty acids, squalene, and sterols isolated from log- and stationary-phase cultures of M. capsulatus (29). Although arguments can be made that the cells are using alternate biosynthetic enzymes or hydrogen donors to produce the changing isotope ratios, another possibility is that the change in isotope ratio of the metabolite merely reflects a difference in the isotope ratio of intracellular water used in its biosynthesis. This possibility was raised by Sessions et al. (29), who proposed that the rate of cellular methane oxidation would determine the fraction of intracellular water hydrogen atoms derived from the substrate and would consequently affect the hydrogen isotope ratio of lipids being synthesized. Our data provide direct evidence that the oxygen isotope ratio of intracellular water is indeed linked to metabolic activity. It is logical that changes in both the hydrogen and oxygen isotope ratios of intracellular water would be reflected in the isotope ratios of organic components that use water as a donor of hydrogen or oxygen atoms, and we therefore suggest that future studies of fractionation between growth water and organic molecules examine this possibility.

Conclusion

The data presented here indicate that a substantial fraction of intracellular water extracted from log-phase E. coli cell cakes produced in 2× LB is metabolic water. At this growth stage, ≈70% of the intracellular water is generated via metabolism, and two different approaches independently estimate that the δ¹⁸O value of the metabolic water is approximately –3.5‰. Intracellular water from stationary-phase and quiescent cells showed a substantially smaller contribution from metabolism.