Abstract
The energy landscape of proteins is thought to have an intricate, corrugated structure. Such roughness should have important consequences on the folding and binding kinetics of proteins, as well as on their equilibrium fluctuations. So far, no direct measurement of protein energy landscape roughness has been made. Here, we combined a recent theory with single-molecule dynamic force spectroscopy experiments to extract the overall energy scale of roughness ɛ for a complex consisting of the small GTPase Ran and the nuclear transport receptor importin-β. The results gave ɛ>5kBT, indicating a bumpy energy surface, which is consistent with the ability of importin-β to accommodate multiple conformations and to interact with different, structurally distinct ligands.
Keywords: energy landscapes, protein folding and binding, roughness, single-molecule experiments, dynamic force spectroscopy
Introduction
The way we think about protein folding and binding has changed markedly in recent years. Replacing classical notions, which describe protein folding and binding as a series of sequential events, the ‘new view' (Baldwin, 1994, 1995) sees them as diffusion-like processes, whereby individual molecules reach their final state by gliding down the slopes of a funnelshaped free-energy landscape along multiple coexisting routes (Frauenfelder et al, 1991; Bryngelson et al, 1995; Wolynes et al, 1995; Thirumalai & Woodson, 1996; Dill & Chan, 1997; Karplus, 1997; Onuchic et al, 1997; Dill, 1999; Dobson & Karplus, 1999; Kumar et al, 2000; Onuchic & Wolynes, 2004). The funnel shape of the landscape guides the molecules to the final state at the bottom of the funnel, whereas the dynamics of the transition is determined by the steepness of the slopes and the details of the underlying energy surface. These surfaces are generally not smooth. Rather, they are traversed by energy barriers of varying heights that render them highly corrugated or rugged. Diffusion must therefore proceed through a series of hills and valleys in the energy landscape.
The ruggedness of the energy landscapes that describe proteins has numerous effects on their folding and binding as well as on their behaviour at equilibrium (Bryngelson & Wolynes, 1987, 1989; Frauenfelder et al, 1991; Bryngelson et al, 1995; Wolynes et al, 1995; Thirumalai & Woodson, 1996; Dill & Chan, 1997; Onuchic et al, 1997; Dill, 1999; Kumar et al, 2000; Onuchic & Wolynes, 2004). Superimposed on the slopes of the funnel, roughness controls transition rates and mechanisms, for example, whether transitions will be fast, involving only two states, or slowed down by kinetic traps and involve intermediates. At the bottom of the funnel, the extent of ruggedness determines the number of conformational isomers and their transition dynamics. Fluctuations between these conformations and states define functional motions, such as those involved in catalysis or exchange of ligands. In addition, they allow proteins to accommodate different conformations and, hence, to have different properties that are important to their function. Thus, to understand how proteins fold, bind and function, we need to know not only the energy of their initial and final states, but also the roughness of the energy surface that connects them. Our present knowledge of roughness comes solely from theory and computer simulations of small model proteins. So far, no direct measurement of energy landscape roughness of proteins or other biomolecules has been made.
In the current work, we used single-molecule dynamic force spectroscopy to measure the energy landscape roughness of a bimolecular protein complex. The results indicate a rugged free-energy surface, in accord with the complex dynamics of the interaction and consistent with the ability of one of the proteins of the complex to interact with multiple, competing ligands in a highly specific and regulated manner. The results are also in line with previous studies showing that the complex can accommodate alternative conformations separated by high-energy barriers (Nevo et al, 2003, 2004).
Results
Theoretical background
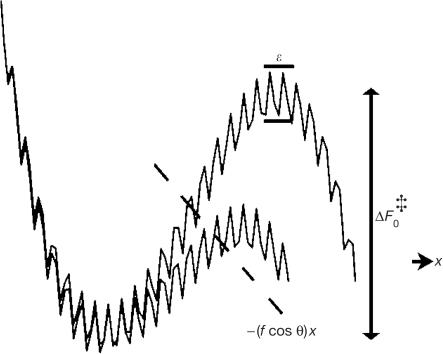
Experimental analysis of protein folding and binding by conventional bulk methods is limited because such methods rely on the assumption that the ensemble is made up of identical members that follow the same path along the reaction coordinate. For these cases, the average of a measured parameter represents each of the individual members. This, however, does not hold for inhomogeneous ensembles, such as proteins, the statistics of which are unknown. By adopting the theory of diffusion in rough potentials by Zwanzig (1988), Hyeon & Thirumalai (2003) recently proposed that the energy landscape roughness of proteins can be measured from single-molecule mechanical unfolding experiments conducted at different temperatures. In particular, their simulations showed that, at a constant loading rate rf (=Δf/Δt), the most probable force for unfolding, f*, increases because of roughness that acts to attenuate diffusion. Because this effect is temperature dependent (Zwanzig, 1988; Bryngelson & Wolynes, 1989; Thirumalai et al, 1989), an overall energy scale of roughness, ɛ, can be derived from plots of f* versus rf acquired at two arbitrary temperatures T1 and T2. The result is representative of the whole of the energy landscape independent of position and nature of the underlying reaction coordinate. The approach is valid as long as ɛ/ΔF0‡<1, where ΔF0‡ denotes the average height of the activation energy barrier for dissociation (Fig 1).
Figure 1.
A rough energy landscape of an unbinding reaction driven by external mechanical force. In this representation, drawn after Hyeon & Thirumalai (2003), ɛ and ΔF0‡ were set to their experimentally determined values of 23.5 and 122 pN nm, respectively. The application of force adds a mechanical potential –(f cos θ)x that tilts the landscape and lowers the height of the prominent energy barrier for dissociation.
In the current study, we expanded the theory of Hyeon & Thirumalai to derive roughness for a bimolecular protein complex from single-molecule mechanical unbinding experiments. The complex consisted of the classical nuclear import receptor importin-β (imp-β) and the Ras-like GTPase Ran, loaded with a non-hydrolysable GTP analogue (GppNHp). We have previously shown that this complex can assume alternative conformations of different adhesion strengths (Nevo et al, 2003, 2004). The analysis made here was performed on the lowerstrength conformation of the complex for which the most probable unfolding forces (f*) could be determined more accurately.
Unbinding of single Ran–imp-β pairs
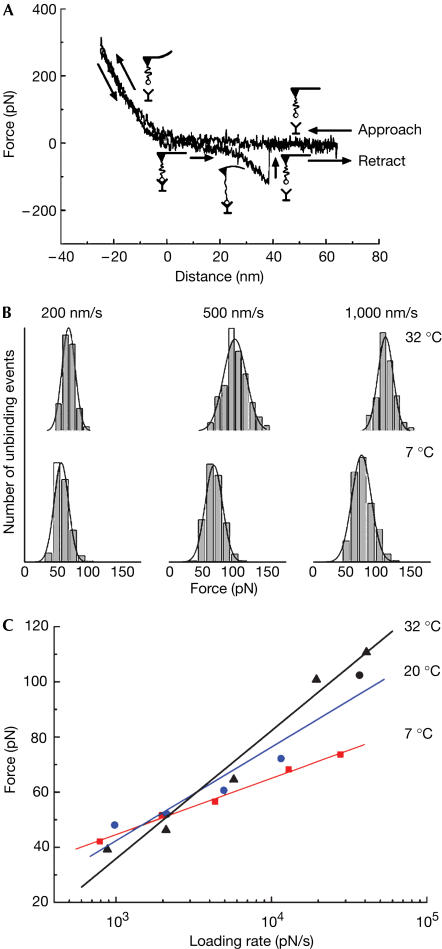
The experimental strategy used for the measurements is shown in Fig 2A. Ran(GppNHp) and imp-β were immobilized through short polymer linkers (polyethylene glycol) onto a cantilevered tip, used in the atomic force microscope (AFM), and on mica, respectively. The unbinding forces were measured by following cantilever deflection, using the AFM set-up. Measurements were carried out at five different loading rates, spanning almost three orders of magnitude in scale, and at three temperatures, ranging from 7 to 32°C.
Figure 2.
Dynamic force spectroscopy measurements of single imp-β–RanGppNHp pairs at different temperatures. RanGppNHp and imp-β were immobilized on an atomic force microscope cantilevered tip and on mica, respectively, by short polyethylene glycol (PEG) linkers (Nevo et al, 2003). The use of linkers allowed for unconstrained recognition and minimized rebinding of the molecules after rupture. It also enabled ready discrimination between binding events and nonspecific interactions with the surface. To achieve single-molecule recognition, both the ligand and the receptor were immobilized on the surfaces at low densities (200–500 molecules/μm2). The AFM tip was repeatedly brought to and retracted from the surface and the interaction force was measured by following the cantilever deflection, using the AFM set-up. Measurements were carried out at different probe velocities, leading to different loading rates rf=Δf/Δt. (A) Representative force–distance cycle recorded at 5 Hz. Unbinding is indicated by the sharp spike in the retraction curve; the parabolic delay antecedent to the spike reflects the extension of the polymer linkers used to immobilize the proteins. (B) Distributions of unbinding forces recorded for the lowerstrength conformation of the complex at different loading rates at 7 and 32°C. Roughness acts to increase the separation between the distributions recorded at different temperatures. Data are presented as gaussian fits of histograms; the width of the bins represents the thermal noise of the cantilever. (C) Force spectra used in the analysis. Most probable unbinding forces f* were plotted against the logarithm of the loading rate. The maximal error was ±10% because of uncertainties in determining the spring constant of the cantilevers. Statistical significance of the differences between the slopes of the spectra was confirmed by analyses of covariance test.
Fig 2B shows representative unbinding force distributions of RanGppNHp–imp-β trapped in the lowerstrength conformation at three different loading rates at 7 and 32°C. As expected, increasing the loading rate led to an increase in the measured unbinding forces (Evans & Ritchie, 1997). For each loading rate, a change in temperature is associated with a pronounced shift in the force distribution.
Fig 2C shows the f* versus rf plots used to derive roughness; f* was taken as the maximum of the unbinding force distribution. For the loading rates used in this study, f* should scale linearly with the logarithm of the loading rate:
![]()
where xβ is a small molecular length that marks the thermally averaged projection of the transition state along the direction of the force (Evans & Ritchie, 1997). At each temperature, the force spectra consist of single linear regimes, indicating a single activation energy barrier along the dissociation path. Increasing the temperature led to an increase in the slope of the curves, consistent with a progressive shortening of the thermal lifetime (toff=1/νD) of the interaction. The increase in slope also indicates a decrease in the distance between the transition and bound states. Such changes in the position of the transition state ensemble are expected for proteins, the potential of which includes solvent contributions, which are strongly temperature dependent (Bryngelson et al, 1995).
Calculation of energy landscape roughness
To calculate ɛ, we modified equation (8) of Hyeon & Thirumalai (2003) to account for the variation in xβ with temperature:
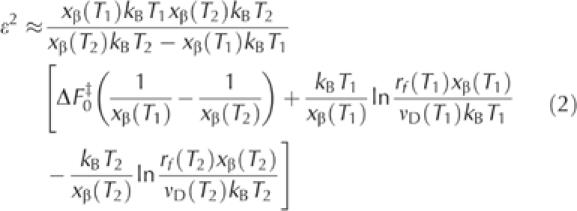
where rf(T1) and rf(T2) are the loading rates that give rise to identical unbinding forces at T1 and T2. The term νD, which represents the escape rate at zero force and includes the temperature-dependent friction coefficient, was determined at each temperature by extrapolation of the force versus loading rate curves. The length scale used by Hyeon & Thirumalai in their derivation for mechanical unfolding is expressed here by xβ(T), which provides a natural measure of the reaction coordinate. The values of xβ (±10%) obtained from the slopes of the force versus loading rate curves in Fig 2C were 0.44 nm (7°C), 0.27 nm (20°C) and 0.21 nm (32°C). For comparison, mechanical unfolding measurements of poly-I27 (Ig module 27 of the I band of human cardiac titin) have yielded an xβ value of 0.25 nm at 25°C (Carrion-Vazquez et al, 1999). Table 1 summarizes the results we have derived for ɛ for the three temperature pairs at three different unbinding forces. The results indicate that ɛ does not vary with the applied force, as expected (Hyeon & Thirumalai, 2003). The average value is 23.5±4.7 pN nm (5.7 kBT at 25°C). This value is about 20% of the height of the prominent energy barrier for dissociation ΔF0‡ (∼120 pN nm, by Arrhenius analysis), well in the limits set by inequality ɛ/ΔF0‡<1.
Table 1.
Values of ɛ derived from mechanical unbinding of RanGppNHp–imp-β
|
f* (pN) |
ɛ (pN nm) |
||
|---|---|---|---|
| |
T1, T2 (°C) |
||
| 7, 20 | 7, 32 | 20, 32 | |
| 40 |
22.9 |
23.5 |
24.0 |
| 60 |
22.9 |
23.5 |
24.0 |
| 75 | 23.0 | 23.5 | 23.9 |
Discussion
In the current work, we used single-molecule dynamic force spectroscopy to measure the energy landscape roughness of a bimolecular protein complex. Although our experiments allow probing of only a fraction of the free-energy surface, the energy scale of roughness ɛ derived from the measurements is expected to reflect typical fluctuations throughout the energy landscape (Hyeon & Thirumalai, 2003).
Rough potentials occur in frustrated systems—systems that are unable to satisfy all their interactions in any given arrangement (Anderson, 1978; Bryngelson et al, 1995). Although evolution tends to lower frustration in proteins, multiple sequencespecific competing interactions and topological constraints dictate that some degree of frustration remains (Bryngelson & Wolynes, 1989; Frauenfelder et al, 1991; Thirumalai & Woodson, 1996; Evans & Ritchie, 1997; Onuchic et al, 1997; Zwanzig, 1988; Hyeon & Thirumalai, 2003; Onuchic & Wolynes, 2004). Generally, frustration is expected to increase with protein size and flexibility. Estimates of energy landscape roughness for small, minimally frustrated model proteins fall in the range of 0<ɛ/kBT<5 (Thirumalai & Woodson, 1996). This is supported by studies on diffusion-limited loop enclosure in small peptides from which an amplitude of about 2 kBT was inferred (Lapidus et al, 2000). The value derived here for ɛ is higher, 5.7 kBT. This relatively high value may reflect differences in size and complexity between the proteins used here and small peptides or the models used in the simulations. However, it probably has a more specific origin that reflects the complex dynamics of the interaction between imp-β and Ran, which, in turn, is dictated by the unique structural properties of imp-β. Binding of RanGTP (or RanGppNHp) to imp-β is associated with both local and global conformational changes in imp-β (Chook & Blobel, 1999, 2001; Vetter et al, 1999; Stewart, 2003; Fukuhara et al, 2004; Xu & Massague, 2004). Similarly, large changes in conformation are also induced in imp-β on binding to its cargo adapter importin-α (Cingolani et al, 1999, 2000). Such processes, which occur at different length scales and/or timescales, are known to lead to frustration. The ability of imp-β to interact with various structurally distinct ligands is achieved by having a highly flexible structure that can accommodate grossly different conformations on binding to different substrates (Cingolani et al, 1999; Lee et al, 2000, 2003). Alternative conformations were also reported for complexes of imp-β with the same ligand (Nevo et al, 2003). This structural polymorphism is shared by all members of the imp-β/karyopherin-β family and is essential for their function and regulation (Chook & Blobel, 2001). Bumpy landscapes are thus expected for all complexes made by imp-β-like transport receptors.
Is there any advantage to having a highly corrugated energy surface? Imp-β functions in the nuclear import of proteins across the nuclear pore complex. On arrival in the nucleus, the imp-β/cargo complexes must dissociate to free the cargo and to allow recycling of imp-β back to the cytoplasm. This dissociation is induced by RanGTP, which binds to the complexes through imp-β. After cargo release, the newly formed imp-β–RanGTP complex shuttles back to the cytoplasm where it again needs to disassemble into free imp-β for another round of transport. This is achieved by the concomitant action of importin-α and one of two effectors of Ran (called RanBP1 and RanBP2), which bind to the complex and displace imp-β (Gorlich & Kutay, 1999, and references therein). Uncoupling between these, as well as other interactions of imp-β, requires that conformational transitions be affected only by ligand binding. Thus, to evolve to its function, imp-β had to adopt a rugged energy landscape in which secondary energy barriers, higher than kBT, oppose thermally induced transitions between different conformations with similar free energy. The same mechanistic principle probably applies to other complexes of imp-β and may be relevant to other proteins, the function of which demands highly specific and regulated interactions with multiple, structurally distinct ligands.
Methods
Proteins and surface immobilization. His-tagged (carboxy-terminal) human imp-β was expressed, purified and stored as described previously (Nevo et al, 2003). His-tagged (amino-terminal) human Ran was obtained from the soluble phase of Escherichia coli BL21 (DE3; trxB™) induced with 0.25 mM isopropyl-β-D-thiogalactoside for 8 h at 30 °C. After purification (metal affinity and sizing), the protein was loaded with GppNHp according to Nevo et al (2003). Before use in the force measurements, proteins were assayed for binding by enzyme-linked immunosorbent assay, sizing chromatography and native gel electrophoresis. Immobilization of Ran and imp-β over the AFM tip and the surface (mica) was made by short polyethylene glycol (PEG) linkers, as described by Nevo et al (2003).
Dynamic force spectroscopy. Force measurements were carried out in 50 mM Tris (pH 7.5)/150 mM NaCl, using a PicoSPM AFM (Molecular Imaging, Phoenix, AZ, USA). The specificity of the interaction was verified by control experiments showing that addition of free imp-β or RanGppNHp to the solution effectively blocked binding whereas the addition of a nonspecific protein (lysozyme) had no effect on the interaction. Force–distance cycles were performed at amplitudes of 100 nm and at frequencies ranging from 0.5 to 10 Hz (loading rates indicated in the figure are corrected for linkage compliance). Temperature was maintained ±0.1°C of the set-point temperature by a temperature controller integrated into the sample plate. Between 100 and 300 rupture events were recorded for each loading rate–temperature combination (each point in Fig 2C). The spring constants of the cantilevers used in the different experiments (TM Microscopes, CA, USA) were determined using the thermal noise method (Hutter & Bechhoefer, 1993). The instantaneous loading rates were calculated according to Kienberger et al (2000), and data were processed and analysed as described earlier (Nevo et al, 2003).
Acknowledgments
We thank H. Gruber and C. Riener for the synthesis of the PEG linkers and O. Bogin for his help in the expression of imp-β. We also thank the anonymous reviewers for helpful comments and suggestions. This work was supported by grants from the Minerva Foundation and the Human Frontier Science Program.
References
- Anderson PW (1978) The concept of frustration in spin glasses. J Less-Common Metals 62: 291–294 [Google Scholar]
- Baldwin RL (1994) Protein folding. Matching speed and stability. Nature 369: 183–184 [DOI] [PubMed] [Google Scholar]
- Baldwin RL (1995) The nature of protein folding pathways: the classical versus the new view. J Biomol NMR 5: 103–109 [DOI] [PubMed] [Google Scholar]
- Bryngelson JD, Wolynes PG (1987) Spin-glasses and the statistical-mechanics of protein folding. Proc Natl Acad Sci USA 84: 7524–7528 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bryngelson JD, Wolynes PG (1989) Intermediates and barrier crossing in a random energy-model (with applications to protein folding). J Phys Chem 93: 6902–6915 [Google Scholar]
- Bryngelson JD, Onuchic JN, Socci ND, Wolynes PG (1995) Funnels, pathways, and the energy landscape of protein folding: a synthesis. Proteins 21: 167–195 [DOI] [PubMed] [Google Scholar]
- Carrion-Vazquez M, Oberhauser AF, Fowler SB, Marszalek PE, Broedel SE, Clarke J, Fernandez JM (1999) Mechanical and chemical unfolding of a single protein: a comparison. Proc Natl Acad Sci USA 96: 3694–3699 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chook YM, Blobel G (1999) Structure of the nuclear transport complex karyopherin-β2-Ran × GppNHp. Nature 399: 230–237 [DOI] [PubMed] [Google Scholar]
- Chook YM, Blobel G (2001) Karyopherins and nuclear import. Curr Opin Struct Biol 11: 703–715 [DOI] [PubMed] [Google Scholar]
- Cingolani G, Petosa C, Weis K, Muller CW (1999) Structure of importin-β bound to the IBB domain of importin-α. Nature 399: 221–229 [DOI] [PubMed] [Google Scholar]
- Cingolani G, Lashuel HA, Gerace L, Muller CW (2000) Nuclear import factors importin-α and importin-β beta undergo mutually induced conformational changes upon association. FEBS Lett 484: 291–298 [DOI] [PubMed] [Google Scholar]
- Dill KA (1999) Polymer principles and protein folding. Protein Sci 8: 1166–1180 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dill KA, Chan HS (1997) From Levinthal to pathways to funnels. Nat Struct Biol 4: 10–19 [DOI] [PubMed] [Google Scholar]
- Dobson CM, Karplus M (1999) The fundamentals of protein folding: bringing together theory and experiment. Curr Opin Struct Biol 9: 92–101 [DOI] [PubMed] [Google Scholar]
- Evans E, Ritchie K (1997) Dynamic strength of molecular adhesion bonds. Biophys J 72: 1541–1555 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frauenfelder H, Sligar SG, Wolynes PG (1991) The energy landscapes and motions of proteins. Science 254: 1598–1603 [DOI] [PubMed] [Google Scholar]
- Fukuhara N, Fernandez E, Ebert J, Conti E, Svergun D (2004) Conformational variability of nucleo-cytoplasmic transport factors. J Biol Chem 279: 2176–2181 [DOI] [PubMed] [Google Scholar]
- Gorlich D, Kutay U (1999) Transport between the cell nucleus and the cytoplasm. Annu Rev Cell Dev Biol 15: 607–660 [DOI] [PubMed] [Google Scholar]
- Hutter JL, Bechhoefer J (1993) Calibration of atomic-force microscope tips. Rev Sci Instrum 64: 1868–1873 [Google Scholar]
- Hyeon CB, Thirumalai D (2003) Can energy landscape roughness of proteins and RNA be measured by using mechanical unfolding experiments? Proc Natl Acad Sci USA 100: 10249–10253 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karplus M (1997) The Levinthal paradox: yesterday and today. Fold Des 2: S69–S75 [DOI] [PubMed] [Google Scholar]
- Kienberger F, Pastushenko VP, Kada G, Gruber HJ, Riener C, Schindler H, Hinterdorfer P (2000) Static and dynamical properties of single poly(ethylene glycol) molecules investigated by force spectroscopy. Single Mol 1: 123–128 [Google Scholar]
- Kumar S, Ma B, Tsai CJ, Sinha N, Nussinov R (2000) Folding and binding cascades: dynamic landscapes and population shifts. Protein Sci 9: 10–19 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lapidus LJ, Eaton WA, Hofrichter J (2000) Measuring the rate of intramolecular contact formation in polypeptides. Proc Natl Acad Sci USA 97: 7220–7225 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee SJ, Imamotos N, Sakai H, Nakagawa A, Kose S, Koike M, Yamamoto M, Kumasaka T, Yoneda Y, Tsukihara T (2000) The adoption of a twisted structure of importin-β is essential for the protein–protein interaction required for nuclear transport. J Mol Biol 302: 251–264 [DOI] [PubMed] [Google Scholar]
- Lee SJ et al. (2003) The structure of importin-β bound to SREBP-2: nuclear import of a transcription factor. Science 302: 1571–1575 [DOI] [PubMed] [Google Scholar]
- Nevo R, Stroh C, Kienberger F, Kaftan D, Brumfeld V, Elbaum M, Reich Z, Hinterdorfer P (2003) A molecular switch between alternative conformational states in the complex of Ran and importin-β1. Nat Struct Biol 10: 553–557 [DOI] [PubMed] [Google Scholar]
- Nevo R, Brumfeld V, Elbaum M, Hinterdorfer P, Reich Z (2004) Direct discrimination between models of protein activation by single-molecule force measurements. Biophys J 87: 2630–2634 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Onuchic JN, Wolynes PG (2004) Theory of protein folding. Curr Opin Struct Biol 14: 70–75 [DOI] [PubMed] [Google Scholar]
- Onuchic JN, Lutheyschulten Z, Wolynes PG (1997) Theory of protein folding: the energy landscape perspective. Annu Rev Phys Chem 48: 545–600 [DOI] [PubMed] [Google Scholar]
- Stewart M (2003) Nuclear trafficking. Science 302: 1513–1514 [DOI] [PubMed] [Google Scholar]
- Thirumalai D, Woodson SA (1996) Kinetics of folding of proteins and RNA. Accounts Chem Res 29: 433–439 [Google Scholar]
- Thirumalai D, Mountain RD, Kirkpatrick TR (1989) Ergodic behavior in supercooled liquids and in glasses. Phys Rev A 39: 3563–3574 [DOI] [PubMed] [Google Scholar]
- Vetter IR, Arndt A, Kutay U, Gorlich D, Wittinghofer A (1999) Structural view of the Ran–importin-β interaction at 2.3 Å resolution. Cell 97: 635–646 [DOI] [PubMed] [Google Scholar]
- Wolynes PG, Onuchic JN, Thirumalai D (1995) Navigating the folding routes. Science 267: 1619–1620 [DOI] [PubMed] [Google Scholar]
- Xu L, Massague J (2004) Nucleocytoplasmic shuttling of signal transducers. Nat Rev Mol Cell Biol 5: 209–219 [DOI] [PubMed] [Google Scholar]
- Zwanzig R (1988) Diffusion in a rough potential. Proc Natl Acad Sci USA 85: 2029–2030 [DOI] [PMC free article] [PubMed] [Google Scholar]