Near-Critical Phenomena in Intracellular Metabolite Pools

Abstract

The supply and consumption of metabolites in living cells are catalyzed by enzymes. Here we consider two of the simplest schemes where one substrate is eliminated through Michaelis-Menten kinetics, and where two types of substrates are joined together by an enzyme. It is demonstrated how steady-state substrate concentrations can change ultrasensitively in response to changes in their supply rates and how this is coupled to slow relaxation back to steady state after a perturbation. In the one-substrate system, such near-critical behavior occurs when the supply rate approaches the maximal elimination rate, and in the two-substrate system it occurs when the rates of substrate supply are almost balanced. As systems that operate near criticality tend to display large random fluctuations, we also carried out a stochastic analysis using analytical approximations of master equations and compared the results with molecular-level Monte Carlo simulations. It was found that the significance of random fluctuations was directly coupled to the steady-state sensitivity and that the two substrates can fluctuate greatly because they are anticorrelated in such a way that the product formation rate displays only small variation. Basic relations are highlighted and biological implications are discussed.

INTRODUCTION

Recent advances in experimental techniques have made it possible to test hypotheses based on mathematical modeling of biochemical reactions in single cells (Becskei and Serrano, 2000; Cluzel et al., 2000; Gardner et al., 2000; Ozbudak et al., 2002; Surrey et al., 2001). These reactions often take place far from equilibrium (Haken, 1982; Joel, 1987), their rates frequently depend nonlinearly on metabolite concentrations and they sometimes involve very small numbers of molecules (Guptasarama, 1995). Such features motivate mesoscopic approaches, where the stochastic properties of intracellular reactions are analyzed with master equations (van Kampen, 1997). The importance of stochastic analyses of gene expression systems was stressed by Berg (1978) and more recently by others (Cook et al., 1998; Elowitz et al., 2002; Hasty et al., 2000; Kepler and Elston, 2001; Ko, 1992; McAdams and Arkin, 1997; Metzler, 2001; Paulsson et al., 2000; Thattai and van Oudenaarden, 2001).

The kinetics of compounds present in high copy number (e.g., metabolites) is, in contrast, typically described from the macroscopic perspective (Cornish-Bowden, 1995; Heinrich and Schuster, 1996; Morton-Firth and Bray, 2001), where random fluctuations are neglected. However, such macroscopic analysis can be misleading when the rate of turnover of metabolite pools is high compared to the rate of relaxation at the stationary state. The importance of fluctuations in such systems has been demonstrated for microtubule formation (Dogterom and Leibler, 1993), ultrasensitive modification and demodification reactions (Berg et al., 2000), plasmid copy number control (Paulsson and Ehrenberg, 2001) and noise-induced oscillations near a macroscopic Hopf bifurcation (Vilar et al., 2002).

Here we address these issues for intracellular metabolite concentrations using a combination of analytical treatments of master equations with elimination of fast variables (Gardiner, 1985), the linear noise approximation (van Kampen, 1997), and molecule-level Monte Carlo simulations (Gillespie, 1977). We focus on Michaelis-Menten mechanisms and enzymatic couplings of two substrates in parameter regions where phase-transition-like behavior emerges. Elimination of fast variables has made it possible to extend earlier mesoscopic analysis of similar systems (Paulsson et al., 2000; Paulsson and Ehrenberg, 2001).

There are two closely related properties of such systems: ultrasensitive responses (Koshland et al., 1982) in metabolite steady-state levels to variations in their rates of synthesis, and large fluctuations in metabolite concentrations. These phenomena are accentuated in the two-substrate case when the rates of supply of the metabolites are balanced and the coupling enzyme is unsaturated. The reason is that the system's overall flow properties can remain more or less unchanged for many combinations of molecule concentrations, resulting in near-critical kinetic behavior. These results extend the earlier description of zero-order behavior (Berg et al., 2000; Goldbeter and Koshland, 1981) from one to several dimensions.

ANALYSIS

Enzyme-catalyzed mono- and bimolecular reactions in the cell

First, we consider a one-substrate case where a metabolite X is synthesized with a rate f_x and is transformed to a product P with a rate v. The reactions are summarized in the scheme

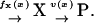(1)

The rate v is of Michaelis-Menten type (Cornish-Bowden, 1995), according to

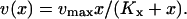(2)

The concentration x of X is diluted by exponential cell growth with a rate μ, related to the cell generation time τ_G through μ=ln2/τ_G.

Second, we consider a two-substrate case where metabolites X and Y are synthesized with rates f_x and f_y, respectively, and irreversibly linked together with a rate v. The reactions are summarized in the scheme

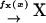(3)

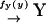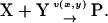The concentrations x and y of X and Y are diluted or degraded with the rate μ as in the one-substrate case. The enzyme that joins X and Y is assumed to equilibrate rapidly and noncooperatively with its substrates as in the scheme

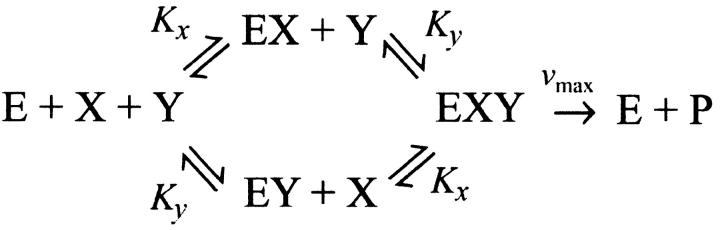(4)

The rate v(x, y) by which X and Y molecules are transformed to product is given by

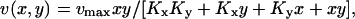(5)

where K_x and K_y are dissociation constants (Cornish-Bowden, 1995).

Macroscopic analysis

Macroscopically, the time evolution of the concentration x in the one-substrate case is determined by

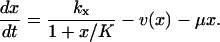(6)

The first term to the right is the rate k_x by which X is produced, constrained by competitive (product) inhibition with inhibition constant K (Cornish-Bowden, 1995) and the second term v(x) is defined in Eq. 2. The last term accounts for dilution by exponential volume growth but could also describe first-order degradation of X.

The time evolution of the metabolite concentrations x and y in the two-substrate case is determined by

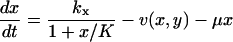(7)

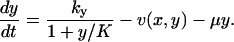The first term to the right in each equation is the rate of synthesis of a metabolite constrained by product inhibition as in Eq. 6. The second term v(x, y) is given in Eq. 5 and the last term accounts for dilution by volume growth or degradation.

Eqs. 6 and 7 have interesting properties, visible already in the steady state (dx/dt = dy/dt = 0). To illustrate, Fig. 1 A shows how the steady-state value x̄ of x varies with k_x, when all other parameters in Eq. 6 are constant. Fig. 2 A shows how 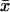and the steady-state value 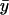of y vary when k_x changes and all other parameters are held constant.

FIGURE 1.

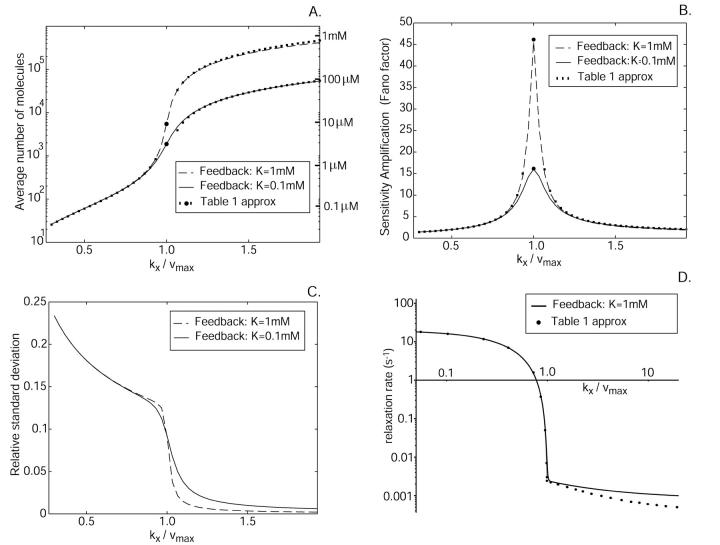
Characterization of the one-substrate system. x-axis: The uninhibited rate of synthesis, k_x, normalized to v_max. (A) The average number and concentrations of X-molecules for different product inhibition constants. The lines are calculated from the stationary probability density function. The dots and small squares correspond to values from the analytical approximations in Table 1 (with μ′ = 2.4 × 10⁻³ s⁻¹ or 2.04 × 10⁻² s⁻¹). At this level of detail the lines are indistinguishable from the macroscopic stationary values, which are not plotted. (B) The Fano factor (σ²/〈X〉) calculated from the stationary probability distribution (lines) compared to the analytical approximation of the sensitivity amplification from Table 1 (dots). (C) The relative standard deviation (σ/〈X〉) calculated from the stationary probability function. (D) The relaxation rate (solid) compared to the approximations from Table 1 (dots). Parameters: The Michaelis-Menten K_m parameter is K_x = 0.1 μM and is v_max = 2 μM s⁻¹. The exponential growth rate μ = 4 × 10⁻⁴ s⁻¹ and the volume is Ω = 10⁻¹⁵ liters.

FIGURE 2.

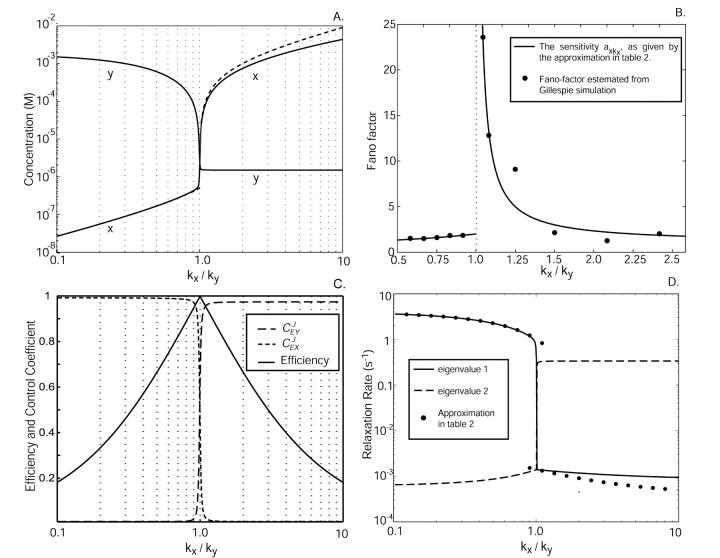
Characterization of the two-substrate system. x axis: uninhibited rate of synthesis of X-molecules, k_x, normalized to the uninhibited rate of synthesis of Y-molecules k_y, where k_y is kept constant. (A) Solid lines represent stationary concentrations of x and y. Dashed lines represent the approximations that are given in Table 2. The curves are overlapping for k_x < k_y. (B) The Fano factor (σ²/〈X〉) as approximated by the expressions in Table 2 (solid line) is compared to estimates from Gillespie simulations (dots). The deviation between the line and the dots for high k_x/k_y is a result of too-short sampling, which is due to the very slow relaxation rate and a large number of X molecules. The estimated value from the Gillespie simulations at the balance point, where k_x/k_y = 1, is 140. (C) The solid line represents the efficiency, i.e., the rate of product formation rate compared to maximal 2 v(x, y)/(k_x + k_y). The dashed lines show the flow control coefficients, i.e., the sensitivity in rate of product formation to a change in either k_x or k_y. (D) Relaxation rates (i.e., eigenvalues for the Jacobian evaluated in the stationary state). The solid line corresponds to the relaxation rate of the X-pool in the unbalanced cases. The dots are the approximations from Table 2. Parameters: k_y = 1 μM s⁻¹, K_y = 1.5 μM, K_x = 0.5 μM, μ = 0.0004 s⁻¹, and K = 1 mM.

In the one-substrate case (Fig. 1 A), 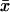increases slowly with increasing k_x until the rate of synthesis of X approaches v_max, where 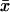increases sharply in a narrow interval of k_x-values. When k_x > v_max, the increase in x is more gradual. In the two-substrate case (Fig. 2 A), 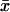behaves very much like the one-substrate case when k_x varies, with a very sharp increase near the point where k_x = k_y. When k_x increases from small values, 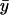decreases gradually until k_x approaches k_y, at which point 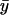decreases sharply. When k_x varies in excess over k_y, 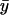displays little further change.

Parameter constraints for analytical approximations

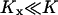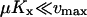The parameters used in Figs. 1 and 2 (see figure legends) have been chosen so that the turnover time of a limiting substrate is much shorter than the generation time of the cell and so that product inhibition of its rate of synthesis is weak. For the one-substrate case this means that and . In the two-substrate case the condition is that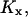 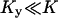and 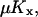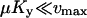. It is also required that 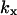or 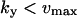to guarantee that the two-substrate reaction is unsaturated. Under these conditions simple, analytical approximations can be found for the different parts of the curves in Figs. 1 A and 2 A (see also Tables 1 and 2, respectively). The same constraints on the parameters are used throughout the paper and lead to simple analytical expressions for sensitivity amplifications (see Eq. 8 below), relaxation rates, and stochastic properties. See Discussion for the biological relevance of this choice of parameters.

TABLE 1.

One-substrate case

Regime	Macroscopic steady state of x	Sensitivity amplification (≈Fano factor)	Relaxation rate constant
kx < vmax		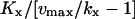vmax/(vmax−kx)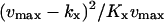
kx = vmax†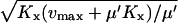
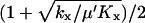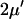kx > vmax	‡

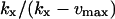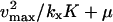^†We use the approximation 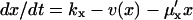and the balance point is really .

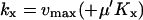^‡Approximation when product inhibition dominates over dilution.

TABLE 2.

Two-substrate case

Regime	Macroscopic steady state of x	Sensitivity amplification (≈Fano factor)	Relaxation rate constant
kx < ky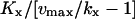
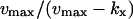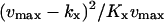kx = ky†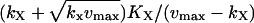
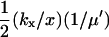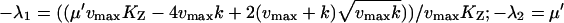kx > ky	‡

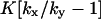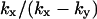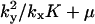^†Assuming K_x = K_y and k_X < v_max. In this regime, the deviation between the macroscopic steady state and the average value is significant.

^‡Approximation when product inhibition dominates over dilution.

The approximations for the one-substrate case in Table 1 are given for three regions: 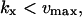and 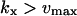. The expressions for 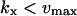and 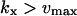are accurate when 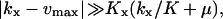which implies that the Michaelis-Menten enzyme should be close to saturated in the 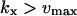region and that the influence of inhibition and dilution should be small in the 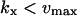region. The approximations for the two-substrate case in Table 2 are also given in three regions: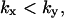 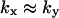and 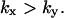The approximations for the 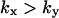region are accurate when 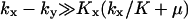, and for 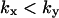accurate when 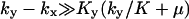, which implies that the nonlimiting substrate saturates the two-substrate reaction.

Ultrasensitivity

The high sensitivity by which 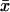responds to changes in k_x near the point where k_x = v_max in Fig. 1 or k_x = k_y in Fig. 2 motivates further analysis. A common measure of the sensitivity of a response, r, to variation in a signal, s, is the logarithmic gain (Savageau, 1976) or sensitivity amplification (Fell, 1997; Goldbeter and Koshland, 1982; Heinrich and Schuster, 1996; Koshland et al., 1982; Savageau, 1971, 1976):

(8)

Parameter a_rs measures the relative (infinitesimal) change in the response (dr/r) normalized to the relative (inifinitesimal) change in the signal (ds/s). With k_x as signal and 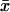as response, 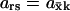is also known as the concentration control coefficient (Cornish-Bowden, 1995; Fell, 1997; Heinrich and Schuster, 1996). It is shown as a function of k_x in Figs. 1 B and 2 B for the one- and two-substrate cases, respectively. The concentration control coefficient is near one for low values of k_x in both cases, reaches a maximum when k_x = v_max (Fig. 1 B) or k_x = k_y (Fig. 2 B), and decreases back to one at high values of k_x.

Analytical approximations for 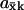were obtained (see Appendix A0) for the different parts of the curves in Figs. 1 B (see also Table 1) and 2 B (see also Table 2). The maximal sensitivity is in the one-substrate case given by

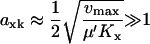(9)

with

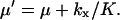(10)

When product inhibition dominates over dilution (k_x/K ≫ μ) Eq. 9 simplifies to

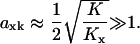(11)

In the two-substrate case the maximal value of 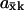is reached at the balance point where 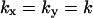and

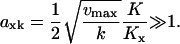(12)

The high sensitivity (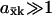) in Eqs. 9 and 11 is quantitatively similar to zero-order ultrasensitivity (Goldbeter and Koshland, 1981), inasmuch as it comes from a delicate balance between formation and elimination reactions that are both of approximately zero kinetic order, i.e., the flows are insensitive to the concentration. The ultrasensitivity in the two-substrate case in Eq. 12 is different and emerges only when the rates of synthesis of two (or more) substrate molecules are approximately balanced and their rates of disappearance are stoichiometrically coupled through a common elimination pathway. One consequence of this difference is that the maximal 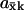in the one-substrate case is proportional to the square root of the ratio between K and K_x, and in the two-substrate case 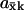is linear in the ratio between K and K_x.

Efficiency

An efficiency parameter E can be defined for two-substrate flow modules according to

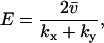(13)

where the parameters k_x and k_y are in general proportional to the concentrations of the enzymes that synthesize X and Y molecules, respectively, so that their sum roughly corresponds to the protein investment a cell has to make to achieve a certain rate v of synthesis of an anabolic product. When E is plotted versus k_x (Fig. 2 C) a sharp maximum occurs for k_x = k_y = k at the point where the sensitivity 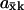is maximal (Fig. 2 B). Maximal efficiency will also occur when k_x = k_y if more precise estimates of the protein investment are used, inasmuch as the overcapacity which arises with one of the two enzymes in excess is wasted. In a more complete analysis, the efficiency parameter would also include the cost of the enzyme in the exit path in the denominator in Eq. 13. In this case, the efficiency displays a ridge at k = k_x = k_y which increases for increasing k until the efficiency passes a global maximum and then decreases due to overcapacity of both inflows. A similar analysis with the cost for both inflow and outflow in the denominator of the efficiency can also be made for the single-substrate case. Here, the efficiency would not have any ridge inasmuch as there is only one inflow, but E would increase in a similar way to a global maximum with increasing k_x and then decrease sharply as k_x exceeds v_max.

Relaxation rates

The high values of the logarithmic gain in both the one- (Fig. 1 B) and the two-substrate (Fig. 2 B) cases reflect system properties reminiscent of phase transitions in thermodynamic systems (see Discussion). Another aspect of the same phenomenon can be illustrated by Taylor-expanding Eqs. 6 and 7 to first-order around their steady-state solutions for different values of k_x and calculating the relaxation rate constants, which describe how rapidly the system returns to the steady state after a perturbation. The results are displayed in Tables 1 and 2, plotted in Figs. 1 D and 2 D, and can be summarized as follows.

In the one-substrate case, when k_x increases toward v_max, the relaxation rate constant decreases as the square of the difference between v_max and k_x until the effects of product inhibition and dilution by volume growth become significant. This behavior reflects the fact that the outflow of substrate approaches zero kinetic order as the enzyme becomes saturated. When k_x is close to v_max the substrate concentration is so large that product inhibition and dilution from volume growth cannot be neglected and at the balance point itself, the relaxation rate constant is very close to 2μ′ (Fig. 1, Table 1).

In the two-substrate case, the rate of relaxation is described by the two eigenvalues of the Jacobian (Strogatz, 1994) to the system in Eq. 7. Both eigenvalues, one small and one large, are plotted as functions of k_x in Fig. 2 D along with their analytical approximations (Table 2). In the unbalanced cases (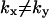) the dynamics of the substrates is decoupled and one eigenvalue is associated with each substrate. When k_x < k_y, 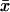is small compared to 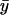and responds rapidly to perturbations from the steady state whereas 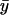is large and relaxes slowly to its steady state. As k_x increases, the fast relaxation rate decreases as the square of the difference between k_x and v_max, as in the one-substrate case. Close to the balance point where k_x ≈ k_y ≈ k, both concentrations have a small and a large relaxation rate constant. The small rate constant is associated with the difference, w = x − y, between x and y that follows the rate equations (Eqs. 7 and A29):

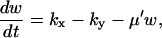(14)

with solution

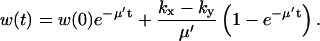(15)

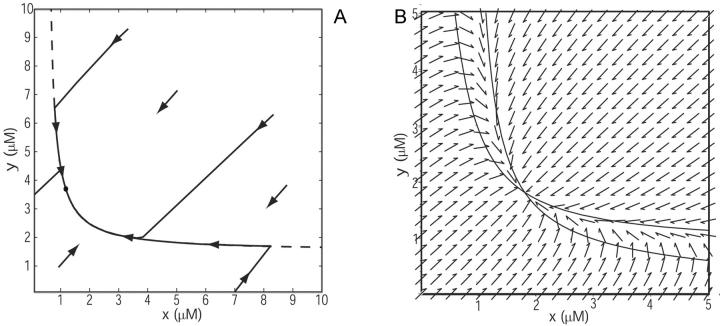
The behavior close to the balance (k_x ≈ k_y) point is further illustrated by phase-plane analysis (Fig. 3 A). All trajectories in the (x, y)-plane first follow diagonals, where w = x − y is constant, until they meet the curve k = v(x, y), which they follow to the steady state (k_x−k_y)/μ′ (Eq. 15 at infinite time). The time scale for the initial, fast concentration changes is determined by the rate of turnover of the pools (Table 2). In Fig. 3 B the influence of product inhibition and dilution is increased to separate the nullclines (the x, y-curves for which dx/dt = 0 and dy/dt = 0, respectively) in the phase plane.

FIGURE 3.

Phase plane illustrating the global macroscopic dynamics close to balanced synthesis. x-axis: concentration of X-molecules (x). y-axis: concentration of Y-molecules (y). (A) The arrows indicate the direction of the trajectories. The dashed line is the curve v(x, y) = k_x, which approximates the nearly overlapping nullclines. Parameters: k_x = 1 μM s⁻¹, k_y = 1.001 μM s⁻¹, K_x = 0.5 μM, K_y = 1.5 μM, μ = 0.0004 s⁻¹ and no product inhibition (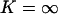). (B) The influence of product inhibition and dilution (or degradation) is increased to separate the nullclines (lines) that have coalesced for the parameters used in A. Parameters: k_x = 1 μM s⁻¹, k_y = 1 μM s⁻¹, K_x = 1 μM, K_y = 1 μM, μ = 0.01 s⁻¹, and K = 10 μM.

As k_x increases above the balance point, the behavior is the reversed where x becomes large and slow, and y becomes small and fast.

Logarithmic gains and the flow control coefficients of metabolic control analysis

Networks of metabolic reactions are often addressed in the language of metabolic control analysis (MCA) (Kacser and Burns, 1973). In MCA steady-state flows of metabolites are described macroscopically and one often wants to derive the fractional change (dJ/J) of a metabolite flow (J) divided by the fractional change (d[E]/[E]) of the concentration [E] of one of the enzymes in the system, i.e., the flux control coefficient, :

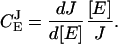(16a)

This is simply the logarithmic gain (Eq. 8) with [E] as signal and J as response. According to the summation theorem (Heinrich and Schuster, 1996; Kacser and Burns, 1973), the sum of all control coefficients that relate to a certain flow is equal to one, provided that there is proportionality between the activity and concentration of every enzyme that contributes to this flow. If the control coefficient for a particular enzyme is close to one, it means that its concentration is a major determinant of the flow. If the control coefficient instead is close to zero, the flow depends little on the concentration of that enzyme.

The two-substrate system in Eq. 7 can be described in MCA by putting the time derivatives equal to zero for steady state, identifying 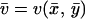with a flow J and assuming that k_x and k_y are proportional to enzyme concentrations [E_x] and [E_y], respectively. One can then define two control coefficients for the flow J, one for each enzyme, according to

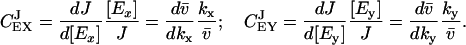(16b)

These control coefficients are plotted as functions of k_x in Fig. 2 C. As long as k_x < k_y, 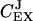is near one and 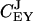near zero. When k_x = k_y, 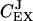rapidly shifts from one to a value near zero and 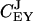changes in the opposite direction from zero to a value near one. This means that for our choice of parameters the flow is almost exclusively determined by k_x to the left and by k_y to the right of the balance point.

Mesoscopic analysis

Macroscopic descriptions are ideally suited for chemical reactions in the test tube where numbers of molecules are large and in the absence of critical phenomena, relative fluctuations tend to be insignificant (Gardiner, 1985; Haken, 1982; Joel, 1987). In contrast, reactions in single cells often involve few molecules or display adjustment rates that are slower then the corresponding turnover rates. Such systems can display large relative fluctuations, motivating that deterministic rate equations for concentrations are replaced by mesoscopic master equations (van Kampen, 1997) for probabilities of discrete copy numbers. In this section we analyze master equation counterparts of Eqs. 6 and 7 using exact analytical methods, linear noise approximations (van Kampen, 1997), and Monte-Carlo simulations (Gillespie, 1977).

The one-substrate case

For the mesoscopic representation of the one-substrate case in Eq. 1 we use the following jump process:

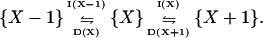(17)

Changes in the number, X, of substrate molecules of type X in the system are determined by the reaction rates for the increments, I, and decrements, D, in Eq. 17. These are defined as (compare with Eqs. 2 and 6):

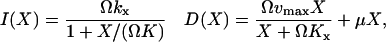(18)

where Ω is the system volume. The effects of volume growth with the rate constant μ and cell divisions at regular time intervals have been approximated by a constant decay rate term μX for substrate molecules (Paulsson and Ehrenberg, 2001). The errors introduced by this simplification are small for the systems in this study (Appendix A5). The master equation (van Kampen, 1997) for the probability, P(X, t), that there are X molecules in the system at time t is given by

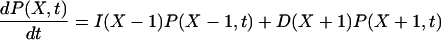(19)

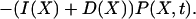The elementary reactions of the intermediate states of the enzymes have been contracted to single pseudo-elementary steps. It can be shown with the technique of adiabatic elimination of fast variables that this is legitimate when the intermediate states of the participating enzymes equilibrate rapidly compared to the fluctuations in the substrate concentrations. The steady-state solution, P(X), of Eq. 19 is

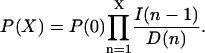Inserting I and D from Eq. 18 leads to the following expression for P(X):

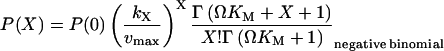(20)

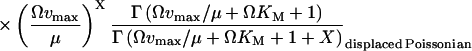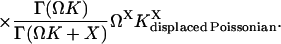When k_x is smaller than v_max, P(X) is of negative binomial type (Råde and Westergren, 1995), and when k_x is larger than v_max, P(X) behaves like a displaced Poissonian (Johnson and Kotz, 1969; Paulsson and Ehrenberg, 2001). When k_x is much smaller or much larger than v_max, Eq. 20 approaches a Poissonian. The mean 〈X〉 and the standard deviation σ were calculated for X from Eq. 20. Plots of the Fano factor, defined as the variance over average, σ²/〈X〉, and the relative standard deviation, σ/〈X〉, are shown as functions of k_x in Fig. 1, B and C, respectively. The Fano factor (Fano, 1947) is typically independent of system volume Ω and measures how much the size of internal fluctuations deviates from what is expected from Poisson statistics, for which the Fano factor equals one. In Fig. 1 B, the Fano factor starts at a value close to one when k_x is small, then increases to a maximum when k_x = v_max (balance point) and then drops again to a value near one as k_x increases further. When k_x = v_max the Fano factor is much larger than one, revealing far from Poissonian system behavior. The relative standard deviation σ/〈X〉, varies little when k_x increases from very small values toward the balance point (Fig. 1 C), although the expected number of molecules per cell increases by three orders of magnitude (Fig. 1 A). The fact that the standard deviation grows almost in proportion to the average is another aspect of the phase-transition like behavior of the one-substrate flow module (see Discussion in this article, and Chapter 7 in Joel (1987)). There is a close correspondence between the Fano factor, calculated from the exact probability distribution in Eq. 20, and the logarithmic gain of the substrate pool with respect to k_x according to Eq. 8 over the whole k_x-interval (Fig. 1 B; Appendix A4).

The two-substrate case

The simplest mesoscopic version of the two-substrate case in Eq. 3 is the following jump process:

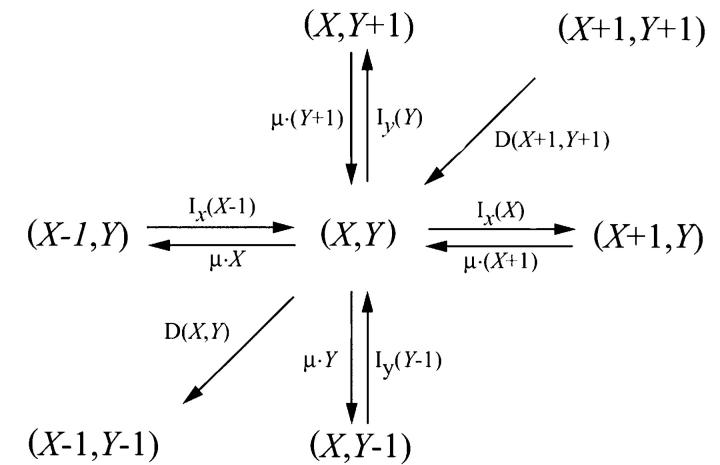(21)

The increment rates I_x(X) and I_y(Y) in Eq. 21, operating on X- or Y-molecules, respectively, are defined as (compare with Eq. 7):

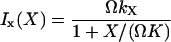(22)

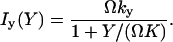The diagonal decrement rate D(X, Y) of X and Y molecules by product formation is defined as (compare with Eq. 5):

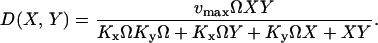(23)

Together with Eqs. 22 and 23, the jump scheme in Eq. 21 defines the master equation for the two-substrate case (Appendix A2). To clarify the stochastic properties of the two-substrate system, we will use approximate solutions for the master equation for different parameter regions (k_x < k_y, k_y < k_x, or k_x ≈ k_y) of the system.

Unbalanced inflows of substrates

When k_x < k_y (or k_y < k_x with X and Y swapped) the macroscopic analysis showed that the linearized version of Eq. 7 has two eigenvalues of very different magnitude (Fig. 2 D). The relaxation of x toward steady state is fast whereas that of y is slow, and the time evolutions of x and y are nearly independent. This system property can be used to simplify also the mesoscopic analysis. When k_x is small in relation to k_y, Y decreases via the enzyme catalyzed pathway with a rate near k_x, independent of Y. X is here small and the synthesis of X-molecules is virtually unaffected by feedback inhibition. These are the conditions described in the earlier section Parameter Constraints for Analytical Approximations. Under these conditions the joint probability distribution P(X, Y, t) for the number of X- and Y-molecules at time t can be factorized as

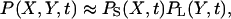(24)

where P_S(X, t) and P_L(Y, t) are the marginal distributions of X and Y, respectively. An equivalent approximation is valid for the corresponding stationary distributions P(X, Y), P_S(X), and P_L(Y).

A one-dimensional jump scheme for Y is

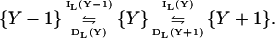(25)

The increment and decrement rates for the large pool, I_L(Y) and D_L(Y), respectively, are given by (compare with Eq. 7):

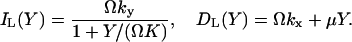(26)

For X the jump scheme is

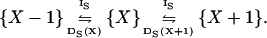(27)

The increment rate (I_S) and decrement rate (D_S) rates for X are given by (compare with Eq. 7):

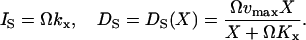(28)

The stationary marginal distribution, P_L(Y), for Y is given by

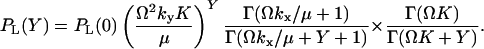(29)

When either feedback inhibition or dilution dominates, Eq. 29 is a displaced Poissonian (Johnson and Kotz, 1969). With feedback inhibition dominating, the average is 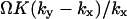and the variance . With dilution dominating, the average is 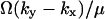and the variance 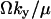. When both factors contribute, the average of Y is approximately 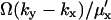and variance is 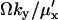. In analogy with Eq. 10, 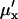is defined as

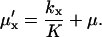(30)

In this approximation, the Fano factor,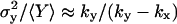, is the same as the logarithmic gain in the macroscopic concentration 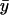to a change in k_y (Table 2; see also Appendix A4).

The marginal distribution, P_S(X) is the negative binomial (Paulsson et al., 2000; Råde and Westergren, 1995):

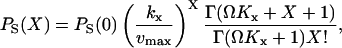(31)

with average 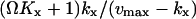and variance 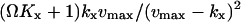. The Fano factor is close to the logarithmic gain for the response in 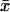to a change in k_x (Table 2; Fig. 2 B; see also Appendix A4).

Balanced inflows of substrates

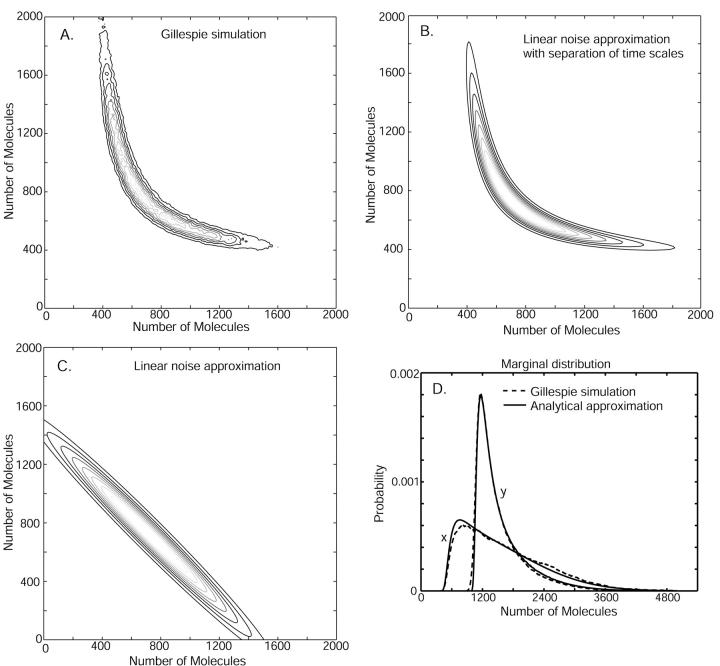
When the inflows to the two-substrate pools are nearly balanced (k_x ≈ k_y ≈ k), variations in X and Y are strongly coupled so that their joint probability distribution, P(X, Y, t), cannot be partitioned as in Eq. 24. (See Figs. 5 and 6). Now, the system has markedly nonlinear kinetics and displays large relative fluctuations (Fig. 4) suggesting that the linear noise approximation (van Kampen, 1997) for P(X, Y, t) might work poorly. We know that, macroscopically, the system moves to its stationary state in two phases with separated time scales (Fig. 3); in the slow time range the relaxation rate is determined by μ′ (Eq. 15) and in the fast time range essentially by the inverse of the turnover time of the metabolite pools (Eq. A37). As in the macroscopic case this property can be used to simplify system dynamics. The difference W = X − Y will display large fluctuations determined by the flow through the metabolite pools divided by the relaxation rate μ′. The sum U = X + Y, in contrast, will display small and rapid fluctuations around a quasi-steady state conditional on W. These rapid fluctuations are determined by the flow through the pools multiplied by the pool turnover time. This suggests a variable change from X and Y to U and W inasmuch as, under those conditions, the joint probability distribution P(U, W, t) can be approximated as (see Appendix A3):

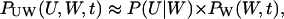(32)

where P(U|W) is the stationary distribution of U conditional on W and P_W(W, t) the distribution of W. Inasmuch as P(U|W) is a narrow distribution, P_W(W, t) is calculated with U = 〈U〉_W, where

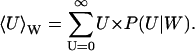(33)

Inasmuch as product formation does not change W, the jump scheme for W is simply

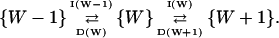(34)

The increment rate I(W) and decrement rate D(W) are given by

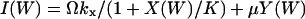(35)

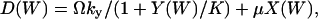where 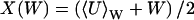and 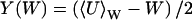. I(W) takes into account that W increases by synthesis of X-molecules and by removal of Y-molecules and D(W) that W decreases by synthesis of Y-molecules and removal of X-molecules. The master equation corresponding to Eqs. 34 and 35 is given in Appendix A3 along with its linear noise approximation, which renders a normal stationary distribution for W with average 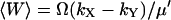and variance 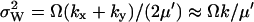. The stationary autocorrelation function, G(τ), of W is given by (compare with Eq. 15 with k_x = k_y = k):

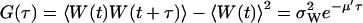(36)

FIGURE 5.

Probability distributions for two-substrate case. In A, B, and C, contour plots for the stationary joint probability distribution function P(X, Y). (A) P(X, Y) is estimated from Monte Carlo simulations by the Gillespie algorithm. (B) P(X,Y) as given by separation of time scales (Eq. 38 and Appendix A3). (C) P(X, Y) as resulting from a direct application of the linear noise approximation (See Appendix A2). Parameters: k_x = k_y = 1 μM s⁻¹, K_x = K_y = 0.5 μM, K = 1 mM, μ = 0.0004 s⁻¹, v_max = 2 μM s⁻¹, Ω = 10⁻¹⁵ liters. In (D), the marginal distributions P(X) and P(Y) are plotted as calculated from only the slow time scale fluctuations (i.e., 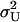= 0). For D, K_x = 0.5 μM and K_y = 1.5 μM.

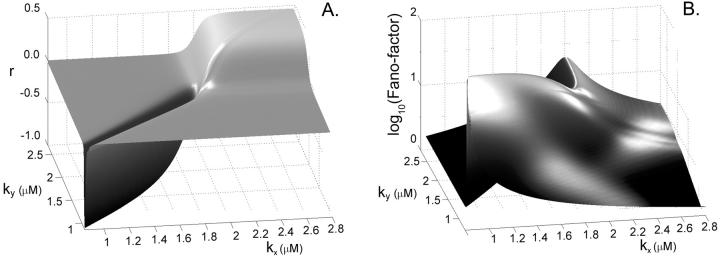
FIGURE 6.

Exploring parameter space with the linear noise approximation. Volume independent stochastic properties are plotted on the z-axis for different values of k_x (x axis) and k_y (y axis). (A) The correlation coefficient 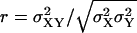, as approximated by 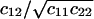. (B) The Fano factor 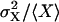as approximated by 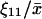(see Appendix A2). Parameters: K_x = 0.5 μM, K_y = 1.5 μM, μ = 0.0004 s⁻¹, K = 1 mM, and v_max = 2 μM s⁻¹.

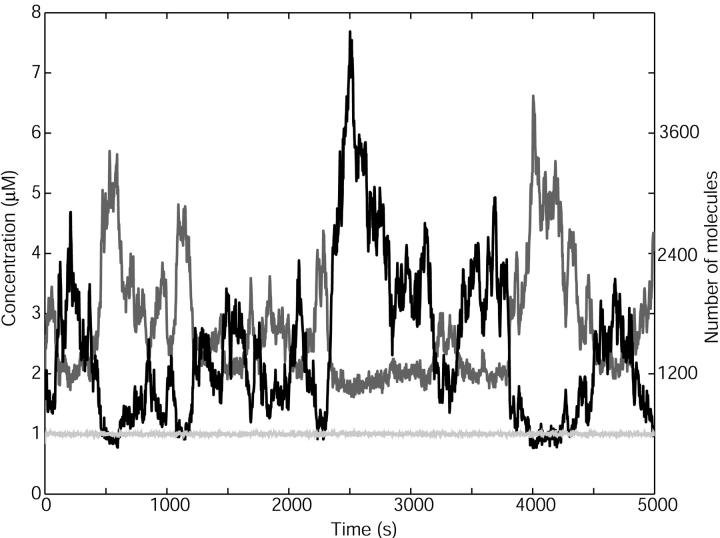
FIGURE 4.

Coupled mesoscopic fluctuations. x axis: Time in seconds. y axis: Concentration and number of molecules in the cell; X-molecules in black and Y-molecules in gray. The light gray line is the nearly constant rate of product formation, v(x, y), given in μM s⁻¹ (left y axis) Parameters: k_x = k_y = 1 μMs ⁻¹, K_x = 0.5 μM, K_y = 1.5 μM, μ = 0.0004 s⁻¹, v_max = 2 μM s⁻¹, Ω = 10⁻¹⁵ liters and no product inhibition ().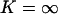

When product inhibition dominates over dilution (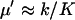) then 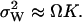In the absence of product inhibition and when volume growth and cell division are approximated by a first-order degradation rate one finds 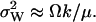In this latter case it is possible to derive an expression for 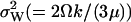directly from the master equation taking cell growth and division fully into account (Appendix A5). The result shows that the error that arises by replacing cell growth and division with a first-order degradation rate is a constant factor 2/3.

On the fast time-scale, when W is approximately constant, the jump scheme for U is approximated by

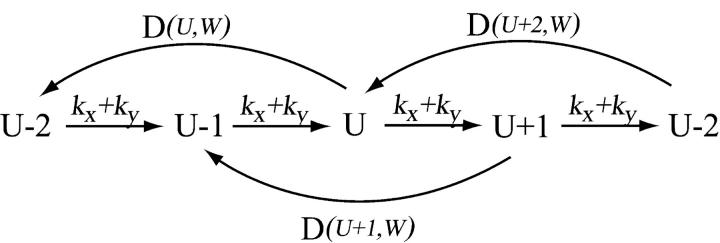(37)

The master equation for this scheme and its linear noise approximation are given in Appendix A3 along with steady-state estimates of the average 〈U〉_W, the variance 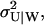and the autocorrelation function for the stochastic variable U, conditional on W. In general, 〈U〉_W and 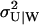must be calculated numerically but an analytical expressions can be found when k_x = k_y and K_x = K_y (Eqs. A36 and A37).

The joint probability distribution for X and Y can be approximated by Eq. 32, taking into account that W = X − Y and U = X + Y. We exemplify with the special case k_x = k_y = k, for which the stationary distribution P(X, Y) for X and Y follows from the normally distributed stationary linear noise estimates for 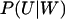and P_W(W) according to

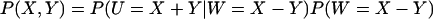(38)

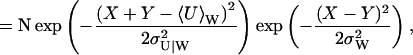where N is a normalization constant. Inasmuch as 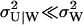(see Eq. A38) the sum U = X + Y will be close to its mean 〈U〉_W defined in Eq. 33. This feature leads to the characteristic shape of P(X, Y) in Fig. 5 B, which is very similar to a Gillespie estimate of the same distribution based on Eqs. 21–23 (Fig. 5 A).

In the limit 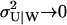are the stationary fluctuations in X and Y confined to a curve in the (X, Y)-plane ( 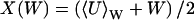and 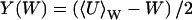). Fig. 5 D shows how this simplification affects the marginal distribution P(X) of X. For comparison we have also applied the linear noise approximation directly to the original master equation (Appendix A2) and, as expected, this leads to a much poorer representation of P(X, Y) (Fig. 5 C).

DISCUSSION

We have analyzed two standard schemes for enzyme-catalyzed elimination reactions: single-substrate Michaelis-Menten kinetics and two-substrate complex formation. To mimic in vivo conditions, we looked at irreversible reactions in growing and dividing cells where the inflow of substrates is inhibited by the substrate concentration (Cornish-Bowden, 1995; Cornish-Bowden and Cárdenas, 2001). We focused mainly on parameter combinations for which enzymatic substrate turnover dominates over dilution and where inhibition is weak. Such conditions would lead to high flow rates with comparatively small enzyme investments. The analysis is based on macroscopic rate equations to describe deterministic changes in a cell population and more realistic mesoscopic master equations to describe stochasticity in single cells. The study shows that even very simple enzymatic reactions display exotic kinetic behavior.

Michaelis-Menten elimination

If a metabolite is consumed in a Michaelis-Menten type reaction, how does its steady-state concentration depend on the rate of its production? When the inflow is much smaller or larger than the maximal outflow capacity (v_max) of the Michaelis-Menten reaction one should expect a direct proportionality, but around the point where the inflow equals v_max, a small percentage change in the production rate can give a very large percentage change in the steady state. Such sensitivity is typical near thermodynamic phase transitions and is intrinsically coupled to large random fluctuation (Haken, 1982; Joel, 1987). Here we show that the stationary Fano factor, i.e., the variance over average, can be simply approximated by the logarithmic gain in the macroscopic steady state to changes in the production rate (Berg et al., 2000; Paulsson, 2000; Paulsson and Ehrenberg, 2001). Thus, the closer to saturation the enzyme operates, the larger the random fluctuations and the slower the relaxation rate for its substrate concentration. Such systems will display near-critical behavior. Critical, because fluctuations become extremely large and relaxation rates extremely slow. Near, because volume growth and product inhibition attenuates the effects such that they disappear in the macroscopic limit.

Substrate-joining reactions

The simplest anabolic reaction is the joining of two metabolites to a higher-level complex. When one metabolite saturates the enzyme or has an externally regulated concentration, the other is typically eliminated through Michaelis-Menten kinetics, following the same type of dynamics as above. When instead the production rates of both metabolites are significantly smaller than the maximal rate (v_max) of complex formation, qualitatively different properties can emerge. For instance, when the two substrates weakly inhibit their own production and complex formation dominates over dilution, the metabolite pools become ultrasensitive to changes in inflow (Fig. 2). The reason is that the outflows are stoichiometrically coupled such that many different combinations of metabolite concentrations result in the same rate of complex formation. At steady state the inflow and outflow are exactly balanced for both metabolites, but there is also a broad range of concentrations where the flows are almost balanced. Mesoscopically, this corresponds to a statistical tendency to conserve the rate of the anabolic reaction rather than the metabolite concentrations individually. The metabolites can thus go on fairly unrestrained “random walks,” where one component can increase as long as the other one has a compensating decrease.

Zero-order ultrasensitivity and mesoscopic fluctuations

The concept of zero-order ultrasensitivity was introduced to characterize systems where both the rates of synthesis and consumption of a chemical compound are independent of its concentration (zero-order kinetics; see Goldbeter and Koshland, 1981). It was later pointed out (Paulsson, 2000) that such sensitivity is not dependent on zero-order rates per se, but occurs more generally when the rates of supply and consumption are of similar kinetic orders. Examples of “first-order ultrasensitivity” can, for instance, be found among self-replicating molecules (Paulsson and Ehrenberg, 2001) or in positive feedback loops (Paulsson and Ehrenberg, 2001). In all such systems, the high sensitivity is accompanied by long relaxation times and large random fluctuations (Berg et al., 2000). The latter are statistically possible because a spontaneous deviation from steady state leaves the net flow almost unchanged, which makes further deviations almost as likely as the return to steady state. Here we generalize this principle to several dimensions such that, even if deviations in a single component are typically followed by the return to steady state, there are combinations of deviations that are not effectively corrected. This leads to high steady-state sensitivities, slow relaxations, large random fluctuations, and strong correlations between different components. All these systems operate near critical points: the real parts of eigenvalues of the Jacobian (Appendix A1) are nonzero, but still much smaller than the turnover rates. Analysis of their stochastic behavior can in general be carried out with the linear noise approximation (Appendix A1; van Kampen, 1997) in combination with suitable variable changes and elimination of fast variables (see Fig. 5; see also Appendix A3; Elf and Ehrenberg, submitted).

Near-Critical Behavior in Living Cells

We have shown that near-critical phenomena can emerge in simple metabolic pathways. The question is if they occur in living cells or if metabolic networks have evolved to eliminate such behavior.

When two substrates are irreversibly joined together by an unsaturated anabolic enzyme (Fig. 2), the fraction of metabolites that form complexes rather than being degraded or diluted has a sharp maximum at the near-critical point where the inflows are balanced (Fig. 2 C). At this point, benefit (product formation) to cost (enzyme investment) ratio is maximal which has been suggested to be an evolutionary advantage for growing cells (Edwards et al., 2001; Ehrenberg and Kurland, 1984). Another potential advantage is to be found in transcriptional regulation. Particularly in those cases where the expression of enzyme encoding genes depends on the concentration of metabolites that determine the affinity of repressors or activators for DNA, sharp maxima of the logarithmic gain as in Fig. 2 B lead to near-Boolean control logic: synthesis of the enzyme responsible for the inflow to a metabolite pool will be fully on when the inflow is just below and fully off when it is just above the maximal rate of consumption (Elf et al., 2001).

Possible drawbacks of near-critical behavior are that the response times of the metabolite pools are long (Fig. 2 D) and the metabolite numbers display large fluctuations (Fig. 4). Response times and fluctuations can be reduced by intracellular feedback and product inhibition mechanisms (Cornish-Bowden and Cárdenas, 2001), but such strategies will also reduce the benefit-to-cost ratio above. This suggests that the optimal strategy for product inhibition is a compromise between fast pool responses and small fluctuations on the one hand and loss of efficiency in metabolite synthesis on the other.

Fluctuations in template directed biosynthetic pathways

There are cases when large fluctuations (or macroscopic variations) in intracellular substrate pools are particularly harmful. One class of such reactions contains DNA replication, transcription, and protein synthesis. In each case the ratios of substrate concentrations determine the substitution errors in the hetero-polymeric products that result from these reactions.

If the intracellular concentrations of deoxyribonucleotides display large fluctuations like the two substrates in Fig. 4, this could greatly increase the mutation rate of an organism. One way that cells can avoid this problem is to have their DNA polymerases always saturated with substrates, which would eliminate the near-critical behavior shown in Fig. 4 (compare with Fig. 6). Another, to carefully control the synthesis of the substrates for DNA replication by careful tuning of the allosteric properties of ribonucleotide reductases (Jordan and Reichard, 1998).

In protein synthesis the flows into the amino acid pools are feedback-inhibited (Neidhardt et al., 1996), which leads to fast pool relaxations and small fluctuations. This, however, does not solve the problem, inasmuch as the amino acids themselves are not the substrates for the ribosome. With the help of ATP the amino acids are first specifically coupled to transfer RNA molecules which subsequently enter the ribosome in ternary complex with a protein factor and GTP (Ibba and Söll, 2000). These ATP-dependent pathways for amino acid activation can decouple the pools of amino acids and ternary complexes. This means that even if the amino acid pools have short response times and small fluctuations due to feedback inhibition, the ternary complex pools can still be near critical with very slow relaxation rates and very large fluctuations (J. Elf and M. Ehrenberg, in preparation).

In summary, finite molecule numbers per cell and irreversible anabolic reactions can lead to near-critical behavior of metabolite pools with ultra-sensitivity, slow relaxation rates and large fluctuations. Such kinetic behavior is potentially harmful in template-directed synthesis of heteropolymers like proteins or DNA, and potentially useful in control systems requiring ultrasensitive responses.

APPENDIX

A0. Analytical expressions for maximal values of the logarithmic gain

One-substrate case

When k_x increases by dk from k in Eq. 6, the deviation dx from 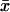is given by

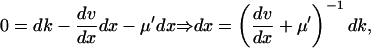(A1)

where

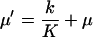(A2)

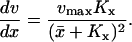The sensitivity a_xk is given by

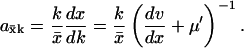(A3)

When feedback inhibition and dilution effects are small (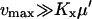), the maximal sensitivity is reached for 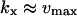and Eq. A3 can then be approximated as

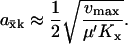(A4a)

When product inhibition dominates over dilution by growth (k/K ≫ μ), Eq. A4a simplifies to

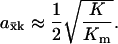(A4b)

Two-substrate case

First, put k_x = k_y = k in Eq. 7 to obtain the steady-state values for x and y. When k_x increases by dk from k, the deviations dx and dy from 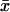and 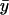, respectively, are given by

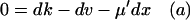(A5a,b)

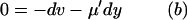where

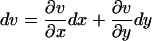(A6)

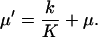Solve Eq. A5b for dy, insert in Eq. A5a and solve for dx

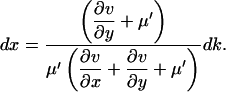(A7)

This gives

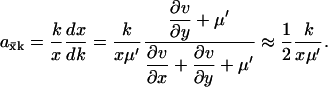(A8)

The approximation in the last step of Eq. A8 follows because when k_x = k_y, and when the flows are large and the concentrations low, then

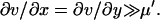(A9)

With 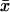from Table 2 for 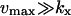, Eq. A8 becomes

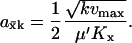(A10)

When k/K ≫ μ, Eq. A10 simplifies to

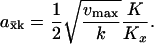(A11)

A1. The linear noise approximation for intracellular metabolite fluctuations

In this section we use the linear noise approximation (van Kampen, 1997) to obtain the fluctuation covariance matrix of the steady state of a system directly from its reaction scheme and macroscopic dynamics. For a biochemical system with R elementary reactions and N different chemical components we ascribe to each elementary reaction i an intensity 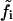that is defined from the probability 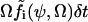that a reaction i occurs in the homogeneous system volume Ω during the short time interval δt. 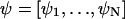is the concentration vector of the chemical components of the system. In the macroscopic limit, where Ω → ∞, 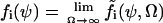. The macroscopic system dynamics is described by N ordinary differential equations:

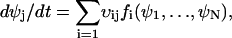(A12)

where v_ij is the number of molecules by which a component j changes when an elementary reaction of type i occurs. The stationary solution of Eq. A12, 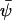, is obtained from

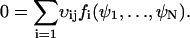(A13)

For sufficiently small deviations 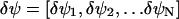from a steady state, 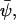the dynamics in Eq. A12 can be approximated by a system of linear differential equations, according to

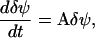(A14)

where the Jacobian matrix A has the elements

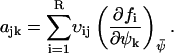(A15)

If all eigenvalues of A have negative real parts, the stationary state is asymptotically stable. The master equation for the probability, P(X, t), of having X = [X₁, X₂, …, X_N] molecules in the system at time t is

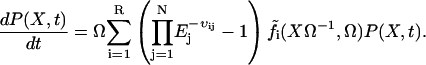(A16)

E is a step operator with the property that 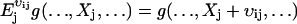. That is, when 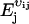acts on a function g(X), the component j of X is increased by v_ij molecules and, similarly, 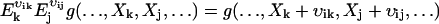. The linear noise approximation for the master equation, Eq. A16, is obtained in two steps. First, a new random vector x = [x₁, …, x_N] is introduced in Eq. A16, with components defined by

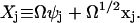(A17)

The stochastic variable X_j is thus described as a macroscopic term 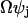plus a stochastic term 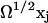, where the properties of x_j are determined by the master equation (Eq. A16).

Subsequent expansion of the resulting master equation to second order in 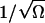(van Kampen, 1997) leads to a linear Fokker-Planck equation for the joint probability distribution 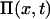of x:

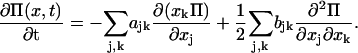(A18)

The matrix elements a_jk are given in Eq. A15. The elements 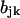of the diffusion matrix B (Risken, 1984) are

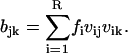(A19)

In the one-dimensional case B will be referred to as the diffusion constant. Generally, the A and B matrices depend on time through the functions , where 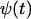is the solution to Eq. A12. Here the analysis will be confined to the special case that 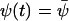, where 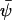is the solution to Eq. A13. Then, the stationary solution to Eq. A18 is the normal distribution, N(0, Ξ). Ξ is the covariance matrix, with elements ξ_ij, is the solution to the matrix Liapunov equation (Horn and Johnson, 1991; van Kampen, 1997)

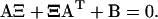(A20)

The covariance matrix, C, for the deviations, 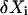, in molecule numbers from their macroscopic values, 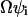, is related to 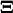through 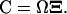In the linear noise approach, the expected value, 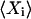, is approximated by the macroscopic value 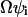, and the true covariance 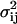by 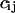. The Fano factor for a chemical component X_i is defined as its variance, 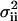, normalized to its expected value, 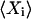, and can often be approximated by normalized to :

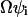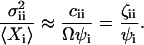(A21)

Inasmuch as the matrix C through Eq. A20 can be directly obtained from macroscopic parameters that all appear in or can be derived from Eq. A12, a preliminary survey of the stochastic properties of a system can be calculated for its entire parameter space in a simple and direct way. To do this, one has to correctly identify the stoichiometry coefficients, 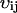, and the macroscopic rate laws, f_i, in Eq. A12, and use these to calculate the matrix A through Eq. A15 and the matrix B through Eq. A19.

A2. Linear noise approximation in the two-substrate case

In this section we will apply the linear noise approximation to the two-substrate case, macroscopically described by Eq. 7 in the main text, according to the method that was outlined in the previous section. To be consistent with the nomenclature in Appendix A1 and with the literature (van Kampen, 1997), we first replace x by 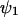, y by 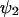and put dψ/dt = 0 in Eq. 7, to obtain the stationary state vector 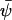. The rate laws, f_i and stoichiometric coefficients, ν_ij, are given by

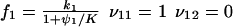(A22)

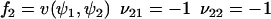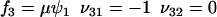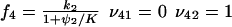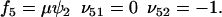The Jacobian matrix, A, in Eq. A15 is given by

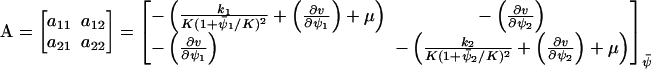(A23)

where

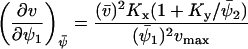(A24)

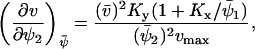and 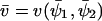. The diffusion matrix, B, in Eq. A19 is given by

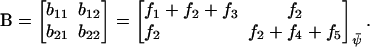(A25)

The covariance matrix, C, for the fluctuations in X and Y can now be obtained from Eq. A20. The linear noise estimate of the correlation coefficient 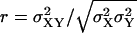is in Fig. 6 A plotted as a function of k_x and k_y. When the enzyme is unsaturated with substrates, i.e., k_x < v_max or k_y < v_max, the figure confirms that when k_x ≈ k_y the fluctuations in X and Y are negatively correlated but otherwise uncorrelated. A result not discussed in the main text is that when both k_x and k_y are larger than v_max, then X and Y are positively correlated, inasmuch as they are consumed as pairs in the same reaction. The linear noise estimate (Eq. A23) of the Fano factor for X is plotted in Fig. 6 B for the same k_x, k_y-range as in Fig. 6 A. By looking at sections for fixed k_y values, we find the behavior from Fig. 2 B, when k_y < v_max, and from Fig. 1 B, when k_y > v_max.

An analytical solution for C can be obtained in the special case when k_x = k_y = k, k < v_max, K_x = K_y = K and 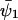, 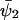≪ K. Then AC in Eq. A20 is symmetric and C approximated by

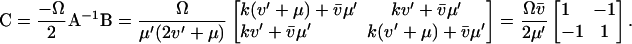(A26)

In the last step we have used that 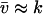, μ′ ≪ v′, where 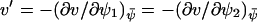. Here, the variances are proportional to the flow, 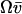, through the pools and inversely proportional to μ′. The fluctuations in X and Y are negatively correlated. The Fano factor, approximated by 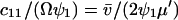, is equal to the sensitivity amplification as given in Eq. A8, where 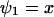and .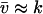

A3. Separation of time scales, followed by linear noise approximation in the balanced two-substrate case

Linear noise approximation for the difference W = X − Y with balanced rates of supply of substrates

When k_x ≈ k_y ≈ k in Eq. 7, it is favorable to change variables before applying the linear noise approximation. We introduce the new variables w = x − y and u = x + y. In this section we will analyze fluctuations in w under the assumption that u has small and rapid fluctuations around its stationary value 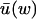for each w, and that x and y are given as functions of w alone; 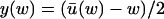and 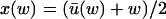. In the next Appendix section we will study fluctuations in u to determine when this separation of time scales is possible.

To connect to Appendix A1 we rename the dynamic variable w to ψ. From Eq. 7 we identify the rate laws, f_i, and stoichiometric coefficients, ν_ij, as

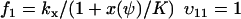(A27)

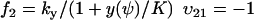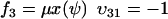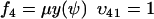From Eq. A12 we obtain the following differential equation for ψ:

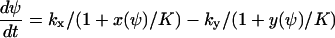(A28)

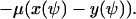The scalar Jacobian A, i.e., the relaxation rate, is obtained by differentiation of Eq. A28 with respect to ψ. This gives (compare with Eq. 15 of the main text):

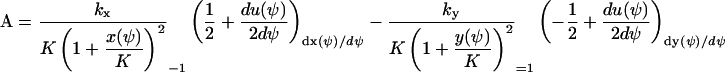(A29)

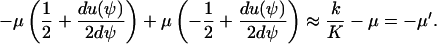We have used that 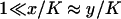and that 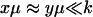when k_x ≈ k_y ≈ k. Under the same conditions, the stationary state, 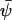, of A16 is given by 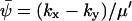(compare with Eq. 15) and the diffusion constant, B, is given by (from Eq. A19):

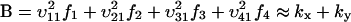(A30)

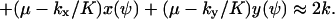It follows that the stationary probability distribution for W = X − Y in the linear approximation is normal with mean, 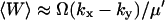, and variance (from Eq. A20).

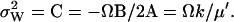(A31)

Linear noise approximation for the sum U = X + Y for balanced rates of substrate supply

In this section we analyze the fluctuations in u = x + y, conditional on W = Ωw = x − y. The single dynamic variable, u, is renamed ψ, i.e., 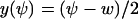and 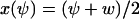, where w is fixed. From the scheme in Eq. 37 and Eqs. 21–23, we identify the rate laws, f_i, and stoichiometric coefficients, ν_ij, for reactions that change ψ:

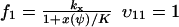(A32)

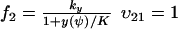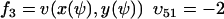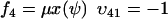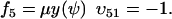To study the parameter dependence analytically, we consider the special case k_x = k_y = k and neglect product inhibition and dilution, which only have marginal influence on the fluctuations in u, when k < v_max. Numerical methods have to be used for a more general treatment. The reduced set of reactions is:

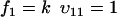(A33)

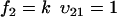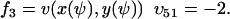This corresponds to the macroscopic rate equation (from A12):

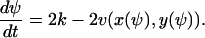The stationary state, 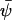, that depends on w is given by the equation 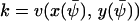(from Eq. A13). This equation also defines the stationary flow 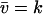. The relaxation rate, A, at the stationary state 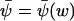(from Eq. A15), is

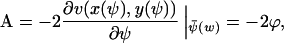(A34a)

where

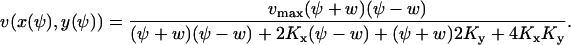(A34b)

Eq. A34b is a restatement of Eq. 5 in the main text. The diffusion constant, B, is evaluated in the stationary state where 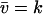(from Eq. A19)

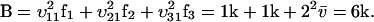(A35)

The average, 〈U〉, is approximated by the macroscopic value, 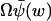, and the variance (from Eq. A20) by

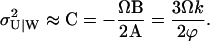(A36)

When v(x, y) is symmetric in x and y, i.e., K_x = K_y = K_z, the stationary value

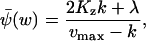where

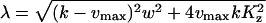and relaxation rate, ϕ, evaluate to

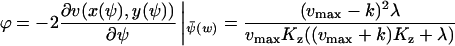(A37)

When k = v_max/2, ϕ changes from 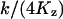, for low w, up to 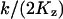, for high w, i.e., 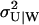changes from 6ΩK_z, for low w, up to 3ΩK_z, for high w. That is, the variance is about the size of the pool and the Fano factor is therefore ∼1. For these parameters (i.e., K_x = K_y = K_z and k = v_max/2), one obtains:

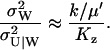(A38a)

Here, the expression for 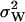from Eq. A31 have been used. The quotient in Eq. A38a tells us that the fluctuations in W are much larger than the fluctuations in U conditional on W, when the relaxation rate of the pools is much smaller than the rate of pool turnover, i.e., 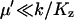. When product inhibition dominates over dilution, i.e., 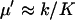, this condition is equivalent to that .

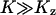As ϕ is the rate of relaxation of U, Eq. A37, and μ′ is the rate of relaxation of W, Eq. A29, the same conditions define when the method of separation of time scales is applicable:

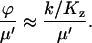(A38b)

A4. Linear noise approximation and sensitivity amplification

The close correspondence between the Fano factor (Eq. A10) and the sensitivity amplification (Eq. 8) has been discussed in previous work (Berg et al., 2000; Paulsson, 2000; Paulsson and Ehrenberg, 2001).

To facilitate reading we reproduce these earlier results in our nomenclature by applying the linear noise approximation as described in Appendix A2 to a simple birth and death process that is defined by the following scheme:

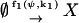(A39)

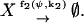X-molecules are increased with the rate f₁, which depends on their concentration ψ and on an external parameter k₁. X-molecules are consumed with the rate f₂, which also depends on ψ and on an external parameter k₂. It is assumed that one X-molecule at the time is either added to or removed from the system. There are two elementary reactions and one chemical component. The stoichiometry parameters, introduced in Eq. A1, are ν₁₁ = 1 and ν₂₁ = −1. The Jacobian A, defined in Eq. A15, is here a scalar that is given by

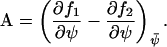(A40)

The steady-state concentration 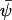is defined by the relation 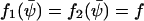. According to Eq. A19, the diffusion constant B is given by 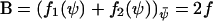. From Eq. A20 follows that C (=ΩΞ) is given by

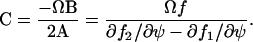(A41)

The Fano factor can, according to Eq. A10, be approximated by dividing C with the macroscopic estimate, Ωψ, for the expected number of X-molecules. That is,

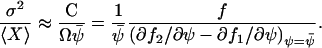(A42)

The Fano factor from the linear noise approximation (A42) is equivalent to the concentration control coefficient in MCA (Cornish-Bowden, 1995; Fell, 1997; Kacser and Burns, 1973). The sensitivity amplification a_ψk1, defined in Eq. 8, of the concentration ψ to a variation in the external parameter k₁ is given by

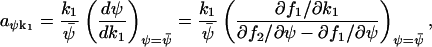(A43)

and the sensitivity amplification of ψ to a variation in k₂ is given by

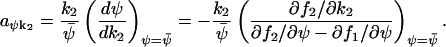(A44)

The expressions for the Fano factor in Eq. A42 and the sensitivity amplification in Eq. A43 are identical if and only if f₁ is linear in k₁. Similarly, the Fano factor and the sensitivity amplification in Eq. A44 have identical numerical values but opposite signs if and only if f₂ is linear in k₂. When one parameter, k, effects both f₁ and f₂, the sensitivity, a_Ψk, is given by

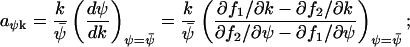(A45)

This expression is equal to Eq. A43 or Eq. A44, when eithe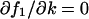r or 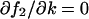. In general, the linear-noise version of the Fano factor is related to the sensitivity amplification a_Ψk through

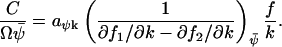(A46)

A5. First-order degradation compared to dilution by exponential growth

There is a subtle difference between the discontinuous cell division and its continuous approximation. With k_x = k_y = k, μ = 0 and in the absence of product inhibition, the scheme in Eq. 34 shows that the variable W is subjected to an unrestricted random walk between cell divisions (a Wiener process for continuous W). In this case, W will have zero mean and a variance that each cell cycle increases by the expected number of synthetic events for X and Y. The current rate of such events in the cell cycle is 2kΩe^μt and the expected total number of synthetic events is obtained by integrating the current rate from time zero to the generation time ln2/μ. This gives a variance increase of 2kΩ/μ per cell cycle. At cell division the number of molecules per cell decreases by a factor of two and this reduces the variance of W by a factor of four. When a cyclic steady state has been established (Paulsson and Ehrenberg, 2001), the variance of W at time zero just after cell division is therefore given by

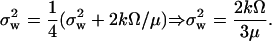(A47)

This is two-thirds of the variance calculated by approximating dilution by a degradation event (compare with Eq. A31). Note that this result is independent of the linear noise approximation. Eq. A47 is very accurate when both the number of reactions that occur every cell cycle and the number of molecules are large (>1000). In the continuous limit the distribution is normal, N(0,σ_w).