Protein Interactions and Membrane Geometry

Abstract

The difficulty in growing crystals for x-ray diffraction analysis has hindered the determination of membrane protein structures. However, this is changing with the advent of a new method for growing high quality membrane protein crystals from the lipidic cubic phase. Although successful, the mechanism underlying this method has remained unclear. Here, we present a theoretical analysis of the process. We show that it is energetically favorable for proteins embedded in the highly curved cubic phase to cluster together in flattened regions of the membrane. This stabilizes the lamellar phase, permitting its outgrowth from the cubic phase. A kinetic barrier-crossing model is developed to determine the free energy barrier to crystallization from the time-dependent growth of protein clusters. Determining the values of key parameters provides both a rational basis for optimizing the experimental procedure for membrane proteins that have not yet been crystallized and insight into the analogous cubic to lamellar transitions in cells. We also discuss the implications of this mechanism for protein sorting at the exit sites of the Golgi and endoplasmic reticulum and the general stabilization of membrane structures.

INTRODUCTION

The in cubo method of growing membrane protein crystals from the cubic phase has produced x-ray diffraction quality crystals of bacteriorhodopsin (bR), halorhodopsin, and sensory rhodopsin II (Belrhali et al., 1999; Kolbe et al., 2000; Luecke et al., 2001; Royant et al., 2001) in a manner that appears to be generally applicable to all membrane proteins (Chiu et al., 2000). For bR the process is understood on a phenomenological level: First, a Pn3m-type cubic phase is formed with the matrix lipid monoolein (MO) in a way that membrane proteins are initially distributed throughout the cubic phase. Next, the system is exposed to salt that osmotically draws water from the interior compartment of the cubic membrane phase. This causes the edge length, or lattice parameter, of the unit cell to shrink by ∼15% (Nollert et al., 2001). In the absence of membrane proteins, such a shrinkage has no effect on the cubic structure of the membrane. However, when proteins are present, they begin to cluster together and locally flatten regions of the cubic phase into lamellar stacks, eventually forming arrays large enough for x-ray analysis (Nollert et al., 2001). The salt concentration is crucial to forming crystals, because counterions mask electrostatics in the close-packed crystal; however, the dehydration of the cubic phase can be carried out at salt concentrations of 100 mM–400 mM. This implies that the major crystallization-inducing factor is the change in membrane structure and not changes in counterion concentration.

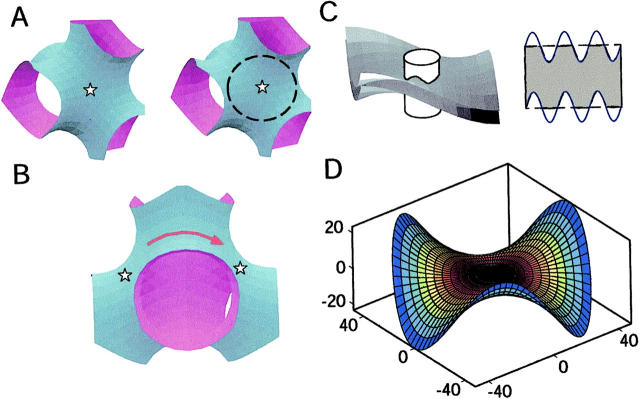
The precise relationship between the lattice parameter and the cubic phase geometry can be understood using as a model the D minimal surface (DMS), a mathematical surface that closely approximates the neutral surface of the Pn3m cubic phase (Scriven, 1976). The DMS is a closed triply periodic surface that divides space into two distinct multiply connected regions (Fig. 1, A and B). Minimal surfaces are characterized by negative Gaussian curvature and zero mean curvature, so that every small piece of the surface is saddle shaped. It is exactly these saddle-shaped curvatures that give rise to membrane-protein interactions, inasmuch as saddle splay exposes the hydrophobic midsection of membrane proteins, as illustrated in Fig. 1 C. The membrane deformation needed to cover these exposed patches requires an elastic work proportional to the preexisting Gaussian curvature (Kim et al., 1998).

FIGURE 1.

Surface plot and curvature of the DMS. (A) Stereo pair showing a unit cell of the DMS, which underlies the geometry of the Pn3m lipidic cubic phase (Brakke, 1992). The extended phase iterates these “tubular units”. Stars mark the centers of monkey saddles where the curvature is a minimum (see D). (B) View of two adjacent monkey saddles. The arrow indicates the path that proteins traverse in passing between monkey saddles. (C) Cartoon of a rigid cylindrical protein embedded in a curved lipid bilayer (left side). If the membrane does not deform from its minimal surface state, undulations arise along the protein-bilayer contact curve. This creates mismatches between the hydrophobic midsections of the protein and the membrane (right side). This is energetically unfavorable, and consequently the membrane distorts to cover up the exposed hydrophobic patches, introducing mean curvature into the membrane surface. (D) The monkey saddle around one of the four sites of minimum Gaussian curvature. See Appendix A for how this is drawn. Level curves of constant Gaussian curvature are represented on the surface for a lattice constant of a = 93.3 Å (−36 (blue), −16 (yellow), 0 (center) × 10⁻⁴ Å⁻²). When proteins move away from these minima, the elastic energy increases several k_BT. This effectively limits the configuration space of the proteins in the bulk cubic phase, and permits the use of a lattice model for nucleation. Axes are in Ångströms.

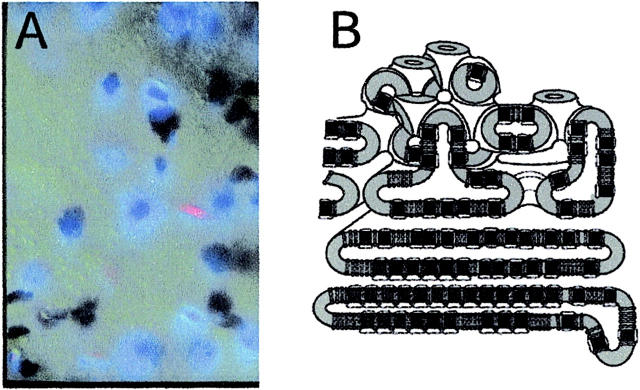
To minimize the elastic energy of deformation, proteins in the Pn3m cubic phase will tend to aggregate at the four “monkey saddle” loci in each cell (shown in Fig. 1 D) where the Gaussian curvature is minimum. Because the size of these loci is comparable to the size of the proteins, the in-plane aggregation of proteins will flatten these regions, making them more energetically attractive for further protein aggregation. Thus, judging from experiment, protein aggregation foments the growth of lamellar regions devoid of Gaussian curvature that are interconnected by tubular regions, the latter of which are the residues of the original connections between unit cells of the cubic phase. As the lamellar stack regions grow, a transition zone separates them from the surrounding bulk cubic phase. Direct evidence of this distortion zone can be seen from cross-polarized light experiments that reveal a “halo” region around crystals (Fig. 2). This noncubic transition structure has some mean curvature, and a concomitant elastic energy cost associated with it. Under crystallization conditions in the absence of proteins, the lamellar phase is transiently observed but never stable. As the lattice parameter decreases, these transients occur more frequently (Caffrey, 2000).

FIGURE 2.

Membrane distortion zone around protein crystals. (A) Protein crystals embedded in the cubic phase viewed with cross-polarized light. The crystals are a deep blue and are surrounded by a hazy blue birefringent halo. Blue birefringence is indicative of a nonisotropic, possibly lamellar, lipid phase. Away from this zone the lack of birefringence is characteristic of a bulk cubic phase. (B) Cartoon representing the disturbance layer in A. The Pn3m cubic phase is thermodynamically stable for MO under the experimental conditions, whereas a lamellar phase is favored by the proteins (see Fig. 3) and the membrane lipids that form the lamellar stacks of the crystal (Landau and Rosenbusch, 1996). The connectedness between the bulk cubic phase and the growing lamellar phase allows proteins to diffuse into the crystal. However, this connection region composed of MO lipids is necessarily a higher energy configuration than the D cubic phase. The energy cost of creating this zone gives rise to an energy barrier to protein aggregation that is treated as an effective surface tension (see Eq. 3).

Standard crystallization experiments occur in liquid solvent; in the cubic phase method the membrane plays the role of the solvent. Despite this difference, all crystallization processes share a fundamental common feature. Nucleation conditions arise when the growth of the crystalline phase acquires a favorable bulk energy and an unfavorable surface energy. We suggest that a substantial component of the favorable bulk energy arises due to the elastic strain relieved as proteins enter the flattened regions of the crystal, whereas the distortion zones surrounding the crystals give rise to an effective surface tension that opposes aggregation. These energies can be computed from the geometry of the cubic phase and characteristics of the protein. Additionally, we develop a general nucleation kinetic scheme to interpret crystallization experiments and to extract information such as free energy barriers and critical cluster sizes. These methods complement each other and present a consistent picture of in cubo membrane protein crystallization.

In the ensuing sections we quantify the qualitative scenario outlined above. In the Discussion, we apply the insights gained from studying the in vivo growth of crystals to discuss how the shapes and curvatures of physiologically relevant membranes might induce the aggregation of membrane proteins. The preponderance of highly curved surfaces in the cell is reviewed and the connection with protein sorting is addressed within the context of our theory of membrane-protein interactions.

A MODEL FOR IN CUBO MEMBRANE PROTEIN CRYSTALLIZATION

Membrane-protein energetics in curved places

We model proteins as rigid bodies that impose clamped boundary conditions on the surrounding membrane neutral surface (Harroun et al., 1999; Kim et al., 1998; Nielsen et al., 1998; Weikl et al., 1998). The far boundary conditions are determined by matching the solution of the model equations to the DMS. Thus, in the absence of proteins, solutions give rise to the unperturbed surface. This imposes constraints on the height and angle of the neutral surface along the protein contact curve. Membrane protein crystals grown in cubo are nearly cylindrical in shape (Chiu et al., 2000). This implies that the protein-bilayer contact boundary forms a circle, and that the membrane locally forms a plane around the protein. The curvature energy of the bilayer is given by the standard Helfrich model (Helfrich, 1973):

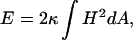(1)

where the integral is over the neutral surface, here represented by the DMS. H is the local mean curvature of the membrane, and κ is the bilayer elastic modulus. The Gauss-Bonnet theorem from differential geometry states that the surface integral of the Gaussian curvature remains constant under deformations that do not change the topology. Inasmuch as the number of proteins, and thus the number of boundaries in the model surface, is constant, the Gaussian curvature term need not be considered in Eq. 1 (Kim et al., 1998). The monolayer bending modulus is 2.8–5.0 k_BT leading to bilayer values in the range 5.6–10.0 k_BT (Chung and Caffrey, 1994; Vacklin et al., 2000).

There are two positions for proteins in the membrane whose energies must be calculated: 1), the center of the monkey saddle where the curvature is a minimum, and 2), the horse saddle that must be traversed by a protein diffusing from one monkey saddle to the next (Fig. 1). In Appendix A, it is shown how the structure of the unperturbed DMS was determined using level set approximations, and we formulate and solve the appropriate biharmonic boundary value problem that arises from the Helfrich model. This determines the membrane bending energy as a function of the lattice parameter, ɛ_elas.(a).

The formation of crystals reduces the system's configurational degrees of freedom, hence there is a significant entropic barrier to their creation. Two aspects of crystallizing from a membrane reduce this entropic barrier, as compared to solution methods: 1), the membrane removes one translational degree of freedom and two rotational degrees of freedom from the protein, and 2), the geometry of the cubic phase further restricts the initial phase space by confining proteins to the monkey saddle regions. As shown in the Results section, the energy cost associated with proteins at positions other than the monkey saddle is large; therefore, these positions have a small associated occupancy. This makes the construction of a lattice model practical. Thus, we posit that N proteins are free to occupy m > N binding sites represented by the monkey saddles. Both of these numbers, N ∼ 9 × 10¹⁴ and m ∼ 52·N, are accessible from the experimental preparations (Nollert et al., 2001). As proteins begin to aggregate into clusters of size k, the total configurations can be explicitly counted leading to the familiar expression for the entropy cost of adding single proteins to the cluster (see Appendix B): Δs = k_BT·log(1/ρ₁). In the thermodynamic limit, ρ_T = N/m ∼1/52 is the total protein density, and ρ₁ is the monomer density. From this model the chemical potential driving the growth of crystals is

(2)

where a lattice parameter independent electrostatic term, ɛ_elec., has been included. At the beginning of an experiment, the total protein density is assumed to be in monomer form; thus, the initial entropic component of the chemical potential is k_BT log(1/ρ₁) ∼ −4 k_BT.

Nucleation kinetics

The analysis of macroscopic crystal growth can be used to reveal additional information regarding the microscopic energies underlying the in cubo crystallization process. For small cluster sizes, surface energy costs make the growth of crystallites energetically unfavorable; however, crystals spontaneously grow once they reach a critical cluster size, K. The overall rate of crystal formation depends exponentially on the height of this barrier at K. Calculating this barrier for ideal hard spheres is possible but computationally intensive (Auer and Frenkel, 2001), and the energy landscape of the in cubo system is sufficiently complicated so as to further hinder such calculations. Therefore, we resort to an analysis of experimental bR crystallization kinetics to extract this energy. The results of this analysis aid the generalization of the in cubo method to the crystallization of other membrane proteins.

The total number and size of clusters formed during a crystallization experiment are readily measured. However, due to monomer depletion, extracting the height of the nucleation barrier from this information is not trivial because the height dramatically changes over the time course of the experiment. To address this issue, we begin with the discrete form of the standard model for the free energy of a crystal of size k:

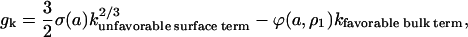(3)

where ϕ(a, ρ₁) can be computed from the model, Eq. 2. The surface tension is obtained by fitting experimental data as described below. The largest cluster energy in Eq. 3, denoted by g_K, is the activation barrier in a nucleation reaction: (k−1 cluster) + monomer ↔ (k cluster). The kinetics of this process are described by a system of ordinary differential equations determining the time evolution of the cluster densities, where the fluxes depend on the cluster densities according to:

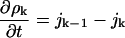(4)

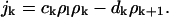Here, the ratio of the creation, c_k, and destruction, d_k, coefficients is determined via the principle of detailed balance using the relative cluster energies, Eq. 3. The value of d_k is determined through correspondence with macroscopic crystallization as shown in Appendix C.

The crystallization process advances through three phases. Initially the nucleation of crystals proceeds slowly as crystallites coalesce and break up, only rarely crossing the large energy barrier. During this nucleation phase, the monomer concentration remains nearly constant. The first crystals that exceed the critical cluster size become the dominant consumers of the monomer concentration. Their growth depletes the monomers, which in turn decreases the chemical potential and further raises the activation energy barrier. The nucleation phase then ends with the large crystals continuing their supercritical growth, with k ≫ K. Eventually the depletion of monomer grows so large that the critical cluster size becomes comparable to the size of the crystals. This signals the end of the supercritical growth phase and the beginning of the coarsening phase described by traditional Lifshitz-Slezov theory (Lifshitz and Slezov, 1961).

Rather than solve the large set of coupled, stiff differential equations in Eq. 4, we use a novel asymptotic analysis. Traditional asymptotics scales the variables to obtain reduced equations as limits of scaled equations. Analysis of this reduction is carried out in Appendix E, and the desired relationship between microscopic energies and crystal size is presented in the Results section. Slezov and co-workers (1996) have carried out a similar calculation starting from the same physical assumptions; however, their model for the growth of large crystals corresponds to a different macroscopic phenomenon.

RESULTS

Elastostatics drives crystal growth

Proteins embedded in the cubic phase induce strain in the surrounding bilayer, which is only relieved by diffusion into the flattened lamellar region near a crystal. We have computed the bending energy associated with a cylindrical protein of the size of a bR molecule located at the center of a monkey saddle. As the lattice parameter decreases, the energy cost of proteins at these sites increases 5–10 k_BT, depending on the value of the experimentally measured bending modulus (Fig. 3 B). The compatible boundary conditions ensure that there is no curvature energy associated with proteins in flat bilayers, so that the curve in Fig. 3 B is exactly the elastic energy component of the chemical potential, ɛ_elas.(a). As shown in Appendix A, ɛ_elas. scales as the fourth power of the protein radius: ɛ_elas. ∼ R⁴. Therefore, large proteins favor the formation of lamellar stacks much more than smaller ones. For instance, a protein with four membrane spanning helices, or a diameter just larger than half that of bR, will have an elastic driving force of ∼0.3–0.6 k_BT at a = 93.3 Å. This poses a problem for crystallizing small proteins and generally limits the broad-based applicability of the in cubo method, although in particular the use of MO-based cubic phases is limited to membrane proteins with five or more transmembrane helices.

FIGURE 3.

Protein energetics in the Pn3m cubic phase. (A) Computed deformation field of the monkey saddle region with a single inclusion in the bulk Pn3m cubic phase. The surface color (red and blue) represents the induced mean curvature radiating outward from the inclusion. (B) Binding energy for adding a single bR-sized protein to a growing lamellar crystal as a function of the lattice parameter. The energy is plotted using an upper and a lower bilayer bending modulus determined from experimentally measured monolayer bending moduli for the monoolein system. The monolayer values are κ_m = 2.8 k_BT (Vacklin et al., 2000), corresponding to the red curve, and κ_m = 5.0 k_BT (Chung and Caffrey, 1994), corresponding to the blue curve. These curves are plotted with bilayer bending moduli twice the recorded monolayer values. This assumes no interdigitation between the monolayer leaflets and is likely an underestimate of the true bilayer bending modulus. The elastic energy increases sharply at smaller lattice parameters, which drives the formation of crystals. (C) The energy barrier for crossing from one minimum energy site to the next is plotted as a function of the lattice parameter. The bilayer bending modulus corresponding to Vacklin et al.'s monolayer value was used (Vacklin et al., 2000). This barrier to diffusion slows the movement of proteins in the cubic phase.

As proteins diffuse through the cubic phase, they encounter horse saddles of high Gaussian curvature (Fig. 1 B). These regions do not play a role in the free energy difference between the dilute and crystal phases, but they are important for the kinetics of nucleation inasmuch as the curvatures present a local energy barrier to protein motion. Applying our analysis to proteins residing at the horse saddles, the elastic energy cost at these intermediate positions was computed. The relevant barrier crossing energy, u(a), in Fig. 3 C is the energy difference between proteins residing at the horse saddle and the monkey saddle. The net diffusion coefficient is obtained by multiplying the flat bilayer value by an Arrhenius factor corresponding to the Kramers jump rate for moving from monkey saddle to monkey saddle: D(a) = D₀exp(−u(a)/k_BT). In Appendix F, we estimate the flat bilayer diffusion coefficient for a protein the size of bR as D₀ ∼ 3.3 μm²/s, using the MO bilayer viscosity measured by Tsapis et al. (2001). The large values of u(a) predict that the diffusion coefficient decreases by several orders of magnitude as the lattice parameter shrinks. In their study of the LH2 complex, Tsapis et al. measured a reduced diffusion coefficient that could not be explained by obstruction factors that take into account distance changes on curved surfaces (Tsapis et al., 2001). However, this reduction is minor compared to the values predicted here, and their experiments were carried out in a different cubic phase at large lattice parameter values, a ∼ 131 Å. At such hydrated states, the height of the crossing barrier is greatly diminished and the elasticity calculations presented herein accordingly predict little change in diffusive motion.

This model allows the computation of the driving force for single proteins to join a sizable crystal, but the complexity of the cubic phase geometry coupled with the difficulty of elastostatic calculations prohibits a detailed calculation of the energetics of small clusters. Computations of up to four proteins have revealed that interactions are attractive in the neighborhood of horse saddles but repulsive around the more stable monkey saddles (data not shown). However, these calculations did not allow for significant local rearrangements of the cubic phase structure, an assumption that becomes suspect for even a few proteins packed in one unit cell. For these reasons, an alternative kinetic analysis of experimental data was carried out to determine the free energy barrier to crystallization and the critical cluster size.

Nucleation kinetics and experiments

The asymptotic approximation to the master equation, Eq. 4, results in an integral equation describing the decrease in the monomer concentration over the time course of the experiment, t:

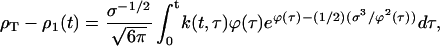(5)

where k(t, τ) is the final size of crystals that were nucleated at time τ, the chemical potential is expressed in terms of time, and its dependence on the lattice parameter has been suppressed. Three elements give rise to this equation: 1), the nucleation rate of new crystals ∝ exp(−(1/2) σ³/ϕ²), 2), the growth of large clusters represented by the remaining terms of the integrand, and 3), the total protein constraint. As qualitatively described in the last section, Eq. 5 contains all of the essential physics of the nucleation process.

From the analysis of Eq. 5, a nucleation period, t_nuc., can be identified:

(6)

where ν is the volume per protein in the crystal, ɛ is the nonentropic component of the chemical potential, and nondimensional energies are in units of k_BT. When the initial value of the chemical potential, ϕ₀, goes to zero, the nucleation time becomes infinitely long. For permissive values of ϕ₀, the logarithm of the nucleation time is ∼2/5 of the initial free energy barrier. After the passage of several nucleation times, the total number of proteins in a crystal is

(7)

From this equation, it is easy to see that large initial free energy barriers give rise to large crystals. This is a result of the reduction in the crystallization rate that decreases the total number of crystals formed allowing those that do form to adsorb more of the protein monomers. However, as can be seen from Eq. 6, these experiments require exponentially more time to carry out. In practice, we use the more complicated counterparts to Eqs. 6 and 7, presented in Appendix E, to relate experimentally measured quantities to microscopic energies.

From the experimental measurements of Nollert et al. (2001), the crystal size was determined as a function of lattice parameter and plotted in Fig. 4 A. Using the known crystal geometry and protein packing fraction, the number of proteins per crystal was estimated and plotted in Fig. 4 B. This completely determines the left-hand side of Eq. 7. The electrostatic contribution to the chemical potential can be computed by realizing that the two equations above have only two unknowns, ϕ₀ and G₀, whereas all other parameters have been experimentally determined or are accessible by theory. The nucleation time in Eq. 6 is required to complete this reduction. We estimated this value at the upper lattice parameter, a = 93.3 Å, where crystals take at least one month but no more than nine months to nucleate. Assuming an approximate nucleation time of three months coupled with the log(k_∞) graph, Eqs. 6 and 7—or more correctly their complicated counterparts found in the supporting material—were simultaneously solved using a standard search algorithm. This gave ɛ_elec. = 4.1 k_BT and a free energy barrier to crystallization of G₀(93.3 Å) = 43.6 k_BT. More importantly, ϕ₀ is determined for all lattice parameter values using the model Eq. 2. Although the uncertainty in the nucleation time is disconcerting, notice from Eq. 6 that t_nuc. is related to the dominant energies through an exponential. This means that errors in t_nuc. are exponentially suppressed when determining energies.

FIGURE 4.

Protein crystal sizes as a function of the lattice parameter. (A) Crystal edge length as a function of the lattice parameter (adapted from Nollert et al., 2001). The longest axis of bR crystals (n ≥ 10) was measured as a function of salt concentration. Separately, the lattice parameter of the cubic phase was determined as a function of the salt concentration. A linear fit was computed to the lattice parameter versus salt concentration and used to determine the crystal edge length as a function of lattice parameter as shown. (B) Natural log of the total number of proteins in a crystal as a function of the lattice parameter. bR crystals pack into hexagonal arrays at a composition of 70% protein and 30% purple membrane lipid. The volume of the crystals is V = (3√3)/8·hl², where h is the height and l is the longest edge as measured in A. The height of the crystals was not accurately measured but was estimated to be linearly proportional to the length with the largest crystals having a height of ∼5 μm and the smallest ∼1 μm. This approximation is not critical inasmuch as the logarithm of the total number is plotted. Finally, the volume of a single bR protein was estimated from the crystal structure as V_bR ∼ π15²·45 ų. The slope of the linear fit is 0.94 Å⁻¹. From Eq. 7, the initial crystallization energy barrier ranges from 32.8 k_BT at 86.3 Å to 43.6 k_BT at 93.2 Å.

Knowing ϕ₀(a), G₀(a) was determined from the cluster size analysis in conjunction with Eq. 7. Subsequently, many parameters of interest were determined by using standard formulas derivable from the energy model, Eq. 7 (see Appendix C). Over the range of crystallization we found that the barrier height G₀ ranges from 32.8 k_BT at 86.3 Å to 43.6 k_BT at 93.3 Å, and the corresponding critical cluster sizes range from 16 to 29 proteins. Thus, the free energy barrier to in cubo crystallization is comparable, yet smaller, than barrier heights determined from simulations of soluble globular proteins (∼50 k_BT) (ten Wolde and Frenkel, 1997). Surprisingly, the surface energy term, σ ∼ 9.8 k_BT, is essentially constant with only a very weak dependence on the lattice parameter. A theoretical determination of this result based on first principles seems daunting; however, phase stability models of the cubics do exist, and extending them to understand the energetics of the interpolation region will be important for a more complete understanding of in cubo crystallization (Anderson et al., 1988; Schwarz and Gompper, 2000; Templer et al., 1998).

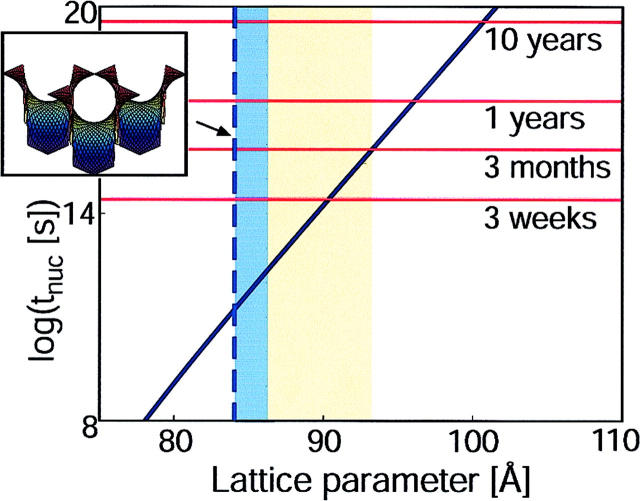
The theoretical nucleation time was determined from Eq. 6, and this time is presented in Fig. 5. Above 93.3 Å, the decrease in ϕ₀ and the concomitant increase in G₀, both appearing in exponentials, quickly drives the nucleation time into an inaccessible range. Therefore, the reason that crystallization stops is not that the chemical potential has gone to zero, but that the free energy barrier to nucleation is too large. At the lower limit of 86.3 Å, our analysis does not predict the inhibition of crystal formation, but the elasticity analysis suggests an explanation. Protein diffusion between monkey saddles is exponentially suppressed by the factor u. If the dependence of u on the lattice parameter is much steeper than the corresponding decrease in the free energy barrier, G₀(a), then the nucleation time is driven back up into an inaccessible range (see Eq. 6). A possible reason why this effect is not evident in our calculations may be due to nonlinear elastic effects caused by the high curvatures. The inset in Fig. 5 shows that at this lower limit, the size of bR is comparable to the size of the membrane regions through which the protein must pass. The true energy cost for traversing these necking regions may not be captured by linear calculations. Another possibility may be that very small crystallites are stabilized effectively annealing microscopic clusters into place. This corresponds to a very small G₀ and K, and because G₀(a) was not predicted from first principles, it is difficult to say how it behaves for lattice parameter values out of the experimental range.

FIGURE 5.

Upper and lower bounds for protein crystallization. The time required to nucleate a crystal has been plotted from Eq. 6 using the experimentally determined crystallization barrier height and the diffusion coefficient for bR (solid blue curve). The flat bilayer diffusion coefficient was modified in accord with the diffusion barrier between adjacent sites plotted in Fig. 3 C. The yellow zone represents the admissible range for growing crystals as shown in Fig. 4. The blue and yellow zones together represent the theoretical bounds on crystallization. Relevant times are indicated by solid red lines. The kinetic analysis predicts that the energy barrier to forming crystals is sufficiently large to prohibit nucleation in less than a year for lattice parameter values larger than 95 Å, as seen experimentally. However, the theory does not predict a lower limit cutoff for crystallization, but suggests the following scenario. At small lattice parameters, the energy barrier prevents proteins from diffusing between adjacent monkey saddle sites. This increases the nucleation time despite the low nucleation barrier. Although this effect is included in the nucleation time prediction (solid blue curve), the barrier to diffusion does not increase fast enough to drive the nucleation time up noticeably. For ∼84 Å the small axis of the protein (∼25 Å) is about equal to the diameter of the aqueous channel of the cubic phase pictured in the inset, D = a/√2 − (lipid bilayer thickness) ∼25 Å. The elastic calculations become suspect at this point and a “pinching off” effect may make the diffusion barrier increase much more quickly than predicted in Fig. 3 C. This limit is represented by the dashed blue line.

DISCUSSION

We have presented a model for in cubo membrane protein crystal growth based upon the elastic interactions between membranes and proteins. The model explains how the osmotic work done by shrinking the cubic phase increases the elastic component of the chemical potential, ultimately inducing the aggregation of proteins and the subsequent formation of crystals. This elastic energy can be computed based on the protein size and the elastic modulus and geometry of the membrane. Our analysis of the membrane bending energy explains the experimental growth of protein crystals and its dependence on the lattice parameter. However, both the compressional and bending modes of the membrane are required to understand membrane mediated interactions in flat bilayers containing gramicidin channels (Harroun et al., 1999). Here we have not modeled the finite thickness of the membrane for reasons discussed in Appendix A. This aspect is required to estimate the compressional energy induced by the hydrophobic mismatch between the proteins and the membrane. It is very likely that compressional energies play a role in in cubo protein crystallization, but a simple estimate based upon the hydrophobic extent of the membrane spanning section of bR and the average MO bilayer thickness would be suspect because there is likely to be significant membrane thinning at different points on the cubic phase surface. To a first approximation, this energy is captured in the constant term in Eq. 2, ɛ_elec., which accounts for all lattice parameter independent energies. Furthermore, as the lattice parameter decreases, a fraction of the osmotic work goes into creating additional cubic cells. This topological change is a consequence of the in-plane incompressibility of the lipids, and alters the total Gaussian curvature of the system. We have neglected the effect of this global change in the Gaussian curvature on the local interactions of the proteins with the cubic and lamellar geometries. However, a more complete analysis would investigate this connection along with the possibility that compressional energy depends on the lattice parameter. Both of these topics are beyond the scope of the present work.

Protein-protein interactions mediated by the bilayer lead to complicated nonpairwise forces (Kim et al., 1998). This complication coupled with the large curvatures and multivalued surface of the DMS approximation to the true Pn3m phase makes a first principal determination of the nucleation barrier a formidable task. Therefore, a lattice nucleation model was developed to determine quantities of interest directly from experimental data. This kinetic analysis applies generally to all nucleation reactions. Some of the parameters deduced are specific to bR crystallization, although the prediction of the surface energy term should apply to all experiments performed in the Pn3m phase. Thus, we have begun to assemble a picture of in cubo crystallization that should ultimately determine whether a protein can be crystallized from the cubic phase, and the model can provide a window within which crystallization will occur. Several experiments must be performed to test aspects of this theory. The diffusion of proteins in the Pn3m cubic phase and nucleation times need to be measured over a range of lattice parameter values. Additionally, crystal size data must be recorded as a function of time as well as lattice parameter. Furthermore, a more complete understanding of this phenomenon will require extending the present work to address multiprotein interactions in an extended DMS as mentioned above. Finally, we note that the notion of lipid phase grain boundaries may contribute to the nucleation mechanism. This does not affect the free energy arguments presented here nor the general barrier analysis carried out on the kinetic data, but it would play a crucial role in actually determining the exact nature of the transition state.

We have shown that the highly curved membranes present in the in cubo method aggregate cylindrical membrane proteins. It is natural to ask whether similar mechanisms play a role in the cell. Although the cubic phases might seem exotic, electron micrograph studies suggest that they may be more commonplace than previously thought. Landh (1995) has identified three families of cubic membranes at sites such as the plasma membrane, smooth endoplasmic reticulum, nuclear membrane, and mitochondria. These membranes are not static but appear to undergo transitions similar to the one investigated here. For example, light induces the transformation of the thylakoid membrane of chloroplasts from a cubic to a lamellar structure (Israelachvili and Wolfe, 1980), and starvation elicits a cubic transition in the mitochondrial cristae of amoeba (Deng et al., 2002). The connection between membrane transformations and the presence of membrane proteins was established in the mitochondria where it was shown that the formation of flat cristae requires clustering of F-ATPase (Paumard et al., 2002), a cylindrical membrane protein (Stock et al., 1999). In mutant yeast cells lacking F-ATPase subunits crucial for protein oligomerization, the inner mitochondrial membrane adopts a morphology similar to an onion peel.

The electron micrograph reconstructions of Alain Rambourg show that the trans-Golgi network is composed of multiple cisternae containing dilated progranules connected by tubular networks (Rambourg and Clermont, 1990). Toward the more distal cisternae the connecting regions appear increasingly tubular and more highly curved whereas the progranules become larger and flatter. Our results suggest that cylindrical proteins preferentially populate the flattened region of the budding progranule. Wu et al. (2001) found that the proper acidification of these budding granules requires both a decrease in the proton leakage and an increase in the density of V-ATPase proton pumps, the structural homolog of the F-ATPase. Our theory provides one mechanistic explanation for how the cylindrically shaped V-ATPase becomes preferentially enriched in the progranular membrane as a direct consequence of the change in the trans-Golgi morphology. Elastic membrane-protein interactions are substantial at these sites of high curvature and must be added to the list of possible players in the organization and stabilization of endomembranes.

APPENDIX A: MINIMAL SURFACES AND MEMBRANE PROTEIN ENERGETICS

Minimal surfaces are those with zero mean curvature. This property implies that they cover spaces with minimum surface area. The cubic phases are represented by triply periodic minimal surfaces, and in particular, we are interested in Schwarz' D (diamond) surface. To simplify the examination of the surface curvature, we employed the trigonometric approximation to the true minimal surface:

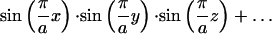(A1)

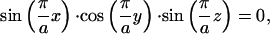where a is the period of the minimal surface or the lattice parameter. This representation can be found on the minimal surfaces web site at the Mathematical Sciences Research Institute: http://www.msri.org/publications/sgp/jim/geom/level/library/triper/index.html.

To study the local properties of a single unit cell, a judicious choice of the origin allows a representation as a continuous surface height, z = h(x, y), that can be found from solving the above equation for z:

(A2)

The surface is thus described by

(A3)

With this representation, the surface curvatures can readily be determined from standard formulas:

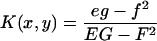(A4)

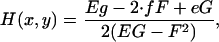where

(A5)

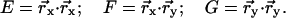Here n is the surface normal and EG − F² is the surface metric.

To obtain a simple expression for the local shape of the minimal surface, we use Eqs. A4 to identify the sites of minimum Gaussian curvature and fit a local polynomial to this region. This approximate representation is used in Fig. 1 C of the main text to plot the distribution of Gaussian curvature on the surface of the unit cell in the vicinity of a point of minimum Gaussian curvature. The polynomial description of this surface patch is a “monkey saddle” given by

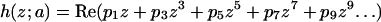(A6)

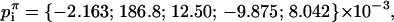where z = r·exp(iθ), and the coefficients have been determined at a lattice parameter of a = π. The surface height at different lattice parameters is determined from the scaling of the coefficients:

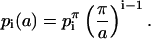This analysis was also been carried out around the horse saddle regions that separate monkey saddles. The additional restriction that the Gaussian curvature at the center of the saddle be equal to the curvature of the DMS restricts the first polynomial coefficient:

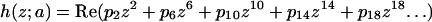(A7)

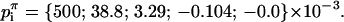The same scaling applies to these coefficients as the ones in Eq. A6.

Membrane protein interactions can now be calculated with the help of Eqs. A6 and A7. The energy of the system is given by the standard representation for the membrane bending energy (Helfrich, 1973):

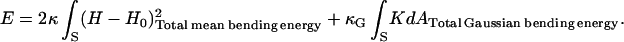(A8)

Here, S is the neutral surface of the bilayer, H is the local mean curvature of the membrane, and K is the Gaussian curvature. H₀ is the spontaneous curvature, reflecting any natural tendency for the surface to bend due to molecular mismatch between the lipid headgroups and the hydrocarbon tails. κ and κ_G are the elastic constants corresponding to the mean and Gaussian bending modes, respectively. Although MO monolayers have a very large spontaneous curvature, H₀ ∼ 0.05 Å⁻¹ (Vacklin et al., 2000), the symmetry of a bilayer formed from a single lipid eliminates the spontaneous curvature (Helfrich, 1999). As mentioned in the main text, the Gauss-Bonnet theorem from differential geometry tells us that the surface integral of the Gaussian curvature does not affect the membrane bending energy.

We consider the energy minima of the Helfrich Hamiltonian in the linearized limit of small curvatures with the assumptions previously stated. This results in a biharmonic boundary value problem where the height, h, of the neutral surface above the base plane satisfies

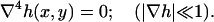The unperturbed height of the surface around the monkey saddle is dominated by the p₃(a) coefficient and the horse saddle by p₂(a). Carrying out the energy calculations around the monkey saddle, Eq. A6 approximates to

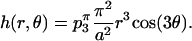(A9)

Here, r and θ are polar coordinates of the tangent plane. Now consider a protein of radius R implanted ∼r = 0. The distortion surface is represented by biharmonic surface that asymptotes to the undisturbed surface Eq. 3 for r ≫ R and satisfies the contact boundary conditions

for all θ. Physically, the circle r = R represents the hydrophobic belt around the circumference of the cylindrical protein and the contact boundary conditions indicate that the tangent planes of the bilayer along the contact circle coincide with the plane of the circle. The required biharmonic solution is

The linearized approximation to the associated mean curvature is

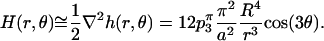The total mean curvature energy around the monkey saddle is then calculated with Eq. (A8):

(A10)

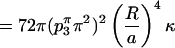and the corresponding elastic energy around a horse saddle is

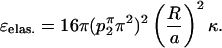(A11)

From Eqs. A10 and A11, all of the graphs in Fig. 3 can be computed. However, we used a biharmonic solver that explicitly includes all the higher order terms in Eqs. A6 and A7 to compute these curves. The difference is negligible and does not change the character of the surface. This solver was formulated and written by M. G. and J. N. and is available upon request.

There are two aspects of the cubic phase that we have not yet addressed. First, to understand the phase stability of membranes, it is necessary to consider lipid chain packing in addition to membrane bending (Anderson et al., 1988; Templer et al., 1998). To date, analysis of packing energetics has required one to posit a priori the shape of the membrane surface and then compute the lipid deformation energy using complicated geometrical analyses (Anderson et al., 1988). Our approach is to solve a biharmonic equation to determine the bending energy of the membrane. It is not clear how to incorporate packing energetics into this scheme, but doing so would permit an analysis of the membrane compression energetics mentioned in the Discussion. Second, constant mean curvature surfaces based on the DMS have been shown to exist and subsequently used to model the Pn3m phase (Andersen et al., 1990; Grosse-Brauckmann, 1997; Templer et al., 1998). We have carried out elastic energy calculations on these surfaces as well, and the protein energetics are not greatly affected (data not shown).

APPENDIX B: NUCLEATION ON A LATTICE

The descriptive summary from the introductory text suggests that the statistical mechanics of nucleation can be treated using a lattice model. This model posits N proteins that are free to occupy m > N binding sites. Let n_j ≥ 0 be the occupation number of site j, j = 1, 2,…, m. The configuration space of the lattice model consists of all sets of occupation numbers, (n₁, n₂, … n_m), consistent with the total particle constraint:

(B1)

The protein crystals are idealized as lattice sites with large occupation numbers. For such large protein clusters, there is clearly a massive disruption of the cubic phase, and a loss of the original binding sites. But in practice, the volume fraction of final crystals is much smaller than the total volume of original cubic phase. Therefore, the fraction of binding sites disrupted by crystals is quite small and the entropy of the protein bilayer system should be well approximated by this lattice nucleation scheme.

Let p_k denote the total number of “k clusters”, which are sites occupied by k particles. The energy of a k cluster relative to an empty binding site is taken as e_k; the actual determination of this value is treated below. The particle constraint and total energy take the form

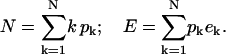(B2)

Defining the binding energy of the k cluster as ɛ_k ≡ ke₁ − e_k and using the particle constraint, the energy can be rewritten as

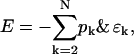(B3)

where the constant term N·e₁ is independent of configurations and is dropped.

The conventional model for binding energy of a nucleating cluster proposes a negative component proportional to the surface area of the cluster, and a positive component proportional to the volume. Because k is the number of proteins in the cluster, the surface area is proportional to k^2/3 and the volume is k, so the conventional model is

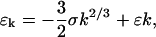(B4)

where ɛ and σ are positive constants with the units of energy. The negative surface component represents the energy cost of the transition zone between the crystal and the bulk Pn3m phase. As discussed before, the bilayer geometry that interpolates between the flat lamellar phase of the crystal to the exterior cubic phase cannot have mean curvature identically zero, and therefore has an elastic mean bending energy. Part of the volume component arises from the elastic energy relieved by removing a protein from the cubic phase and implanting it in the flattened out region of the crystal. There is an additional bending energy component that originates from the purple membrane lipid incorporated into the flattened stacks. These lipids have been shown to favor a lamellar structure under crystallization conditions (Landau and Rosenbusch, 1996). Additionally, electrostatic interactions between the packed proteins will augment this bulk energy in a lattice parameter independent manner. These short-range energies are difficult to calculate, but are very important for protein crystallization in solution inasmuch as they provide the only driving force for crystal growth.

The proceeding discussion has general implications for all nucleation reaction scenarios and does not depend upon the exact nature of the driving forces involved. These results are just as applicable to experiments performed in solution as in cubo. The general properties of energy landscapes that lead to nucleation are summarized in Fig. 6.

FIGURE 6.

Energy barrier in k space. Crystallites smaller than the critical cluster size, K, break up on the average whereas larger clusters deterministically grow. For k ≫ K, the crystal grows with a driving force equal to ɛ.

We now compute the entropy in the lattice model. Let D be the number of distinct configurations, (n₁, n₂, … n_m), consistent with the given numbers, p_k, of k clusters. The entropy of the lattice system is then S = k_B log(D). D is found by counting: the number of ways to choose p₁ monomer sites is

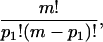and the number of ways to place p₂ dimers in the remaining m − p₁ sites is

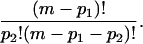In general, the number of ways to place p_k k clusters in the remaining m − p₁ … −p_k − 1 sites is

The total number D of configurations with p_k k clusters, k = 1,…, N is the product of the above factors,

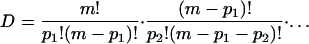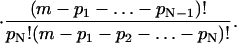After cancellations the entropy becomes

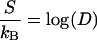(B5)

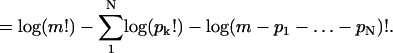In the thermodynamic limit as m → ∞ with N/m → ρ_T fixed, the entropy density becomes

(B6)

The energy density has the form

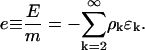(B7)

Equilibria are characterized by the minima of the free energy density, f = e − TS. Equilibrium values of ρ_k are given by ∂_kf = 0, and in the dilute protein limit, ρ ≪ 1, where r ∼ 1 the following relationship holds

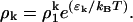(B8)

Various cluster statistics, such as the average cluster size, can be derived from Eq. B8 in conjunction with the thermodynamic limit of the particle constraint Eq. B1.

APPENDIX C: KINETICS OF NUCLEATION

If the particle density is sufficiently large, it is easy to show that the equilibrium condition, Eq. B8, is not compatible with the total particle density constraint. Therefore, we develop a kinetic framework to interpret crystallization experiments. Rewriting the equilibrium condition Eq. B8, as

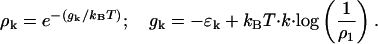(C1)

This allows us to interpret g_k as an activation barrier height in a nucleation reaction

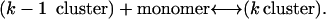Substituting into Eq. C1 Eq. B4 for the binding energy, e_k, gives

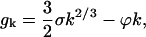(C2)

where ϕ is the chemical potential:

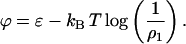(C3)

Fig. 6 is a graph of g_k versus k of j > 0. g_k achieves its maximum at the critical cluster size:

(C4)

It has a maximum value

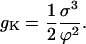(C5)

Notice that as k → ∞, g_k+1 − g_k → −ϕ, so that the chemical potential can be thought of as the driving force for crystallization. The standard kinetics of these reactions is described by a system of ordinary differential equations for the densities as a function of time: ∂_tρ_k = j_k−1 − j_k ≡ −D₋ j_k, where the j's are the cluster creation rates, and we have introduced the discrete difference operator ±D_± X_k ≡ X_k±1 − X_k. These fluxes are related to the densities by

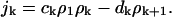(C6)

The first term on the RHS is the bimolecular reaction rate of creation of a k + 1 cluster due to the addition of a single monomer to a k cluster. The prefactors in this equation are the creation rate constants c_k and the destruction rates d_k. The ratio of these two coefficients is determined from the energetics through the principle of detailed balance, which says that the flux should be zero at equilibrium

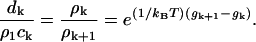(C7)

This relation allows us to rewrite the flux as

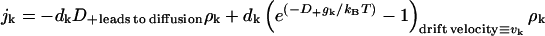(C8)

In Eq. 8, the diffusion coefficient d_k and the drift velocity v_k have been identified. We see that when k < K, the argument of the exponent is positive, g_k − g_k+1 > 0, the drift velocity is negative, and protein clusters dissolve on average. When the cluster size is larger than the critical cluster size, g_k − g_k+1 < 0, the clusters grow on average.

For large k the diffusion component reduces to

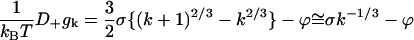(C9)

and the drift velocity becomes

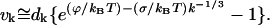(C10)

The asymptotic form of d_k for k ≫ 1 is identified by correspondence with macroscopic crystallization: Consider a single large crystal of roughly spherical shape surrounded by monomer at uniform density. Because p₁ = mρ₁ is the number of sites occupied by monomer, and there are four binding sites per unit cell of side a, the volume density of monomer far from the crystal, c_∞, is determined by

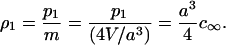(C11)

Here, V is the total volume of the cubic phase. At the surface of the crystal, quasi-static equilibrium prevails, and the local value of ρ₁ at the interface is determined so that g_k+1 = g_k. By Eq. (C9), this means

The corresponding value of the volume density at the interface is given by the quasi-steady diffusion of the monomer into the crystal:

(C12)

The crystal presumably grows slowly so there is quasi-steady diffusion of monomer into the crystal. When the crystal has a radius of R, the concentration field, c = c(r), of the monomer in r > R is given by c(r) = c_∞ − (c_∞ − c_j)·R/π. D is the macroscopic diffusion coefficient of the monomer in the bulk cubic phase, and the flux of monomer into the crystal is given by

Substituting for c_∞ and c_j from Eqs. C11 and C12,

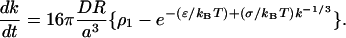Setting ρ₁ = exp((ϕ − ɛ)/k_BT) as follows from the definition of ϕ in Eq. C3, there results

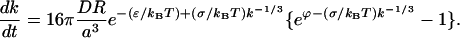(C13)

If ν is the volume per protein in the crystal, then

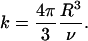So

And Eq. 13 becomes

(C14)

Comparing the drift velocity to ∂_tk leads to the asymptotic identification of d_k,

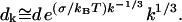(C15)

And when k ≫ 1,

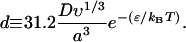(C16)

If k ≫ K ≫ 1, then σk^−1/3 ≪ σK^−1/3 = ϕ. Assuming that ϕ/k_BT is of order 1 or smaller, it follows that σk^−1/3 ≪ 1 and Eq. 6 reduces to

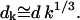(C17)

To nondimensionalize these results, we measure all energies in units of k_BT, and time in units of 1/d given in Eq. 5. The dimensionless equations are

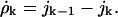(C18)

For j ≥ 2, with

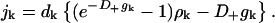(C19)

In Eq. C19,

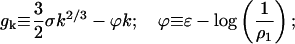(C20)

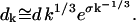To close this system of equations, one more equation governing the monomer concentration is required. This is just the particle constraint:

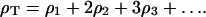(C21)

APPENDIX D: NUCLEATION RATE

If the activation energy barrier g_K is sufficiently high, a quasi-steady condition develops in which j_k is asymptotically uniform, j_k ∼ j for all values of k on the order of the critical cluster size K. As k → ∞, j_k presumably asymptotes to zero. An estimate for j in terms of the energy barrier is now derived: In Eq. C19, set j_k ∼ j to get

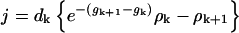(D1)

It follows from Eq. D1 that

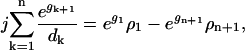(D2)

where g₁ = −ɛ₁ − log(ρ₁) = −log(ρ₁), so exp(g₁) ρ₁ = 1. For n ≫ K, one expects that ρ_n is much less than the equilibrium concentration, exp(−g_n), so that exp(g_n+1)·ρ_n+1 → 0 as n → ∞ and Eq. D2 reduces to a formula for j:

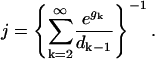(D3)

In Eq. D3, assume that d_k−1 and g_k are values of analytic functions evaluated at integer arguments k, and approximate the sum by an integral,

(D4)

For K ≫ 1, the main contribution to the integral comes from k near K where g_k is a maximum. The standard Laplace approximation to the integral is

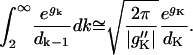(D5)

From Eqs. D3–D5, there follows the asymptotic formula for j,

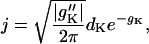(D6)

which has a familiar form from Kramers rate theory. Given g_k and d_k as in Eqs. C20, one obtains

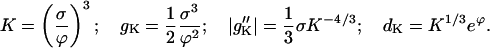Thus, Eq. D6 for j reads

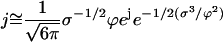(D7)

APPENDIX E: TIME EVOLUTION OF CRYSTALLIZATION

The initial state at t = 0 is pure monomer at density ρ_T. There is an initial transient that establishes the quasi-steady conditions for k on the order of the critical cluster size K: The j_k values are approximated by the uniform value for k on the order of K given by Eq. D7. For k < K, the densities are close to quasi-equilibrium values

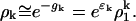(E1)

Initially there are very few large clusters with k > K, so the particle constraint, Eq. C21, is approximated by

For k < K, the ɛ_k are negative and decreasing, so

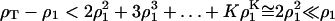for ρ₁ ≪ 1. Hence this initial transient does not significantly change the monomer density from its initial value of ρ_T.

The first clusters to nucleate (i.e., exceed the critical cluster size, K) are the biggest. When these are much greater than K, they are the dominant consumers of monomers. Their growth depletes the monomer, which in turn decreases the chemical potential, ϕ, and raises the activation energy barrier g_K ≅ 1/2 σ³/ϕ². Eventually, nucleation is effectively shut off, but the large crystals continue their supercritical growth, with k ≫ K. Ultimately, there is sufficient depletion of the monomer, and the chemical potential is so small that the critical cluster size, K ≅ (σ/ϕ)³, catches up to the crystals. This signals the end of the supercritical growth phase and the beginning of the coarsening phase.

How does one quantitate this scenario? Traditional asymptotics introduces scalings of the variables and reduced equations are obtained as limits of scaled equations. Here, a priori guessing of scalings is tricky, but the simplest reduced kinetics with the essential mechanisms is clear. So we proceed straight to the reduced kinetics and its predictions. Formal scaling and reduction give a posteriori validation of the method.

In reduced kinetics, ρ_k and j_k are represented as

(E2)

where ρ(k,t) and j(k,t) are values of analytic functions at integer arguments. The time dynamics, Eq. C18, is translated into the local conservation partial differential equation,

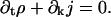(E3)

The approximation to j in Eq. C19 for k ≫ K ≫ 1 is

(E4)

This reduction is based on D₊g_k ≅ −j for k ≫ K and the assumption that D₊ρ_k ≪ ρ_k, which holds if the scale of k in ρ(k,t) is much larger than unity. In summary, ρ(k,t) satisfies the advection equation

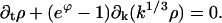(E5)

The nucleation rate in Eq. D7 gives an effective flux boundary condition as k → 0:

(E6)

Finally, the continuous approximation of the particle constraint Eq. C21 is

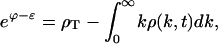(E7)

where ρ₁ has been written in terms of the chemical potential.

The solution of Eqs. E5–E7 for ρ(k,t) and ϕ(t) representing initial nucleation and supercritical growth is constructed as follows. First, we cast the advection equation, Eq. E5, in the characteristic form,

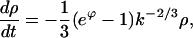(E8)

which holds along characteristic curves in the k,t plane. These curves satisfy

(E9)

For t > τ, the characteristic emanating from (k,t) = (0,τ) is given by

(E10)

In Eq. E10, the chemical potential, ϕ(t), is not yet determined. But because equilibrium is not reached, ϕ(t) is positive. In this case it follows from Eq. E10 that the characteristics have k increasing with t. Fig. 7 is a qualitative picture of the characteristics.

FIGURE 7.

Qualitative characteristic curves. The cut C at time t intersects characteristics giving the size of each crystal. Notice that there is a vanguard of large crystals (i.e., many characteristics) near the red curve, which is the initial characteristic. As time increases, the density of characteristics falls off.

The region of nonzero density is above the t = 0 characteristic given by Eq. E10, with the lower limit replaced by τ = 0. In this region, the τ of the characteristic that passes through (k, t) is a function of k and t,

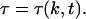(E11)

The values of ρ along each characteristic are determined as solutions of the ordinary differential equation, Eq. E8. But because k is increasing in time, t, one can use k as an independent variable in place of τ. Dividing Eq. E8 by Eq. E9, one obtains

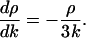And the solution along the characteristic emanating from (0, τ) is

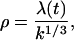(E12)

where λ is a function of τ, to be determined from the flux condition Eq. E6:

(E13)

as k → 0 along the characteristic from (0, τ). Comparing Eqs. E12 and E13, it is evident that

Finally, the solution for ρ is,

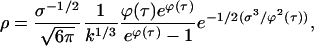(E14)

where τ = τ(x,t) is implicitly determined by Eq. E10. ρ is largest when ϕ(τ) is largest and that happens at τ = 0. Characteristics in the k,t plane can be thought of as the trajectories of individual crystals, so the profusion of early crystals with t near zero is indicated in Fig. 7 by a high density of characteristics near the τ = 0 curve.

We turn now to the determination of the chemical potential ϕ(t). Substitute the solution to Eq. E14 for ρ into the particle constraint, Eq. C21:

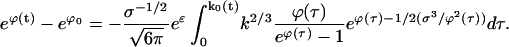(E15)

Here, k₀(t) is the equation for the τ = 0 characteristic, given by Eq. E10 with the lower limit set to zero. In addition ρ_T = ρ₁(t = 0) has been replaced by exp(ϕ₀ − ɛ), where ϕ₀ ≡ ϕ(0). Think of Eq. E15 as a line integral in the k,t plane along the line segment of constant t, as shown in Fig. 7. As k increases from 0 to k₀(t), the values of τ = τ(t,k) decreases from t to 0. Hence τ is used as a variable of integration in place of k. Using

as follows from Eq. E10, there results

(E16)

Here, k = k(t, τ) is given in terms of ϕ(t) by Eq. E10. Hence Eq. E16 is an integral equation for the chemical potential, ϕ(t).

Eq. E16 is a summary of the essential physics. The rate of nucleating clusters is proportional to the factor exp(−1/2 σ³/ϕ²). Supercritical growth of the clusters is represented by k(t, τ) given by Eq. E10. Both effects are evident in the integral on the RHS that represents the number of particles in the supercritical crystals. As this number increases, monomer is depleted and the chemical potential concomitantly decreases toward zero.

The main contribution to the integral in Eq. 16 comes from a neighborhood of τ = 0, when the nucleation rate is largest. This means that the biggest crystals are produced the earliest and deplete the monomer fastest. Notice that a small relative decrease in the chemical potential from its initial value is sufficient to greatly decrease the nucleation rate, exp(−1/2 σ³/ϕ²), and put an end to nucleation. The range of nucleation times, τ, that dominate the integral Eq. E16 is referred to as the nucleation era. A distinguished limit of this equation describing the nucleation era is identified by scaling of the chemical potential differences ϕ₀ − ϕ(τ) and time.

The natural scaling of ϕ₀ − ϕ(τ) is 1/k₀, where k₀ is the initial size of the critical cluster, K₀ ≡ (σ/ϕ₀)³. Define the quantity,

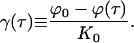(E17)

Then the energy barrier at time τ is approximated by

where

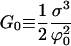(E18)

is the initial energy barrier at the beginning of the crystallization experiment. It follows that

(E19)

The exponential factor in Eq. E19 undergoes a relative change of order unity when the chemical potential changes by an amount of order 1/k₀. For the range of t in which ϕ(t) − ϕ₀ = O(1/k₀), the collection of factors containing the chemical potential in Eq. E16 are approximated by

(E20)

From Eq. E10 the corresponding approximation to k(t,τ) is

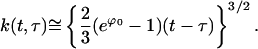(E21)

In the LHS of Eq. E16,

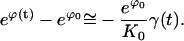(E22)

Under the approximations of Eqs. E19–E22, Eq. 16 reduces to

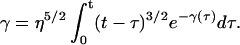(E23)

where η is a constant defined by

(E24)

The pre-factor η^5/2 in Eq. E23 can be absorbed by scaling the time T = ηt, and representing γ as a function of T, γ = γ(T). Then Eq. E23 becomes a parameter-free equation

(E25)

Physically, 1/η is the dimensionless duration of the nucleation era. This can be converted into a dimensional nucleation time,

(E26)

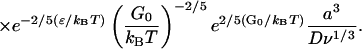The integral equation, Eq. E25, has a unique solution. As T → 0, γ(T) → 0 and the asymptotic behavior of γ is seen from Eq. E25 to be

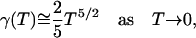(E27)

assuming

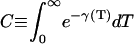(E28)

exists, the large T behavior of γ is seen to be

(E29)

This asymptotic behavior is consistent with the convergence of the integral in Eq. E28. Assuming γ is known, physical predictions about the nucleation era are presented.

The total number of crystals formed during a typical experiment readily follows. The total density of nucleated clusters is

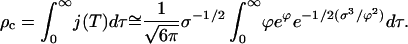(E30)

Here, the approximation Eq. E6 to ϕ is used. The dominant contribution to the integral comes from τ = O(t_nuc) and the relevant approximation is

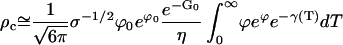Using the values of η in Eq. E24,

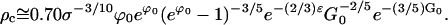(E31)

The total number of nucleated crystals is N_c = mρ_c where m is the total number of binding sites in the whole cubic phase. The approximation to N_c based on the dominant terms in Eq. E31 is log(N_c) ≅ log(m) − 3/5G₀, or restoring G₀ to dimensional form,

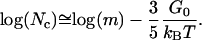(E32)

The time duration of the supercritical growth era determines the size of the nucleated crystals. As noted before, the cluster density, ρ(k,t), has its main concentration about the τ = 0 characteristic in the k,t plane. The detailed structure of this concentration is irrelevant so in effect there is a rough approximation to ρ(k,t):

(E33)

Substituting Eq. E33 into the particle constraint, Eq. C21, there results

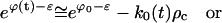(E34)

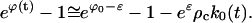As long as the crystals remain much larger than the critical size k₀(t) ≫ K = σ³/ϕ³, the crystal size k₀(t) evolves according to the ordinary differential Eq. E9. Substituting into Eq. E9 with the approximation for exp(ϕ(t)) − 1, there results

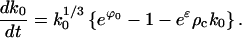(E35)

In Fig. 8 there is a graph of ∂k₀/∂t vs. k₀ based on Eq. E35. According to Eq. E35,

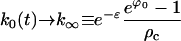(E36)

as t → ∞. Physically, k_∞ is the size of the crystal obtained when most of the monomer is depleted. The time constant associated with the decay of k₀(t) to k_∞ is found from the derivative of the RHS of Eq. E35 at k₀ = k_∞:

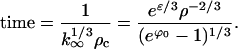Because ρ_c in Eq. E31 is proportional to exp(−2/5G₀), this growth time is proportional to exp(2/5G₀), the same as t_nuc. Hence the supercritical growth era has essentially the same duration as the nucleation era.

FIGURE 8.

Graph showing the dependence of ∂_tk₀ on k₀.

This description of growth breaks down when ϕ(t) becomes so small that the critical cluster size catches up with the size of the existing crystals. An order of magnitude balance between k_∞ in Eq. E36 and the critical cluster size determines this crucial value of ϕ(t):

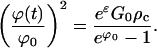Because ρ_c is proportional to exp(−3/5G₀), it is seen that ϕ(t) is a small fraction of its original value of ϕ₀ at the end of the supercritical growth phase. From Eq. E34, it is seen that the crystal size at the end of supercritical growth phase is very close to k_∞ in Eq. E36.

For crystallization experiments that run for several nucleation times t_nuc, the size of crystals produced is k_∞. It follows from Eq. E36 and the result Eq. E31 for ρ_c that

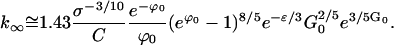(E37)

Using the surface tension model to solve for σ in terms of G₀ and ϕ₀, it is possible to express the two key Eqs. E26 and E27 in only a handful of variables

(E38)

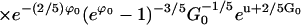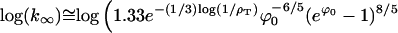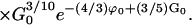The common-sense approximations to these two equations are presented in the main text. Experimental measurements of t_nuc and k_∞ allow a determination of G₀ and ϕ₀ inasmuch as all other parameters are accessible through theory or experiment.

APPENDIX F: CRYSTALLIZATION PREPARATION AND PHYSICAL CONSTANTS

The standard experimental setup used to create Fig. 4 of the main text requires mixing 6 mg of dry MO (initially in the lamellar crystalline phase), with 4 ml of bR solution (10 mg/ml). The approximate number of proteins in this setup can be determined from the molecular weight of bR = 26.79 kDa. The mass of the protein in the sample is

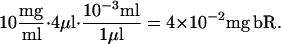Thus, there are 2.41 × 10¹⁹ Da of bR, or ∼9.0 × 10¹⁴ total proteins in the sample. Additionally, the size of a single protein can be determined from the crystal structure, as V_bR ∼ π15²·45 ų = 31792.5 ų (15 Å radius and 45 Å height). This then leads to a bR volume in the crystal of n^1/3 = (V_bR/0.7)^1/3 = 35.7 Å. The factor 0.7 accounts for the fact that the final crystal is only 70% protein.

The diffusion coefficient of bR proteins in MO lipid bilayers can be estimated as follows. The viscosity of an MO bilayer was recently estimated to be η_m = 1.5 ± 0.15 P (Tsapis et al., 2001). Using an estimated radius of 15 Å, the Saffman and Delbruck formula for protein diffusion gives (Saffman and Delbruck, 1975):

where d_m = 35 Å is the bilayer thickness, η = 0.01 P is the viscosity of the bounding fluid (water), and γ′ is Eulers constant (0.5772). k_BT is 4.1 × 10⁻²¹ J at room temperature, which leads to a flat bilayer diffusion coefficient of D₀ = 3.28 × 10⁻¹² m²/s or 3.3 μm²/s (1 P = 0.1 kg/(m·s)).