Fluorescence Resonance Energy Transfer over ∼130 Basepairs in Hyperstable Lac Repressor-DNA Loops

Abstract

Lac repressor (LacI) binds two operator DNA sites, looping the intervening DNA. DNA molecules containing two lac operators bracketing a sequence-directed bend were previously shown to form hyperstable LacI-looped complexes. Biochemical studies suggested that orienting the operators outward relative to the bend direction (in construct 9C14) stabilizes a positively supercoiled closed form, with a V-shaped LacI, but that the most stable loop construct (11C12) is a more open form. Here, fluorescence resonance energy transfer (FRET) is measured on DNA loops, between fluorescein and TAMRA attached near the two operators, ∼130 basepairs apart. For 9C14, efficient LacI-induced energy transfer (∼74% based on donor quenching) confirms that the designed DNA shape can force the looped complex into a closed form. From enhanced acceptor emission, correcting for observed donor-dependent quenching of acceptor fluorescence, ∼52% transfer was observed. Time-resolved FRET suggests that this complex exists in both closed- and open form populations. Less efficient transfer, ∼10%, was detected for DNA-LacI sandwiches and 11C12-LacI, consistent with an open form loop. This demonstration of long-range FRET in large DNA loops confirms that appropriate DNA design can control loop geometry. LacI flexibility may allow it to maintain looping with other proteins bound or under different intracellular conditions.

INTRODUCTION

The E. coli lactose repressor (the lacI gene product, LacI protein, also referred to as LacR) is the archetypal DNA looping protein. Secondary operators upstream and downstream of the primary operator in the lac promoter are essential for highly efficient repression of the lacZYA operon (Brenowitz et al., 1991; Oehler et al., 1990). The protein is a stable homotetramer, with the DNA binding unit being a dimer. Binding of one dimer to an operator increases the local concentration of the other dimer in the neighborhood of nearby operators, potentiating the formation of transient or stable DNA loops bridged by a repressor tetramer. Repression efficiency is strongly dependent on the proper helical phasing between the two operators (Müller et al., 1996), as is seen for other DNA looping proteins such as AraC (Lobell and Schleif, 1991). The dependence on distance along the DNA is less marked, suggesting significant bending flexibility on the part of protein, DNA, or both.

Landmark crystallographic studies from the Steitz and Lewis groups showed that the LacI tetramer is a dimer of dimers in which the two dimers adopt a V-shape, with an angle of ∼28° between the symmetry axes of the dimers in the crystals (Friedman et al., 1995; Lewis et al., 1996). However, both groups pointed out that the tetramerization domain (a C-terminal four-helix bundle) is attached to the body of the protein by flexible linkers, and that the protein may be able to adopt a more open conformation. Experimental evidence from x-ray scattering and electron microscopy suggests that the open form is accessible (McKay et al., 1982; Ruben and Roos, 1997). A proposed geometry of the LacI loop (Lewis et al., 1996) as a tight supercoil away from the protein has been controversial (Fried and Hudson, 1996; Perros and Steitz, 1996), and it is likely that loop geometry is different for different DNA sequences.

Our approach to the geometry of the LacI loop has been to design DNA molecules predisposed to stabilize different possible looping geometries (Mehta and Kahn, 1999). This was done by constructing molecules with lac operators that bracket a sequence-directed phased A-tract bend. The operators are on the same face of DNA (separated by an integral number of DNA helical turns), but in different DNA molecules they are directed either toward the direction of curvature or away from it. The design of the constructs is derived from previous work on the ring closure of molecules containing protein-induced bends separated by varied helical phasing from sequence-directed phased A-tract bends (Davis et al., 1999; Kahn and Crothers, 1992; Kahn and Crothers, 1998). These studies validated the A-tract bend direction previously inferred by extensive electrophoretic and DNA cyclization studies (Koo et al., 1990; Zinkel and Crothers, 1987), and subsequently confirmed by NMR and x-ray crystallography (Hizver et al., 2001; MacDonald et al., 2001). The LacI looping constructs used here employ essentially the same well-characterized A-tract sequence as much of the previous work, and subtle differences in bend direction would not affect the conclusions of our work.

Our “wrapping away” design (denoted as 9C14), with operators directed outward with respect to the bend direction, should stabilize a V-shaped repressor and a tight positive supercoil, as in the Lewis loop model (Lewis et al., 1996). The “simple loop” design (11C12), with operators pointing inward or perpendicular, should stabilize a more open form (see Fig. 1 for models of the DNA structures). The 9C14 and 11C12 looped constructs were both found to be hyperstable (t_1/2 ≥ 24 h), with 11C12 forming the more stable loop (Mehta and Kahn, 1999); this hyperstability indicates that the operators are not significantly misaligned torsionally, as such misalignment decreases loop stability (Bellomy and Record, 1990). Electrophoretic mobility, DNA cyclization kinetics, and the topologies of cyclized products suggested that each construct formed its expected loop geometry. The 9C14 loop was observed to give a mixture of a relaxed topoisomer, a positive supercoil, and a small amount of negative supercoil upon ring closure, whereas 11C12 gave mainly a relaxed topoisomer.

FIGURE 1.

The design of fluorescent 11C12 (simple loop) and 9C14 (wrapping away) constructs. (A) Schematic of the sequences of both DNAs. The dimensions in basepairs of the molecules and the attachment sites for the fluorescein donor and TAMRA acceptor are shown. The 56-bp primer sequences used to generate the labeled constructs are shown. Two different sequences were needed to synthesize the fluorescein-labeled top stand for the two constructs, LEFL56 for 9C14 and FL11TOP for 11C12, because the primers overlap the variable linker region. The primer sequence KTTM56 was used to synthesize the bottom strand of both constructs. (B) Models for the two looping constructs, with the view on the right rotated 90° relative to the view on the left. The dyad axes of the DNA operators, which lie along the symmetry axis of the LacI dimers, are represented by long blue cylinders. The base of attachment of the fluorescein donor is shown as a green ball and the base of attachment of the TAMRA acceptor as an orange ball on both molecules. (C) Design of fluorophore attachment sites. The cocrystal structure of a LacI tetramer-DNA “sandwich” complex (PDB entry 1LBG, Lewis et al., 1996) is shown, with the protein in blue, the tetramerization domain in magenta, and the DNA in red. The black DNA is a modeled B-DNA extension, and the fluorophore attachment points at the thymine C5 position are indicated. The fluorophores project into the major groove, away from the protein.

We sought a more direct method of assessing loop geometry and protein conformation, and turned to fluorescence resonance energy transfer (FRET) to measure distances between donor and acceptor fluorophores attached on opposite sides of the loop in these designed LacI-DNA complexes, next to the operator sequences (Fig. 1). FRET is the transfer of electronic excitation between fluorescent donor and acceptor molecules, which occurs when the emission spectrum of the donor overlaps with the excitation spectrum of the acceptor. The FRET efficiency can be used to quantitatively measure the physical distance (up to 100 Å) between the donor and acceptor. It can be determined from the decrease in quantum yield of the donor, the sensitized emission of the acceptor, or the decrease in lifetime of the donor (Clegg, 1992; Lakowicz, 1999; Selvin, 1995).

The FRET technique has been utilized in the study of structures of various DNA and RNA systems, both with and without bound proteins (Clegg, 1992; Hillisch et al., 2001). Steady-state and time-resolved FRET have been used to study the structure of models for the Holliday junction formed in DNA recombination (Clegg et al., 1994; Clegg et al., 1992), sequence-induced DNA bending (Toth et al., 1998; Wildeson and Murphy, 2000), the deformation of DNA resulting from the binding of the integration host factor (Lorenz et al., 1999a), DNA bending induced by high mobility group proteins (Lorenz et al., 1999b), and the geometry of nucleosomal linker DNA (Toth et al., 2001). Steady-state FRET provides mean distance measurements between the fluorophores in these complexes. Time-resolved FRET has been used to measure distance distributions, to distinguish among multiple conformers in nucleic acid complexes (Klostermeier and Millar, 2002; Parkhurst et al., 2002). It has been used to investigate the distribution of DNA bend angles in the catabolite activator protein (CAP)-DNA complex (Kapanidis et al., 2001) and in various TATA box binding protein (TBP)-TATA box DNA complexes (Wu et al., 2001).

Here, we present the results of FRET experiments on the 9C14 and 11C12 designed LacI-DNA loops, demonstrating that efficient FRET can be observed between fluorophores that are ∼440 Å apart along the linear DNA contour. The FRET studies confirm and extend the conclusions of our previous biochemical studies on loop geometry and LacI flexibility.

MATERIALS AND METHODS

Proteins and nucleic acids

Fluorescein- and tetramethylrhodamine- (TAMRA) labeled oligonucleotides were purchased from the Midland Certified Reagent Company (Midland, TX). The fluorophores are linked to the 5′ position of an internal dT base via a six-carbon linker. Unlabeled oligonucleotides were obtained from Invitrogen/GIBCO/BRL (Gaithersburg, MD). Lac repressor was generously supplied by Dr. Michael Brenowitz (Albert Einstein College of Medicine, Bronx, NY). Its concentration is given in terms of active dimer. Restriction enzymes and T4 polynucleotide kinase were purchased from New England Biolabs (Beverly, MA). Unless otherwise specified all buffer components and reagents were obtained from Fisher Scientific (Pittsburgh, PA).

Synthesis of fluorescently labeled DNA looping constructs

All oligonucleotides were purified on denaturing 10% polyacrylamide gels [39:1 (w/w) acrylamide:bis-acrylamide, 8 M urea, 0.6× TBE (50 mM Tris, 50 mM boric acid, 1 mM EDTA)]. Fluorescently labeled and unlabeled constructs were synthesized by polymerase chain reaction (PCR), using the FailSafe system from Epicentre Technologies (Madison, WI) with the optimized PreMix J buffer. Templates for the 9C14 and 11C12 constructs were previously described plasmids (Mehta and Kahn, 1999) restricted with BstN1 and diluted to 10⁸ molecules/μL. Each PCR reaction contained 1 μL template, 1 μL each 50 μM primer, 0.5 μL FailSafe PCR Enzyme Mix, 25 μL PreMix J, and 22.5 μL H₂O. The primers (sequences are below) used for the 9C14 fluorescein- and TAMRA-labeled construct were LEFL56 and KTTM56, and for the 11C12 fluorescein- and TAMRA-labeled construct FL11TOP and KTTM56 were used. In the sequence listing, a fluorescein dT modification is denoted as F, a TAMRA dT modification is denoted as X, and the lac operator is underlined:

• LEFL56: 5′ CTGCAGGTCAGTCTAGGTAATTGTGAGCGCTCACAATTAFATCTCAATTCGTACGG 3′

• FL11TOP: 5′ CTGCAGGTCAGTCTAGGTAATTGTGAGCGCTCACAATTAFATCTCAATTCCTGTAC 3′

• KTTM56: 5′ CAAGCTTTACCATCAACGAATTGTGAGCGCTCACAATTAXCTAGCTTCGATTCTAG 3′

The primers for the unlabeled or singly labeled constructs were identical to the above sequences except that the positions of the modifications were replaced with unlabeled thymine bases.

Two DNA duplexes, 56 basepairs (bp) in length, labeled with either donor or acceptor, were made to allow the formation of a sandwich complex (two separate DNA duplexes, each containing an operator sequence, bound to one LacI tetramer). The fluorescein-labeled duplex was formed by annealing LEFL56 to an unlabeled complement strand and the TAMRA-labeled duplex was formed by annealing KTTM56 to an unlabeled complement strand, by mixing equimolar amounts of the appropriate oligonucleotides in 100 mM NaCl and 10 mM MgCl₂, heating the sample to 95°C, and letting it cool slowly to 37°C. PCR products and 56 bp DNA duplexes were purified on native 8% polyacrylamide gels (39:1 acrylamide:bis) and eluted by gentle shaking overnight in 400 μL of 50 mM NaOAc (pH 7), 1 mM EDTA. Trace acrylamide was removed from the eluant using a QIAquick Gel Extraction Kit from Qiagen (Valencia, CA). DNA was stored in TE buffer (10 mM Tris, 1 mM EDTA, pH 8.0).

Determination of labeling efficiencies

The [dye]/[DNA] for each of the PCR primers was determined by measuring the absorption spectra of the oligonucleotide annealed to its unlabeled complement in LacI buffer [25 mM Bis-Tris, 5 mM MgCl₂, 100 mM KCl, 2 mM DTT, 0.01% (v/v) Nonidet P-40, pH 8.0] on an HP 8453 diode-array spectrophotometer (Hewlett Packard, Palo Alto, CA). Bis-Tris was used in the LacI buffer for consistency with previous work done at pH 7.0, but careful attention was paid to maintaining the pH at 8.0 so that fluorescein should be found in only one prototropic form, the dianion (Klonis and Sawyer, 1996). The concentrations of the dyes were obtained using the extinction coefficients reported by Midland, the supplier: at their excitation maxima, ɛ^fluorescein(494 nm) = 73,000 M⁻¹ cm⁻¹ and ɛ^TAMRA(558 nm) = 85,000 M⁻¹ cm⁻¹. The contributions of the dyes to absorption at 260 nm were calculated based on their concentrations and their extinction coefficients at 260 nm (ɛ^fluorescein(260 nm) = 20,900 M⁻¹ cm⁻¹; ɛ^TAMRA(260 nm) = 31,900 M⁻¹ cm⁻¹). The contribution of the dye at 260 nm was subtracted out and the concentration of DNA in each sample was then determined using the standard extinction coefficient for double-stranded DNA (50 μg/OD₂₆₀ unit).

The labeling efficiencies for the three labeled oligonucleotides were found to be 83% for KTTM56, 77% for FL11TOP, and 57% for LEFL56. Note that these calculations do not consider a possible decrease in the fluorescein extinction coefficient upon conjugation to DNA (Sjöback et al., 1998), which would increase the actual labeling efficiencies for FL11TOP and LEFL56. The donor labeling efficiency appears in energy transfer calculations only multiplied by the extinction constant (see Eq. 5 below), so this would not affect any of our conclusions.

Steady-state fluorescence measurements

Fluorescence data were collected using a PC1 photon counting spectrofluorometer (ISS, Champaign, IL) with a temperature regulated cell holder set at 21°C. All measurements were carried out in LacI buffer. Emission spectra from 505–700 nm were collected for the fluorescein-labeled and the fluorescein/TAMRA-labeled constructs, with λ_ex at 495 nm, whereas emission spectra for the TAMRA-labeled construct were collected from 565–700 nm, with λ_ex at 560 nm. The slit widths for the excitation and emission monochromators were 0.5 mm and 2.0 mm, respectively. A concentrated stock of LacI was titrated directly into a 2.5-nM sample of looping construct DNA, or into 12.5 nM each 56-bp duplex for sandwich complex formation, and spectra were collected after each addition of protein.

Spectral decomposition calculations

The emission and excitation spectra of the fluorescein/TAMRA-labeled constructs were decomposed into the individual contributions of the donor and acceptor as follows: Reference emission spectra of double-stranded 56-bp oligonucleotides labeled individually with fluorescein or TAMRA were obtained. These reference spectra were used as the basis set for determining contribution factors from fluorescein and TAMRA in experimental spectra of the double-labeled constructs. Microsoft Excel's Solver module was used to determine the contribution factors that minimize the least-squares difference between the experimental spectrum and a model consisting of a sum of variable contribution factors multiplied by the reference spectra. In particular, a and b in Eq. 1 below were chosen to minimize the sum of the residual errors:

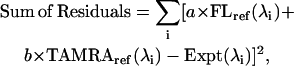(1)

where FL_ref(λ_i), TAMRA_ref(λ_i), and Expt(λ_i) refer to reference intensities for fluorescein and TAMRA and the experimental intensity, respectively, all as a function of wavelength. The results are presented in terms of the spectral contributions of the donor and acceptor, as areas integrated over wavelength. These values were used to calculate energy transfer as described below. Excitation spectra were decomposed analogously into fluorescein and TAMRA components. In all cases, emission data collected at a wavelength less than 20 nm greater than the excitation wavelength was excluded from the analysis to avoid scattering artifacts. None of the fit residuals showed any dependence on wavelength, indicating that there were no systematic shifts in the fluorescence spectra upon addition of LacI.

The fit curves in Fig. 2, B and D, and Fig. 3 B were obtained by assuming stoichiometric binding of LacI to DNA (the concentrations used here are at least 10-fold greater than K_d), and allowing variation of (1) the actual concentration of the LacI stock used for the particular experiment, (2) the slopes of the lines at [LacI] <5 nM, and (3) the endpoint integrated areas for each component. The fit was constrained by the assumption that 5 nM and 10 nM LacI were considered to be at saturation. In all cases these two concentrations give very similar results, although typically slight quenching is observed when LacI is in excess over DNA (in this case, 10 nM), perhaps due to nonspecific binding. The same actual concentration of LacI is enforced for both donor quenching and enhanced acceptor emission, and the best fit was determined simultaneously for the two processes. The actual concentration of LacI was typically found to be 3–5 nM for a nominal 5-nM concentration, suggesting some adsorption of protein to the cuvette. In practice, the fits are essentially to guide the eye: simply using the fluorescence observed at 5-nM LacI gave essentially identical results for the endpoint representing complete binding, and these values are used for all energy transfer calculations.

FIGURE 2.

Fluorescence resonance energy transfer in the 11C12-LacI and 9C14-LacI complexes. Excitation was at the excitation maximum of the fluorescein donor, 495 nm. The DNA concentration was 2.5 nM (5-nM operator), and the LacI concentration is reported in terms of dimer. (A) Fluorescence emission spectra of the 11C12 fluorescein/TAMRA-labeled DNA construct at increasing concentrations of LacI. Reference spectra for fluorescein-only and TAMRA-only labeled duplexes are reduced by 50%. (B) Spectral decomposition of the donor and acceptor contributions to the emission spectra of the 11C12-LacI complex, in terms of integrated area, versus LacI concentration. A small amount of energy transfer is apparent as a decrease in the contribution of the fluorescein donor and an increase in the contribution of the TAMRA acceptor. The fits shown assume stoichiometric binding of LacI, with the actual active concentration constrained to be the same for each data set, as described in Materials and Methods. (C) Fluorescence emission spectra of the 9C14 fluorescein/TAMRA-labeled DNA construct at increasing concentrations of LacI, showing dramatic energy transfer. At saturating LacI (10 nM), IPTG was added to the sample. A decrease in the efficiency of energy transfer is apparent. The fluorescence spectrum does not return to that in the absence of protein; apparently IPTG does not remove LacI from the DNA, rather it changes the DNA conformation. (D) Spectral decomposition of the donor and acceptor contributions to the emission spectra of the 9C14-LacI complex, in terms of integrated area, versus LacI concentration. A significant amount of energy transfer is detected in the DNA-protein complex, apparent as a large decrease in the contribution of the fluorescein donor and a large increase in the contribution of the TAMRA acceptor. The fits are as described for B.

FIGURE 3.

Demonstration of LacI and donor-dependent quenching of acceptor fluorescence in the donor and acceptor labeled 9C14-LacI complex. (A) Fluorescence excitation spectra for 9C14 labeled with fluorescein and TAMRA at increasing concentrations of LacI, with the emission wavelength fixed at the emission maximum of TAMRA at 580 nm. The DNA concentration was 2.5 nM (5 nM operator) and the LacI concentration is reported in terms of dimer. Reference spectra for fluorescein-only and TAMRA-only labeled duplexes are shown, reduced by 50%. (B) Spectral decomposition of the donor and acceptor contributions to the excitation spectra, in terms of integrated area. There is a significant decrease in the contribution from the direct excitation of the acceptor to the excitation spectra, due to quenching of acceptor fluorescence. The fluorescein contribution remains essentially constant, probably due to efficient energy transfer to acceptor accompanied by quenching of the acceptor fluorescence (see the text). In this experiment, 5 nM LacI caused 31.6% quenching of acceptor fluorescence. The fits in B were performed as in Fig. 2.

The extent of energy transfer in this system can be measured with a single sample of doubly labeled DNA, in contrast to other systems where measurements typically must be made on separate donor-only and donor/acceptor samples. (This requires the absence of energy transfer in the absence of LacI; see Results for this control experiment.) Energy transfer is calculated by comparing spectra measured in the absence of LacI and at 5-nm LacI (at which concentration the DNA is saturated with protein, as described above). The energy transfer efficiency based on the decrease in the quantum yield of the donor was calculated using Eq. 2 from Lakowicz (1999) below. The efficiency can also be calculated from the donor lifetime as in the expression on the right in Eq. 2, which is useful in interpreting the time-resolved results described below.

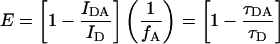(2)

Here E is the efficiency of transfer, I_DA is the integrated area due to fluorescein at 5 nM LacI (20 nM LacI for the sandwich complex), I_D is the integrated area due to fluorescein in the absence of LacI, f_A is the labeling efficiency of the acceptor, τ_DA is the lifetime of the donor in the presence of the acceptor (for the population which is in fact double-labeled), and τ_D is the unperturbed donor lifetime. The transfer efficiency for steady-state experiments was also calculated based on the sensitized emission of the acceptor, using Eq. 3 adapted from Selvin (1996):

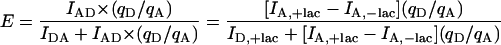(3)

Here I_AD is the integrated area of the sensitized emission of the acceptor, I_DA is the integrated area under the donor emission curve in the presence of the acceptor, q_D is the quantum yield of the donor, and q_A is the quantum yield of the acceptor. Adapting the equation to our system, we express I_AD as the difference between I_A,+lac, the integrated area under the acceptor emission curve in the presence of 5 nM LacI, and I_A,−lac, the integrated area under the acceptor emission curve in the absence of LacI. I_DA is replaced by I_D,+lac, the integrated area under the donor emission curve in the presence of 5 nM LacI. During the course of the experiments, we characterized LacI-dependent quenching of acceptor fluorescence in the donor and acceptor labeled 9C14 construct (see Results). The energy transfer corrected for acceptor quenching is given by Eq. 4:

(4)

Here, Q_AV is the average quenching of acceptor fluorescence by LacI, and q_D/q_A is the original ratio of quantum yields of the donor to acceptor. The factor (1 − Q_AV) multiplying I_{A, −lac} takes account of the fact that the observed acceptor intensity in the absence of LacI is larger than the intensity that would have been observed in the presence of quenching but in the absence of energy transfer. The factor (1 − Q_AV)⁻¹ multiplying (q_D/q_A) corrects for the underestimation of the observed I_A,+lac due to decreased acceptor quantum yield. The second expression in Eq. 4 makes it clear that the quenching Q_AV is not being double-corrected.

To apply Eqs. 3 and 4, the absolute quantum yields of the donor and acceptor need not be determined, only the ratio (q_D/q_A), derived from the definition of quantum yield and given by Eq. 5 (Cantor and Schimmel, 1980):

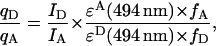(5)

where I_D and I_A are the integrated fluorescence intensities of donor and acceptor in the absence of quenching or energy transfer, ɛ^D and ɛ^A are their extinction coefficients, and f_D and f_A are the labeling efficiencies. The extinction coefficients of both of the dyes at the excitation maximum of fluorescein were provided by Midland [ɛ^D(494 nm) = 73,000 M⁻¹cm⁻¹, ɛ^A(494 nm) = 14,300 M⁻¹cm⁻¹].

The interfluorophore distance is calculated from the efficiency using Eq. 6:

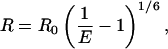(6)

where R is the physical distance between the donor and the acceptor and R₀ is the Förster radius for the donor and acceptor pair (assumed to be 55 Å). We make the standard assumption that the orientations of the fluorophores average, to give a κ² factor of 2/3. None of our qualitative conclusions depend on the accuracy of absolute distances.

Time-resolved fluorescence measurements

Time-resolved fluorescence data were collected on samples in which LacI was titrated into 50 nM fluorescein/TAMRA-labeled 9C14 DNA. During acquisition of the time-resolved data, efficient energy transfer in the same samples was verified by collection of emission spectra on a steady-state fluorometer as described above. Time-resolved fluorescence was measured using a single photon counting fluorometer setup (Han et al., 2002), briefly as follows: a synchronously pumped, mode-locked, cavity-dumped Spectra-Physics 3520 dye laser (Mountain View, CA) was used as the light source at 335 nm, providing pulses of width <10 ps, with a repetition rate of 4 MHz and an average power of 200 μW. Vertically polarized ultraviolet pulses were obtained by frequency doubling of horizontally polarized dye laser pulses. The channel width was 47 ps and the data were collected in 512 channels. A monochromator and microchannel plate photomultiplier combination yielded a transit time spread of ∼120 ps, allowing one to resolve correlation times as short as 50 ps. The exciting light time profile was obtained with a light-scattering Ludox suspension (DuPont, Wilmington, DE). The intensity decay profiles were collected through an emission sheet polarizer oriented 55° from the vertical symmetry axis. Emission was selected by a computer-controlled JYH10 monochromator with the bandwidth set at 8 nm, and a glass slide was added to further reject stray excitation as needed. Decay curves were recorded by using standard time-correlated single photon counting modules and a Spectrum-Master multichannel analyzer (Ortec, Oak Ridge, TN) under computer control. Amplitude and lifetime values were recovered using the custom software package Decayfit. We are grateful to Drs. Jay Knutson and John Harvey (Laboratory of Biophysical Chemistry, National Heart, Lung, and Blood Institute, National Institutes of Health) for the collection of this data and decomposition into decay components.

Monte Carlo simulations

Monte Carlo simulation methods for DNA loops (R.C., R.A. Mehta, L.M.E., and J.D.K., unpublished) were derived from previous work on DNA cyclization kinetics (Hagerman and Ramadevi, 1990; Kahn and Crothers, 1998; Koo et al., 1990). Essentially, a plausible description of possible open Lac repressor geometries was derived by examination of the cocrystal structure (Lewis et al., 1996); one LacI dimer was modeled as rotating relative to the other about an axis parallel to the axis of the C-terminal four-helix bundle. For a given simulation, the repressor geometry was held fixed. The DNA loop geometry was obtained by combining DNA half-chains as in previous work, but one set of half-chains contained a discontinuous segment where the DNA jumps from one operator to the other. Fig. 5 shows representative examples of chains that cyclized at the apices of the loops shown. Short DNA segments were grafted onto the operators of cyclized molecules to generate a picture of the actual loop. The simulation procedures will be described in detail elsewhere.

FIGURE 5.

Models of (A) the 11C12-LacI “open” complex and (B) the 9C14-LacI “closed” complex, obtained by Monte Carlo simulations as described in Materials and Methods. The model in (B) agrees with previous demonstrations that 9C14 can form a loop with a positive writhe crossover and with the FRET results reported here. The interfluorophore distance is much larger for the open form 11C12 loop in (A), in accord with the much lower FRET efficiency.

RESULTS

Our previous work on the DNA-LacI loop geometry suggested that loop geometry can be controlled by the appropriate design of DNA sequences between two lac operators (Mehta and Kahn, 1999). The previously designed DNA constructs have two operator sequences that bracket a sequence-directed phased A-tract bend. The stabilities of specific loop shapes were controlled by altering the helical phasing of the operators relative to the bend, via altering linker lengths between each operator and the A-tract bend (see Fig. 1). The 9C14 construct was designed with the operator dyad symmetry axes directed away from the center of curvature, such that upon LacI binding the DNA is more likely to adopt a closed form loop directed away from the protein, as in the Lewis model (Lewis et al., 1996). The 11C12 construct was designed with operator dyad axes directed inward, to prefer a more U-shaped open form loop around the protein.

Previous results using this system showed that both the 9C14 and 11C12 constructs form hyperstable loops, with half-lives on the order of days. LacI titrations and also relative kinetic stabilities in competitor challenge experiments suggested that the 11C12 construct is the most stable. Gel mobility shift experiments suggested that the 9C14 loop is in fact more compact than 11C12, as expected from the model. Ring closure experiments on loops with extended tails (∼345 bp total length) indicated that the 9C14 loop can give both relaxed and positive topoisomers, whereas the 11C12 loop gives predominantly relaxed topoisomers. Analysis of the cyclization kinetics suggested that 9C14 may adopt both open and closed forms, and that the two do not interconvert rapidly. A control looping construct in which there is no sequence-directed bend was much less stable, but its gel mobility and topology suggested that its shape is very similar to the open form 11C12.

Electrophoretic mobility and topology results are subject to multiple interpretations, so we sought a more direct method of analyzing shape in the DNA loops, as well as more information concerning the proposed multiple populations of the 9C14 construct. We turned to fluorescence resonance energy transfer (FRET). Because the operators are ∼130 bp (∼440 Å) apart along the DNA contour, we reasoned that a significant level of FRET would be a strong confirmation of the 9C14 closed form loop. For comparison, we also characterized energy transfer in the 11C12 open form loop as well as in sandwich complexes, in which a separate DNA duplex is bound to each of the two LacI dimers in the tetramer. (The x-ray crystal structure of Lewis et al. (1996), Fig. 1 C, is a sandwich complex with two 21-bp operator DNAs bound to the protein tetramer.)

Design, synthesis, and characterization of fluorescent DNA constructs

We examined the structure (Lewis et al., 1996) and chose positions for fluorophore attachment in the major groove, on the face of the DNA helix facing away from the bound LacI and not included within the operator (Fig. 1 C). Accordingly, looping constructs were synthesized, using PCR, with a fluorescein donor molecule two bases toward the A-tract segment from the edge of one operator sequence and a TAMRA acceptor molecule two bases toward the A-tracts from the other operator (thus, both fluorophores are inside the final DNA loops; Fig. 1). In a closed form loop with the same LacI shape as seen in the crystal structure, the fluorophores should come into close proximity (30 Å) of each other, allowing energy transfer to occur. The energy transfer was predicted to be much lower in the 11C12 open form loop. In addition, two 56-bp DNA duplexes, one labeled with fluorescein and the other with TAMRA, were used to form sandwich complexes.

Before FRET analysis of the 11C12-LacI, 9C14-LacI, and sandwich complexes, several initial experiments that would have a bearing on the subsequent calculations of energy transfer efficiencies were performed. First, electrophoretic mobility shift assays using radiolabeled DNA were performed on all DNA constructs, both fluorescently labeled and unlabeled, to verify that LacI binds and loops the DNA or forms sandwich complex as previously seen (data not shown). Second, titrations of LacI into 2.5-nM samples of donor-only and acceptor-only fluorescently labeled looping constructs were used to measure LacI-induced quenching of donor and acceptor fluorescence. Emission spectra were collected throughout the titration and the spectra were integrated for each concentration of LacI (data not shown). The quenching of donor-only and acceptor-only fluorescence in the three complexes analyzed was ∼5%. Except as discussed below, this low level of quenching should lead to minimal error in the calculated energy transfer efficiencies. (Subsequent experiments, however, suggest that a higher level of quenching of acceptor fluorescence by LacI in the donor/acceptor labeled 9C14-LacI complex may partially explain an observed discrepancy between the energy transfer efficiencies measured from sensitized emission of the acceptor and from donor quenching.)

The assumption is made throughout that in the absence of protein no energy transfer occurs between the donor and acceptor, as the average distance between the fluorophores should exceed 200 Å. This is significant because it allows the efficiency to be measured from a single sample as opposed to separate donor-only and doubly labeled samples. The lack of energy transfer for each unbound DNA construct was verified using a restriction digestion assay: The emission spectrum for each construct labeled with donor and acceptor was obtained. Then, the blunt cutting restriction enzyme RsaI (recognition sequence 5′ GT/AC 3′), was added directly to the samples. This enzyme cuts the DNA at a site ∼12 bp interior to the first operator in Fig. 1, inside the loop region. Upon complete restriction (verified by electrophoresis of subsequently radiolabeled products), the donor and acceptor are on separate molecules and can no longer transfer energy. No changes in the emission spectra were detected after a complete restriction (data not shown), confirming that in the intact samples no energy transfer had been occurring.

Energy transfer in the 11C12-LacI open complex

Based on our previous results (Mehta and Kahn, 1999) the 11C12 construct was proposed to adopt an open form loop around the protein. It was hypothesized that the protein can adopt an open configuration by rotating one LacI dimer relative to the other about the axis of the four-helix bundle tetramerization domain at the base of the protein (Friedman et al., 1995). Therefore, there should be a relatively large distance between the two DNA-binding domains of the tetramer and hence between the two fluorophores. Fig. 2 A shows emission spectra from the titration of LacI into a 2.5-nM sample of fluorescein/TAMRA-labeled 11C12, with excitation at the donor excitation maximum at 495 nm. There appears to be a small extent of energy transfer in this complex, suggested by a small decrease in the intensity at the donor emission maximum at 520 nm and a corresponding increase at the acceptor emission maximum at 580 nm.

To quantify the extent of energy transfer, emission spectra were decomposed into the individual contributions of the donor and acceptor over all wavelengths, as described in Materials and Methods (Fig. 2 B). As protein is added and looped complex forms, the integrated area attributed to the donor decreases slightly, and the contribution of the acceptor increases to a similar extent, as expected for energy transfer. The changes in the integrated areas of both the donor and the acceptor level off at 5 nM LacI dimer, the concentration at which the tetramer concentration ([LacI_tetramer] = 0.5 × [LacI_dimer]) equals the 2.5 nM DNA concentration, and therefore all of the DNA is found as a bound loop (binding is stoichiometric at these concentrations).

Using Eqs. 2 and 3 in Materials and Methods, the energy transfer efficiencies in the 11C12 loop, based on the decrease in the quantum yield of the donor and the sensitized emission of the acceptor, were found to be 11% and 8%, respectively (all the energy transfer results are collected in Table 1). As expected from the design of 11C12, these efficiencies are low, corresponding to distances of 78 Å and 83 Å, respectively (Table 1). The observed spectra are not the result of quenching: as discussed above, LacI quenches donor-only 11C12 by only ∼2%, and the enhanced emission of acceptor confirms energy transfer rather than some other quenching mechanism. The measured distances indicate that the DNA operators are substantially farther apart than they are in the crystal structure of the sandwich complex (Lewis et al., 1996). This confirms the earlier claim that the protein may adopt a relatively open form to accommodate the preferred looping geometry of the 11C12 construct. The observed weak energy transfer could reflect an ∼80 Å separation between fluorophores in a uniform looped complex population, or it could be due to efficient transfer in a rare closed form population; the steady-state experiment cannot distinguish these possibilities.

TABLE 1.

Energy transfer efficiencies and apparent interfluorophore distances for the 11C12-LacI, 9C14-LacI, and sandwich complexes

Sample	Method	Efficiency	Apparent distance (Å)
11C12-LacI	Donor quenching†	11%	78
	Uncorrected acceptor emission	8%	82
9C14-LacI	Donor quenching†	74%	46
	Uncorrected acceptor emission	38%	60
	Corrected for acceptor quenching	52%	54
Sandwich*	Donor quenching†	12%	77
	Uncorrected acceptor emission	9%	81

^*Sandwich is a mixture containing 20 nM LacI and 12.5 nM each of two 56-bp duplexes: [LEFL56 (Fluorescein) + complement] and [KTTM56 (TAMRA) + complement].

^†Non-Förster donor quenching due to LacI binding was measured in experiments on donor-only DNA as 2.1% for 11C12 and 6.9% for 9C14. This is not taken into account in the energy transfer calculation.

Energy transfer in the 9C14-LacI closed complex

Previous studies showed that upon LacI binding to a 9C14 construct and subsequent DNA cyclization to form an ∼320-bp minicircle, a positive topoisomer appears, suggesting a tight loop wrapping away from the protein (Mehta and Kahn, 1999). A relaxed topoisomer is also formed. Thus, the cyclization kinetics results suggested that the 9C14-LacI complex exists as a mixture of two populations, one in which the closed loop forms at the cost of bending strain and the other in which an open loop forms at the cost of twisting strain. We expected to detect substantial energy transfer for the closed loop complex. As shown in Fig. 2 C, as protein is added to the 2.5 nM DNA there is a significant decrease in the intensity of the fluorescein emission. A slight increase in intensity at the acceptor's emission maximum at 580 nm was also observed. The observed increase is not as large as might be expected intuitively, partly because the increased contribution from the acceptor is balanced by a decreased contribution from the donor.

Spectral decomposition (Fig. 2 D) of the emission spectra in Fig. 2 C confirms a substantial decrease in the contribution of the fluorescein donor and a significant increase in the contribution of the acceptor as looped complex is formed. The amount of sensitized acceptor emission is smaller than the amount of donor quenching; subsequent experiments showed that acceptor fluorescence is quenched in this complex, which decreases the observed sensitized emission (see below). As seen for the 11C12-LacI complex, the changes in the contributions of the donor and acceptor are complete at 5 nM LacI. Based on this data, an energy transfer efficiency of 74% was calculated based on the decrease in quantum yield of the donor, which corresponds to a distance of 46 Å. A significantly lower efficiency of 38% was calculated based on the sensitized emission of the acceptor, corresponding to a larger distance of 60 Å. Before discussing the origin of this discrepancy, we mention one additional experiment on the loop geometry.

Isopropyl-β-D-thiogalactopyranoside (IPTG) is an artificial inducer of the lac operon. It acts by shifting the orientation of DNA binding headpieces relative to each other (Bell and Lewis, 2000; Lewis et al., 1996). However, the protein remains a DNA binding protein, albeit with a ∼1000-fold lower affinity (Müller-Hartmann and Müller-Hill, 1996; O'Gorman et al., 1980a). IPTG (1.5 mM, twice the concentration typically used to induce transcription in media) was added to the 9C14-LacI complex (2.5 nM DNA, 10 nM LacI dimer). The resulting emission spectrum is intermediate between the spectrum observed for maximum energy transfer (5 nM LacI) and the spectrum in the absence of energy transfer (0 nM LacI), indicating a decreased efficiency of energy transfer (Fig. 2 C). Addition of more IPTG led to no further change in the spectrum, and IPTG addition to donor-only and acceptor-only complexes showed that IPTG did not cause quenching of either fluorophore (data not shown). These results suggest that IPTG binding leads to a rearrangement of the loop, but not the release of the protein; the concentrations of protein and DNA here would still be expected to afford complete binding based on the results of O'Gorman et al. (1980b) The geometric change induced by IPTG was not studied further.

The interfluorophore distance along the DNA contour in these molecules is ∼130 bp, or ∼440 Å. Thus, the qualitative fact of energy transfer provides a definitive verification of DNA looping. These results are the first demonstration of FRET in a true DNA loop, defined here as a complex where much of the loop DNA is not contacted; experiments on IHF (Lorenz et al., 1999a) and the nucleosome (Toth et al., 2001) provide examples of end-to-end FRET in complexes where the proteins wrap DNA about themselves over the entire DNA length.

Donor-dependent quenching of acceptor fluorescence in the 9C14-LacI complex

What is the origin of the disagreement described above between donor quenching and acceptor emission results? LacI causes only minimal quenching of donor and acceptor fluorescence in donor-only and acceptor-only loops that behave identically to the doubly labeled loop in biochemical experiments. This suggests that a feature specific to the presence of donor in the doubly labeled looped complex may be quenching the fluorescence emitted from the acceptor. Such quenching would explain the observed net quenching of total fluorescence as well as the smaller apparent energy transfer efficiency calculated based on sensitized emission relative to the efficiency calculated based on donor quenching. Experiments focusing on acceptor emission and excitation were performed to investigate this issue.

Emission spectra of the donor/acceptor labeled 9C14 complex were collected at the TAMRA acceptor's excitation maximum, 560 nm, where fluorescein absorbance is negligible. As the concentration of LacI increased, there was significant quenching of acceptor fluorescence, but no change in the shape of the emission curve (data not shown). Area integration of the emission spectra showed that LacI quenches the acceptor, causing an 18.1% decrease in fluorescence at 5 nM LacI, the concentration at which maximal energy transfer occurs. The protein quenches the acceptor by only 5.3% in the 9C14 acceptor-only complex (data not shown).

Donor-dependent quenching of acceptor fluorescence was further verified by collecting excitation spectra of the doubly labeled 9C14 loop complex at several LacI concentrations, monitoring emission at the TAMRA emission maximum at 580 nm (Fig. 3 A). Uncomplicated energy transfer in the looped complex would give an increase in the excitation spectrum component matching the donor's absorbance spectrum, due to absorption of a photon by the donor, transfer to acceptor, and then emission characteristic of the acceptor. The fluorescein component is observed, however, to change very little (notice the nearly constant peak at 495 nm, the excitation maximum of fluorescein), whereas there is a significant decrease in intensity of the acceptor's excitation component (notice the decrease at the acceptor excitation maximum of 560 nm). The result for fluorescein (495 nm) is actually consistent with energy transfer: overall, the donor is being quenched, and the constant intensity masks a shift from inefficient direct donor emission at 580 nm to emission via energy transfer to the acceptor. Had there been no acceptor quenching, we would have observed an increase in the fluorescein component. The decrease in the excitation spectra at 560 nm confirms quenching of directly excited acceptor, and quenching is presumably also occurring for acceptor excited via energy transfer.

To determine the magnitude of quenching, these excitation spectra were decomposed into components from excitation spectra of fluorescein-only and TAMRA-only duplexes, as described in Materials and Methods (Fig. 3 B). Based on the integrated areas, 5 nM LacI causes 31.6% quenching of acceptor fluorescence. We do not know why quenching measurements from emission spectra versus excitation spectra give somewhat different answers.

The average extent of acceptor quenching in the 9C14 donor/acceptor-LacI looped complex from the two experiments above (Q_AV = 24.9%) was used to correct the observed energy transfer efficiency according to Eq. 4 (Materials and Methods), which accounts for both the decrease in the observed acceptor fluorescence due to quenching and also the decrease that quenching would have caused in the baseline acceptor emission. The corrected calculated efficiency based on the sensitized emission of the acceptor is 52% (versus the uncorrected 38%), corresponding to a smaller distance of 54 Å versus the previous 60 Å (Table 1). A significant discrepancy remains between the efficiency calculated based on sensitized emission and that calculated based on donor quenching. It is possible that this is due to a reciprocal non-Förster effect, acceptor-dependent donor quenching by a mechanism other than energy transfer, but we cannot evaluate this possibility from our present data. Further discussion of the results is based on the efficiency calculated based on the decrease in the quantum yield of the donor, but the qualitative conclusions would be the same for either value.

There are several possible mechanisms for donor-dependent acceptor quenching (and the possible reciprocal effect). The presence of the donor fluorophore could have an allosteric effect on the protein-DNA complex and/or could change the electrostatic environment, either of which could alter the environment of the acceptor. However, there do not appear to be dramatic conformational changes, as we did not observe effects on electrophoretic mobility or complex stability for donor/acceptor versus singly labeled complexes. The photophysics of the two fluorescent molecules could be altered if they approach each other very closely, although we did not observe any spectral shifts in excitation or emission spectra. Note that for the inefficient energy transfer exhibited by the 11C12-LacI looped complex, the donor quenching and acceptor emission measurements agreed better, to within ∼20%, suggesting that whatever the quenching mechanism is for 9C14-LacI, it requires close approach of fluorophores.

There is ample precedent in the literature for disagreement between energy transfer efficiencies measured by donor quenching versus acceptor emission. Parkhurst and Parkhurst (1995) described a similar phenomenon in kinetic studies of DNA duplex formation, which used fluorescein and X-rhodamine labeled oligonucleotides. They show that an X-rhodamine attached to the 5′ end of one oligonucleotide causes a conformational perturbation that affects the interaction of a fluorescein attached to the 3′ end of the oligonucleotide with the DNA itself. They attribute their detection of abnormal static quenching of fluorophores to this perturbation. Clegg and co-workers have performed an extensive study of the spectral properties of 5-carboxytetramethylrhodamine attached to the 5′ end of DNA in both single-stranded and double-stranded complexes (Vamosi et al., 1996). They found that unlike the free dye, TAMRA-DNA molecules (both single- and double-stranded) exhibit at least three different spectroscopic states with different quantum yields, and their relative populations are temperature and salt dependent. Their work suggests that these various states are due to multiple orientations of the dye relative to the DNA, arising from TAMRA stacking with the nucleotides or interactions of the charged groups of TAMRA with the DNA backbone or salt. By comparing time-resolved and steady-state fluorescence measurements they identified two fluorescent states, with lifetimes in the 0.5–1-ns and 2.5–3-ns range, and one nonfluorescent or “dark” state. Balasubramanian and co-workers have similarly identified multiple orientations of TAMRA relative to the DNA for molecules that have internal dye modifications, as in our molecules (Furey et al., 1998). If the distribution among TAMRA populations changes due to allosteric or electrostatic effects of one dye on the other, this could contribute to the discrepancy observed here between the two efficiencies obtained for the 9C14-LacI complex.

Regardless of the origin of the quantitative discrepancy between our efficiency measurements, the essential result is that efficient energy transfer was detected for the 9C14-LacI complex and inefficient transfer for 11C12-LacI. The corresponding distance estimates should be useful in setting limits for models of the closed form 9C14 loop and the open form 11C12 loop.

Time-resolved fluorescence of the 9C14-LacI complex

Energy transfer in the 9C14-LacI complex was also analyzed by measuring fluorescence lifetimes in the time domain, because time-resolved measurements can identify the presence of a mixed population of conformational states. The steady-state efficiency of ∼70% measured above for this complex could be due to a uniform population of looped complexes transferring with 70% efficiency, or it could be due to 70% of the complexes existing in a closed form exhibiting nearly 100% transfer efficiency and the remaining 30% of the complexes in an open form, supporting little to no energy transfer. Any intermediate combination of these scenarios is also possible. A uniform population should give a single donor lifetime at saturating LacI, whereas different populations should have different donor lifetimes, manifested as multiple decay components in fluorescein fluorescence.

The decay curves for the fluorescein donor in doubly labeled 9C14 were measured as a function of LacI concentration. Fluorescein was excited in its second excitation band at 335 nm using a pulsed dye laser, and the fluorescence decay was collected in the time domain at 515 nm. The decay curve was measured in the absence of protein at a DNA concentration of 50 nM. Then, LacI protein was titrated in to achieve saturation and the decay curve was measured at several LacI concentrations. During collection of the time-resolved data, emission spectra collected on a steady-state fluorometer showed that the same samples engaged in energy transfer with an efficiency essentially identical to that observed above for titration of 2.5 nM DNA with LacI (data not shown). The time-resolved data were globally fit to a four-component multiexponential decay curve, with the lifetimes constrained to be the same for each decay curve but with amplitudes free to vary, yielding a global χ² of 1.004 with a total of twenty parameters. The quality of the fit from this analysis was as good as the quality from several other models with more parameters (for example, 32 parameters from allowing lifetimes to vary for each decay curve); in contrast, the χ² values were much larger for models with fewer lifetime components.

In Fig. 4 the component amplitudes of the four measured lifetimes are plotted versus LacI concentration. The 0.01 and 15.5-ns lifetime components remain essentially constant and are assigned to scattering and to background, respectively. The 3.56-ns lifetime of the unperturbed fluorescein donor molecule decreases in amplitude as looped complex is formed and energy transfer occurs. However, at 150 nM LacI, a concentration at which the DNA is saturated with protein, this lifetime component remains present at 45% of its initial amplitude. (At this high concentration there also appears to be some nonspecific quenching, because the total amplitude has decreased slightly relative to 100 nM LacI.) Note that although fluorescein residing on a molecule lacking TAMRA would give the unperturbed lifetime even in a closed form loop, based on the measured labeling efficiency for TAMRA the fluorescein-only molecules should comprise no more than ∼17% of the fluorescein-labeled pool. Thus, the continued presence of the 3.56-ns component suggests that some of the LacI-9C14 loop is in an open form.

FIGURE 4.

Time-resolved fluorescence monitoring the fluorescein donor emission (at 515 nm) of the 9C14-LacI complex. The DNA concentration was 50 nM. Looped complex is formed as LacI is titrated into the sample. The best global fit to the data was obtained using four constant lifetime components and variable amplitudes. The 0.01 and 15.5 ns lifetime components correspond to scattering and to background, respectively. The 3.56 ns lifetime corresponds to an unperturbed lifetime of the donor, which decreases significantly in amplitude as looped complex is formed and energy transfer occurs, but at saturation still remains present. This suggests the presence of two populations, one population involved in efficient energy transfer and another population that does not engage in any energy transfer. The 0.61 ns lifetime corresponds to the observed energy transfer efficiency and increases as looped complex forms, but it is surprising that it is present in the absence of protein. There may also be a quasistatic self-quenching component; see the text for details.

There is also a 0.61-ns lifetime population, which may represent fluorescein engaged in energy transfer (0.61 ns would correspond to 83% efficiency), because the amplitude increases as looped complex is formed. However, the 0.61-ns component is also observed in the absence of LacI, and as [LacI] increases the 0.61-ns component does not increase in proportion to the decreased amplitude of the 3.56-ns component. The 0.61-ns component may derive partially from a population of fluorescein with altered photophysics, for example in a different orientation relative to the DNA; multiple lifetimes for fluorescein conjugated to DNA, including a 0.7-ns lifetime, have been reported previously (Lee et al., 1995; Sjöback et al., 1998). Fluorescein that is allosterically quenched by the presence of nearby TAMRA, as speculated above, might also contribute to the 0.61-ns component. The decreased amplitude of the 0.61-ns component at 150 nM relative to 100 nM LacI could be due to overall non-Förster quenching or to a decrease in energy transfer due to the conversion of looped DNA into a form bound to two LacI tetramers (Brenowitz et al., 1991).

It is not necessarily to be expected that a fluorescein in an altered conformation and one that was quenched by energy transfer would exhibit the same 0.61-ns lifetime, but our experiments do not have the resolution needed to distinguish two very similar lifetimes. Adding a fifth lifetime component to the analysis was not justified.

Finally, there may be a very short lifetime component, with τ less than 100 ps, that was not detected with the time-resolution of the system used. Such “quasistatic self quenching” (Chen et al., 1991) appears as net static quenching: the total fluorescence amplitude at zero time decreases throughout the LacI titration (as seen in our steady-state data). The quenching is, however, due to efficient quenching of the excited state donor via transfer, as opposed to ground state formation of a dark state. An interfluorophore distance of ∼30 Å in our system would give a 100-ps lifetime.

All in all, the time-resolved data are consistent with the presence of at least two populations of the looped 9C14-LacI complex, one a closed form population involved in efficient or undetectably rapid energy transfer, and another a more open form population that does not engage in any energy transfer and therefore exhibits an unperturbed fluorescein fluorescence lifetime. The data presented here is consistent with the previous biochemical results (Mehta and Kahn, 1999). We did not characterize time-resolved spectra of the 11C12 loop, as the extent of energy transfer was so low that it would have been difficult to detect changes due to transfer. In principle, more complete characterization of the time-dependent emission over the entire emission spectrum of both fluorophores would address whether the observed lifetimes of the fluorescein and TAMRA are consistent with the mutual donor-acceptor quenching mechanism suggested here.

Energy transfer in the DNA-LacI sandwich complex

The LacI tetramer can bind two operators simultaneously. If the operators are on different DNA molecules, a DNA-LacI “sandwich” complex can form (Fickert and Müller-Hill, 1992; Fried and Crothers, 1981; O'Gorman et al., 1980b). In the absence of constraining loop DNA, electrostatic repulsion between the bound DNA molecules could favor a more open form where the DNA-binding domains are farther apart. The magnitude of any such effect would presumably depend on the DNA length and the ionic strength.

We characterized the sandwich complex for comparison with the DNA loops. Preliminary experiments attempting to form sandwich complex using two 26-bp duplexes with fluorophores at their ends confirmed that nonspecific DNA flanking the operators was required to increase the stability of the complexes (data not shown). Record and co-workers have previously demonstrated that stable LacI binding requires flanking nonoperator sequences (Levandoski et al., 1996; Tsodikov et al., 1999).

Subsequently, we employed two 56-bp duplexes with centered operators that contain either a fluorescein or TAMRA modification attached two bases away from the operator, using the same fluorescent oligonucleotides that were used as PCR primers above annealed to unlabeled complementary DNA. Equal amounts of donor and acceptor duplexes were mixed, LacI was titrated into the sample to form sandwich complex, and emission spectra were collected as above (data not shown). An energy transfer efficiency of 12% was measured by donor quenching and 9% by sensitized acceptor emission, an energy transfer similar to the open form 11C12. However, data analysis is complicated by several factors. First, assuming that stable sandwich complexes form randomly, only half of the complexes will contain both donor and acceptor duplexes. Also, the operator sequence is symmetric, which allows for four orientational isomers in which the donor and acceptor molecules can each be on one side or the other of the protein. Therefore, to give a distance estimate corresponding to the same locked fluorophore orientation provided by the continuous double-labeled molecules, the measured energy transfer efficiency should be multiplied by a factor between two and eight to account for the various isomers formed. It is, however, impossible to estimate from our data whether the distribution of compositional and positional isomers is in fact random, or what contribution might be made to the observed energy transfer by isomers in which the orientation of one or the other DNA is reversed. Therefore, the most that can be concluded about the sandwich complex is that at least some fraction of the LacI tetramers must be in a conformation significantly more closed than the LacI in 11C12 to give the observed transfer efficiency, which is similar to that of 11C12.

DISCUSSION

The steady-state fluorescence resonance energy transfer experiments reported here confirm that stable Lac repressor loops can adopt at least two different conformations, one in which the two operators are in close proximity and one in which they are significantly farther apart. The populations of the two forms are strongly modulated by the orientations of DNA bending sequences in the loop regions. This is the first demonstration of FRET between the ends of a true DNA loop (as opposed to a complex in which the DNA is contacted along its entire length). The two conformations were predicted based on the design and biochemical characterization of the prebent hyperstable 9C14 and 11C12 loops used. Furthermore, the time-resolved experiments reported here, though preliminary, support the existence of two separate conformers for the 9C14 loop, as previously suggested based on DNA cyclization kinetics experiments. More elaborate time-resolved experiments and single-molecule FRET studies could make possible a detailed analysis of the loops' equilibrium distance distribution and dynamic properties. The size and hyperstability of these complexes also make them ideal for atomic force microscopy or high-resolution footprinting experiments.

It is perhaps surprising that the 9C14 loop can adopt two (at least) conformations: for both to exist, they must be quite similar in free energy, and a priori there is no reason this should be true. There are, however, several lines of evidence for multiple populations. In cyclization kinetics experiments (Mehta and Kahn, 1999), we found that an extended 9C14 yields both positively supercoiled circles and relaxed circles, but that formation of relaxed circles is complete before the positive supercoils accumulate substantially. This suggests non-interconverting loop precursors; interconversion is slow because it requires the release of one operator. (In principle, slow interconversion means that the observed loop distribution reflects the kinetics rather than the thermodynamics of loop formation, but the transition state for formation is likely to require most of the DNA deformation of the final complex.) The observed cyclization kinetics can be quantitatively rationalized by Monte Carlo simulations (Kahn and Crothers, 1998) that consider multiple loop geometries (R.C., R.A. Mehta, L.M.E., and J.D.K., unpublished), with the assumption that the loop energetics and also a preference intrinsic to DNA-bound LacI protein for the open form dictate which loop forms. In the current work, the fact that a population of fluorescein donors retains the unperturbed fluorescein lifetime (3.56 ns) even at saturating protein suggests that some of the 9C14 loops exhibit no energy transfer. We suspect that the same is true of 11C12, that the low level of fluorescence observed reflects a small population of closed form loops as opposed to a uniform ∼100-Å separation, but the measured FRET efficiency is too low to test this experimentally.

Plausible loop shapes derived from Monte Carlo simulations are illustrated in Fig. 5. They are in accord with the structural features suggested by the biochemical and FRET experiments, as described above. They also confirm a previously suggested possible origin for the two 9C14 populations: the closed form loop clearly has a great deal of bending strain throughout the loop, and might be expected to be less stable than the open form loop. This is confirmed experimentally and in the simulations (R.C., R.A. Mehta, L.M.E., and J.D.K., unpublished). The 9C14 molecule also appears to be able to adopt an open form geometry of some kind, as described above. Intuition and simulation suggest that this is due to a conformation where the DNA is twisted so that the operators are directed inward relative to the direction of curvature, allowing the formation of an open form with much less bending strain than the closed form but much more twisting strain. Monte Carlo simulations of DNA cyclization (Kahn and Crothers, 1998) show that the formation of DNA circles from strongly bent molecules does not proceed through bend inversion; it is less energetically costly to make local twist changes that bring the DNA bends into alignment with each other. The same should be true for loop formation. Fig. 6 qualitatively illustrates the energetic tradeoff between bending strain and twisting strain in the two conformations of 9C14-LacI, and rationalizes the greater stability of 11C12-LacI by the fact that no such tradeoff is incurred when it forms the open loop.

FIGURE 6.

Illustration of the proposed balance between DNA bending strain and twisting strain in different DNA loops. The green bars represent the dyad axes of the DNA operators, which must align as shown to form a DNA loop; the sketch is not intended to suggest that LacI dimers are relevant intermediates. The arrows in the sketches at the left indicate the DNA deformations needed to form the loops on the right. Sketch A shows the formation of two possible 9C14 loops. The open form at the top shows that the linkers have overtwisted and undertwisted to allow formation of a conformation with reduced bending strain, but at a cost of increased twist strain. The closed form for 9C14, at the center on the right, is substantially more bent than its equilibrium shape and therefore is highly strained, although this form appears to be preferred for 9C14. Sketch B shows the 11C12 loop, which can adopt an open form (low bending strain) at a low cost in twist and is therefore more stable than either 9C14 loop. The small extent of FRET observed for 11C12 could be due to the open form shown or to smaller populations with other geometries.

The model in Fig. 5 B resembles but is not identical to that of Schulten and co-workers (Balaeff et al., 1999), which was based on minimizing the elastic energy of the wild-type lac operon loop. Their preferred model (the “odd” solution) has the DNA loop largely in a plane perpendicular to the direction of the operator DNA helix axes, but their “even” solution has a crossover similar to Fig. 5 B. The differences arise because the sequences and loop lengths are different; specifically, the A-tracts in our molecules alter the bending energetics substantially. Also, Balaeff et al. use strongly asymmetric bending potentials, whereas ours are isotropic. In any case, their model treats the Lac repressor geometry as fixed, and because the fluorophores in our molecules are close to the edge of the bound operator (and hence anchored by the protein geometry), any such model would not predict the dramatic differences in FRET demonstrated here.

Zhurkin, Adhya, and co-workers (Geanacopoulos et al., 2001) have modeled the DNA loop that regulates the gal operon, which is formed by the Gal repressor (GalR) and the HU protein. GalR is related to LacI but it lacks the C-terminal tetramerization domain, and instead tetramerizes via surface interactions on the body of the dimer. Geanacopoulos et al. therefore use a rigid model for GalR, and again their results would not have predicted our FRET results. They do point out that the four loop orientations are possible, and demonstrate that an antiparallel loop is more stable than the parallel structures: our results are consistent with their work in that only the designed bending in 9C14 allows the positively supercoiled parallel loop to form.

Record and co-workers have performed extensive studies of the salt dependence of LacI-operator and sandwich complex formation at a variety of DNA lengths, for single-operator molecules (Levandoski et al., 1996; Tsodikov et al., 1999). They suggest that Coulombic interactions between the negatively charged phosphates on the flanking DNA and the positively charged protein core may lead to local and global wrapping of the DNA around the protein, especially at low salt. They suggest that this may be a feature of many protein-DNA complexes (Saecker and Record, 2002). At the salt concentrations used here (100 mM KCl and 5 mM MgCl₂), their LacI work suggests that only local wrapping is likely to be significant (Tsodikov et al., 1999). In our looped molecules, binding of the two specific operators to the helix-turn-helix recognition elements is likely to dominate over nonspecific wrapping, and within the looped segment the DNA bending energetics probably do not permit wrapping. A static wrapping model could not explain the FRET changes observed here; Saecker and Record (2002) have also pointed out that changes in the tetramer conformation would change the nature of the DNA looping or wrapping, and that for dual operator constructs there is likely to be a mixture of through-space looping and DNA wrapping. Our data do not address whether the DNA outside the looped segment wraps locally on the protein surface.

In summary, the work described here shows that protein-DNA loop geometry can be controlled to a significant degree by designing DNA sequences that prefer a chosen geometry, and that FRET provides a definitive assay for the closed form LacI-DNA loop. Loop design offers the potential of controlling large-scale structure via self assembly, with implications for the design of nanoscale biomaterials from DNA (Seeman, 1998). The designed loops are hyperstable, with half-lives measured in days (Mehta and Kahn, 1999), much more stable than the natural O1-O3 loop. The stability of the natural loop has presumably been optimized, but not maximized, by evolution: the repressor must be released rapidly upon induction.

The flexibility of the Lac repressor allows it to adapt to a variety of operator-operator separations (Mossing and Record, 1986). Similar versatility has been observed for the AraC transcriptional repressor/activator (Lee and Schleif, 1989), and transcriptional activators are able to adapt to a wide variety of geometries (Ross et al., 2001; Ross et al., 2000; Schulz et al., 2000; A. Lilja and J.D.K., unpublished). In the case of the Lac repressor, this flexibility might seem unnecessary: the in vivo O1-O3 loop (from +11 to −82) is always the same length, and the O1-O2 loop (+11 to +401) is long enough to adapt to a rigid protein. However, the repressor does have to adapt to variations in DNA bending and flexibility, for example from variations in the cations present, from simultaneous CAP binding (Fried and Daugherty, 2001; Vossen et al., 1996), or from HU or other semispecific bending proteins binding preferentially to bent DNA in the loop (which is essential to GalR repression: see Kar and Adhya, 2001). Thus, it is likely that the Lac repressor's ability to form loops with varying geometries allows it to maintain stable repression under a variety of conditions.