Abstract
The Photoactive Yellow Protein (PYP) from Halorhodospira halophila (formerly Ectothiorhodospira halophila) is increasingly used as a model system. As such, a thorough understanding of the photocycle of PYP is essential. In this study we have combined information from pOH- (or pH-) dependence and (kinetic) deuterium isotope effects to elaborate on existing photocycle models. For several characteristics of PYP we were able to make a distinction between pH- and pOH-dependence, a nontrivial distinction when comparing data from samples dissolved in H2O and D2O. It turns out that most characteristics of PYP are pOH-dependent. We confirmed the existence of a pB′ intermediate in the pR to pB transition of the photocycle. In addition, we were able to show that the pR to pB′ transition is reversible, which explains the previously observed biexponential character of the pR-to-pB photocycle step. Also, the absorption spectrum of pB′ is slightly red-shifted with respect to pB. The recovery of the pG state is accompanied by an inverse kinetic deuterium isotope effect. Our interpretation of this is that before the chromophore can be isomerized, it is deprotonated by a hydroxide ion from solution. From this we propose a new photocycle intermediate, pBdeprot, from which pG is recovered and which is in equilibrium with pB. This is supported in our data through the combination of the observed pOH and pH dependence, together with the kinetic deuterium isotope effect.
INTRODUCTION
The photoactive yellow protein (PYP) from Halorhodospira halophila (formerly Ectothiorhodospira halophila) is on its way to become a model system in multiple disciplines. PYP is a small (125 amino acids, 14 kDa) water-soluble protein that can be activated with blue light. It has already been labeled as the prototype for the PAS folding motif (Pellequer et al., 1998). Proteins containing one or more PAS domains are predominantly involved in signal transduction pathways and can be found in organisms from all kingdoms of life (Taylor and Zhulin, 1999). Recently, PYP has also been used to study protein folding (Lee et al., 2001a,b), where the possibility to influence (un)folding events with light provides unique control over these (un)folding events. Also as a model for photo-sensory proteins PYP is becoming more and more popular and rivals in this respect the rhodopsins. PYP owes this popularity not only to its favorable handling characteristics and (photo)chemical stability, but also to the availability of high resolution crystal structures, of not only its dark state (Borgstahl et al., 1995), but also of transient photocycle intermediates (Genick et al., 1997a, 1998; Perman et al., 1998; Ren et al., 2001). Also, the relatively simple chromophore, a 4-hydroxycinnamic acid (containing only a single isomerizable double bond) linked to Cys69 via a thiol ester bond, is a clear advantage of this protein.
A detailed understanding of the photocycle of PYP is essential if this protein is to be used as a model system. This photocycle can be divided into three basic steps. In the first the chromophore is isomerized. This step is initiated by absorption of a photon in the ground state, pG (also known as P, PYP), and is completed within a few nanoseconds upon formation of the pR intermediate (also known as I1, PYPL). At least two excited states and the photocycle intermediates I0 and I0‡ are intermediates in this part of the photocycle (Devanathan et al., 1999; Gensch et al., 2002; Ujj et al., 1998). The chromophore, which is deprotonated and has the trans configuration in pG, changes its isomerization state to cis by flipping its carbonyl group (Xie et al., 1996), thus isomerizing the chromophore with a minimum of chromophore movement. The chromophore is already in the cis configuration upon formation of I0 (Gensch et al., 2002). In this step the hydrogen bonding network with residues Tyr42, Glu46, and Thr50, which helps to stabilize the negative charge on the chromophore in pG, stays intact (Brudler et al., 2001). For the current study this first basic photocycle step is instantaneous. In the second basic photocycle step, the chromophore is protonated and structural changes take place in the protein. The extent of these structural changes is dependent on the mesoscopic context of the protein. In crystals (Genick et al., 1997a; Xie et al., 2001), at low temperatures (Kandori et al., 2000), and under low hydration conditions (Hoff et al., 1999), very little structural change takes place. In contrast, in solution (Xie et al., 2001) and in sufficiently hydrated films (Hoff et al., 1999) large structural changes take place. The second photocycle step is initiated at pR and is completed upon formation of the signaling state, pB (also known as I2, PYPM). It has been shown that protonation of the chromophore precedes the structural changes (Xie et al., 2001). The most likely proton donor in chromophore protonation is Glu46. The intermediate, signifying the protonation change of the chromophore, without the structural change in the protein, has been named pB′. This intermediate has thus far only been identified in Fourier Transform Infrared (FTIR) spectroscopic experiments (Xie et al., 2001) and is postulated to have an absorption spectrum very similar to pB in the UV/Vis region. Interestingly, the possibility of the existence of an additional intermediate in the transition from pR to pB was hinted at previously, on the basis of the biexponential behavior of this transition in the UV/Vis region (Meyer et al., 1987). However, this idea was later dismissed (Meyer et al., 1989). Several characteristics of the second basic photocycle step have been shown to be pH-dependent, like photocycle kinetics (Genick et al., 1997b) and structural change (Hendriks et al., 2002). In the third basic photocycle step, the protein returns to its ground state fold and the chromophore returns to its ground state configuration, i.e., deprotonated and trans. Very little detail is known about this step other than that it shows pH-dependent kinetics (Genick et al., 1997b) and that it can be accelerated three orders of magnitude by isomerizing the chromophore photoactively (Hendriks et al., 1999b).
In PYP, as in all proteins, there are many exchangeable protons that can be exchanged for deuterium atoms easily and rapidly. PYP contains 235 exchangeable hydrogen atoms, 42 of which are from (de)protonatable groups. As such, for any characteristic of PYP, in which exchangeable protons play a significant role, it might be possible to observe a deuterium isotope effect (DIE) upon deuteration of the exchangeable protons. In this study we will be mostly concerned with the kinetic deuterium isotope effect (KDIE) of the different photocycle transitions. Both normal and inverse KDIEs can be observed, i.e., in deuterium oxide the reactions can be slower and faster, respectively. For H/D exchange, often a factor of 1.41 (square root of 2) is observed in KDIE experiments, which is caused by the difference in mass of the hydrogen and the deuterium atom. Nevertheless, larger factors are also frequently measured, reflecting hydrogen-tunneling mechanisms (Kohen and Klinman, 1999). The KDIE will not only help to determine reaction mechanisms within the photocycle, but by analyzing it in combination with the pH dependence that most PYP photocycle reactions display, it is possible to determine whether these reactions are dependent on the hydronium ion or on the hydroxide ion concentration. This is of crucial importance when comparing data obtained in H2O and D2O at different pH or pD values.
In this study we have been able to confirm known reaction mechanisms in the photocycle of PYP, elaborate on certain photocycle transitions, and obtain more information about the details of the third basic photocycle step. Combining the pOH (or pH) dependence and the KDIE has been crucial in our approach. Furthermore, the results from this study will aid in choosing optimal conditions in future studies of specific photocycle events and/or intermediates.
MATERIALS AND METHODS
Materials
Recombinant wild type apoPYP was produced heterologously in Escherichia coli, as described previously (Kort et al., 1996). Wild type apoPYP was reconstituted with a derivative of p-coumaric acid as described previously (Hendriks et al., 2002). The genetically introduced hexa-histidine containing N-terminal tag was removed by proteolysis with enterokinase (from Boehringer Mannheim). The purity index (OD278/OD446) of the samples was <0.5.
Sample preparation
Samples for the time trace experiments were prepared by mixing the following four solutions: 1) water or deuterium oxide (1.8–2.0 ml); 2) a buffer mixture in water or deuterium oxide (176 μl), consisting of citric acid, 1,3-bis[tris(Hydroxymethyl)methylamino]propane, and 3-[Cyclohexylamino]-1-propanesulfonic acid (250 mM each); 3) wild type PYP in deuterium oxide buffer mixture (4.8 μl); and 4) a 1-M sodium hydroxide or sodium deuteroxide solution (0–160 μl). After mixing, the pH was measured with a Mettler Toledo InLab®423 pH-electrode. The pD was obtained by adding 0.4 to the electrode reading (Glasoe and Long, 1960). Samples ranging in pH from 5.1 to 10.6 and ranging in pD from 5.7 to 11.5 were obtained. The optical density at the absorption maximum of wild type PYP of the samples was ∼0.5.
Samples for the time-gated spectra experiments were prepared by making a batch solution of wild type PYP in 20 mM of the buffer mixture in water described above at pH 8.10 and 9.55.
Transient (ms/s) UV/Vis measurements
An HP 8453 UV/Vis diode array spectrophotometer (Hewlett-Packard Nederland BV, Amstelveen, NL) was used with its maximum time resolution of 100 ms. Spectra were collected from 210 to 600 nm. Samples were flashed with a 500 μs photoflash. Samples were measured at room temperature, just before the start of the accompanying laser-flash photolysis measurements.
Laser-flash photolysis spectroscopy
We used an Edinburgh Instruments Ltd. LP900 spectrometer (Livingston, West Lothian, UK), equipped with a photomultiplier and a charge-coupled device (CCD) camera, in combination with a Continuum Surelite OPO laser (for further details, see Hendriks et al., 1999b). The PYP sample was excited with 446-nm laser flashes of ∼5–6 mJ/pulse (pulse width 6 ns). During the measurements the sample was kept at 20°C in a Peltier controlled cuvette holder. Time traces were recorded at 500, 450, and 360 nm with the slow-board option of the photomultiplier (time resolution ∼2 μs). Optical interference filters were used before the sample to minimize measurement artifacts induced by probe light. The following time windows were measured for all three wavelengths, −10 to 190 μs (0.2-μs resolution), and −1 to 19 ms (20-μs resolution). In addition, for traces at 450 and 360 nm one of the following time windows was used, depending on recovery rate: −0.25 to 4.75 s (5-ms resolution), −0.5 to 9.5 s (10-ms resolution), or −1 to 19 s (20-ms resolution).
Time-gated spectra were recorded pseudo-randomly with the CCD camera to prevent long-term trends in the data. 80 time points were chosen, evenly spaced on a logarithmic time scale between 30 ns and 2 s. A gate of 5% of the delay time was chosen with 10 ns as minimum and 10 ms as maximum.
Data analysis
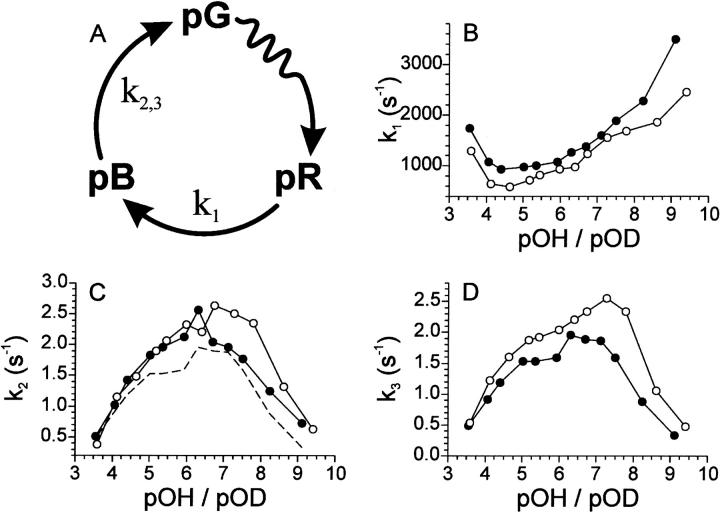
Data from the different time windows were merged, correcting for any intensity differences between the traces. Merged traces obtained at a single pH or pD were analyzed simultaneously. For the initial analysis with a simple sequential model, the program Origin 6.0 (Microcal Software, Inc.) was used. For analysis with more complex models the merged traces were analyzed with a global fitting program described elsewhere (Van Stokkum et al., 1994), making use of the Target Analysis method (van Stokkum and Lozier, 2002). For the Target Analysis to succeed, several spectral constraints needed to be introduced for the model depicted in Fig. 4 A. The intermediate pR has no contribution at 360 nm. The intermediates pB and pB′ only have a contribution at 360 nm and do not contribute to the 450- and 500-nm traces. The intermediate pBdeprot only contributes to the 450-nm trace. Due to a discrepancy between the recovery kinetics of the 360- and 450-nm trace, which is caused by a branching reaction induced by probe light in the 360-nm trace, a correction needed to be introduced in the model. Two corrections were tried, which are described in the Results section.
FIGURE 4.
KDIE obtained with the complex model. In (A) the photocycle model used to analyze the data presented in (B–H) is shown. Data obtained in H2O is represented with solid symbols; data obtained in D2O by open symbols. Triangles denote values that were forced in the analysis. Error bars are shown for data points where the error is larger than the size of the symbol. Data is plotted as function of pOH/pOD with the exception of the data in (F), which is plotted as function of pH/pD. In (B) the rate representing pB′ formation (k1) is shown. The dashed line represents the values for the reverse reaction in H2O. The KDIE of this reverse reaction (k−1) is illustrated in (C). In (D) the formation of pB from pB′ (k2) is represented. In (E) the rate representing pBdeprot formation (k3) is shown. The dashed line represents the values for the reverse reaction in H2O. The KDIE of this reverse reaction (k−3) is illustrated in (F). In (G and H) the formation of pG from pBdeprot is plotted for data recorded at 450 nm (k4) and 360 nm (k5), respectively.
For the analysis of the CCD data, the complex model used for the analysis of the time traces was found to be too complex with regard to ground state recovery. As such the part of the complex model describing pB formation was used in conjunction with a simple one-step recovery from pB to pG (see Fig. 5 A). Two constraints were used in the Target Analysis, i.e., both pB′ and pB have zero absorbance above 425 nm. These constraints were found valid by also testing the constraints that pB′ and pB do not absorb at wavelengths longer than 460 nm, which indeed resulted in approximately zero absorption between 425 and 460 nm for both pB′ and pB. In addition, as a reference, a calculated absorption spectrum of the ground state was used (see Results section).
FIGURE 5.
Spectral analysis of the photocycle of PYP at pH 8.1. In (A) the photocycle model used to analyze the CCD data is shown. (B) shows the measured ground state spectrum as dots (one out of every six data points is shown). The calculated ground state spectrum is shown as a solid line, with the contribution of the 425 nm and 452.4 nm skewed Gaussian to this fit shown as dashed lines. In (C) the absorption spectrum of pR1 (dashed line) and pR2 (solid line) obtained in the analysis are shown. (D) represents the absorption spectrum of pB′ (dashed line) and pB (solid line) obtained in the analysis.
RESULTS
Inasmuch as the photocycle kinetics of PYP are pH-dependent (Genick et al., 1997b), a kinetic analysis was carried out in a large pH range (5.1–10.6) and pD range (5.7–11.5), to distinguish between pH and deuterium isotope effects on the photocycle kinetics. At 20°C the dissociation constant of water pKw (with Kw in mol × l−1) is 14.1669 for H2O and 15.049 for D2O (Weast, 1988). Due to this difference in pKw, a clear distinction can be made in plotting data as a function of pH/pD or pOH/pOD, when comparing data obtained in H2O and D2O. In fact, data obtained in D2O appears to shift 0.88 units with respect to the same data obtained in H2O when plotted as function of pOH/pOD instead of pH/pD. For a property with a clear pH dependence it is then possible to determine if this dependence is indeed a pH (hydronium ion) or in fact a pOH (hydroxide ion) dependence. Both types of dependence can be observed in PYP and data is plotted accordingly in this study. The choice between pH and pOH dependence is mainly based on an alignment of the shape of the curves, whereas in some cases the underlying chemistry of the actual photocycle model was used to choose between different dependencies.
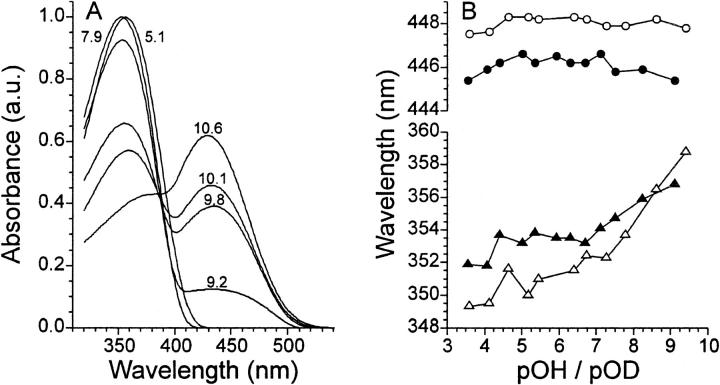
Besides kinetic effects, there may also be some spectral effects due to the substitution of hydrogen atoms for deuterium atoms. Therefore transient spectra were recorded with a time resolution of 100 ms for each sample and the difference spectra, representing the recovery component, were determined. After subtracting the contribution of the pG spectrum (using a calculated pG spectrum) from these difference spectra, the absorption bands of species other than pG were obtained (see Fig. 1 A). At high pH the chromophore in pB becomes deprotonated, forming a species which is red-shifted with respect to pB and appears with an apparent pKa of 10 and a cooperativity constant, n, in the Henderson-Hasselbalch equation of 0.74. This is in line with earlier observations (Hendriks et al., 1999a). From these spectra the absorption maxima of the pB state were determined. In the case where pB is present with both a protonated and deprotonated chromophore, the peak maximum of pB with a protonated chromophore was determined via deconvolution of the spectrum. In Fig. 1 B the peak maxima of pG and pB are compared for the protein in H2O and in D2O. As these absorption maxima appear to be dependent on the hydroxide/deuteroxide ion concentration of the solution, they are plotted as function of pOH/pOD. For pG a red shift of 2 nm is observed for the deuterated samples. For pB the deuterated samples show a blue shift of ∼2 nm over a large range, which changes to a red shift above pOH ∼8.5. In addition, pB shows a clear pOH dependence of the peak maximum, which shifts over a range of 5 nm in H2O. Contrary to pB, pG shows a negligible pOH dependence of the peak maximum. As a control we also carried out a titration of the chromophore in a protein sample denatured with 8 M guanidine hydrochloride. In this titration the chromophore has a pKa of 8.7 and an n of 1 (data not shown).
FIGURE 1.
Spectral deuterium isotope effect. In (A), the fitted spectra of the species involved in ground state recovery are shown for pH 5.1, 7.9, 9.2, 9.8, 10.1, and 10.6. The transition between the two peaks has a pKa of 10. In (B) the absorption maximum of pG (circles) and pB with a protonated chromophore (triangles) is plotted as a function of pOH/pOD for the samples in H2O (solid symbols) and D2O (open symbols).
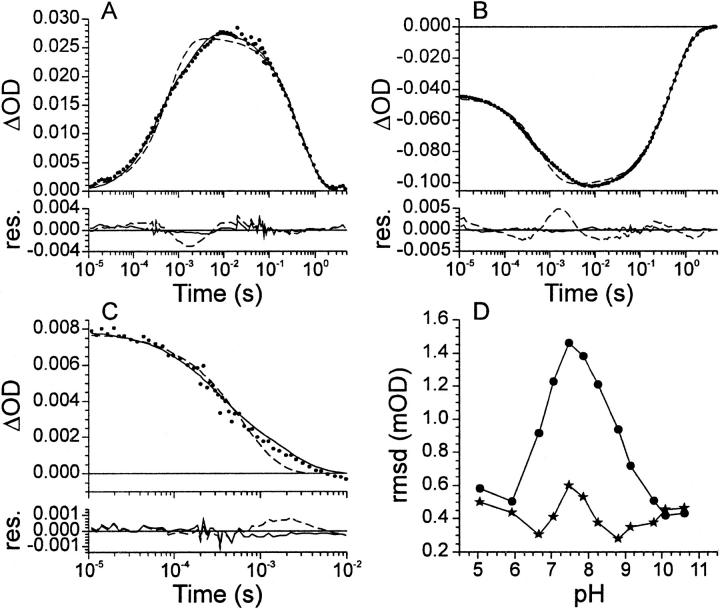
To determine the photocycle kinetics with μs time resolution, traces were recorded at 360, 450, and 500 nm (see Fig. 3, A–C for representative traces at pH 7.06). To start with, the data was analyzed using a simple 2-exponent sequential model (see Fig. 2 A). This model was also used in an earlier study on the pH dependence of the photocycle of PYP (Genick et al., 1997b). In Fig. 2 the pOH dependence obtained with this simple model is shown. As a result of the measurement conditions, the recovery rate measured at 450 nm is slower than that measured at 360 nm (see Fig. 2 C). This is caused by the 360-nm probe light, which initiates the photocycle branching reaction, leading to an accelerated pG recovery (Hendriks et al., 1999b; Miller et al., 1993). At low pOH the rates at 360 and 450 nm are almost identical. This is probably caused by the simultaneous presence of pB with either a protonated or a deprotonated chromophore at these pOH values (see Fig. 1 A and below). Because of this, both 360- and 450-nm light is able to initiate the branching reaction via pB with a protonated or a deprotonated chromophore, respectively. The rate of formation of pB (see Fig. 2 B) shows a normal KDIE (i.e., rate in deuterium oxide is slower) over the entire measured pH range. For ground state recovery (see Fig. 2, C and D) an inverse KDIE (i.e., rate in deuterium oxide is faster) can be observed. However, at low pOH this effect diminishes. Interestingly, when measured at 360 nm (see Fig. 2 C) the KDIE disappears below pOH ∼6, whereas when it is measured at 450 nm it disappears below pOH 4. Presumably this difference is caused by the photocycle branching reaction. The shape of the pOH dependence, both of pB formation and of pG recovery, is similar to the previously determined pH dependency for these reactions (Genick et al., 1997b). The simple model (see Fig. 2 A) only provides an acceptable fit at the pH extremes, and is not able to properly describe the data over the entire measured pH range. This is illustrated in Fig. 3 D where the root mean square deviation (RMSD) of the fits with the simple model (circles) are plotted as function of pH. The increased RMSD values between pH 6 and 9.5, together with residuals from the fit of the traces (see Fig. 3, A–C for representative fits at pH 7.06) clearly show the inadequacy of this simple model.
FIGURE 3.
Comparison between the simple and the complex model. Data recorded at 360 (A), 450 (B), and 500 nm (C) is shown for pH 7.06. The data is represented by dots. The solid line gives the fit with the complex model and the dashed line with the simple model. Accompanying residuals are shown in the lower part of the panels. Note the different scales. In (D) the RMSD obtained for the fits of the data in water with the simple (circles) and complex (stars) model are shown as function of pH.
FIGURE 2.
KDIE obtained with the simple photocycle model. In (A) the photocycle model, used to analyze the data presented in (B–D), is shown. Data obtained in H2O is represented with solid symbols; data obtained in D2O with open symbols. All data is plotted as function of pOH/pOD. In (B) the rate representing pB formation (k1) is shown. In (C) the ground state recovery, measured at 360 nm (k2), is shown. The dashed line represents recovery at 450 nm in H2O. In D the ground state recovery, measured at 450 nm (k3), is shown.
A more complex model was subsequently constructed on the basis of what is known from literature and what was inferred from the KDIE observed with the simple model. On the basis of FTIR measurements it was shown that an additional intermediate pB′ is formed from pR, which precedes pB (Xie et al., 2001). This pB′ has very similar, or possibly the same, spectral characteristics as pB. The pB′ intermediate differs from pR only in one important respect, i.e., where in pR a buried negative charge resides on the chromophore where it can be effectively neutralized via delocalization of the charge, a hydrogen bonding network and the vicinity of a positive charge from Arg52, in pB′ this buried negative charge resides on Glu46 where it no longer can be effectively neutralized. This is a stressful situation for the protein that potentially can be resolved in two different ways. One, Glu46 could be protonated by the chromophore, i.e., a return to the pR state. Two, formation of pB. Indeed, only when the formation of pB′ from pR is considered to be reversible, does the incorporation of this intermediate significantly improve the fit. This is illustrated by a fit on the data at pH 7.06 (see Fig. 3). Here the root mean square deviation (RMSD) obtained with the simple model represented in Fig. 2 A is 1.32 mOD. The addition of the pB′ intermediate in a unidirectional reaction scheme results in an RMSD of 1.29 mOD, which is only a very small decrease. However, by making the pR to pB′ reaction reversible, an RMSD of 0.62 mOD is obtained, which is a significant reduction. With respect to pB formation, the addition of the pB′ intermediate in equilibrium with pR was sufficient to obtain an acceptable fit of the part of the data representing pB formation.
On the basis of the inverse KDIE of the recovery rate obtained with the simple model, we conclude that deprotonation of the chromophore by a hydroxide ion from solution is likely involved before isomerization of the chromophore takes place (see Discussion). Therefore we included a new photocycle intermediate, which we have named pBdeprot, that is formed from pB. As this intermediate is formed through a (de)protonation reaction, it is most likely that this reaction is reversible. As a result of the addition of this equilibrium between pB and pBdeprot, the RMSD of the fit at pH 7.06 was further lowered from 0.62 to 0.50 mOD. Note that the incorporation of the pBdeprot intermediate in the recovery step is purely based on the observed KDIE, not on the UV/Vis traces themselves. The resulting model as depicted in Fig. 4 A was then used to fit the data. As indicated by the analysis with the simple model, it is necessary to correct for the fact that the recovery kinetics differ between the 360- and 450-nm traces. Two types of correction were tried. For the first a branching reaction from pB directly to pG, only present in the 360-nm data, was incorporated. In the second the pBdeprot to pG reaction is considered separately in the 360- and 450-nm traces. The results obtained with both types of correction were very similar, with the exception of the pB to pBdeprot equilibrium. The rate constants obtained for this equilibrium showed relatively large errors with the first branching correction, whereas the second branching correction did not display this problem. Therefore, the more complex model was used with the incorporation of the second branching correction. With the described more complex model an acceptable fit over the entire measured pH range was obtained (see Fig. 3 D).
For the pR to pB′ reaction (see Fig. 4 B) a normal KDIE can be observed over the entire pOH range. The reverse reaction (see Fig. 4 C) shows a normal KDIE between pOH 5.7 and 6.5, no KDIE at higher pOH values, and an inverse KDIE at lower pOH values. Formation of pB from pB′ (see Fig. 4 D) shows no clear KDIE at low pOH values, a normal KDIE at intermediate pOH values going to a normal or inverse KDIE for higher pOH values. It is good to note here that at the pH extremes the simple photocycle model was able to describe the data equally well (see Fig. 3 D) and showed a normal KDIE at both pH extremes for the formation of pB (see Fig. 2 B).
For the formation of pBdeprot from pB (see Fig. 4 E), no KDIE is observed at lower pOH values and an inverse KDIE at pOH values above ∼5. The reverse reaction (see Fig. 4 F) shows a pH dependence with no KDIE at lower pH values and an inverse KDIE at pH values above ∼8. For the last step in the photocycle, i.e., formation of pG from pBdeprot, rates were obtained specific for the 450-nm data set (see Fig. 4 G) and the 360-nm data set (see Fig. 4 H). In the 450-nm data set a pOH dependence is observed with no KDIE below pOH ∼6.5, and an inverse KDIE for pOH values above ∼6.5. In the 360-nm data set no clear KDIE could be observed due to the relatively large error in the rate constants. Interestingly, we have been able to dissect the observed KDIE of the simple photocycle model into reactions with different dependencies (pOH and pH), and with different KDIEs using the more complex model depicted in Fig. 4 A. This supports the application of this more complex model.
In addition to the kinetic traces at specific wavelengths with microsecond time resolution, spectral data with nanosecond time resolution were collected at pH 8.10 and 9.55. For the analysis of these data it is necessary to use the absorption spectrum of the ground state as a reference. However, we have noticed that the measured ground state spectrum is less suitable. This is indicated by the following: when the measured ground state spectrum is subtracted from spectra obtained with 100-ms time resolution or through accumulation of the pB intermediate with continuous wave irradiation, we find a pR-like residue. In these spectra the presence of a significant amount of pR is not expected. Also, when the measured ground state spectrum is used as a reference in the analysis of time-gated spectra on a nanosecond to second timescale, the spectrum of pR contains a long, offset-like tail, on the blue side of the absorption peak (Hoff et al., 1994). Lastly, when the complex model depicted in Fig. 4 A is used, the pR intermediate has a clear fast decay component similar to that found in the absorption traces, but also a slow decay component similar to the decay rate of pB, which is not observed in the absorption traces. In an attempt to simulate a ground state spectrum we found that the ground state spectrum can be simulated very well by two skewed Gaussians (Fraser and Suzuki, 1969; Sevilla et al., 1989) above 385 nm. The maxima of these two skewed Gaussians were selected to be at 425 and 452.4 nm, values that have been observed in a low temperature study (Masciangioli et al., 2000). We determined an appropriate calculated ground state spectrum via a global analysis of five time-gated difference spectra that did not contain a pR signal, using the Origin 6.0 program. The resulting calculated ground state spectrum is very similar to the measured ground state spectrum, but has a little less absorption on the red side of absorption spectrum and has no residual absorption on the blue side of the absorption spectrum (see Fig. 5 B). This calculated ground state spectrum was then used as reference in the Target Analysis. The calculated ground state spectrum improved the analysis significantly, which is demonstrated by the absence of the offset-like blue absorption in the absorption spectra of pR that were determined with the Target Analysis (see Fig. 5 C).
As the time resolution of the CCD dataset was higher than the one of the time traces, we were able to see a relaxation of the pR intermediate. This relaxation has also been observed recently in transient grating experiments (Takeshita et al., 2002a,b). Therefore an additional step in the photocycle was introduced that reflects this, i.e., a unidirectional reaction from pR1 to pR2 (Fig. 5 A). With the time traces we saw that the RMSD of the analysis improved tremendously upon introduction of the reversible character of the pR to pB′ transition. In the CCD data the improvement in RMSD is not as dramatic, with a change from an RMSD of 4.59 mOD for the simple model (see Fig. 2 A) to an RMSD of 3.86 mOD for the more complex model depicted in Fig. 5 A (compare the RMSD change of 1.32 mOD to 0.62 for the time traces at pH 7.06). Though we also tried the complex model depicted in Fig. 4 A, the quality of the data was not sufficient to use this model confidently. As such we present the results obtained with the somewhat less complex model as depicted in Fig. 5 A. As Fig. 5 C indicates the absorption spectra of both pR species are very similar, with pR1 having a slightly higher extinction coefficient than pR2. Note that the offset-like blue absorption of the pR spectra observed before (Hoff et al., 1997) has disappeared as a result of using the calculated ground state spectrum as a reference. Also, the pB′ intermediate seems to be slightly red-shifted with respect to the pB intermediate (see Fig. 5 D). The spectra of the intermediates obtained at pH 9.55 (not shown) are very similar to those found at pH 8.10. The rate constants obtained in the analysis of the CCD data at pH 8.10 and pH 9.55 (see Table 1) agree with those found with the UV/Vis traces.
TABLE 1.
Rate constants obtained from the CCD data sets, using the model depicted in Fig. 5 A
| pH | k1 (s−1) | k2 (s−1) | k−2 (s−1) | k3 (s−1) | k4 (s−1) |
|---|---|---|---|---|---|
| 8.10 | 59(7) × 104 | 2400(130) | 2700(400) | 1840(160) | 4.65(4) |
| 9.55 | 20(4) × 105 | 2350(80) | 710(100) | 440(70) | 4.49(6) |
The estimated standard error in the last digit is indicated in parentheses.
The effect of acid denaturation of PYP was also studied. The pKa for pBdark formation in H2O and D2O were determined as 2.7 and 3.2, respectively. In both solvents the cooperativity constant n in the Henderson-Hasselbalch equation is 1.5, which is within the previously reported range for this value (Hoff et al., 1997). This indicates that PYP is less stable in D2O. Ionic hydrogen bonds could therefore play an important role in the stability of PYP, as these bonds are less strong in D2O.
DISCUSSION
As a result of changing the solvent from H2O to D2O, exchangeable hydrogen atoms in PYP are exchanged for deuterium atoms. Consequently, any property of the protein in which an exchangeable hydrogen atom is involved may be influenced. Additionally, there are several (de)protonatable groups that may induce a pH or pOH dependence in any property of PYP. It is possible to distinguish between a pH and pOH dependence via the DIE. We have mainly investigated effects on photocycle kinetics, but also, e.g., information concerning the absorption maximum of the ground and signaling state was obtained.
Spectral tuning of the 4-hydroxycinnamic acid chromophore in the ground state of PYP can be divided into three contributions (Yoda et al., 2001), i.e., counterion effect (5300 cm−1), medium effect of the protein matrix (700 cm−1), and hydrogen-bonding effect (−1600 cm−1). This latter contribution is likely the cause of the observed 2-nm red shift of the ground state spectrum in D2O (see Fig. 1 B). In the ground state the phenolic group of the chromophore is involved in two ionic hydrogen bonds (Borgstahl et al., 1995). Such hydrogen bonds become weaker when deuterium is the bridging atom (Scheiner, 2000). As such, in D2O the contribution of the hydrogen-bonding effect to the spectral tuning is less, i.e., a smaller blue shift, which effectively results in a red shift of the main band in the visible absorption spectrum. For the signaling state, pB, a spectral deuterium isotope effect was also observed. Interestingly, the isotope effect changes from a blue to a red shift as a function of pOH. When the absorption maxima are plotted as a function of pH the change from a blue to a red shift occurs at ∼pH 7.5. No property with an apparent pKa of 7.5 has been observed for PYP as of yet. When plotted as a function of pOH (see Fig. 1 B) the change from a blue to a red shift occurs at ∼pOH 8.5, which is equal to a pH of 5.5. In earlier studies a pKa of 5.5 has been correlated with a change in folding state of pB (Hendriks et al., 2002; 1999a). A pOH dependence of the absorption maximum of pB is therefore likely. Especially inasmuch as a change in folding state of pB could also explain the change from a blue to a red shift. As in pB the chromophore is protonated, it is likely that any effect on tuning in pB involving exchangeable hydrogen atoms is mainly caused by hydrogen bond(s) formed by the hydroxy group of the chromophore. Here a distinction can be made between neutral and ionic hydrogen bonds. Whereas ionic hydrogen bonds become weaker when deuterium becomes the bridging atom, in neutral hydrogen bonds, the bond becomes stronger when deuterium is the bridging atom (Scheiner, 2000). Consequently, a blue shift would indicate involvement of (a) neutral hydrogen bond(s) and a red-shift involvement of ionic hydrogen bonds. It is unclear whether the change from neutral to ionic hydrogen bonding is due to a change in hydrogen-bonding partner or a change of the protonation state of that partner. Interestingly, the possible ionic hydrogen bond is formed in the pB state that is supposedly more folded (Hendriks et al., 2002). Furthermore, it has now been shown for the first time that the absorption spectrum of pB is pOH-dependent. The interpretation that in pB the phenolic hydroxy group is involved in (a) hydrogen bond(s) with the protein is supported by the fact that the pKa of this hydroxy group in pB is ∼10 (Hendriks et al., 1999a), as is shown in Fig. 1 A. Without such an interaction one would expect the pKa to be 8.7 as indicated by pH titration of the denatured protein, assuming that the pKa of the chromophore in the cis configuration is very similar to that of the chromophore in the trans configuration.
To determine the KDIE for the photocycle of PYP, the progress of the photocycle was monitored at three representative wavelengths. The resulting traces were first analyzed with a simple photocycle model (see Fig. 2 A). Although the shape of the pOH dependence (see Fig. 2, B–D) compares well with the previously published pH dependence for pB formation and pG recovery (Genick et al., 1997b), our rate constants are about a factor-of-3 lower for both transitions. The reason for this discrepancy is unclear, but may lie in the fact that different buffers were used in the two studies. Also different illumination conditions may have had an influence. E.g., a difference in intensity of light that can induce the photocycle branching reaction, can lead to significant differences in the rate of pG recovery (Miller et al., 1993). Note that, in previous studies, not focusing on pH dependency, recovery rates were reported that are similar to those found in this study (Hoff et al., 1994; Meyer et al., 1989; Hendriks et al., 2002). As the simple photocycle model is not able to accurately fit the data over the entire measured pH range (only at the extremes of pH it is), a more complex model (see Fig. 4 A) was designed. With respect to pB formation, the different photocycle reactions in this complex model reflect the following reactions. The formation of pB′ from pR is characterized by the protonation of the chromophore by Glu46. This results in a shift of the buried negative charge from the chromophore to Glu46, where it can no longer be effectively stabilized. This introduces a stress situation for the protein that can be resolved by either returning to pR or by forming pB. During the formation of pB from pB′ the protein undergoes a structural change. We have shown that formation of pB, as described by the complex model, is able to accurately describe pB formation over a large pH range. As such, it also explains the previously observed biexponential behavior of the pR to pB transition (Hoff et al., 1994; Meyer et al., 1987). The large improvement in RMSD shown in Fig. 3 D for the fit with the complex model (see Fig. 4 A), compared to the simple model (see Fig. 2 A), is mainly caused by the improvement of the model regarding pB formation.
For the recovery step a reasonable fit was obtained with the simple model. However, an inverse KDIE was observed for pG recovery (see Fig. 2 D). An inverse KDIE could indicate that the breaking of an ionic hydrogen bond is part of a rate determining step, as ionic hydrogen bonds are weaker when deuterium is the bridging atom (Scheiner, 2000). In light of the spectral deuterium isotope effect described above, this is unlikely. The spectral deuterium isotope effect suggests that the chromophore is most likely involved in a neutral hydrogen bond for most of the measured pH range. Alternatively, the inverse KDIE could suggest that deprotonation of the chromophore by a hydroxide ion from solution is a rate-determining step. As the deuteroxide ion is a stronger base than the hydroxide ion (Scheiner, 2000), it is a more potent proton extractor. This also explains the apparent pOH dependence of this reaction. Furthermore, it has already been shown that when the chromophore is deprotonated it isomerizes more easily (Sergi et al., 2001). This makes it likely that the chromophore needs to be deprotonated before re-isomerization of the chromophore can take place. A mechanism also proposed on the basis of an in-depth analysis (Demchuk et al., 2000) of the previously reported pH dependency of PYP photocycle kinetics (Genick et al., 1997b). Therefore, an additional intermediate, representing the pB intermediate in a deprotonated form, pBdeprot, was introduced in the model. As formation of pBdeprot is a (de)protonation event it is likely that this reaction is reversible. The model incorporating these characteristics is presented in Fig. 4 A. This complex model provided an accurate fit of the data over the entire measured pH range. However, at the pH extremes the model was too complex for the data, resulting in an increased inaccuracy of the obtained rate constants.
pR to pB′
Formation of pB′ from pR (Fig. 4 B) shows a pOH dependence. A normal KDIE is observed over the whole measured pH range. The pR to pB′ reaction describes a proton transfer reaction, for which a normal KDIE is expected (Scheiner, 2000). It has been suggested in the past that upon pB formation the chromophore is protonated by the solvent (Genick et al., 1997a). A normal KDIE would then only be observed if protonation of the chromophore is achieved via water, as D2O is a weaker acid than H2O. Protonation via the hydronium ion would lead to an inverse KDIE as the deuterated form of the hydronium ion is a stronger acid, like the deuteriumoxide ion is a stronger base than the hydroxide ion (Scheiner, 2000). Although protonation of the chromophore by water is also compatible with the obtained data, we favor the interpretation that the chromophore is protonated via Glu46, as suggested on the basis of FTIR results (Xie et al., 1996; 2001).
pB′ to pR
Formation of pR from pB′ shows a different pOH dependence as pB′ formation from pR (compare Fig. 4, B and C). From this pOH dependence it is clear that at the pH extremes the equilibrium between pR and pB′ shifts toward pB′. This explains why the simple model is able to accurately describe pB formation at the pH extremes. Though the transition from pB′ to pB is spectrally silent at 360 nm (see Fig. 5 D), the reversible character of the pR to pB′ reaction makes the transition visible through the biexponential character of the formation of the spectral species representing both pB′ and pB. With a shift of the equilibrium toward pB′ it is no longer possible to make a clear distinction between pB′ and pB on a kinetic basis.
One would expect the pB′ to pR reaction to be a proton transfer reaction like the pR to pB′ reaction. As such a normal KDIE is expected for the whole measured pH range. However, a normal KDIE is only observed for a small pOH range (pOH 5.7–6.5). At low pOH values an inverse KDIE and at higher pOH values no KDIE is observed. It is therefore likely that the pB′ to pR reaction may have more than one reaction mechanism. Between pOH 5.7–6.5 a proton transfer mechanism, i.e., one in which Glu46 is protonated by the chromophore, may dominate. At low pOH values, a mechanism in which a hydroxide ion extracts a proton from the chromophore and then protonates Glu46 could explain the observed KDIE at low pOH values. In such a mechanism it is likely that the protein is already starting to change its fold, allowing a hydroxide ion to enter the chromophore pocket. Then after the proton is transferred via the hydroxide ion, the protein may return to the pR fold. Here the proton extraction by the hydroxide ion is the rate-determining step. If the rate-determining step would be protonation of Glu46 by the newly formed water molecule, a normal KDIE would be expected. Likewise, at higher pOH values, indirect proton transfer via a hydronium ion could explain the absence of a KDIE. Only here, protonation of Glu46 by the hydronium ion and deprotonation of the chromophore via the newly formed water molecule are both rate-determining steps, effectively canceling each other's inverse and normal KDIEs. Again, for this mechanism to work it is likely that the protein has already started to change its fold, before returning to pR. Alternatively, a water molecule could first deprotonate the chromophore after which the newly formed hydronium ion would protonate Glu46. In a recent molecular dynamics study (Groenhof et al., 2002) it was calculated that after Glu46 donates its proton to the chromophore, the hydrogen bonding network is very quickly lost and structural changes start to occur, which is in line with the above hypotheses.
pB′ to pB
Formation of pB from pB′ shows no clear KDIE at low pOH, a normal one at intermediate pOH, which turns into no KDIE at higher pOH values (see Fig. 4 D). Basically the protein changes its fold in this step, exposing the chromophore to solvent. The normal KDIE can be explained by the need to break neutral backbone hydrogen bonds. As neutral hydrogen bonds are stronger when deuterium is the bridging atom, it is more difficult to drastically change the protein fold in D2O. At low pOH values, either it is not necessary to break the backbone hydrogen bonds, or breaking them is no longer rate-determining, e.g., due to the presence of a buried charge (Xie et al., 2001) which would then drive the structural change. As at very high pOH values the data are not reliable enough, it is not possible to draw conclusions about the KDIE at those pOH values. However, it is clear that the normal KDIE diminishes in going to higher pOH values. This could be explained by a decrease in the extent of structural change accompanying pB formation, as is also suggested to occur at low pH values (Hendriks et al., 2002; 1999a), and thus at high pOH values. Less structural change implies that fewer backbone hydrogen bonds need to be broken, which would lead to a smaller KDIE. The diminished need for structural change can be explained by protonation of Glu46 by either water or a hydronium ion, effectively removing the buried charge on Glu46, which has been suggested to be the driving force for structural change in the pB′ to pB reaction (Xie et al., 2001). Coincidentally, protonation of Glu46 by a hydronium ion is also the first step in one of the suggested mechanisms for pR formation from pB′ at high pOH.
pB to pBdeprot
As suggested by the analysis with the simple model, the pB to pBdeprot reaction represents deprotonation of the chromophore by a hydroxy ion. This reaction therefore must show a pOH dependence. Interestingly, the inverse KDIE expected for deprotonation of the chromophore via a hydroxide ion is only observed above pOH ∼5 (see Fig. 4 E). The absence of a KDIE at lower pOH values could be explained by the fact that at low pOH the concentration of hydroxide ions is high and as such the small difference in basicity between hydroxide and deuteroxide ions no longer makes a significant difference for the rate of deprotonation.
In the reverse reaction the chromophore is most likely protonated by a hydronium ion and therefore this reaction is presumably pH-dependent. This results in a similar picture as observed for the pB to pBdeprot reaction (see Fig. 4 F). As KDIE is only observed for higher pH values, at low pH (below pH ∼8) the concentration of hydronium ions is sufficient to mask the difference in acidity between the deuterated and protonated form of the hydronium ion.
The mechanisms described for the reversible reaction of the pB to pBdeprot transition imply that the obtained rate constants contain a contribution from the hydroxide or hydronium ion concentration, i.e., k3 = k3c [OH−] and k−3 = k−3c [H3O+]. However, after correction of the rate constants, the new rate constants predict that the equilibrium between pB and pBdeprot is reached within 100 ns and has a pKa of ∼7.3. This is in contradiction with the pKa of 10 that is found experimentally for the equilibrium between pB and pBdeprot (see above and Fig. 1 A). Therefore, the pBdeprot in the complex model not only represents deprotonation of the chromophore, but also implies a certain protein fold that allows isomerization to take place. Here, deprotonation of the chromophore by hydroxide ions is a rate-determining step only at higher pOH values. Otherwise, structural change is the rate-determining step. The structural change leads to no KDIE at lower pOH values either due to the small amount of structural change necessary or to cancellation of opposite isotope effects. Similarly, protonation of the chromophore in the return reaction is only a rate-determining step at higher pH values and structural change is rate-determining where no KDIE is observed.
The inverse KDIE for the pB to pBdeprot reaction disappears below pOH ∼5. A pKb of 4 (pKa 10) was determined for the equilibrium between pB and pBdeprot, with a cooperativity constant n in the Henderson-Hasselbalch equation of 0.74. As such, at pOH ∼5 the equilibrium contains ∼15% pBdeprot and 85% pB. Assuming that in pBdeprot the phenolate part of the chromophore no longer is involved in hydrogen bonds with the protein and is exposed to solvent, the pKa of the chromophore would be expected to be 8.7 with n is 1, as suggested by pH titration of the chromophore in the denatured protein (assuming that the pKa of the chromophore in the cis and trans configuration is very similar; see above). Then, at the point the KDIE disappears (∼pH 8) in the pBdeprot to pB reaction, an equilibrium between these two intermediates is expected to have 85% pBdeprot and 15% pB. These values are the inverse of the values found in the pB to pBdeprot reaction. Note that the true equilibrium between pB and pBdeprot has a pKa of 10, but that the pKa that is felt by the pBdeprot species in the reaction from pBdeprot to pB is 8.7 in the above assumption. The observation that the implied pBdeprot to pB ratios coincide inversely with the disappearance of the observed KDIE is evidence that the introduction of the pB to pBdeprot equilibrium reaction, in the recovery step of PYP, is justified.
The precise characteristics of the structural change in the pB to pBdeprot step are unclear. It is likely, though, that the protonation state of the Glu46 residue has an influence on this step. This is based on information about the recovery rate of the Glu46Gln mutant, which displays a faster recovery of the ground state than the wild type protein (Genick et al., 1997b). In the Glu46Gln protein, an amide group effectively replaces the carboxyl group of residue 46. As this is a neutral group, it is likely that Glu46 needs to be protonated in pBdeprot in order for the final recovery step to take place. This is in line with an earlier observation where it was proposed that for recovery to take place, the chromophore has to be in a deprotonated state and Glu46 needs to be protonated (Demchuk et al., 2000).
pBdeprot to pG
In the final reaction from pBdeprot to pG (see Fig. 4 G) it is likely that isomerization is the rate-determining step. As isomerization is not likely to involve any exchangeable protons, no KDIE is expected for this reaction. However, this only seems true below pOH ∼6.5. Above pOH ∼6.5 an inverse KDIE is observed. Interestingly, this is very similar to what was observed in the analysis with the simple model of the 360-nm data (see Fig. 2 C), in which isomerization occurs, at least in part, photoactively. It would therefore seem that the observed KDIE is characteristic of the refolding event in the recovery after isomerization has taken place. However, any structural changes after isomerization will likely occur at least 2 orders of magnitude faster than the rates observed for the pBdeprot to pG photocycle step. This conclusion is based on experiments in which acid-denatured PYP is renatured (Lee et al., 2001a) in a pH range overlapping with the pH range showing the inverse KDIE. An alternative explanation is that, due to the unfavorable pKa of 10 for deprotonation of the chromophore in pB, at high pOH (low pH) the presence of hydroxide ions may be important for the dark isomerization step to keep the chromophore deprotonated long enough for isomerization to take place.
When ground state recovery is compared between the simple and complex model, it is worth noting that an inverse KDIE was observed over almost the entire measured pH range with the simple model, where the kinetics showed a pOH dependence. With the complex model, the obtained rates showed an inverse KDIE for only part of the measured pH range for the pB to pBdeprot equilibrium and the pBdeprot to pG step. Also, not only reactions that showed a pOH dependence were observed but also a reaction that showed a pH dependence. Additionally, through plausible assumptions we were able to show that the point at which the KDIE disappears in both reactions of the pB to pBdeprot equilibrium occur inversely at the same implied pB to pBdeprot ratios. All this supports the relevance of the introduction of the pBdeprot intermediate.
Spectral kinetic analysis
With the insight we have obtained through the analysis of the time traces, we have applied the new photocycle model to spectral data of the photocycle recorded at pH 8.10 and 9.55. As these data had nanosecond time resolution, we were also able to observe a transition from one pR-like intermediate to another.
Such a transition was recently observed in transient grating experiments (Takeshita et al., 2002a,b), and reflects structural relaxation of the protein far from the chromophore. Although it is claimed that this transition is not observable via UV/Vis spectroscopy, an earlier UV/Vis study (Hoff et al., 1994) already noted that an additional pR-like component could be observed. However, it was ignored, because the quality of the data was deemed not good enough to confidently make the distinction between two separate pR components. Inclusion of the transition from pR1 to pR2 shows that the two pR intermediates have a very similar absorption spectrum, differing mainly in their extinction coefficient. The obtained rate constant for this transition compares well to that found with transient grating. The reversible character of the pR to pB′ reaction is clearly observed in the datasets recorded at pH 8.10 and pH 9.55. This enabled us to determine an absorption spectrum for both pB′ and pB. It is notable that these two spectra are very similar but not identical. The absorption spectrum of pB′ is slightly red-shifted with respect to pB. As the quality of the CCD data was not good enough, we were not able to obtain reliable information with regard to the pBdeprot intermediate, introduced on the basis of the KDIE of the photocycle recovery step. This lack of quality of the data is evident from the absence of an additional small shoulder at ∼430 nm in the pB spectrum at pH 9.55 (data not shown) as would be expected on the basis of the spectra shown in Fig. 1 A. It is likely that the absorption spectrum of the pBdeprot intermediate is very similar to that of pG. This is also suggested by the fact that not only deprotonation of the chromophore but also the folding state of PYP is an important feature of this proposed intermediate. As such the absorption spectrum is not necessarily the same as that of the shoulder observed in the pB spectrum at high pH (see Fig. 1 A), which is also caused by a pB species with a deprotonated chromophore. The different fold of pBdeprot may cause an additional red shift. In fact, an analysis incorporating pBdeprot resulted in a pG-like spectrum for pBdeprot (data not shown). However, as mentioned before, we feel the data is not of sufficient quality to confidently draw such a conclusion. It would, however, explain why this intermediate has not been observed before. Also, it is in line with the observation that refolding, as measured via Nile Red fluorescence (Hendriks et al., 2002), seems to be slightly slower than recovery monitored with UV/Vis spectroscopy at 468 nm.
Acid denaturation
When acid denaturation is compared in H2O and D2O it appears that PYP is less stable in D2O. As ionic hydrogen bonds are less strong in D2O, it is likely that such (a) bond(s) causes the decreased stability. The prime candidates for this are the hydrogen bonds between the chromophore, and Glu46 and Tyr42. These two hydrogen bonds then have a greater influence than the neutral hydrogen bonds which are much more abundant and are stronger when deuterium is the bridging atom.
CONCLUSIONS
By comparing pH effects using both H2O and D2O as solvent, we have been able to show that most characteristics in PYP are not pH-, but rather pOH-dependent; an essential distinction when comparing data obtained in H2O and D2O. Furthermore, we have shown that the pB′ intermediate (introduced on the bases of FTIR experiments and containing a protonated chromophore; see Xie et al., 2001), is in equilibrium with pR. Its absorption spectrum is slightly red-shifted with respect to pB. On the basis of the KDIE of the photocycle-recovery reaction we were able to show that deprotonation of the chromophore is an essential step before re-isomerization can take place. This necessitates the introduction of a new photocycle intermediate, pBdeprot, to represent this step. This intermediate is in equilibrium with pB. We have shown for the first time that the absorption maximum of pB (containing a protonated chromophore) is pH-dependent. Furthermore, the stability of PYP is mainly governed by ionic hydrogen bonds.
Acknowledgments
This research was supported by the Netherlands Foundation for Chemical Research, with financial assistance from the Netherlands Organization for Scientific Research.
References
- Borgstahl, G. E., D. R. Williams, and E. D. Getzoff. 1995. 1.4 Å structure of photoactive yellow protein, a cytosolic photoreceptor: unusual fold, active site, and chromophore. Biochemistry. 34:6278–6287. [DOI] [PubMed] [Google Scholar]
- Brudler, R., R. Rammelsberg, T. T. Woo, E. D. Getzoff, and K. Gerwert. 2001. Structure of the I1 early intermediate of photoactive yellow protein by FTIR spectroscopy. Nat. Struct. Biol. 8:265–270. [DOI] [PubMed] [Google Scholar]
- Demchuk, E., U. K. Genick, T. T. Woo, E. D. Getzoff, and D. Bashford. 2000. Protonation states and pH titration in the photocycle of photoactive yellow protein. Biochemistry. 39:1100–1113. [DOI] [PubMed] [Google Scholar]
- Devanathan, S., A. Pacheco, L. Ujj, M. Cusanovich, G. Tollin, S. Lin, and N. Woodbury. 1999. Femtosecond spectroscopic observations of initial intermediates in the photocycle of the photoactive yellow protein from Ectothiorhodospira halophila. Biophys. J. 77:1017–1023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraser, R. D. B., and E. Suzuki. 1969. Resolution of overlapping bands. Functions for simulating band shapes. Anal. Chem. 41:37–39. [Google Scholar]
- Genick, U. K., G. E. Borgstahl, K. Ng, Z. Ren, C. Pradervand, P. M. Burke, V. Srajer, T. Y. Teng, W. Schildkamp, D. E. McRee, K. Moffat, and E. D. Getzoff. 1997a. Structure of a protein photocycle intermediate by millisecond time-resolved crystallography. Science. 275:1471–1475. [DOI] [PubMed] [Google Scholar]
- Genick, U. K., S. Devanathan, T. E. Meyer, I. L. Canestrelli, E. Williams, M. A. Cusanovich, G. Tollin, and E. D. Getzoff. 1997b. Active site mutants implicate key residues for control of color and light cycle kinetics of photoactive yellow protein. Biochemistry. 36:8–14. [DOI] [PubMed] [Google Scholar]
- Genick, U. K., S. M. Soltis, P. Kuhn, I. L. Canestrelli, and E. D. Getzoff. 1998. Structure at 0.85 Å resolution of an early protein photocycle intermediate. Nature. 392:206–209. [DOI] [PubMed] [Google Scholar]
- Gensch, T., C. C. Gradinaru, I. H. M. van Stokkum, J. Hendriks, K. J. Hellingwerf, and R. van Grondelle. 2002. The primary photoreaction of photoactive yellow protein (PYP): anisotropy changes and excitation wavelength dependence. Chem. Phys. Lett. 356:347–354. [Google Scholar]
- Glasoe, P. K., and F. A. Long. 1960. Use of glass electrodes to measure acidities in deuterium oxide. J. Phys. Chem. 64:188–190. [Google Scholar]
- Groenhof, G., M. F. Lensink, H. J. Berendsen, and A. E. Mark. 2002. Signal transduction in the photoactive yellow protein. II. Proton transfer initiates conformational changes. Prot. Struct. Funct. Gen. 48:212–219. [DOI] [PubMed] [Google Scholar]
- Hendriks, J., T. Gensch, L. Hviid, M. A. van Der Horst, K. J. Hellingwerf, and J. J. van Thor. 2002. Transient exposure of hydrophobic surface in the photoactive yellow protein monitored with nile red. Biophys. J. 82:1632–1643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hendriks, J., W. D. Hoff, W. Crielaard, and K. J. Hellingwerf. 1999a. Protonation/deprotonation reactions triggered by photoactivation of photoactive yellow protein from Ectothiorhodospira halophila. J. Biol. Chem. 274:17655–17660. [DOI] [PubMed] [Google Scholar]
- Hendriks, J., I. H. van Stokkum, W. Crielaard, and K. J. Hellingwerf. 1999b. Kinetics of and intermediates in a photocycle branching reaction of the photoactive yellow protein from Ectothiorhodospira halophila. FEBS Lett. 458:252–256. [DOI] [PubMed] [Google Scholar]
- Hoff, W. D., I. H. van Stokkum, H. J. van Ramesdonk, M. E. van Brederode, A. M. Brouwer, J. C. Fitch, T. E. Meyer, R. van Grondelle, and K. J. Hellingwerf. 1994. Measurement and global analysis of the absorbance changes in the photocycle of the photoactive yellow protein from Ectothiorhodospira halophila. Biophys. J. 67:1691–1705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoff, W. D., I. H. M. Van Stokkum, J. Gural, and K. J. Hellingwerf. 1997. Comparison of acid denaturation and light activation in the eubacterial blue-light receptor photoactive yellow protein. Biochim. Biophys. Acta. B. 1322:151–162. [Google Scholar]
- Hoff, W. D., A. Xie, I. H. Van Stokkum, X. J. Tang, J. Gural, A. R. Kroon, and K. J. Hellingwerf. 1999. Global conformational changes upon receptor stimulation in photoactive yellow protein. Biochemistry. 38:1009–1017. [DOI] [PubMed] [Google Scholar]
- Kandori, H., T. Iwata, J. Hendriks, A. Maeda, and K. J. Hellingwerf. 2000. Water structural changes involved in the activation process of photoactive yellow protein. Biochemistry. 39:7902–7909. [DOI] [PubMed] [Google Scholar]
- Kohen, A., and J. P. Klinman. 1999. Hydrogen tunneling in biology. Chem. Biol. 6:R191–R198. [DOI] [PubMed] [Google Scholar]
- Kort, R., W. D. Hoff, M. Van West, A. R. Kroon, S. M. Hoffer, K. H. Vlieg, W. Crielaand, J. J. Van Beeumen, and K. J. Hellingwerf. 1996. The xanthopsins: a new family of eubacterial blue-light photoreceptors. EMBO J. 15:3209–3218. [PMC free article] [PubMed] [Google Scholar]
- Lee, B. C., P. A. Croonquist, and W. D. Hoff. 2001a. Mimic of photocycle by a protein folding reaction in photoactive yellow protein. J. Biol. Chem. 276:44481–44487. [DOI] [PubMed] [Google Scholar]
- Lee, B. C., A. Pandit, P. A. Croonquist, and W. D. Hoff. 2001b. Folding and signaling share the same pathway in a photoreceptor. Proc. Natl. Acad. Sci. USA. 98:9062–9067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masciangioli, T., S. Devanathan, M. A. Cusanovich, G. Tollin, and M. A. el-Sayed. 2000. Probing the primary event in the photocycle of photoactive yellow protein using photochemical hole-burning technique. Photochem. Photobiol. 72:639–644. [DOI] [PubMed] [Google Scholar]
- Meyer, T. E., G. Tollin, J. H. Hazzard, and M. A. Cusanovich. 1989. Photoactive yellow protein from the purple phototrophic bacterium, Ectothiorhodospira halophila. Quantum yield of photobleaching and effects of temperature, alcohols, glycerol, and sucrose on kinetics of photobleaching and recovery. Biophys. J. 56:559–564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer, T. E., E. Yakali, M. A. Cusanovich, and G. Tollin. 1987. Properties of a water-soluble, yellow protein isolated from a halophilic phototrophic bacterium that has photochemical activity analogous to sensory rhodopsin. Biochemistry. 26:418–423. [DOI] [PubMed] [Google Scholar]
- Miller, A., H. Leigeber, W. D. Hoff, and K. J. Hellingwerf. 1993. A light-dependent branching-reaction in the photocycle of the yellow protein from Ectothiorhodospira-Halophila. Biochim. Biophys. Acta. 1141:190–196. [Google Scholar]
- Pellequer, J. L., K. A. Wager-Smith, S. A. Kay, and E. D. Getzoff. 1998. Photoactive yellow protein: a structural prototype for the three-dimensional fold of the PAS domain superfamily. Proc. Natl. Acad. Sci. USA. 95:5884–5890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perman, B., S. Srajer, Z. Ren, T. Teng, C. Pradervand, T. Ursby, D. Bourgeois, F. Schotte, M. Wulff, R. Kort, K. Hellingwerf, and K. Moffat. 1998. Energy transduction on the nanosecond time scale: early structural events in a xanthopsin photocycle. Science. 279:1946–1950. [DOI] [PubMed] [Google Scholar]
- Ren, Z., B. Perman, V. Srajer, T. Y. Teng, C. Pradervand, D. Bourgeois, F. Schotte, T. Ursby, R. Kort, M. Wulff, and K. Moffat. 2001. A molecular movie at 1.8 Å resolution displays the photocycle of photoactive yellow protein, a eubacterial blue-light receptor, from nanoseconds to seconds. Biochemistry. 40:13788–13801. [DOI] [PubMed] [Google Scholar]
- Scheiner, S. 2000. Calculation of isotope effects from first principles. Biochim. Biophys. Acta. 1458:28–42. [DOI] [PubMed] [Google Scholar]
- Sergi, A., M. Gruning, M. Ferrario, and F. Buda. 2001. Density functional study of the photoactive yellow protein's chromophore. J. Phys. Chem. B. 105:4386–4391. [Google Scholar]
- Sevilla, J. M., M. Dominguez, F. Garcia-Blanco, and M. Blazquez. 1989. Resolution of absorption spectra. Comput. Chem. 13:197–200. [Google Scholar]
- Takeshita, K., Y. Imamoto, M. Kataoka, K. Mihara, F. Tokunaga, and M. Terazima. 2002a. Structural change of site-directed mutants of PYP: new dynamics during pR state. Biophys. J. 83:1567–1577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takeshita, K., Y. Imamoto, M. Kataoka, F. Tokunaga, and M. Terazima. 2002b. Thermodynamic and transport properties of intermediate states of the photocyclic reaction of photoactive yellow protein. Biochemistry. 41:3037–3048. [DOI] [PubMed] [Google Scholar]
- Taylor, B. L., and I. B. Zhulin. 1999. PAS domains: Internal sensors of oxygen, redox potential, and light. Microbiol. Mol. Biol. Rev. 63:479–506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ujj, L., S. Devanathan, T. E. Meyer, M. A. Cusanovich, G. Tollin, and G. H. Atkinson. 1998. New photocycle intermediates in the photoactive yellow protein from Ectothiorhodospira halophila: picosecond transient absorption spectroscopy. Biophys. J. 75:406–412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Stokkum, I. H. M., and R. H. Lozier. 2002. Target analysis of the bacteriorhodopsin photocycle using a spectrotemporal model. J. Phys. Chem. B. 106:3477–3485. [Google Scholar]
- Van Stokkum, I. H. M., T. Scherer, A. M. Brouwer, and J. W. Verhoeven. 1994. Conformational dynamics of flexibly and semirigidly bridged electron donor-acceptor systems as revealed by spectrotemporal parameterization of fluorescence. J. Phys. Chem. 98:852–866. [Google Scholar]
- Weast, R. C., editor. 1988. Handbook of Chemistry and Physics. CRC Press, Boca Raton, Florida.
- Xie, A., W. D. Hoff, A. R. Kroon, and K. J. Hellingwerf. 1996. Glu46 donates a proton to the 4-hydroxycinnamate anion chromophore during the photocycle of photoactive yellow protein. Biochemistry. 35:14671–14678. [DOI] [PubMed] [Google Scholar]
- Xie, A., L. Kelemen, J. Hendriks, B. J. White, K. J. Hellingwerf, and W. D. Hoff. 2001. Formation of a new buried charge drives a large-amplitude protein quake in photoreceptor activation. Biochemistry. 40:1510–1517. [DOI] [PubMed] [Google Scholar]
- Yoda, M., H. Houjou, Y. Inoue, and M. Sakurai. 2001. Spectral tuning of photoactive yellow protein. Theoretical and experimental analysis of medium effects on the absorption spectrum of the chromophore. J. Phys. Chem. B. 105:9887–9895. [Google Scholar]