An Empirical Correlation between Secondary Structure Content and Averaged Chemical Shifts in Proteins

Abstract

It is shown that the averaged chemical shift (ACS) of a particular nucleus in the protein backbone empirically correlates well to its secondary structure content (SSC). Chemical shift values of more than 200 proteins obtained from the Biological Magnetic Resonance Bank are used to calculate ACS values, and the SSC is estimated from the corresponding three-dimensional coordinates obtained from the Protein Data Bank. ACS values of ¹H_α show the highest correlation to helical and sheet structure content (correlation coefficient of 0.80 and 0.75, respectively); ¹H_N exhibits less reliability (0.65 for both sheet and helix), whereas such correlations are poor for the heteronuclei. SSC estimated using this correlation shows a good agreement with the conventional chemical shift index-based approach for a set of proteins that only have chemical shift information but no NMR or x-ray determined three-dimensional structure. These results suggest that even chemical shifts averaged over the entire protein retain significant information about the secondary structure. Thus, the correlation between ACS and SSC can be used to estimate secondary structure content and to monitor large-scale secondary structural changes in protein, as in folding studies.

INTRODUCTION

Since the first observation of the chemical shift in NMR spectra in 1957 by Gutowsky et al., it has been used as a powerful indicator of the type of secondary structure that a biopolymer can adopt. Thus, most development of modern experimental methods is driven by the goal to increase the resolution and sensitivity by which the chemical shift of a nucleus can be measured. In addition to structural information (Dalgarno et al., 1983; Pastore and Saudek, 1990; Williamson, 1990; Wishart et al., 1991a; Laws et al., 1993; Oldfield, 1995; Cornilescu et al., 1999), chemical shifts provide detailed information about the nature of hydrogen exchange dynamics, ionization and oxidation states, ring current influence of aromatic residues, and hydrogen bonding interactions (Szilagyi, 1995). Several recent and excellent review articles describe a variety of experimental and computational methods to correlate chemical shifts to protein three-dimensional structural information (Szilagyi, 1995; Case et al., 1994; Wishart and Nip, 1998; Ando et al., 2001; Wishart and Case, 2001).

Here, we would like to explore whether any meaningful structural information could still be obtained from chemical shifts before completion of resonance assignments. Thus, the extensive information found in the Biological Magnetic Resonance Bank and Protein Data Bank was used to determine whether there is a correlation between protein secondary structure content (SSC) and the average chemical shift (ACS) value for a particular type of nucleus. We have determined that the highest correlation with secondary structure content is found with the ¹H_α ACS value, followed by ¹H_N ACS. No reliable correlations could be determined for backbone heteronuclei ¹³C_α and ¹⁵N. The correlation between ¹H_α and ¹H_N ACS values and SSC was used to estimate the percentage of helical and sheet content for a set of proteins that have complete chemical shift information available in the BMRB, but the NMR or x-ray determined three-dimensional structures of which are not yet available. The estimates are then compared with estimates calculated using a more conventional method, the chemical shift index (CSI), which uses the individual chemical shifts of each resonance instead of an average. The results show a good agreement for the helical content between the two estimates, whereas the agreement is only moderate for the sheet content. Though determination of CSI values is superior in obtaining SSC estimates in cases where the resonances can be readily assigned, estimates of SSC could be obtained from a simple ACS value as well, especially in cases where assignments would be difficult if not impossible to obtain (e.g., under denaturing conditions). Though circular dichroism also be used to estimate SSC, and requires less sample and experimental time, circular dichroism cannot be used in cases where the signal is masked by the solvent signal, such as when high concentrations of urea are used.

METHODS

Chemical shift values corresponding to the protein backbone atoms (¹H_N, ¹⁵N, ¹H_α, and ¹³C_α) were obtained from the Biological Magnetic Resonance Bank (BMRB, http://www.bmrb.wisc.edu/) star files (Seavey et al., 1991). If the information on the structure of the protein was also present in the star file, it was extracted, as was the information on the amino acid sequence. Structure files obtained from the Rutgers Center for Structural Biology (PDB format, http://www.rcsb.org/pdb/) (Berman et al., 2000) were cross-checked against the corresponding BMRB star file manually to ensure a correct match. NMR determined structures were used whenever possible, but if they were not available, the corresponding x-ray structure was used instead. Only proteins with more than 50 amino acid residues were considered, inasmuch as these were expected to contain a significant amount of secondary structure.

The averaged chemical shift (ACS) of a nucleus “i” is defined by:

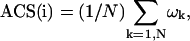(1)

where N is the total number of observed crosspeaks (typically in a single bond correlated spectrum, such as a heteronuclear single quantum correlation (HSQC)) and ω_k is the corresponding chemical shift of the k^th resonance (referenced using recommended procedures (Wishart et al., 1995)).

To evaluate the secondary structure content for the set of proteins, the program probability-based protein secondary structure identification (PSSI) was used (Wang and Jardetzky, 2002). In this method, CSI of the set of backbone atoms are used to define the probability with which the secondary structure (sheet or helix) is assigned. Secondary structure content in percentage is then calculated with respect to the total number of residues in the sequence.

The structure-based percentage of sheet and helix (sum of α and 3₁₀) was determined using the program PROMOTIF (http://www.biochem.ucl.ac.uk/gail/promotif/promotif.html) (Hutchinson and Thornton, 1996), which uses the atomic coordinate files obtained from the RCSB. All the analyses were performed using codes written using C⁺⁺ and other scripts (awk or perl) on a Silicon Graphics UNIX work station (copies of the code are available from the authors). A complete list of the 213 proteins (comprised of ¹H_N, ¹⁵N, ¹H_α, and ¹³C_α chemical shifts) and 25 additional proteins (with only ¹H_N and ¹⁵N chemical shifts), their individual ACS values and the structure based secondary structure content estimates are available from the authors.

RESULTS

Correlations between averaged chemical shifts and secondary structure content

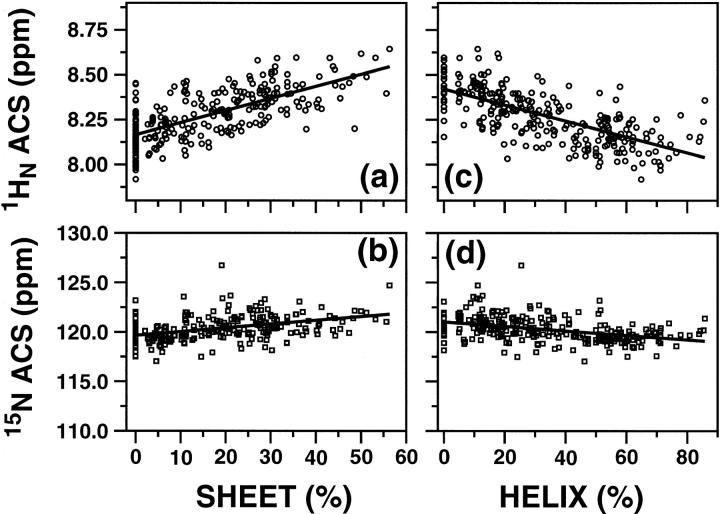
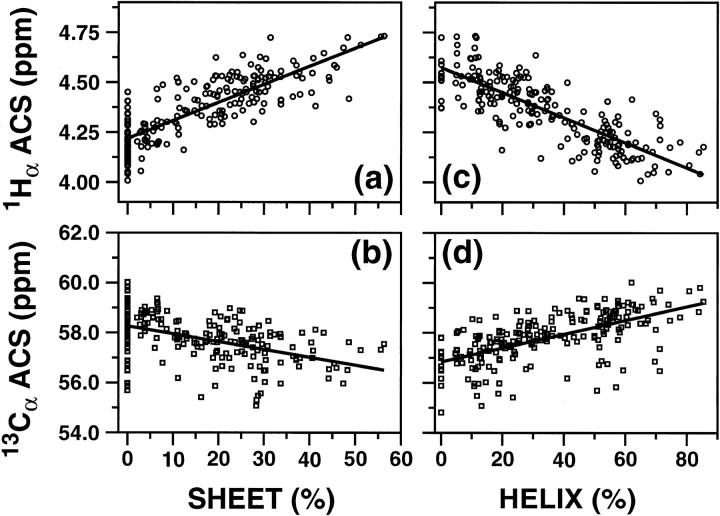
Fig. 1 shows the ACS values of ¹H_N and ¹⁵N nuclei (top and bottom rows, respectively) plotted against the respective sheet and helical content (left and right columns, respectively). Fig. 2 shows a similar plot for ¹H_α and ¹³C_α nuclei. A total of 238 and 213 proteins were used in Figs. 1 and 2, respectively (Supporting Information Table S1). The continuous lines in Figs. 1 and 2 correspond to linear regression analyses of the data, and Table 1 lists the results of the analyses. ACS values of both ¹H_N and ¹H_α are much more indicative of the overall secondary structure content than those of the heavy atoms. Correlation coefficients for the plots of ¹H_N, ¹⁵N, ¹H_α, and ¹³C_α versus percent sheet content are 0.64, 0.44, 0.75, and 0.44, respectively, whereas the coefficients obtained in the plots versus percent helix content are 0.65, 0.40, 0.80, and 0.58, respectively (Table 1). Although ¹³C_α ACS values show a wider dispersion with respect to helical content (Fig. 2 d) than the corresponding ¹⁵N data (Fig. 1 d), the correlation coefficients for the plots of heteronuclei are equally poor. Overall, the best correlations were obtained with the ¹H_N and ¹H_α data.

FIGURE 1.

Plots of ACS values versus the secondary structure contents estimated from the three-dimensional structures using the program PROMOTIF. (a) and (b) show the correlation of ¹H_N and ¹⁵N ACS values, respectively, to the percentage of β-sheet structures, whereas (c) and (d) correlate the same ACS values with respect to the percentage of helical structure (sum of α and 3₁₀ helices). Continuous lines represent the linear regression analysis results.

FIGURE 2.

Plots of ACS values versus the secondary structure contents estimated from the three-dimensional structures using the program PROMOTIF. (a) and (b) show the correlation ¹H_α and ¹³C_α ACS values, respectively, to the percentage of β-sheet structures, whereas (c) and (d) correlate the same ACS values with respect to the percentage of helical structure (sum of α and 3₁₀ helices). Results of the linear regression analysis are shown by continuous lines.

TABLE 1.

Linear correlation of ACS to secondary structure content

	*Sheet (%)			*Helix (%)
ACS (ppm)	†CC	‡Slope	‡Intercept	†CC	‡Slope	‡Intercept
1HN	0.64	60.9 ± 4.4	−488.0 ± 36.3	0.65	−95.0 ± 6.7	818.9 ± 55.4
15N	0.44	5.1 ± 0.63	−598.4 ± 75.5	0.40	−7.2 ± 1.0	899.1 ± 118.6
1Hα	0.75	66.2 ± 3.7	−273.1 ± 16.0	0.80	−102.8 ± 5.2	482.1 ± 22.6
13Cα	0.44	−6.27 ± 0.9	377.6 ± 49.8	0.58	12.4 ± 1.2	−680.0 ± 67.5

^*Secondary structures defined based on PROMOTIF.

^†CC: Correlation coefficient for linear regression analysis.

^‡Slope and intercept are defined based on a linear equation ACS (ppm) = Slope× Secondary Structure Content + Intercept.

A notable feature of these results is that the slopes of the lines for the ACS values versus helix and sheet content are opposite to each other (most clearly seen in panels a and c of Figs. 1 and 2). The change in the sign of the slope indicates that changes in ACS values can allow differentiation of increasing or decreasing helical or sheet secondary structural elements upon changes in environment. The ACS values increase with an increase in the total sheet content and decrease with an increase in the total helical content.

Estimation of SSC for proteins having no determined three-dimensional structure

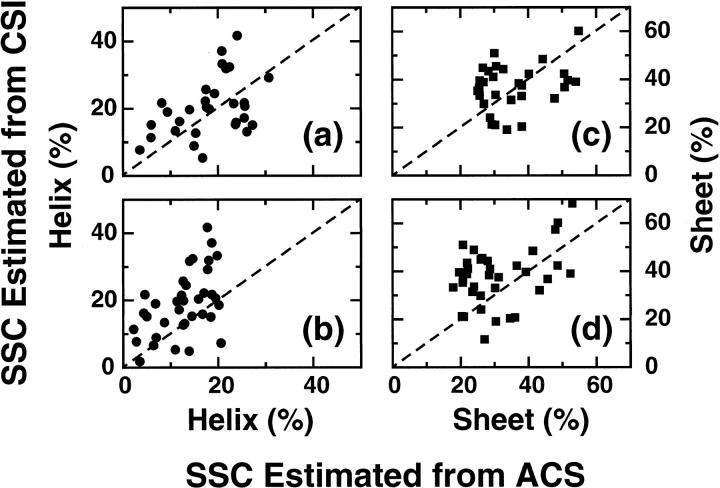
A set of 36 proteins obtained from the BMRB for which complete assignments of the backbone atoms are known, but for which structures have not yet been determined, were used to estimate SSC by using the empirical correlation between SSC and ¹H_α or ¹H_N ACS values. SSC was also calculated using the consensus chemical shift indices using the program PSSI (Methods) using all the backbone atoms. The list of all the proteins and their estimated SSC, using the correlation and CSI-based methods is given in Table 2. There is an overall agreement between the SSCs estimated using these two methods (Fig. 3). Larger deviations were observed in the ¹H_N ACS values compared to the ¹H_α ACS values. The correlation between ¹H_N ACS and secondary structure (Table 1) is worse than that for the ¹H_α ACS, as shown in Fig. 3, b and d.

TABLE 2.

Estimated SSC using ACS- and CSI-based methods for proteins with no three-dimensional structural information

		Helix (%) from			Sheet (%) from
BMRB	Protein name	*ACS (1Hα)	*ACS (1HN)	†CSI	*ACS (1Hα)	*ACS (1HN)	†CSI
4840	Adenylate kinase	15.31	12.65	12.70	38.11	34.58	20.40
4834	Staphylococcus aureus peptide deformylase	25.56	18.69	21.70	25.54	20.70	36.50
4825	Recombinant RC-RNase 2	27.28	18.45	15.10	25.70	19.60	39.60
4821	DcuS	17.62	15.87	20.40	33.70	30.37	19.10
4795	Human D187N gelsolin domain 2	20.83	18.67	37.10	28.73	26.01	24.10
4794	Human wild-type gelsolin domain 2	25.69	19.45	20.70	25.06	20.62	35.30
4787	Apical membrane antigen 1	26.10	12.95	13.10	29.25	20.36	21.30
4784	Tyrosine repressor	n.a.	6.38	6.60	n.a.	47.90	57.40
4776	Sud dimer	14.03	11.31	19.70	40.21	36.56	42.30
4771	Tola3	8.18	4.57	21.70	50.72	45.64	36.80
4752	gpnu1-E68	11.92	4.32	16.20	51.62	39.25	39.70
4735	Olfactory marker protein	23.33	12.27	21.50	29.68	22.13	41.10
4722	Shikimate kinase	9.34	6.80	19.00	47.78	43.28	32.10
4716	Auxilin	3.53	2.78	7.70	54.01	52.33	39.00
4712	Newt acidic FGF	16.76	10.94	5.30	30.54	26.34	45.50
4711	RNA-binding protein	n.a.	13.99	31.70	n.a.	36.02	20.80
4698	Transforming growth factor beta type II receptor	n.a.	13.86	4.90	n.a.	28.66	41.00
4688	L18	22.46	14.66	32.40	34.98	23.48	31.50
4670	PIN1At	30.71	17.80	29.20	25.68	17.80	33.30
4664	Lipocalin Q83	25.54	11.77	17.20	30.01	20.71	51.00
4579	FYVE domain of EEA1	n.a.	20.16	18.60	n.a.	27.05	11.60
4567	Catalytic domain of yUBC1	19.30	13.23	24.50	37.21	28.38	38.40
4558	YopH-NT monomer	17.48	12.64	25.70	38.13	31.21	37.50
4463	Ras-binding domain of Byr2	21.74	18.02	31.90	30.37	23.95	33.60
4447	p23fyp	20.93	19.80	33.30	26.97	25.85	29.80
4353	p13 C-terminal domain	23.81	16.69	15.90	26.84	21.82	38.90
4335	Calerythrin	5.88	2.21	11.40	54.90	48.68	60.20
4313	E2	24.09	17.73	41.70	30.19	20.94	21.10
4294	Human MBF1(57-148) core domain	5.96	4.99	15.20	50.59	48.55	42.40
4271	Calcium binding protein from Entamoeba histolytica	11.00	8.70	13.40	44.27	41.27	48.50
4239	f29-SSB bacteriophage	23.69	14.46	15.30	28.27	21.90	43.50
4147	Cold shock domain	14.95	6.93	8.90	32.65	27.95	44.30
4136	Escherichia coli multidrug Resistance protein E	n.a.	3.46	1.80	n.a.	52.96	68.20
4132	Human ubiquitin-conjugating enzyme	18.15	12.68	19.90	38.07	30.17	33.10
4027	S. aureus DHFR(F98Y)-NADPH-TMP ternary complex	17.36	17.00	22.20	26.64	25.96	44.90
1583	Micrococcal nuclease	n.a.	20.59	7.30	n.a.	23.89	48.90

^*Secondary structure content estimated using the correlation listed in Table 1.

^†Secondary structure content estimated using probability-based protein secondary structure identification (Wang and Jardetzky, 2002).

n.a.: not determined due to absence of chemical shift information.

FIGURE 3.

Comparison of helical and sheet content percent calculated using ¹H_α or ¹H_N ACS values to that obtained using a consensus chemical shift index-based method for a set of proteins for which no three-dimensional structures are available. (a) and (b) correspond to the helical content using the ¹H_α and ¹H_N ACS values, respectively, whereas (c) and (d) are the corresponding sheet content using the same ACS values. The dashed lines correspond to a perfect correlation between these two methods.

DISCUSSION

Previously, Wishart and co-workers (Wishart et al., 1991b; Wishart and Sykes, 1994) have suggested two methods to estimate secondary structure content from two-dimensional NMR data. In one of their methods, the total number of crosspeaks over a preselected region of a homonuclear two-dimensional correlation spectrum is counted to estimate the SSC. Here we show that even the averaged chemical shift values of a backbone atom of a protein can retain significant information about the proteins secondary structure. In particular, the ¹⁵N-¹H_N chemical shift values, which are often underutilized as indicators of secondary structure because they are liable to change with small variations in temperature and pH (Glushka et al., 1989; Le and Oldfield, 1994), can be used to estimate SSC from ¹H_N ACS values as a function of varying buffer conditions. In addition to the backbone atoms ¹H_N, ¹⁵N, ¹H_α, and ¹³C_α, ACS versus SSC correlations for the other backbone and side-chain nuclei ¹³CO, ¹³C_β, and ¹H_β were also evaluated (data not shown). The correlation coefficients for the plots of ACS values for these nuclei versus SSC were good, in particular for the carbon atoms. However, estimates of SSC using the ¹³CO, ¹³C_β, and ¹H_β ACS were not considered further because residue-specific secondary structure determination can readily be accomplished with chemical shift assignments by using other empirical methods, such as TALOS, developed by Cornilescu et al. (1999).

The statistical analysis of the correlation between ACS and SSC is relatively good for the ¹H_α ACS values (75–80%), whereas a moderate correlation (65%) is obtained with the ¹H_N ACS values. As the number of proteins that can be added into the correlations of ACS with secondary structure increases, the correlation coefficients should improve significantly. However, certain factors may result in lowering the correlation coefficient. ACS values were based on the total number of crosspeaks that were observed, and not on the total number of residues in the protein. For example, a ¹⁵N-HSQC spectrum will not contain resonances from a proline residue, which will consequently not be included in the ACS value, though it is present in the sequence. Significant contributions in lowering the correlation are expected from the residues that are present in the turns that will contribute to the ACS value as a sheet or helix. For example, residues that are part of a β-turn will be considered as β-sheet when the average values are calculated. The distribution of chemical shifts for each of the amino acids found in the BMRB database suggests that no particular amino acid dominates the ACS values, and hence the chemical shifts, for a particular type of amino acid. Therefore no particular amino acid expected to bias the correlation. Moreover, Sharman et al. (2001) have used rigorous statistical analyses of ¹H_α chemical shifts to show that there is no correlation between amino acid type and propensity to fall within helical or sheet regions. However, it is possible that certain proteins will contain a large number of one type of residue (or a preponderance of a few types of residues) that may skew the ACS value. The relatively low correlation coefficients (0.64–0.8) for the ACS versus SSC correlations may result from these and other factors. However, estimating SSC from ACS values may still be a way to detect secondary structural changes, especially increases or decreases in helical content.

From a practical point of view, this correlation would be most useful if a sufficient number of individual crosspeaks are observed in an HSQC spectrum. Although the correlations were not evaluated by systematically eliminating a certain percentage of peaks from the data, it is recommended that a minimum of 70% of the total number of peaks expected should be observed in the spectra to determine a reliable ACS value. Experimental methods based on transverse relaxation optimized spectroscopy (Pervushin et al., 1997, 1998) can provide an additional advantage for estimating SSC from ACS values.

In summary, the observed correlation between ACS and SSC can be used to monitor structural changes in real time, such as in protein folding experiments, to detect large-scale structural changes in complex formation and to identify initial protein folds in high throughput proteomics applications.

SUPPORTING MATERIAL

Table S1: List of all the proteins, BMRB and pdb codes, ACS values and PROMOTIF estimates of secondary structure content is available from the authors. (15 pages, data used in Figs. 1 and 2).