Cascades of Transient Pores in Giant Vesicles: Line Tension and Transport

Abstract

Under ordinary circumstances, the membrane tension of a giant unilamellar vesicle is essentially nil. Using visible light, we stretch the vesicles, increasing the membrane tension until the membrane responds by the sudden opening of a large pore (several micrometers in size). Only a single pore is observed at a time in a given vesicle. However, a cascade of transient pores appear, up to 30–40 in succession, in the same vesicle. These pores are transient: they reseal within a few seconds as the inner liquid leaks out. The membrane tension, which is the driving force for pore opening, is relaxed with the opening of a pore and the leakage of the inner liquid; the line tension of the pore's edge is then able to drive the closure of a pore. We use fluorescent membrane probes and real-time videomicroscopy to study the dynamics of the pores. These can be visualized only if the vesicles are prepared in a viscous solution to slow down the leakout of the internal liquid. From measurements of the closure velocity of the pores, we are able to infer the line tension, 𝒯. We have studied the effect of the shape of inclusion molecules on 𝒯. Cholesterol, which can be modeled as an inverted cone-shaped molecule, increases the line tension when incorporated into the bilayers. Conversely, addition of cone-shaped detergents reduces 𝒯. The effect of some detergents can be dramatic, reducing 𝒯by two orders of magnitude, and increasing pore lifetimes up to several minutes. We give some examples of transport through transient pores and present a rough measurement of the leakout velocity of the inner liquid through a pore. We discuss how our results can be extended to less viscous aqueous solutions which are more relevant for biological systems and biotechnological applications.

INTRODUCTION

Transport of ions and molecules across membranes is central to many biological processes. Understanding transmembrane transport is also a key ingredient in the development of new technologies such as gene therapy (Verma and Somia, 1997), which requires transport of DNA fragments through cellular and nuclear membranes, and targeted drug delivery systems based on vesicular “baggies” where drug molecules initially contained in vesicles need to be released in a well-controlled fashion (Lawrence, 1994; Lasic and Needham, 1995; Moase et al., 2001; Cao and Suresh, 2000; Yu et al., 1999; Zasadzinski, 1997).

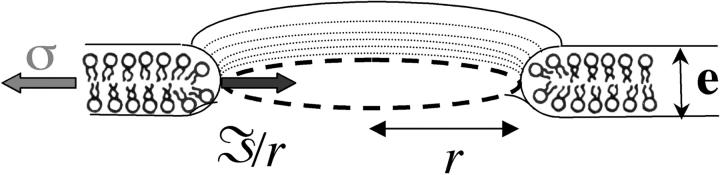
Inasmuch as there exists a large body of empirical results on these subjects, there is little understanding of the fundamental mechanisms involved. An important step in this direction is the visualization of the dynamics of membrane reorganization. We have previously reported visualization of transient pores in tense vesicles (Sandre et al., 1999). These were unilamellar synthetic vesicles, 10–100 μm in radius, tensed either by adhesion to appropriately treated surfaces, or by intense optical illumination in the presence of fluorescent probes embedded in the membrane (Fig. 1). Pore opening is driven by the membrane tension, σ, and pore closure by the line tension, 𝒯, as drawn schematically in Fig. 3 (Sandre et al., 1999; Brochard-Wyart et al., 2000). We observe only a single pore in a vesicle at a time. A hydrodynamic model which explains the dynamics of pore opening and closure was also presented (Brochard-Wyart et al., 2000). Optically induced tension was reported by Bar-Ziv and co-workers as well, who used unlabeled vesicles and laser tweezers as the light source (Bar-Ziv et al., 1995, 1998). In this article we report the effect of adding cholesterol or detergents to the vesicle systems. Cholesterol increases the line tension, 𝒯, and the lifetime of the pores are consequently reduced. Conversely, detergents reduce 𝒯 and increase pore lifetimes by stabilizing the pores' borders. Pore lifetimes, which are normally a few seconds, can increase up to several minutes in the presence of certain detergents.

FIGURE 1.

(a) At the beginning of the observation under a fluorescence microscope the vesicles are relaxed: their surface tension, σ, is very small and their membrane undergoes large amplitude fluctuations. (b) Over tens of minutes of observation with maximum available incident light intensity, illuminated vesicles gradually become tense and perfectly spherical. The width of the white bar is 10 μm. (For experimental conditions, see Materials and Methods.)

FIGURE 3.

Transverse view of a pore, with radius r, drawn schematically. Pore opening is driven by the membrane tension, σ, and is opposed by the line tension term, 𝒯/r.

In addition, we present our observations of transport across transient pores. The most convenient cargo to be transported is another vesicle: indeed, in a vesicle preparation it is not unusual to find a vesicle containing a smaller one inside. When the external vesicle makes a pore, the smaller one is dragged toward the hole by the liquid leaking through it. If the internal vesicle is very small compared to the pore size, it acts as a probe of the flow field. On the other hand, if the internal vesicle is larger than the pore size it can still be transported out due to its soft, deformable nature. Finally we present our observations concerning the regularity of intervals between successive pores: a given vesicle makes a series of pores (up to 30 or 40 in succession), separated by regular time intervals.

Let us now summarize the essential features of the model quantitatively, following Brochard-Wyart et al. (2000). The overall geometry of the system is provided in Fig. 2. Just before the pore opening (Fig. 2 A) the vesicle has radius R_i, membrane tension σ_o, and projected area A_p = 4πR_i². It is more convenient to express the projected area in terms of the radius, R_o, that the vesicle would adopt were its membrane tension, σ, equal to zero. A finite membrane tension stretches the membrane area by a factor 1 + σ/E, whenc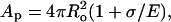e where 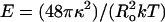is a two-dimensional modulus, related to the unfolding of the “wrinkles” of the surface, with the Helfrich bending constant κ and thermal energy kT. When a pore opens up, the overall spherical shape of the vesicle is by and large conserved (Fig. 2). We assume that the total amount of lipid is conserved during the opening and closure of a pore. Thus, we can relate the membrane tension σ to the pore (r) and vesicle (R) radii simply by counting areas:

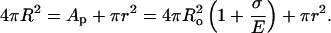(1)

We define a critical pore radius, r_c, by writing 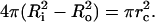This is the radius corresponding to the complete relaxation of the membrane tension (σ = 0 in Eq. 1), assuming zero leakage (R = R_i). Using r_c, Eq. 1 can be rearranged to:

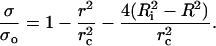(2)

In Eq. 2 two separate mechanisms which, in general, act simultaneously to relax the tension are apparent: 1), Opening of the pore provides the lipid to be distributed in a smaller area; the membrane surface wrinkles, relieving tension. The ratio 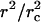increases, and σ decreases. 2), When a pore opens, the internal liquid leaks out through the pore, due to the excess Laplace pressure, ΔP = 2σ/R. This leakout decreases the vesicle radius, making the ratio 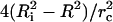larger in Eq. 2, thereby reducing tension.

FIGURE 2.

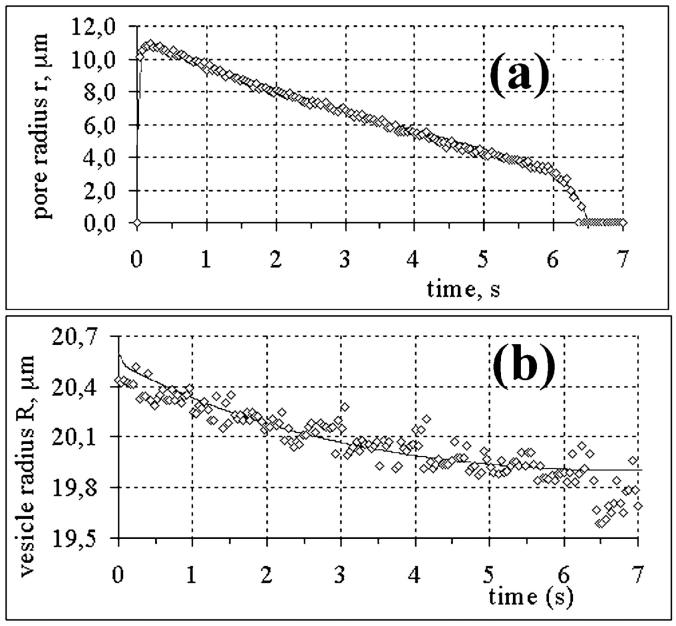
Appearance of a transient pore in a DOPC vesicle having initial radius R_i. (a), When the membrane tension reaches a critical value, the vesicle responds by the sudden opening of a pore. The pore size reaches its maximum very rapidly (b), thereafter decreasing slowly until complete resealing (c–f). The sizes of the pore (r) and vesicle (R) radii are plotted in Fig. 4 as a function of time. The white bar in (f) corresponds to 10 μm. The vesicle in this example contains 20 mol % cholesterol (see Materials and Methods; also see Cholesterol increases the line tension).

The dynamics of the pore radius, r, are somewhat reminiscent of bursting of soap films. However, in a soap film a hole grows at constant velocity, surrounded by a rim which collects the liquid. The growth kinetics are driven by inertia (Mysels et al., 1959; de Gennes, 1996). In contrast, we have never observed a rim collecting the lipid around a growing pore. In fact, pores in vesicles are more closely analogous to the opening of pores in viscous bare films which do not contain any surfactant. In these bare films pore opening is governed by the transfer of surface energy to viscous losses, and rims are absent (Debrégeas et al., 1995; Diederich et al., 1998). Pores in vesicles are more complex, however, inasmuch as i), the membrane tension relaxes as the pore grows (Eq. 2), and ii), the line tension 𝒯, negligible in bare viscous films, becomes important and drives the closure of pores when the membrane tension has relaxed sufficiently. Thus, for pores in vesicles the following dynamics apply (Sandre et al., 1999; Brochard-Wyart et al., 2000):

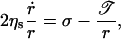(3)

where η_s ≡ η₂ e is the surface viscosity in N s/m, defined as the product of the lipid viscosity, η₂, and the membrane thickness, e (Fig. 3).

The dynamics of the vesicle radius, R, on the other hand, are provided by considering the flux through the pore, 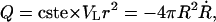where V_L is the velocity of the leaking liquid at the center of the orifice, and r is the pore radius. The leakout velocity can be estimated by equating the Laplace pressure, ΔP = 2σ/R, which is present due to the nonzero membrane tension and acts to drive the internal liquid out, to the shear stresses involved, which are of order η_oV_L/r, where η_o is the viscosity of the internal liquid. A rigorous calculation (Happel and Brenner, 1983) of the flux through a circular orifice provides the numerical prefactors:

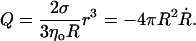(4)

Strictly speaking, Eq. 4 only applies to flow through an orifice with constant radius. However, it is a good approximation for our problem as long as r changes slowly: .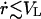

In summary, we have related the dynamics of the pore radius r (Eq. 3) to that of the vesicle radius R (Eq. 4), through the common constraint provided by the membrane tension (Eq. 2). Thus, we have three equations for three unknowns (r, R, and σ). In Fig. 4 we have plotted the numerical solutions of Eqs. 2, 3, and 4 for r(t) and R(t) along with experimental measurements. Details of numerical solutions are given in Brochard-Wyart et al. (2000).

FIGURE 4.

For the vesicle of Fig. 2, (a) pore radius as a function of time and (b) vesicle radius as a function of time. Diamonds are experimental measurements, whereas the continuous curves are numerical fits to the data, with 𝒯 = 10 pN, r_c = 12 μm, R_o = 19.7 μm, σ_o = 1.7 × 10⁻⁵ N/m, η_s = 3.4 × 10⁻⁷ N s/m, and η_o = 32 cP.

The organization of the article is as follows. In Materials and Methods, we provide experimental details. In Life of Transient Pores, we present analytical solutions to the pore dynamics in the limit of slow leakout which corresponds to our measurements. In the subsequent section, we present measurements of the line tension, 𝒯, for bare DOPC vesicles, and show how 𝒯 is increased in the presence of cholesterol and decreased in the presence of surfactants. In Pores and Transport across Membranes, we discuss transport through pores, and present a rough measurement of the leakout velocity. In Cascades of Pores under Illumination, a peculiarity of transient pores is presented: these appear at highly regular time intervals. In Final Remarks, we summarize and discuss our results.

MATERIALS AND METHODS

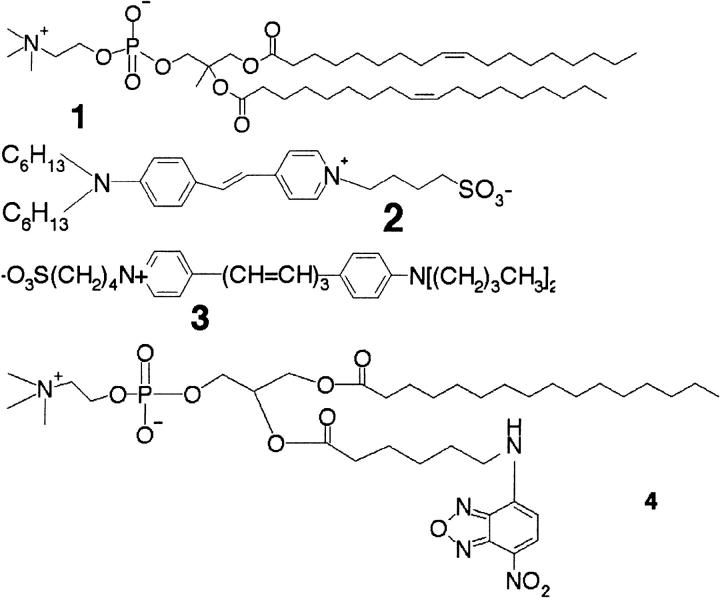
We use the “electroformation” method (Angelova, 2000), which produces giant unilamellar vesicles (GUVs) with high efficiency and very few multilamellar aggregates. The lipid is 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC, Sigma, structure 1 in Fig. 5) which is in the L_α fluid phase at room temperature and forms vesicles in arbitrary mixtures of water and glycerol (Öradd et al., 1994).

FIGURE 5.

Chemical structures of the phospholipid DOPC (1) and the fluorescent markers, di6ASP-BS (2), RH237 (3), and NBD-C6-HPC (4), used in the experiments.

A solution of pure lipid (1 mg/ml in a 2:1 chloroform/methanol mixture) is cast onto both windows of a homemade preparation chamber composed of two transparent electrodes (formed by glass plates coated with indium tin oxide) separated by a 1-mm-thick Teflon spacer. The cast lipid film is dried overnight in a vacuum oven, then filled with ∼1.5 ml of aqueous buffer, containing 0.1 M sucrose or glucose to control the osmolarity and 66% v/v glycerol to obtain a viscosity of η_o = 32.1 ± 0.4 cP, measured with an Ubbelohde viscometer. An AC voltage of ∼1.1 V at 7 Hz is applied between the electrodes to allow the gentle swelling of the lipid film to form GUVs of 10–100 μm diameters at the end of ∼6 h. The vesicles are let to “relax” overnight in the preparation chamber, then are drawn out carefully. This stock solution contains ∼0.1 mg/ml lipid (≈130 μM).

Unless noted otherwise, the vesicles are labeled using the lipophilic fluorescent dye n-(4-sulfopropyl)-4-(4-(dihexylamino)styryl)pyridinium (di6ASP-BS; kindly provided by Mireille Blanchard-Desce, UMR 6510 CNRS, U. de Rennes, France, Fig. 5), which is spontaneously inserted into the bilayer. 1% v/v of 560 μM of the dye (in ethanol) is incubated for a few hours with the vesicle solution before observation. The vesicles are either observed as such, or after sedimentation in an equiosmolar solution, in a closed microscope chamber (two glass slides spaced by parafilm of 200 μm thickness and sealed with hot paraffin), using a Reichert-Jung MET upright microscope equipped with an OLYMPUS 60× /0.90 LUMPlanFL water immersion objective. Epifluorescence excitation is provided by a 200-W mercury lamp and a 455–490 nm band-pass filter. The fluorescence peak at 580 nm is detected with a standard CCD camera. Images are digitized on an 8-bit frame grabber (LG-3, Scion, Frederick, MD) and analyzed using Scion Image software (Scion).

In some experiments, the fluorescent marker n-(4-sulfobutyl)-4-(6-(4-(dibutylaminophenyl)hexatrienyl) pyridinium (RH237; Fig. 5), or 2-(6-(7-nitrobenz-2-oxa-1,3-diazol-4-yl) amino) hexanoyl-1-hexadecanoyl-sn-glycero-3-phosphocholine (NBD-C6-HPC, Fig. 5) is used instead of di6ASP-BS, as noted.

For experiments in which surfactants are added to vesicles, a stock solution of the surfactant Tween 20 (Sigma; Fig. 9; also see section called Line Tension, 𝒯) is prepared in aqueous solutions identical to those in which the vesicles are kept, 100 mM sucrose in a 2:1 v/v glycerol/water mixture. These stock solutions are introduced into the vesicle preparation through an opening in the observation cell. This method provides a front of surfactants diffusing into the vesicle suspension, allowing the immediate observation of the effect of surfactants on vesicles. This is essential at high surfactant concentrations wherein vesicles are quickly destroyed by the surfactant. The main disadvantage of the method is that the concentration of the surfactant is inhomogeneous, and thus not known precisely.

FIGURE 9.

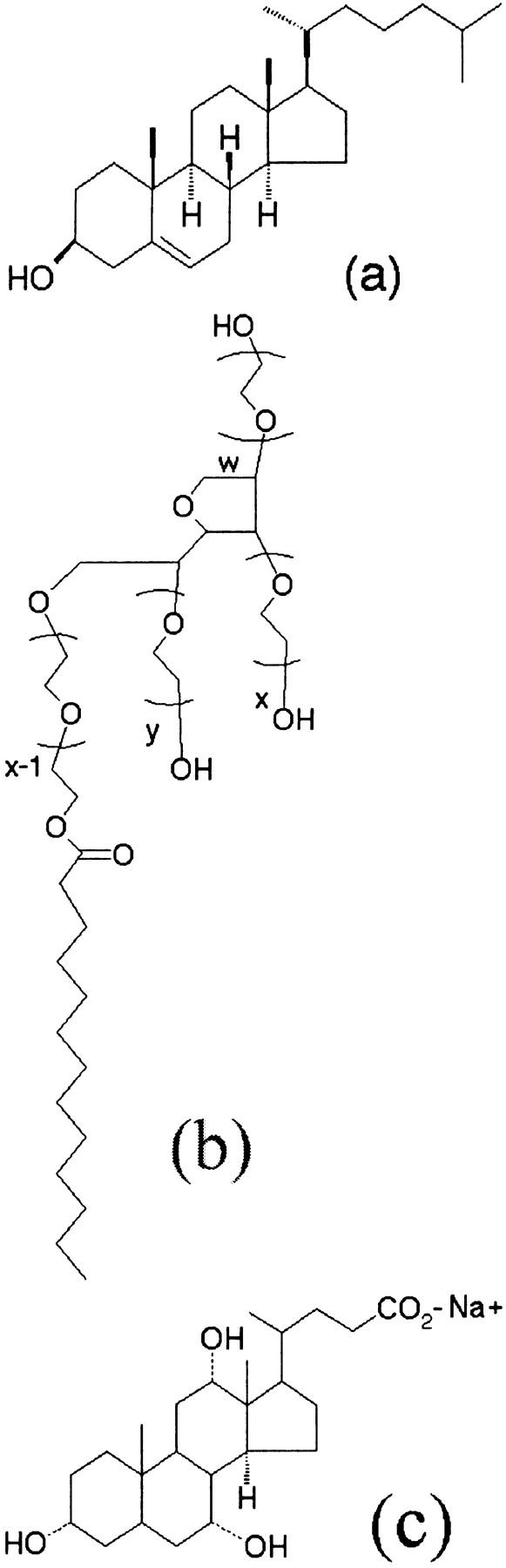
(a) Cholesterol, (b) Tween 20 (x + y + w = 20), and (c) Sodium cholate.

In experiments where cholesterol (Fig. 9; also see section called Line Tension, 𝒯) is added to the bilayers, a different approach is taken inasmuch as cholesterol is insoluble in the aqueous phase and its presence in bilayers is not detrimental to the stability of vesicles. Cholesterol is co-cast with the lipid onto glass plates, at the desired molar ratio, before electroformation. The rest of the procedure is similar to what is described above.

LIFE OF TRANSIENT PORES

In this section we first summarize analytical solutions to the pore dynamics in different stages of the pore's lifetime, following Brochard-Wyart et al. (2000). In the following section we will use these results to infer the line tension from experimental data under various conditions.

Consistent with the experimental observations in Figs. 2 and 4, we consider small variations in the vesicle radius R: R = R_o(1 + δ) and R_i = R_o(1 + δ_o), where 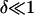and 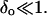The critical pore radius, r_c, of Eq. 2 then becomes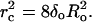

Using the reduced units, 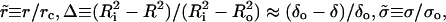and 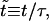where τ ≡ 2η_s/σ_o, Eq. 2 becomes

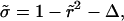(5)

whereas Eqs. 3 and 4 can be written as

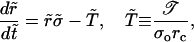(6)

and

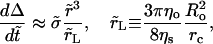(7)

respectively. The initial conditions for Eqs. 6 and 7 are: 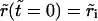and 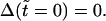In Eq. 7, Δ represents the decrease of the vesicle radius from its initial value, whereas the ‘leakout parameter’ 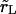separates the following two regimes:

1. Fast leakout 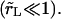Relaxation of the membrane tension, σ, is dominated by the leakout of the internal liquid. The pore size remains small 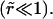In the limit 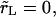the contents are released instantly, and the pore never opens.

2. Slow leakout 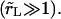The leakout time, 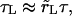is much longer than the pore opening time, τ (see below). Thus, the pore opens as if the contents were rigid, nearly up to its critical value, then closes back very slowly as the contents leak out, keeping the surface tension very small. In the limit 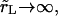the contents are gelified, Δ = 0, and the pore opens to its maximum value, r_m, and remains open.

From Figs. 2 and 4 we see that the pore opening time is on the order of 100 ms, whereas the vesicle radius drops over the course of a few seconds. Thus, our experimental conditions correspond to the slow leakout regime 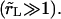This is due to the fact that our experiments are carried out using highly viscous mixtures of glycerol and water (viscosity ∼30 times that of pure water). Beside placing us in the slow leakout regime where the pore opening is decoupled from the leakout, which simplifies the analysis, this also has the important effect of slowing down the dynamics sufficiently to enable observation at video rate.

We summarize below analytical solutions to Eqs. 5, 6, and 7 in the case of slow leakout 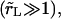where the leakout time scale, τ_L, is much longer than the pore opening time, 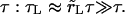There are four stages in the life of a pore in this regime:

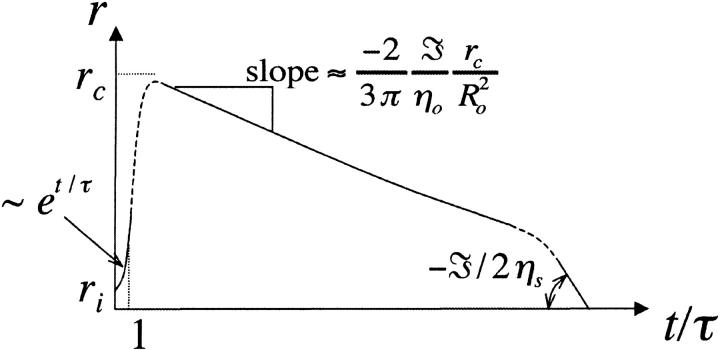
Growth

At time t = 0 a pore nucleates with radius r_i ≈ 𝒯/σ_o, as derived from the pore energy πr²σ_o − 2πr𝒯. This is likely to be induced by a surface defect, and not by thermal activation, since the energy barrier to open a pore, of order 𝒯²/σ_o ≈ 10⁻¹⁷ J (using values reported below), is high compared to kT ≈ 10⁻²¹ J at room temperature. The idea of nucleation by defects is also corroborated by the fact that pores often nucleate in series at or near the same site on a given vesicle. Now, for 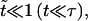we have 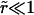and 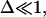and so 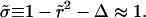With these, Eq. 6 becomes 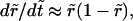that is,

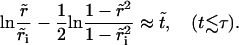(8)

In the initial stages of pore opening 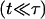we have 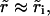and the opening is exponential: r ≈ r_ie^t/τ, from Eq. 8.

Maximum pore radius

When the pore reaches its maximum size, r_m, we hav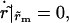e i.e., 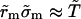from Eq. 6, where 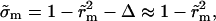inasmuch as the approximation 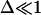is still valid. Thus, we obtain 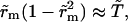whose solution is:

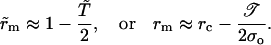(9)

As we saw above, the ratio 𝒯/σ_o represents the nucleation radius, r_i, which is small compared to r_c. Thus the pore opens nearly up to its critical value, r_m ≈ r_c, for which the surface tension is very small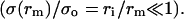

Quasi-static leakout

After the fast opening of the pore up to its maximum radius, the inner liquid of the vesicle starts leaking very slowly through the pore. Inasmuch as the pore radius changes very slowly, we make the quasi-static approximation rσ ≈ 𝒯 from Eq. 3. Equally slowly changing is the surface tension, σ: the leaking out of the liquid tends to relax σ, whereas the slow closure of the pore works in the opposite direction. The net result is that σ remains very small, and is nearly constant (increasing very slightly) over the course of this regime: 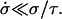After use of Eq. 2, this condition leads to:

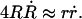(10)

From the leakout equation (Eq. 4), with σ ≈ 𝒯/r and Eq. 10, we obtain the closure equation,

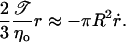(11)

Introducing r₂₃ and t₂₃ as the crossover values between stages 2 and 3, and approximating R ≈ constant, we integrate Eq. 11 to obtain:

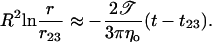(12)

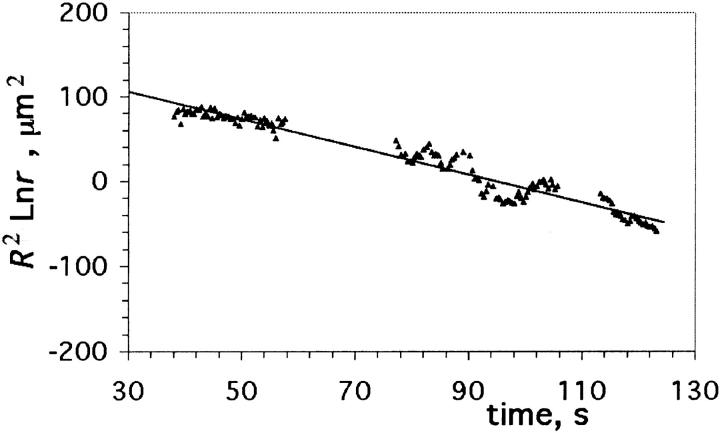
We note that a plot of R² ln r versus t in this stage should be linear with a slope −2𝒯/(3πη_o), allowing the measurement of the line tension, 𝒯, since η_o is known from independent measurements.

Fast closure

When the size of the pore becomes sufficiently small, σ becomes small compared to 𝒯/r, and Eq. 3 reduces to:

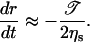(13)

Thus, the pore closes with a final velocity that is constant: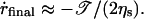

These different stages are shown schematically in Fig. 6. In principle, experimental measurements of the pore (r(t)) and vesicle (R(t)) radii should allow the determination of all the relevant parameters: the membrane viscosity, η_s, the initial membrane tension, σ_o, and the line tension, 𝒯. However, the pore opening (stage 1) and the fast closure (stage 4) occur too fast to allow a precise determination of η_s or σ_o. On the other hand, as can be seen in Fig. 4, a pore spends the overwhelming majority of its lifetime in the quasi-static leakout stage (stage 3), and we can measure the line tension, 𝒯, quite accurately from a plot of R² ln r versus t in this stage. Below, we concentrate on the experimental determination of 𝒯, first in bare DOPC lipid bilayers, then in the presence of additives which modify the line tension.

FIGURE 6.

Theoretical prediction of the pore radius, r, as a function of scaled time in the limit of slow leakout, drawn schematically. The time axis is scaled with the pore opening time, τ = 2η_s/σ_o.

LINE TENSION, 𝒯

The formation of a pore in a lipid bilayer implies the existence of a membrane edge. It is expected that the lipids near the edge reorient themselves to minimize the exposure of their hydrophobic chains to the aqueous environment. A plausible molecular arrangement is the formation of a cylindrical rim (Litster, 1975), as shown schematically in Fig. 3 (Introduction). The modified molecular packing of the lipids gives rise to an excess free energy with respect to the unperturbed bilayer. This energy, expressed per unit edge length, is the line tension, 𝒯. Experimentally, it has been rather delicate to measure the line tension, partly due to the difficulty of creating long-lived bilayer edges. Previously reported values of 𝒯 are in the range 10–30 pN for a number of lipid bilayers, based on various experimental techniques, such as osmotic shock (Taupin et al., 1975), or electroporation of either GUVs (Harbich and Helfrich, 1979; Zhelev and Needham, 1993; Moroz and Nelson, 1997) or black lipid membranes (Genco et al., 1993).

On the theoretical side, there exist two different approaches to describe the line tension. Molecular lipid models (Israelachvili et al., 1980) usually start with defining geometrical parameters to characterize the lipids which are then allowed to interact with one another through both attractive (hydrophobic) and repulsive forces (head group repulsion, hydration forces, etc.). In more elaborate molecular lipid models, the lipid chains may possess a conformational energy as well (May, 2000).

The second approach is to use the membrane elasticity theory to calculate 𝒯. In this approach, one regards the membrane edge as an elastic deformation of a lipid monolayer (Helfrich, 1973, 1974; Chernomordik et al., 1985). Membrane elasticity theories are strictly valid only if the deformation of the membrane is sufficiently small. Thus, application of such a model to calculate the line tension (wherein the deformation involves curvatures of the order of the reciprocal bilayer thickness) may be questionable. Nevertheless, we may expect to obtain correct scaling laws.

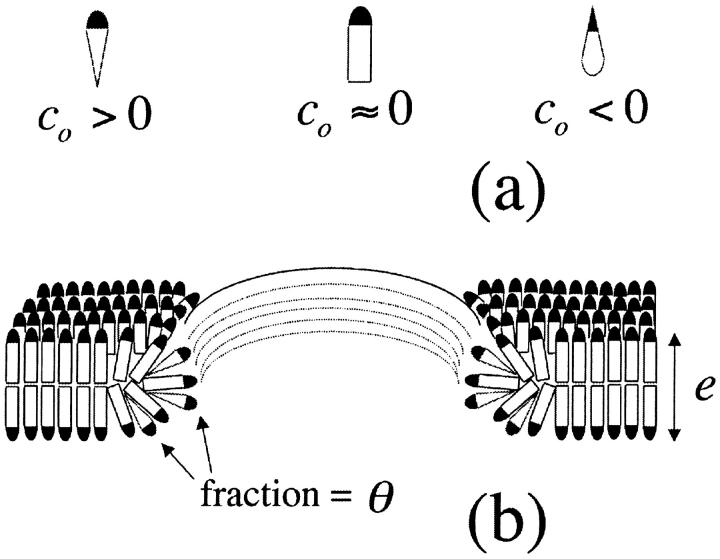
We are interested, in particular, on how the line tension, 𝒯, would be modified by the addition of molecules which stabilize or destabilize the pore edge. Let us consider a bilayer edge, composed of phospholipid molecules possessing spontaneous curvature 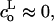and a small fraction, θ, of inclusion molecules having roughly the same equilibrium head group area as the lipids but a nonzero spontaneous curvature, c_o, which can be either negative or positive (Fig. 7). Assuming that the contributions of the individual components of the bilayer to the spontaneous curvature are additive, the mean spontaneous curvature in the rim is θc_o. Considering the monolayer as an elastic sheet with bending modulus κ, and assuming that the molecules at the edge of the pore organize in a semicylindrical rim, the bending energy, integrated over the rim surface, is E_rim = (κ/2) (2/e + 1/r − θc_o)²π²er, where e/2 is the monolayer thickness, and r the pore radius (Fig. 7). Equating this bending energy to the line tension integrated over the pore perimeter, E_line = 2πr𝒯, we obtain 𝒯 = (πeκ/4) (2/e + 1/r − θc_o)², which becomes (Chernomordik et al., 1985), in the limit 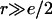and dilute inclusions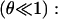

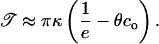(14)

Thus, the line tension is proportional to the difference between one-half the curvature of the membrane edge (1/e) and the mean spontaneous curvature (θc_o). Before proceeding further, let us make a few remarks on Eq. 14. First, the fraction θ in this equation refers to the fraction of inclusion molecules in the semicylindrical rim around the pore. This fraction may be different from that in the unperturbed regions of the bilayer, θ_m, especially in the case of inclusion molecules, such as sodium cholate (Fig. 9), having a high “edge activity” (Inoue, 1996). An extreme example is the edge-active protein talin, which localizes only at membrane edges (Saitoh et al., 1998). Secondly, in general the bending modulus, κ, will be modified in the presence of inclusion molecules. However, we may hope that this modification will be small if the inclusions are dilute. Bearing these qualifications in mind, we will analyze our results below in light of Eq. 14.

FIGURE 7.

(a) Spontaneous curvature. Detergents typically have c_o > 0, whereas phospholipids have c_o ≈ 0. Some molecules, such as cholesterol, can be modeled as inverted cones and possess negative spontaneous curvature. (b) A fraction θ of molecules with nonzero curvature, c_o, in the rim of a pore's edge in a bilayer composed of lipid molecules having zero spontaneous curvature. The mean curvature in the rim is θc_o.

Line tension of bare DOPC bilayers

We first consider the case of “bare” DOPC bilayers, in which the membrane is devoid of any additives, except for the presence of the fluorescent probes (whose spontaneous curvatures are ≈0, due to their structural similarity with double chained lipid molecules).

In the previous section, we have seen that a plot of R² ln r versus t in the quasi-static leakout regime should be linear with a slope k = −2𝒯/(3πη_o), from which 𝒯 can be obtained readily, after using η_o = 32.1 ± 0.4 cP, measured independently (see Materials and Methods) for our samples which contain 66% v/v glycerol.

Linear portions of plots of R² ln r versus time are shown in Fig. 8 a for bare DOPC vesicles of various sizes. As an example let us consider the data for a vesicle of initial radius R_i = 13.8 μm (inverted triangles in the inset of Fig. 8 a). A least-squares fit to this set of data (0.28 s < t < 2.4 s) yields a slope k = −48.77 μm²/s, from which we infer 𝒯 = 7.3 pN. Repeating this analysis for data for other vesicles and pores shown in Fig. 8 a and averaging, we obtain 𝒯 = 6.9 ± 0.42 pN for bare DOPC bilayers. Note that despite the important variation of vesicle sizes, the plots yield the same slope within experimental error, for a given bilayer composition.

FIGURE 8.

Linear portions of R² ln r versus time plots for different DOPC/cholesterol compositions. (a) Bare DOPC vesicles, of initial sizes R_i = 10.0–40.3 μm. The data for the two smallest vesicles (R_i = 10.0 and 13.8 μm) are shown in detail in the inset. (b) Vesicles containing 10 mol % (or 5 weight %) cholesterol, with R_i = 18.7–24.2 μm. (c) Vesicles containing 20 mol % (10 weight %) cholesterol, with R_i = 10.1–26.0 μm. (d) Vesicles containing 30 mol % (15 weight %) cholesterol, with R_i = 10.4–12.9 μm.

It should be mentioned that measurements of the line tension are quite sensitive to the presence of small impurities which may be inserted into the pore's edge. This is in line with the observations of Harbich and Helfrich (1979) who measured lower 𝒯 values for lipid samples which were aged. In our case, we have consistently measured similar values of 𝒯, provided the lipid was purchased through the same supplier. Thus, the values reported above were obtained for DOPC supplied by Sigma (Saint Quentin Fallavier, France), while using DOPC from Fluka (Saint Quentin Fallavier, France) or Avanti Polar Lipids (Alabaster, AL, USA), we have measured 𝒯 = 20.7 ± 3.5 pN. Thus, in our studies of the effect of inclusion molecules of the line tension reported below, we were careful to use the same supplier for a given set of (comparative) measurements. We speculate that the differences in line tensions obtained using lipid from different suppliers may be due to the presence of small amounts of impurities.

Cholesterol increases the line tension

Cholesterol, shown in Fig. 9, is a central component in the regulation of the properties of eukaryotic cell membranes (Simons and Ikonen, 2000; Rukmini et al., 2001). It can be modeled as an inverted cone (Israelachvili et al., 1980; Carnie et al., 1979) (spontaneous curvature c_o < 0), and is thus expected to increase the line tension according to Eq. 14.

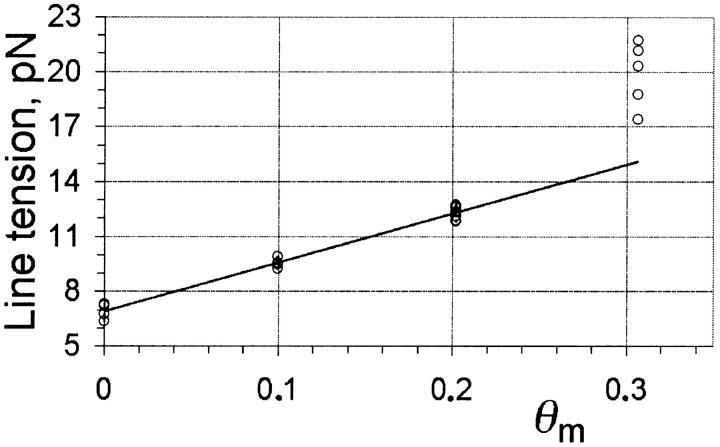
Inferring the line tension from the slopes of R² ln r versus t plots shown in Fig. 8 for a number of different vesicles and pores in the presence of varying amounts of cholesterol we have obtained the results shown in Fig. 10. For this set of experiments, we have used DOPC supplied by Sigma, and co-cast the cholesterol at given mole fractions with the lipid before the electroformation of the vesicles (see Materials and Methods). Thanks to this procedure, and due to the low solubility of cholesterol in the aqueous phase, we may assume that all the cholesterol that was co-cast with the lipid is incorporated into the bilayers. The cholesterol mole fraction in Fig. 10 refers to the nominal fraction (θ_m) of cholesterol co-cast with lipid before the formation of vesicles, which may differ from the actual fraction of cholesterol around the pore edge, θ. We see from Fig. 10 that the line tension increases linearly up to ∼θ_m = 0.20, then appears to increase more rapidly for higher cholesterol content. The higher dispersity of data points for θ_m = 0.30 is explained in part by the increased uncertainty in the determination of the line tension due to shorter pore lifetimes at higher cholesterol content (see Fig. 8 d; the effect of the line tension on pore lifetimes will be discussed shortly). Another possibility for the higher dispersity of data points at 0.3 mol fraction cholesterol is that we may be close to the solubility limit of cholesterol in DOPC bilayers. In fact, when we tried to incorporate 50% cholesterol in the bilayers we obtained precipitates of cholesterol.

FIGURE 10.

Line tension, 𝒯, as a function of cholesterol mole fraction, θ_m, for DOPC vesicles. The straight line is a least-squares fit for 0–0.2 mol fraction cholesterol (𝒯_fit = 26.7 θ_m + 6.90, R² = 0.98). (mass fraction cholesterol ≈ θ_m/2.)

If we assume that the fraction of cholesterol in the unperturbed membrane is the same as the fraction around the pore (θ = θ_m), we can attempt to analyze the results of Fig. 10 in light of Eq. 14. As predicted by this equation for an inclusion compound having a negative spontaneous curvature, at small θ the line tension 𝒯 increases linearly for increasing θ. Fitting a straight line through the data points for 0 ≤ θ ≤ 0.20 yields 𝒯 = 26.7 θ + 6.90, with a correlation coefficient of 0.98 (Fig. 10). Comparison with Eq. 14 provides κ ≈ 0.9 × 10⁻²⁰ J and c_o ≈ −0.9 nm⁻¹, after using a bilayer thickness e ≈ 4 nm.

For comparison, published values of the bending moduli κ range between (2–40) × 10⁻²⁰ J for a number of phospholipid bilayers in their fluid state (Lipowsky, 1995). In particular, for DOPC monolayers, Chen and Rand (1997) have measured κ ≈ 4.0 × 10⁻²⁰ J. The value of κ we have estimated thus seems to be somewhat lower than those previously reported. However, as noted above, when we use DOPC from Fluka or Avanti Polar Lipids, we find 𝒯 = 20.7 ± 3.5 pN (for bare DOPC bilayers), i.e., a value ∼3 times larger than what is measured using DOPC supplied by Sigma. Thus, we estimate κ ≈ 2.7 × 10⁻²⁰ J, using 𝒯 ≈ 21 pN, measured using DOPC from Fluka or Avanti Polar Lipids, after making use of κ ≈ 𝒯e/π from Eq. 14 at zero cholesterol content. This value for the bending modulus κ is in quite satisfactory agreement with the measurements of Chen and Rand (1997).

As for the spontaneous curvature of cholesterol, using x-ray diffraction and the osmotic stress method in DOPC/cholesterol inverted hexagonal phases, Chen and Rand (1997) have found c_o = 2/R_curv ≅ −0.74 nm⁻¹, where R_curv is the radius of curvature. Interestingly, they also found that cholesterol exhibits a larger spontaneous curvature when incorporated into DOPE (dioleoylphosphatidylethanolamine) phases (c_o ≅ −0.88 nm⁻¹). Meanwhile, Carnie et al. (1979) modeled cholesterol as having a hydrocarbon volume ν = 400 ų, optimum head group area a = 19 Ų, and a critical chain length l_c = 17.0–17.5 Å, which results in a packing parameter f ≡ ν/(al_c) ≅ 1.20–1.24. This corresponds to a spontaneous curvature c_o ≅ 0.11–0.14 nm⁻¹, after using f ≅ 1 − l_cc_o (to first order in l_cc_o ≪1; see also Chernomordik et al., 1985).

It is known that in the presence of cholesterol, the rigidity of lipid bilayers is increased: hydrocarbon chains of the lipids are straightened, the bilayer is thickened, and its fluidity is reduced (Israelachvili et al., 1980). These effects are reflected in a corresponding increase in the bending modulus κ in Eq. 14 as cholesterol is added to the bilayer. Thus, the increase in the line tension that we observe as a function of increasing cholesterol content in Fig. 10 may be influenced by this increase in κ. However, Chen and Rand (1997) measured a bending modulus that is independent of cholesterol content for DOPC/cholesterol mixed monolayers containing up to θ_m ≈ 0.30 mol fraction cholesterol. Increasing θ_m further to 0.50 resulted in only a 30% increase in κ. Similarly, they obtained only a modest increase in the bending modulus of DOPE/cholesterol monolayers as cholesterol content was increased from 0 to 0.30 mol fraction. Chen and Rand (1997) noted that the increase they measured in the bending modulus by the incorporation of cholesterol in their hexagonal phase monolayers is much smaller than might be expected from cholesterol's increase of the area compressibility modulus in bilayers (Evans and Rawics, 1990; Needham and Nunn, 1990). Eliminating several possibilities for this discrepancy, they suggested that the difference may be due to the inadequacy of the treatment of the phospholipid monolayer as one of homogeneous mechanical properties through its thickness, with concomitant coupling of area and bending moduli.

Detergents reduce the line tension

Detergents are water-soluble amphiphiles which form micelles spontaneously when dissolved at a concentration above the critical micelle concentration. They can typically be modeled as cone-shaped molecules possessing positive spontaneous curvature; c_o > 0 (Fig. 7). The detergent micelles have an ability to dissolve insoluble or sparingly soluble materials in the aqueous solution by incorporating them into the micellar interior to form mixed micelles. Detergents can also solubilize phospholipids and other constituents of biomembranes. Due to this property, detergents are widely used in membranology, for example to disintegrate biomembranes to mixed micelles for isolation and purification of membrane proteins (Lichtenberg et al., 1983; Dennis, 1986; Silvius, 1992). The reverse course of action, the removal of detergent molecules from the solution of detergent/phospholipid mixed micelles by, e.g., gel filtration or dialysis, leads to the formation of phospholipid vesicles. Thus, detergents are also used in reconstituting functional membranes (Eytan, 1982; Rigaud et al., 1998) and in preparing phospholipid vesicles of controlled and homogeneous size (Ueno et al., 1984). Thanks to these important applications, the interaction of detergents with vesicles has received great attention (for recent reviews, see Inoue, 1996; Lasch, 1995; Heerklotz and Seelig, 2000).

An emerging application with great potential is the use of vesicles as drug delivery vehicles (Lawrence, 1994; Lasic and Needham, 1995; Moase et al., 2001; Cao and Suresh, 2000; Yu et al., 1999; Zasadzinski, 1997), wherein the release of drugs entrapped in the vesicle's interior becomes an important problem. Vesicles are required to act as tight containers of a given drug, and to release their cargo under desired conditions. The membrane barrier efficiency for vesicles is affected by their interaction with amphiphilic molecules, when the vesicles are delivered into physiological fluids (Inoue, 1996). Thus, it is essential for the use of vesicles as a drug delivery system to know the manner in which the vesicular cargo is released in the presence of foreign molecules. The study of how detergents affect the permeability of vesicle membranes may provide useful information about this problem.

We have studied the effect of the detergent Tween 20 (Fig. 9) on transient pores and the line tension in DOPC bilayers. Tween 20 is a common detergent used in the solubilization of membrane proteins (Kawasawa et al., 1999), having a hydrophilic-lipophilic balance of 16.7 which places it among good emulsifiers for oil-in-water emulsions (de Gennes et al., 2002). Thanks to its bulky polar head relative to its hydrophobic tail (Fig. 9 b), it can be modeled as a cone-shaped molecule with a positive spontaneous curvature, c_o > 0 (Fig. 7 a). Thus, we expect that it should insert itself into the highly curved edge of a pore, as shown schematically in Fig. 7 b. This should reduce the line tension, according to Eq. 14.

In Fig. 11, a transient pore for a vesicle of size R_o ≈ 10 μm is shown in the presence of the detergent Tween 20. A striking feature is the very long duration, over 2 min, of the pore lifetime. This is consistent with a huge reduction in the line tension, estimated to be 𝒯 ≈ 0.2 pN, from a plot of R² ln r against t, as shown in Fig. 12. For this set of experiments, we used DOPC supplied by Fluka (see Materials and Methods) for which we have measured 𝒯 ≈ 20 pN for bare (detergent-free) bilayers. Thus, the addition of Tween 20 can reduce the line tension, 𝒯, by two orders of magnitude. Pore lifetimes, t_pore, are increased by the same factor (for a given vesicle size), inasmuch as t_pore varies inversely with 𝒯: t_pore ≈ (3π/2)(η_oR_o²/𝒯) (Brochard-Wyart et al., 2000).

FIGURE 11.

A long-lived pore in the presence of the detergent Tween 20 (R_o ≈ 10 μm).

FIGURE 12.

The linear portion of a plot of R² ln r against t for the pore shown in Fig. 11, in the presence of the detergent Tween 20. The straight line is a least-squares fit, with slope −1.64, which implies 𝒯 ≈ 0.2 pN (see text).

In these experiments, a concentration gradient was used (see Materials and Methods), inspired by the work of Nomura et al. (2001), who have recently visualized effects of some detergents on topological transformations of giant liposomes in low viscosity solutions using dark-field microscopy. For the example shown in Fig. 11, the concentration of the surfactant varied from zero to 0.6 mM (∼10× the critical micelle concentration in water) across the gradient. Using another surfactant, sodium cholate (Fig. 9 b), we have observed similar increases in pore lifetimes. A difficulty with detergents is that they solubilize some of the dye and consequently increase the background fluorescence; this deteriorates the image quality.

The propensity of amphiphiles with positive spontaneous curvature for facilitating transient pore formation was already noted (Israelachvili et al., 1980) in considering the increased permeability of lecithin vesicles to ions and small molecules in the presence of lysolecithin (which is similar to lecithin, but has only one rather than two hydrophobic tails and hence possesses positive spontaneous curvature). It was also observed that addition of cholesterol possessing negative spontaneous curvature into lecithin vesicles produced the opposite effect; it reduced permeabilities (Israelachvili et al., 1980). Our direct visualization of the effects of cholesterol and surfactants on transient pores are consistent with these previous observations.

We are currently studying the effects of surfactant at much lower (sublytic) concentrations wherein the vesicles are not solubilized rapidly. The results of these studies will be reported elsewhere.

PORES AND TRANSPORT ACROSS MEMBRANES

Transient pores are intimately connected with transport across lipid bilayers. In this section we present two examples of transport through pores. The “cargo” to be transported in both cases is in fact a smaller vesicle initially residing in a larger one. This is the most convenient type of cargo, as a GUV preparation usually contains a small amount of such vesicle configurations.

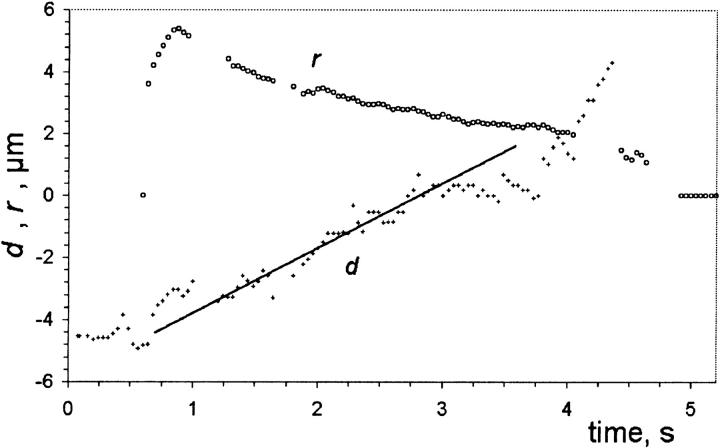
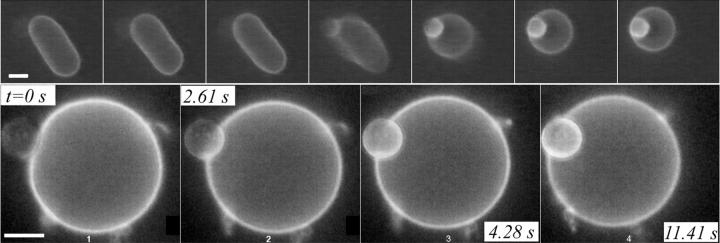
In Fig. 13 a small vesicle, of radius R_cargo ≈ 0.6 μm, marked by an arrow, is initially inside a larger one (R ≈ 16 μm, first frame in Fig. 13). When a pore appears in the container vesicle (second frame in Fig. 13, t = 0.76 s), the cargo is dragged toward the pore by the leaking fluid, eventually exiting the container vesicle just before the pore reseals (frames 3–6, Fig. 13). Inasmuch as the cargo vesicle is rather small, we may expect that it does not significantly perturb the flow field and it can be used as a rough probe of the fluid's leakout velocity. To this end, we plot the position, d, of the cargo vesicle's center with respect to the center of the pore, as a function of time, in Fig. 14. We set d = 0 when the cargo vesicle is in the middle of the pore, and d < 0 (d > 0) when it is inside (outside) the container vesicle. As can be seen in Fig. 14, d varies almost linearly with time, implying a constant velocity, V_cargo = dd/dt ≈ 2.1 μm/s. Also plotted in Fig. 14 is the radius, r, of the pore as a function of time.

FIGURE 13.

Exit of a small vesicle through a transient pore. The small vesicle (marked by an arrow) of radius R_cargo ≈ 0.6 μm is initially inside a larger one, of radius R ≈ 16 μm (first frame, t = 0 s). When a pore opens (second frame, t = 0.76 s), the small vesicle starts moving, dragged by the leaking fluid. It passes through the pore (fourth frame, t = 3.93 s) just before the pore reseals (sixth frame, t = 5.24 s). The position of the small vesicle and the pore radius are plotted as a function of time in Fig. 14. The vesicles are labeled using the dye RH237 (Fig. 5; also see Materials and Methods).

FIGURE 14.

The position of the small vesicle, d, and the pore radius, r, in Fig. 13, plotted as a function of time. We measure d from the center of the pore to the center of the small vesicle, and take d < 0 (d > 0) when the small vesicle is inside (outside) the container vesicle. The straight line is a least-squares fit to the position data for the region corresponding to the slow leakout regime (∼1.2 s < t < 3.1 s, see text). It has slope equal to 2.1 μm/s.

The leakout velocity of the fluid through the pore, V_L, is equal to V_L = Q/(πr²), where Q = 2 σ r³/(3 η_o R) is the flux through the pore of radius r (Eq. 4, Introduction). During the quasi-static leakout regime (see Life of Transient Pores), we have σr ≈ 𝒯, and the leakout velocity becomes V_L ≈ 2𝒯/(3πη_o R). Thus, we can estimate the line tension, taking V_L ≈ V_cargo: 𝒯 ≈ (3τ/2) η_o R V_cargo ≈ 5.1 pN, after using η_o = 32 cP = 3.2 × 10⁻² N s/m² and R ≈ 16 μm. This estimate of 𝒯 is slightly smaller than what is obtained from the slope of a plot of R² ln r versus time, the method presented in Life of Transient Pores (𝒯 ≈ 7.7 pN, data not shown; DOPC supplied by Sigma). This difference is perhaps not surprising: our probe is likely to move somewhat slower than the fluid surrounding it, thus reporting a fluid velocity lower than the actual value, which we would actually expect to be V_cargo ≤ V_L. The size of our probe may also be large enough to perturb the flow field, especially when it is just exiting the pore (Fig. 13) when the pore size becomes comparable to the probe size. Nevertheless, the two values of the line tension obtained by two independent ways are consistent with each other and thus provide a test of the model.

What happens if the size of the vesicle to be transported through the pore is larger than the pore size? The internal vesicle can still exit thanks to its deformable nature, as shown in Fig. 15. In this example, soon after the opening of a pore, the internal vesicle, dragged toward the pore by the leaking fluid, plugs the pore (first frame in Fig. 15). The vesicles remain in this configuration for a few minutes. However, slow buildup of further membrane tension increases the pressure inside the container vesicle, pushing the cargo vesicle further through the pore (second and third frames). We remark that the contact line between the pore's edge and the exiting vesicle must be very tight. Otherwise, some leakout would occur, reducing the pressure pushing the cargo vesicle out. Once half the cargo vesicle has passed through the pore (which process takes ∼400 s) things speed up considerably: now the force exerted by the line tension of the pore's edge works in the same direction as the pressure pushing the cargo vesicle out. Notice that the small displacement of the exiting vesicle between t = 389 s (third frame) and t = 504 s (fourth frame) removes enough volume from inside the container vesicle to relax its membrane tension considerably: large amplitude membrane fluctuations are apparent at t = 504 s (fourth frame), indicating a nearly nil membrane tension. Beyond this point the major driving force for the exit of the cargo vesicle is the line tension of the pore. An intriguing event occurs at the very end: the cargo vesicle is cut in two by the rapidly closing pore (see frames at t = 517 s and t = 520 s). The smaller cut portion remains inside the container vesicle after complete sealing of the pore. Thus, a closing pore in a phospholipid membrane may not only do work to displace a vesicle but also disrupt the integrity of another membrane!

FIGURE 15.

A vesicle larger than the pore diameter can still exit through, by deforming. (First frame), As the internal vesicle plugs the pore soon after its opening, the vesicles remain locked in this configuration for a few minutes. Buildup of further tension pushes out the internal vesicle very slowly until half of it passes through the pore. Beyond this point, the internal vesicle is pushed out both by the excess Laplace pressure and the line tension squeezing the internal vesicle. However, by t = 504 s, the exiting vesicle has removed enough volume from the container vesicle to relax its membrane tension, as evidenced by large amplitude membrane fluctuations. Thereafter it is mainly the constriction force applied by the closing pore that pushes the internal vesicle out. A portion of the exiting vesicle is cut by the closing pore (t = 517 s and t = 520 s) and remains inside after complete resealing.

CASCADES OF PORES UNDER ILLUMINATION

When a given vesicle is illuminated by the mercury arc lamp of our microscope (see Materials and Methods), a rather irreproducible induction period is required from the start of the illumination until the appearance of the first transient pore. The length of this induction period, which can vary from ∼10 min to a few hours, is determined (for fixed illumination intensity) largely by the amount and nature of lipidic structures surrounding the observed vesicle. For example, thin lipid “wires”, or tubes, connecting the chosen, large vesicle to smaller vesicles and/or lipid aggregates are often observed to be incorporated into the large vesicle by being “sucked” into it, as tension is built up. It is also likely that there exist smaller lipidic structures, that cannot be resolved optically, which may undergo similar rearrangements. This slow incorporation of the smaller structures into larger ones results in the cleaning up of the environment of the chosen vesicle (for an example, see Fig. 5 of Sandre et al., 1999). When there are no more aggregates to be incorporated into the larger vesicle to relieve tension, the vesicle becomes completely spherical, and a transient pore appears. After the appearance of this first pore, subsequent ones appear at highly regular intervals.

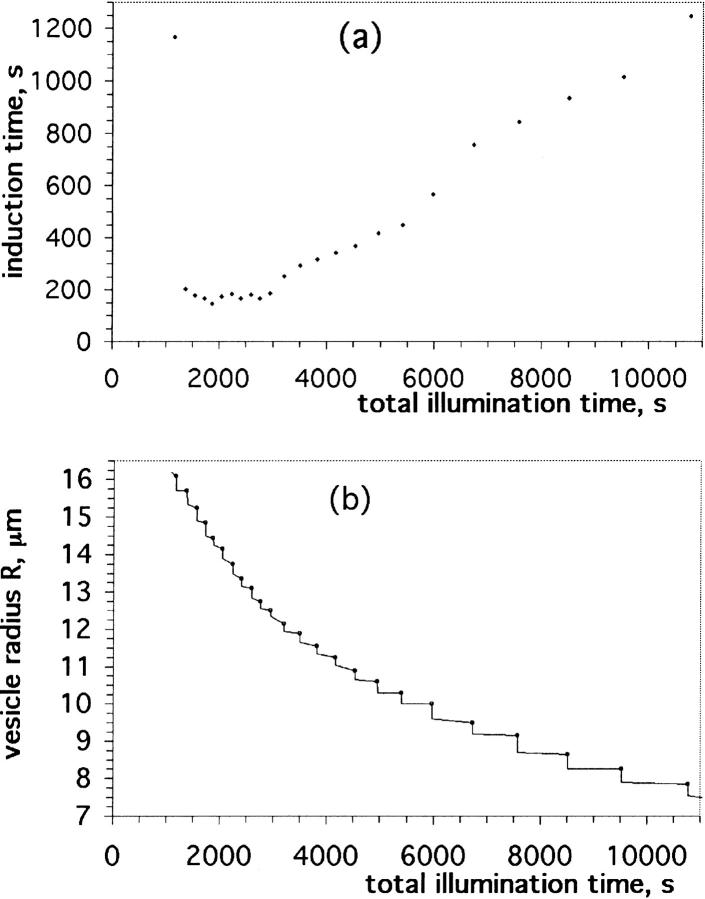
A typical observation is shown in Fig. 16 a, in which we have plotted the induction (or waiting) time between successive pores in a DOPC vesicle containing 20% cholesterol against the total time of illumination/observation. The first pore appeared 1165 s (or 19 min 25 s) after the start of the illumination. For the subsequent 10 pores, the waiting time was nearly constant and equal to ∼3 min (175 ± 15 s). After the 10th pore, the waiting time started increasing almost linearly with the illumination time. In Fig. 16 b we have plotted the vesicle radius, R, as a function of the total illumination time for the same vesicle. A series of steps are apparent in this figure. Measurements of R taken just before the opening of a pore are marked by circles. When a transient pore opens, R drops abruptly, due to the leakout of the internal liquid, until the pore reseals a few seconds later. After the sealing of a pore, the vesicle radius remains constant or decreases very slightly (below optical resolution), until the next pore appears a few minutes later. This process is repeated many times, until the vesicle becomes very small, and the waiting time impractically long (up to 20 min for the last few pores). An interesting, but unexplained feature is the appearance of little bright fluorescent spots on the vesicle membrane beyond about the 22nd pore for the vesicle considered in Fig. 16. These spots are somewhat reminiscent of “particles” observed by Kummrow and Helfrich (1996) on collapsing giant phosphatidylcholine vesicles. The particles were interpreted by these workers to consist of the more stable cubic phases of phosphatidylcholine.

FIGURE 16.

A cascade of transient pores in a DOPC vesicle containing 20 mol % cholesterol. (a) Induction, or waiting time between successive pores in a bare DOPC vesicle, plotted against the total time of illumination. (b) Vesicle radius, R, plotted as a function of the total illumination time for the same vesicle as in a. Measurements taken just before the opening of a pore are marked by circles. When a transient pore opens, R drops rapidly due to the leakout of the internal liquid, until the pore reseals a few seconds later.

Just after the sealing of a pore, the membrane tension, σ_f, is lower than its value just before the pore opening, σ_o (numerical calculations indicate σ_f/σ_o ≈ 0.3–0.4; Brochard-Wyart et al., 2000). Thus, after the closure of a pore, the vesicle must recover its membrane tension to σ_o before the subsequent pore can appear. Inasmuch as R does not vary significantly between two successive pores, we conclude that the tension buildup is due to a loss of membrane surface, presumably in the form of small-sized lipidic aggregates not resolvable optically. We remark that the radius R measured by optical microscopy is a rather poor estimate of the true lipid surface area because of the unresolved excess area contained in thermal fluctuations. Thus, the true lipid area may change, whereas the measured, projected area remains constant within experimental error.

Currently, the mechanism leading to the loss of phospholipid from vesicle membranes is unexplained. To check whether the lipid loss could be due to local heating of the sample, we measured the temperature change at the illuminated region of the sample by a small thermocouple. We recorded temperature increases of 3–4°C which level off after ∼10 min, under conditions similar to those employed in the observation of transient pores in GUVs. It is unlikely that such a temperature change be relevant, except in the vicinity of a phase transition (DOPC bilayers remain fluid down to −22°C; Ladbrooke and Chapman, 1969).

We have also qualitatively tested the effect of reducing the incident light intensity by use of neutral density filters. Cutting the incident light intensity by a factor of 100 resulted in longer waiting times to tense the vesicles (a few hours), but at the end, series of transient pores appeared in DOPC vesicles. Similarly, illuminating only part of a vesicle by closing down the diaphragm of the microscope resulted in a longer wait for tension buildup, but eventually a series of pores appeared, with rather long waiting times between successive pores (several minutes).

A possible explanation for the loss of surface is the oxidation of the lipid. Most phospholipid oxidation products are lower molecular weight compounds with increased solubility in the aqueous phase (Gunstone, 1994). Oxidation can be accelerated considerably by photooxygenation, which involves interaction between a double bond and singlet oxygen produced from ordinary triplet oxygen by light in the presence of a sensitizer. Thus, photooxidized products may leave the membrane, perhaps in the form of small aggregates also containing intact phospholipid. Unfortunately, standard methods of removing oxygen are difficult to apply to our suspensions of GUVs. For example, bubbling argon gas through the solution not only damages vesicles but causes foaming due to the presence of glycerol, as well. To test whether the dye could act as a sensitizer for generating singlet oxygen we varied the lipid-to-dye ratio between 13:1 and 13:3 DOPC:RH237, hoping to see different rates of surface loss. Presumably, different rates of surface loss would result in different waiting periods between successive pores (in the early, constant period regime, see Fig. 16 a). For similarly sized vesicles, we were not able to observe any systematic variation in the waiting time as a function of the dye-to-lipid ratio. The difficulty here is that pores are formed through inhomogeneous nucleation (see Life of Transient Pores). Thus, the interval between pores is hard to reproduce: this interval is determined not only by the rate of lipid loss, but also by the nature of the nucleation defect. It would be quite useful to have a well-characterized nucleation defect to study systematically the rate of photoinduced surface loss.

We have observed cascades of transient pores using any one of the dyes di6ASP-BS, RH237, or NBD-C6-HPC (Fig. 5, Materials and Methods), with periods which are hard to relate to the nature of the dye. A good test to determine the role of dye would be to illuminate the vesicles in the absence of dye. However, in the glycerol-water mixtures we employ, vesicles are hardly visible using bright-field microscopy techniques such as phase contrast, due to the small difference between the refractive indices of the lipid bilayers and the solvent (n = 1.43 for 66% glycerol). In solutions not containing glycerol, we have rarely observed vesicles becoming tense. However, we have never observed measurable changes in vesicle sizes in such low viscosity solutions, even after several hours of intense illumination. Finally, focusing the 488-nm beam of an Ar laser (Beamlock, Spectra Physics) at the equator of a marked DOPC vesicle, we were able to tense it in glycerol-water solutions, in a way similar to Bar-Ziv et al. (1998). Further application of the laser spot on the vesicle resulted in the appearance of a series of transient pores, away from the laser spot. We were unable to correlate the period between pores with the laser intensity which was varied.

FINAL REMARKS

Opening of pores in lipid bilayers is an ubiquitous process in cellular biology, implicated in the transport of small molecules and ions across membranes and in membrane fusion. In liposome-based drug delivery applications, pores are implied in the release of the encapsulated cargo molecules.

In this article, we have concentrated on the closure dynamics of transient pores in giant unilamellar vesicles, prepared in viscous solutions (containing 66% by volume glycerol). Here, we have used optical illumination to put the vesicles under tension. Other methods, such as adhesion to a surface (Bernard et al., 2000), shearing (Guedeau-Boudeville, 2002), or the spreading of the excess vesicle membrane onto an adhesive bead (Dietrich et al., 1997) could also be used to increase the membrane tension for practical applications. Examples of the latter method are shown in Fig. 17, wherein beads covered by the polycation poly(allylamine hydrochloride) are brought into contact with DOPC vesicles, using laser tweezers (A. Fery, Max Planck Institute, Potsdam, Germany; private communication, 2001).

FIGURE 17.

Epifluorescence videomicroscopy frames of DOPC vesicles put under tension upon adhesion to beads, in water. Latex beads covered by the polycation poly(allylamine hydrochloride) strongly adhere to DOPC membranes carrying residual negative charges. (Top row), When the excess area of a vesicle is sufficiently large, a latex bead is completely covered by the phospholipid membrane. The decrease in the surface-to-volume ratio resulting from the membrane surface lost to the bead tenses the vesicle. Frames are taken (from left to right) at t = 0, 1.12, 1.72, 1.76, 1.80, 1.88, and 3.40 s. (Bottom row), When the excess area of a vesicle is limited, the bead surface is only partially covered by membrane. The bar in the first frame in each row corresponds to 3 μm. The beads, unmarked initially, are manipulated using laser tweezers. They become visible when the membrane (containing the dye di6ASP-BS) wraps around them (images by A. Fery, Max Planck Institute, by permission).

When σ reaches a sufficiently high value, a pore suddenly appears in a vesicle. During the fast opening of a pore, the inner liquid does not have time to leak out due to its high viscosity: in this regime the membrane tension is relaxed by the redistribution of the lipid over a smaller projected area. When the pore reaches its maximum radius, nearly all the membrane tension has relaxed. The remaining membrane tension is balanced by the weak restoring force, the line tension 𝒯. This balance between the opening force r σ (r is the pore radius), and the restoring force 𝒯 is retained for some time as the pore closes back slowly, thanks to the slow leakout of the inner, viscous liquid. This quasi-static regime, limited by leakout, allows us a precise determination of the line tension: plotting the quantity R² ln r versus time yields a straight line, whose slope is −2𝒯/(3πη_o), where R is the vesicle radius and η_o = 32 cP is the independently measured solution viscosity.

Using this method, we have first measured the line tension for bare DOPC vesicles. We have found that using phospholipids from different suppliers results in different measured values: 𝒯 = 6.9 ± 0.42 pN for DOPC from Sigma, and 𝒯 = 20.7 ± 3.5 pN for DOPC supplied by Avanti Polar Lipids. Then we have investigated the role of the shape of inclusion molecules on the line tension. We have shown that cholesterol, which can be modeled as an inverted cone-shaped molecule, increases the line tension. From this increase we have estimated the spontaneous curvature of cholesterol to be c_o ≈ −0.9 nm⁻¹, a value somewhat larger than that measured by Chen and Rand (1997) (c_o ≈ −0.74 nm⁻¹) using x-ray diffraction and the osmotic stress method in DOPC/cholesterol inverted hexagonal phases. We note the possibility that our measurements may be influenced by an increase in the monolayer bending modulus κ in the presence of cholesterol. However, Chen and Rand (1997) investigated the role of cholesterol on κ up to 0.5 mol fraction cholesterol in DOPC monolayers and (somewhat surprisingly) found only a modest increase, and this only beyond 0.3 mol fraction.

We have demonstrated that the detergent Tween 20, with a large polar head group, relatively small hydrophobic tail, and thus possessing positive spontaneous curvature, has the opposite effect on the line tension: 𝒯 is reduced in the presence of detergent. We have shown that the reduction in 𝒯 can be by up to two orders of magnitude. Consequently, pore lifetimes, 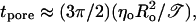are increased up to several minutes (for typically sized vesicles, R_o ≈ 10–30 μm).

Quantitative analysis of our data in the presence of detergent is complicated by several factors. First, unlike cholesterol, the detergent has significant solubility in the aqueous phase. Thus, it is not trivial to estimate its fraction in the vesicle membranes. Secondly, at the concentrations of detergent employed, the vesicles become fragile, and are solubilized in the course of several hours. Thus, to see the immediate effect of the detergent on the vesicles we used a concentration gradient. This makes it difficult to quantify the total concentration of detergent in the vicinity of a given vesicle.

Some of these difficulties can be overcome by using lower concentrations of detergent (the amount of lipid is fixed). When sublytic concentrations of detergent are used, vesicles are not solubilized. Thus, homogeneous mixtures of detergent and vesicles, at known total detergent concentration, can be prepared before observation. The phase behavior of detergent/vesicle mixtures is also simpler, and analogous to Langmuir adsorption, at low detergent content. We have recently started investigating the variation of the line tension at sublytic detergent concentrations. The results of this study will be reported in a future article.

In our discussion of the effect of inclusion molecules on the line tension, we mentioned the possibility that the pore edge may be enriched or depleted in inclusion molecules compared to their fraction in the unperturbed regions of the bilayer. In fact, we expect that the energy of a molecule with c_o < 0 (c_o > 0) should be higher (lower) at the bilayer edge. Thus, cholesterol, having c_o < 0, should be depleted at the edges of the pore compared to its number density in the unperturbed bilayer. Conversely, the pore edge should be enriched in molecules with c_o > 0, such as Tween 20. This problem will be treated quantitatively in a forthcoming article.

We presented examples of how cargo can be transported through transient pores. The cargo in the first example given was a small vesicle whose exit velocity allowed us to have an independent estimate of the line tension, 𝒯, which was found to be consistent with the value obtained using the “standard” method, from the slope of a plot of R² ln r versus time. In the second example, the cargo was again a vesicle, but with a size larger than the pore diameter. This large vesicle could pass through the pore only after deforming considerably. A remarkable observation was that the sealing pore cut the exiting vesicle in two smaller vesicles, with the smaller one remaining inside the container vesicle.

Finally, we presented a peculiarity of the transient pores: these appear in series in a given vesicle, with regular time intervals between two successive pores. Two regimes are observed: first, the waiting time between pores is constant for about a dozen pores, then it increases almost linearly as a function of the observation time. We have argued that the increase of the membrane tension is due to a loss of lipid from the vesicle membrane. However, the mechanism of this loss is unexplained for the moment. In their studies of lipid bilayers (not containing any dye) excited by laser tweezers, Bar-Ziv and colleagues also observed loss of vesicle surface area (Bar-Ziv et al., 1995, 1998; Moroz et al., 1997). Their interpretation is that lipid is pulled into the optical trap by the familiar dielectric effect, is disrupted, and finally is repackaged into an optically unresolvable suspension of colloidal particles. In our studies using a microscope lamp with a much lower photon flux, the loss of surface is quite unlikely to be due to the same mechanism.

We have been able to visualize transient pores only in sufficiently viscous solutions. If the inner liquid is a low viscosity liquid, such as water, leakout through a pore becomes fast and limits the size and lifetime of pores, making it difficult to visualize them (Brochard-Wyart et al., 2000; Sandre et al., 1999). However, the presence of pores in such systems have been suggested by indirect measurements: anomalously high permeation rates, explained by the presence of small, transient pores, have been observed for vesicles tensed by adsorption in water (Sandre et al., 1999; Guedeau-Boudeville et al., 1995; Bernard et al., 2000). Other researchers have been able to visualize long-lived, large pores in low viscosity solutions by creating the pores by electroporation, and maintaining large membrane tensions using micropipette aspiration (Zhelev and Needham, 1993; Moroz and Nelson, 1997). If the driving force for pore opening, the membrane tension, is allowed to relax, as is the case with freely floating vesicles, then pores would be aborted before reaching observable sizes in water.

Lipid membranes do not like having edges. They possess a self-healing capacity: if punctured, a membrane reseals itself. This is essential for maintaining the integrity of all membranous cellular compartments and hence for maintaining life itself. This amazing capacity of lipid membranes is due to the line tension. Despite its foremost importance, the line tension has received little attention in the past, partly due to a lack of a convenient, simple, and robust method for its measurement. We hope that the method described here will help in filling this void.