Statistical Analysis of Fluorescence Correlation Spectroscopy: The Standard Deviation and Bias

Abstract

We present a detailed statistical analysis of fluorescence correlation spectroscopy for a wide range of timescales. The derivation is completely analytical and can provide an excellent tool for planning and analysis of FCS experiments. The dependence of the signal-to-noise ratio on different measurement conditions is extensively studied. We find that in addition to the shot noise and the noise associated with correlated molecular dynamics there is another source of noise that appears at very large lag times. We call this the “particle noise,” as its behavior is governed by the number of particles that have entered and left the laser beam sample volume during large dwell times. The standard deviations of all the points on the correlation function are calculated analytically and shown to be in good agreement with experiments. We have also investigated the bias associated with experimental correlation function measurements. A “phase diagram” for FCS experiments is constructed that demonstrates the significance of the bias for any given experiment. We demonstrate that the value of the bias can be calculated and added back as a first-order correction to the experimental correlation function.

INTRODUCTION

Fluorescence correlation spectroscopy (FCS) is a powerful technique for measuring diffusion coefficients and chemical reaction rates both in vivo and in vitro. The fundamental idea of these experiments is to measure the relaxation of spontaneous fluctuations of fluorescence from a defined volume of a sample. These fluctuations can arise from diffusion of fluorescent molecules into or out of a sampling volume defined by a focused laser, or from chemical reactions or photophysical processes.

To obtain information about conventional rate parameters one typically analyzes the fluctuations statistically by computation of a fluorescence fluctuation autocorrelation function. Knowing the mechanism by which the fluctuations occur, one can also calculate the expected correlation function. The reaction rates or diffusion coefficients are extracted by fitting the theoretical model to the experimentally determined correlation function (Elson and Magde, 1974). Hence, the accuracy with which the rate coefficients are determined depends on the statistical accuracy of the experimental correlation function.

The experimental correlation function is calculated from a finite data set and thus is only a statistical estimation of the theoretical ensemble averaged correlation function used to model FCS data. Note that the theoretical ensemble averaged correlation function is calculated assuming infinite experiment time. Due to statistical variance the measured experimental correlation function always deviates from the theoretical correlation function. When the data set is finite but very long, these deviations are random and so when the experiments are repeated many times and averaged, the average will approach the true ensemble averaged correlation function apart from systematic measurement errors. The behavior of these random deviations has been the focus of investigation by previous authors and has been included in the calculation of standard deviation for the experimental correlation functions. In contrast, when the data set is short, even when averaged over many repeats of the experiment, the final averaged result will have a systematic deviation from the theoretical ensemble averaged correlation function calculated for an infinite experiment time. This systematic deviation is called “bias,” and thus the experimental correlation function is called a biased estimator. This problem has previously been recognized for experimental correlation function calculations (Oliver, 1979; Schatzel et al., 1988), but here we present the first derivations of it in the context of an FCS experiment.

Koppel provided the first statistical analysis of the standard deviations for experimental correlation functions in FCS (Koppel, 1974). In his pioneer analysis Koppel derived analytical expressions for the standard deviation of the correlation function of fluorescence under assumptions of Gaussian statistics. The analysis assumed an exponential correlation function, and in the analysis he derived an expression for the dependence of the standard deviation of the measurements on the duration of the experiment, i.e., the data acquisition time, and the photon yield of the particles. The underlying assumption that the fluorescence signal is Gaussian is valid, however, only when the contribution of the detector to the statistics is negligible and the number of particles in the laser beam is much larger than one. Qian extended the analysis to include the contributions of the detector and the effects of a small number of molecules in the beam, both of which contribute to the Poissonian nature of the statistics of fluorescence (Qian, 1990).

Further improvements were made by considering the effects of a more realistic hyperbolic correlation function and of the contributions from different laser profiles on the statistical analysis, but only the derivations by Koppel and Qian have provided the errors for the nonzero lag times in the correlation function (Qian, 1990; Kask et al., 1997).

By the late 1980s advances in the field of light scattering pushed researchers to develop new methods for correlation function measurements, which would enable the calculation of the correlation functions over a large range of lag times (Schatzel et al. 1988). These “multi-tau” correlators calculate the correlation function using many different dwell times in comparison with the single dwell time used in earlier linear correlators. Multi-tau correlators were soon found useful in FCS experiments as they provide a logarithmic scale of lag times and facilitate evaluation of the correlation function over a wide time range (Rigler et al., 1993; Schwille et al., 1999). Wohland showed that the proper weighting of the experimental correlation function by error estimates (error bars) before fitting to a theoretical model could dramatically improve the parameter estimation of a FCS measurement. Thus knowledge about the standard deviation of the experimental correlation function was shown to be crucial for the analysis of FCS. It was also demonstrated that the theoretical estimations based mainly on Koppel's calculations fail to predict the measured errors of the correlation function (Wohland et al., 2001). The error bars for the correlation function were measured either by repetition of FCS experiments, which was both time-consuming and uninformative about the nature of the errors, or by computer simulations.

The extension of Koppel's approach used by Wohland fails to properly take into account the Poissonian nature of the fluorescence signal, the hyperbolic character of diffusion correlation functions, and the use of multi-tau correlators (Wohland et al., 2001).

An empirical solution for the noise analysis has been offered by Starchev et al. (2001), in which an empirical equation is introduced to account for the noise on FCS. Although this approach might be useful for establishing the errors on the correlation function after calibrating the instrument, it reveals little about the underlying mechanisms of noise.

In the first part of this paper we have developed a theoretical framework in which the Poissonian nature of the fluorescence signal and the effects of varying dwell times in multi-tau correlators are both taken into account. The calculations have been performed for free diffusion, and arbitrary beam profiles. Very good agreement with experimental data has been demonstrated.

In the second part of the paper we focus on the bias associated with FCS experiments. The experimental correlation function is a biased estimator of the desired ensemble averaged correlation function. Bias is a systematic error in experimentally measured correlation functions that results from limiting the data accumulation time over which fluctuations are measured. As the data accumulation time increases, the magnitude of the bias decreases and the estimator approaches the ensemble averaged theoretical correlation function calculated for an infinite data set. In general the presence of bias in experimental correlation function estimators has been recognized for many years (Oliver, 1979; Schatzel et al., 1988). Here we present a derivation of bias for FCS experiments and calculate the conditions under which the bias would be significant. A method for a first-order correction of bias errors is also included in the analysis.

THEORY OF FCS NOISE

Correlation function

A laser spot tightly focused inside the sample provides a very small excitation volume for the particles that diffuse into and out of the beam. The volume from which fluorescence is detected is further reduced by using a pinhole in one of the image planes of the microscope to reject out-of-focus light (Koppel et al., 1976). This can also be achieved through a two-photon excitation of the molecules that effectively happens only in the focal plane of the objective (Denk et al., 1990). The result is a small observation volume that can be approximated by a three-dimensional Gaussian (Rigler et al., 1993).

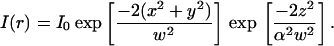(1)

I₀ is the central intensity of the laser beam; w is the radius at which the intensity in the focal plane has fallen by e⁻²; and α is the ratio of the effective beam radius along the optic axis to w. As the molecules diffuse into and out of this excitation profile, the fluorescence intensity fluctuates. Although each one of these fluctuations is stochastic, their average rate of decay toward equilibrium will be governed by the macroscopic rate constants of the sample. By making the observation volume small, thereby decreasing the number of molecules within it, the fluctuation amplitude increases. This enables the detection and analysis of the fluctuations (Elson and Magde, 1974). Here, the fluorescence at time t is represented by F(t), and to analyze the fluctuations of fluorescence, a normalized correlation function, G(τ), is defined as

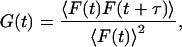where 〈F(t)F(t + τ)〉 represents an ensemble average or, equivalently, the following time average, which is independent of t inasmuch as F is assumed to be stationary,

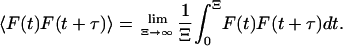The correlation function of the fluctuating fluorescence signal measured in the FCS experiment over a limited data accumulation time, Ξ, is an approximation to the ideal correlation function in which Ξ → ∞. This measured correlation function is then fitted with an appropriate theoretical model to deduce rate constants and concentrations. For a simple single component diffusion model in which m is the average number of molecules in the observation volume, the calculated correlation function is

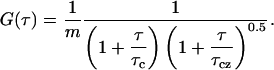(1b)

Here, 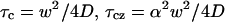, and D is the diffusion coefficient.

Statistical analysis

When the photons emitted by fluorescent particles are detected, electrical pulses are generated in the photo detector which can be stored either as individual pulse arrival times or as the number of pulses that arrive in an interval T (dwell time). The latter is used for correlation function calculations. The experimental correlation function estimator is defined as,

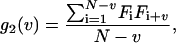(2)

in which F_i is the number of pulses counted during the interval T at time index i, and v is the lag index. To obtain information independent of laser intensity and brightness of the particles, the correlation function is normalized as follows:

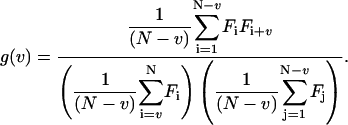(3)

This normalization is called “symmetric” normalization due to the symmetric boundary on the sums appearing in the denominator. Symmetric normalization reduces the effect of the boundary conditions on the variance of the correlation function at large lag times, and has first been implemented by Schatzel et al. (1988).

As the time for data accumulation (Ξ = NT) is finite, the experimental normalized correlation function defined in Eq. 3 becomes a biased estimator of the desired correlation function (Oliver 1979; Schatzel et al. 1988):

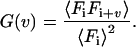(4)

Both the variance and bias of g(v) in Eq. 3, can be calculated by expanding g(v) in terms of fluctuations of fluorescence:

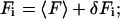(5)

inserting this into Eq. 3,

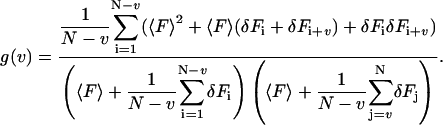(6)

By expanding the denominator one obtains:

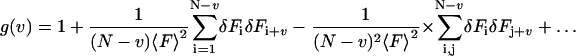(7)

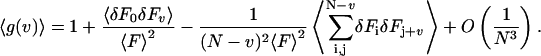(7a)

The third term represents the bias (Schatzel et al., 1988). The variance of the estimator is defined as,

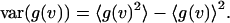(8)

The variance can be calculated by inserting Eq. 6 into Eq. 8. The denominator of the estimator must be expanded again in terms of the fluctuations, which yields

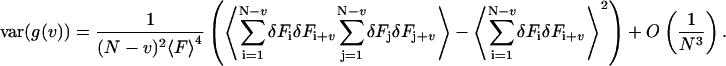(9)

Equations 7 and 9 are very general. In an FCS experiment the ensemble averages in these equations can be calculated using theoretical higher order correlation functions. To calculate these higher order moments one needs to understand the statistics of the diffusing molecules and their photon emission.

Statistics of fluorescence for simple diffusion

A sample has a total of M identical fluorescent molecules that are free to diffuse in a volume V. The molecules are completely independent of one another so that each molecule interacts only with the solvent molecules. The observation volume Ω, created by the tightly focused laser beam defined in Eq. 1, occupies only a very small fraction of the whole sample volume V.

In Equations. 9 and 7 we have expressed the variance and the bias of the normalized correlation function in terms of moments of fluctuations of fluorescence. The next step is to represent the moments of the fluctuations in terms of the moments of individual particle fluorescence, as previously shown (Saleh, 1978; Qian, 1990):

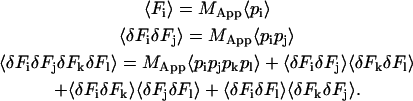(10)

Here p_i is the fluorescence of a single molecule and represents the number of photons that are detected from a single particle during the dwell time T at the index time i. When T is comparable to or larger than the diffusion time of the particles, the particles can move in and out of the beam during the dwell time. The average number of molecules that contribute to the fluorescence during large dwell times is larger than the average number in the sample volume. To take this into consideration we introduce M_App to be the apparent number of molecules in the sample during measurements with large dwell times. The concentration of molecules is simply the total number of molecules divided by the volume of the sample (M/V). During the larger dwell time the apparent concentration can be defined as (M_App/V). The number of molecules in the beam is then just the apparent concentration times the observation volume. The relation between M_App and M will be derived later.

Calculation of moments of fluorescence for single particles

The moments of fluorescence of individual particles (p) are related to the higher order diffusion correlation functions plus a shot noise contribution. This result is derived from the analysis of the diffusion of the particle through the laser profile using the probability distribution function for simple diffusion and the beam profile characteristics in Eq. 1. The motion of the molecules during the dwell time should be considered if the dwell and diffusion times are comparable. The first moment is calculated as below (Qian, 1990; Kask et al., 1997):

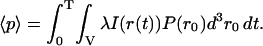(11a)

Here P(r₀) is the probability of finding the particle at position r₀, at time zero. For independent particles in the sample of volume V, this probability is equal to 1/V. λ is an optical factor that includes the absorption coefficient and quantum yield multiplied by the detection efficiency; I(r) is the laser intensity defined in Eq. 1; and r(t) is the position of the molecule at time t. The second moment of fluorescence of the single particles becomes

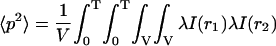(11b)

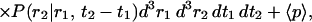in which

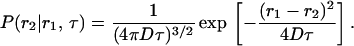(11c)

The second term in Eq. 11b is the shot noise contribution, which is related to the detector statistics (Saleh, 1978; Qian, 1990). Inserting (11c) into (11b), the second moment is calculated as

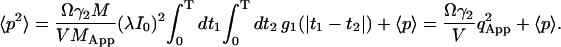(12)

Here, g₁ is the first order correlation function of diffusion:

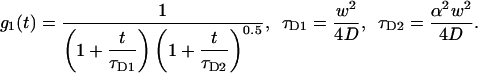(12a)

If the dwell time is short compared to the diffusion time, we can express the second moment of the particle fluorescence as (Qian, 1990),

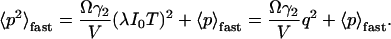(12b)

The photon yield parameter q represents the number of photons that have been detected from a single particle during the dwell time T. 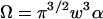is the observation volume and 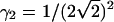is the normalized second moment of the laser intensity profile. The k′th moment is defined as

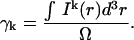(12c)

To retain the functional form of Eq. 12b and keep the notation consistent with previous work, the apparent photon yield q_App is defined in Eq. 12. The exact solution for q_App is expressed as (Palo et al., 2000)

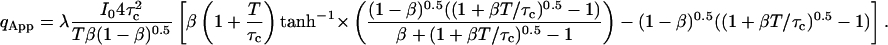(13)

Here 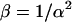and T is the dwell time. Now that we have calculated the apparent photon yield we can use it to calculate all the moments of individual particles for any dwell time T:

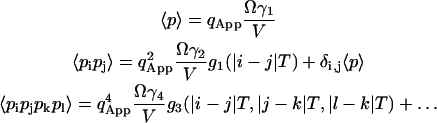(14)

For a three-dimensional Gaussian excitation intensity profile, the parameters are derived as

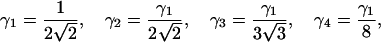and g₃ is the fourth-order correlation function for free diffusion. It is calculated using Eq. 1 and the probability distribution function of particles undergoing free diffusion.

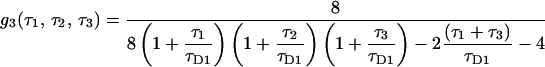(15)

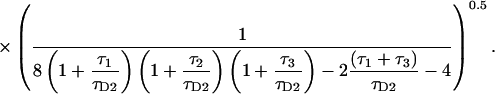To summarize, we have expressed the variance and bias of the normalized correlation function in terms of the higher moments of the total fluorescence, F, Eqs. 7 and 9. We also have derived the dependence of the total fluorescence moments on the moments of fluorescence of single molecules, p, Eq. 10. At the end we have calculated the moments of fluorescence of single molecules in terms of the higher-order correlation functions for simple diffusion in Eq. 14.

Calculation of the variance

Inserting Eq. 14 into Eq. 10, we derive the dependence of the moments of the fluorescence intensity on the higher-order diffusion correlation functions:

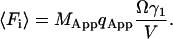(16a)

The average fluorescence count in each bin can also be directly calculated:

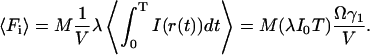(16b)

By inserting Eq. 13 into Eq. 16a, and comparing with Eq. 16b, the apparent number of particles M_App can be derived:

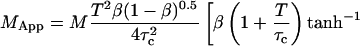(17)

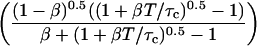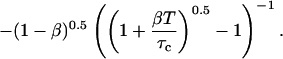The apparent number of molecules in the observation volume is the apparent concentration times the volume of the observation region which yields

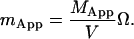(18)

Continuing with Eq. 10, the higher moments of the fluorescence become:

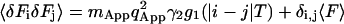(19)

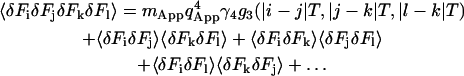(20)

in which 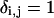when i = j and is zero otherwise.

When the moments in Eqs. 19 and 20 are introduced into Eq. 9, the summation of the fluctuation moments becomes the summation of higher-order correlation functions:

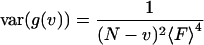(21)

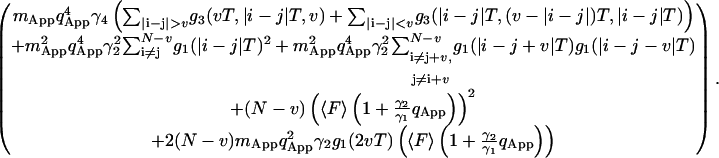It is important to note that the contributions from the first term in Eq. 21, are negligible because the fourth-order correlation function (g₃) decays to zero much faster than the second-order correlation function (Fig. 1 of Qian, 1990). For the purpose of this calculation we will neglect the first term in Eq. 21 that contains the fourth-order correlation function summation. The shot noise contributions are shown on lines 3 and 4 of Eq. 21. When the two sums on the second line of Eq. 21 are studied in more detail, it can be seen that the difference between the two should be of the order of contributions from the fourth-order correlation function. Using the above argument, the two sums in line 2 of Eq. 21 will be approximated equal:

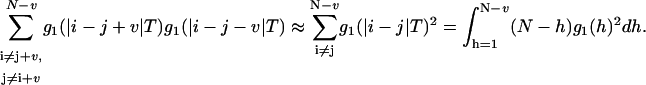(22)

The integral in Eq. 22 can be calculated using the three-dimensional correlation function in Eq. 12a:

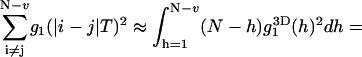(23)

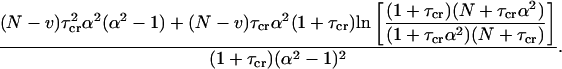Here 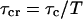. By applying these approximations, the final variance can be calculated as

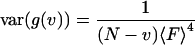(24)

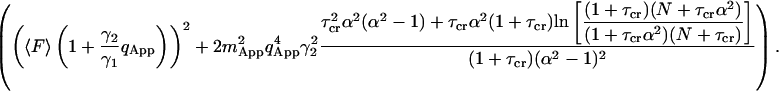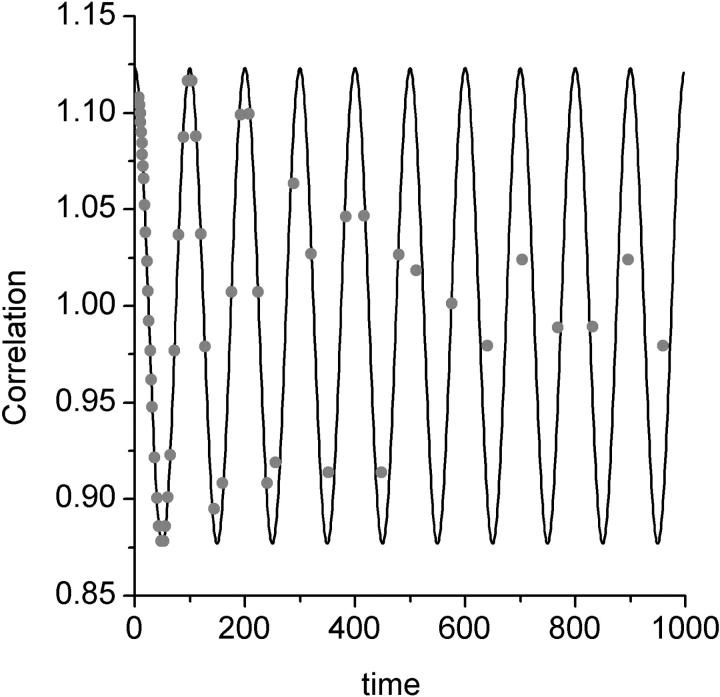
FIGURE 1.

Processing an extended oscillatory signal using linear and multi-tau correlators. The correlation function of an oscillatory signal is calculated using a linear correlator (continuous line) and a multi-tau correlator (individual data points). In a multi-tau correlator the spacing between the calculated points increases as the lag time increases. The software multi-tau correlator was designed according to Wohland et al. (2001).

The first term in this equation is the zero time, second-order moment of fluctuations of fluorescence to the power of two 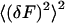. It contains a shot noise term and a particle noise term. These contributions to the noise will be discussed further in the Results section. The second part of the equation is the noise associated with correlated molecular dynamics (correlated fluctuations noise).

Calculating the bias

The bias of the experimental correlation function has been derived in terms of fluctuations of the fluorescence in Eq. 7. By inserting Eq. 19 into Eq. 7a, the bias of the correlation function becomes

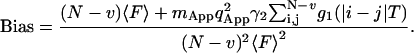(25)

Here the first term represents the shot noise contributions to the bias. To calculate the bias the sum in Eq. 25 must be executed. It can be approximated by an integral and represented as

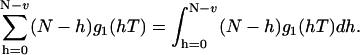(26)

The three-dimensional diffusion correlation function can be integrated in Eq. 26:

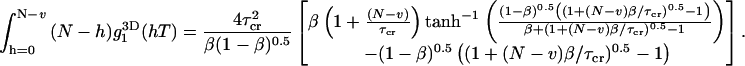(27)

The complete bias is calculated by inserting Eq. 27 into Eq. 25:

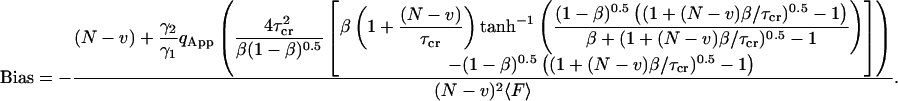(28)

Again, the first term 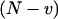is the shot noise: 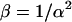and .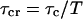

MATERIALS AND METHODS

FCS experiments

The laser beam from a titanium sapphire laser cavity, Mira 900 (Coherent Inc. Laser Group, Santa Clara, CA), pumped with a diode-pumped Verdi V-10 laser (Coherent) was used in the experiments. The repetition rate of the laser was 80 MHz, and the pulse width 120 fs. The laser light was directed to the side port of an Olympus IX 70 microscope using gold-coated mirrors. A glass filter (RG715, Chroma Technology Corp., Brattleboro, VT) was used to eliminate pump beam contamination from the laser beam. A 5× beam expander mounted on the side of the microscope expanded the beam to over-fill the back aperture of an Olympus 60× water immersion objective. The IR laser beam was reflected toward the objective using a dichroic mirror (725 dcspxr, Chroma) that reflects the IR beam. The fluorescence of the sample that passes the dichroic mirror cited above was collected using the same objective. A low-pass filter (e700SP special, Chroma) was used to filter out the remaining scattered laser light. The fluorescence of the sample was collected from the image plane at the side port of the microscope and was then collimated using a simple convex lens. The collimated fluorescence was then passed through a 50/50 beam splitter and focused onto two avalanche photodiode units (Photon Counting Module SPCM-QC, Perkin Elmer Optoelectronics, Fremont, CA). The TTL pulses generated were then collected by a correlator card (FLEX01, Correlator.com, Bridgewater, NJ), which enables both the storage of photon arrival times and real-time correlation function calculations. A test Rhodamine sample in alcohol was always used for calibration of the beam profile. All the data analysis was performed using Origin software (Originlab Corporation, Northampton, MA).

Sample preparation

Fluorescein-labeled dextran molecules (molecular weights, 150 kDa, 464 kDa, 70 kDa, and 2.5 MDa)), were obtained from Sigma (Sigma-Aldrich, St. Louis, MO). Each experiment was performed using a single molecular weight of dextran. The molecules were then dissolved in a phosphate buffer pH 7, which included 0.1 mg/ml of casein. To prevent aggregation the samples were probe-sonicated and filtered using a 20-μm sterile filter before use.

RESULTS

To understand the statistics of FCS, the details of the correlation function measurements as well as the dynamic processes that occur in the sample and the detector properties must be considered. There is a considerable freedom in the way the correlation function can be measured. In theory there are no limitations on how fast the data can be binned and how long the data can be stored, but in practice a balance between practical restrictions in the instrumentation and accuracy of the correlation functions must be taken into account. Our theoretical analysis of FCS is developed so that it can be applied to all methods of correlation function measurements. It is useful to point out the limitations of different methods for correlation function measurements.

The multi-tau correlator

In early FCS experiments the data were always analyzed with a constant dwell time. This dwell time was usually fixed by the speed of data acquisition by the correlator and was always much smaller than the correlation time of the process under investigation. In general when a correlation function is calculated, all the data collected during the longest lag time of the correlator must be stored in the memory. Thus if the lag time is much longer than the dwell time, a large number of dwells must be saved and shifted during this process. This restricts the lag time of the correlation function due to memory constraints. When a wide range of lag times is to be calculated in real time, and the speed and memory of the instrument is limited, a single dwell time design becomes impractical. To overcome this problem, multiple dwell times are used in multi-tau correlators to reduce the number of dwells that have to be stored in the memory.

A multi-tau correlator is a combination of many linear correlators, each with a different dwell time. Each linear correlator usually calculates a few lag times. The final correlation function is a combination of the results from all the linear correlators (Schatzel et al., 1988).

Although the wide range of dwell times used does solve the problem presented by the wide range of lag times, its important to know that not all the lag times are calculated using the same dwell time. When the signal is correlated with a dwell time much longer than its frequency, the signal gets effectively averaged out in each dwell time and the calculated correlation function gets damped. This is most apparent when an oscillatory signal is correlated by both a linear and a multi-tau correlator. We have demonstrated this effect by passing a sine wave through both types of correlators. In a linear correlator with a dwell time much smaller than the period of the oscillation, the correlation function is oscillatory as expected. In the multi-tau correlator the sine wave correlation is oscillatory in the timescales in which the dwell time is smaller than the period, but becomes damped at longer lag times in which larger dwell times are used (Fig. 1). In typical fluctuation relaxation measurements the dwell time is always kept at least one order of magnitude smaller than the lag times corresponding to the fluctuation relaxation time, and so the effects of filtering can be neglected when signals are not oscillatory.

This simple example demonstrates how different methods for measuring the correlation function might show drastically different results, suggesting that one must always be mindful of the properties of the correlator used. For FCS when the samples under study do not have an undamped oscillatory behavior, the application of the multi-tau correlator is well justified. In our statistical analysis of FCS we have paid direct attention to the effects of different dwell time lengths on the statistics of FCS. We begin our analysis of noise with the fastest dwell times in the multi-tau correlator.

The shot noise

One of the simple sources of noise is the detector noise also called shot noise. Detector noise is most easily observed when light of constant intensity impinges on a photodetector. The detector photocurrent is a Poisson transform of the incident intensity (Saleh, 1978). So the distribution of the measured fluorescence intensity after the detector is wider than the distribution of intensity emitted by the sample. This additional broadening that happens at the detector is called the shot noise or the detector noise, (Qian, 1990).

If the fluorescence signal is completely uncorrelated, the second moment of fluorescence fluctuations equals the mean fluorescence registered in the dwell time.

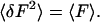(29)

Equation 29 is a special case of Eq. 19. Although the variance of the fluorescence signal grows with the average fluorescence, the ratio of the variance to signal squared decreases with increase in fluorescence signal. Thus, the higher the fluorescence signal, the lower the relative shot noise contribution.

For the purpose of this section we can simplify by assuming that the fluorescence of the sample is completely uncorrelated. This implies that,

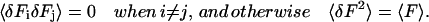(30)

Then substituting Eq. 10 into Eq. 9, the variance of the correlation function can be easily calculated as:

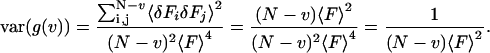(31)

By comparing this result to the complete analysis of Eq. 24, one sees that the first term in Eq. 24 includes the shot noise contribution. As expected if the sample has no correlations, the variance of the correlation function is determined only by the number of dwells and the total fluorescence in each dwell.

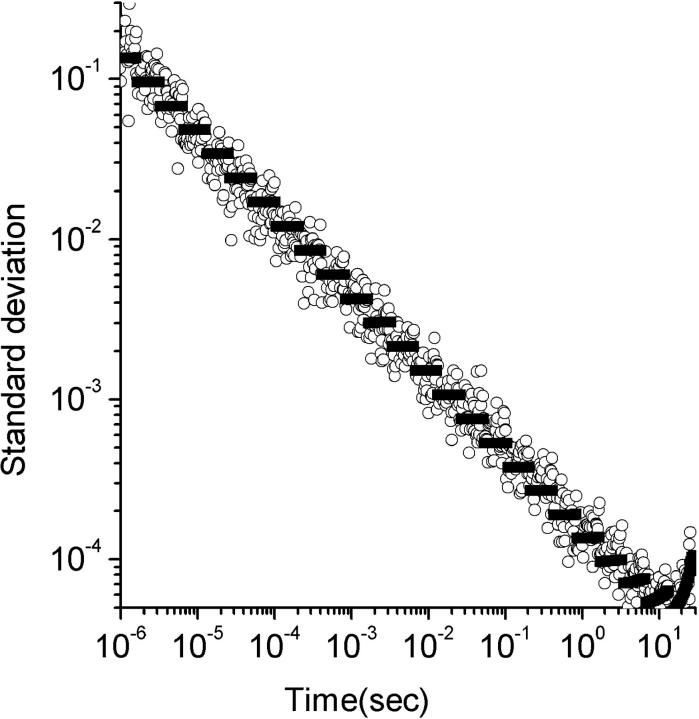
We have generated a completely uncorrelated fluorescence signal by reducing the laser intensity and increasing the fluorophor concentration so that each particle that enters the beam has a very small probability of fluorescing, and the probability of a particle emitting two photons is negligible. The agreement between the measured variance of such a sample, versus the theoretical prediction from Eq. 31, is demonstrated in Fig. 2.

FIGURE 2.

Theoretical and experimental variance for shot noise. The standard deviation is plotted versus lag times. The circles are standard deviations measured from an experimental sample as discussed in the text and the black data points are theoretical predictions from Eq. 31. The standard deviations in this experiment were completely dominated by shot noise. The experiments were performed for 30 s and were repeated 10 times for standard deviation calculations.

In a multi-tau correlator the smallest dwell times are very short, and so the average numbers of photons registered in the fast dwells are very small. The statistics of the noise at these timescales is governed by shot noise contributions described in Eq. 31.

The particle noise

In the previous section we demonstrated the effects of very small dwell times on the statistics of the noise of the correlation function. At this point we consider the very long dwell times. By a very long dwell time, we mean a dwell time that is much longer than the diffusion time of the molecules.

The very long dwell times, like the very short ones, do not correlate with one another. The correlation between any given two dwells comes from a single particle emitting fluorescence during both of those dwells. When the dwell time is very long, the probability of finding the same particle in two consecutive dwells becomes very small. Thus, the second moment of fluorescence fluctuation can be written as:

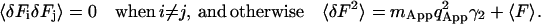(32)

Equation 32 is derived from Eq. 19. As the dwell time increases, the apparent number of molecules in the beam increases correspondingly because more molecules can diffuse in and out of the beam during the longer dwell time. At the same time the correlation between the dwells decreases inasmuch as no one molecule can be found that has stayed in the observation volume long enough to contribute fluorescence into two dwells. The calculation of Eq. 32 assumes that there is no correlation between the dwells at very long dwell times.

The apparent photon yield 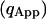increases linearly with the dwell time for very short dwell times, but reaches a saturating level after the dwell time increases beyond the diffusion time. If we use Eq. 31, and insert Eq. 10 into Eq. 9, the variance of the correlation function becomes:

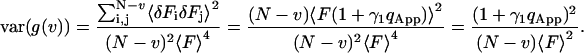(33)

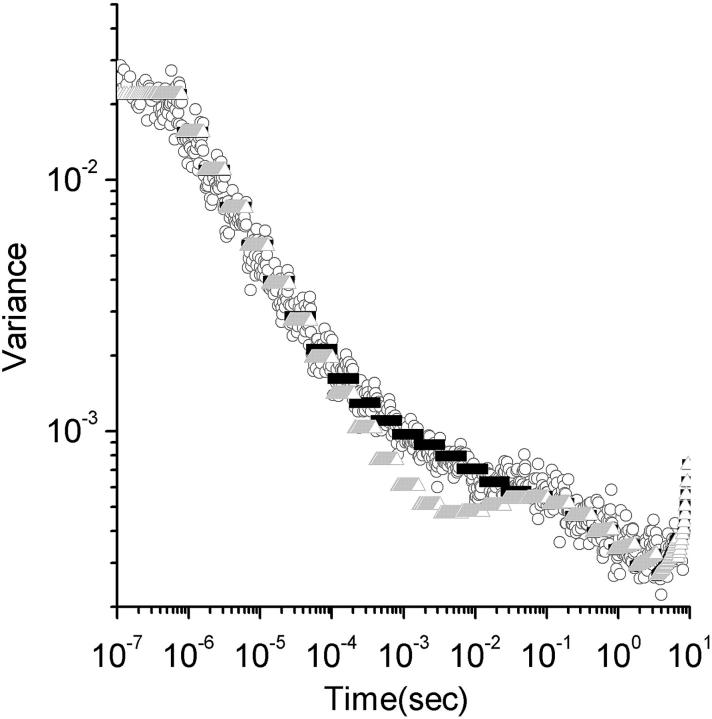
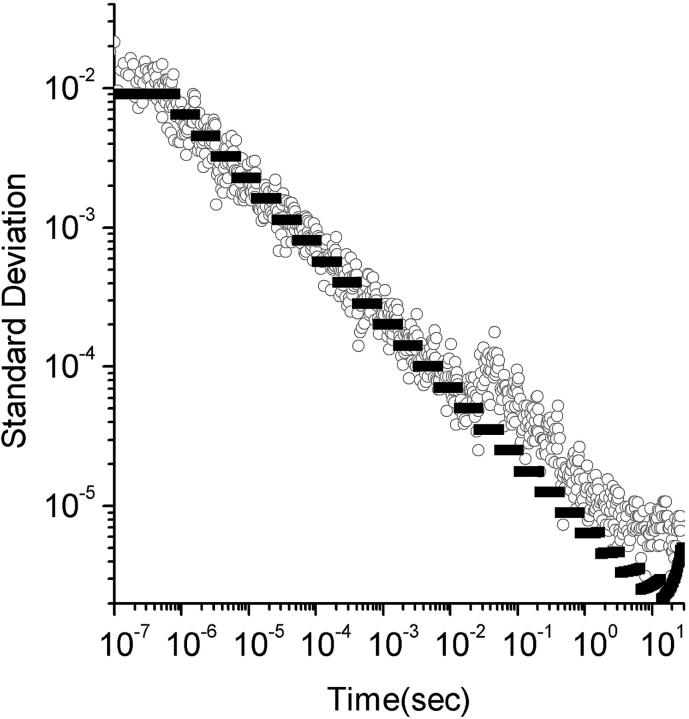
The difference between Eqs. 31 and 33 is the particle noise. The particle noise becomes important only at lag times much longer than the diffusion time of the particles. A fit to the experimental data using Eq. 33 is demonstrated in Fig. 3. As seen in the Figure, Eq. 33 captures the behavior of the noise at very short lag times as well as very long lag times.

FIGURE 3.

Theoretical and experimental variance including all noise contributions. The standard deviation versus lag time for a sample of 150-kDa Dextran molecules labeled with fluorescein. The experimental points are presented as circles. The complete analytical noise calculation are represented by the black triangles. The gray triangles are the predicted standard deviation from shot noise and particle noise without contributions from correlated fluctuations noise (Eq. 33). The theoretical points appear as black and gray bars due to their density.

The correlated fluctuations noise

When the particle emits enough photons and the dwell time is such that photons emitted by a specific particle are registered in consecutive series of dwells, the intensities in these dwells become correlated with one another. Under these conditions the sums presented in Eq. 21 become important in the noise analysis. This region of the noise analysis has been studied intensively by Koppel and others, but a detailed solution for lags greater than zero has not been found. Here we have used several approximations to reduce the complexity of these calculations without losing significant accuracy in evaluating the noise.

Our first and major approximation has been to ignore the sums in Eq. 21 which are carried over the fourth-order correlation functions. This approximation is justified because the fourth-order correlation functions decay to zero much faster than the second-order correlation functions. Thus, when summations are compared, the sums over fourth-order correlation functions are much smaller than the other terms in Eq. 21. Although this is valid in most practical cases, the fourth-order correlation functions are multiplied by m whereas the other terms are multiplied by m². Hence, the effects of the fourth-order correlation terms might need to be included if very sparse and bright molecules are studied. We have also omitted the part of the variance represented in the last term of Eq. 21. This term comes from a multiplication of shot noise and correlated fluctuations noise, but its effects will be negligible inasmuch as, when the shot noise is dominant, the correlated fluctuations noise is small, and vice versa. The complete theoretical representation of the variance in Fig. 3, in which all the sources of noise have been considered, agrees well with the experimental data.

The analysis of signal to noise

The signal-to-noise ratio has been calculated using Eq. 24 and is presented as

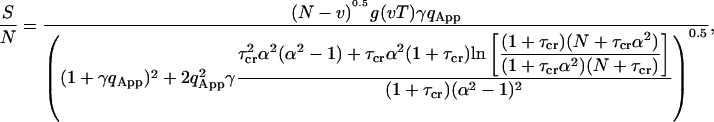(34)

in which 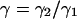. Equation 34 is independent of the number of molecules in the beam as observed by Koppel. This is so because the contributions of the fourth-order correlation functions in Eq. 21 have been ignored. When the analysis is extended to low concentrations of highly fluorescing molecules, the fourth-order correlation terms must be considered. Then the signal-to-noise ratio will depend on the number of particles (Qian, 1990).

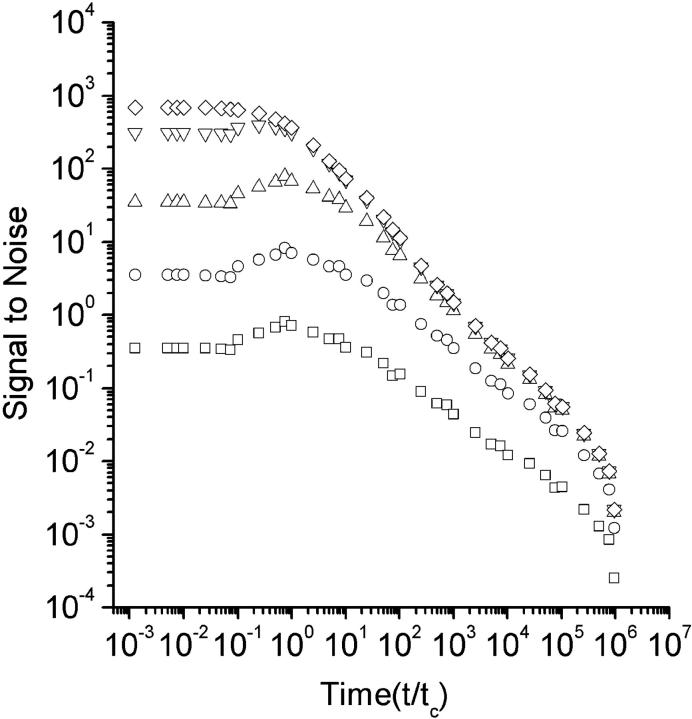
The signal-to-noise derived in Eq. 34 is a function of the photon yield per particle and the total experiment time. We have calculated the signal-to-noise for different photon yield parameters in Fig. 4. As seen in the Figure, increasing the photon yield per molecule increases the signal-to-noise. In theory, even without shot noise the signal-to-noise is always limited by the statistical error due to the finite experiment time and the stochastic nature of fluorescence fluctuations. When the photon yield is increased, the signal-to-noise ratio approaches its statistical limit faster at the long lag times. When the emitted intensity reaches a critical 1-photon-per-molecule per correlation time, the signal-to-noise in the range of the diffusion time approaches its limit (Koppel, 1974). It is important to know that even under these conditions the faster lag times are still below saturation and a much higher photon yield is needed to saturate the whole range.

FIGURE 4.

Theoretical signal-to-noise for various photon yields. The signal-to-noise, as defined in Eq. 34, is plotted versus all the lag times normalized to the diffusion time. The plots represent signal-to-noise values for different photon yields. For the symbols □, ○, ▵, ▿, and ◊, the photon yields are 0.01, 0.1, 1, 10, and 100 photons per particle per diffusion time, respectively.

The analysis of bias in FCS

The analysis of Eq. 7a clearly demonstrates that the measured correlation function is biased from the ensemble averaged theoretical correlation function obtained from Eq. 4. The bias can be further calculated using a three-dimensional diffusion model. Eq. 28 demonstrates the dependence of the bias on both the photon yield and total duration of the experiment. To investigate the bias we define signal-to-bias ratio (S/B) as the ratio of the normalized correlation function to the bias calculated at the diffusion time of the process:

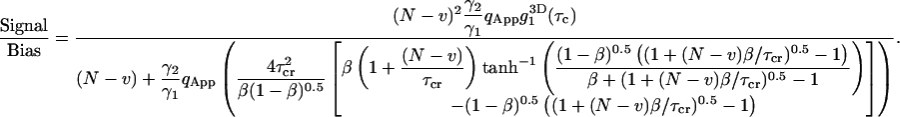(35)

Further we derive the photon yield as a function of signal-to-bias and the duration of the experiment:

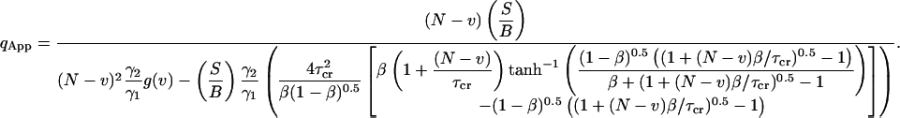(36)

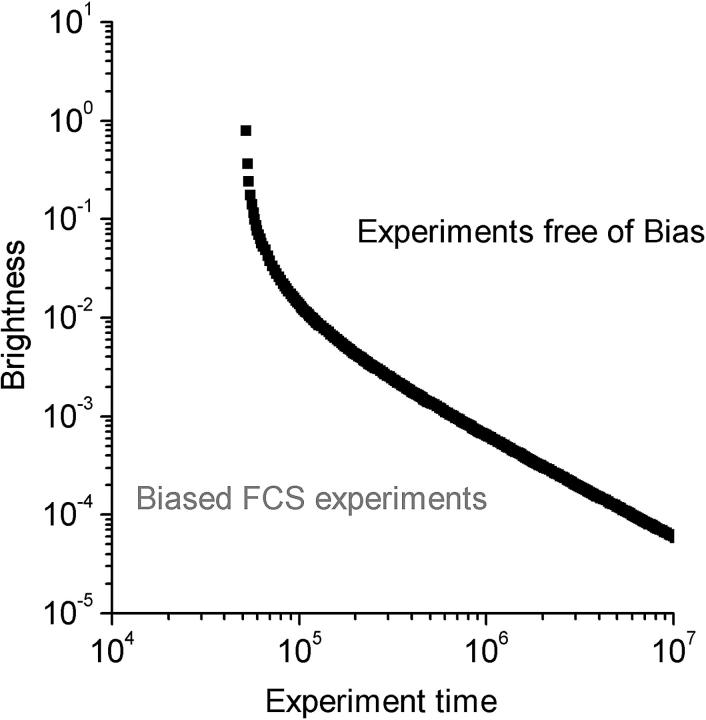
By plotting the photon yield versus the total duration of the experiment (Fig. 5), a diagram can be constructed in which each FCS experiment can be represented by its coordinates in the photon yield V_s duration plot. We call this the FCS phase diagram inasmuch as the bias of the experiment can be judged by looking at the position of the experiment in the diagram. For a specified value of S/B a plot of photon yield versus duration defines a reference curve. When the coordinates for a given FCS experiment fall on the right side of the reference curve, the S/B ratio for that experiment is higher than the specified reference value. For an experiment that falls on the left side of the curve, S/B is lower than the reference value. From experimental observations we have found the contributions of the bias to the resulting fitting parameters to be negligible for values of S/B larger than 100. Thus we would use S/B = 100 as the boundary between biased and bias-free FCS experiments.

FIGURE 5.

FCS phase diagram for analysis of bias. The FCS phase diagram as defined by Eq. 36 with the signal-to-bias = 100. The photon yield (q) is calculated for a dwell time of 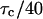. The behavior of the boundary is dominated by the shot noise when the photon yield becomes small. This plot shows that to obtain a given S/B, longer measurement times are required for lower photon yields.

To demonstrate this concept we performed FCS measurements on 2.5 MDa dextran molecules labeled with fluorescein. Three different durations for the experiments were chosen so that the longest and shortest experiments would have S/B larger and smaller than 100, respectively. The laser intensity and sample conditions were kept the same between the experiments. The resulting correlation functions were weighted by their respective errors, and a means squared data fit was performed to obtain values for the number of molecules and the diffusion time. The data presented in Table 1 show a significant decrease for the fitted value of the correlation time when the S/B was below 100.

TABLE 1.

Corrections to biased experiments

Duration of the experiments	Measured diffusion time	Signal to bias at diffusion time	Diffusion time after correction by calculated bias
3 s	3800 ± 250 μs	48	4100 ± 250 μs
10 s	4200 ± 200 μs	116	4300 ± 200 μs
30 s	4400 ± 150 μs	296	4450 ± 150 μs

The diffusion time is measured for 2.5 MDa dextran molecules in water, in conjunction with the diffusion times measured after the addition of the theoretical bias to the experimental correlation function.

Inasmuch as the actual value of the bias can be estimated from the knowledge of the diffusion time and photon yield of the fluorophores, we corrected the experimental correlation functions with the predicted bias from Eq. 28. The correlation time used in Eq. 28 was derived from fitting the initial correlation functions. The results from this secondary fit to corrected data are also shown in Table 1. The diffusion times calculated using the corrected curves do converge to the value obtained by the longest experiment, thereby corroborating the correction of the correlation function by the addition of the calculated bias.

DISCUSSION

Fluorescence correlation spectroscopy is a powerful method for characterizing the dynamics of molecular processes in systems that remain, unperturbed by the measurement, in equilibrium or in a steady state. In contrast, transient kinetic methods typically observe the relaxation of systems that have been displaced macroscopically from equilibrium. In the latter experiments the macroscopic displacement from equilibrium effectively synchronizes a multimolecular relaxation process. The conventional phenomenological rate parameters, e.g., diffusion coefficients or chemical rate constants, can be determined from a single relaxation transient to the limits of accuracy of the measurement of that transient. FCS, however, measures spontaneous unsynchronized stochastic fluctuations. Measurement of an individual fluctuation, no matter how accurate, is insufficient to determine accurately the phenomenological rate parameters. Accurate measurements require statistical analysis of many fluctuations. This analysis is embodied in the fluorescence fluctuation autocorrelation function. At the very low concentrations at which FCS experiments are typically carried out, the systems measured are effectively ideal, and so each molecule is correlated only with itself. Cross-correlations between molecules are not seen unless those molecules are linked. Hence, in FCS the average dynamic behavior of single molecules is measured without need for synchronization.

In the past, application of FCS to small labile systems such as living cells was hampered by the need to acquire many fluctuations over a period of time in which the system was not likely to remain stationary. As a result of technological improvements (Rigler et al., 1993), it has been possible to minimize the confocal detection volume, originally introduced by Koppel (Koppel et al., 1976). This has decreased the diffusion time and has made possible measurements in which small numbers, even less than one, of fluorescent molecules are present on average in the observation volume (Rigler et al., 1993, 1995; Maiti et al., 1997). Decreasing the number of fluorophores in the observation volume increases the amplitude of the correlation function (compare to Eq. 1b). The decreased diffusion time and increased fluctuation signal amplitude have decreased the time required to acquire a correlation function and so has enhanced the application of FCS to cells. Very slow fluctuations that might occur in cells or other labile systems can be filtered out by doing the experiments in very short intervals and then averaging the results (Qian et al., 1992).

From the observations above, it is clearly important to know the limit to which the experiment time can be shortened, without producing systematic errors. Also the statistical analysis of FCS is essential for obtaining accurate estimates of molecular dynamic parameters from the FCS measurements. It has been demonstrated (Wohland et al., 2001) that proper weighting of the measured correlation function by errors yields a much better estimation of the values of the dynamic parameters. Due to the lack of a complete theoretical model for the error estimation, however, it was previously necessary to measure the variance of the correlation function experimentally or to calculate it using a Monte Carlo approach. Using our analysis of noise, one can predict the errors in an FCS experiment for all the lag times of the correlation function. By knowing the errors of the experiment a priori, one can either omit repetitions of the measurement to determine variance, or one can use the theoretical values versus the experimental noise as a troubleshooting tool for finding the additional sources of noise contributing to the experiment.

As an example, we have used this approach to isolate the contributions of the laser fluctuations to our overall noise. The laser fluctuations appear as an additional source of noise at ∼0.1 s as shown in Fig. 6. The amplitude of the noise corresponding to a signal smaller than 1% rms fluctuation is well within the specifications for our titanium sapphire laser.

FIGURE 6.

Detection of small laser fluctuations. The standard deviations versus lag times (circles) were measured from an experimental sample as discussed in the text. The black data points are theoretical predictions from Eq. 31. In this experiment the average fluorescence intensity is 200 kHz, which is higher than that shown in Fig. 2. Inasmuch as the shot noise is smaller than the laser fluctuations, we can more easily observe the fluctuations in this figure than in Fig. 2.

By understanding the statistics of FCS one can optimize the experimental conditions to allow the shortest possible measurement time within the limits of required accuracy. Knowing the photon yield of the measured fluorophores, one can determine from the FCS phase diagram introduced in the last section the minimum data acquisition time consistent with an acceptable S/B ratio. Hence, when designing experiments on labile systems that require short data acquisition times, the resulting systematic bias errors can be estimated and possibly kept to an acceptable level.

In some systems, however, e.g., relatively active cells, it may be necessary to use data acquisition times too short to avoid significant bias. Inasmuch as we have calculated the value of the bias for the correlation function, these fast FCS experiments can be corrected to the first order by adding the calculated bias to the measured correlation function. This method enables improved parameter estimation for experiments that have a total duration of one order of magnitude less than what would be considered bias free according to the phase diagram (Table 1).

The methods developed here can also be extended to analysis of single molecule fluorescence trajectories. Inasmuch as all the single molecules eventually photo-destruct, the total fluorescence record available for each is limited. There can be a significant bias to a correlation function calculated from these trajectories. Using an analysis similar to that presented in this paper, one should be able to predict both the bias and the noise on the correlation function. If a model is assumed for the process, the bias can be calculated and added back to the correlation function, reducing the effect of bias on parameter estimation.

In conclusion, we have derived analytical equations for calculating the variance and the bias for FCS autocorrelation functions and have validated them by comparison with experimental measurements. The most important consequence of this work is that using these equations one can substantially shorten the time required for acquisition of FCS data. The calculation of the variance at each point of the correlation function eliminates the need for repetitive measurements to obtain this information and thereby facilitates determining optimal rate parameters by fitting measured to theoretical correlation functions. Calculation of bias further accelerates FCS data acquisition both by allowing a determination of the minimum data acquisition time consistent with a specified bias level, and by enabling the correction of correlation functions obtained using brief data collection times that produce bias.