Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Apr;84(4):2137–2148. doi: 10.1016/S0006-3495(03)75020-6

Simulating Structural and Thermodynamic Properties of Carcinogen-Damaged DNA

Shixiang Yan *, Min Wu *, Dinshaw J Patel †, Nicholas E Geacintov *, Suse Broyde ‡
PMCID: PMC1302781  PMID: 12668423

Abstract

A pair of stereoisomeric covalent adducts to guanine in double-stranded DNA, derived from the reaction of mutagenic and tumorigenic metabolites of benzo[a]pyrene, have been well characterized structurally and thermodynamically. Both high-resolution NMR solution structures and an array of thermodynamic data are available for these 10S (+)- and 10R (−)-trans-anti -[BP]-N2-dG adducts in double-stranded deoxyoligonucleotides. The availability of experimentally well-characterized duplexes containing these two stereoisomeric guanine adducts provides an opportunity for evaluating the molecular mechanics Poisson–Boltzmann surface area (MM-PBSA) method for computing thermodynamic properties from molecular dynamics ensembles. We have carried out 3-ns molecular dynamics simulations, using NMR solution structures as the starting models for the 10S (+)- and 10R (−)-trans-anti-dG adducts in a DNA duplex 11-mer using AMBER 6.0. We employed the MM-PBSA method to compute the free energies, enthalpies, and entropies of the two adducts. Our complete thermodynamic analysis agrees quite well with the full experimental thermodynamic characterization of these adducts, showing essentially equal stabilities of the two adducts. We also calculated the nuclear Overhauser effect (NOE) distances from the molecular dynamics trajectories, and compared them against the experimental NMR-derived NOE distances. Our results showed that the simulated structures are in good agreement with the NMR experimental NOE data. Furthermore, the molecular dynamics simulations provided new structural and biological insights. Specifically, the puzzling observation that the BP aromatic ring system in the 10S (+)-trans-anti-dG adduct is more exposed to the aqueous solvent than the 10R (−)-trans-anti-dG adduct, is rationalized in terms of the adduct structures. The structural and thermodynamic features of these stereoisomeric adducts are also discussed in relation to their reported low susceptibilities to nucleotide excision repair.

INTRODUCTION

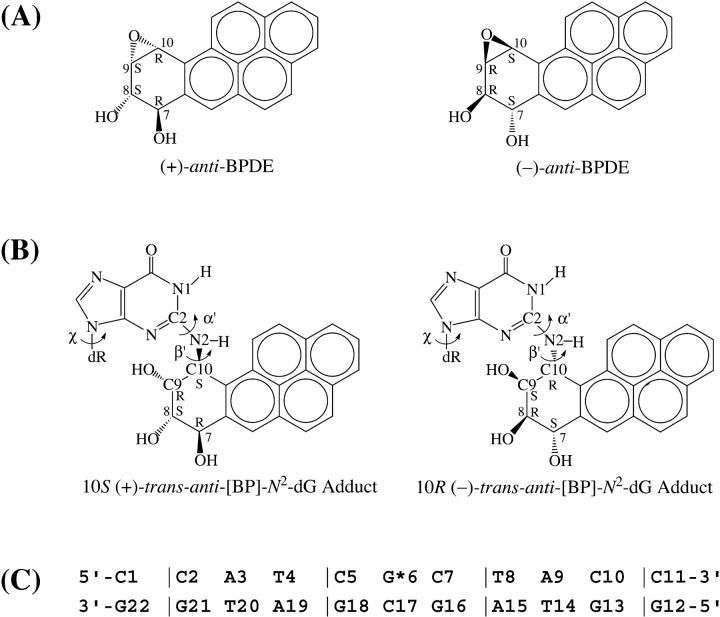
The recently developed molecular mechanics Poisson–Boltzmann surface area (MM-PBSA) methodology employs molecular dynamics (MD) simulations to generate ensembles of structures from which free energies can be calculated (Kollman et al., 2000; Beveridge and McConnell, 2000; Cheatham and Young, 2001; Srinivasan et al., 1998a). Assessing this computational technique requires a system that has been experimentally fully characterized, both structurally and thermodynamically. DNA containing guanine that is covalently modified through reaction with mutagenic and tumorigenic metabolites of benzo[a]pyrene (BP) is among the few such well-studied macromolecules. Both high-resolution NMR solution structures (Cosman et al., 1992; de los Santos et al., 1992; Fountain and Krugh, 1995) and an array of thermodynamic data (Marky et al., 1996; Ya et al., 1994) are available for such a pair of stereoisomeric 10S (+)- and 10R (−)-trans-anti-[BP]-N2-dG adducts (Fig. 1), and they therefore provide an ideal system for evaluating the MM-PBSA method. The structural and thermodynamic characteristics of these two BP adducts in the d(CCATCG*CTACC)·d(GGTAGCGATGG) duplex sequence context have been extensively and rigorously investigated experimentally by high-resolution solution NMR (Cosman et al., 1992; de los Santos et al., 1992), thermal melting (Marky et al., 1996; Ya et al., 1994), and a combination of calorimetry and magnetic suspension densimetry techniques (Marky et al., 1996). The NMR solution studies revealed that the bulky aromatic BP residues in both the 10S (+)- and 10R (−)-trans-anti-[BP]-N2-dG adducts reside in the minor groove of the DNA double helix (Cosman et al., 1992; de los Santos et al., 1992). Moreover, the 10S (+)-trans-anti-dG adduct has the BP pyrenyl ring system directed 5′ along the modified strand, whereas in the 10R (−)-trans-anti-dG adduct this ring system is oriented in the 3′ direction. In addition, thermodynamic studies of the 10S (+)- and 10R (−)-trans-anti-dG adduct duplexes in the same sequence (Marky et al., 1996; Ya et al., 1994) showed that both adducts have similar thermal stabilities, defined by the melting points Tm, which characterize the 50% dissociation point of the duplexes into single strands. Also, calorimetry revealed similar duplex formation free energies, enthalpies, and entropies (Marky et al., 1996).

FIGURE 1.

FIGURE 1

Open in a new tab

Structures of (A) (+)- and (−)-anti-BPDE and (B) 10S (+)- and 10R (−)-trans-anti -[BP]-N2-dG adducts. Torsion angles α′ and β′ are defined as: α′, N1–C2–N2–C10(BP); β′, C2–N2–C10(BP)–C9(BP). (C) Sequence context in the NMR solution structures (Cosman et al., 1992; de los Santos et al., 1992), where G*6 is the modified guanine.

The capabilities of the combination of molecular dynamics simulations and MM-PBSA free energy calculations have recently been demonstrated. A number of examples showing that the structural or thermodynamic properties of a variety of biological macromolecules can be quite well-reproduced have been published (Cheatham and Young, 2001; Cheatham and Kollman, 2000, 1996; Beveridge and McConnell, 2000; Kollman et al., 2000; Jayaram et al., 2002, 1998; Cheatham et al., 1998; Srinivasan et al., 1998a; Spector et al., 1997; Elizondo-Riojas and Kozelka, 2001; Miaskiewicz et al., 1996; Yan et al., 2001; Wu et al., 2002; Srinivasan et al., 1998b; Reyes and Kollman, 2000). However, there are few examples in which both the structural and thermodynamic properties have been experimentally examined in the same system, and compared with results obtained from MD simulations and MM-PBSA calculations. In this work, one goal is to evaluate the MM-PBSA methodology by comparing the results of these calculations with the known structures and thermodynamic properties of the stereoisomeric pair of 10S (+)- and 10R (−)-trans-anti-dG adducts. We also show that this approach provides new insights into the properties of these two adducts in double-stranded DNA that were not evident from the NMR solution structures and thermodynamic studies alone. Our previous investigation (Yan et al., 2001) of the stereochemically analogous adenine adducts, 10S (+)- and 10R (−)-trans-anti-[BP]-N6-dA, did not provide the opportunity for this type of comparison of the computational results with experiment, inasmuch as microcalorimetry data was not available on these systems, and an NMR solution structure opposite the normal partner base dT was available only in the case of the 10R (−)-trans-anti-[BP]-N6-dA isomer adduct (Zegar et al., 1996).

We have carried out 3-ns MD simulations using, as starting conformations, the NMR solution structures of the 10S (+)- and 10R (−)-trans-anti-[BP]-N2-dG adducts in a DNA duplex 11-mer in the same d(CCATCG*CTACC)·d(GGTAGCGATGG) sequence context (Cosman et al., 1992; de los Santos et al., 1992). Then we applied the MM-PBSA method (Kollman et al., 2000) to compute the free energies of the two adducts. We also calculated the NOE distances from the MD trajectories, and compared them against the experimental NMR NOE distances. Our results show that the simulated ensembles of structures are in good agreement with the NMR experimental NOE data, and our complete thermodynamic analysis agrees quite well with the experimental thermodynamic characterization of these same adducts (Marky et al., 1996). Moreover, the puzzling enhanced exposure to solvent of the BP aromatic ring system in the 10S (+)-trans-anti-dG adduct, deduced from magnetic suspension densimetry investigations (Marky et al., 1996), is structurally rationalized. In addition, we discuss the thermodynamic and structural features of the adduct pair in relation to their similar, low, yet detectable, susceptibilities to nucleotide excision repair (NER) in human cell extracts (Hess et al., 1997a), in the light of current models for recognition and excision by the nucleotide excision repair machinery, which indicate that the NER machinery responds to distortions and destabilization of the modified DNA duplexes (Wood, 1999; Sancar, 1996; Batty and Wood, 2000; Hess et al., 1997b, 1998; Sugasawa et al., 2001; Buschta-Hedayat et al., 1999).

METHODS

Starting structures

The NMR solution structures (Cosman et al., 1992; de los Santos et al., 1992) were the starting structures for the DNA duplex 11-mer in the d(CCATCG*CTACC)·d(GGTAGCGATGG) sequence context containing a 10S (+)- or 10R (−)-trans-anti-[BP]-N2-dG adduct (Fig. 1). The starting structure for the unmodified DNA duplex in the d(CCATCGCTACC)·d(GGTAGCGATGG) sequence context was an energy-minimized B-form DNA computed with DUPLEX (Hingerty et al., 1989) from a B-DNA fiber diffraction model (Arnott et al., 1976).

Force field

To obtain partial charges for the 10S (+)- and 10R (−)-trans-anti-[BP]-N2-dG nucleosides, we excised them from the NMR duplex structures (Cosman et al., 1992; de los Santos et al., 1992). We used Hartree–Fock calculations with 6-31G* basis set, without geometry optimization, to calculate the electrostatic potential, using Gaussian 98 (Frisch et al., 1998). The charge was then fitted to each atomic center with restrained electrostatic potential fitting (RESP) (Bayly et al., 1993) using the RESP module in the AMBER 6.0 suite (Case et al., 1999). The partial charges for the modified nucleotide were then obtained from the RESP charges for the modified nucleoside through our normalization protocol (Wu et al., 1999), which yields a charge of −1 on the modified nucleotide, consistent with the −1 charge for unmodified nucleotides. Bond angles added to the force field for the two adducts were assigned by analogy to chemically similar atom types already available in the parm98 parameter set (Cheatham et al., 1999). Table S1 (Supporting Information) gives the partial charges and atom types, and Table S2 (Supporting Information) gives the added force field parameters.

Molecular dynamics simulations

We carried out the molecular dynamics simulations using the AMBER 6.0 package (Case et al., 1999) with the force field of Cornell et al., (1995) and the parm98 parameter set (Cheatham et al., 1999). The particle mesh Ewald (PME) method (Darden et al., 1993; Essmann et al., 1995) was applied to treat long-range electrostatic interactions, and a 9-Å cutoff was used for the nonbonded Lennard-Jones interactions. We applied the SHAKE algorithm (Ryckaert et al., 1977) to constrain all bonds involving hydrogen atoms with a tolerance of 10−6 Å. A 2-fs time step was used in the dynamics simulations, and the translational motion of the center of mass was removed every 1 ps (Harvey et al., 1998). Removal of the global rotational motion in a periodic system is technically uncertain and hence was not implemented. However, visual inspection of the trajectories revealed no abnormal overall rotation of the DNA duplexes, indicating that energy leakage from internal motion to global rotation through the “flying ice-cube effect” (Harvey et al., 1998) is not contributing in this specific case. In all, we added 20 Na+ ions to neutralize the system using the LEap module in AMBER 6.0 package (Case et al., 1999), and then solvated the whole system with a rectangular box of TIP3P water molecules (Jorgensen et al., 1983) which extended ∼10 Å from the DNA atoms in each direction. This yielded a periodic box size of ∼50 Å × 50 Å × 65 Å for the 10S (+)-trans-anti-dG adduct, the 10R (−)-trans-anti-dG adduct, and the unmodified control structure. In total, we added 3639, 3470, and 3686 water molecules for the 10S (+)-trans-anti-dG adduct, the 10R (−)-trans-anti-dG adduct, and the unmodified control, respectively. We used the same minimization and equilibration protocols for all the systems. First, the water molecules and counterions were minimized for 1000 steps of steepest descent, followed by 50-ps dynamics with DNA fixed to relax the solvent. The whole system was then minimized for 1000 additional steps of steepest descent, followed by 3-ps dynamics with 25 kcal/mol restraints on the DNA, which further allowed the solvent to relax. The system was minimized for five rounds of 600 steps of steepest descent with the restraints on the DNA reduced by 5 kcal/mol each round, from 20 to 0 kcal/mol. Finally, the whole system was heated from 10 K to 300 K over 40 ps using the Berendsen coupling algorithm (Berendsen et al., 1984) with a coupling parameter of 1.0 ps. After an additional 20-ps unrestrained dynamics for further equilibration, production simulation was then continued at atmospheric pressure with a 1.0 ps coupling parameter and 300 K for 3 ns.

Free energy analyses

We took snapshots from the MD trajectories of the 10S (+)- and 10R (−)-trans-anti-dG adducts with water and counterions removed for the free energy calculations. The difficulties associated with inclusion of counterions have been discussed (Srinivasan et al., 1998a; Jayaram et al., 1998, 2002; Cheatham and Young, 2001). A total of 150 snapshots were selected at 10-ps intervals from each of the last 1.5-ns trajectory.

The free energy (Gtot) was estimated from the molecular mechanical energy (EMM), the solvation free energy (Gsolvation), and the vibrational, rotational, and translational entropies for the DNA, following previously developed methods (Srinivasan et al., 1998a; Jayaram et al., 1998; Cheatham et al., 1998; Kollman et al., 2000):

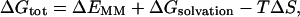graphic file with name M1.gif (1)

where T is the temperature, and S is the entropy. The molecular mechanical energy (EMM) was calculated from internal energy (Eint) stemming from deviations of the bonds (Ebonds), angles (Eangles), and dihedral angles (Edihedrals) from their equilibrium values, van der Waals interaction energy (EvdW), and electrostatic energy (Eelec), using the Anal module in the AMBER 6.0 package (Case et al., 1999):

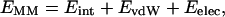graphic file with name M2.gif (2)

where:

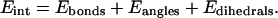graphic file with name M3.gif (3)

We applied the same force field (Cornell et al., 1995) and parameter set (Cheatham et al., 1999) used in the MD simulations to compute the molecular mechanical energy (EMM) but without cutoff for nonbonded interactions.

The solvation free energy (Gsolvation) was estimated from the electrostatic solvation energy (GPB) and the nonpolar solvation energy (Gnonpolar):

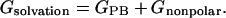graphic file with name M4.gif (4)

The electrostatic contribution to the solvation free energy (GPB) was calculated using the nonlinear Poisson–Boltzmann method (Sharp and Honig, 1990a,b), as implemented in the DelPhi program (Nicholls et al., 1990; Honig and Nicholls, 1995). This method approximates the electrostatic solvation free energy (GPB) as the reaction field energy of removing a solute from vacuum to water (Nicholls et al., 1990; Honig and Nicholls, 1995). The vacuum dielectric constant was 1, and the water dielectric constant was set to 80 (Srinivasan et al., 1998a). We employed a physiological 0.15-M salt concentration (Alberts et al., 1994) to calculate salt effect on the solvation free energies. Atomic charges for DNA and adducts are the same as those used in the molecular mechanical energy calculations (Srinivasan et al., 1998a). We applied the PARSE parameter set (Sitkoff et al., 1994) for atomic radii, and used a probe radius of 1.4 Å (Srinivasan et al., 1998a; Massova and Kollman, 2000) to define the dielectric boundary. A grid spacing of 2.0 grid/Å, in which the longest linear dimension of the solute occupied 80% of the lattice, was used to determine the size of the cubic lattice, and the boundary potentials were set to the sum of the Debye–Hückel values (Gilson and Honig, 1987). A total of 300 linear iterations followed by 1000 nonlinear iterations were performed for each snapshot to reach convergence, as further judged by the root-mean-square deviation (RMSD) between successive iterated potential maps being less than 10−5.

The nonpolar contribution to the solvation free energy (Gnonpolar) was estimated as:

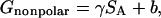graphic file with name M5.gif (5)

where γ = 0.00542 kcal/Å2, b = 0.92 kcal/mol (Sitkoff et al., 1994), and SA is the solvent-accessible surface area (SASA). We computed SASA using Sanner's algorithm implemented in the MSMS program (Sanner et al., 1996) with a solvent probe radius of 1.4 Å and the PARSE atomic radii parameters (Sitkoff et al., 1994).

Solute entropies were approximated with normal mode calculations (Srinivasan et al., 1998a,b; Cheatham et al., 1998; Chong et al., 1999; Reyes and Kollman, 2000) by using the Nmode module in the AMBER 6.0 package (Case et al., 1999), which computes vibrational, rotational, and translational entropies. We employed the following protocol: first, seven structures at 200-ps intervals were selected from the last 1.5 ns in each trajectory; then, using a distance-dependent dielectric function (ɛ = 4r, where r is the interatomic distance in Å) to mimic solvent effects, steepest descent and conjugate gradient minimizations, followed by Newton–Raphson minimizations, were carried out with no cutoff for all nonbonded interactions until the RMSD of the elements in the gradient vector was less than 10−4 kcal/(mol × Å) for each structure. Finally, we chose the minimized structure with the smallest RMSD compared to the MD average structure for each adduct, to estimate the translational, rotational, and vibrational entropies at 300 K.

Quality of Watson–Crick hydrogen-bonding, hydration, and DNA backbone torsion and helical parameter analyses

Our hydrogen bond quality index (Hingerty et al., 1989), IH, was employed to quantitatively assess the quality of Watson–Crick hydrogen bonding, in terms of the deviation from ideal Watson–Crick hydrogen bond distances and angles:

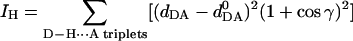graphic file with name M6.gif (6)

where dDA is the instantaneous donor–acceptor distance, 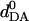Inline graphic is an ideal donor–acceptor distance (Saenger, 1984) [O6 (G) to N4 (C) is 2.91 Å, N1 (G) to N3 (C) is 2.95 Å, and N2 (G) to O2 (C) is 2.86 Å], and γ is the instantaneous D–H⋯A-bond angle with ideal value of 180°. The summation is over the Watson–Crick hydrogen bonds in any selected set of base pairs. IH adopts a value of 0 when ideal Watson–Crick hydrogen bonding is maintained over all the base pairs selected.

The solvent-accessible surface area for the BP aromatic ring system was computed and visualized using the Connolly algorithm (Connolly, 1983) implemented in the InsightII 97.0 program (Accelrys, Inc., a subsidiary of Pharmacopeia, Inc.) with a probe radius of 1.4 Å. The number of water molecules within the first solvation shell of the BP aromatic ring system was calculated with the ptraj program developed by Dr. Thomas Cheatham, using 3.4 Å as the first solvation shell boundary.

We also computed the DNA backbone torsional angles and helicoidal parameters using Dials and Windows (Ravishanker et al., 1989).

RESULTS AND DISCUSSION

MD simulations reproduce NMR-derived interproton distances

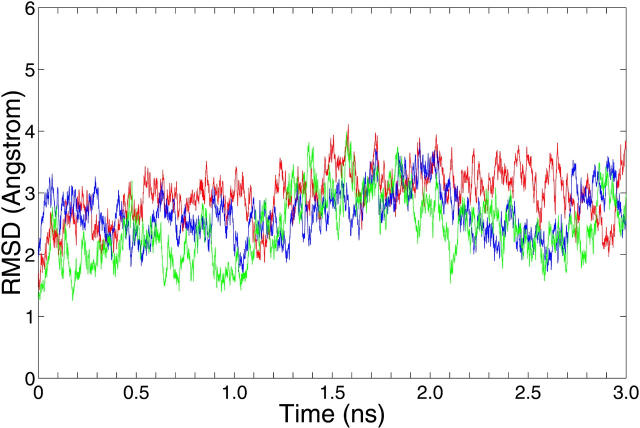
The RMSDs of the 10S (+)-trans-anti-dG adduct, 10R (−)-trans-anti-dG adduct, and the unmodified control computed relative to the NMR solution starting structures (Cosman et al., 1992; de los Santos et al., 1992) are shown in Fig. 2. The average RMSD of all atoms is 3.2 ± 0.4 Å for the 10S (+)-trans-anti-dG adduct, 2.8 ± 0.4 Å for the 10R (−)-trans-anti-dG adduct, and 2.6 ± 0.4 Å for the unmodified B-DNA control over the 1.5–3 ns time frame, respectively.

FIGURE 2.

FIGURE 2

Open in a new tab

Root-mean-square deviations (RMSDs) for the 10S (+)-trans-anti-dG adduct (red), 10R (−)-trans-anti-dG adduct (blue), and the unmodified control duplex (green) over the 3-ns production MD simulation. The RMSDs were calculated relative to the starting structures for the 10S (+)- and 10R (−)-trans-anti-dG adducts and the unmodified control duplex, respectively.

To compare our simulated structures to experimental observations, we computed our trajectory-averaged distances involving the key protons of the BP OH-containing benzylic and pyrenyl ring systems with DNA protons. These govern the positioning of the BP with respect to the DNA, and were identified in the NMR experiments. We then compared them to the experimental NMR NOE data for the 10S (+)- and 10R (−)-trans-anti-dG adducts (Cosman et al., 1992; de los Santos et al., 1992; and unpublished NOE bounds). The results are shown in Tables 1 and 2. We calculated the average distances of these interproton distances for the 1.5–3 ns time frame.

TABLE 1.

Experimental (Cosman et al., 1992) and trajectory-averaged intermolecular NOE-derived distances involving BP benzylic and pyrenyl rings for the 10S (+)-trans-anti-dG adduct.

Experimental NOE Range Computed NOE
HC11 G*6 H1′ G18 [2.76, 4.76] 4.37 (0.43)
HC9 G*6 H1′ C7 [2.03, 3.23] 2.31 (0.30)
HC10 G*6 H1′ C7 [2.81, 4.41] 4.24 (0.52)
HC2 G*6 H4′ A19 [2.94, 4.54] 3.16 (0.45)
HC9 G*6 H1′ G*6 [4.00, 6.00] 4.65 (0.49)
HC10 G*6 H1′ G*6 [2.85, 4.45] 3.74 (0.25)
HC10 G*6 HN G*6 [2.50, 4.50] 2.97 (0.06)
HC8 G*6 HN G*6 [2.00, 4.00] 2.37 (0.20)
HC9 G*6 HN G*6 [3.00, 5.00] 3.22 (0.17)
HC8 G*6 H1 G*6 [2.68, 4.68] 3.91 (0.23)
HC9 G*6 H1 G*6 [3.53, 5.53] 4.50 (0.20)
HC8 G*6 H1 G16 [3.25, 5.25] 4.69 (0.50)
HC8 G*6 H1 G18 [3.30, 5.30] 7.29 (0.37)
1HC4 G*6 H5′1 G18 [3.17, 5.17] 6.32 (0.72)
1HC4 G*6 H5′2 G18 [3.17, 5.17] 6.74 (0.73)
1HC5 G*6 H5′1 G18 [3.17, 5.17] 4.91 (0.52)
1HC5 G*6 H5′2 G18 [3.17, 5.17] 4.84 (0.57)
2HC6 G*6 H5′1 G18 [2.13, 4.13] 5.01 (0.46)
2HC6 G*6 H5′2 G18 [2.13, 4.13] 4.11 (0.41)
3HC4 G*6 H4′ G18 [2.31, 4.31] 4.46 (0.58)
3HC4 G*6 H4′ A19 [2.31, 4.31] 4.15 (0.93)
3HC5 G*6 H4′ G18 [2.31, 4.31] 2.93 (0.37)
3HC5 G*6 H4′ A19 [2.31, 4.31] 5.85 (0.86)
4HC1 G*6 H4′ A19 [2.69, 4.69] 4.09 (0.79)
4HC3 G*6 H4′ A19 [2.69, 4.69] 2.98 (0.64)
Open in a new tab

NOEs for grouped proton pairs (groups 1, 2, 3, and 4) were assigned to any one of the pair members. Consequently they have identical bounds, as they could not be distinguished (Cosman et al., 1992).

TABLE 2.

Experimental (de los Santos et al., 1992) and trajectory-averaged intermolecular NOE-derived distances involving BP benzylic and pyrenyl rings for the 10R (−)-trans-anti-dG adduct

Experimental NOE Range Computed NOE
HC9 G*6 H1′ G*6 [4.10, 5.60] 3.11 (0.29)
HC9 G*6 H1 G*6 [2.68, 4.28] 4.84 (0.17)
HC9 G*6 HN G*6 [2.20, 3.80] 3.64 (0.14)
HC10 G*6 HN G*6 [1.96, 3.56] 2.72 (0.10)
HC10 G*6 H1′ G*6 [4.20, 5.70] 4.53 (0.33)
HC10 G*6 H1′ C7 [1.98, 3.38] 2.76 (0.50)
HC11 G*6 H1′ C7 [2.14, 3.14] 2.68 (0.47)
HC11 G*6 H4′ C7 [3.63, 5.13] 4.36 (0.62)
HC11 G*6 HN G*6 [1.95, 3.55] 2.78 (0.23)
HC11 G*6 H1 G*6 [2.23, 3.83] 4.15 (0.28)
HC11 G*6 H1 G16 [2.85, 4.45] 4.69 (0.28)
HC12 G*6 H1′ C7 [3.18, 4.18] 4.04 (0.77)
HC12 G*6 H4′ T8 [1.91, 3.91] 3.44 (0.83)
HC12 G*6 HN G*6 [2.51, 4.11] 4.70 (0.22)
HC12 G*6 H1 G*6 [2.84, 4.44] 5.66 (0.32)
HC12 G*6 H1 G16 [2.58, 4.18] 4.91 (0.38)
HC4 G*6 H4′ C17 [2.80, 4.40] 4.09 (0.62)
HC4 G*6 H4′ G18 [4.00, 5.50] 4.70 (0.70)
HC5 G*6 H4′ G18 [2.86, 3.86] 2.84 (0.51)
HC6 G*6 H1′ G18 [3.78, 5.28] 3.71 (0.54)
HC6 G*6 H4′ G18 [2.25, 3.25] 2.82 (0.34)
HC1 G*6 H1′ T8 [2.16, 3.16] 3.95 (1.27)
HC1 G*6 H4′ T8 [2.22, 3.22] 3.67 (1.13)
HC2 G*6 H1′ C17 [3.59, 5.09] 5.10 (0.37)
HC2 G*6 H1′ T8 [2.37, 3.37] 6.03 (1.37)
HC3 G*6 H4′ C17 [3.25, 4.75] 3.35 (0.42)
HC3 G*6 H1′ C17 [2.76, 4.36] 5.06 (0.34)
Open in a new tab

For the 10S (+)-trans-anti-dG adduct, a total of 17 intermolecular NOEs between BP benzylic and pyrenyl protons and DNA protons were identified from the NMR experiments, among which 13 were assigned unambiguously, whereas four could be assigned only to one or another of a pair of protons (Cosman et al., 1992); for the 10R (−)-trans-anti-dG adduct, a total of 27 intermolecular NOEs were identified and assigned (de los Santos et al., 1992). Only one of the 17 NOE distances taken from the MD trajectory for the 10S (+)-trans-anti-dG adduct (Table 1) deviates from the experimental NOE-based distance range; whereas 12 of 27 NOE distances for the 10R (−)-trans-anti-dG adduct (Table 2) deviate from the experimental NOE-based distance range; however, all but three of these violations are only ∼0.5 Å beyond the experimental range. Tables S3 and S4 (Supporting Information) also show the average NOE distances over different segments (1.5–2.0 ns and 1.5–2.5 ns) of the trajectory for the 10S (+)- and 10R (−)-trans-anti-dG adducts, respectively. Only very modest variations were observed for these computed distances in the different time frames. Also, for the 10S (+)-trans-anti-dG isomer, excluding the one most deviant distance in the trajectory, the bounds are met 99.5% of the time over 1.5–3.0 ns to within ±0.75 Å. For the 10R (−)-trans-anti-dG isomer, excluding the two very deviant distances, the bounds are met 86.8% of the time within the ±0.75 Å range. Thus, our MD trajectories are in quite good agreement with the NMR experimental NOE data.

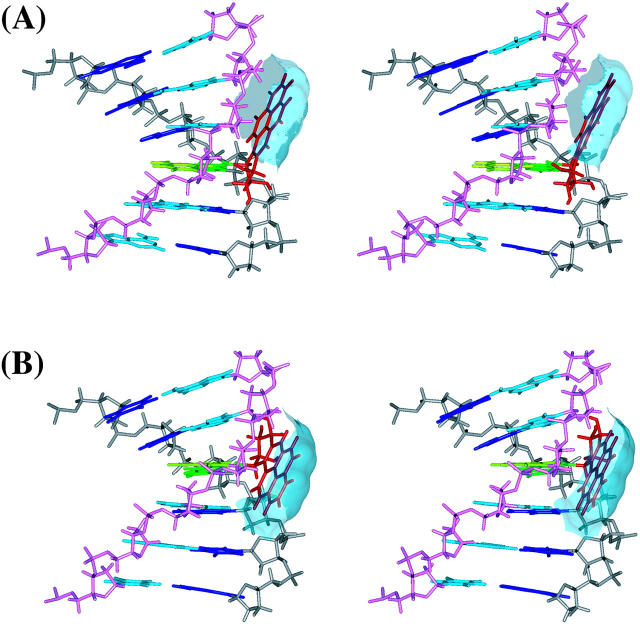
The average structures for the 10S (+)-trans-anti-dG adduct, 10R (−)-trans-anti-dG adduct, and the control B-DNA structure are shown in stereo in Fig. 3. The stable position of the BP residue in both the 10S (+)- and 10R (−)-trans-anti-dG adducts over the course of the simulations is demonstrated by the time-dependence of the torsion angles α′ and β′ for both adducts over the 3-ns simulations (Fig. S1, Supporting Information). The average values for α′ and β′ (over 1.5–3 ns time frame) are −184.1° ± 8.2° and −97.4° ± 13.1°, respectively, for the 10S (+)-trans-anti-dG adduct; they are 171.3° ± 8.9° and 52.1° ± 12.7° for the 10R (−)-trans-anti-dG adduct, respectively. In the NMR solution structures, the α′, β′ values for the 10S (+)- and 10R (−)-trans-anti-dG adducts are respectively −223°, −102° and 152°, 78° (Cosman et al., 1992; de los Santos et al., 1992).

FIGURE 3.

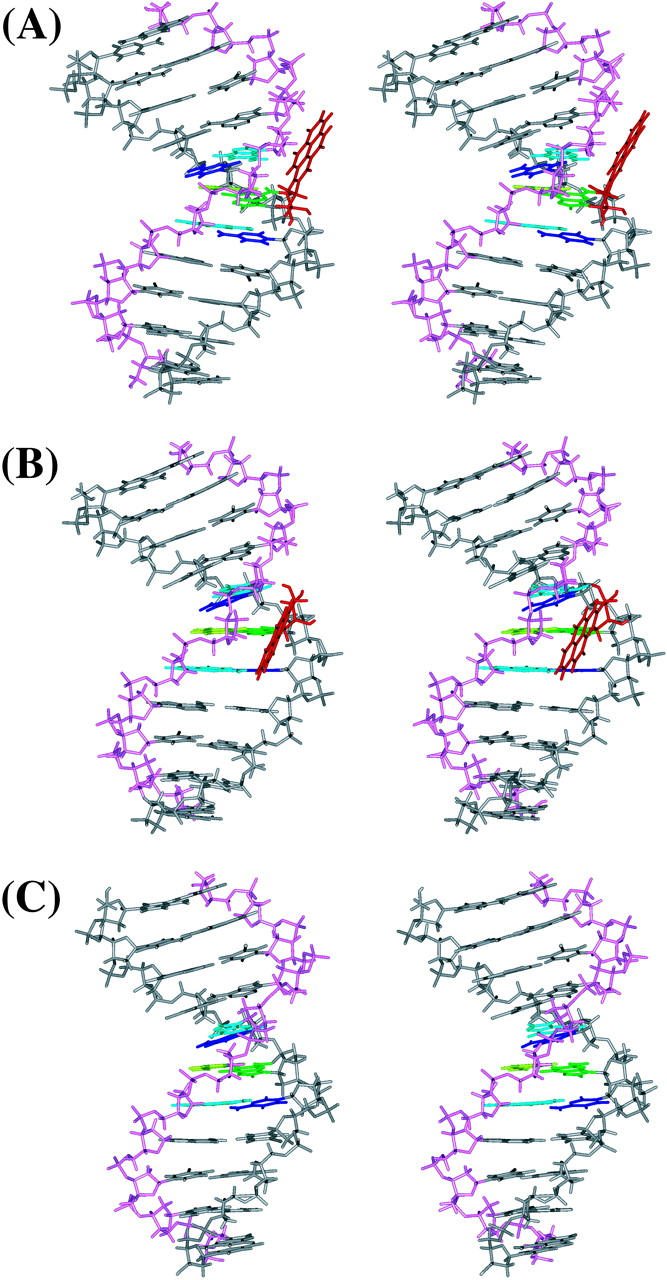
FIGURE 3

Open in a new tab

Stereo views of the MD average structures for (A) 10S (+)-trans-anti-dG adduct, (B) 10R (−)-trans-anti-dG adduct, and (C) unmodified control duplex over 1.5–3 ns. BP is red, G*6 (G6 in the unmodified control) is green, T17 is light green, C5 and C7 are blue, A16 and A18 are light blue, and other residues are gray. The backbone, sugar atoms from C1 to C11 are gray, and those from G12 to G22 are light magenta. All structures are aligned to have 5′-OH at the top left. All stereo images are constructed for viewing with a stereo viewer.

Computed thermodynamic profiles for the 10S (+)- and 10R (−)-trans-anti-dG adducts compare well with experimental measurements

Experimental determinations of melting and duplex formation data for the 10S (+)- and 10R (−)-trans-anti-dG adducts (Marky et al., 1996) show similar thermal stabilities of these two adducts. The melting temperature Tm, obtained from UV melting curves, for the 10S (+)-trans-anti-dG adduct in the d(CCATCG*CTACC)·d(GGTAGCGATGG) sequence context is 54°C, whereas it is 58°C for the 10R (−)-trans-anti-dG adduct in the same sequence. Moreover, the favorable enthalpic contribution to the duplex formation free energy, determined by calorimetry, for the 10S (+)-trans-anti-dG adduct is −49 ± 2 kcal/mol, whereas it is −47 ± 2 kcal/mol for the 10R (−)-trans-anti-dG adduct (Marky et al., 1996). The unfavorable entropic contribution to the duplex formation free energy is 44 ± 3 kcal/mol and 42 ± 3 kcal/mol for the 10S (+)- and 10R (−)-trans-anti-dG adducts, respectively (Marky et al., 1996). In total, the duplex formation free energy is −5.1 ± 0.6 kcal/mol for the 10S (+)-trans-anti-dG adduct, whereas it is −5.4 ± 0.6 kcal/mol for the 10R (−)-trans-anti-dG adduct, resulting from partial compensation of favorable enthalpy changes and unfavorable entropy changes (Marky et al., 1996). The difference in the duplex formation free energy between the 10S (+)- and 10R (−)-trans-anti-dG adducts is only 0.3 kcal/mol, favoring the 10R (−)-trans-anti-dG adduct. Within the experimental errors, these thermodynamic measurements showed that the 10S (+)- and 10R (−)-trans-anti-dG adduct duplexes have very similar stabilities.

We computed the free energies, enthalpies, and entropies for the 10S (+)- and 10R (−)-trans-anti-dG adducts over the 1.5–3-ns time frame using the MM-PBSA method (Table 3). The computed enthalpy difference between the stereoisomeric pair is 2.5 kcal/mol, favoring the 10S (+)-trans-anti-dG adduct. This value is reasonably consistent with the aforementioned experimental data based on DNA duplex formation (Marky et al., 1996). Such comparisons of enthalpies for the 10S (+)- and 10R (−)-trans-anti-dG modified DNA duplexes assume similar conformations in the modified stereoisomeric single strands (Yan et al., 2001; Chalikian et al., 1999). As shown in Table 3, the calculated entropic free energy difference is 1.4 kcal/mol favoring the 10R (−)-trans-anti-dG adduct. This is also in line with the experimental data. In all, the computed total free energy difference between the 10S (+)- and 10R (−)-trans-anti-dG adducts is 0.9 kcal/mol favoring the 10S (+)-trans-anti-dG adduct. Moreover, we observed a maximum variation of only ∼3 kcal/mol in the total enthalpic contributions to the free energies over different blocked and windowed time frames for each of the two adducts, as shown in Table S5 (Supporting Information). Given the uncertainties in both the experimental determination and the MM-PBSA methodology, our calculated free energy difference agrees quite well with the experimental data. In this connection it is also of interest that our previous simulations for two other systems, one involving adenine adducts derived from BP, and a second involving adenine adducts to a different carcinogen derived from benzo[c]phenanthrene, also revealed good agreement between thermal melting data and computed enthalpy differences between S and R stereoisomeric adducts (Yan et al., 2001; Wu et al., 2002). These combined findings suggest that our assumption of similarity in the modified single strands of S and R isomers, needed to compare with experiment, is reasonable in this case. Furthermore, our results together with those from a number of other systems (Cheatham and Young, 2001; Cheatham and Kollman, 2000, 1996; Beveridge and McConnell, 2000; Kollman et al., 2000; Jayaram et al., 2002; Cheatham et al., 1998; Srinivasan et al., 1998a,b; Jayaram et al., 1998; Spector et al., 1997; Reyes and Kollman, 2000; Wang et al., 2001; Huo et al., 2002) indicate that agreement between computed and experimental thermodynamic data is encouraging. Nonetheless, in the current MM-PBSA methodology, uncertainties in the calculation of the entropic components to the free energy as well as issues concerning computation of the counterion contributions (Srinivasan et al., 1998a; Kollman et al., 2000; Jayaram et al., 1998; Cheatham and Young, 2001) are yet to be resolved. Future developments in the methodology are needed to address these limitations.

TABLE 3.

Free energy analysis of the 10S (+)- and 10R (−)-trans-anti-dG adducts

10S (+)-trans 10R (−)-trans Δ
〈Eelec〉 321.8 (44.6) 315.2 (45.7) 6.7
〈EvdW〉 −193.0 (9.7) −195.4 (9.5) 2.5
〈Eint〉 1014.6 (22.6) 1017.3 (19.4) −2.7
〈EMM〉 1143.5 (45.0) 1137.0 (46.9) 6.4
〈Gnonpolar〉 25.0 (0.2) 24.8 (0.2) 0.2
〈GPB〉 −5709.3 (39.6) −5700.3 (43.1) −9.0
〈Gsolvation〉 −5684.3 (39.7) −5675.5 (43.2) −8.9
〈GPB + Eelec〉 −5387.5 (12.0) −5385.1 (11.8) −2.4
〈EMM + GPB〉 −4565.8 (19.8) −4563.3 (18.2) −2.5
−TS −586.5 −587.9 1.4
Gtot −5127.3 −5126.4 −0.9
Open in a new tab

All energies are in kcal/mol. Values in parentheses are standard deviations. Δ is defined as 10S (+)-trans − 10R (−)-trans.

Observed differential hydration of the BP ring system in the 10S (+)- and 10R (−)-trans-anti-dG adducts is reproduced by MD simulations and can be accounted for in terms of structural differences

Experimental determinations of hydration using magnetic suspension densimetry for the 10S (+)- and 10R (−)-trans-anti-dG adducted DNA duplexes in the same sequence context unambiguously indicate a greater exposure of hydrophobic residues to solvent in the 10S (+)-trans-anti-dG adduct than in the 10R (−)-trans-anti-dG adduct (Marky et al., 1996). Our MD simulations are in agreement with this experimental observation and a structural basis for the origin of this puzzling finding can now be provided.

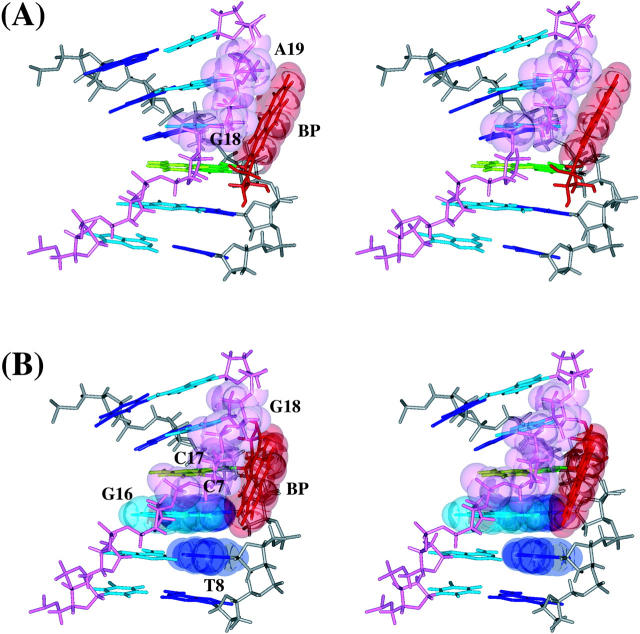
The dynamics average structures of the 10S (+)- and 10R (−)-trans-anti-dG adducts show that although the BP ring resides on the minor groove side in both adducts, the BP in the 10S (+)-trans-anti-dG adduct is more exposed to solvent (Fig. 4). The computed solvent-accessible surface area for the BP aromatic moiety in the average structure is 121 Å2 in the 10S (+)-trans-anti-dG adduct, whereas it is 107 Å2 in the 10R (−)-trans-anti-dG adduct. The trajectory-averaged number of water molecules within the first solvation shell of the BP aromatic rings is 19 for the 10S (+)-trans-anti-dG adduct over 1.5–3 ns, whereas it is 16 for the 10R (−)-trans-anti-dG adduct over the same time frame. This may be compared with the experimental difference of four water molecules per adduct pair. [We estimated the difference in number of water molecules based on the magnetic suspension densimetry results (Marky et al., 1996). ΔΔV = ΔV10S(+) − ΔV10R(−) = (−209) − (−136) mL/mol = −73 mL/mol = −121.3 Å3/molecule. Therefore, the difference between the 10S (+)- and 10R (−)-trans-anti-dG adducts is 121.3 A3. Given that the water density is 1 g/cm3, this 121.3 Å3 volume difference would correspond to four water molecules.] As shown in Fig. 5, one face of the BP ring is stacked over the sugar-phosphate backbone atoms of G18 and A19 in the 10S (+)-trans-anti-dG adduct, whereas the other face and both edges of the BP aromatic moiety are totally exposed to solvent. However, in the 10R (−)-trans-anti-dG adduct, in addition to the stacking between one face of the BP ring and the sugar-phosphate backbone atoms of C17 and G18, a pocket mainly comprised of C7, T8, and G16, nicely shields one edge of the BP aromatic moiety. In total, one face and one edge of BP are solvent-exposed in the 10R (−)-trans-anti-dG adduct, whereas both edges and one face are solvent-exposed in the 10S (+)-trans-anti-dG adduct.

FIGURE 4.

FIGURE 4

Open in a new tab

Differential hydration of BP aromatic moiety in the 10S (+)- and 10R (−)-trans-anti-dG adducts. Stereo views of (A) the d(ATCG*CT)·d(AGCGAT) region of the 10S (+)-trans-anti-dG adduct and (B) the d(TCG*CTA)·d(TAGCGA) region of the 10R (−)-trans-anti-dG adduct with solvent-accessible surfaces of BP. BP is red, G*6 is green, T17 is light green, residues from A3 to A9 are blue, and residues from T14 to T20 are light blue. The backbone and sugar atoms from A3 to A9 are gray, and those from T14 to T20 are light magenta. The solvent-accessible surface of BP is transparent and in light blue. The structures are aligned to have the 5′ residue of the modified strand at top left.

FIGURE 5.

FIGURE 5

Open in a new tab

Key van der Waals contacts between BP aromatic ring system and DNA residues. Stereo views of (A) the d(ATCG*CT)·d(AGCGAT) region of the 10S (+)-trans-anti-dG adduct and (B) the d(TCG*CTA)·d(TAGCGA) region of the 10R (−)-trans-anti-dG adduct with transparent van der Waals surfaces of relevant residues. The color scheme is given in the caption to Fig. 4. The structures are aligned to have the 5′ residue of the modified strand at top left.

We also computed the van der Waals interaction energy between the BP aromatic moiety with each DNA residue in the 10S (+)- and 10R (−)-trans-anti-dG adducts (Table 4). In the 10S (+)-trans-anti-dG adduct, the BP ring interacts primarily, if not exclusively, with G18 and A19 on the complementary strand. On the other hand, in the 10R (−)-trans-anti-dG adduct, the BP ring interacts not only with C17 and G18 on the complementary strand, but also with C7 and T8 on the adducted strand. This indicates that the BP aromatic ring system has more contact with DNA on both strands in the 10R (−)-trans-anti-dG adduct than in the 10S (+)-trans-anti-dG adduct. This is in line with our analysis that greater solvent exposure of BP is observed in the 10S (+)-trans-anti-dG adduct.

TABLE 4.

Van der Waals interaction energies between BP aromatic rings and DNA residues

10S (+) 10R (−) 10S (+) 10R (−)
C1 0.0 0.0 G22 0.0 0.0
C2 0.0 0.0 G21 0.0 0.0
A3 0.0 0.0 T20 −0.5 0.0
T4 0.0 0.0 A19 −5.4 −0.4
C5 −0.3 −0.1 G18 −7.3 −4.5
G*6 −0.4 0.8 C17 −1.0 −7.4
C7 −0.6 −1.6 G16 −0.1 −1.3
T8 −0.1 −2.7 A15 0.0 −0.1
A9 0.0 −0.4 T14 0.0 0.0
C10 0.0 0.0 G13 0.0 0.0
C11 0.0 0.0 G12 0.0 0.0
Open in a new tab

All energies are in kcal/mol.

The origins of the differential hydration can be explained on the basis of our previous studies of the 10S (+)- and 10R (−)-trans-anti-[BP]-N2-dG adducts on the nucleoside level (Xie et al., 1999; Geacintov et al., 1997). These revealed that the orientation of the BP is near mirror-image with respect to the modified guanine in the stereoisomer pair (Xie et al., 1999), because the BP OH-containing benzylic rings are nearly mirror images of one another. The α′, β′ (see Fig. 1) domains that the BP ring system can adopt in each stereoisomer are strongly restricted by steric hindrance between the BP and the covalently linked guanine, and this dominates the allowed BP orientation. To maintain the favored α′, β′ domains in duplex DNA, the BP is 3′-directed along the modified strand in the 10R (−)-trans-anti-dG adduct. The BP ring system is partially accommodated inside the minor groove with extensive van der Waals contacts with the neighboring backbone atoms, as well as 3′-side neighboring bases on both strands (Fig. 5 B); in this case the BP orientation, dictated by the required α′, β′ domains, nicely follows the curve of the minor groove (Fig. 6 B). By contrast, the aromatic BP residue in the 10S (+)-trans-anti-dG adduct is 5′-directed along the modified strand to maintain the favored α′, β′ domains and avoid the steric hindrance; however, the 5′-neighboring base pairs together with the minor groove exhibit a righthand twist in a direction that places them further away from the BP residue (Fig. 6 A). Therefore, the BP aromatic ring system in the 10S (+)-trans-anti-dG adduct cannot be accommodated as well within the minor groove on the 5′-side of the modified guanine, and can only interact with the complementary strand, thus resulting in greater solvent exposure of the BP moiety.

FIGURE 6.

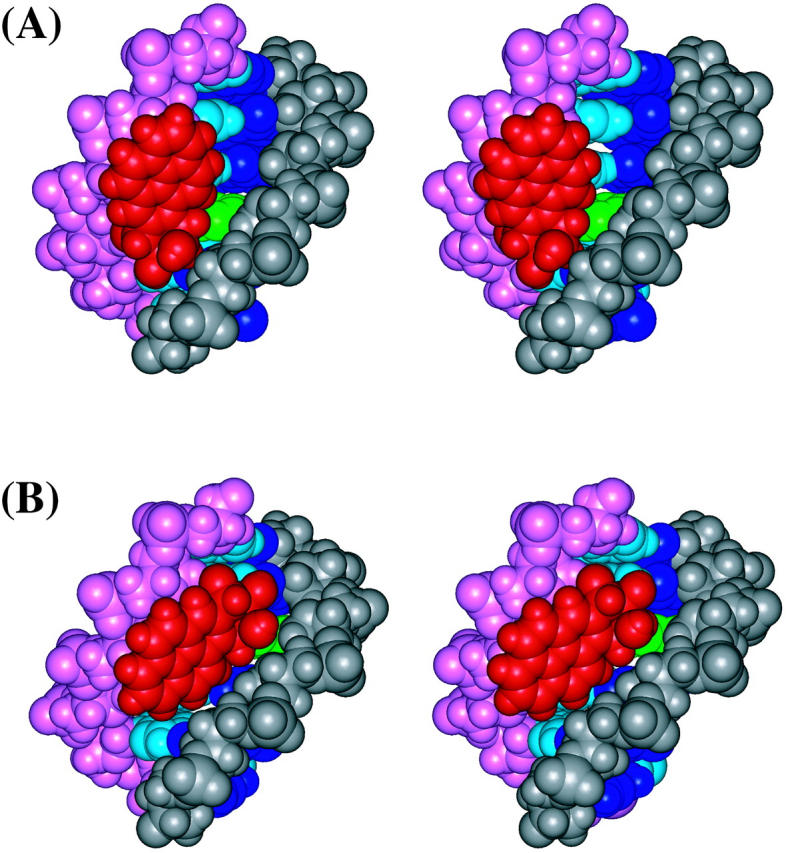
FIGURE 6

Open in a new tab

Stereo views of (A) the d(ATCG*CT)·d(AGCGAT) region of the 10S (+)-trans-anti-dG adduct and (B) the d(TCG*CTA)·d(TAGCGA) region of the 10R (−)-trans-anti-dG adduct from the minor groove side. All atoms are in CPK, and the color scheme is given in the caption to Fig. 4. The structures are aligned to have the 5′ residue of the modified strand at top right.

These differences in accommodation within the minor groove also cause more minor groove widening in the 10S (+)-trans-anti-dG adduct (Fig. 6). The trajectory-averaged minor groove widths for the 10S (+)-trans-anti-dG adduct, 10R (−)-trans-anti-dG adduct, and the unmodified control B-DNA are shown in Table 5. Compared to the control B-DNA structure, most of the minor groove regions in the 10R (−)-trans-anti-dG adduct are similar or marginally widened, except for the C7–T20, T8–A19, and A9–G18 regions, in which the minor groove is ∼2–3 Å wider than in the unmodified B-DNA (Table 5). On the other hand, the minor groove opening, particularly at the 5′-side of the modified guanine, is more pronounced in the 10S (+)-trans-anti-dG adduct (Table 5). Specifically, at G*6–G21, C7–T20, T8–A19, and A9–G18 regions, the minor groove is widened by ∼3–4 Å as compared to the unmodified B-DNA control simulation.

TABLE 5.

Trajectory-averaged minor groove widths

10S (+)-trans 10R (−)-trans B-DNA
C5–G22 5.7 4.8 4.5
G*6–G21 7.2 5.3 4.1
C7–T20 8.2 6.6 5.0
T8–A19 7.7 7.0 4.5
A9–G18 5.7 5.8 2.5
C10–C17 4.3 5.5 4.2
C11–G16 3.8 3.9 4.6
Open in a new tab

Minor groove width is calculated from the indicated interstrand phosphate to phosphate distance for each structure over the 1.5–3 ns time frame. All distances are in Å.

Small perturbations to the DNA helical structures in both 10S (+)- and 10R (−)-trans-anti-dG adducts correlate with low nucleotide excision repair susceptibilities

Bulky DNA lesions formed by polycyclic aromatic chemicals are removed by the nucleotide excision repair (NER) system in mammals (Wood, 1999). It is currently believed that distortions in DNA helical structure induced by the lesions are recognized by NER factors (Wood, 1999; Evans et al., 1997; Fujiwara et al., 1999), and DNA helical destabilization facilitates NER (Hess et al., 1997b, 1998; Buschta-Hedayat et al., 1999). The disruption or weakening of Watson–Crick hydrogen bonding, DNA bending, and unwinding of the DNA double helix are considered to be among the distortions recognized by NER factors (Hess et al., 1997b; Buschta-Hedayat et al., 1999; Missura et al., 2001; Shi et al., 1992; Verhoeven et al., 2001).

Hess et al. (1997a) found that the susceptibilities of the [BP]-N2-dG adducts to excision catalyzed by NER enzymes in cell-free extracts from human HeLa cells in vitro are markedly dependent on the stereochemistry-dependent conformations of these adducts in double-stranded DNA. The external, minor groove 10S (+)- and 10R (−)-trans-anti-[BP]-N2-dG adducts in the same sequence context studied here have revealed a relatively low excision activity of ∼7–10% relative to the stereoisomeric 10S (−)- and 10R (+)-cis-anti -[BP]-N2-dG adducts that are intercalated between adjacent base pairs, but with a displacement of the modified guanine base and partner strand dC out of the helix (“base-displaced intercalation”) (Cosman et al., 1993, 1996). The relative low efficiency of NER for both the 10S (+)- and 10R (−)-trans guanine adducts suggest relatively small deviations of the DNA helix structural parameters from their normal values in an unmodified DNA duplex of the same sequence. We analyzed our MD simulation trajectories to determine helical distortions that might relate to these observations.

As shown in Fig. S2 (Supporting Information), some modest deviations in the helicoidal parameters compared to the unmodified control were observed for both the 10S (+)- and 10R (−)-trans-anti-dG adducts. Whereas a small amount of unwinding was observed at the T4–A19 to C5–G18 step in the 10S (+)-trans-anti-dG adduct, total unwinding in both modified DNA duplexes is small. Moreover, our backbone analysis (Fig. S3, Supporting Information) also indicated that the backbone parameters in both the 10S (+)- and 10R (−)-trans-anti-dG adducts are modestly perturbed compared to the unmodified control. The greatest differences occur primarily at C17, G18, and A19 in sugar-pucker pseudorotation angle P (also reflected in backbone torsion angle δ), particularly in the 10S (+)-trans-anti-dG adduct. Interaction of the BP aromatic ring system with the sugar-phosphate backbone in both adducts (Table 4, Fig. 5) likely accounts for the deviations in sugar pucker.

We also assessed the quality of Watson–Crick hydrogen bonding for the 10S (+)- and 10R (−)-trans-anti-dG adducts at the lesion site using our hydrogen bond quality index, IH, and results were compared to the unmodified control B-DNA. The lower the value of IH, the better the quality of the Watson–Crick hydrogen bonding. The summed value for this index is 297, 362, and 190 for the 3000 structures of the 10S (+)-trans-anti-dG adduct, 10R (−)-trans-anti-dG adduct, and the unmodified control, respectively, over the 1.5–3 ns time frame. According to this index, both the 10S (+)- and 10R (−)-trans-anti-dG adducts have a similar marginally diminished quality of Watson-Crick hydrogen bonding, as compared to the unmodified B-DNA. Taken together, the small extent of helix perturbation in both stereoisomeric adducts is consistent with the observed low, yet detectable, NER susceptibility (Hess et al., 1997a). However, NER is a very complex, multistep process, and such correlations must be interpreted with caution. Therefore, it is important to increase our available data base to further support such correlations between adduct-induced deviations in the helix structural parameters and DNA nucleotide excision repair efficiencies. Our previous structural and thermodynamic analyses of other polycyclic aromatic adducts, together with the current results, are encouraging in terms of relating thermodynamic stabilities, structural perturbations, and the observed susceptibilities of these bulky DNA adducts to NER (Yan et al., 2001; Wu et al., 2002; Geacintov et al., 2002).

CONCLUSIONS

In conclusion, our MD simulations for the 10S (+)- and 10R (−)-trans-anti-[BP]-N2-dG stereoisomeric adducts in an 11-mer DNA duplex have produced trajectories over 3 ns that preserve the NMR-derived interproton distance bounds (NOEs) for the key distances governing the orientation of the BP moiety with respect to the DNA quite well, showing the capability of molecular dynamics in simulating structural properties of carcinogen-damaged DNA. The MM-PBSA free energy analysis revealed free energy differences between the two stereoisomeric adducts that are quite consistent with experimental thermodynamic measurements. Furthermore, the enhanced exposure to solvent of the BP aromatic ring system in the 10S (+)-trans-anti-dG adduct, deduced from experimental thermodynamic investigations (Marky et al., 1996), is structurally rationalized. Steric hindrance between the bulky BP residue and the modified guanine to which it is attached covalently (Geacintov et al., 1997), combined with the righthand helical twist in B-DNA, leads to a poorer fit in the minor groove of the 5′-oriented 10S (+)-trans-anti-dG adduct; this results in a greater widening of the minor groove and more solvent exposure. In addition, the observed similar, low, yet detectable, susceptibilities of the 10S (+)- and 10R (−)-trans-anti-dG adducts to nucleotide excision repair in human cell extracts (Hess et al., 1997a) correlate with the relatively minor perturbations of the DNA structures induced by these covalent adducts positioned in the B-DNA minor groove. This finding is in line with current evidence that the NER machinery responds to distortions and destabilization of the modified DNA double helices (Wood, 1999; Sancar, 1996; Batty and Wood, 2000; Hess et al., 1997b, 1998; Sugasawa et al., 2001; Buschta-Hedayat et al., 1999).

Supporting information

Supporting Information contains five tables and three figures. These are available at http://www.biophysj.org. Table S1 gives partial charges, atom types, and topologies for the 10S (+)- and 10R (−)-trans-anti-[BP]-N2-dG nucleotide adducts; Table S2 gives added force field parameters; Tables S3 and S4 give the experimental and trajectory-averaged intermolecular NOE-derived distances involving BP benzylic and pyrenyl rings for the 10S (+)- and 10R (−)-trans-anti-dG adducts, respectively, over additional different time frames; Table S5 gives free energy analysis of the 10S (+)- and 10R (−)-trans-anti-dG adducts over additional different blocked and windowed time frames; Figure S1 shows the time dependence of the torsional angles α′ and β′ for the 10S (+)- and 10R (−)-trans-anti-dG adducts over the 3-ns MD simulation; Figures S2 and S3 show the average helicoidal parameters and backbone torsional parameters, respectively, for the 10S (+)- and 10R (−)-trans-anti-dG adducts over 1.5–3 ns.

Supplementary Material

[Figure]
biophysj_84_4_2137__index.html (684B, html)

Acknowledgments

Computations were carried out on our own Silicon Graphics Octane workstations.

This research is supported by National Institutes of Health grants CA-28038 to S.B., CA-20851 to N.E.G., and CA-46533 to D.J.P.

Abbreviations used: (+)-anti-BPDE, (+)-(7R,8S,9S,10R)-7, 8-dihydroxy-9,10-epoxy-7,8,9,10-tetrahydrobenzo[a]pyrene; (−)-anti-BPDE, (−)-(7S,8R,9R,10S)-7,8-dihydroxy-9,10-epoxy-7,8,9,10-tetrahydrobenzo[a]pyrene; BP, benzo[a]pyrene; BPDE, benzo[a]pyrene diol epoxide; DNA, deoxyribonucleic acid; MD, molecular dynamics; MM-PBSA, molecular mechanics Poisson–Boltzmann surface area; NER, nucleotide excision repair; NMR, nuclear magnetic resonance; NOE, nuclear Overhauser effect; PME, particle mesh Ewald; RESP, restrained electrostatic potential fitting; RMSD, root-mean-square deviation; SASA, solvent-accessible surface area.

References

  1. Alberts, B., D. Bray, J. Lewis, M. Raff, K. Roberts, and J. D. Watson. 1994. Molecular Biology of the Cell, 3rd edition. Garland Publishing, Inc., New York, NY.
  2. Arnott, S., P. J. C. Smith, and R. Chandrasekaran. 1976. Handbook of Biochemistry and Molecular Biology, 3rd edition. CRC Press, Cleveland, OH. pp411–422.
  3. Batty, D. P., and R. D. Wood. 2000. Damage recognition in nucleotide excision repair of DNA. Gene. 241:193–204. [DOI] [PubMed] [Google Scholar]
  4. Bayly, C. I., P. Cieplak, W. D. Cornell, and P. A. Kollman. 1993. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: the RESP model. J. Phys. Chem. 97:10269–10280. [Google Scholar]
  5. Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, A. DiNola, and J. R. Haak. 1984. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81:3684–3690. [Google Scholar]
  6. Beveridge, D. L., and K. J. McConnell. 2000. Nucleic acids: theory and computer simulation, Y2K. Curr. Opin. Struct. Biol. 10:182–196. [DOI] [PubMed] [Google Scholar]
  7. Buschta-Hedayat, N., T. Buterin, M. T. Hess, M. Missura, and H. Naegeli. 1999. Recognition of nonhybridizing base pairs during nucleotide excision repair of DNA. Proc. Natl. Acad. Sci. USA. 96:6090–6095. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Case, D. A., D. A. Pearlman, J. W. Caldwell, T. E. Cheatham, W. S. Ross, C. L. Simmerling, T. A. Darden, K. M. Merz, R. V. Stanton, A. L. Cheng, J. J. Vincent, M. Crowley, D. M. Ferguson, V. Tsui, R. J. Radmer, Y. Duan, J. Pitera, I. Massova, G. L. Seibel, U. C. Singh, P. K. Weiner, and P. A. Kollman. 1999. AMBER 6.0. University of California, San Francisco, CA.
  9. Chalikian, T. V., J. Völker, G. E. Plum, and K. J. Breslauer. 1999. A more unified picture for the thermodynamics of nucleic acid duplex melting: a characterization by calorimetric and volumetric techniques. Proc. Natl. Acad. Sci. USA. 96:7853–7858. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Cheatham, T. E., P. Cieplak, and P. A. Kollman. 1999. A modified version of the Cornell et al. force field with improved sugar pucker phases and helical repeat. J. Biomol. Struct. Dyn. 16:845–862. [DOI] [PubMed] [Google Scholar]
  11. Cheatham, T. E., and P. A. Kollman. 1996. Observation of the A-DNA to B-DNA transition during unrestrained molecular dynamics in aqueous solution. J. Mol. Biol. 259:434–444. [DOI] [PubMed] [Google Scholar]
  12. Cheatham, T. E., and P. A. Kollman. 2000. Molecular dynamics simulation of nucleic acids. Annu. Rev. Phys. Chem. 51:435–471. [DOI] [PubMed] [Google Scholar]
  13. Cheatham, T. E., J. Srinivasan, D. A. Case, and P. A. Kollman. 1998. Molecular dynamics and continuum solvent studies of the stability of polyG-polyC and polyA-polyT DNA duplexes in solution. J. Biomol. Struct. Dyn. 16:265–280. [DOI] [PubMed] [Google Scholar]
  14. Cheatham, T. E., and M. A. Young. 2001. Molecular dynamics simulation of nucleic acids: successes, limitations, and promise. Biopolymers. 56:232–256. [DOI] [PubMed] [Google Scholar]
  15. Chong, L. T., Y. Duan, L. Wang, I. Massova, and P. A. Kollman. 1999. Molecular dynamics and free energy calculations applied to affinity maturation in antibody 48G7. Proc. Natl. Acad. Sci. USA. 96:14330–14335. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Connolly, M. L. 1983. Solvent-accessible surfaces of proteins and nucleic acids. Science. 221:709–713. [DOI] [PubMed] [Google Scholar]
  17. Cornell, W. D., P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell, and P. A. Kollman. 1995. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 117:5179–5197. [Google Scholar]
  18. Cosman, M., C. de los Santos, R. Fiala, B. E. Hingerty, V. Ibanez, E. Luna, R. Harvey, N. Geacintov, S. Broyde, and D. J. Patel. 1993. Solution conformation of the (+)-cis-anti-[BP]dG adduct in a DNA duplex: intercalation of the covalently attached benzo[a]pyrenyl ring into the helix and displacement of the modified deoxyguanosine. Biochemistry. 32:4145–4155. [DOI] [PubMed] [Google Scholar]
  19. Cosman, M., C. de los Santos, R. Fiala, B. E. Hingerty, S. B. Singh, V. Ibanez, L. A. Margulis, D. Live, N. E. Geacintov, and S. Broyde. 1992. Solution conformation of the major adduct between the carcinogen (+)-anti-benzo[a]pyrene diol epoxide and DNA. Proc. Natl. Acad. Sci. USA. 89:1914–1918. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Cosman, M., B. E. Hingerty, N. Luneva, S. Amin, N. E. Geacintov, S. Broyde, and D. J. Patel. 1996. Solution conformation of the (−)-cis-anti-benzo[a]pyrenyl-dG adduct opposite dC in a DNA duplex: intercalation of the covalently attached BP ring into the helix with base displacement of the modified deoxyguanosine into the major groove. Biochemistry. 35:9850–9863. [DOI] [PubMed] [Google Scholar]
  21. Darden, T., D. York, and L. Pedersen. 1993. Particle mesh Ewald: an N·log(N) method for Ewald sums in large systems. J. Chem. Phys. 98:10089–10092. [Google Scholar]
  22. de los Santos, C., M. Cosman, B. E. Hingerty, V. Ibanez, L. A. Margulis, N. E. Geacintov, S. Broyde, and D. J. Patel. 1992. Influence of benzo[a]pyrene diol epoxide chirality on solution conformations of DNA covalent adducts: the (−)-trans-anti-[BP]G·C adduct structure and comparison with the (+)-trans-anti-[BP]G·C enantiomer. Biochemistry. 31:5245–5252. [DOI] [PubMed] [Google Scholar]
  23. Elizondo-Riojas, M.-A., and J. Kozelka. 2001. Unrestrained 5 ns molecular dynamics simulation of a cisplatin-DNA 1,2-GG adduct provides a rationale for the NMR features and reveals increased conformational flexibility at the platinum binding site. J. Mol. Biol. 314:1227–1243. [DOI] [PubMed] [Google Scholar]
  24. Essmann, U., L. Perera, M. L. Berkowitz, T. Darden, H. Lee, and L. G. Pederson. 1995. A smooth particle mesh Ewald method. J. Chem. Phys. 103:8577–8593. [Google Scholar]
  25. Evans, E., J. G. Moggs, J. R. Hwang, J.-M. Egly, and R. D. Wood. 1997. Mechanism of open complex and dual incision formation by human nucleotide excision repair factors. EMBO J. 16:6559–6573. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Fountain, M. A., and T. R. Krugh. 1995. Structural characterization of a (+)-trans-anti-benzo[a]pyrene-DNA adduct using NMR, restrained energy minimization, and molecular dynamics. Biochemistry. 34:3152–3161. [DOI] [PubMed] [Google Scholar]
  27. Frisch, J. M., W. G. Trucks, B. H. Schlegel, E. G. Scuseria, A. M. Robb, R. J. Cheeseman, G. V. Zakrzewski, A. J. Montgomery, E. R. Stratmann, C. J. Burant, S. Dapprich, M. J. Millam, D. A. Daniels, N. K. Kudin, C. M. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, A. G. Petersson, Y. P. Ayala, Q. Cui, K. Morokuma, K. D. Malick, D. A. Rabuck, K. Raghavachari, B. J. Foresman, J. Cioslowski, V. J. Ortiz, G. A. Baboul, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, L. R. Martin, J. D. Fox, T. Keith, A. M. Al-Laham, Y. C. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, W. M. P. Gill, B. Johnson, W. Chen, W. M. Wong, L. J. Andres, C. Gonzalez, M. Head-Gordon, S. E. Replogle, and A. J. Pople. 1998. Gaussian 98, Revision A7. Gaussian, Inc., Pittsburgh, PA.
  28. Fujiwara, Y., C. Masutani, T. Mizukoshi, J. Kondo, F. Hanaoka, and S. Iwai. 1999. Characterization of DNA recognition by the human UV-damaged DNA-binding protein. J. Biol. Chem. 274:20027–20033. [DOI] [PubMed] [Google Scholar]
  29. Geacintov, N. E., S. Broyde, T. Buterin, H. Naegeli, M. Wu, S. Yan, and D. J. Patel. 2002. Thermodynamic and structural factors in the removal of bulley DNA adducts by the nucleotide excisin repair machinery. Biopolymers. 65:202–210. [DOI] [PubMed] [Google Scholar]
  30. Geacintov, N. E., M. Cosman, B. E. Hingerty, S. Amin, S. Broyde, and D. J. Patel. 1997. NMR solution structures of stereoisometric covalent polycyclic aromatic carcinogen-DNA adduct: principles, patterns, and diversity. Chem. Res. Toxicol. 10:111–146. [DOI] [PubMed] [Google Scholar]
  31. Gilson, M. K., and B. H. Honig. 1987. Calculation of electrostatic potentials in an enzyme active site. Nature. 330:84–86. [DOI] [PubMed] [Google Scholar]
  32. Harvey, S. C., R. K.-Z. Tan, and T. E. Cheatham. 1998. The flying ice cube: velocity rescaling in molecular dynamics leads to violation of energy equipartition. J. Comp. Chem. 19:726–740. [Google Scholar]
  33. Hess, M. T., D. Gunz, N. Luneva, N. E. Geacintov, and H. Naegeli. 1997a. Base pair conformation-dependent excision of benzo[a]pyrene diol epoxide-guanine adducts by human nucleotide excision repair enzymes. Mol. Cell. Biol. 17:7069–7076. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Hess, M. T., H. Naegeli, and M. Capobianco. 1998. Stereoselectivity of human nucleotide excision repair promoted by defective hybridization. J. Biol. Chem. 273:27867–27872. [DOI] [PubMed] [Google Scholar]
  35. Hess, M. T., U. Schwitter, M. Petretta, B. Giese, and H. Naegeli. 1997b. Bipartite substrate discrimination by human nucleotide excision repair. Proc. Natl. Acad. Sci. USA. 94:6664–6669. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Hingerty, B. E., S. Figueroa, T. L. Hayden, and S. Broyde. 1989. Prediction of DNA structure from sequence: a build-up technique. Biopolymers. 28:1195–1222. [DOI] [PubMed] [Google Scholar]
  37. Honig, B., and A. Nicholls. 1995. Classical electrostatics in biology and chemistry. Science. 268:1144–1149. [DOI] [PubMed] [Google Scholar]
  38. Huo, S., J. Wang, P. Cieplak, P. A. Kollman, and I. D. Kuntz. 2002. Molecular dynamics and free energy analyses of cathepsin D-inhibitor interactions: insight into structure-based ligand design. J. Med. Chem. 45:1412–1419. [DOI] [PubMed] [Google Scholar]
  39. Jayaram, B., K. McConnell, S. B. Dixit, A. Das, and D. L. Beveridge. 2002. Free-energy component analysis of 40 protein-DNA complexes: a consensus view on the thermodynamics of binding at the molecular level. J. Comp. Chem. 23:1–14. [DOI] [PubMed] [Google Scholar]
  40. Jayaram, B., D. Sprous, M. A. Young, and D. L. Beveridge. 1998. Free energy analysis of the conformational preferences of A and B forms of DNA in solution. J. Am. Chem. Soc. 120:10629–10633. [Google Scholar]
  41. Jorgensen, W. L., J. Chandreskhar, J. D. Madura, R. W. Imprey, and M. L. Klein. 1983. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79:926–935. [Google Scholar]
  42. Kollman, P. A., I. Massova, C. Reyes, B. Kuhn, S. Huo, L. Chong, M. Lee, T. Lee, Y. Duan, W. Wang, O. Donini, P. Cieplak, J. Srinivasan, D. A. Case, and T. E. Cheatham. 2000. Calculating structures and free energies of complex molecules: combining molecular mechanics and continuum models. Acc. Chem. Res. 33:889–897. [DOI] [PubMed] [Google Scholar]
  43. Marky, L. A., D. Rentzeperis, N. P. Luneva, M. Cosman, N. E. Geacintov, and D. W. Kupke. 1996. Different hydration thermodynamics of stereoisomeric DNA-benzo[a]pyrene adducts derived from diol epoxide enantiomers with different tumorigenic potentials. J. Am. Chem. Soc. 118:3804–3810. [Google Scholar]
  44. Massova, I., and P. A. Kollman. 2000. Combined molecular mechanical and continuum solvent approach (MM-PBSA/GBSA) to predict ligand binding. Perspect. Drug Discovery Des. 18:113–135. [Google Scholar]
  45. Miaskiewicz, K., J. Miller, M. Cooney, and R. Osman. 1996. Computational simulations of DNA distortions by a cis, syn-cyclobutane thymine dimer lesion. J. Am. Chem. Soc. 118:9156–9163. [Google Scholar]
  46. Missura, M., T. Buterin, R. Hindges, U. Hubscher, J. Kasparkova, V. Brabec, and H. Naegeli. 2001. Double-check probing of DNA bending and unwinding by XPA-RPA: an architectural function in DNA repair. EMBO J. 20:3554–3564. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Nicholls, A., K. A. Sharp, and B. Honig. 1990. DelPhi. Department of Biochemistry and Molecular Biophysics, Columbia University, New York, NY.
  48. Ravishanker, G., S. Swaminathan, D. L. Beveridge, R. Lavery, and H. Sklenar. 1989. Conformational and helicoidal analysis of 30 ps of molecular dynamics on the d(CGCGAATTCGCG) double helix: “curves,” dials and windows. J. Biomol. Struct. Dyn. 6:669–699. [DOI] [PubMed] [Google Scholar]
  49. Reyes, C. M., and P. A. Kollman. 2000. Structure and thermodynamics of RNA-protein binding: using molecular dynamics and free energy analyses to calculate the free energies of binding and conformational change. J. Mol. Biol. 297:1145–1158. [DOI] [PubMed] [Google Scholar]
  50. Ryckaert, J. P., G. Ciccotti, and H. J. C. Berendsen. 1977. Numerical integration of Cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comp. Phys. 23:327–341. [Google Scholar]
  51. Saenger, W. 1984. Principles of Nucleic Acid Structure. Springer-Verlag New York, Inc., New York, NY.
  52. Sancar, A. 1996. DNA excision repair. Annu. Rev. Biochem. 65:43–81. [DOI] [PubMed] [Google Scholar]
  53. Sanner, M. F., A. J. Olson, and J. C. Spehner. 1996. Reduced surface: an efficient way to compute molecular surfaces. Biopolymers. 38:305–320. [DOI] [PubMed] [Google Scholar]
  54. Sharp, K. A., and B. Honig. 1990a. Calculating total electrostatic energies with the nonlinear Poisson-Boltzmann equation. J. Phys. Chem. 94:7684–7692. [Google Scholar]
  55. Sharp, K. A., and B. Honig. 1990b. Electrostatic interactions in macromolecules: theory and applications. Annu. Rev. Biophys. Biophys. Chem. 19:301–332. [DOI] [PubMed] [Google Scholar]
  56. Shi, Q., R. Thresher, A. Sancar, and J. Griffith. 1992. Electron microscopic study of (A)BC excinuclease DNA is sharply bent in the UvrB-DNA complex. J. Mol. Biol. 226:425–432. [DOI] [PubMed] [Google Scholar]
  57. Sitkoff, D., K. A. Sharp, and B. Honig. 1994. Accurate calculation of hydroation free energies using macroscopic solvent models. J. Phys. Chem. 98:1978–1988. [Google Scholar]
  58. Spector, T. I., T. E. Cheatham, and P. A. Kollman. 1997. Unrestrained molecular dynamics of photodamaged DNA in aqueous solution. J. Am. Chem. Soc. 119:7095–7104. [Google Scholar]
  59. Srinivasan, J., T. E. Cheatham, P. Cieplak, P. A. Kollman, and D. A. Case. 1998a. Continuum solvent studies of the stability of DNA, RNA, and phosphoramidate-DNA helices. J. Am. Chem. Soc. 120:9401–9409. [Google Scholar]
  60. Srinivasan, J., J. Miller, P. A. Kollman, and D. A. Case. 1998b. Continuum solvent studies of the stability of RNA hairpin loops and helices. J. Biomol. Struct. Dyn. 16:671–682. [DOI] [PubMed] [Google Scholar]
  61. Sugasawa, K., T. Okamoto, Y. Shimizu, C. Masutani, S. Iwai, and F. Hanaoka. 2001. A multistep damage recognition mechanism for global genomic nucleotide excision repair. Genes Dev. 15:507–521. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Verhoeven, E. E., C. Wyman, G. Moolenaar, J. H. Hoeijmakers, and N. Gooseen. 2001. Architecture of nucleotide excision repair complexes: DNA is wrapped by UvrB before and after damage recognition. EMBO J. 20:601–611. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Wang, J., P. Morin, W. Wang, and P. A. Kollman. 2001. Use of MM-PBSA in reproducing the binding free energies to HIV-1 RT of TIBO derivatives and predicting the binding mode to HIV-1 RT of efavirenz by docking and MM-PBSA. J. Am. Chem. Soc. 123:5221–5230. [DOI] [PubMed] [Google Scholar]
  64. Wood, R. D. 1999. DNA damage recognition during nucleotide excision repair in mammalian cells. Biochimie. 81:39–44. [DOI] [PubMed] [Google Scholar]
  65. Wu, M., S. Yan, D. J. Patel, N. E. Geacintov, and S. Broyde. 2002. Relating repair susceptibility of carcinogen-damaged DNA with structural distortion and thermodynamic stability. Nucleic Acids Res. 30:3422–3432. [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Wu, X., R. Shapiro, and S. Broyde. 1999. Conformational analysis of the major DNA adduct derived from the food mutagen 2-amino-3-methylimidazo[4,5-f]quinoline. Chem. Res. Toxicol. 12:895–905. [DOI] [PubMed] [Google Scholar]
  67. Xie, X. M., N. E. Geacintov, and S. Broyde. 1999. Stereochemical origin of opposite orientations in DNA adducts derived from enantiomeric anti-benzo[a]pyrene diol epoxides with different tumorigenic potentials. Biochemistry. 38:2956–2968. [DOI] [PubMed] [Google Scholar]
  68. Ya, N.-Q., S. Smirnov, M. Cosman, S. Bhanot, V. Ibanez, and N. E. Geacintov. 1994. Thermal stability of benzo[a]pyrene diol epoxide-modified oligonucleotide duplexes: effects of mismatched complementary strands and bulges. In Structural Biology: The State of the Art. R. H. Sarma, and M. H. Sarma, editors. Adenine Press, Schenectady, NY. pp. 349–366.
  69. Yan, S., R. Shapiro, N. E. Geacintov, and S. Broyde. 2001. Stereochemical, structural and thermodynamic origins of stability differences between stereoisomeric benzo[a]pyrene diol epoxide deoxyadenosine adducts in a DNA mutational hot spot sequence. J. Am. Chem. Soc. 123:7054–7066. [DOI] [PubMed] [Google Scholar]
  70. Zegar, I. S., S. J. Kim, T. N. Johansen, P. J. Horton, C. M. Harris, T. M. Harris, and M. P. Stone. 1996. Adduction of the human N-ras codon 61 sequence with (−)-(7S,8R,9R,10S)-7,8-dihydroxy-9,10-epoxy-7,8,9,10-tetrahydrobenzo[a]pyrene: structural refinement of the intercalated SRSR(61,2) (−)-(7S,8R,9S,10R)-N6−[10−(7,8,9,10-tetrahydrobenzo[a]pyrenyl)]-2′-deoxyadenosyl adduct from 1H NMR. Biochemistry. 35:6212–6224. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Figure]
biophysj_84_4_2137__index.html (684B, html)
biophysj_84_4_2137__1.pdf (346.5KB, pdf)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES