Mechanically Probing the Folding Pathway of Single RNA Molecules

Abstract

We study theoretically the denaturation of single RNA molecules by mechanical stretching, focusing on signatures of the (un)folding pathway in molecular fluctuations. Our model describes the interactions between nucleotides by incorporating the experimentally determined free energy rules for RNA secondary structure, whereas exterior single-stranded regions are modeled as freely jointed chains. For exemplary RNA sequences (hairpins and the Tetrahymena thermophila group I intron), we compute the quasiequilibrium fluctuations in the end-to-end distance as the molecule is unfolded by pulling on opposite ends. Unlike the average quasiequilibrium force-extension curves, these fluctuations reveal clear signatures from the unfolding of individual structural elements. We find that the resolution of these signatures depends on the spring constant of the force-measuring device, with an optimal value intermediate between very rigid and very soft. We compare and relate our results to recent experiments by Liphardt et al. (2001).

INTRODUCTION

The advent and refinement of techniques to apply and measure forces on single molecules have allowed remarkable experiments probing the elastic properties and structural transitions of biomolecules such as DNA (see, e.g., Bockelmann et al., 1998; Maier et al., 2000; Smith et al., 1996) and proteins (see, e.g., Rief et al., 1997). Recently, single-molecule experiments using optical tweezers were also performed to study the unfolding of small RNA molecules under an applied force (Liphardt et al., 2001, 2002). RNA molecules, besides functioning as messengers of sequence information in the process of protein synthesis, also have many biological functions that intricately depend on a precisely folded RNA structure, e.g., as ribosomal RNA or as self-splicing introns (Cech, 1993). The formation of RNA structure (RNA folding) is therefore an important biophysical process, which, however, is currently not understood in sufficient detail (Tinoco and Bustamante, 1999). Pulling experiments (Liphardt et al., 2001, 2002), possibly in combination with single-molecule fluorescence methods (Zhuang et al., 2000, 2002), promise to reveal important aspects of RNA structure, its folding pathways and kinetics, and eventually its biological function.

The experiment of Liphardt et al. (2001) has shown that pulling on simple structural units of RNA, e.g., a single hairpin, yields characteristic features in the force-extension curve (FEC), which can be used to deduce the unfolding free energy and the size of the structural element. Moreover, the observation of end-to-end distance time traces at constant force revealed that the unfolding and refolding of these simple structures proceeds directly without intermediates, and the opening/closing rates could be extracted from the time traces. From the theoretical side, it is interesting to ask how far, in principle, the pulling approach could be pushed to study larger RNA molecules and how the resolution of such approaches depends on parameters of the experimental setup. Here, we expand our previous model for RNA pulling experiments (Gerland et al., 2001), and address these questions. The model incorporates the experimentally known free energy rules for RNA secondary structure (Walter et al., 1994) and a polymer model for the elastic properties of single-stranded RNA (ssRNA), but neglects pseudoknots and tertiary interactions, the energetics of which are currently poorly characterized.

Our model yields predictions for force-extension measurements, including fluctuations, and the mechanical (un)folding pathway for any given RNA sequence. Below, we begin with the P5ab hairpin used by Liphardt et al. (2001) and demonstrate that our model yields an FEC that is in semiquantitative agreement with the experimental curve. This agreement gives us confidence that our model is sufficiently realistic to permit its use to explore general questions regarding sequence-dependent signatures in mechanical single-molecule experiments on RNA.

We first address the question of intermediates in the unfolding pathway and show that, according to our model, a small modification in the sequence of the P5ab hairpin can change its two-state folding behavior and introduce a locally dominant intermediate. However, whether this intermediate state can be observed through quasiequilibrium fluctuation measurements critically depends on the experimental conditions: If the force-measuring device is a soft spring, the hairpin unfolds without any visible intermediates. Only when the force is measured with a stiff spring can an intermediate state be observed.

We then consider a larger RNA molecule, the group I intron of Tetrahymena thermophila with a sequence of ∼400 bases and a known secondary structure containing many individual elements (Cech, 1993). Previous theoretical work predicted that equilibrium FECs of large RNAs are smooth and display no secondary structure dependent features, due to a compensation effect between individual structural elements (Gerland et al., 2001). Here, we find that even in the absence of structure-based features in the FEC, measurements of the equilibrium fluctuations of the entire molecule can still be useful to obtain information on the (un)folding pathway. Also, for this longer molecule, a good choice of the stiffness of the force-measuring device is important for the determination of the pathway.

Finally, we compare the mechanical unfolding process studied here with the more conventional thermal unfolding. Again using the group I intron as an example, we find that the individual structural elements display significantly sharper opening transitions for force-induced than for thermal denaturation within our model. Indeed, in UV absorption experiments (Banerjee et al., 1993), thermal melting of the intron shows only one broad signature associated with the opening of the secondary structure.

MODEL

We consider an experimental setup where the two ends of an RNA molecule are attached to a force- and extension-measuring device, e.g., an atomic force microscope or beads trapped by optical tweezers. For the sake of concreteness, we use the optical tweezer setup sketched in Fig. 1 a as an example here. In an idealized theoretical model, the RNA molecule (in essence, a highly nonlinear elastic element for the present context) is connected in series with a linear harmonic spring, and the total extension is externally controlled (see Fig. 1 b). The linear spring models the force-measuring device. E.g., for optical tweezers, its harmonic potential approximates the potential of the optical trap, and the spring constant λ is adjustable in the experiment through the laser intensity. The extension of the spring, R_s, corresponds to the position of the bead with respect to the minimum of the trapping potential, and is measured as a function of the total extension R_t. The average force acting on the RNA molecule and its average extension are

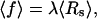(1)

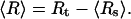(2)

Here, 〈…〉 denotes a thermal average over all accessible conformations of the RNA molecule and the spring at fixed total extension R_t. Throughout this article, we assume that the pulling experiment is performed slowly enough, such that the RNA molecule can fully sample its conformational space on timescales that are short compared to the external timescale of the imposed stretching process. This limit corresponds to the quasiequilibrium regime, where the work dissipated in the pulling process is negligible. The average 〈…〉 then includes an average over all possible secondary structures of the molecule.

FIGURE 1.

Sketch of the system considered. (a) In a typical experimental setup, the two ends of an RNA molecule are attached to beads, the position of which is controlled, e.g., with optical tweezers. (b) In a theoretical model, the potential of the optical trap can be approximated by a linear spring (with spring constant λ). This spring is connected in series with a highly nonlinear elastic element (the RNA molecule, usually with an additional linker). The total extension, R_t, is externally controlled, whereas the individual extensions, R_s and R, undergo thermal fluctuations.

Partition function

To calculate the averages in Eqs. 1 and 2, as well as the averages of other observables to be introduced below, we first determine the partition function, Z(R_t), of the RNA molecule and the spring at fixed total extension R_t. In previous work (Gerland et al., 2001), we computed the partition function of the RNA molecule alone in the fixed distance ensemble. Here, we explicitly take the force-measuring spring into account; varying the spring constant λ interpolates between the fixed distance ensemble for stiff springs (large λ) and the fixed force ensemble for soft springs (small λ). Intermediate spring constants effectively put the RNA molecule into a mixed ensemble. The explicit consideration of the spring in the model is necessary here, not only for a closer modeling of the actual experimental setup, but also from a theoretical point of view, since the force fluctuations diverge in the fixed distance ensemble and our aim is to study fluctuation measurements.

A model for an experimental setup such as the one sketched in Fig. 1 a requires two separate parts, one that contains only information on the free energies for the secondary structures of the RNA sequence, and another that describes the polymer properties of ssRNA (Gerland et al., 2001). The coupling between these two parts is through the total length of the exterior ssRNA segments of the molecule, i.e., the number m of bases that actually “feel” the applied force (see Fig. 1 a). For every fixed total extension R_t, the system has to find a compromise between lowering the RNA binding energy by decreasing m, and gaining entropy (plus lowering elastic energy) by increasing m. The secondary structure part is given by the partition function, Q(m), summed over all secondary structures of the RNA molecule with a fixed number m of exterior single-stranded bases. (We account for the width of stems within the exterior single strand by increasing the base count m by three for each stem.) The polymer properties of ssRNA then enter through a function W_tot(R_t;m), which denotes the total end-to-end distance distribution of an ssRNA molecule of m bases in series with the spring. (For simplicity, we restrict the spring to be collinear with the end-to-end distance of the RNA molecule.) The total partition function, Z(R_t), is then simply the convolution of Q(m) with W_tot(R_t;m),

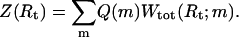(3)

The detailed calculation of Q(m) is described in Gerland et al. (2001). Briefly, the calculation takes the experimentally determined rules for the binding free energies of RNA secondary structures (Walter et al., 1994) into account, but neglects tertiary structure effects and pseudoknots. Our method is based on a recursive method to calculate the partition function (McCaskill, 1990) as implemented in the “Vienna RNA Package” (Hofacker et al., 1994), but introduces an additional recursion relation for the calculation of Q(m).

The total end-to-end distance distribution of an ssRNA molecule of m bases in series with the spring can be expressed as

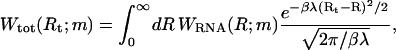(4)

where W_RNA(R;m) denotes the distribution of the ssRNA molecule alone. We model the ssRNA as an elastic freely jointed chain, i.e., as a chain of segments with unrestricted relative orientations, whereas the segment length r is constrained by a harmonic potential V(r) = κ(r − b)²/2. The average segment length b corresponds to the Kuhn length of a noninteracting ssRNA chain. The number of segments of the elastic freely jointed chain used to represent an RNA molecule with m bases is chosen as ml/b where l is the base-to-base distance of ssRNA. This yields 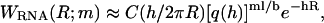where C is a normalization constant, 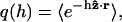and h is determined from 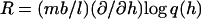(Gerland et al., 2001). Such a model has been shown to describe the elastic properties of ssDNA molecules (Maier et al., 2000; Montanari and Mézard, 2001). Since we are not aware of the corresponding data for RNA, we use the DNA values for the polymer parameters as obtained by Montanari and Mézard (2001) through fitting to the experiment of Maier et al. (2000), i.e., l = 0.7 nm, b = 1.9 nm, and (κ/k_BT)^−1/2 = 0.1 nm (we do not expect a large difference in the single-strand properties of DNA and RNA because of the high similarity between their chemical structures). We take the free energy parameters for RNA secondary structure as supplied with the Vienna package (version 1.3.1) at room temperature T = 25°C. The salt concentrations at which the free energy parameters were measured are [Na⁺] = 1 M and [Mg²⁺] = 0 M.

Observables

From the partition function (Eq. 3), we get the total free energy F(R_t) = −k_BT log Z(R_t), the average force 〈f〉 = ∂F(R_t)/∂R_t, and through Eqs. 1 and 2 also the average extension 〈R〉 of the RNA molecule. The equilibrium fluctuations in the extension of the RNA molecule are given by (δR)² = 〈R²〉 − 〈R〉² = [λ − ∂²F/∂R_t²]/βλ². Using these relations, one can show (the derivation is straightforward after observing that 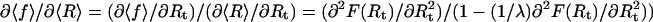that the variance is related to the derivative of the FEC as measured in the mixed ensemble through

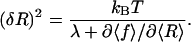(5)

This exact relation simply expresses the intuitive result that the extension of the molecule undergoes large thermal fluctuations in the flat regions of the FEC.

To study the unfolding pathway, we introduce the weight x_m(R_t) for the secondary structures with m exterior open bases at a given value of R_t,

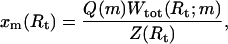(6)

which satisfy the normalization condition 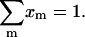The binding probability of base i and j at given R_t may then be expressed as

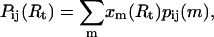(7)

where p_ij(m) denotes the basepairing probability in the ensemble of structures with fixed m, which can be calculated as described previously (Gerland et al., 2001).

RESULTS

We first consider the P5ab hairpin, which is the simplest RNA molecule studied in the experiment of Liphardt et al. (2001), and is of a size that typically occurs as a structural subunit in larger RNAs. Fig. 2 a shows its native structure and the experimental FEC for P5ab with added linker, taken with permission from Liphardt et al. (2001). The superimposed solid line shows the FEC that results from our model as described above with a spring constant of λ = 0.2 pN/nm (the native structure of P5ab contains two nonstandard G-A basepairs for which no quantitative information on the binding energies is available. We therefore follow the suggestion of Liphardt et al. (2001) and approximate the binding energy of G-A basepairs by replacing them with G-U pairs). Here, we modeled the RNA-DNA hybrid linker, which in the experiment connects the RNA molecule to the beads, as a wormlike chain (WLC) with an experimentally known length of L = 320 nm. We used the WLC interpolation formula (Bustamante et al., 1994)

(8)

where the value for the persistence length, l_p = 3.57 nm, and the (experimentally unknown) origin of the distance scale were obtained by fitting to the experimental FEC at low forces. The shape of the experimental FEC is well captured by the theoretical curve, with a characteristic “hump” indicating the opening of the hairpin (the force drop in the hump occurs, because the released single-strand creates “slack” in the polymer). However, the force at which the hairpin opens is overestimated by the theoretical model. To assess the origin of this discrepancy, we applied a simple salt correction to the RNA-binding (free) energies (SantaLucia, 1998) to account for the different ionic conditions between the single-molecule experiment ([Na⁺] = 0.25 M) and the standard conditions ([Na⁺] = 1.0 M). The resulting FEC (dashed line in Fig. 2 a) yields near-quantitative agreement with the experiment, indicating that the difference in ionic conditions accounts for most of the discrepancy. The remaining discrepancy could be caused, for instance, by the freely jointed chain model for ssRNA or the unknown stacking energies for G-A basepairs. However, the good agreement we have achieved seems sufficient to justify the use of our model as a tool to study the general questions outlined in the Introduction (in the following, we keep the salt concentration at the standard conditions).

FIGURE 2.

Force-extension curve for the P5ab hairpin with added linker. (a) Native structure of the hairpin, its FEC as experimentally determined by Liphardt et al. (2001), and the FEC resulting from our model for two different salt concentrations. (b) FEC for P5ab as results from our model for two different spring constants λ (solid and dashed lines; see main text for details). The dotted line represents the FEC for a nonbinding sequence of the same length as P5ab. (Inset) End-to-end distance fluctuations as a function of the average extension.

The FECs in Fig. 2 contain useful information on the RNA molecule. For instance, the total binding free energy and the size of the hairpin can be read off by comparing to the FEC for a nonbinding control sequence. Within our theoretical model, such control curves are obtained through a convolution of the WLC model (Eq. 8) for the linker with the freely jointed chain model for the single-stranded RNA. The resulting curves could also be used as a reference for the experimental data, although ideally the control curve should be measured, using, e.g., an oligonucleotide with a homogeneous sequence (note that it suffices to record the control for a single-sequence length, since it can be straightforwardly rescaled to an arbitrary length). Fig. 2 b shows our theoretical FEC for P5ab both for a stiff spring (λ = 0.2 pN/nm, solid line) and a soft spring (λ = 0.01 pN/nm, dashed line), together with the control FEC (dotted line) for a sequence of commensurate length. Since stretching the control sequence requires only work against entropic and elastic forces, whereas stretching of the P5ab hairpin requires additional work to break the basepairs, the area between the two FECs equals the total binding free energy of P5ab. As Fig. 2 b shows, not only the region of the P5ab FEC where the basepairs are opened (the “hump” region) contributes to this area, but there is also a significant contribution from the initial part of the FEC. The initial part of the P5ab FEC corresponds to stretching the exterior single-stranded chain of the molecule, which is shorter than the full molecule and hence has higher entropic/elastic forces at the same extension. However, this additional entropic/elastic energy is “stored” in the molecule and is fully released when the hairpin is (adiabatically) unzipped, i.e., in the “hump” region. Note that as long as the experiment is performed in quasiequilibrium, the area under the FEC is independent of the spring constant, and therefore the same in the fixed-force and the fixed-distance ensemble. Loosely speaking, the FEC in the fixed-force ensemble could therefore be considered as the “Maxwell construction” of the FEC in the fixed-distance ensemble.

We now seek to characterize the unfolding process of the P5ab hairpin within our model. In the experiment of Liphardt et al. (2001), the time traces of the end-to-end extension at fixed forces around 14 pN show the characteristic pattern of a bistable system, i.e., the unfolding proceeds directly, without intermediates. To calculate theoretical time traces would require a full kinetic treatment of the RNA folding/unfolding process, which is beyond the scope of the present article. Instead, we determine the amplitude of the equilibrium fluctuations in the end-to-end extension, δR, as a function of the mean force or extension. Experimentally, this amplitude would be determined as a time-average, 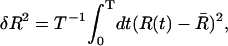where R(t) denotes the recorded time trace of the end-to-end extension and 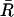its average. Our theoretical prediction is for the infinite time limit, T → ∞, of this average. Note that the exact relation Eq. 5 directly links the equilibrium fluctuations to the derivative of the averaged FEC. In practice, where the averaging period T is finite and limited to a few minutes by instrumental drift (Liphardt et al., 2001), the amplitude δR can be determined with much greater accuracy than the derivative of the time-averaged FEC, since taking the derivative strongly amplifies the statistical error. Therefore, the quasiequilibrium FEC and the equilibrium fluctuations, δR, can effectively be regarded as two independent and complementary sources of information.

The inset of Fig. 2 b shows the fluctuations δR as a function of the average extension, 〈R〉, in the range of extensions over which the hairpin opens. We observe a single peak of the fluctuations at the force/extension where the transition takes place, which is consistent with the two-state behavior found experimentally. Physically, this peak is caused by continual kinetic fluctuations between the open and the closed state of the hairpin.

Hairpin with intermediate

Next, we address the question whether the simple two-state behavior observed for P5ab is a generic property for hairpins of this typical size. The discussion of this question also serves as a preparation for our ensuing study of a larger RNA with more complicated structure. To this end, we modify the sequence of the P5ab hairpin slightly by replacing the two G-A basepairs with U's on both strands, which leads to a small interior loop in the hairpin. This change does not significantly affect the FEC (see Fig. 3 a); however the fluctuations δR take on a qualitatively different behavior, as shown in Fig. 3 b: For a soft spring, the δR curve shows only a single peak as before, but a stiff spring yields two maxima with a pronounced minimum in between. At this minimum, the configurational distribution of the molecule is localized on an intermediate state, which strongly reduces the fluctuations in the extension. This is demonstrated explicitly in Fig. 4, which shows the probability distribution in m-space, i.e., x_m as given by Eq. 6 (see figure legend for details).

FIGURE 3.

Calculated force-extension characteristics for the modified P5ab hairpin (G-A basepairs replaced by A-A) for a hard (λ = 0.2 pN/nm) and a soft (λ = 0.01 pN/nm) harmonic potential of the optical tweezer. (a) The average FEC, which resembles very much the FEC in Fig. 2 b. (b) The fluctuations of the extension as a function of the average extension. Although the curve is very similar to the inset of Fig. 2 b for a soft spring, it develops a pronounced minimum corresponding to an intermediate state for a hard spring. The arrows indicate the positions at which the x_m distributions shown in Fig. 4 were calculated.

FIGURE 4.

Probability distributions in m-space for the modified P5ab hairpin. The left column is calculated with a soft spring (λ = 0.01 pN/nm), and the right column with a stiff spring (λ = 0.2 pN/nm). The curves in the top, middle, and bottom rows are calculated for different average extensions 〈R〉 corresponding to the positions indicated by the arrows in Fig. 3 b (first peak, minimum, and second peak in the fluctuation curve, respectively). For the stiff spring, the distribution at the minimum is almost entirely localized on the intermediate state. In contrast, the distribution is spread out over all three states for the soft spring at the same average extension.

The stiffness of the external spring therefore limits the attainable resolution of the measurements: At low resolution, the hairpin appears as a two-state folder, whereas an intermediate state appears at higher resolution. This observation is in line with the comment of Fernandez et al. (2001) who discuss the experiment of Liphardt et al. (2001) by analogy to patch-clamp experiments, where an intermediate state in the opening of an ion channel appears only at high resolution. While an increase in the spring constant increases the resolution, it decreases the amplitude of the fluctuations, which renders them harder to detect. For the present purpose, the optimal value for λ results from a trade-off between low resolution and low amplitude. Clearly, increasing λ can increase the resolution only up to the point where the floppiness of the RNA plus linker becomes resolution-limiting (this point corresponds approximately to λ = 0.5 pN/nm for the hairpin sequences with linker discussed above). This point marks the optimal choice for λ, unless the spacial resolution of the experimental apparatus is restrictive already at smaller values of λ. The role of the spring constant in dynamic force spectroscopy measurements is discussed by Heymann and Grubmüller (2000).

Intuitively, the fact that the appearance of the intermediate state depends on the spring constant is best understood by mapping the unzipping problem onto the problem of a particle with an attached spring in a random potential and coupled to a thermal bath (see Fig. 5). As the other end of the spring is moved in one direction, the particle performs a “stick-slip” motion (Bockelmann et al., 1998). With a stiff spring, the particle hops over short distances and tends to be localized, whereas the particle can make long jumps, sliding over many valleys, when the spring is soft.

FIGURE 5.

Particle with an attached spring in the free energy landscape of the modified P5ab hairpin. The other end position of the spring is externally controlled (see Gerland et al., 2001, for the details of the mapping to the RNA unzipping problem). The spring in this picture represents the measurement device, the linker, and the ssRNA, and has an effective spring constant 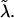Its harmonic potential for λ = 0.01 pN/nm and λ = 0.2 pN/nm is shown as the dashed and dash-dotted lines, respectively. With the soft spring, the particle can jump from the closed to the open state immediately as soon as the force is strong enough to overcome the energy barrier. The hard spring has a steeper harmonic, potential and thus the particle will first jump into the intermediate state and later into the open state as the end of the spring is moved toward larger m.

RNA molecule with multiple structural subunits

Longer RNA molecules typically have a complex structure with many structural subunits interacting through weak tertiary contacts (Tinoco and Bustamante, 1999). A typical example for a structural subunit is the P5ab hairpin studied above, which is indeed extracted from a larger RNA molecule, the self-splicing intron of T. thermophila with a sequence of 419 bases (GenBank No. J01235). The known secondary structure of this intron comprises 19 structural elements labeled P1, P2, P2.1, P3, etc. It was the first RNA molecule to be shown to have a catalytic activity and has since been studied in great detail (Cech, 1993). Its active, i.e., self-splicing, conformation contains a pseudoknot, which is essential for the function. However, it also has a known stable and well-characterized inactive conformation without pseudoknot (Pan and Woodson, 1998; Zhuang et al., 2000). The minimum free energy structure obtained from the Vienna RNA Package (which supplies the basis to our model) is shown in Fig. 6. The overall structure, and almost all individual basepairs, are identical to one of the inactive conformation as determined by Pan and Woodson (1998) (we follow the labeling introduced there), which confirms that the RNA free energy rules describe the nucleotide interactions quite well. For the cyclized form of this intron, a very similar secondary structure was obtained by Jaeger et al. (1990).

FIGURE 6.

Secondary structure of the Tetrahymena thermophila group I intron as obtained from the Vienna package. The overall structure, and almost all individual basepairs, are identical to the one of the inactive conformation as determined by Pan and Woodson (1998) (we follow the labeling introduced there).

For complex secondary structures such as the one shown in Fig. 6, it is interesting to study the physical process of structure formation, whereby e.g., a newly produced RNA molecule folds into its preferred structure(s). For instance, one may ask, in which order do the structural elements in Fig. 6 form, i.e., what is the folding pathway? Mechanical single-molecule experiments offer a very controlled way to probe the folding process. In the quasiequilibrium limit that we consider, the mechanical folding pathway is independent of i), the direction, i.e., unfolding and refolding pathway are identical, and ii), specific experimental parameters such as the spring constant λ. The latter is clear from the fact that the number of exterior unpaired bases, m, is a natural and well-defined reaction coordinate in the quasiequilibrium limit. On average, the distribution x_m will always shift to larger m when R_t is increased, and hence λ can only affect the resolution of individual states in m-space, but not the average order in which they are visited.

How can one determine the (un)folding pathway in a single-molecule experiment? As we have seen, pulling on an isolated subunit produces a characteristic signature in the FEC (see Fig. 2). If every structural subunit in a larger RNA molecule would produce such a characteristic signature, one could directly read off the folding pathway from the FEC. However, our previous theoretical study predicted that the quasiequilibrium FEC of RNAs with many subunits will typically show no distinguishable signatures of individual subunits opening (Gerland et al., 2001). This prediction is consistent with the experimental observation of smooth FECs for long ssDNA molecules (Maier et al., 2000). Three physical effects are responsible for the smoothness: i), the “floppiness” of the external single strand and the linkers, ii), thermal fluctuations in the secondary structure, i.e., the contribution of suboptimal structures, and most importantly, iii), the fact that changes in the extension of individual structural subunits can compensate each other, since only the total end-to-end distance is measured (Gerland et al., 2001). As a result, quasiequilibrium FECs cannot be used to study the folding pathway (or the secondary structure) of larger RNA molecules.

The smoothing mechanisms (ii and iii) can be strongly suppressed by performing the experiments at large pulling speeds, which do not leave sufficient time for the molecule to sample the entire ensemble of different secondary structures with similar number of exterior unpaired bases, m, and free energy of folding. Hence, nonequilibrium FECs of larger RNA molecules should be very rugged and display signatures of individual structural elements opening (see also the discussion in Gerland et al., 2001). This was indeed observed recently in the Berkeley group (S. Dumont and I. Tinoco, Jr., private communication). From the theoretical side, the calculation of nonequilibrium FECs is challenging, since the simple particle-in-a-landscape picture of Fig. 5 breaks down in nonequilibrium: The free energy landscape is no longer well-defined. The secondary structures that are accessible for a molecule at a given extension and within a given time window depend on the present structure of the molecule and the detailed folding kinetics. Although important steps toward a kinetic theory of RNA folding have been taken (Isambert and Siggia, 2000), there is currently insufficient experimental information available to construct a full theoretical model.

Here, we consider instead the equilibrium fluctuations in the end-to-end distance of the entire intron, and explore, within our theoretical model, how much information on the folding pathway can be obtained from this. Although looking at the equilibrium fluctuations does not suppress any of the above-mentioned smoothing mechanisms, it does provide a greater resolution for the observation of structural transitions, as already discussed. We will see in the following that this enhanced resolution, which is dependent on the spring constant, is sufficient to reveal major steps of the unfolding process.

The quasiequilibrium FEC of the intron is shown in Fig. 7 a. Here, we have not added an additional linker in the calculation, since the intron is already fairly large and flexible, so that the effect of a comparatively short and stiff double-stranded linker is negligible. As expected, the FEC displays no signatures of the secondary structure, mostly due to “compensation” between different structural elements (Gerland et al., 2001). As for the P5ab hairpin above, we compute the equilibrium fluctuations δR, which would correspond to the average standard deviation in an infinitely long experimental time trace R(t). Obviously, our averaged δR contains less information than experimental R(t) traces. Nevertheless, as Fig. 7 b shows, already the equilibrium fluctuations δR display interesting sequence-dependent features, i.e., local maxima and minima. The minima can again be interpreted as intermediate states along the (un)folding pathway, and the maxima as structural transitions. Note that the central peak close to 〈R〉 = 150 nm splits into two peaks as the stiffness of the spring is increased, indicating the appearance of a new intermediate on the (un)folding pathway. This illustrates again how the ability to resolve intermediate states depends on the stiffness of the force-measuring device. For the choice of the latter, a trade-off between resolution of intermediate structures and fluctuation amplitude has to be respected.

FIGURE 7.

Calculated force-extension characteristics of the Tetrahymena thermophila group I intron. (a) FEC. (b) Fluctuations in the extension of the ribozyme for different stiffness λ of the force-measuring device. (c) Fractional opening for all of the structural elements at λ = 0.02 pN/nm. A black square indicates that the structural element is completely intact whereas a white square indicates that all basepairs of the element have been opened. It can be seen that the FEC lacks all structural features. In contrast, the fluctuations display pronounced peaks that coincide with the disappearance of specific structural elements.

Within our theoretical model, it is a simple matter to identify the structural transitions associated with the peaks in Fig. 7 b. To obtain a measure for the likelihood to find a given structural element at a given mean extension of the molecule, we have summed the basepair probabilities for all basepairs in the element and divided by the total number of basepairs in the intact element. Here, the basepair probabilities at a given extension are computed using Eqs. 6 and 7. For each of the labeled structural elements in Fig. 6, we plotted the normalized total basepair probabilities as a function of the mean extension at λ = 0.02 pN/nm in Fig. 7 c using a gray-scale code (black corresponds to presence of the element with probability 1 and white to absence of the element). We observe that the opening of most structural elements is localized to a relatively small extension interval, however, typically the opening of several elements takes place simultaneously. Roughly, the structural elements open in the following order: P7, Alt P3, P4, P5, P5a, P1, P2.1, P6a, P9.1, P9.1a, P9.2, P2, P9, P8, P6b, P5c, and P5b.

By simultaneous inspection of Fig. 7, b and c, we can assign particular peaks in the fluctuation curve to the opening of particular elements. For instance, the central peak is associated with the parallel opening of P9.1, P9.1a, and P9.2, whereas the most stable elements P5b, P5c open at the final hump. Generally, elements that free a lot of single strand upon opening, such as a stem-loop structure with a large loop (e.g., P2.1), are associated with a distinct peak in the fluctuation curve. This peak reflects the large difference in extension between the open and closed state of the element.

To obtain the information displayed in Fig. 7 c in the experiment will be more laborious, but should be possible given the known secondary structure. Since at every mean extension (or force) only a small number (up to three) structural elements open in parallel, one can expect a small number of characteristic plateaus in the experimental R(t) traces. The identification of the plateaus with the corresponding elements can be obtained by cutting the molecule at several places between the known secondary structure elements and performing the same measurement on subsequences. A similar approach was taken for recent nonequilibrium experiments in the Berkeley group (S. Dumont and I. Tinoco, Jr., private communication). Obtaining the mechanical (un)folding pathway for a moderately sized RNA with known secondary structure therefore appears feasible by measuring the fluctuations.

It is interesting to compare the mechanical unfolding studied so far with thermal unfolding. The thermal unfolding process of the group I intron can be studied theoretically with the Vienna RNA Package (Hofacker et al., 1994). Fig. 8 b shows the fractional opening of all structural elements as in Fig. 7 c, but plotted against temperature. We observe that the individual stems show a less sharp transition from closed to open than in Fig. 7 c. As a result, the specific heat curve shown in Fig. 8 a displays only a single broad peak for the unfolding of the secondary structure (the specific heat is obtained from the total folding free energy, ΔG, through −T ∂²(ΔG)/∂T²). This is consistent with UV absorption experiments (Banerjee et al., 1993) that found only two broad peaks for the same RNA, where the low-temperature peak could be associated with melting of the tertiary structure and the high-temperature peak with the secondary structure.

FIGURE 8.

Thermal unfolding of the intron. (a) Specific heat curve. (b) Fractional opening for all of the structural elements. Analogously to Fig. 7 c, a black square represents a fully formed structure whereas a white square represents a structure that has fully opened up.

From Fig. 8 b, a rough order for thermal opening of the structural elements can be discerned: P4, P5, P5a, P6a, P7, Alt P3, P1, P2.1, P9, P8, P9.1a, P9.2, P9.1, P6b, P5b, P2, P5c. No structural element in this thermal (un)folding pathway is more than four list positions away from its place in the mechanical (un)folding pathway discussed above. This suggests that the thermal and mechanical unfolding pathways, although different in detail, can still be used as reasonable priors for each other.

SUMMARY AND DISCUSSION

Single-molecule experiments are particularly useful when the molecule under study can take on several conformations, e.g., folding intermediates, because in these cases bulk measurements usually yield only average properties, whereas single-molecule measurements can characterize each of the different conformations. Here, we predicted experimental signatures of such folding intermediates in the quasiequilibrium fluctuations of the end-to-end distance. We found that a local minimum in the fluctuations curve indicates a locally stable intermediate state in the average mechanical unfolding pathway (which is well-defined and identical to the (re)folding pathway). The number of local minima in the fluctuations curve can therefore serve as a lower estimate of the number of locally stable intermediate states in this pathway. Furthermore, these signatures could be used to reconstruct the (un)folding pathway of an RNA molecule with a known secondary structure by cutting the sequence at appropriate positions and individually probing different substructures of the molecule.

We also showed that the stiffness of the force-measuring device plays a crucial role in determining the resolution of the quasiequilibrium fluctuations curve. If the device is too soft, some local minima can be lost, whereas a too rigid device has a low fluctuation amplitude and therefore a low signal-to-noise ratio. The optimal choice for the stiffness (see Results) leads to the best estimate for the number of locally stable intermediate states along the pathway and increases the degree to which the pathway could be reconstructed with the “cutting approach”. The dependence on the stiffness has a simple intuitive explanation within the statistical mechanics problem of a particle with an attached spring in a one-dimensional energy landscape (see Fig. 5): A stiff force-measuring device corresponds to a rigid spring, which tends to localize the particle in valleys of the landscape (i.e., locally stable intermediates) and forces it to make small jumps as it is pulled along the landscape. On the other hand, a soft spring allows the particle to spread out and make long jumps, effectively hiding the intermediates in the equilibrium curve.

We hope that this view, which also explains the smoothness of quasiequilibrium FECs for large RNAs (Gerland et al., 2001), will be useful for the design and interpretation of future experiments. Of course, experiments typically record not only the average fluctuations, but the detailed time traces of the end-to-end distance (Liphardt et al., 2001). These traces probe the kinetics of structural rearrangements in RNA, and could provide even more detailed resolution of intermediate states (if the kinetics is slow enough to be resolvable in the experiment). However, we expect that it is still helpful to make the choice for the stiffness of the force-measuring device as discussed above, to limit the number of states that contribute to each of the time traces.

Although single-molecule experiments on RNA have already produced remarkable results, there are many desirable future developments. For instance, it appears that the current approaches are not well suited to measure the secondary structure of an unknown molecule (e.g., in the cutting approach, one would not know where to cut and it would be too laborious to try all positions). Is there a direct way to mechanically measure the secondary structure? Also, could one detect signatures of pseudoknots or even tertiary interactions? We hope that theoretical models of the type presented here can be useful for the planning and design of new experimental approaches in the future.