Abstract
We present a model for cooperative myosin binding to the regulated actin filament, where tropomyosins are treated as a weakly-confined continuous flexible chain covering myosin binding sites. Thermal fluctuations in chain orientation are initially required for myosin binding, leaving kinked regions under which subsequent myosins may bind without further distortion of the chain. Statistical mechanics predicts the fraction of sites with bound myosin-S1 as a function of their affinities. Published S1 binding curves to regulated filaments with different tropomyosin isoforms are fitted by varying the binding constant, chain persistence length ν (in actin monomers), and chain kink energy A from a single bound S1. With skeletal tropomyosin, we find an S1 actin-binding constant of 2.2 × 107 M−1, A = 1.6 kBT and ν = 2.7. Similar persistence lengths are found with yeast tropomyosin. Larger values are found for tropomyosin-troponin in the presence of calcium (ν = 3.7) and tropomyosins from smooth muscle and fibroblasts (ν = 4.5). The relationship of these results to structural information and the rigid-unit model of McKillop and Geeves is discussed.
INTRODUCTION
The regulation of contractility in striated muscle by calcium is effected via tropomyosin on the actin filament (Ebashi, 1969). The tropomyosin molecule is a coiled-coil 42 nm in length, which covers seven monomers on one strand of the actin double helix. On each strand these units are disposed end-to-end to form what appears to be a continuous chain (Lorenz et al., 1995; Vibert et al., 1997). The steric blocking model of Haselgrove (1973) and Huxley (1973) proposes that myosin binding sites are blocked by tropomyosin·troponin (TmTn) in the absence of calcium, and that tropomyosin moves to a position which allows myosin binding when calcium is bound to troponin-C. The two positions of tropomyosin may be viewed as two states of an allosteric system if transitions between them are rapid and in equilibrium (Lehrer and Geeves, 1998). The steric blocking model is broadly confirmed by a variety of experiments (Gordon et al., 2000), although the fact that myosin binds weakly in the absence of calcium suggests that a two-state model may be oversimplified.
The statistical-mechanical model of thin filament regulation proposed by Hill, Eisenberg, and Greene (Hill et al., 1980a) is based on these ideas. The key assumptions of their model are that 1), each tropomyosin molecule can be treated as a rigid unit moving between two discrete orientations which generate different actin affinities for myosin; 2), states of the same kind are favored by weak end-to-end interactions between adjacent tropomyosins; and 3), Tm-Tm interaction energies vary with the number of calcium ions bound to the nearest molecule of TnC. This model contains two mechanisms for cooperativity in myosin binding; a single bound myosin activates the six additional actin monomers covered by one tropomyosin, and this activation is partially transmitted to neighboring tropomyosins by end-to-end interactions. Cooperativity is observed in solution studies of the extent and kinetics of myosin binding (Greene and Eisenberg, 1980; Trybus and Taylor, 1980; McKillop and Geeves, 1991) and of actomyosin ATPase (Bremel et al., 1972; Lehrer and Morris, 1982). In vertebrate striated muscle, the high sensitivity of isometric force to changes in calcium level can also be explained in terms of calcium-dependent Tm-Tm interactions (Hill, 1985).
Later cryo-EM studies show that there are actually three orientational states of tropomyosin (Vibert et al., 1997), designated by Lehman et al. (2000) as B (blocked), C (calcium-induced), and M (myosin-induced). A model with three regulatory states of the thin filament (blocked, closed, and open) was previously proposed by McKillop and Geeves (1993), based on solution studies of myosin-S1 binding to thin filaments. However, this model did not invoke end-to-end Tm interactions; the regulatory unit was originally identified as the structural repeat unit of one tropomyosin and seven actin monomers (A7Tm). The development of assay methods sensitive to the size of the regulatory unit showed that cooperativity could extend significantly beyond the structural unit size for both actin-Tm and actin-Tm-Tn filaments (Geeves and Lehrer, 1994, Lehrer et al., 1997, Maytum et al., 1999). For these systems, a model of independent regulatory units is structurally inappropriate. A version of the Hill-Eisenberg-Greene model with three regulatory states would provide a way out of these difficulties.
In fact, we wish to argue for a more radical revision of existing regulatory models, in which individual tropomyosin molecules have intrinsic flexibility and are coupled by strong end-to-end interactions to form a semiflexible chain. Evidence which points in this direction is as follows.
In solution, tropomyosin readily polymerizes end-to-end at ionic strengths below ∼0.3 M, and the polymer is flexible with a persistence length of 50–200 nm (Howard, 2001). However, individual molecules of tropomyosin have a very low affinity for actin (Wegner, 1979), so that the binding of Tm filaments to actin can also be described as a polymerization process (Vilfan, 2001). This view is supported by the observation that minor modifications to either the N-terminus (loss of acetylation) or the C-terminus (loss of the terminal amino acid) of the Tm polypeptide chain does not greatly affect the stability of Tm but results in loss of polymerization and actin binding (Heald and Hitchcock-deGregori, 1988; Maytum et al., 2001). Thus the head-to-tail interactions between tropomyosins along the actin filament are essential for actin affinity. High-resolution structural data (Brown et al., 2001, Whitby and Phillips, 2000) also suggest that tropomyosin is a semiflexible molecule (see also Stewart, 2001). Atomic modeling of tropomyosins on the actin surface suggests that Tm is bound by weak electrostatic interactions which are not highly stereospecific (Lorenz et al., 1995). Furthermore, both the Hill-Eisenberg-Greene and McKillop-Geeves models give an equilibrium constant of 0.2 for the transition between closed and open states of the actin-Tm filament, so that the Gibbs energy difference between these states is 1.6 × thermal energy. The rate of transitions between these states is estimated at above 500 s−1 (Geeves and Lehrer, 1994), suggesting a low activation barrier between binding positions. If a single Tm molecule in a Tm chain were to move between the discrete binding sites on actin inferred from EM and x-ray scattering, a major reorganization of the Tm-Tm contacts would be required, yet these are the contacts which are essential for binding to actin.
Whatever the exact nature of Tm-Tm and Tm-actin interactions, there is now a body of evidence which suggests that tropomyosin molecules on actin form a loosely-confined quasi-continuous semiflexible chain which spans the whole actin filament. We propose a new model of thin-filament regulation along these lines. To make the problem mathematically tractable the tropomyosin chain is treated as elastically homogeneous. Similarly, the potential well which provides angular confinement is assumed to have a single minimum in the absence of myosin or troponin. As discussed in the last section, the second hypothesis is still open.
In this article, the continuous-flexible-chain (CFC) model is applied to actin-tropomyosin systems in the absence of troponin. Mathematical developments appear in a self-contained section (Theory), which can be omitted if desired. Here we show that the model can fit published experimental myosin binding curves in solution, using reasonable values of parameters such as chain stiffness and the distortion energy of the chain accompanying myosin binding. The results are in broad agreement with those obtained from the independent-rigid-unit model (McKillop and Geeves 1991, 1993). Chen et al. (2001) have shown that the same binding curves can also be fitted with the model of Hill, Eisenberg, and Greene (Hill et al., 1980a). Thus the CFC model should be tested against a much wider range of experiments. In the following article, the model is generalized to actin-Tm-Tn systems and regulation by calcium.
Definitions of model parameters and other symbols are collected in Table 1. Fortran programs for numerical predictions and data-fitting to the model are available at www.kcl.ac.uk/depsta/biomedical/randall/dasmith.html.
TABLE 1.
| Key model parameters | |
|---|---|
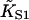 |
Second-order binding constant of myosin to actin |
| A | Chain kink energy for one bound myosin |
| ν | Persistence number = 1/ξc |
| Associated parameters, variables, and constants
| |
| α | Strength of the chain confining potential |
| κ | Chain bending stiffness per unit length (see under Eq. 1) |
| ξ | Inverse persistence length = (α/4κ)1/4 |
| φ+ | Myosin kink angle (>0) |
| δφ | Angular standard deviation of free chain = (8βκξ3)−1/2 |
| n | Hill coefficient |
| s | Distance along the chain |
| [S1] | Free myosin concentration |
| KS1 | First-order myosin affinity to actin 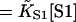
|
| K | Myosin affinity under the chain = KS1exp(−βA) |
| θ | Myosin bound fraction (of actin sites with myosin bound) |
| φ(s) | Angular displacement of the chain at position s |
| c | Actin monomer spacing (5.5 nm) |
| kB | Boltzmann's constant |
| T | Absolute temperature |
| β | =1/kBT |
Definitions of mathematical symbols appearing outside the Theory section. In this article, ln and log denote logarithms to base e and 10 respectively.
REGULATION BY A CONTINUOUS FLEXIBLE CHAIN
This section gives the basic assumptions of the proposed model, its mathematical formulation, and a qualitative description of how it regulates the energetics of myosin binding. Exact results quoted without proof are derived in a preliminary article (Smith, 2001). Kinetic aspects of myosin regulation will be considered elsewhere.
1. Tropomyosin units on the surface of F-actin are intrinsically flexible and linked to form a continuous semiflexible chain along the length of the actin filament (Fig. 1 A).
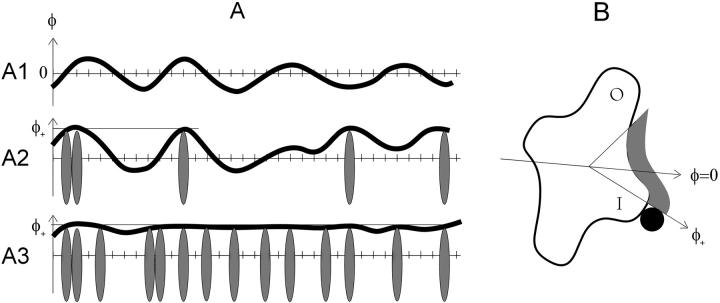
FIGURE 1.
Schematics of orientational configurations of a continuous flexible tropomyosin chain on actin (A), and a cross section of the actin filament (B). A1, A chain configuration in the absence of myosin (upper diagram), with thermally excited angular fluctuations about φ = 0, close to the groove between the inner and outer domains of G-actin depicted in B (see also Lehman et al., 2000). These fluctuations cover the myosin binding interface and collectively define a closed regulatory state. A2, The tropomyosin chain with a low density of myosins bound to actin, which push the chain beyond angle φ+ toward the inner domain. A local open state is created by each myosin-induced kink. A3, At higher myosin density, an extended open state is created. If the persistence length covers several actin sites, this can occur even when most sites are unoccupied.
2. This chain is confined to a range of orientations on one strand of the actin double helix (here termed the closed state) by a weak electrostatic potential, arising from ionic or van der Waals interactions.
This model becomes mathematically tractable if we suppose that the chain is elastically homogeneous, with a finite bending stiffness κTm per unit length, and the confining potential is a quadratic function of chain orientation φ (in radians) from a preferred orientation which tracks one helical strand. A distorted chain configuration is specified by angular displacements φ(s) at each position s along a chain of length L. The energy of this configuration is
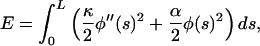 |
(1) |
where κ = κTmR2 and R the radius at which tropomyosin sits on the actin filament. Estimates of κTm from the persistence length of tropomyosin in solution (Howard, 2001; Hvidt et al., 1983, Phillips and Chacko, 1996) and by scaling as (radius)4 from actin measurements (Yanagida et al., 1984, Yasuda et al., 1996) suggest that κTm ∼ 0.4–1.6 × 10−27 N·m2. With R = 4–5 nm (Vibert et al., 1997; Xu et al., 1999), κ ∼ 0.6–4.0 × 10−44 N·m4. For estimation we use a value of 2.5 × 10−44 N·m4.
If the chain is forcibly pinned to angle φ+ at one point, the rest of the chain adopts a minimum-energy configuration in which displacements away from the pinning point revert smoothly to zero over a characteristic distance called the persistence length. The persistence length is estimated by minimizing the energy of a smooth kink of half-width l, which is of the form κ(φ+/l2)2l + αφ+2l apart from numerical factors of order unity. This energy is minimized when l = (3κ/α)1/4. An exact calculation gives the kink energy A as
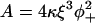 |
(2) |
where
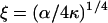 |
(3) |
and 1/ξ is the persistence length. It will be shown later that myosin binding data can be fitted to the model if ξ−1 = 16.5 nm (three actin repeats). Hence, α = 1.34 × 10−12 J/m, which implies that the energy required to displace a single 42-nm tropomyosin unit from its resting angle by 30° is ∼8 × 10−21 J, or twice thermal energy kBT (kB = Boltzmann's constant; T = absolute temperature).
3. In the absence of bound myosin, the chain makes thermal fluctuations about its preferred orientation. The standard angular deviation from thermal noise can be estimated by equating the energy of a kink of amplitude δϕ to kBT. This argument is not rigorous because thermal noise excites fluctuations on a range of wavelengths above the persistence length, but gives the correct result,
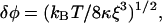 |
(4) |
apart from a numerical factor. The preceding estimates for κ and α give δϕ ∼ 0.30 radians (17°), which is physically reasonable. These fluctuations are intrinsic to the closed state.
4. In the absence of myosin, myosin-binding sites on the actin filament are covered by most thermally-driven configurations of the chain (Fig. 1), which define a closed state.
5. A myosin binding site is exposed only by a sufficiently large positive kink φ > φ+ in chain angle. To achieve myosin binding rates comparable with unregulated actin (Trybus and Taylor 1980), φ+ should not exceed two standard deviations from thermal noise, as above. Equivalently, the kink energy A should not exceed 2kBT. The binding site should span a range of angles from φ+ to a larger negative angle (Fig. 1 B), to prevent exposure by negative deviations of the chain.
Fig. 1 A shows how this model leads to cooperative myosin binding. The first myosin to bind under thermal fluctuations of the Tm or Tm-Tn chain produces a positive kink of amplitude φ+ and a half-width of one persistence length (a local open state). We define a persistence number as
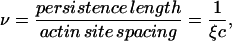 |
(5) |
so the first bound myosin exposes ν sites on either side, and the kink size (the number of actin sites exposed by the kink) is 2ν + 1.
Let 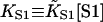 be the first-order affinity of S1 to actin in the absence of chain distortion, proportional to free myosin-S1 concentration in solution. The first myosin to bind does so with affinity
be the first-order affinity of S1 to actin in the absence of chain distortion, proportional to free myosin-S1 concentration in solution. The first myosin to bind does so with affinity
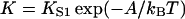 |
(6) |
reduced by the probability of a kink fluctuation. Those that follow are presented with a predominantly unkinked filament, so that at low S1 concentration the fraction θ of occupied sites is K/(K + 1). At higher concentrations, late-binding myosins see a significant fraction of sites exposed by kinked regions of the chain, and may bind to these sites at a higher affinity approaching KS1, enlarging the kinks. As more myosins bind, all kinked regions eventually overlap and further bindings are not inhibited by the chain.
The cooperative transition between these regimes should occur when the bound fraction θ ≈ (2ν + 1)−1. If θ = K/(K + 1), switching occurs when K ≈ (2ν)−1. Hence the switching value of KS1, here denoted by K*, is estimated at exp(A/kBT)/2ν. This formula exaggerates the dependence on A, because the binding curve lies between K/(K + 1) and KS1/(KS1 + 1). A better estimate can be obtained from predicted binding curves.
The structure of the model is now specified. To make quantitative predictions, expressions for the free energy of the kinked chain are needed for at least two kinks of the same angle as a function of their separation. For two kinks of angle φ+ at separation ξx, the energetic component of the distortion energy can be written in terms of the single-kink energy A as
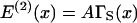 |
(7) |
(Smith, 2001). The function ΓS(x) tends to unity when x → 0 and to 2 for x ≫ 1. When the kinks are merged, the pair energy is that of a single kink, but when widely separated the pair energy is the sum of the energies of each kink in isolation. The entropic contribution is expected to vary similarly with x, in which case A can be regarded as a free energy.
Please note the following corrections to the article (Smith, 2001) in which the interaction potentials were derived:
Eq. 3.2: Replace 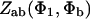 by
by 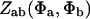 in both denominators.
in both denominators.
Eq. 4.7: The lower limit of the second sum should be i, not i + 1.
MYOSIN BINDING TO ACTIN-TROPOMYOSIN
This section develops the statistical mechanics of equilibrium myosin-S1 binding to actin regulated by a continuous flexible chain. The theoretical formalism can be used to predict the bound S1 fraction as a function of the free S1 concentration in solution, and other statistical measures of occupancy such as the correlation length between occupied sites. This model is applied to the actin-tropomyosin system in the absence of troponin. It should also be applicable to the actin-tropomyosin-troponin system at saturating levels of calcium, as troponin-I does not bind significantly to actin under these conditions.
Theory
The fraction of monomers with myosin bound can be calculated if the distortion energy of the kinked chain with an arbitrary number and position of bound myosins is known. Let F(n) (sn) be the free energy of the distorted chain covering N monomers on one strand of F-actin, with n myosins bound to monomers at positions sn = (s1,…,sn), listed in increasing order. The equilibrium probability of this configuration is a Boltzmann factor in the corresponding Gibbs energy, which is the sum of the above distortion energy and the Gibbs energy 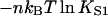 of myosin binding. Thus the probability of all configurations with n myosins bound is
of myosin binding. Thus the probability of all configurations with n myosins bound is
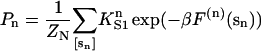 |
(8) |
where β = 1/kBT and
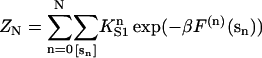 |
(9) |
is the partition function for regulated binding; the inner sum is over all ordered arrangements of n sites out of N. Hence the mean number 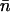 of occupied sites is given by
of occupied sites is given by
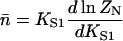 |
(10a) |
and the bound fraction is 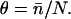 Similarly, the mean square deviation in n is
Similarly, the mean square deviation in n is
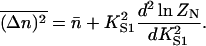 |
(10b) |
It is instructive to apply these formulae to a rigid chain covering N sites, as envisaged by Geeves and Halsall (1987) for protomeric tropomyosin with N = 7. If one bound myosin displaces the whole chain, 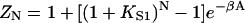 where A is the displacement energy. The corresponding formula for the bound fraction θ is equivalent to that of Geeves and Halsall if
where A is the displacement energy. The corresponding formula for the bound fraction θ is equivalent to that of Geeves and Halsall if 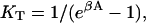 where KT is the equilibrium constant between the closed and open states of their model. Nevertheless, the rigid-chain model considered here is different, because the totality of chain configurations in the absence of bound myosin defines a closed state, but a subset of these configurations with excitation energy > A allow myosin binding. If βA ≪ 1, nearly all configurations permit binding and the fraction of nonbinding configurations, which should be associated with the closed state of the Geeves-Halsall model, becomes small. Hence KT ≫ 1 as predicted above.
where KT is the equilibrium constant between the closed and open states of their model. Nevertheless, the rigid-chain model considered here is different, because the totality of chain configurations in the absence of bound myosin defines a closed state, but a subset of these configurations with excitation energy > A allow myosin binding. If βA ≪ 1, nearly all configurations permit binding and the fraction of nonbinding configurations, which should be associated with the closed state of the Geeves-Halsall model, becomes small. Hence KT ≫ 1 as predicted above.
Apart from end effects, the distortion energy F(n)(sn) depends only on the spacings 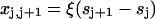 between bound myosins as a fraction of chain persistence length 1/ξ. For n = 2, a closed analytic expression is available via Eq. 7. For convenience, each bound myosin is assumed to pin the chain to angle φ+ at the point of contact. It can be argued that pinning is more realistic than the one-sided constraint φ > φ+. Both types of constraint have similar consequences, but the former is easier to handle mathematically.
between bound myosins as a fraction of chain persistence length 1/ξ. For n = 2, a closed analytic expression is available via Eq. 7. For convenience, each bound myosin is assumed to pin the chain to angle φ+ at the point of contact. It can be argued that pinning is more realistic than the one-sided constraint φ > φ+. Both types of constraint have similar consequences, but the former is easier to handle mathematically.
The partition function can be evaluated by the transfer-matrix method if F(n)(sn) can be expressed in terms of localized interactions between the n bound myosins. For n = 1, F(1)(s1) ≡ A is the energy of a single kink. Chain energies expressing the interaction of localized pairs, triplets of bound myosins are defined as
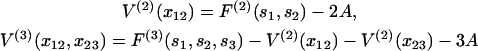 |
(11) |
and
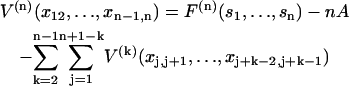 |
(12) |
for a localized n-myosin interaction. By construction, these functions tend to zero when all spacings between bound myosins are increased beyond the persistence length. Using Eq. 7 for the distortion energy of two kinks gives the pair-interaction energy 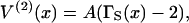 which varies from −A at x = 0 to zero when x ≫ 1 (Fig. 2). These definitions imply that the higher-order interactions approach zero when at least one spacing between adjacent myosins approaches zero or becomes much greater than the persistence length. They also vanish in the limit of large persistence lengths, when the kink from a single myosin spans many binding sites. Hence the distortion energy will be approximated by the sum of nearest-neighbor pair interactions, namely
which varies from −A at x = 0 to zero when x ≫ 1 (Fig. 2). These definitions imply that the higher-order interactions approach zero when at least one spacing between adjacent myosins approaches zero or becomes much greater than the persistence length. They also vanish in the limit of large persistence lengths, when the kink from a single myosin spans many binding sites. Hence the distortion energy will be approximated by the sum of nearest-neighbor pair interactions, namely
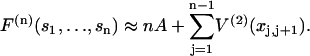 |
(13) |
The accuracy of this approximation can be investigated numerically from recursion formulae for the n-body free energy function (Smith, 2001).
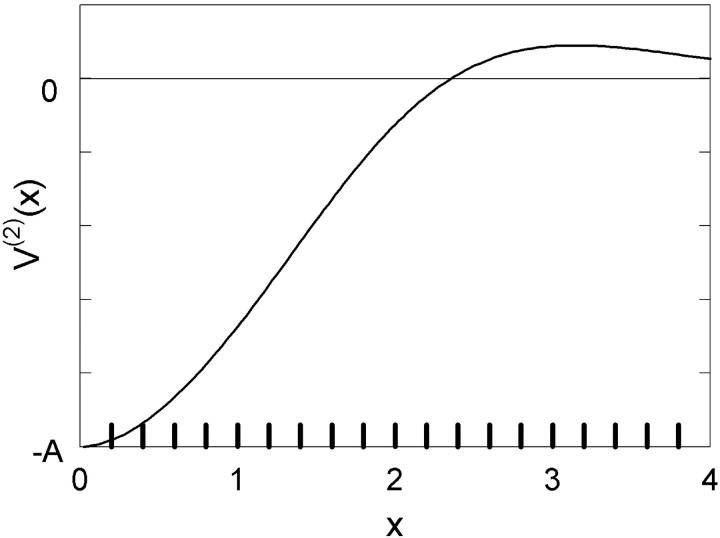
FIGURE 2.
The universal chain-induced interaction potential 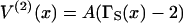 for a pair of bound myosins at separation x in units of the persistence length. Ticks on the x-axis denote binding sites on actin for a persistence length of five actin sites (ν = 5). The interaction is attractive (V(2)(x) < 0) almost everywhere, because the energy of two isolated kinks has been subtracted. A closed analytic formula is available (Smith, 2001).
for a pair of bound myosins at separation x in units of the persistence length. Ticks on the x-axis denote binding sites on actin for a persistence length of five actin sites (ν = 5). The interaction is attractive (V(2)(x) < 0) almost everywhere, because the energy of two isolated kinks has been subtracted. A closed analytic formula is available (Smith, 2001).
The transfer-matrix method for pair interactions
Under the pair approximation (Eq. 13), the partition function of Eq. 9 can be calculated by the transfer-matrix method if the range of interactions is limited and interactions over all pairs within that range are included correctly. To this end, the pair energy V(2)(x) is assumed to be zero for x > 2, which neglects an oscillating tail of order 10% (Fig. 2). The range of this truncated potential is r actin sites, where r = 2ν.
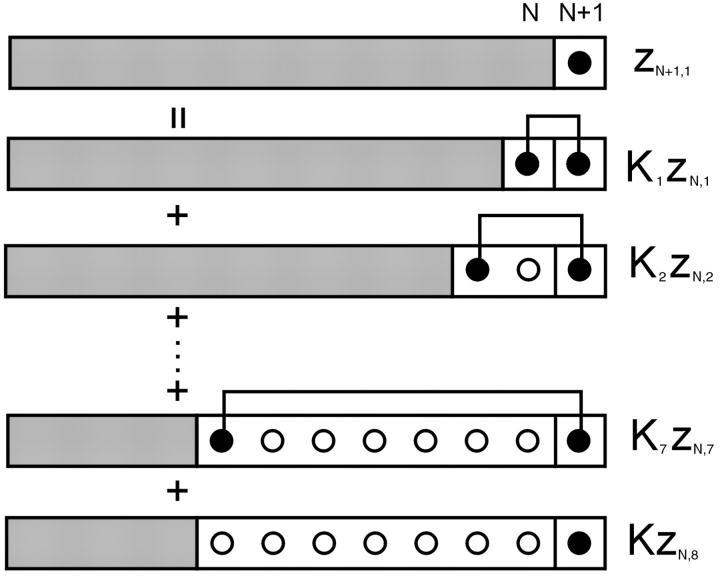
The transfer-matrix method for ZN proceeds by a recursion on the number of sites N. For this purpose, the following set of constrained N-site partition functions are sufficient. Let zN1 be the partition function with the leading site occupied by myosin. For j = 2,…,r, let zNj be the partition function with the leading j−1 sites empty and the site behind occupied. We also need the partition function with the leading r sites empty; it is convenient to denote this quantity by zN,r+1, although zN,j then has different meanings for j = r + 1 and j < r + 1. As shown in Fig. 3, adding one more site gives
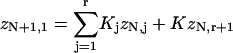 |
(14a) |
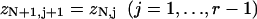 |
(14b) |
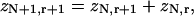 |
(14c) |
where 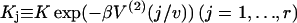 is myosin affinity under the chain but enhanced by a jth-nearest-neighbor myosin. In vector-matrix form,
is myosin affinity under the chain but enhanced by a jth-nearest-neighbor myosin. In vector-matrix form, 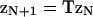 where T is a transfer matrix of dimension r + 1. For r = 7,
where T is a transfer matrix of dimension r + 1. For r = 7,
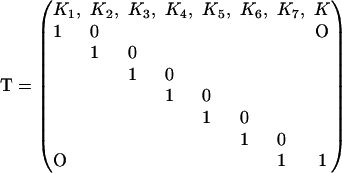 |
(15) |
For the interaction potential in Fig. 2 with A > 0, K1 > K2 >…Kr > K so the transfer matrix has rank r + 1. Although this matrix is not symmetric, it has a simple form which facilitates the construction of eigenvalues and eigenvectors. As shown below, a symmetric transfer matrix is not required to calculate the partition function.
FIGURE 3.
Diagrams illustrating iterative rules (Eq. 14) for components of the N-site myosin-only transfer matrix ZN, with interaction range r = 7. The component zN+1,1 in which the leading site is occupied by myosin (•), can be expressed in terms of N-site components, zNj, in which the leading j − 1 sites are unoccupied (○) and the jth site is occupied (j ≤ 7) or unoccupied (j = 8). In the bottom diagram, the leading myosin binds independently and requires a multiplicative factor K (Eq. 6). Interacting myosins within range r are linked, and require a factor 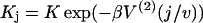 when separated by j sites. Similar diagrams apply for the zN+1,j.
when separated by j sites. Similar diagrams apply for the zN+1,j.
Let λα be an eigenvalue of T, with right and left eigenvectors u(α) and v(α) respectively. All eigenvalues are assumed to be distinct, though not necessarily real. Hence the eigenvectors satisfy mutual orthogonality and completeness conditions, which in terms of the matrices 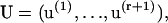
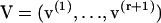 can be written as VTU = I and UVT = I respectively. I is the unit matrix and superscript T indicates the transposed matrix. Then
can be written as VTU = I and UVT = I respectively. I is the unit matrix and superscript T indicates the transposed matrix. Then
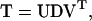 |
(16) |
where D is the diagonal matrix of eigenvalues λ1,…,λr+1.
These results determine the required partition function ZN. The vector form of Eq. 14 has the solution 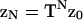 where z0 is a constant vector. With Eq. 16,
where z0 is a constant vector. With Eq. 16, 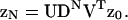 The sum of the elements of this vector gives ZN in the form
The sum of the elements of this vector gives ZN in the form
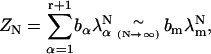 |
(17) |
where λm is the maximum eigenvalue and the bα are determined by the eigenvectors. In the limit of large N, the Gibbs energy of the system is 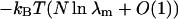 and extensive thermodynamic variables such as
and extensive thermodynamic variables such as 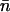 are determined by the maximum eigenvalue. The limiting form
are determined by the maximum eigenvalue. The limiting form
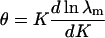 |
(18) |
of the bound fraction is independent of N.
The secular equation for the eigenvalues of T is the polynomial
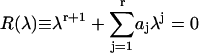 |
(19) |
with coefficients 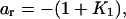
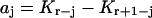 (j = 1,…,r) and
(j = 1,…,r) and 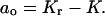 Manipulations based on this polynomial allow the bound fraction to be written in the form
Manipulations based on this polynomial allow the bound fraction to be written in the form
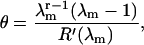 |
(20) |
which is used for numerical calculations.
Numerical predictions
Binding curves for θ as a function of the first-order binding constant KS1 have been computed from Eq. 20 using the pair interaction in Eq. 7. Three parameters are involved; the ratio βA of kink energy to thermal energy, the persistence number ν, and the range r of the truncated potential such that r ≥ 2ν.
Fig. 4 shows the predicted fraction of actin sites occupied by myosin as a function of its first-order affinity KS1. At low affinity, myosin binding is inhibited by the need to create kinked regions of the chain. As KS1 rises through a characteristic switching value K*, this inhibitory mechanism is removed as the kinks overlap and the binding curve switches smoothly to a higher-level curve. As the persistence number ν is increased, less myosin is required to effect switching and the width of the switching range of KS1 values decreases. With a bigger kink energy, the initial inhibition is increased and more myosin is required to overcome it.
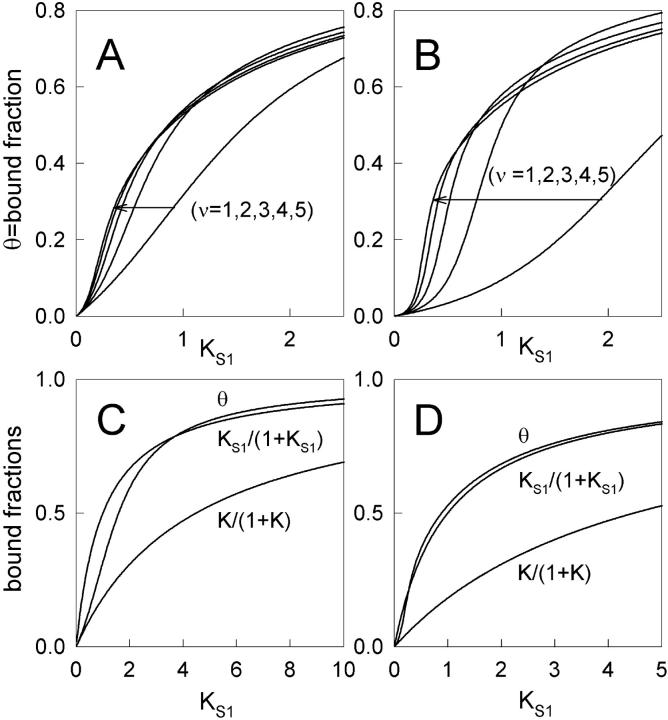
FIGURE 4.
The fraction θ of actin sites occupied by myosin-S1 as a function of first-order myosin affinity KS1, as predicted by Eq. 20. Graphs A and B show binding curves for kink energies 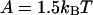 and 3kBT respectively; plots selected along the arrow from right to left are in increasing order of the persistence number ν. Graphs C and D show the above curves for ν = 1 and 5 respectively, and
and 3kBT respectively; plots selected along the arrow from right to left are in increasing order of the persistence number ν. Graphs C and D show the above curves for ν = 1 and 5 respectively, and 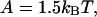 accompanied by the hyperbolic curves K/(K + 1) and KS1/(KS1 + 1) for independent binding in the presence and absence of inhibition. The crossover effect is discussed in the main text.
accompanied by the hyperbolic curves K/(K + 1) and KS1/(KS1 + 1) for independent binding in the presence and absence of inhibition. The crossover effect is discussed in the main text.
Fig. 4, C and D show that as KS1 → 0 the bound fraction approaches the function K/(1 + K) where K is affinity under the chain (Eq. 6). When KS1 ≫ 1, binding is not inhibited, and the asymptotic form slightly exceeds 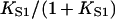 and therefore approaches unity more slowly. The overshoot is most pronounced for persistence lengths of the order of the actin site spacing (ν ≈ 1), and appears to be due to the neglect of triplet and higher-order interactions as defined by Eq. 11. This claim is substantiated by analyzing the behavior of the chain model for ν ≤ 1, when the range of myosin interaction is substantially limited to nearest neighbors (Fig. 2). In this case, the model is mathematically equivalent to a one-dimensional lattice gas with a one-particle energy
and therefore approaches unity more slowly. The overshoot is most pronounced for persistence lengths of the order of the actin site spacing (ν ≈ 1), and appears to be due to the neglect of triplet and higher-order interactions as defined by Eq. 11. This claim is substantiated by analyzing the behavior of the chain model for ν ≤ 1, when the range of myosin interaction is substantially limited to nearest neighbors (Fig. 2). In this case, the model is mathematically equivalent to a one-dimensional lattice gas with a one-particle energy 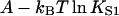 and a nearest-neighbor pair energy
and a nearest-neighbor pair energy 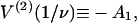 for which an analytic solution exists (Baxter, 1982). The correct partition function per site is the maximum eigenvalue of the transfer matrix
for which an analytic solution exists (Baxter, 1982). The correct partition function per site is the maximum eigenvalue of the transfer matrix
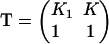 |
for r = 1 (see Eq. 15), from which the binding curve follows as before. This nearest-neighbor model also generates an overshoot effect but only when ν > 0.58, for which A1 > A/2 (Fig. 2). This condition relates to the change in Gibbs energy, 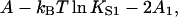 when myosin binds to a single vacant site between occupied sites—the overshoot that occurs when ν > 0.58 is a consequence of lowering the chain energy by
when myosin binds to a single vacant site between occupied sites—the overshoot that occurs when ν > 0.58 is a consequence of lowering the chain energy by 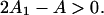 However, when the chain energy is not approximated by a sum of pair interactions, it is clear that adding one more myosin always increases the distortion energy of the chain. Thus the overshoot effect is a consequence of the neglect of triplet and higher-order interactions.
However, when the chain energy is not approximated by a sum of pair interactions, it is clear that adding one more myosin always increases the distortion energy of the chain. Thus the overshoot effect is a consequence of the neglect of triplet and higher-order interactions.
The chain model also shows an opposing effect at small ν which is not an artifact of the pair approximation; with the interaction potential in Fig. 2, the chain is unable to open fully for a single actin site between two bound myosins. This effect changes the expected high-affinity binding law from KS1/(1 + KS1) to K1/(1 + K1) where K1/KS1 = exp{−β[A + V(2)(1/ν)]} ≤ 1. Taken together, these effects imply that the second-order affinity 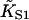 cannot be correctly estimated from experimental binding curves by fitting the high concentration region to KS1/(1 + KS1). Rather, the whole curve should be fitted to Eq. 20 or its counterpart for the tropomyosin-troponin system. The reliability of the pair approximation can then be assessed by the degree of overshoot.
cannot be correctly estimated from experimental binding curves by fitting the high concentration region to KS1/(1 + KS1). Rather, the whole curve should be fitted to Eq. 20 or its counterpart for the tropomyosin-troponin system. The reliability of the pair approximation can then be assessed by the degree of overshoot.
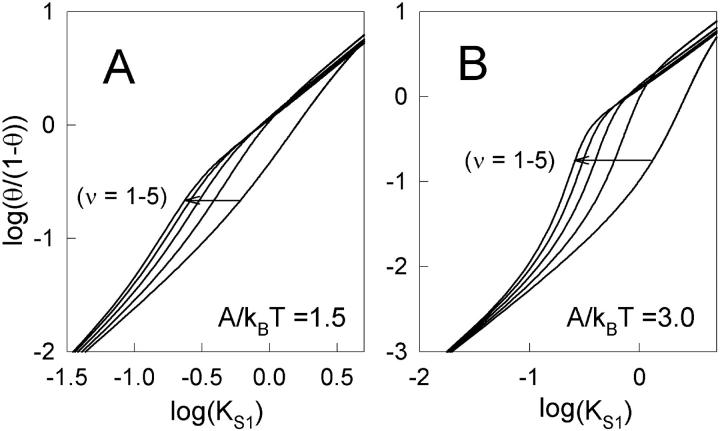
It is desirable to have a general method for characterizing cooperative binding curves, without invoking a specific model. The value of KS1 at the point of inflection in the binding curve can be interpreted as a switching affinity K*. However, the slope of the curve at this point reflects the degree of binding as well as the tightness of the switch and is therefore not a unique measure of cooperativity. One approach is to construct a Hill plot (Hill, 1913), which is based on the approximate binding fraction xn/(1 + xn) where x ∝ KS1 in this context. Hill plots for the binding curves of Fig. 4 are shown in Fig. 5. Each plot has a characteristic sigmoidal shape, so that the slope is not constant but varies with KS1. In fact n ≈ 1 at low and high values of KS1, reflecting first-order binding kinetics with or without inhibition, whereas larger values are found in the switching region KS1 ∼ K*. The customary definition of the Hill coefficient, as the slope at half activation (zero ordinate), underestimates the maximum slope if K* < 1, and in this article the Hill coefficient is defined as the maximum slope of the Hill plot. Even so, the Hill coefficients from Fig. 5, A and B generally underestimate the persistence number ν, which is the basic measure of cooperativity in the present model, and a different kind of data analysis is required.
FIGURE 5.
Hill plots corresponding to Fig. 4 for the bound myosin fraction θ against myosin affinity KS1. The Hill coefficient nH, defined as the maximum slope of the Hill plot, is generally less than the persistence number ν (nH = 1.1 and 1.9 for ν = 1 and 5, respectively, in A) but also increases with kink energy A (nH = 2.6 and 3.8 for ν = 1 and 5 in B). The persistence number is better estimated from the binding curves by the method described in the Appendix. The plots are indexed as described under Fig. 4.
A general method for quantifying the degree of cooperativity in an autocooperative binding curve is presented in the Appendix. Cooperative binding curves which switch from one affinity to another as a function of enzyme concentration x can be characterized by deriving an associated switching function F(x). The point of inflection of this function determines the switching concentration x* and the corresponding affinity K*. The slope S* at this point is a useful index of cooperativity if 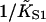 is used as the unit of concentration. The relationship between the switching parameters K*, S* and the parameters A, ν of the continuous-flexible-chain model are tabulated in this Appendix. In particular, the empirical relation ν ≈ S* (Eq. A4) is usually accurate to within 10%. The same method also extracts the apparent second-order affinity at high concentrations, which falls below
is used as the unit of concentration. The relationship between the switching parameters K*, S* and the parameters A, ν of the continuous-flexible-chain model are tabulated in this Appendix. In particular, the empirical relation ν ≈ S* (Eq. A4) is usually accurate to within 10%. The same method also extracts the apparent second-order affinity at high concentrations, which falls below 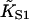 at small persistence numbers as expected.
at small persistence numbers as expected.
When A is zero, myosin affinity for actin is not inhibited by the chain, and the bound fraction is equal to KS1/(1 + KS1). This result is duplicated numerically as A → 0. However, the calculation is technically invalid when A = 0 because the transfer matrix then has rank r, the top row being K times the sum of the remaining rows.
The model predicts that the extent of myosin binding depends on free myosin concentration [S1] and second-order affinity 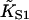 only through their product
only through their product 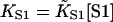 (the first-order affinity). For specific proteins, the second-order affinity is fixed and titrations are performed against [S1], but the theory applies equally to the binding of different myosins at the same concentration. For this reason, model curves are plotted against KS1. The second-order affinity refers to binding at high concentrations, in the absence of inhibition.
(the first-order affinity). For specific proteins, the second-order affinity is fixed and titrations are performed against [S1], but the theory applies equally to the binding of different myosins at the same concentration. For this reason, model curves are plotted against KS1. The second-order affinity refers to binding at high concentrations, in the absence of inhibition.
EXPERIMENTAL BINDING CURVES
Myosin binding data for various regulated actin systems have been fitted by the CFC model. As this data has already been fitted by the rigid-regulatory-unit model of McKillop and Geeves (1991), it is convenient to discuss the fits in relation to the parameters of this model, namely KT (equilibrium constant between closed and open states) and nU (number of actin sites per unit). Numerically, KT tracks the Boltzmann factor exp(−βA) of the chain model, although the latter quantity is usually larger. If the regulatory unit is equivalent to a single chain kink in the CFC model, then nU = 2ν + 1. In fact, this condition is not observed and the comparison highlights an essential difference between the models.
Skeletal tropomyosin
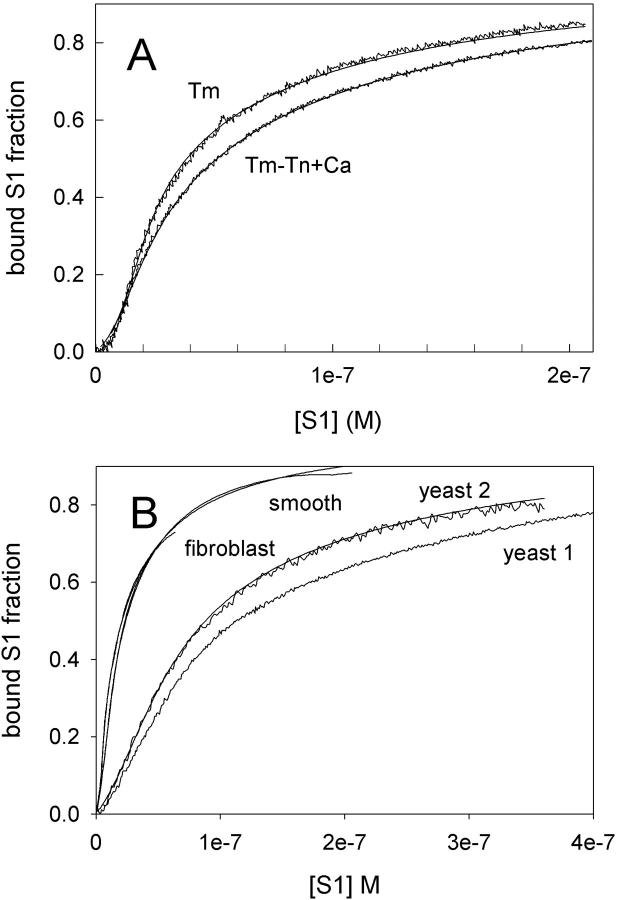
Fig. 6 A shows myosin-S1 binding curves of Maytum et al. (1999) against free S1 concentration to actin-Tm and actin-Tm-Tn filaments, and fitted curves generated from Eq. 20. The fitting process was well-conditioned and gave unique optimum values of the three adjustable parameters 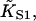 A and ν, summarized in Table 2. Myosin kink energy A is typically 1.6 kBT, so exp(−βA) = 0.22 compared with KT = 0.15. Both curves are fitted by similar values of the second-order affinity
A and ν, summarized in Table 2. Myosin kink energy A is typically 1.6 kBT, so exp(−βA) = 0.22 compared with KT = 0.15. Both curves are fitted by similar values of the second-order affinity 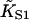 in the absence of chain distortion. The persistence length is increased by adding troponin if calcium is present at 0.1 mM or more. The corresponding kink sizes, namely 6.5 and 8.4 for A-Tm and A-Tm-Tn+Ca respectively, should be compared with unit sizes of 7 and 11 from the rigid-unit model.
in the absence of chain distortion. The persistence length is increased by adding troponin if calcium is present at 0.1 mM or more. The corresponding kink sizes, namely 6.5 and 8.4 for A-Tm and A-Tm-Tn+Ca respectively, should be compared with unit sizes of 7 and 11 from the rigid-unit model.
FIGURE 6.
Experimental myosin binding curves versus free S1 concentration for regulated actin systems and curves of best-fit to the CFC model. (A) from skeletal muscle (Maytum et al., 1999) and (B) from nonskeletal actin-tropomyosin filaments as listed (Maytum et al., 2001). Fitting procedures and values of fitted parameters are given in Table 2. For filaments from smooth muscle, the data falls below the fitted curve at the highest concentrations used.
TABLE 2.
| Regulated actin system (size of Tm molecule in actin monomers) | Binding constant 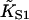 (M−1) (M−1) |
Kink energy βA | Kink size 2ν + 1 | χ2/N |
|---|---|---|---|---|
| Skeletal-Tm* (7) | 2.2 × 107 | 1.6 | 6.4 ± 0.2 (6.8) | 0.11 |
| Skeletal-Tm† (7) | 2.2 × 107 | 1.7 | 6.6 ± 0.2 | 1.6 |
| Skeletal-Tm-Tn+Ca* (7) | 1.7 × 107 | 1.6 | 8.4 ± 0.2 (8.8) | 0.12 |
| Smooth† (7) | 2.2 × 107 | 0.93 | (10.0) | − |
| Fibroblast† (6) | 4.2 × 107 | 1.5 | 10.0 ± 0.6 | 0.065 |
| Yeast 1† (5) | 7.9 × 106 | 0.95 | 6.6 ± 0.2 | 0.045 |
| Yeast 2† (4) | 1.1 × 107 | 0.91 | 5.0 ± 0.4 | 0.19 |
Fitting parameters and goodness-of-fit for myosin binding curves of Maytum et al. (*1999, †2001) for various actin-tropomyosin systems, fitted to Eq. 20. Least-squares fitting was performed with the Levenberg-Marquardt method. Fits were made to raw data as shown and to data filtered by averaging both coordinates over a centered running window of 50 points. Fitted parameter values were not significantly affected by filtering, but listed values of χ2/N (chi-squared per data point) are for filtered data, relative to a standard deviation of 0.02 for raw data points. Bracketed values of the kink size were obtained by weighted fitting in favor of the lowest S1 concentrations, which did not change the fitted values of 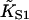 and A. Where bracketed values are not given, weighted and unweighted fits gave the same results. Values of
and A. Where bracketed values are not given, weighted and unweighted fits gave the same results. Values of 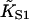 have not been corrected for the overshoot effect described in the main text.
have not been corrected for the overshoot effect described in the main text.
The fits show that the persistence length of the tropomyosin chain is increased by troponin, but not to the extent indicated by the McKillop-Geeves model. This may be due to the dynamic nature of chain kinks in the CFC model. Kink size 2ν + 1 and unit size nU should be equal only at low myosin concentrations where bound myosins are well separated and their associated kinks do not overlap. At higher concentrations, myosin kinks begin to overlap and the correlation length of the multipally kinked chain increases with the density of kinks. Thus the apparent unit size may correspond to a concentration-averaged correlation length. The dynamic nature of chain kinks implies that the discrepancy between these measures is bigger in systems with a high persistence length, as observed.
Other actin systems
Myosin binding data of Maytum et al. (2001) for actin-tropomyosin from smooth muscle and nonmuscle cells, which contain no troponin, are also fitted by the chain model. These systems use structurally different tropomyosins, which may be shorter than skeletal tropomyosin. A key assumption of the present model, that these molecules interact to form a continuous semiflexible chain, can be tested by using A-Tm constructs with a common actin structure and tropomyosins of different lengths.
Fitted binding curves for tropomyosins from smooth muscle, fibroblasts, and two kinds of yeast tropomyosin are shown in Fig. 6 B; the fitted parameters are also in Table 2. In contrast to skeletal tropomyosin, we find kink sizes significantly greater than the length of the tropomyosin molecule in all four systems, and especially for smooth-Tm and fibroblast-Tm where the kink size is almost twice the monomer length. Thus, actin-tropomyosin systems exist where the tropomyosins behave as a continuous semiflexible chain.
In these systems also, the kink size obtained from the CFC model generally tracks the unit size obtained from the rigid-unit model (Table 2; see also Maytum et al., 2001). There is also a general correlation between values of exp(−βA) from myosin kink energy A and the closed-to-open equilibrium constant KT of the rigid-unit model; both quantities are two to three times bigger for yeast-Tm relative to skeletal-Tm, although the kink sizes (and unit sizes) are similar. In the CFC model, the reduced value of A for yeast-Tm can be produced by a 25% drop in kink angle φ+, say by 5–7°. As the myosin binding interface is the same in both systems, this shift implies that the resting position (φ = 0 in Fig. 1 B) of the chain in yeast actin has shifted slightly toward the inner domain. Cryo-EM studies (Lehman et al., 2000) suggest that there is no shift in resting orientation. However, Table 2 predicts a similar small shift toward the inner domain for smooth-muscle Tm, whereas Lehman et al. (2000) report a large shift toward the outer domain. This discrepancy may have a structural explanation, but the available binding data for smooth-Tm was less well fitted (see text under Table 2), and for this system the value of A may be unreliable.
Myosin binding data of Tobacman and Butters (2000) for mutant tropomyosins with internal deletions suggests that myosin kink energy has been raised, perhaps because of a shift in the resting orientation of the chain toward the outer domain of actin. Their binding curves for mutant and wild-type tropomyosins should be compared with those in Fig. 4, B and A respectively, with the same value of ν. Fitting the CFC model to their data should reveal whether the persistence length is also altered by these mutations.
In general, the fitted binding curves overshoot the curve 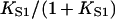 expected in the absence of inhibition, by 1.5–3% at
expected in the absence of inhibition, by 1.5–3% at 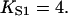 We have argued that this effect is an artifact of the model, produced by the neglect of chain-induced interactions between bound myosins not reducible to pair interactions. Hence the best-fit value of the second-order affinity
We have argued that this effect is an artifact of the model, produced by the neglect of chain-induced interactions between bound myosins not reducible to pair interactions. Hence the best-fit value of the second-order affinity 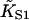 should be corrected upwards so that the hyperbola
should be corrected upwards so that the hyperbola 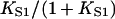 does not lie below the measured binding curve; this procedure gives affinity corrections of the order of 10% for the data presented here. It is desirable to predict myosin binding curves from the chain model without invoking the pair approximation. The inclusion of triplet interactions complicates the transfer-matrix approach considerably and a different methodology may be required; this task should be addressed in the future.
does not lie below the measured binding curve; this procedure gives affinity corrections of the order of 10% for the data presented here. It is desirable to predict myosin binding curves from the chain model without invoking the pair approximation. The inclusion of triplet interactions complicates the transfer-matrix approach considerably and a different methodology may be required; this task should be addressed in the future.
In conclusion, the CFC model is able to generate similar results to the rigid-unit model for the binding of S1 to regulated actin systems. In addition, the optimum values of fitted parameters appear to be consistent with thin-filament structure within the assumption of a continuous semiflexible tropomyosin chain.
DISCUSSION
Any discussion of the merits and predictive power of models of thin-filament regulation inevitably reverts to the structural assumptions underlying each model. The structural motivation for the CFC model is given in the Introduction and under Fig. 1. As the key assumption of this model (that tropomyosins act as a continuous semiflexible chain which fluctuates about a single resting position in the absence of myosin and troponin) runs counter to all previous regulatory models, a closer look at the evidence is desirable before returning to the models themselves.
The structural basis of regulatory models
The steric blocking model of Haselgrove and Huxley supposed that individual tropomyosin molecules switched between two discrete orientational states on actin, and did not determine whether these regulatory units switched independently or not. Two discrete orientations are observed but under different conditions: the closed state is observed in the absence of myosin and the open state in the presence of enough bound myosin to force all tropomyosins open. This observation does not imply that each unit has two possible resting orientations in the absence of myosin, as assumed by all previous models except the alternative model of Hill et al. (1980b). The observation of a third orientation, in the Tm-Tn-Ca system only (Vibert et al., 1997), appears to confirm the model of McKillop and Geeves (1993) in which three orientational states of tropomyosin are always present, with myosin and calcium (through troponin-I) acting as allosteric effectors by changing the balance of equilibrium between them (Lehrer and Geeves, 1998). More recent cryo-EM studies of various actin-tropomyosin systems with no troponin reveal only a single resting orientation; however, this orientation may vary significantly with troponin and actin isoforms (Lehman et al., 2000). Studies of filaments sparsely decorated with myosin show a gradual shift in tropomyosin position toward the closed state on moving away from the border of a myosin-decorated area, as far as 100 nm (Vibert et al., 1997). The spatial persistence of this effect is larger than the persistence lengths estimated in this article, perhaps because of hidden myosins. Similar effects are found in x-ray diffraction studies of the thin filament in vertebrate muscle stretched to zero overlap (Poole et al., 1995, 1996). The corresponding effect on moving away from a bound troponin-I has been reported by Lehman et al. (2001). Thus there is reasonable evidence for a single resting orientation of tropomyosin on actin, but with the capacity to depart from that orientation by 10–20° in either direction in the presence of bound myosin or troponin-I. On the other hand, a double orientational potential well, with minima separated by an energy barrier of order kBT, cannot be ruled out.
Evidence for semiflexible rather than rigid tropomyosins, and for the end-to-end interactions required to make a chain, is given in the Introduction. In fact, the observed flexibility of polymeric Tm in solution implies a bending stiffness at the lower end of values quoted in this article. It is possible that tropomyosin is stiffened by electrostatic interactions with actin, in addition to the postulated confining potential in Eq. 1. If end-to-end interactions are interpreted as an elastic link, the resulting chain will appear homogeneous if the bending stiffness of the link is similar to that between tropomyosin residues. With troponin present, this may be achieved by end-to-end interactions via troponin-T, which also links the other components of troponin to tropomyosin and is required for activation (Greaser and Gergely, 1971). The validity of the CFC model for tropomyosin-only systems is less clear, but is supported by comparing estimated kink sizes in systems with tropomyosins of different length, as discussed in the previous section.
Weakly-bound actomyosin states (Chalovich et al., 1991) have not been incorporated in the chain model. This was done for simplicity, and because these states are not populated at the low myosin concentrations used for titrations. Nevertheless, a weakly-bound actin-myosin-products state may be an intermediate in the ATP-hydrolyzing actin-myosin cycle, and one can ask how it would be affected by tropomyosin in the present model. Atomic reconstructions of the actin-myosin interface suggest that weak-binding regions lie at negative angles in Fig. 1 B, not substantially covered by tropomyosin in its thermal fluctuations ∼φ = 0, whereas the strong-binding interface requires additional contacts over a wider range of angles of both sign (Holmes, 1995; Hodgkinson et al., 1997), requiring myosin to skew as well as tilt axially in the force-generating transition (Corrie et al., 1999). Thus, only strongly-bound myosin states are inhibited by tropomyosin in the closed state of the CFC model, as assumed by McKillop and Geeves for the closed state of the rigid-unit model. In the presence of a more strongly-bound final state, as expected for nucleotide-free myosin and myosin-ADP (Geeves, 1991), the weakly-bound state will not be populated significantly and its omission should not be significant.
The quadratic angular confining potential used in Eq. 1 is necessary for mathematical developments and is intended only as a parody of orientational confinement of tropomyosin by electrostatic interactions, which also provide radial confinement. Hence the CFC model does not address tropomyosin binding data, in particular the observation that the binding of vertebrate tropomyosin to actin is increased fourfold by one bound myosin-S1, or 47-fold when all seven sites are occupied (Tobacman and Butters, 2000). This suggests that when myosin binds to regulated actin, it captures the tropomyosin chain at a point of contact after displacing it to the open position (Fig. 1), leaving it pinned to actin rather than free to make larger displacements; in fact this assumption was made in developing the model. The related observation that myosin-S1 binds four times more strongly to actin-tropomyosin than unregulated actin implies only that the second-order myosin affinity 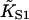 of the model is not transferable to unregulated actin. An operational definition may not be available, since
of the model is not transferable to unregulated actin. An operational definition may not be available, since 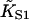 was defined in the absence of chain distortion and the chain must distort to allow myosin binding at low density.
was defined in the absence of chain distortion and the chain must distort to allow myosin binding at low density.
Outlook
The form of the myosin binding curve against myosin concentration does not provide a complete test of the CFC model, and can generally be fitted by all current models. Better tests are posed by 1), the calcium dependence of myosin binding, which requires an explanation of its high cooperativity and asymmetry as observed in the muscle fiber; and 2), the calcium dependence of calcium binding to TnC, which is more cooperative when the troponin complex is bound to tropomyosin on actin and more cooperative again with bound myosin present. These tests are addressed in the accompanying article.
The available models can be ranked in order of complexity, both conceptual and numerical (more complex models generally contain more parameters). The McKillop-Geeves model, despite its use of three regulatory states, is perhaps the simplest as it divides the tropomyosin assembly into independent rigid units, using four parameters in general and three parameters for A-Tm and A-Tm-Tn+Ca systems; in its current form this model does not make predictions as a function of calcium level. The model of Hill, Eisenberg, and Greene (1980a) has only two regulatory states, equivalent to the closed and open states of the preceding model, and identifies the tropomyosin molecule as the rigid regulatory unit, but invokes state-dependent and calcium-dependent interactions between units, requiring 17 parameters in all. This model has been applied to a variety of experiments. Motivated by the modulation of actin-myosin affinity by tropomyosin, the recent model of Tobacman and Butters (2000) adds complexity by postulating a cooperative conformational change in the actin filament. This four-parameter model also fits myosin binding curves for different filament systems.
What level of complexity in a mechano-kinetic model is desirable? One way of answering the question is by reference to molecular structure. In this sense, a model with independent regulatory units is inadequate when the unit size does not match the tropomyosin molecule. The CFC model is able to deal with filament systems with shortened tropomyosins and show that the regulatory unit can be dynamically determined and unrelated to the length of the tropomyosin molecule. The Hill-Eisenberg-Greene models apparently require calcium-dependent end-to-end tropomyosin interactions which cannot easily be interpreted in terms of known interactions between calcium, TnC and TnT. Devising mechanokinetic models which encapsulate key features of the wealth of structural information on these proteins will continue to be a major challenge.
On the other hand, the CFC and Tobacman-Butters models have not been tested against a sufficient variety of experiments. The CFC model needs to be developed further to explore kinetic aspects of thin filament regulation, which has been treated empirically by Razumova et al. (2000). The time courses of myosin binding and tropomyosin movements in A-Tm-Tn have been interpreted in terms of a regulatory unit of 10–12 monomers moving between discrete orientations (Geeves and Lehrer, 1994), but a similar kink size in the CFC model might not be necessary.
Acknowledgments
We wish to thank Prof. T. Burkhardt for reprints of his previous work on the harmonically confined polymer chain (Burkhardt, 1995), which uses a different methodology to that in Smith (2001), and Drs. S.S. Lehrer and J.L. Hodgkinson for discussions and comments on the manuscript. We acknowledge constructive comments from reviewers, especially a correspondence that led to an explanation of the overshoot phenomenon.
This work was supported by program grants from the Wellcome Trust (D.A.S., R.M., and M.A.G.) and the National Institutes of Health (M.A.G.).
APPENDIX: A Switching Function for an Auto-Cooperative Binding Curve
Suppose an enzyme M binds auto-cooperatively to a substrate, so that M binds with low affinity at a low concentration of M and binds with high affinity at high concentration. We seek to characterize this transition by a switching function F(x) which ranges from zero at low x to unity at high x, where x = [M]. The essential parameters of this function are the switching concentration x* at which F(x) has a point of inflection, and the slope S* at this point. x* is an inverse measure of the sensitivity of the transition to enzyme concentration. S* measures intrinsic cooperativity, and 1/S* is the range of concentrations over which switching occurs. In the context of this article, the motivation for constructing a switching function is to estimate the parameters of the chain model from a given binding curve without fitting to the model.
An auto-cooperative binding curve, which switches from a weak binding form with affinity 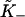 at small x to a strong binding form with affinity
at small x to a strong binding form with affinity 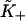 at large x, can be described by the function
at large x, can be described by the function
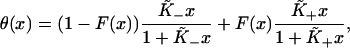 |
(A1) |
where F(x) is a function which switches smoothly from zero for x ≪ x* to unity for x ≫ x*. The binding curves predicted by our model are of this form. The switching function for a given binding curve can be calculated by the following procedure. An empirical partition function is first constructed numerically from the integral form
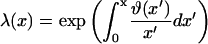 |
(A2) |
of Eq. 18, where λ(0) = 1. The expected forms of λ(x) at low and high concentrations are straight lines of slopes 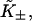 which can be extracted graphically once asymptotic straight-line behavior has been established. The point of maximum slope locates the switching concentration x*. The maximum slope S* of F(x) is a useful measure of cooperativity if defined with respect to a dimensionless unit of concentration, such as first-order affinity. For this purpose, F(x) should be plotted against the first-order affinity
which can be extracted graphically once asymptotic straight-line behavior has been established. The point of maximum slope locates the switching concentration x*. The maximum slope S* of F(x) is a useful measure of cooperativity if defined with respect to a dimensionless unit of concentration, such as first-order affinity. For this purpose, F(x) should be plotted against the first-order affinity 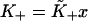 and S* defined as the maximum value of
and S* defined as the maximum value of 
The switching function has been calculated for modeled and experimental myosin-S1 binding curves. We describe results for the model curves of Fig. 4 A. For this purpose, it is convenient to set x = KS1 rather than [S1], which is equivalent to setting 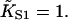 Figure 7 shows the resulting plots of
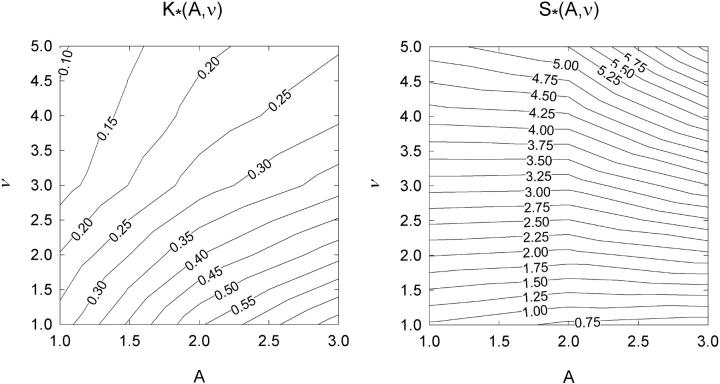
Figure 7 shows the resulting plots of 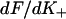 and values of the switching parameters K*, S*. Their relation with the parameters A,ν of the chain model is shown graphically in Fig. 8, which enables the latter to be determined numerically. The empirical relations
and values of the switching parameters K*, S*. Their relation with the parameters A,ν of the chain model is shown graphically in Fig. 8, which enables the latter to be determined numerically. The empirical relations
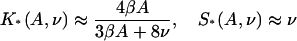 |
(A3) |
are generally accurate to 10%, though the second equation is unreliable when βA > 2.
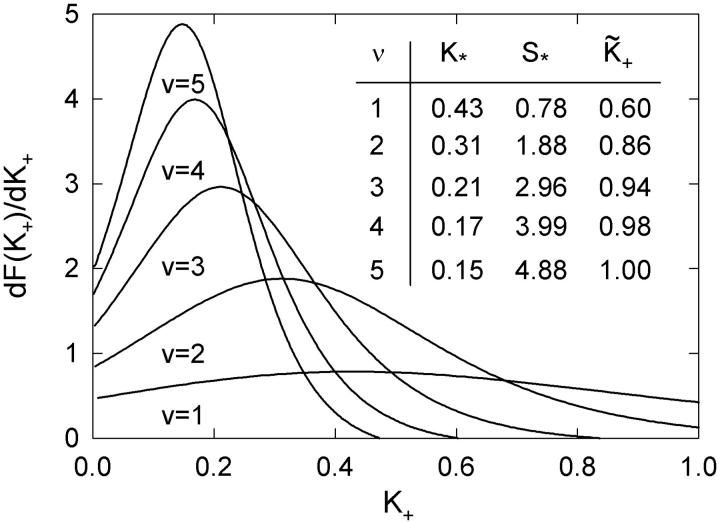
FIGURE 7.
Derivative of the switching function F(K+) of the Appendix, computed for the chain model with A = 1.5 kBT. The abscissa is defined as 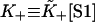 where the apparent second-order affinity
where the apparent second-order affinity 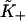 is determined numerically as described in the Appendix. For each value of the persistence number ν, the inset table gives the coordinates K*,S* of the maximum, which characterize the cooperative binding curve, and
is determined numerically as described in the Appendix. For each value of the persistence number ν, the inset table gives the coordinates K*,S* of the maximum, which characterize the cooperative binding curve, and 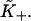 When ν > 2, S* is very close to ν. The values of
When ν > 2, S* is very close to ν. The values of 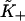 are within 2% of those predicted by the expression
are within 2% of those predicted by the expression 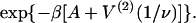
FIGURE 8.
Contour maps for the switching variables K*(A,ν), S*(A,ν) of the Appendix, computed for the chain model as functions of its parameters A and ν.
Values of 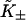 determined by this procedure were in good agreement with those predicted from the expressions
determined by this procedure were in good agreement with those predicted from the expressions 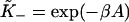 and
and 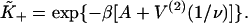 The latter is generally close to unity except when ν ≈ 1 and/or βA > 2, when the chain is unable to open fully for actin sites next to an occupied site. Thus
The latter is generally close to unity except when ν ≈ 1 and/or βA > 2, when the chain is unable to open fully for actin sites next to an occupied site. Thus 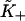 is only a lower estimate for the fundamental second-order myosin affinity
is only a lower estimate for the fundamental second-order myosin affinity 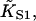 although the difference is usually small if ν > 2.
although the difference is usually small if ν > 2.
A Fortran program for generating the switching function and values of  K*, S* from an experimental binding curve is listed on the website mentioned at the end of the Introduction.
K*, S* from an experimental binding curve is listed on the website mentioned at the end of the Introduction.
References
- Baxter, R. J. 1982. Exactly Solved Models in Statistical Mechanics. Academic Press, New York and London.
- Bremel, R. D., J. M. Murray, and A. Weber. 1972. Manifestations of cooperative behavior in the regulated actin filament during actin-activated ATP hydrolysis in the presence of calcium. CSH Sympos. Quant. Biol. 37:267–275. [Google Scholar]
- Brown, J. H., K.-H. Kim, G. Jun, N. J. Greenfield, R. Dominguez, N. Volkmann, S. E. Hitchcock-deGregori, and C. Cohen. 2001. Deciphering the design of the tropomyosin molecule. Proc. Natl. Acad. Sci. USA. 98:8496–8501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burkhardt, T. W. 1995. Free energy of a semiflexible polymer confined along an axis. J. Phys. A. Math. Gen. 28:L629–L635. [Google Scholar]
- Chalovich, J. M., L. C. Yu, and B. Brenner. 1991. Involvement of weak binding crossbridges in force production in muscle. J. Muscle Res. Cell Mot. 12:503–506. [DOI] [PubMed] [Google Scholar]
- Chen, Y.-D., B. Yan, J. M. Chalovich, and B. Brenner. 2001. Theoretical kinetic studies of models for binding myosin subfragment-1 to regulated actin: Hill model versus Geeves model. Biophys. J. 80:2338–2349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corrie, J. E. T., B. D. Brandmeier, R. E. Ferguson, D. R. Trentham, J. Kendrick-Jones, S. C. Hopkins, U. A. van der Heide, Y. E. Goldman, C. Sabido-David, R. Dale, S. Criddle, and M. Irving. 1999. Dynamic measurement of myosin light-chain-domain tilt and twist in muscle contraction. Nature. 400:425–430. [DOI] [PubMed] [Google Scholar]
- Ebashi, S. 1969. Control of muscle contraction. Q. Rev. Biophys. 2:351–384. [DOI] [PubMed] [Google Scholar]
- Geeves, M. A. 1991. The dynamics of actin and myosin association and the crossbridge model of muscle contraction, Biochem. J. 274:1–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geeves, M. A., and D. J. Halsall. 1987. Two-step ligand binding and cooperativity; a model to describe the cooperative binding of myosin subfragment 1 to regulated actin. Biophys. J. 52:215–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geeves, M. A., and S. S. Lehrer. 1994. Dynamics of the muscle thin filament regulatory switch: the size of the cooperative unit. Biophys. J. 67:273–282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon, A. M., E. Homsher, and M. Regnier. 2000. Regulation of contraction in striated muscle. Physiol. Rev. 80:853–924. [DOI] [PubMed] [Google Scholar]
- Greaser, M., and J. Gergely. 1971. Reconstitution of troponin activity from three protein components. J. Biol. Chem. 246:4226–4233. [PubMed] [Google Scholar]
- Greene, L. E., and E. Eisenberg. 1980. Cooperative binding of myosin subfragment-1 to the actin-troponin-tropomyosin complex. Proc. Natl. Acad. Sci. USA. 77:2616–2620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haselgrove, J. C. 1973. X-ray evidence for a conformation change in the actin-containing filaments of vertebrate striated muscle. CSH Sympos. Quant. Biol. 37:341–352. [Google Scholar]
- Heald, R. W., and S. E. Hitchcock-deGregori. 1988. The structure of the amino terminus of tropomyosin is critical for binding to actin in the absence and presence of troponin. J. Biol. Chem. 263:5254–5259. [PubMed] [Google Scholar]
- Hill, A. V. 1913. The combinations of haemoglobin with oxygen and with carbon monoxide. Biochem. J. 7:471–480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill, T. L. 1985. Cooperativity Theory in Biochemistry. Springer-Verlag, New York.
- Hill, T. L., E. Eisenberg, and L. Greene. 1980a. Theoretical model for the cooperative equilibrium binding of myosin subfragment 1 to the actin-troponin-tropomyosin complex. Proc. Natl. Acad. Sci. USA. 77:3186–3190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill, T. L., E. Eisenberg, and L. Greene. 1980b. Alternate model for the cooperative equilibrium binding of myosin subfragment 1-nucleotide complex to actin-troponin-tropomyosin. Proc. Natl. Acad. Sci. USA. 80:60–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkinson, J. L., S. B. Marston, R. Craig, P. Vibert, and W. Lehman. 1997. Three-dimensional image reconstruction of reconstituted smooth muscle thin filaments: effects of caldesmon. Biophys. J. 72:2398–2404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmes, K. C. 1995. The actomyosin interaction and its control by tropomyosin. Biophys. J. 68:2s–7s. [PubMed] [Google Scholar]
- Howard, J. 2001. Mechanics of Motor Proteins and the Cytoskeleton. Sinauer Associates Inc., Sunderland, Massachusetts.
- Huxley, H. E. 1973. Structural changes in the actin- and myosin-containing filaments during contraction. CSH Sympos. Quant. Biol. 37:361–376. [Google Scholar]
- Hvidt, S., J. D. Ferry, D. L. Roelke, and M. L. Greaser. 1983. Flexibility of light-meromyosin and other coiled-coil alpha-helical proteins. Macromolecules. 16:740–745. [Google Scholar]
- Lehman, W., V. Hatch, V. Korman, M. R. L. Thomas, R. Maytum, M. A. Geeves, J. E. van Eyk, L. S. Tobacman, and R. Craig. 2000. Tropomyosin and actin isoforms modulate the localization of tropomyosin strands on actin filaments. J. Mol. Biol. 302:593–606. [DOI] [PubMed] [Google Scholar]
- Lehman, W., M. Rosol, L. S. Tobacman, and R. Craig. 2001. Troponin organization on relaxed and activated thin filaments revealed by electron microscopy and three-dimensional reconstruction. J. Mol. Biol. 307:739–744. [DOI] [PubMed] [Google Scholar]
- Lehrer, S. S., and M. A. Geeves. 1998. The muscle thin filament as a classical cooperative allosteric regulatory system. J. Mol. Biol. 277:1081–1089. [DOI] [PubMed] [Google Scholar]
- Lehrer, S. S., N. L. Golitsina, and M. A. Geeves. 1997. Actin-tropomyosin activation of myosin subfragment 1 ATPase and thin filament cooperativity. The role of tropomyosin flexibility and end-to-end interactions. Biochemistry. 36:13449–13454. [DOI] [PubMed] [Google Scholar]
- Lehrer, S. S., and E. P. Morris. 1982. Dual effects of tropomyosin and troponin-tropomyosin on actomyosin subfragment 1 ATPase. J. Biol. Chem. 257:8073–8080. [PubMed] [Google Scholar]
- Lorenz, M., K. J. V. Poole, D. Popp, G. Rosenbaum, and K. C. Holmes. 1995. An atomic model of the unregulated actin filament obtained by x-ray fiber diffraction on oriented actin-tropomyosin gels. J. Mol. Biol. 246:108–119. [DOI] [PubMed] [Google Scholar]
- Maytum, R. M., S. S. Lehrer, and M. A. Geeves. 1999. Cooperativity and switching within the three-state model of muscle regulation. Biochemistry. 38:1102–1110. [DOI] [PubMed] [Google Scholar]
- Maytum, R. M., M. Konrad, S. S. Lehrer, and M. A. Geeves. 2001. Regulatory properties of tropomyosin: effects of length, isoform and N-terminal sequence. Biochemistry. 40:7334–7341. [DOI] [PubMed] [Google Scholar]
- McKillop, D. F. A., and M. A. Geeves. 1991. Regulation of the actin-myosin subfragment 1 interaction by troponin/tropomyosin. Biochem. J. 279:711–718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKillop, D. F. A., and M. A. Geeves. 1993. Regulation of the interaction between actin and myosin subfragment 1: evidence for three states of the thin filament. Biophys. J. 65:693–701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips, G. N., and S. Chacko. 1996. Mechanical properties of tropomyosin and implications for muscle regulation. Biopolymers. 38:89–95. [DOI] [PubMed] [Google Scholar]
- Poole, K. J. V., K. C. Holmes, G. Evans, G. Rosenbaum, I. Rayment, and M. Lorenz. 1995. Control of the actomyosin interaction. Biophys. J. ET J. 68:S348. [Google Scholar]
- Poole, K. J. V., M. Lorenz, G. Evans, G. Rosenbaum, and K. C. Holmes. 1996. A low angle diffraction investigation of the structural changes in the muscle thin filament that regulates contraction. J. Muscle Res. Cell Mot. 17:119. [Google Scholar]
- Razumova, M. V., A. E. Bukatina, and K. B. Campbell. 2000. Different myofilament nearest-neighbour interactions have distinctive effects on contractile behaviour. Biophys. J. 78:3120–3137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith, D. A. 2001. Path integral theory of an axially-confined worm-like chain. J. Phys. A. Math. Gen. 34:4507–4523. [Google Scholar]
- Stewart, M. 2001. Structural basis for bending tropomyosin around actin in muscle filaments. Proc. Natl. Acad. Sci. USA. 98:8165–8166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tobacman, L., and C. A. Butters. 2000. A new model of cooperative myosin-thin filament binding. J. Biol. Chem. 275:27587–27593. [DOI] [PubMed] [Google Scholar]
- Trybus, K., and E. W. Taylor. 1980. Kinetic studies of the cooperative binding of subfragment 1 to regulated actin. Proc. Natl. Acad. Sci. USA. 77:7209–7213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vibert, P., R. Craig, and W. Lehman. 1997. Steric model for activation of muscle thin filaments. J. Mol. Biol. 266:8–14. [DOI] [PubMed] [Google Scholar]
- Vilfan, A. 2001. The binding dynamics of tropomyosin to actin. Biophys. J. 81:3146–3155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wegner, A. 1979. Equilibrium of the actin-tropomyosin interaction. J. Mol. Biol. 131:839–853. [DOI] [PubMed] [Google Scholar]
- Whitby, F. G., and G. N. Phillips. 2000. Crystal structure of tropomyosin at seven Ångstroms resolution. Proteins: Structure. Funct. Gen. 38:49–59. [PubMed] [Google Scholar]
- Xu, C., R. Craig, L. Tobacman, R. Horowitz, and W. Lehman. 1999. Tropomyosin positions in regulated thin filaments revealed by cryoelectron microscopy. Biophys. J. 77:985–992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yanagida, T., M. Nakase, K. Nishiyama, and F. Oosawa. 1984. Direct observation of motion of single F-actin filaments in the presence of myosin. Nature. 307:58–60. [DOI] [PubMed] [Google Scholar]
- Yasuda, R., H. Miyata, and K. Kinosita. 1996. Direct measurements of the torsional rigidity of single actin filaments. J. Mol. Biol. 263:227–236. [DOI] [PubMed] [Google Scholar]