Single-Strand Stacking Free Energy from DNA Beacon Kinetics

Abstract

DNA beacons are short single-stranded chains which can form closed hairpin shapes through complementary base pairing at their ends. Contrary to the common polymer theory assumption that only their loop length matters, experiments show that their closing kinetics depend on the loop composition. We have modeled the closing kinetics and in so doing have obtained stacking enthalpies and entropies for single-stranded nucleic acids. The resulting change of persistence length with temperature effects the dynamics. With a Monte Carlo study, we answer another polymer question of how the closing time scales with chain length, finding τ ∼ N^2.44±0.02. There is a significant crossover for shorter chains, bringing the effective exponent into good agreement with experiment.

INTRODUCTION

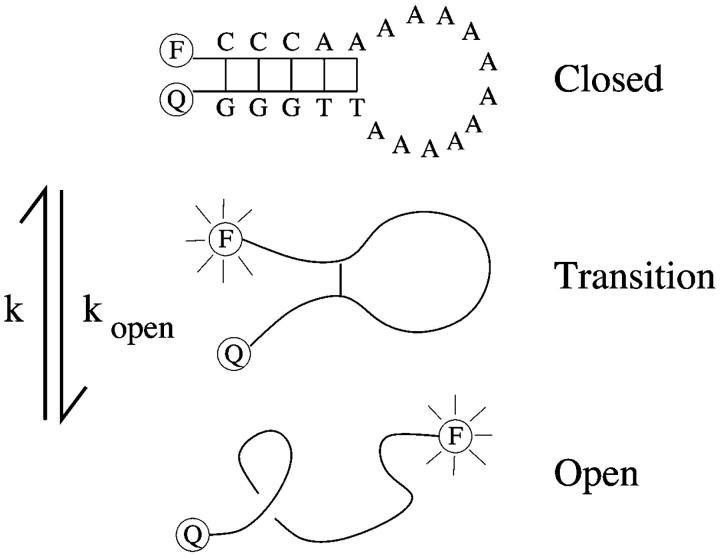
Hairpin conformations of single-stranded nucleic acids dominate secondary structure and have been implicated as important regulatory elements for transcription and replication (Lodish et al., 2000). Molecular beacons (see Fig. 1), self-complementary single-stranded (ss) DNA with fluorophore and quencher tags, serve as a simple example of hairpins. They were invented as probes for identifying specific ssDNA sequences—one can observe a distinct fluorescence change from dark to light when they hybridize to a target (Tyagi and Kramer, 1996). The Libchaber group has recently used beacons as probes of conformational dynamics (Bonnet et al., 1998; Goddard et al., 2000). How those dynamics reveal stacking interactions is our interest.

FIGURE 1.

Beacons fluctuate between closed and open states, with opening k_open and closing k rates measured using a fluorophore (F) and quencher (Q).

The free energies for duplex formation of nucleic acids have been exhaustively measured by SantaLucia, Turner, and others (SantaLucia, 1998; Turner et al., 1988; Mathews et al., 1999; Sugimoto et al., 1995). Hydrogen bonding stabilizes the double-helical form, but the van der Waals energy gained in stacking of nucleotides is thought to be the primary contribution to its enthalpy. Nucleotide stacking in single-stranded nucleic acids is also known (Saenger, 1984). Nearest-neighbor stacking free energies of simple single strands—poly(rA), poly(rU), and poly(rC)—have been measured using calorimetry and optical techniques (Turner, 2000). The enthalpies of single-strand stacking are remarkably large; indeed they are comparable to those of forming double-helical segments.

Libchaber and co-workers (Bonnet et al., 1998; Goddard et al., 2000) have measured melting curves for beacons of different loop length and composition (poly(dA) or poly(dT)) with fixed stem composition. Fluorescence correlation spectroscopy was then used to measure timescales of the thermal fluctuations between open and closed conformations. Opening rates were found to be insensitive to loop sequence and length variation; closing rates were found to vary dramatically with both, contrary to the common assumption that the loop entropy depends only on length. (The assumed functional form—Mathews et al., 1999—for a loop of length N is ΔG⁰ (N) = ΔG⁰ (10) + 1.75RT log(N/10), independent of sequence.)

A transition energy barrier of 0.5 kcal/mol/base for poly(dA) is reported by Goddard and co-workers (Goddard et al., 2000) and it is suggested there that this is the nucleotide stacking enthalpy. We shall show that stacking enthalpies consistent with measured closing rates are, in fact, an order-of-magnitude larger, in agreement with calorimetry. Ansari and co-workers has argued this discrepancy could be due to competing effects with misfolded states (Ansari et al., 2001, 2002). We argue instead that the effect results from the entropy change with persistence length.

Fluorescence correlation spectroscopy measurements (Bonnet et al., 1998) indicate that the closing (end-to-end collision) rate scales as a power law of chain length, τ ∼ N^2.6±0.3. Recently, Ansari and co-workers have argued the relaxation time scales as τ_r ∼ N^2.0±0.2 (Ansari et al., 2001, 2002) based on temperature jump experiments. Rouse theory suggests a random polymer relaxation time that scales like τ_r ∼ N², and the Kirkwood approximation proposes a self-avoiding polymer relaxation time that scales like τ_r ∼ R_F³ ∼ N^9/5 (de Gennes, 1979). Using a Monte Carlo approach to address this polymer physics question, we find a closing time asymptotic scaling of τ ∼ N^2.44±0.02 for self-avoiding polymers and large finite size corrections which make the power appear larger.

MONTE CARLO APPROACH

An off-lattice bond fluctuation method (BFM) type algorithm was used for Monte Carlo simulations of polymer dynamics (Carmesin and Kremer, 1988). Beads are tethered 1 < r < 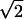with minimum and maximum separation radii chosen to prevent chain crossings (Kantor et al., 1986; Aalberts, 1996). We modify the BFM to incorporate nucleotide stacking.

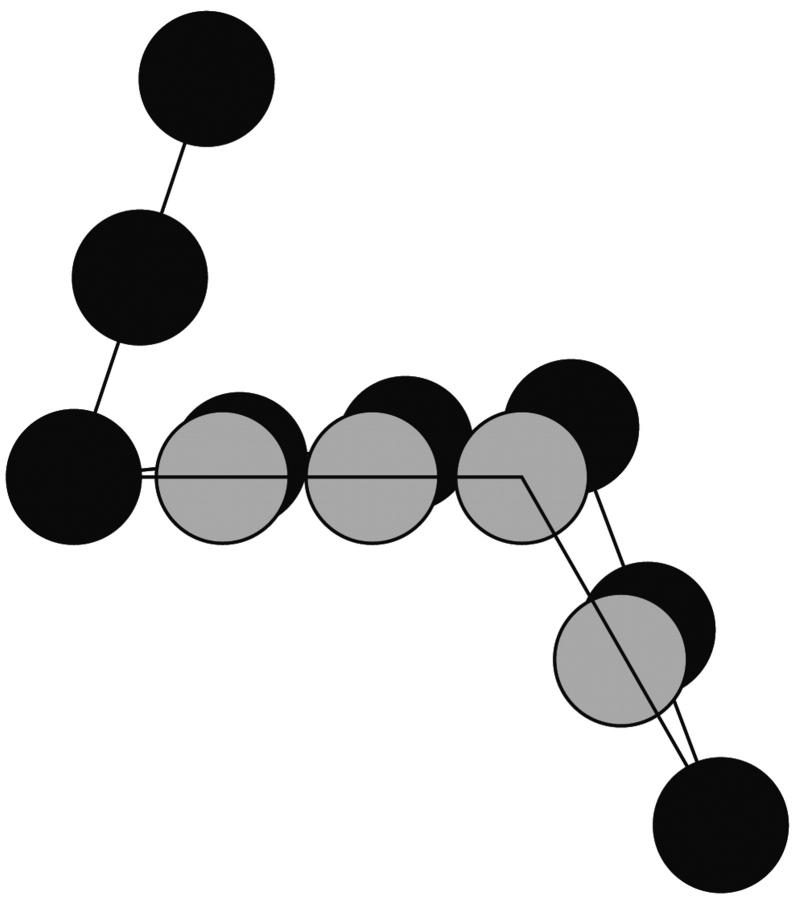
In each Monte Carlo step (MCS), an attempt is made to randomly displace each vertex bead a small distance. Because the backbone persists in the same direction when nucleotides are stacked, the beads between the displaced vertex and its neighboring vertices are also moved to keep stacked backbone segments straight, as depicted in Fig. 2. Simulations of chains with stacks were done using an ensemble of randomly chosen instances of stack locations (or, equivalently, the vertices bracketing stacked regions).

FIGURE 2.

The ssDNA beacon is modeled as a string of uniform beads with each bead representing one nucleotide. A Monte Carlo move consists of randomly choosing one of the vertices and randomly displacing it and any stacked neighbors to new positions (gray). If the new positions do not violate bond length or self-avoidance constraints, the beads are moved to the new positions.

We concentrate on measuring closing events because the beacon opening rate was found to be insensitive to loop composition (Bonnet et al., 1998), while the closing rate was found to vary substantially with loop composition (Bonnet et al., 1998; Goddard et al., 2000). (Using N_loop > N_stem, Shen and co-workers (Shen et al., 2001) have found variations for short loops N_loop ≤ N_stem. Enhanced stability has been reported for certain triloops and tetraloops.) In our simulations, the chain ends do not attract each other, as that would only result in slowing the simulation and reducing the closing event rate. The primary statistic measured is the number of MCS between closing events, when opposite ends of the chain come into close proximity. Since the closing distance is not known, we made measurements at a series of threshold values. Scaling of simulation results proved to be insensitive to the choice of closing radius r_c.

In the absence of other interactions, the probability of being in the closed state is the ratio of the multiplicities of states:

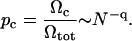(1)

Standard polymer theory (de Gennes, 1979; Grosberg and Khokhlov, 1994) says that, for a random walk, q = 3/2, whereas for a self-avoiding random walk, q ≈ 2. If configurations were sampled in an unbiased manner, the closing time would scale as τ ∼ N^q. However, the sampling of states is autocorrelated. In Monte Carlo simulations we find that ends rapidly cross any threshold separation. Nevertheless, it is the longer-lived open states which determine the effective closing time.

Closing times must be weighted to account for the greater likelihood of the long intervals. If t_j represents the time between the (j−1)^th opening and the j^th closing, then p(j) = t_j/Σ_k t_k is the probability of being in the j^th open interval. Thus the average closing time, which we measure in our Monte Carlo simulations, is

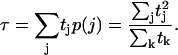(2)

We can uncover how τ scales with N from numerical data. Monte Carlo simulation data for self-avoiding BFM chains with no stacks is well fit by

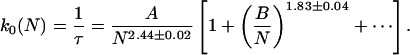(3)

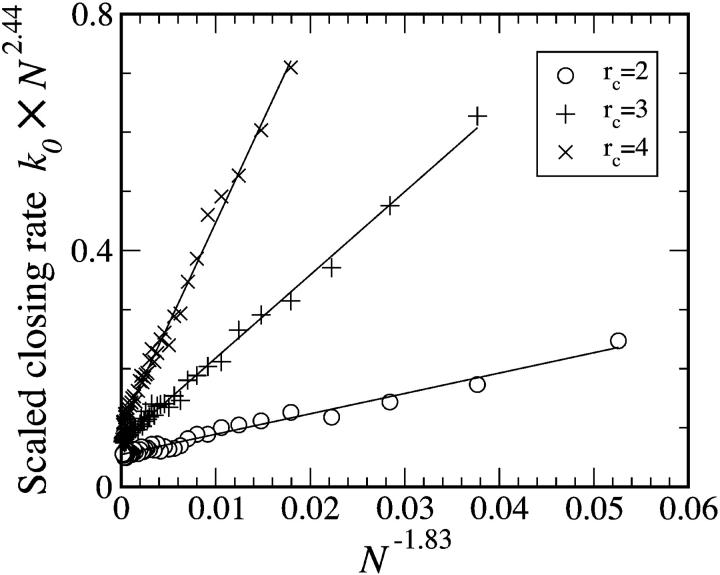
In Eq. 3, the constants A and B depend on the closing radius r_c. In Fig. 3, one sees that there are strong corrections to simple power law scaling. The correction term makes the effective scaling exponent for short chains appear to be somewhat larger than the asymptotic scaling τ ∼ N^q, with q = 2.44 ± 0.02. Eq. 3 disagrees somewhat with simple-polymer theory (Ansari et al., 2002) but agrees with the measurement of q = 2.6 ± 0.3 (Bonnet et al., 1998).

FIGURE 3.

The closing rate scaling of BFM Monte Carlo simulations of unstacked chains. The scaling form, Eq. 3, works well regardless of choice of closing radii r_c (measured in units where the minimum bead separation is r_min = 1), though intercept A and slope B depend on these details. Asymptotically, k₀ ∼ N^−q with q = 2.44 ± 0.02, but for small N the effective power q appears somewhat larger because of a significant correction to scaling.

EXTRACTING FREE ENERGIES FROM KINETICS

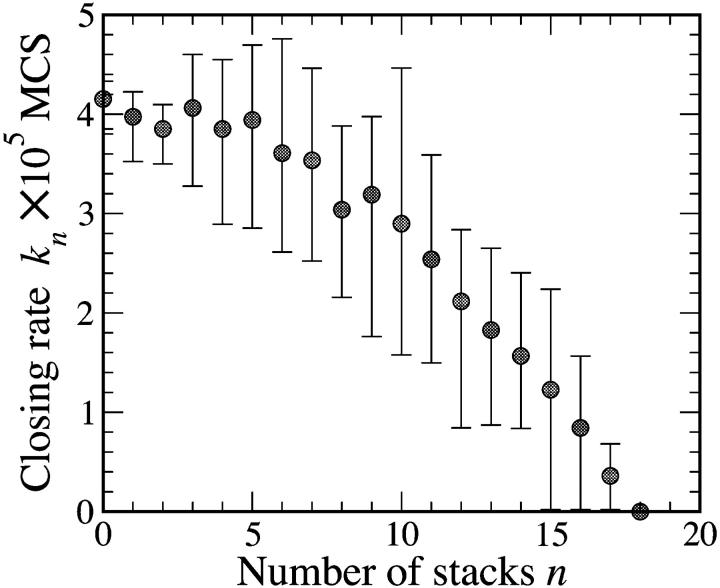
When the polymer backbone is more rigid, the closing kinetics slow dramatically, as shown in Fig. 4. Chains explore many chain stack configurations before closing (the rate of making and breaking of stacks is estimated—Pörschke, 1978—to be O(100 ns), whereas the closing rates are O(100 μs)). Even though chains with a sufficiently large number of stacks cannot close, the measured closing rate will be dominated by faster folding configurations.

FIGURE 4.

The closing rate of a chain of N = 21 beads as a function of the number of stacks n. The error bars indicate the 25% and 75% fluctuations around the average closing rate from the 30 different runs done with n stacks distributed at different locations (and r_c = 2). As the number of stacks increases, the closing rate decreases.

The closing rate k can be calculated as the thermal average of the closing rates k_n which are measured in simulations (see Fig. 4) for n stacks. The temperature dependence enters via a Boltzmann factor,

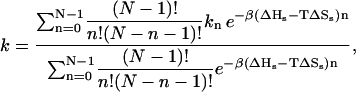(4)

where β = 1/RT, and where ΔH_s and ΔS_s are the enthalpy and entropy change of stacking. Note that in Eq. 4 there is a binomial degeneracy factor for the number of configurations with n stacks. Our analysis indicates that for lowest temperatures measured in the experiments the probability of stacking in poly(dA) is 80%. Thus the average persistence length λ approaches the total loop length of some beacons considered, and plays an important role in the kinetics.

The question of how to relate simulations to experiment remains to be addressed. To eliminate time dependences (MCS and seconds) we computed ratios. By taking the ratio of closing rates for poly(dA) and poly(dT) chains k_dA/k_dT, we see the effect of stacking and eliminate the viscosity dependence. Likewise, measuring k/k₀ in the Monte Carlo context largely eliminates dependences on the details of Monte Carlo moves. (We normalize with respect to zero stacking k₀ because calorimetry studies have indicated no preference for stacking of poly(dT) chains; see Turner, 2000.)

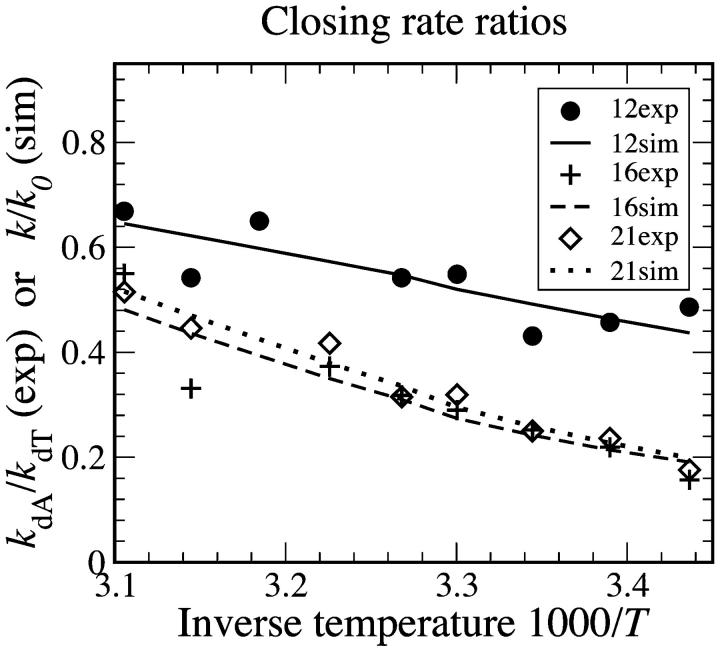
It is possible to extract ΔH_s and ΔS_s from closing rates. We used a least-squares approach to optimize the agreement of simulation k/k₀ and experiment k_dA/k_dT closing rate ratios. Our fits are presented in Fig. 5, and derived values for ΔH_s and ΔS_s are given in Table 1. The single-stranded stacking enthalpy and entropy obtained from beacon kinetics is in good agreement with calorimetry data presented in Table 2.

FIGURE 5.

The poly(dA) to poly(dT) closing rate ratio is plotted as a function of temperature for loop lengths of 12, 16, and 21 bases. The experimental values k_dA/k_dT are compared with simulation values k/k₀. Here k₀ is the rate with zero stacks (where poly(dT) is assumed to have no stacking) and k is given by Eq. 4. The optimized stacking free energy parameters ΔH_s and ΔS_s derived from this fit are given in Table 1.

TABLE 1.

Thermodynamic parameters for single-stranded stacking of poly(dA) in 0.25 M NaCl, obtained by fitting simulation (with threshold radius r_c = 2) to experimental (Goddard et al., 2000) closing rates

Loop N beads	ΔHs kcal/mol	ΔSs cal/mol/K	ΔGs (310 K) kcal/mol
12	−4.5	−14	−0.2
16	−8.2	−25	−0.5
21	−7.4	−21	−0.9

TABLE 2.

Thermodynamic parameters for single-stranded stacking of poly(rA) from three experiments cited in (Turner, 2000)

Reference	ΔHs kcal/mol	ΔSs cal/mol/K	ΔGs (310 K) kcal/mol
Filimov	−3.0	−10	+0.1
Suurkuusk	−8.5	−27	−0.1
Freier	−6.8	−22	0.0

ARRHENIUS BEHAVIOR OF CLOSING

In Goddard et al., (2000), an Arrhenius closing enthalpy of ΔH_c^‡ = 0.5 kcal/mol/base was found for poly(dA). The authors associated ΔH_c^‡ with the base stacking enthalpy; however, in the previous section we have shown (from that same data set) that the enthalpy of an AA stack is an order-of-magnitude larger, ΔH_s ≈ −8 kcal/mol. Let us now attempt to resolve that discrepancy.

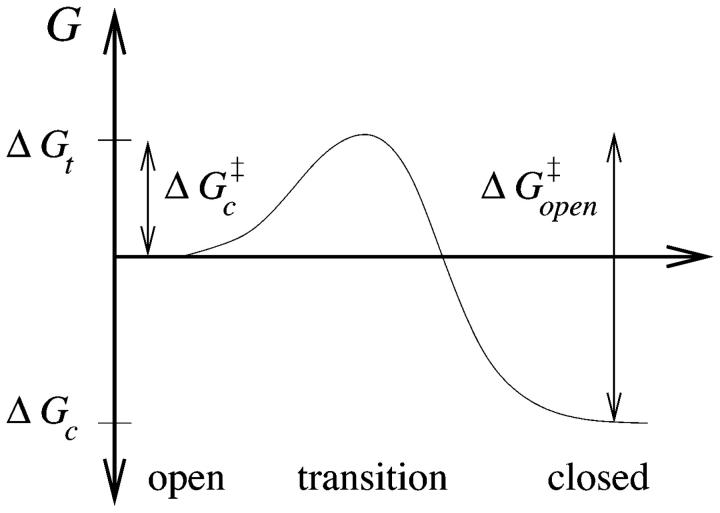
The closing free energy difference (relative to the open state and see Fig. 6) is

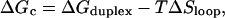(5)

and the presumed free energy of the transition state is

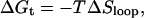(6)

without the benefit of forming a duplex at the stem, but with the entropic cost of forming a loop. This picture is consistent with the independence of loop composition of the Arrhenius opening rat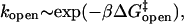e, since 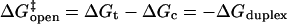depends only on the stem.

FIGURE 6.

Schematic of free energy states for Arrhenius Behavior of Closing.

The Arrhenius picture says that the closing rate should vary as

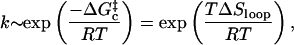(7)

which appears, at first glance, to be temperature independent, consistent with the treatment in preceding works (Bustamante et al., 1994; Smith et al., 1996; Shen et al., 2001). However, single-strand stacking increases the persistence length λ, thereby reducing the loop closure probability. An Arrhenius-type activation energy arises from ΔS_loop(λ(T)).

Our theoretical context to estimate ΔS_loop(λ(T)) is a simple one, a nonreversal random walk picture to calculate λ merged with standard expressions for the Flory radius. Despite this simplicity, the qualitative aspects are observed and even surprisingly good numerical agreement is obtained.

Because the nonreversal random walk lacks correlations, the persistence length λ can be related to the thermal average of the dot products of neighboring segments:

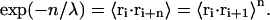(8)

For a nonreversal random walk with stacking interactions, the dot product can be computed

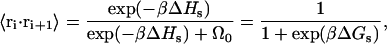(9)

which gives

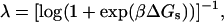(10)

where ΔG_S = ΔH_s − TΔS_s is the free energy difference for stacked versus unstacked states of neighboring nucleotides.

The loop closing entropy change can be estimated by comparing the probabilities of closed and open configurations,

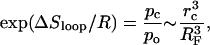(11)

where the Flory radius (Grosberg and Khokhlov, 1994) is

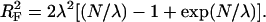(12)

Putting it all together yields

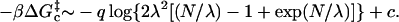(13)

Fixing λ and taking the large N limit here would result in the standard loop entropy expression. As is often done, to partially correct for self-avoidance in our calculations, we shall replace the q = 3/2 factor that is indicated in the derivation with q = 2.

To obtain the Arrhenius activation energy we differentiate with respect to β,

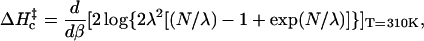(14)

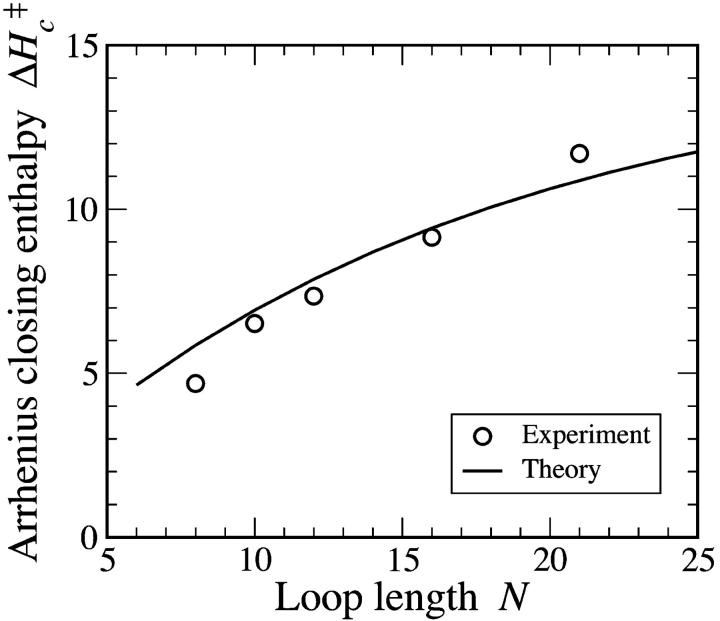
thereby eliminating temperature-independent terms. (Terms that go as higher powers of β are also eliminated in Eq. 14. Reports of non-Arrhenius kinetics given in Wallace et al., 2001, might be understood in this way.) Our results are given in Fig. 7.

FIGURE 7.

The Arrhenius activation energy as a function of chain length. Stacking parameters ΔH_g = −9 kcal/mol and ΔS_s = −25.6 cal/mol/K were used, and ΔH_c^‡ = d(βΔG_t)/dβ was evaluated at T = 310 K.

This simple theory resolves the discrepancy between ΔH_c^‡ and ΔH_s measurements. Quantitative agreement is already fairly good. Constructing a more sophisticated theory which describes a few self-avoiding segments would be a next step toward improving the fit.

INFLUENCE OF DEFECTS ON CLOSING TIME KINETICS

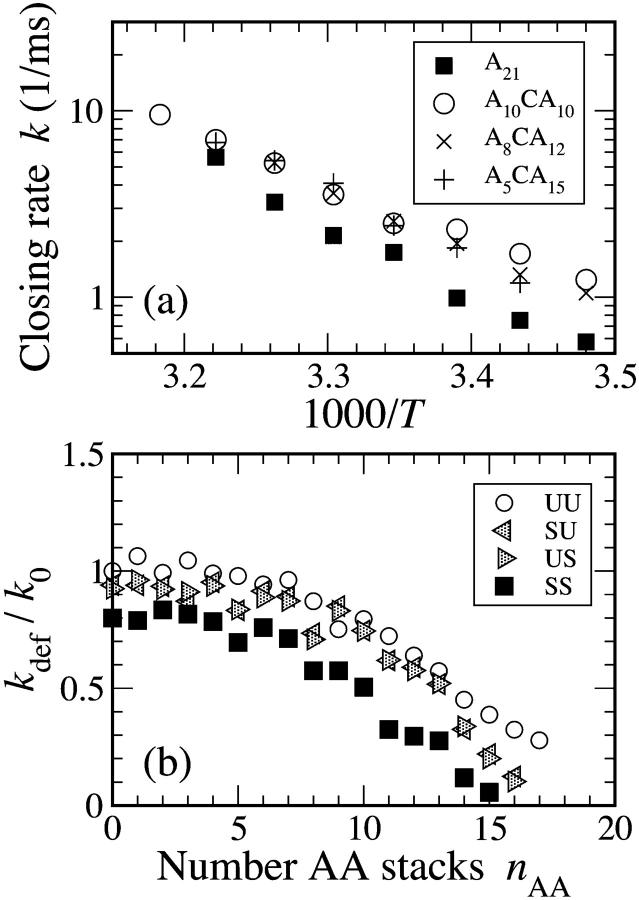
Goddard and co-workers also measured the closing times of chains with a single cytosine “defect” in the loop region along with 20 adenines (Goddard et al., 2000). Such a defect has a major impact on the closing kinetics of beacons—it is twice as fast for low temperatures (see Fig. 8 a).

FIGURE 8.

(a) Experimental data (Goddard et al., 2000) shows that the inclusion of a cytosine defect among an N = 21, poly(dA) chain cuts the closing time substantially. (b) To simulate a defect at a central location (A₁₀CA₁₀), the status of central AC and CA stacks (either unstacked, U, or stacked, S) is specified. As temperature decreases, the number of AA stacks in the rest of the chain will increase. Note how the difference between stacked SS (more like A₂₁) and unstacked UU/SU/US (more like A₁₀ CA₁₀) rates widens.

There is no reason to expect that there would be significant stacking stabilization of AC pairs (Friedman and Honig, 1995). There was insufficient data for us to estimate ΔH_AC and ΔS_AC, but it is clear that the defects are not stacked as often as AA pairs (see Fig. 8 b, which shows that when there are breaks in stacking at the defect position, the closing rate increases).

Others have suggested that misfolded states contribute to folding kinetics by roughening the folding energy landscape (Ansari et al., 2001; Ying et al., 2001). Alternate folds may be important to the kinetics of beacons with heterogeneous loop regions, but we see no evidence for them in studying the melting curves of these experiments. Using 37°C values from Turner (2000), we may estimate the free energies of alternate states. An AA/TT bound loop contributes weakly ΔG_alt ∼ +3.5 kcal/mol relative to the open state (−1 kcal/mol for AA/TT pair, −1.5 kcal/mol for terminal mismatches, +6 kcal/mol for loop formation).

The inclusion of a cytosine defect yields an AAC sequence which can bind to the TTG sequence of the stem much more tightly than any AA/TT pair. By the same estimates, an AAC/TTG bound loop contributes ΔG_def ∼ +2 kcal/mol relative to the open state (−2.5 kcal/mol for AAC/TTG pairs, −1.5 kcal/mol for terminal mismatches, +6 kcal/mol for loop formation; the m-fold algorithm—Zuker, 1989—yields free energies of alternate and defect states of ΔG_alt ∼ +1.0 kcal/mol and ΔG_def ∼ +0.2 kcal/mol, at 37°C).

Alternate conformations increase the likelihood of remaining in a fluorescing (unclosed) configuration,

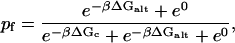(15)

and with

(16)

the effective closing rate becomes k_eff = k/(1 + e^−βΔG_alt). Alternate configurations only increase the closing time; however, this is not what was observed in experiment.

What has been observed is that defect states close more quickly, a fact which is consistent with a nucleotide stacking model.

CONCLUSIONS

Stacking plays an important role in the kinetic behavior and folding conformations of nucleic acids in solution. As temperature decreases, stacked regions become longer and closing times increase. While current RNA folding algorithms (Zuker, 1989; Isambert and Siggia, 2000) do include the free energies for forming double-stranded regions, they neglect sequence-specific persistence lengths. Stacking of unhybridized (ss) nucleotides may significantly stabilize the nucleic acid conformations (certain RNA tetraloops where free energy bonuses have been described; Mathews et al., 1999). Interestingly, we have been able to measure these nearest-neighbor interactions from kinetic simulations and time-resolved experiments.

We have shown it is possible to extract persistence lengths and local thermodynamic properties from comparing time-resolved experimental measurements to simulated kinetics. The stacking enthalpy and entropy for AA was shown to be in good agreement with calorimetric measurements.

We also present a solution to the closing penalty puzzle. The persistence length is not constant, but depends on ΔH_s, ΔS_s, and T. A simple theory indicates why the Arrhenius closing enthalpy ΔH_c^‡ is an order-of-magnitude smaller than the stacking enthalpy ΔH_s. Scaling results for end-to-end closing rates of self-avoiding polymers were also presented, clarifying a disputed result.