Mechanisms of Microtubule-Based Kinetochore Positioning in the Yeast Metaphase Spindle

Abstract

It has been hypothesized that spatial gradients in kMT dynamic instability facilitate mitotic spindle formation and chromosome movement. To test this hypothesis requires the analysis of kMT dynamics, which have not been resolved at the single kMT level in living cells. The budding yeast spindle offers an attractive system in which to study kMT dynamics because, in contrast to animal cells, there is only one kMT per kinetochore. To visualize metaphase kMT plus-end dynamics in yeast, a strain containing a green fluorescent protein fusion to the kinetochore protein, Cse4, was imaged by fluorescence microscopy. Although individual kinetochores were not resolvable, we found that models of kMT dynamics could be evaluated by simulating the stochastic kMT dynamics and then simulating the fluorescence imaging of kMT plus-end-associated kinetochores. Statistical comparison of model-predicted images to experimentally observed images demonstrated that a pure dynamic instability model for kMT dynamics in the yeast metaphase spindle was unacceptable. However, when a temporally stable spatial gradient in the catastrophe or rescue frequency was added to the model, there was reasonable agreement between the model and the experiment. These results provide the first evidence of temporally stable spatial gradients of kMT catastrophe and/or rescue frequency in living cells.

INTRODUCTION

In eukaryotic cells, chromosome segregation during mitosis is accomplished with high fidelity by the mitotic spindle, which consists of MTs attached at their minus ends to spindle poles and attached at their plus ends to kinetochores on the chromosomes. Chromosome motion is directly tied to the dynamics of the attached kMTs, and therefore an understanding of kMT dynamics is essential to deciphering the mechanisms of chromosome movement (Rieder and Salmon, 1998). Many models have been proposed to explain the congression and oscillating behavior of microtubule-bound chromosomes about the spindle equator during metaphase (for review, see Mitchison, 1989; Rieder and Salmon, 1998; Kapoor and Compton, 2002). Until the late 1980s, the most accepted of these had been the “traction fiber” model, where the strength of the pulling force on a chromosome is proportional to the length of the attached kMT fiber (Ostergen, 1951; Fuge, 1989; Hays and Salmon, 1990). As evidence has accumulated against this theory (Rieder et al., 1986; Nicklas, 1989; Mitchison and Salmon, 1992; Skibbens et al., 1993), recent models of congression have centered upon the dynamic behavior of kMTs.

MTs exhibit dynamic instability, characterized by alternating cycles of extended polymerization and depolymerization (Mitchison and Kirschner, 1984; Skibbens et al., 1993). The growth and shortening rates are approximately constant from one growth or shortening excursion to the next. A switch from the growth to shortening state (catastrophe) or the reverse transition (rescue) occurs abruptly and apparently at random. Generally, MT dynamics are characterized by four parameters: growth and shortening rates, and catastrophe and rescue rates (inverse of mean growth and shortening durations, respectively). This characterization implicitly assumes a random first-order transition between the growth and shortening states. MTs can continue to exhibit abrupt transitions between growth and shortening with chromosomes bound at their plus-end tip (Skibbens et al., 1993; Hunt and McIntosh, 1998; Maddox et al., 2000).

To explain the oscillation and congression of chromosomes, various models have been proposed in which kMT dynamics are dependent upon the position of the attached kinetochore relative to the spindle and/or relative to its sister kinetochore (Mitchison, 1989; Skibbens et al., 1993; Murray and Mitchison, 1994). One proposed mechanism of position sensing is that the kinetochore acts as a tensiometer dictating the state of MT polymerization and therefore chromosome movement (Skibbens et al., 1993, 1995; Skibbens and Salmon, 1997). Microneedle chromosome manipulation (Nicklas, 1988), centromere laser ablation (Skibbens et al., 1995), and comparison of mono-oriented and bioriented chromosome movements (Skibbens et al., 1993) have suggested that tension across the chromosome between sister kinetochores affects the direction of chromosome motion. Other experiments have demonstrated that MT-dependent “polar ejection forces” (Rieder et al., 1986; Salmon, 1989; Rieder and Salmon, 1994) appear to bias chromosome motion away from the nearest pole. Although the mechanism of this phenomenon is still not well understood, steric interaction and motor localization along chromosome arms have both been hypothesized, and recent experiments have begun to reveal molecules that are involved (Antonio et al., 2000; Funabiki and Murray, 2000; Levesque and Compton, 2001). Another mechanism by which kMT dynamics could be regulated based on chromosome position relative to the spindle is via a concentration gradient of signaling molecules (Mitchison, 1989). This might include microtubule-associated proteins, MT destabilizers, tubulin itself, or any molecule that influences kMT dynamics. Although it is not obvious how such a mechanism by itself would accomplish congression in animal spindles, where sister kinetochores are separated by less than a few micrometers whereas the pole-to-pole spindle length is many tens of micrometers (Rieder and Salmon, 1994), it is possible that chemical gradients could mediate metaphase alignment in concert with other mechanisms.

Whereas the complexity of most eukaryotic mitotic spindles obscures the relationship between MT dynamics and the movement of the attached chromosome, the budding yeast Saccharomyces cerevisiae offers a simpler model system that may reveal certain conserved features. Electron microscopy has shown that the yeast mitotic spindle contains 16 kMTs anchored at each pole that apparently bind to the 16 chromosomes (Winey et al., 1995; O'Toole et al., 1999). With only one kMT per kinetochore, chromosome motion is directly coupled to single kMT length fluctuations, a phenomenon that has been directly observed only in vitro (Hunt and McIntosh, 1998). Although electron microscopy has provided information about the structure of the mitotic spindle, live cell imaging via light microscopy is required to gather temporal information concerning MT length fluctuations and chromosome positions. However, the small size of the yeast nucleus (1500 nm diameter) makes direct visualization of individual kMT dynamics very challenging. Recent advances in fluorescence imaging techniques have enabled the visualization of spindle poles, chromosomes, microtubules, and kinetochores in living yeast cells (Straight et al., 1997; Goshima and Yanagida, 2000; He et al., 2000; Maddox et al., 2000; Tanaka et al., 2000; Pearson et al., 2001). Labeling of centromere proximal markers showed that sister centromeres on a single chromosome oscillated relative to each other (He et al., 2000), and were often separated by distances of up to 800 nm (Goshima and Yanagida, 2000). The oscillation in separation distance found in yeast suggests that the centromere proximal regions of the chromosome are elastic, stretching to accommodate their dynamic kMT attachments. To characterize kMT dynamics on this scale, centromere proximal markers are therefore insufficient, as their distance from the MT attachment site at the kinetochore may fluctuate (Pearson et al., 2001). Fluorescent kinetochore proteins, however, can be used to track kMT plus-end locations (Pearson et al., 2001), assuming that the kinetochore remains attached to the plus-end tip of the kMT, as is observed in other eukaryotic spindles (Rieder, 1981; Wise et al., 1991). Although individual kinetochores cannot be resolved, this technique allows visualization of the kinetochore population and therefore kMT population dynamics. Pearson et al. (2001) found that during metaphase, kinetochores labeled with Cse4-GFP often appeared as two clusters of fluorescence, ∼600 nm apart, with transient movements between the two clusters.

Here we developed computer simulations to predict kMT tip positions in the spindle based on three models of kMT dynamics during metaphase in yeast: 1), pure dynamic instability, 2), dependence of the rescue frequency on tension between sister kinetochores, and 3), spatial dependence of either the rescue or catastrophe frequency on the position of the kMT tip in the spindle. To evaluate these models requires a direct comparison to experimental observations of kMT tip markers. However, the inability to resolve individual kinetochores experimentally, even by deconvolution, required that an additional component be added to our models: the fluorescence imaging process. We accomplished this by incorporating an experimentally determined three-dimensional point spread function (Agard et al., 1989) with which we convolve the model's predicted fluorescent kinetochore localization to generate a simulated image. We call this approach “model-convolution,” a technique inspired by previous efforts to predict microscope images of cellular features (Waterman-Storer and Salmon, 1998; Jiang et al., 1999). The mean spatial distribution of simulated kinetochore fluorescence relative to the spindle poles and ACF of the simulated kymographs were produced for each model of kMT dynamics and directly compared to the same statistics calculated from experimentally obtained images. We found that a pure dynamic instability model was insufficient to reproduce the observed mean spatial distribution of Cse4-GFP fluorescence, whereas models incorporating a spatial gradient in either the catastrophe or rescue frequency relative to the spindle poles could predict both the mean spatial distribution and the temporal dynamics of the Cse4-GFP fluorescence.

EXPERIMENTAL METHODS

Fluorescent constructs

Cse4-GFP and Spc29-CFP were used as previously described to label kinetochores and spindle pole bodies, respectively (Pearson et al., 2001). All experiments were done using S. cerevisiae strain KBY2012 (MATa trp1-63 leu2-1 ura3-52 his3-200 lys2-801 cse4::HB SPC29-CFP-KAN pKK1). The cells were transfected with the pKK1 plasmid, which contains CSE4 fused to GFP (CSE4-GFP) under its native promoter. Construction of pKK1 was previously described by Chen et al. (2000). This plasmid was introduced into a strain with the endogenous CSE4 gene knocked out, so that all Cse4p was fluorescently labeled. Previously this cell line has been demonstrated to proceed through mitosis normally and to have Cse4p localization similar to other kinetochore proteins (Pearson et al., 2001). SPBs were labeled by fusing CFP to the C-terminus of SPC29. KBY2012 was maintained in YEPD medium (2% glucose, 2% peptone, and 1% yeast extract).

Imaging

The fluorescence imaging techniques and equipment were similar to those previously described (Shaw et al., 1997; Maddox et al., 2000; Pearson et al., 2001). All imaging was done with a Nikon Eclipse TE600FN fixed stage upright microscope using a 100×/1.4 NA Plan Apo DIC oil immersion objective and a 100-W mercury arc lamp fluorescent-light source. Images were acquired using Metamorph software (Universal Imaging., West Chester, PA), which controlled a Hamamatsu Photonics (Bridgewater, NJ) Orca II C4742-98 chilled charge-coupled-device camera, a Nikon z axis stepping motor, and a Uniblitz shutter (Vincent Associates, Rochester, NY). Each camera pixel element represented an area 66 nm × 66 nm in the specimen field. Two-color imaging was performed using the Chroma CFP-YFP narrow pass excitation and emission filters (86002 series; Chroma Technology, Brattleboro, VT) and the FITC filter set (Chroma FITC filters). The CFP signal was imaged using CFP emission and excitation filters, whereas GFP was excited with the YFP excitation filter and imaged with the FITC emission filter. YFP filters were used for GFP excitation to minimize the overlap between CFP and GFP fluorescence, which is significant when using GFP excitation filters (Pearson et al., 2001).

For single snapshot images, metaphase cells were selected based on spindle length (∼1–2 μm) and cell morphology (bud greater than ⅓ size of mother cell). For each cell, an optical z-series of five images with 0.75 μm steps in both the GFP and CFP channels was taken to determine the 3-D position of the spindle pole bodies. Of 101 examined yeast cells, 52 spindles had both poles in the same plane of focus, as judged by the position of the SPBs. These spindles were selected for analysis of their spatial distribution of kinetochore (Cse4-GFP) fluorescence.

Dual color time-lapse movies of single cells were created by recording a single image plane in both the Cse4-GFP and Spc29-CFP channels every 5 s. Kymographs were then created from these movies as described in Pearson et al. (2001). Briefly, a 20-pixel (1320-nm) wide line was drawn through the long axis of the mitotic spindle, and the maximum intensity of the 20 pixels was recorded at each pixel length along the spindle to create a single line characterizing that image. This procedure was repeated for each frame of the dual color movies and each line stacked along the x axis to show the entire time series as a kymograph.

PSF determination and background fluorescence measurement

To effectively simulate the microscope imaging system, it was necessary to measure the PSF of the microscope, background fluorescence in cells, and system noise. To determine the PSF, small diameter beads (D = 100 nm, excitation 480 nm, emission 520 nm, Bangs Laboratories, Fishers, IN) were used to approximate a single point source of light (Agard et al., 1989; Hiraoka et al., 1990). The beads were attached to the coverslip using poly-l-lysine and then mounted in a 50% glycerol solution with a small amount of n-propyl galate (an antioxidant) to prevent photobleaching. Imaging was done using the YFP excitation filters and FITC emission filters, as used for Cse4-GFP imaging. An optical z-series image stack with axial steps of 100 nm was obtained to create a 3-D image of the single beads, extending 1 μm above and below each bead. Stacks of five different beads were averaged to measure the mean decay of fluorescence intensity away from the bead in both the focal plane and direction of the image axis.

Fig. 1 shows the appearance of a bead from focal planes 500 nm below to 500 nm above the bead, in 100 nm steps. With the bead in focus, the intensity decays to half maximum by ∼150 nm in the radial direction. As the level of defocus is adjusted in the z direction, the maximum intensity decays to half maximum by ∼300 nm above and below the focal plane, although there is a slight asymmetry to the profile. The slight asymmetry in both the radial and image axis direction indicates small aberrations in the microscope lens (Hiraoka et al., 1990).

FIGURE 1.

PSF determination. The PSF of the microscope system used for acquiring the experimental Cse4-GFP images was determined by imaging 100-nm diameter fluorescently labeled beads at varying levels of defocus in the z direction (indicated in nanometers in upper right hand corner of images). Bar = 1000 nm, 1 pixel = 66 nm. The PSF was then applied to the simulated distribution of Cse4-GFP fluorescence to generate a simulated fluorescence image.

Background fluorescence was estimated from the microscope images of the Cse4-GFP/Spc29-CFP cells. In both the GFP and CFP channels, the mean fluorescence was measured in a 5 pixel × 5 pixel (330 nm × 330 nm) region in 10 cells, away from the bright SPB and kinetochore spots. The background noise in the cell was measured from these images by calculating the standard deviation of fluorescence in these areas.

SIMULATION METHODS

A computer program was written using MATLAB (Version 6.0, The MathWorks, Natick, MA) to predict the fluorescence distribution of labeled kinetochores in the spindle, based on various models of kMT dynamics. The simulation involved two distinct processes: 1), simulating the position of the kMTs and kinetochores, and 2), simulating the formation of a fluorescence image of these kinetochores by a light microscope.

Simulation of microtubule dynamics

A Monte Carlo technique was used to simulate the length life histories of individual kMTs undergoing dynamic instability. It was assumed that each kMT was always in one of two states: growth or shortening. Switching between states was assumed to occur via a catastrophe (growth to shortening) or rescue (shortening to growth) event. kMT positions were tracked using a three-dimensional matrix representing the x, y, and z planes. Each element of the matrix corresponded to a volume 30 nm × 16.5 nm × 30 nm, corresponding to the transverse axis (y direction), spindle axis (x direction), and optical axis (z direction), respectively (Fig. 2 A). Consistent with electron micrographs of the yeast spindle (Winey et al., 1995), the location (in y-z space) of the base of each microtubule at a simulated SPB was randomly assigned within a 120 nm radius of the SPB center (Fig. 2 B), at x = 0 and x = 1500 nm. Since electron micrographs and live cell fluorescence also showed few MTs extending off the spindle axis (Winey et al., 1995; Maddox et al., 2000), kMT plus-end tips were only allowed to grow straight out from the SPB. No curving in the y or z directions was allowed; a kMT was only allowed to change its tip position in the x direction, as it grew or shortened along the axis of the spindle.

FIGURE 2.

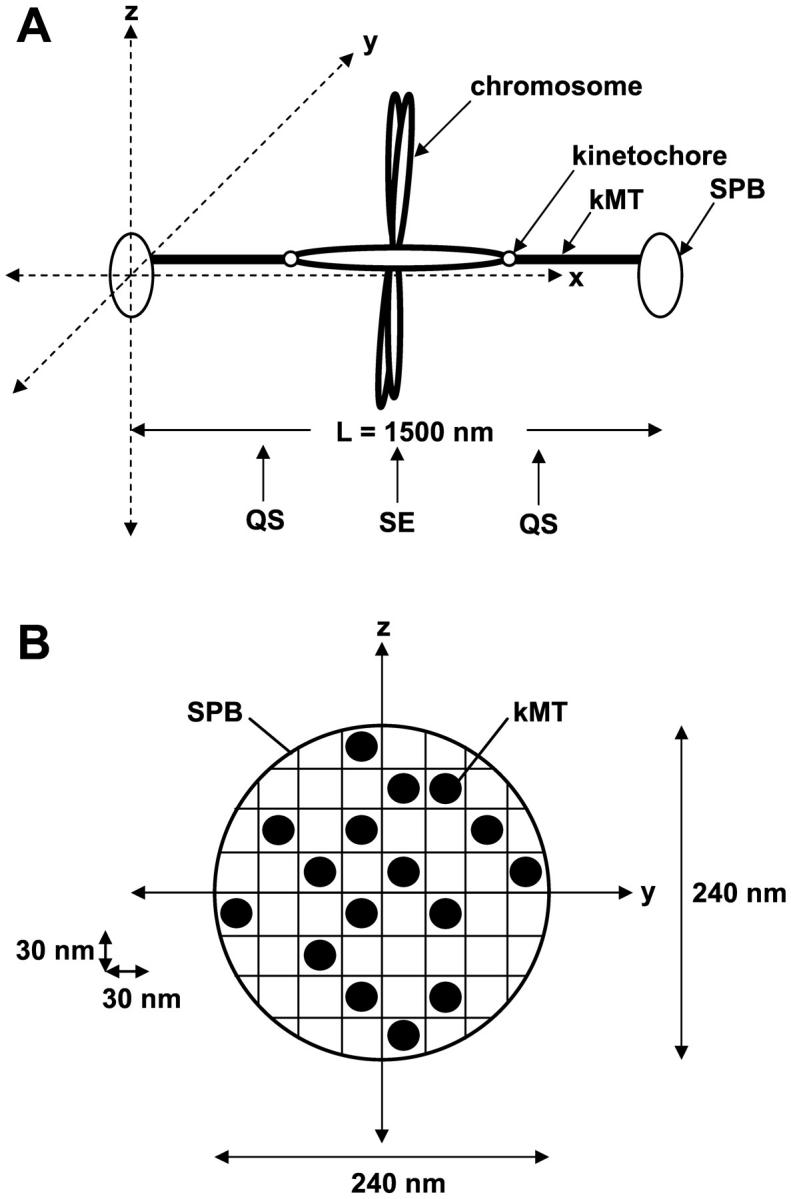
Diagram of spindle orientation assumed in computer simulation of kMT dynamics. (A) kMTs grow in the x direction toward the opposite SPB. The z direction corresponds to the optical axis for imaging. The location of the quarter spindle (QS) and spindle equator (SE) in the x direction are noted. (B) Cross section of the SPB. At the start of each simulation, kMT minus-end anchor positions at the SPB were chosen randomly within a 240-nm circle at x = 0 and x = 1500 nm. 16 kMTs were nucleated per SPB.

Thirty-two kMTs (16 from each SPB) were simulated to allow all 16 yeast chromosomes a single kMT attachment to each pole. Initially each microtubule was randomly assigned to either the growth or shortening state, and assigned a random initial length (in x space), chosen from a uniform distribution across the entire length of the spindle. To match the mean experimentally observed spindle length (1520 nm ±230 nm; see Results section), a spindle length of 1500 nm (91 matrix elements) was assumed for all simulated spindles. Since in yeast and in mammalian tissue cells the majority of kMT dynamics appears to take place at the plus-end tip (Cassimeris and Salmon, 1991; Mitchison and Salmon, 1992; Maddox et al., 2000), only plus ends were allowed to exhibit dynamic instability, whereas the minus ends were held fixed at the spindle pole bodies. At time steps of 0.9 s, the position of each microtubule plus-end tip was updated based on the assigned growth and shortening rates (V_g, V_s). The probability of catastrophe or rescue occurring during a single time step, τ_step, was calculated by the equation,

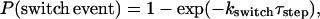(1)

where k_switch may be either the rescue (k_r) or catastrophe (k_c) frequency, depending on the present growth state of the kMT.

After each time step, a uniformly distributed random number between 0 and 1 was generated and compared with the computed switching probability (Eq. 1), to determine if a kMT underwent a transition event. If the random number was less than P(switch event), the switch event was executed. Such a transition was assumed to be instantaneous. Any kMT that completely shortened to its SPB was automatically switched into the growth state, whereas any kMT that grew the entire length of the spindle was automatically switched to the shortening state. It was assumed that each kinetochore remained attached to the tip of its microtubule throughout the duration of the simulation. A warm-up time of 5 min (333 time steps) was provided to allow the kMT length distribution to reach steady state. To ensure that steady state had been reached, the simulation was run for 5 more min before the kinetochore positions were fed into a simulation of the imaging process.

V_g and V_s were adjustable parameters but treated as constants in each model. The switching frequencies, k_c and k_r, were determined at each time step based on the model chosen for kMT dynamics.

Models for MT dynamics

Model 1: pure dynamic instability

Each kMT underwent dynamic instability with constant parameters of dynamic instability (V_g, V_s, k_c, k_r). Each parameter was independent of time, position in the spindle, and distance between sister kinetochores.

Model 2: tension between sister kinetochores

To investigate the effects of tension between sister kinetochores, we created a model in which the rescue frequency, k_r, for a kMT at any given time depended on the amount of tension felt between the kMT's kinetochore and its sister kinetochore. Similar to other chromosome models (Joglekar and Hunt, 2002), the tensile force between sister kMTs was modeled as a Hookean spring:

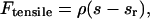(2)

where s is the separation distance in the x direction between the tips of sister kMTs, s_r is the rest length between sister kMT tips, and ρ is the spring constant. Previous experiments demonstrated that fluorescent tags ∼1 kb from the centromere on sister chromosomes appear as a single indistinguishable spot of fluorescence in ndc10-1 mutant cells (missing essential kinetochore protein) or normal cells in the presence of nocodazole (Goshima and Yanagida, 2000; He et al., 2000). Given the spatial resolution of the conventional epifluorescence microscope, 250 nm (Kohlwein, 2000), this provides an upper bound on an estimate of the rest length between sister kinetochores. We assumed a value of 200 nm for s_r.

The following equation was used to calculate the rescue frequency as a function of the tensile force:

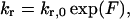(3)

where k_r,0 is the rescue frequency in the absence of any net polar ejection or tensile force, and the force, F, in this case is F_tensile (Fig. 3 A). The exponential dependence of a first-order rate constant on force is generally assumed from first principle thermodynamic arguments (Hill, 1987). The exponential shape of the curve allows k_r to increase with increasing F, while preventing negative rescue frequencies at low or negative values of F. Since the argument of the exponential must be dimensionless, the units of ρ are μm⁻¹. Failure to specify the units of force is acceptable because the prefactor to the exponential in Eq. 3, k_r,0, is itself an adjustable parameter. Therefore, any arbitrary change in the units of force can be compensated for by a change in the adjustable prefactor to the exponential. The adjustable parameters k_c, V_g, and V_s were treated as constants.

FIGURE 3.

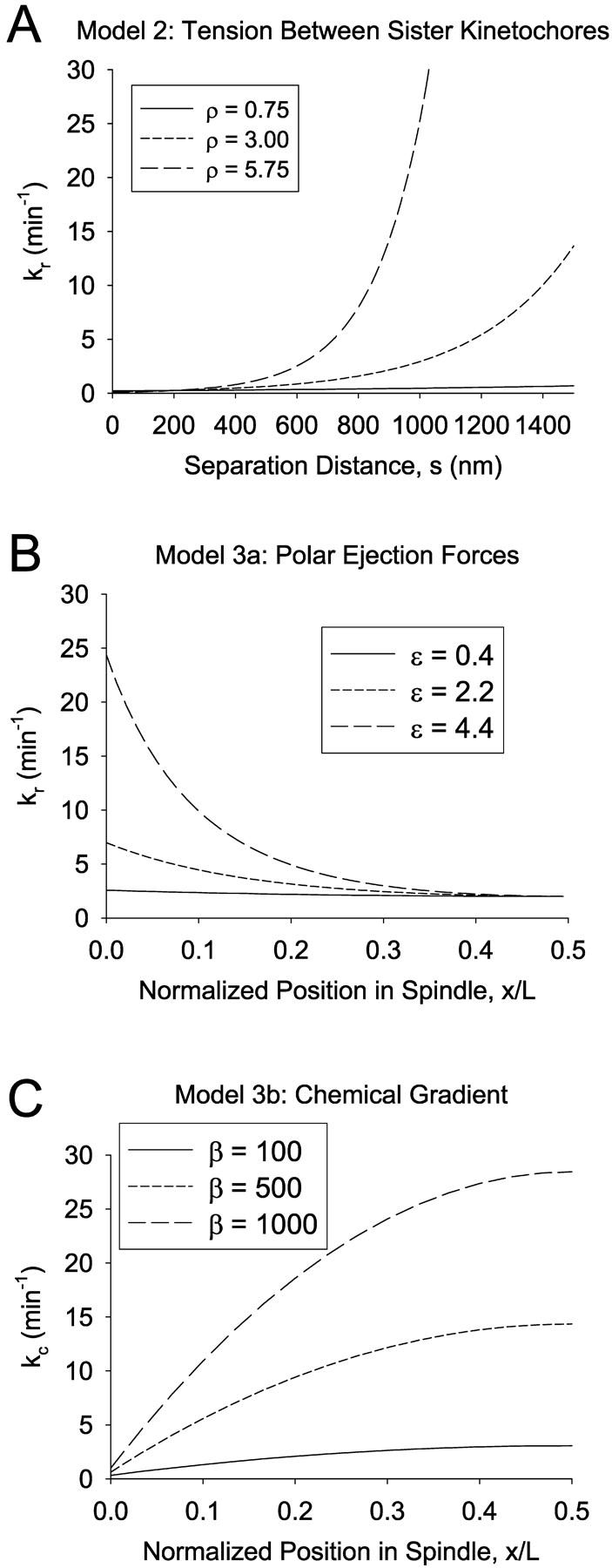
Functional dependence of switching frequencies in models 2 and 3. (A) Model 2: Tension between sister kinetochores. Rescue frequency is plotted as a function of the separation distance between the tips of sister kMTs (see Eqs. 2 and 3; k_r,0 = 0.25 min⁻¹, ρ indicated in μm⁻¹). As the separation distance increases, the magnitude of the tensile force becomes greater, leading to a larger rescue frequency. (B) Model 3 a: Polar ejection force model. The rescue frequency for a kMT anchored at x/L = 0 is plotted as a function of the normalized kMT plus end tip position in the spindle according to Eqs. 3 and 4 (k_r,0 = 2.0 min⁻¹, ɛ indicated in units of μm⁻²). As ɛ increases, the magnitude of the polar ejection force becomes larger, increasing the effect on k_r. The net ejection force is always zero at the spindle equator (x/L = 0.5), where the forces from the opposing SPBs balance each other. (C) Model 3 b: Chemical gradient model. The catastrophe frequency is plotted as a function of the normalized kMT plus-end tip position in the spindle according to Eq. 12 (k_c,0 = 0.25 min⁻¹, β indicated in units of min⁻¹ c_B⁻¹]. c_B is defined as a function of position by Eqs. 7 and 10 (k = 1 s⁻¹and D = 10⁻¹¹ m²/s]. As β increases, the effective range of catastrophe frequencies in the spindle increases as well.

Model 3: spatial dependence of dynamic instability

Two models were created to investigate temporally stable spatial gradients in the rescue or catastrophe frequency relative to the spindle: a), a polar ejection force model, and b), a chemical gradient model.

a) Polar ejection force model. The magnitude of the polar ejection force, F_ejection, was modeled as proportional to the square of the distance from the kMT tip to the center of the spindle:

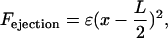(4)

where ɛ is an adjustable parameter and L is the pole-to-pole spindle length. This form has been employed in a previous model of the polar ejection force (Joglekar and Hunt, 2002). As in previous models (Salmon, 1989; Rieder and Salmon, 1994; Skibbens and Salmon, 1997; Joglekar and Hunt, 2002), it was assumed that the polar ejection forces are applied at the chromosome arms, particularly the centromeric chromatin, leading to tension at the kinetochore with magnitude F_ejection. F_ejection was always directed toward the center of the spindle, and defined as a positive value when directed away from the SPB at which the kMT was anchored. The rescue frequency, k_r, was then calculated by Eq. 3, with F = F_ejection, yielding a spatial gradient in k_r (Fig. 3 B). Again, the argument of the exponential must be dimensionless, as argued above in the presentation of the tension between sister kinetochores model. As a result, in the polar ejection force model the units of ɛ are μm⁻². The adjustable parameters k_c, V_g, and V_s were treated as constants in this model.

For the case in which both polar ejection forces and tension between sister kinetochores were modeled, the net force at the kinetochore was calculated as:

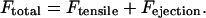(5)

The net force, F_total, was then used in Eq. 3 to calculate the rescue frequency.

b) Chemical gradient model. To simulate a chemical gradient that might produce kinetochore clustering, we modeled a hypothetical spatially segregated kinase/phosphatase system that regulates a kMT catastrophe promoter. The kinase reaction was modeled as a first-order heterogeneous surface reaction at the SPBs, whereas the phosphatase reaction was modeled as a first-order homogeneous reaction occurring throughout the nucleus. The diffusive transport and interconversion of species A and B can be described by the following equations:

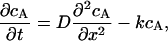(6)

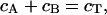(7)

where c_A is the concentration of the phosphorylated (deactivated) catastrophe promoter, c_B is the concentration of unphosphorylated (activated) catastrophe promoter, c_T is the total concentration of both species of catastrophe promoter, D is the diffusivity of the catastrophe promoter, and k is the homogenous reaction rate constant. The boundary conditions are:

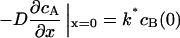(8)

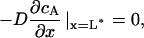(9)

where L^* = L/2 (the half-length of the spindle), and k^* is the first-order heterogeneous reaction rate constant at the SPB surface. The analytical solution to Eqs. 6–9 at steady state is:

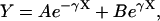(10)

where

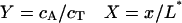(11a)

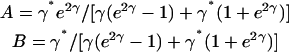(11b)

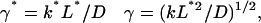(11c)

where x is the distance from the nearest spindle pole. The following values were assigned to produce a stable spatial gradient in c_B via Eq. 7 and Eq. 10: k = 1 s⁻¹ and D = 10⁻¹¹ m²/s. These values are similar to those found experimentally for proteins in the cytoplasm (for review, see Brown and Kholodenko, 1999). The specific values chosen are not critical to the model, as a variety of physically plausible parameter combinations can give rise to substantial gradients over the dimensions of the nucleus.

The catastrophe frequency, k_c, was then related to the concentration of the activated catastrophe promoter, c_B, in a linear fashion:

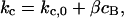(12)

where k_c,0 is the catastrophe frequency in the absence of the catastrophe promoter and β is an adjustable parameter that describes the magnitude of the catastrophe promoter's effect (Fig. 3 C). The free parameter k_c,0 was assumed to be 0.25 min⁻¹ in all cases to maximize the size of the gradient while minimizing the maximum catastrophe frequency at the spindle center. This value is consistent with previously measured catastrophe frequencies of cytoplasmic microtubules in yeast (Carminati and Stearns, 1997; Tirnauer et al., 1999; Kosco et al., 2001).

At each time step in the simulation, the concentration of activated catastrophe promoter at each kMT tip was determined based on its distance from the spindle pole bodies so that the effective catastrophe rate constant (k_c) could then be computed using Eq. 12. The adjustable parameters, k_r, V_g, and V_s were treated as constants in this model.

For the case in which the chemical gradient model was combined with the tension between sister kinetochores model, the catastrophe frequency was calculated via Eq. 12 as a function of the catastrophe promoter concentration, whereas the rescue frequency was calculated via Eq. 3 where F = F_tensile.

Simulation of the imaging process

It was assumed that each kinetochore remained attached to the tip of its kMT throughout the duration of the simulation. At the conclusion of the simulation (∼10 min of kMT dynamics), the kinetochore positions were mapped to a matrix with voxels matching the size of those in the microscope images (66 nm × 66 nm × 100 nm). To generate a fluorescence image of the simulated kinetochores, this kinetochore position matrix was convolved with the experimentally determined three-dimensional PSF. The convolution was done by summing the contributions of fluorescence to the image focal plane from each z plane of the kinetochore position matrix (for review of fluorescence image formation in three dimensions, see Agard et al.,1989):

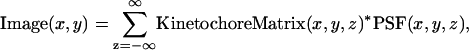(13)

where the ^* operator represents the 2-D convolution of the kinetochore matrix plane with its corresponding PSF plane. The summation was carried out with z steps of 100 nm, across the entire z dimension of the spindle (three steps), with the simulated image always focused at the midplane of the spindle. After summing the contributions from each kinetochore matrix plane, the intensities were scaled so that the mean signal intensity matched that of the signal in the experimentally observed eight-bit images (pixel intensity range: 0–255). Background fluorescence and Gaussian white noise were added at levels measured in the experimental images. Any pixel intensity >255 was set to 255.

Statistical analysis

Spatial distribution of kinetochore-associated fluorescence

All image analysis was done in MATLAB. The mean spatial distribution of kinetochore (Cse4-GFP) fluorescence of 52 spindles in both the experimental and simulated images was calculated in the same way. In each image the total fluorescence in the spindle area was calculated. This area was designated to begin at the center of one spindle pole body fluorescent marker and end at the opposite spindle pole body, and included 15 pixels (990 nm) in the direction perpendicular to the spindle axis (y direction in Fig. 2 A), which was sufficiently wide to encompass all spindle fluorescence. The percentage of the total spindle fluorescence was then measured as a function of relative distance along the spindle axis (x/L), by integrating the fluorescence intensity of each 15-pixel column and dividing by the total spindle fluorescence. The distribution was binned into 24 equal intervals (each ∼4.2% of the spindle length, L, corresponding to the pixel width of 66 nm) to facilitate the analysis of slightly different size spindles. This data was then pooled as 104 half spindles and the mean percentage of total spindle fluorescence in each bin calculated.

To compare the simulation results with the experimentally observed fluorescence distribution, we calculated the mean distribution of fluorescence of 52 simulated spindles 100 times for every set of parameters investigated. A single curve was fit to the 100 simulated mean curves, and the sum-of-squares errors between this fit curve and the experimentally observed distribution (SSE_exp) was calculated. The sum-of-squares error between each of the 100 simulated mean curves and the fit curve (SSE_sim) was also calculated. The SSE_exp was then ranked in the set of 100 SSE_sim to determine the probability of fit a given model parameter set. For example, if the SSE_exp ranked as the 20th largest in the set of SSE_sim, then p = 20/100 = 0.2. The model parameters were rejected if p < 0.05.

To run the simulations, MATLAB code was compiled and run as a stand-alone C program. It took ∼1 h to run 100 simulations on a GenuineIntel computer with 256 MB RAM and a Pentium III 933 MHz processor.

Temporal dynamics

To evaluate the temporal rate of change in spindle fluorescence intensity in the models, the ACF of spindle fluorescence in experimental and simulated kymographs was calculated at 25% (quarter spindle) and 50% (spindle equator) of the total spindle length. The pattern of change in fluorescence intensity at any point in the spindle will be reflected in the behavior of the autocorrelation function. For example, white noise would result in ACF values of zero for all time intervals greater than zero. Alternatively, a diffusionlike random walk from the initial fluorescence intensity would result in an exponential decay in the ACF. To account for photobleaching in the experimentally observed kymographs, an exponential curve was fit to the decay of the total linescan fluorescence intensity in both the Cse4-GFP and Spc29-CFP channels of the kymographs. The intensities in each line scan of the kymographs were then corrected by multiplying by the reciprocal of the exponential curve at each time frame.

In the experimental kymographs, the position of the spindles fluctuated slightly in the z direction during the recording of time series data, resulting in shifts out of focus for transient time periods. To add this component to the simulated kymographs, the maximum Spc29-CFP intensity in each line scan of the experimental kymographs was recorded, and the mean and standard deviation over the duration of each kymograph was calculated. Using the experimentally determined point spread function, the amount of “defocus” necessary to reproduce these fluctuations in SPB fluorescence was determined by simulation. The focal plane of each image acquisition in simulated spindle movies was then modeled as having a mean of z = 0 (center of the spindle), with a standard deviation (Gaussian white noise) sufficient to produce the observed mean intensity of maximum Spc29-CFP fluorescence over time. For example, if the maximum Spc29-CFP fluorescence had a mean intensity of 255 over all the line scans of an experimental kymograph, then the focal plane at each time step in the corresponding simulated kymograph would have mean z = 0 ± 0 (always in focus), resulting in a simulated mean maximum intensity of 255. If Spc29-CFP fluorescence in the experimental kymograph had a mean maximum intensity of 200, then the simulated kymograph would have a mean focal plane of z = 0 ± 300 nm, so that enough frames were sufficiently out of focus to reduce the simulated mean maximum intensity to 200.

In both the experimental and simulated kymographs, severely out-of-focus line scans were eliminated from the autocorrelation calculation. Any line scan in which the intensity of both SPBs was not greater than two standard deviations above background was replaced for purposes of calculating the ACF with the mean intensities of all “in-focus” line scans.

In both experimental and simulated kymographs, quarter spindle and spindle equator intensity was recorded at each time frame and the ACF of the intensity at each of these two locations was calculated using the following formula:

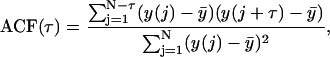(14)

where τ = time lag, N is the total number of time steps in the kymograph, y(j) is fluorescence intensity at a particular location under consideration (either the quarter spindle or spindle equator) at frame j, and 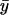is the mean fluorescence intensity at the quarter spindle or spindle equator over all frames.

To determine the probability of fit between a model and the observed kymographs, the mean ACF at time lag of one frame (5 s) was calculated for 12 simulated kymographs 100 times for every set of parameters tested. The mean value of the mean ACF over the 100 simulations was recorded, and the squared error between this average mean and the 100 individual means (SE_sim) was calculated. The squared error between the simulated average mean and the experimental observed mean (SE_exp) was also calculated. SE_exp was then ranked in the set of 100 SE_sim to determine the probability of fit of a given model parameter set. The model parameters were rejected if p < 0.05.

EXPERIMENTAL RESULTS

Spatial distribution of kinetochore-associated fluorescence

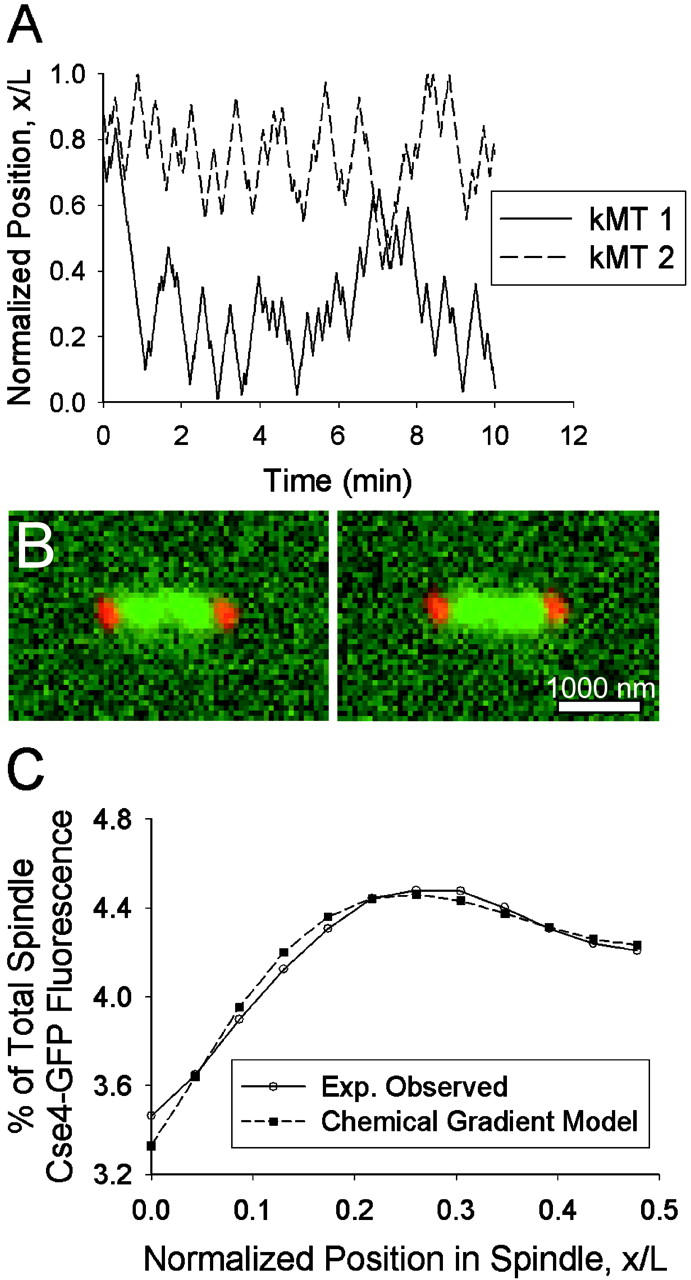
In images of the budding yeast spindle during metaphase, kinetochore protein Cse4-GFP generally appeared as two clusters of fluorescence in opposite halves of the spindle (Fig. 4 A). Cse4-GFP fluorescence was confined to the area directly between the spindle pole bodies (SPBs), which were visualized by imaging Spc29-CFP fluorescence (red). As in Pearson et al. (2001), the centroid positions of Cse4-GFP clusters were located relative to the SPBs. The mean separation distance between cluster centroids was 750 ± 220 nm, approximately half the mean spindle length of 1520 ± 230 nm (N = 52 spindles). The mean midpoint between clusters was at 50.6 ± 3.0% of the spindle length, suggesting that the chromosomes in these spindles have on average a metaphaselike alignment with respect to the spindle equator. Individual kinetochores could not be resolved, as the 32 kinetochores are distributed along the 1500-nm-long spindle, giving a mean axial separation of ∼50 nm, which is much less than the spatial resolution of the microscope (0.61λ/NA = ∼250 nm).

FIGURE 4.

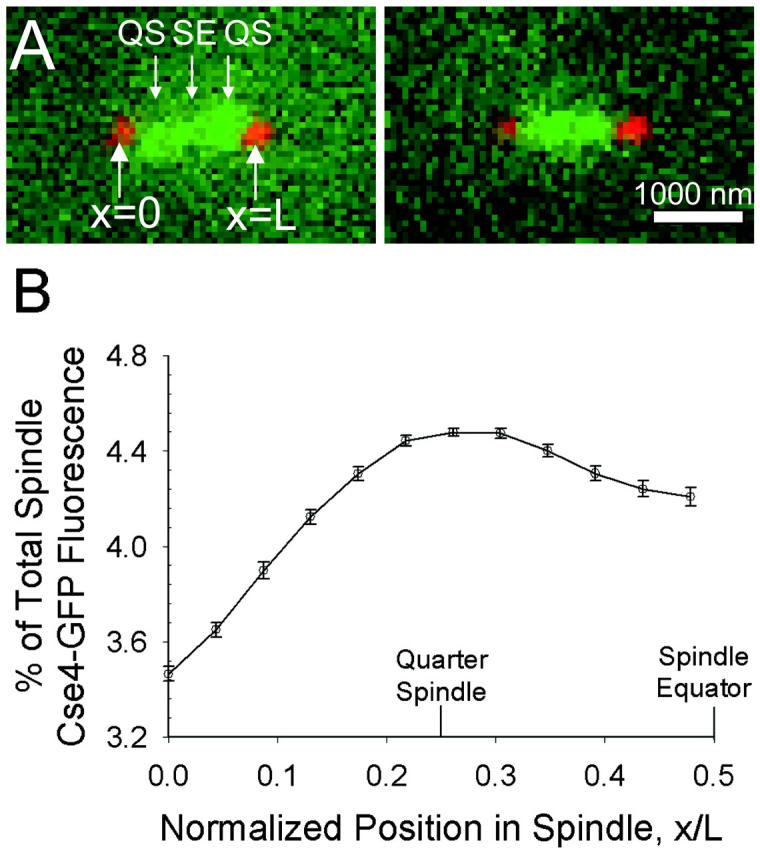
Experimentally observed kinetochore (Cse4-GFP) spatial distribution. (A) Two representative images of kinetochore (green) localization relative to the SPBs (red) (N = 52 total). The location of the quarter spindle (QS) and spindle equator (SE), and the x coordinates of the SPBs are noted (compare with Fig. 2 A). The individual positions of each of the 32 kinetochores could not be resolved. However, note clustering of kinetochore fluorescence in opposite spindle halves near the QS location. Bar = 1000 nm. (B) Plot of mean spatial distribution of kinetochore fluorescence in a half spindle (N = 104 half spindles). Position on the x axis is normalized over the pole-to-pole spindle length, L. The locations of the quarter spindle and spindle equator are again noted. Error bars indicate standard error. Quantitative analysis demonstrates clustering at the QS, confirming visual perception of Fig. 4 A.

The mean distribution of Cse4-GFP fluorescence in the 104 half spindles, normalized over spindle length and total spindle fluorescence, is shown in Fig. 4 B. Fluorescence was dimmest near the spindle poles while peaking at the quarter spindle (25% of the total spindle length), corresponding to an average separation of 750 nm between the peaks in each half spindle. At the spindle equator, fluorescence decreased relative to the peaks, reflecting the gap in fluorescence often observed between Cse4-GFP clusters.

Temporal dynamics

Representative kymographs constructed from fluorescence movies of Cse4-GFP and Spc29-CFP are shown in Fig. 5 A. The frame rate in all movies was one frame per 5 s. The kymographs depict the motion of the Cse4-GFP clusters along the spindle axis (x direction) over time relative to the SPBs. Cse4-GFP tended to appear as two distinct clusters throughout the length of the movie, with motion of smaller fluorescent spots or transient merging of the clusters also observed. This suggests that single or small numbers of kinetochores often move between clusters of fluorescence, across the length of the spindle. Vertical shifting of the SPBs in Fig. 5 A (i.e., in the x direction) indicates movement of the entire spindle relative to the imaging system. Movement of the spindle in the direction of the optical axis (z direction) is also evident as the SPBs occasionally drop out of focus.

FIGURE 5.

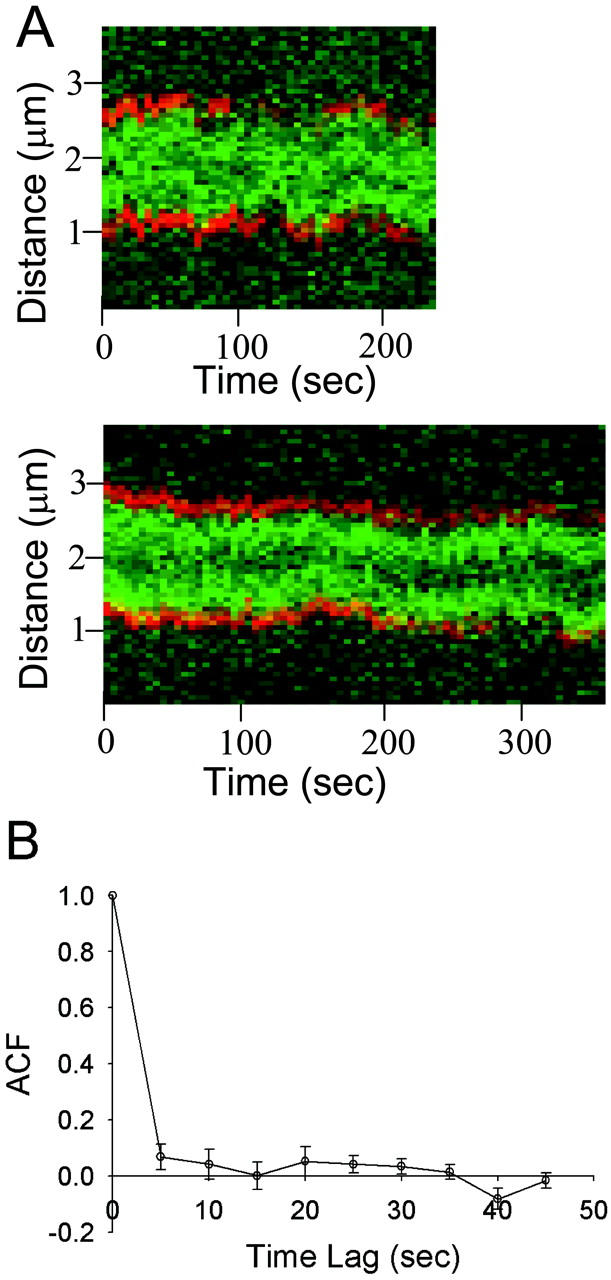
Experimentally observed Cse4-GFP temporal dynamics. (A) Two representative kymographs depicting Cse4-GFP fluorescence (green) over time relative to the SPBs (red), produced from time-lapse movies with 5-s intervals (N = 12 experimental kymographs total). (B) The ACF of quarter spindle fluorescence decays rapidly to zero. The ACF at the spindle equator behaves similarly. Error bars indicate standard error.

In each of the 12 spindle movies, the Cse4-GFP fluorescence intensity at the quarter spindle and spindle equator were recorded over the length of the movie, after correcting for bleaching due to imaging. The ACF of this time series data was then determined. Fig. 5 B shows the mean ACF of quarter spindle fluorescence in the 12 spindles. The error bars indicate the standard error of the 12 kymograph ACFs. It was found that the ACF at both the quarter spindle and spindle equator (data not shown) decays to zero within a 5-s time lag.

SIMULATION RESULTS

Model 1: Pure dynamic instability

MT dynamics were simulated with constant values for V_g, V_s, k_r, and k_c. Then, using the experimentally determined PSF, 3-D convolution was performed to simulate the imaging of the kinetochores at the plus ends of simulated kMT tips. Previously, no parameter estimates for dynamic instability in the budding yeast spindle have been made. However, values have been reported for cytoplasmic MTs during metaphase, with the following estimates: V_g = 0.5 μm/min; V_s = 1.35 μm/min; k_r = 0.36 min⁻¹; and k_c = 0.12 min⁻¹ (Carminati and Stearns, 1997; see also Tirnauer et al., 1999; Kosco et al., 2001).

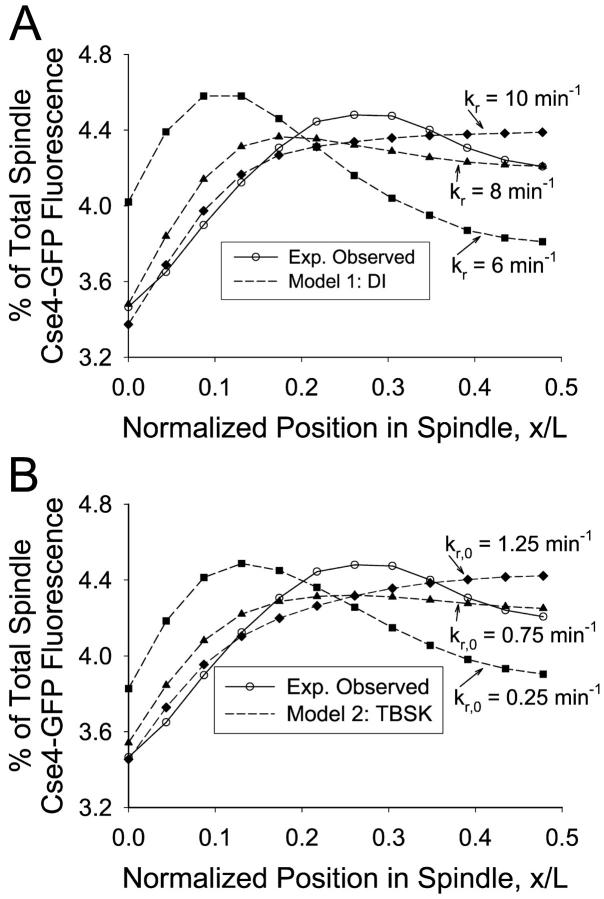
With these parameters assigned to spindle dynamics in our model, microtubules tended to grow all the way across the spindle before a catastrophe occurred, and then shortened completely to the SPB to which they are anchored (Fig. 6 A). The low rescue and catastrophe rates, relative to the size of the spindle and the growth and shortening velocities, ensure that kMT tips are likely to be located throughout the spindle. The predicted images generated by this model (Fig. 6 B) appear by eye to be similar to those observed experimentally (Fig. 4 A). However, quantitative analysis reveals that the predicted mean distribution of kinetochore fluorescence is much flatter than that observed experimentally and fails to give rise to the peak observed at the quarter spindle (Fig. 6 C). These results indicate that kMT spindle dynamics are different from cytoplasmic MT dynamics during metaphase in budding yeast (p < 0.01).

FIGURE 6.

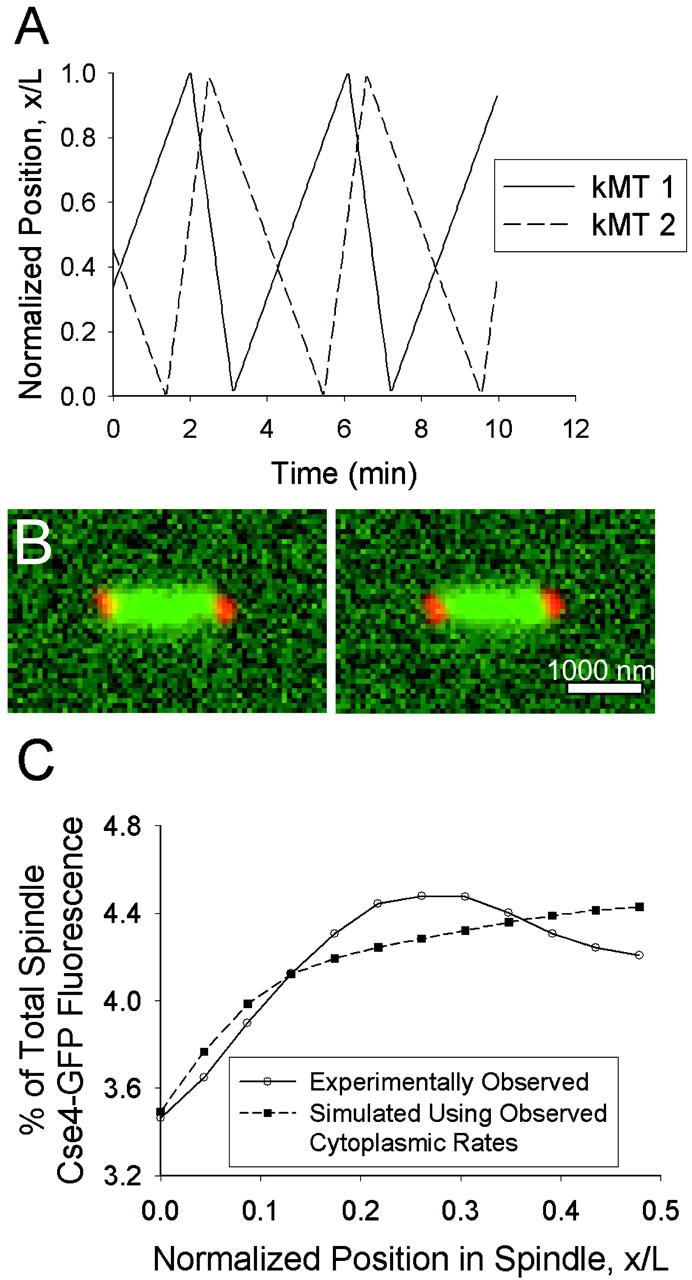
Simulated Cse4-GFP behavior assuming kMTs undergo pure dynamic instability with cytoplasmic rates (V_g = 0.5 μm/min, V_s = 1.35 μm/min, k_c = 0.12 min⁻¹, k_r = 0.36 min⁻¹). (A) Sister kMT plus-end tip positions during 10 min of simulated dynamics. The minus end of kMT 1 is anchored to the SPB located at x/L = 0, whereas the minus end of kMT 2 is anchored at x/L = 1. (B) Representative predicted images of kinetochore fluorescence (green) relative to SPBs (red). Bar = 1000 nm. (C) Predicted mean spatial distribution of kinetochore fluorescence in a half spindle (p < 0.01; N = 100 simulations of 52 spindles). Note the lack of elevated fluorescence at the quarter spindle relative to that observed experimentally.

By adjusting any or all of the four parameters, the kMT dynamics can be influenced to prevent repeated excursions across the entire length of the spindle. For example, increasing the catastrophe frequency results in shorter kMTs on average and therefore higher kinetochore fluorescence near the poles. However, we found that within this model of pure dynamic instability, no set of four parameter values can predict the experimentally observed mean distribution of Cse4-GFP fluorescence (p < 0.01; see Table 1 for the range of parameter values tested). The predicted distribution tended to remain flat until the parameters were adjusted so that the kMTs were dramatically shorter on average and a peak of fluorescence arose near the pole (Fig. 7 A). The peak in fluorescence at the quarter spindle observed experimentally cannot be matched regardless of parameter choice.

TABLE 1.

Ranges of model parameter values tested

Parameter	Units	Model 1 DI	Model 2 TBSK	Model 3 a PEF	Model 3 b CG
Vg	μm/min	0.25–5	0.25–5	0.25–5	0.25–5
Vs	μm/min	0.25–5	0.25–5	0.25–5	0.25–5
kc	min−1	0.1–30	0.1–30	0.1–30	0.1–30
kr	min−1	0.1–30	0.1–30	0.1–30	0.1–30
ρ	μm−1	—	0.2–7.5	—	—
ɛ	μm−2	—	—	0.5–5	—
β	catastrophes/min/[cB]	—	—	—	50–2000

DI, pure dynamic instability model; TBSK, tension between sister kinetochores model; PEF, polar ejection force model; CG, chemical gradient model.

FIGURE 7.

Model 1 and model 2 results. (A) Pure dynamic instability with arbitrary parameters. Predicted mean spatial distribution of kinetochore fluorescence of pure dynamic instability model (V_g = 1.5 μm/min, V_s = 1.5 μm/min, k_c = 10 min⁻¹, k_r noted; N = 100 simulations of 52 spindles). The mean distribution of fluorescence shifts away from the SPB as k_r is increased to produce longer kMTs on average. However, a peak in fluorescence at the quarter spindle is never observed, and the experimentally observed fluorescence distribution cannot be matched regardless of parameter choice (p < 0.01). (B) Tension between sister kinetochores model (V_g =3 μm/min, V_s = 3 μm/min, k_c = 10 min⁻¹, ρ = 3.75 μm⁻¹, k_r,0 noted). The mean distribution of fluorescence shifts away from the SPB as k_r,0 is increased; a peak in fluorescence at the quarter spindle is never observed (p < 0.01).

We also constructed models of dynamic instability with nonfirst-order kinetics, based on previous studies that indicated MT growth is characterized by history-dependent switching frequencies (Odde et al., 1995; Dogterom et al., 1996; Howell et al., 1997). Although the range of kMT lengths became slightly more narrowed with history-dependent kinetics, the effect was insufficient by itself to match the peak in the mean distribution of Cse4-GFP fluorescence observed experimentally (p < 0.01; data not shown).

Model 2: Tension between sister kinetochores

It was hypothesized that a tensile force between sister kMTs might bias kinetochores away from the SPBs and result in clustering at the quarter spindle as observed experimentally. However, a model in which increasing tensile forces between sister kinetochores increased rescue frequency, superimposed on pure dynamic instability, could not reproduce the experimentally observed fluorescence distribution, regardless of parameter choice (p < 0.01; see Table 1 for the range of parameter values tested). A peak in fluorescence could be generated near the spindle poles when kMT dynamics were biased toward short kMT lengths. However, as the parameters were adjusted to produce longer kMT lengths, the fluorescence distribution flattened out (Fig. 7 B), indicating a broad distribution of kMT lengths incompatible with the kinetochore clustering observed experimentally. The spring constant, ρ, gave control over the distance between sister kMT tips but was insufficient to bias kMT lengths away from the SPB and simultaneously away from the middle of the spindle.

Similar results were found when a dependency of the catastrophe frequency on tension (i.e., k_c = k_c,0 exp(−F_tensile)) was added to tension between sister kinetochore model (data not shown). A model that contained history-dependent catastrophe rates coupled with a dependence of the rescue frequency on the tension between sister kinetochores also failed (data not shown). A peak in the mean distribution of kinetochore fluorescence could still not be reproduced at the quarter spindle.

Model 3: Spatial dependence of dynamic instability

a) Polar ejection force model

The polar ejection force model was constructed in an attempt to bias kinetochore positions away from the SPBs. The model assumes that polar ejection forces act on the chromosome arms, causing tension at the kinetochore, and inducing a higher kMT rescue frequency. Fig. 8 A shows how sister kMT dynamics in this model differ from the simple dynamic instability model with cytoplasmic rates (compare to Fig. 6 A). Each sister tends to remain in the half of the spindle nearest the SPB to which it is anchored. Occasional excursions are made to the opposite half, sometimes resulting in transient “crossing” of kMT tips as one kMT grows past its sister. It is also apparent that kMTs rarely shorten entirely to the SPB at which they are anchored, with no occurrences in Fig. 8 A during a 10-min period.

FIGURE 8.

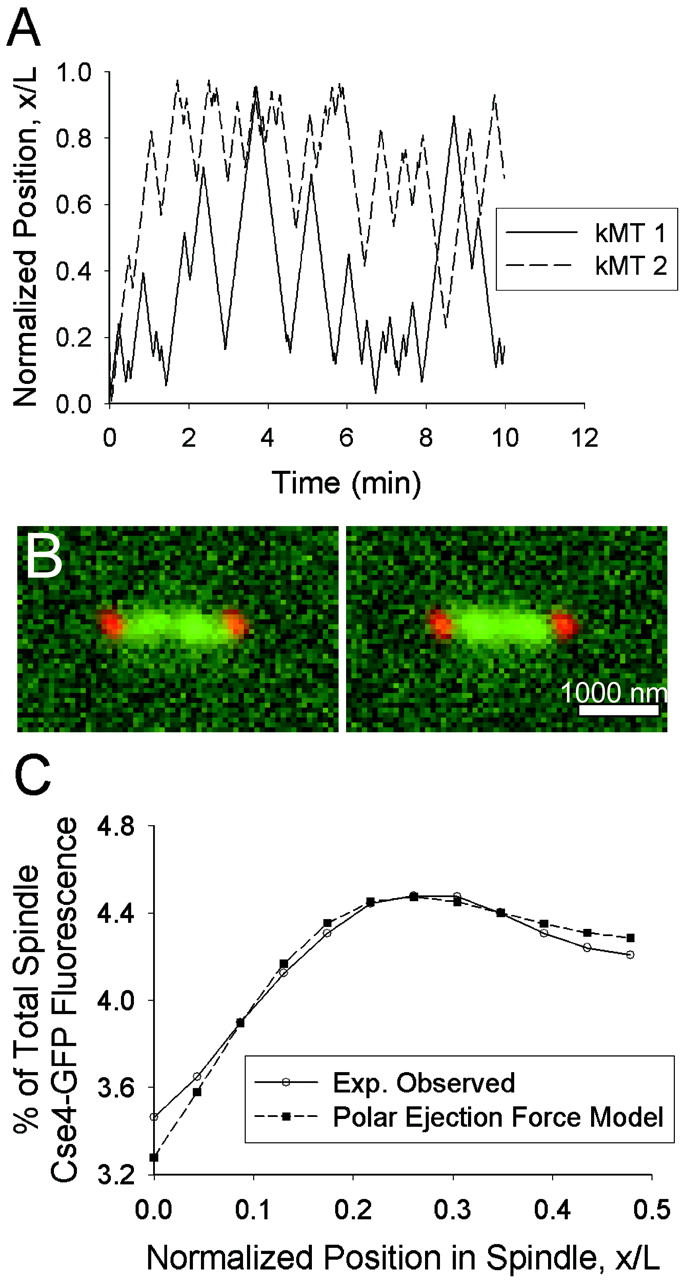
Model 3 a: Polar ejection force model. (A) Plot of sister kMT plus-end tip positions over time (V_g = 1.5 μm/min, V_s = 1.5 μm/min, k_c = 5 min⁻¹, k_r,0 = 0.75 min⁻¹, ɛ = 2.2 μm⁻²]. The minus end of kMT 1 is anchored to the SPB at x/L = 0, and the minus end of kMT 2 is anchored at x/L = 1. Each kMT tip spends most of its time in the spindle half to which its minus end is anchored, with occasional excursions to the opposite spindle half sometimes resulting in a crossing of its sister kMT plus end. (B) Representative predicted images of kinetochore fluorescence (green) relative to SPBs (red). Note clustering in opposite spindle halves near the quarter spindle. Bar = 1000 nm. (C) The experimentally observed mean spatial distribution of kinetochore fluorescence can be predicted by this model (p ∼ 0.1). Note the peak in fluorescence at the quarter spindle (N = 100 simulations of 52 spindles).

The model predicted spindle images with clusters of Cse4-GFP fluorescence in opposite halves of the spindle (Fig. 8 B) and was capable of successfully reproducing the observed mean spatial distribution of kinetochore fluorescence (Fig. 8 C). At sufficiently large values of k_c (≥5 min⁻¹), a given set of V_g, V_s, ɛ, and k_r,0 could be found to produce a peak in fluorescence at the quarter spindle. kMT tip “clustering” at the quarter spindle occurs because a high k_c prevents kMTs from growing too long whereas the polar ejection force resists kMT shortening to the SPB via its effect on k_r. Successful parameter values for ɛ and k_r,0 ranged from 0.5 to 3.0 μm⁻² and 0.25 to 15 min⁻¹, respectively. The resulting fluorescence distribution indicated a strong correlation between ɛ and k_r,0. The maximum probability of fit to the experimental data was relatively low (p ∼ 0.1), but the model could not be formally rejected.

To assess the temporal dynamics of this model, kymographs were created from simulated time-lapse movies of kinetochore fluorescence (Fig. 9 A). Similar to experimentally observed kymographs, maximum fluorescence is generally located near the quarter spindle, but fusing of these clusters and movements of fluorescent spots between clusters can also be observed. The ACF of quarter spindle and spindle equator fluorescence was calculated for sets of parameter values that matched the experimentally observed mean spatial distribution of kinetochore fluorescence. Fig. 9 B shows the quarter spindle ACF for a set of parameter values in which V_g = V_s = 1.5 μm/min. Like the experimentally observed ACF, the predicted ACF decays rapidly to zero. It was found that as k_r,0 and the gradient in k_c were increased, the ACF decreased slightly at any given time lag. V_g and V_s had little effect on the ACF values (data not shown). All sets of parameter values that predicted an appropriate mean spatial distribution of kinetochore fluorescence also produced ACF values at the quarter spindle and spindle equator that were not significantly different than those observed experimentally (p > 0.05).

FIGURE 9.

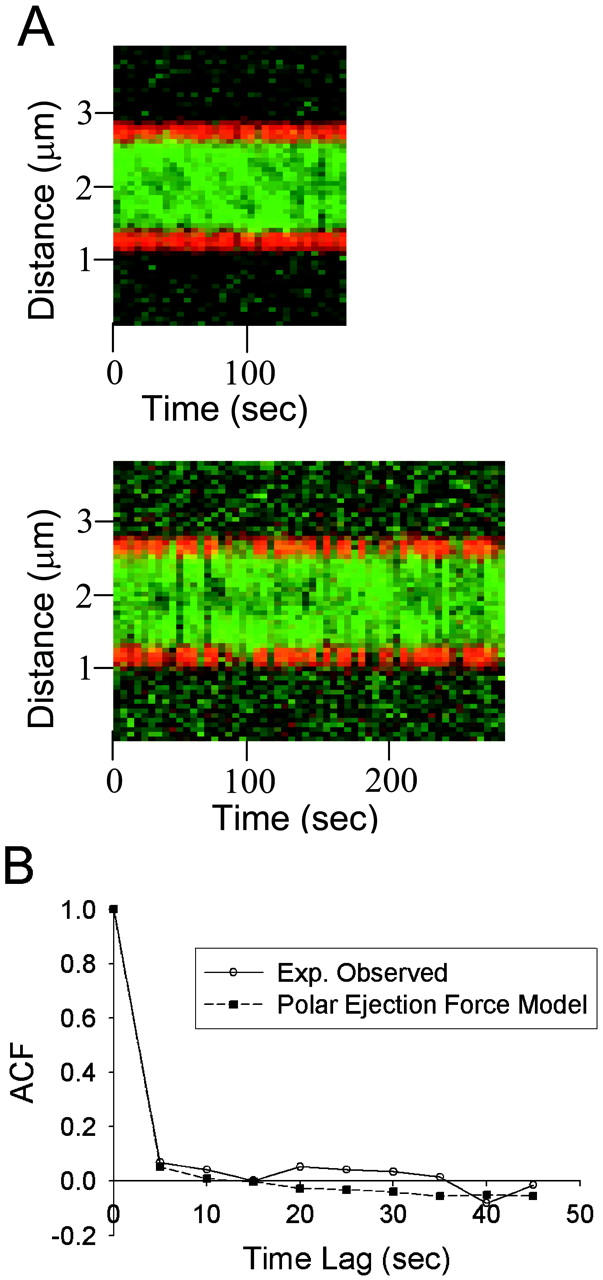
Temporal dynamics of model 3 a: Polar ejection force model (V_g = 1.5 μm/min, V_s = 1.5 μm/min, k_c = 5 min⁻¹, k_r,0 = 0.75 min⁻¹, ɛ = 2.2 μm⁻²). (A) Predicted kymographs from simulated time-lapse movies (5-s intervals) of kinetochore fluorescence. As observed in experimental kymographs, kinetochore fluorescence (green) appears clustered in opposite spindle halves but with transient merging of clusters and movement of fluorescence between clusters. (B) Predicted mean autocorrelation function of quarter spindle fluorescence (N = 100 simulations of 12 kymographs). The simulated ACF decays rapidly to zero, providing reasonable agreement with the experimentally observed ACF (p ∼ 0.25). The chemical gradient model produced similar results.

Combining the polar ejection force model with the tension between sister kinetochores model by summing the two forces on the kinetochore (Eq. 5) and using this net force to calculate the rescue frequency (Eq. 3) did not have a dramatic effect on the acceptable ranges of parameter values. The most significant effect was to reduce the amount of “crossing” of sister kMT tips (data not shown). The tensile force element gives rise to a significant decrease in the rescue frequency when the separation distance between sister kMTs becomes less than the rest length, s_r = 200 nm. Combined with a high k_c, the probability of maintaining a significantly negative separation distance is low.

b) Chemical gradient model

As an alternative to force-based effects, we investigated another mechanism by which the MT length distribution could be concentrated toward the quarter spindle: a chemical gradient model that hypothesizes a spatial gradient in the catastrophe frequency. This could be produced by a spatial gradient of activated catastrophe promoter molecules, stably generated via a spatially segregated kinase/phosphatase system described in the Methods section. This gradient in concentration of activated catastrophe promoter was coupled via a linear relationship to produce a spatial gradient in the effective catastrophe frequency.

The dynamics of sister kMT tips were similar to those of the polar ejection force model. The kMT tips tended to stay in the same half of the spindle as the SPB to which they were anchored, with occasional excursions to the other half and transient crossing of sisters kMTs (Fig. 10 A). Complete kMT shortening to the SPB at which it was anchored was rare; ∼1 occurrence is apparent in Fig. 10 A over a 10-min period.

FIGURE 10.

Model 3 b: Chemical gradient model. (A) Plot of sister kMT plus-end tip positions over time (V_g = 1.5 μm/min, V_s = 1.5 μm/min, k_r = 9.5 min⁻¹, k_c,0 = 0.25 min⁻¹, β = 500 min⁻¹ c_B⁻¹). The minus end of kMT 1 is anchored to the SPB at x/L = 0, and the minus end of kMT 2 is anchored at x/L = 1. Each sister kinetochore spends the majority of its history in the spindle half at which it was anchored. (B) Representative predicted images of kinetochore fluorescence (green) relative to SPBs (red). Note clustering in opposite spindle halves near the quarter spindle. Bar = 1000 nm. (C) The experimentally observed mean spatial distribution of kinetochore fluorescence can be predicted by this model (p ∼ 0.25). Note the peak in fluorescence at the quarter spindle (N = 100 simulations of 52 spindles).

With this effect in place, the model predicted images that appeared to contain kinetochore clustering (Fig. 10 B) and the mean distribution of kinetochore fluorescence observed experimentally could be reproduced (Fig. 10 C). It was found that for sufficiently large values of β, k_r could be adjusted to produce the desired fluorescence distribution (p ∼ 0.25). As k_r was increased, the peak in fluorescence moved away from the pole and maintained a peaked shape at the quarter spindle. The greater the growth and shortening velocities, the greater k_r and β had to be to contain the kMTs within the desired length distribution. With V_g = V_s = 1.5 μm/min, the rescue frequency needed to be at least 7.5 min⁻¹, whereas the effective catastrophe frequency gradient varied from 0.25 min⁻¹ near the poles to ∼11 min⁻¹ at the center of the spindle. The experimental fluorescence distribution could also be reproduced with V_g ≠ V_s or with a range of values for k_c,0, given a compensatory change in β or k_r.

Kymographs constructed from simulated fluorescence time-lapse movies also appeared similar to those of the polar ejection force model (see Fig. 9). Again, the ACF of fluorescence at the quarter spindle and spindle equator was calculated for sets of parameter values that matched (p > 0.05) the spatial kinetochore fluorescence distribution. As the rescue frequency and gradient in catastrophe frequency increased, the ACF at each location became smaller. All tested sets of parameter values produced ACF values that were not significantly different from those observed experimentally (p > 0.05).

As was done with the polar ejection force model, the chemical gradient model was also combined with the tension between sister kinetochore model to determine the effect of adding a dependence of the kMT dynamics on sister kMT tip separation. The catastrophe frequency was calculated via Eq. 12 as a function of the catastrophe promoter concentration, whereas the rescue frequency was calculated via Eq. 3, in which F = F_tensile. This did not significantly affect the range of acceptable parameter values for the chemical gradient model. It did, however, reduce the incidence of “crossing” of sister kMT tips (data not shown).

DISCUSSION

In experimental images, the fluorescently labeled kinetochore protein, Cse4-GFP, appeared as clusters in opposite halves of the mitotic spindle during metaphase. This was reflected as a peak in the mean distribution of Cse4-GFP fluorescence at the quarter spindle, relative to the fluorescence at the spindle poles and spindle equator. Experimental time-lapse movies of Cse4-GFP were characterized by low autocorrelation at the quarter spindle and spindle equator at time lags greater than or equal to 5 s (minimum frame rate). Computer simulations of models of pure dynamic instability predicted kMT length distributions that gave rise to mean distributions of Cse4-GFP fluorescence that were inconsistent with that observed experimentally. Models in which the switching frequencies were dependent on the tension between sister kinetochores or were history-dependent also failed. However, models incorporating spatial gradients in the rescue or catastrophe frequency were able to correctly predict the mean distribution of Cse4-GFP fluorescence. Spatially dependent models also predicted the low autocorrelation observed experimentally. These results are consistent with the hypothesis that position-based cues guide kMT assembly/disassembly and kinetochore positions in the yeast metaphase spindle.

Why models without spatial gradients in switching fail

Model 1: Pure dynamic instability

It is apparent from Fig. 6 A that kMT growth characteristics in the mitotic spindle of yeast must be significantly different than those of cytoplasmic MTs. With low rescue and catastrophe frequencies, kMTs would grow back and forth the entire distance of the small yeast spindle (∼1.5 μm). This would not be consistent with the Cse4-GFP clustering (Fig. 4) and the restrained motion of centromere proximal markers observed during metaphase (Pearson et al., 2001). In addition, we found that not only are the cytoplasmic rates of dynamic instability inconsistent with experimental observation, but also any set of the four parameters of pure dynamic instability was found to be inconsistent.

The most obvious failure of the pure dynamic instability model is an inability to produce peaks in fluorescence near the quarter spindle. With any set of the four parameters (V_g, V_s, k_c, and k_r), the same pattern was apparent: a flat mean distribution of Cse4-GFP fluorescence persisted until the parameters were adjusted to promote very short kMT lengths, which gave rise to a peak in fluorescence near the spindle pole (Fig. 7 A). This was consistently observed throughout the entire range of tested parameter values; a fluorescence peak never arose at the quarter spindle. From this observation it is apparent that pure dynamic instability predicts an expected range of kMT lengths that is inconsistent with the clustering of fluorescence at metaphase.

Model 2: Tension between sister kinetochores

To determine which elements beyond pure dynamic instability are important for achieving Cse4-GFP clustering, we investigated models in which a single parameter of dynamic instability was treated as a nonconstant during the dynamics of kMT growth. The first was a model in which the rescue frequency depended upon the tension between sister kMT tips. As the distance between sister kMT tips increased, the tension rose and caused an increase in the rescue frequency for those kMTs. Although the model provided a control over the distance between sister kMT tips, the position of the kMT tips relative to the spindle poles remained unbiased. This again translated into flat Cse4-GFP fluorescence profiles unless the parameters were adjusted to promote short kMT lengths, which could only produce a fluorescence peak near the SPB (Fig. 7 B). Therefore, this model was also incapable of predicting the peaks in the mean distribution of Cse4-GFP fluorescence at the quarter spindle observed experimentally.

Why models incorporating spatial gradients in switching do not fail

Alternatively, we constructed two models incorporating a spatial dependence of either the rescue or catastrophe frequency upon the position of the kMT plus-end tip relative to the spindle. Whether this was based on a polar ejection force or chemical gradient model (Fig. 3, B and C, respectively), the experimentally observed peaks in fluorescence could be predicted (Fig. 8, B and C; Fig. 10, B and C). Both mechanisms gave rise to kMT length distributions that could be maintained within a limited range so that the Cse4-GFP fluorescence appeared as two clusters. Although the polar ejection force and chemical gradient model are similarly position-based, there is a subtle difference that discriminates between the two. In the chemical gradient model, the concentration of activated catastrophe promoters, and therefore the catastrophe frequency, is highest at the center of the spindle (Fig. 3 C). But if a kMT happens to penetrate through this zone, the catastrophe promoter concentration begins to decrease and the kMT experiences a progressively smaller catastrophe frequency. In contrast, in the polar ejection tension model where the rescue frequency is related to the amount of force felt, the rescue frequency decreases as the kMT plus-end tip moves further away from the pole to which it is anchored and continues to do so even after passing through the spindle midzone (Fig. 3 B).

Both the polar ejection force model and the chemical gradient model predicted low autocorrelation at time lags greater than or equal to 5 s. The low autocorrelation observed experimentally, and the ease with which the models matched this autocorrelation, are most likely due to the relatively large growth and shortening rates of kMTs relative to the size of the spindle. Previous work has suggested that centromere proximal GFP markers move at velocities near 1.5 μm/min. This corresponds to 125 nm per 5 s, a distance equal to ∼2 pixels in our imaging system. So one would expect low correlation at a given location in the spindle for 5-s time lags. Higher autocorrelation might become apparent at shorter time lags, allowing further discrimination of the models and the successful parameter space; however, technical limitations in our two-color imaging system required a minimum time lag of 5-s intervals.

The fact that both of these models can predict the observed mean distribution of Cse4-GFP fluorescence demonstrates a robustness in the ability of position-based models to explain the experimentally observed results. This indicates that position sensing is an important element to any model of chromosome movements during metaphase in yeast. These results do not rule out other position-based models beyond those considered here. For example, spatial gradients emanating from other locations within the spindle, such as the chromosomes or MTs, may also be capable of producing an effective gradient in kMT dynamics.

Parameter limits of the spatially dependent models

The main limitation of the polar ejection force model was the small parameter space that provided a strong enough polar ejection force to bias kMT lengths toward the quarter spindle while still allowing some kMTs to shorten all the way to the SPBs. Fig. 8 C displays the challenge of implementing this effect: the peak in fluorescence is at the quarter spindle position, but the fluorescence near the pole is already less than that observed experimentally. Consequently the predicted probability of fit of polar ejection alone models was relatively low (p ∼ 0.1).

In the chemical gradient model, the minimum catastrophe frequency gradient required to match the experimentally observed mean spatial distribution of Cse4-GFP fluorescence was correlated with the growth velocity. At V_g = 1.5 μm/min, the speed at which centromere proximal markers have been observed (Pearson et al., 2001), a gradient in catastrophe frequency from 0.25 to ∼11 min⁻¹ was required. A larger growth velocity, such as 3.0 μm/min, required a larger gradient, 0.25 to ∼27 min⁻¹, to achieve the same effect. This was necessary to limit the range of kMT lengths so that the kinetochores appeared as two clusters of fluorescence. The shortening velocity, V_s, and rescue frequency, k_r, could vary widely as long as they balanced each other to produce a suitable average shortening length excursion (i.e., as V_s increases, k_r also must increase).

Time-series analysis of experimental Cse4-GFP movies revealed low autocorrelation at all time lags, indicating that the fluorescence intensity at any pixel in a kymograph was equally likely to be greater or less than the mean intensity of the pixel over time, regardless of the intensity of the pixel at the previous time step. It was found that the sets of parameter values in both the polar ejection force and chemical gradient model that produced a mean spatial distribution of kinetochore fluorescence matching the observed distribution also predicted ACF values that were not significantly different than those observed experimentally (p > 0.05). A slight increase in autocorrelation was observed when the effective switching (k_r and k_c) frequencies were decreased at any given pair of V_g and V_s values, but the increase was never enough for the predicted ACF values to become statistically different from the experimental autocorrelation (p > 0.05).

The range of acceptable parameter values may also be affected by experimental phenomena that we did not take into account in our models. Although we believe their effects to be minor, thermal motion of kMTs, tilting of the spindle, and other unaccounted effects may influence the range of acceptable combinations of parameter values in the models.

Potential limitations of the analysis

Certainly these models are simple formulations of presumably complex interactions in the mitotic spindle that dictate MT lengths and chromosome positions. There are many ways one might implement polar ejection forces and tensile forces between sister kMT tips and the relationships between these forces and the parameters of dynamic instability. We examined a limited number of scenarios with simple linear and exponential relationships. In addition, we did not examine treadmilling (minus-end dynamics), a traction fiber model, or kinetochore sliding along the length of its kMT away from the plus-end tip. Tubulin flux from the plus end to the minus end of kMTs, termed treadmilling, has been observed in a variety of cell types (Desai et al., 1998; Lafountain et al., 2001). However, the pattern of fluorescence recovery of bleached GFP-tubulin has suggested that treadmilling is not prevalent during metaphase in yeast (Maddox et al., 2000). Furthermore, the addition of treadmilling would not impact our conclusion against pure dynamic instability: any minus-end dynamics would simply offset plus-end dynamics, changing the effective V_g and V_s but not the pattern of kinetochore fluorescence localization with pure dynamic instability.

Recently, Joglekar and Hunt presented a mechanistic model for chromosome directional instability during mitosis that relied on the ability of kinetochores to gain and lose kMT attachments (Joglekar and Hunt, 2002). It is not clear how this model would function in the budding yeast spindle, in which a kinetochore losing its single kMT attachment would appear to be a severe setback in the progression of mitosis. However, their conclusion that polar ejection forces are essential for biasing chromosome motion is consistent with the evidence for a spatial gradient of dynamic instability in the yeast spindle presented here. In general, our model and the Joglekar and Hunt model do not have any assumptions that are contradictory to each other.

The analysis may also suffer some technical limitations. For example, we used in vitro bead images to estimate the point spread function of the imaging system. Although this provides a good characterization of the microscope system, the PSF of a fluorophore in a living yeast cell may suffer from spatial inhomogeneities or temporal instability (Kam et al., 2001). We also measured the background fluorescence of Cse4-GFP from areas in the cytoplasm of yeast cells. However, the background levels in the nucleus, which remains intact during mitosis in yeast, may differ as a result of regulated nuclear trafficking. Technical challenges in characterizing the PSF in live cells and measuring the background Cse4-GFP fluorescence make our estimates the best currently available. In addition, it is not clear how the uncertainty in these estimates would give rise to a spatial bias sufficient to not reject the pure dynamic instability model. Our conclusions are dependent upon the exclusive localization of Cse4-GFP to the kinetochore. Immunofluorescence and previous work with Cse4-GFP suggest that this is a valid assumption (Meluh et al., 1998; Pearson et al., 2001).

Sister communication and position sensing

The failure of the tension between sister kinetochores model suggests that communication between sister kinetochores and their attached MTs may be less essential to proper chromosome alignment at metaphase in yeast. Adding this tensile element to either our polar ejection force (see Eq. 5) or chemical gradient model did not corrupt the models, however, indicating that sister kinetochore communication could complement a position-based mechanism and may be utilized for other aspects of mitosis such as the spindle assembly checkpoint and biorientation (Nicklas et al., 2001). Recent experimental evidence in Scc1p and Ipl1 mutants suggests that tension between sister chromatids is necessary for normal centromere separation and reassociation dynamics in yeast (Tanaka et al., 2000, 2002). However, it is not clear if tension's role is in establishing biorientation or in coordinating kinetochore motion after biorientation is established, or both.

To discriminate between the simulation results of a spatially defined mechanism alone versus one coupled with sister kMT communication could potentially be achieved by an examination of the kMT tip positions over time. With a spatially defined mechanism alone, the separation distance between sister kMT tips was widely variable, showed little coordination, and the tips met or crossed infrequently over a 10-min time frame (Fig. 8 A). In contrast, the model incorporating a tensile element between sister kMT tips showed a steadier separation distance, loose coordination, and very rare crossing (data not shown). Further evaluation of these models would therefore require an analysis of experimentally observed sister kinetochore positions over time in yeast. Fluorescent tagging studies using lac operators at chromosomal sites proximal to the centromere allowed the tracking of DNA as close as 1 kb from the kinetochore (Goshima and Yanagida, 2000; He et al., 2000; Pearson et al., 2001). However, since both centromeres are labeled with the same fluorescent tag, it is impossible to distinguish one from the other during sister centromere separation and reassociation (a process distinct from sister chromosome arm separation during anaphase). It is therefore impossible to assess the degree of crossing of sister kinetochores on the spindle axis, if it is indeed present. Furthermore, the analysis of the localization of these probes has demonstrated that the ∼1 kb distance between the centromere and the marker results in a significant (∼150 nm) and time-dependent displacement of the tag from the kinetochore (Pearson et al., 2001). In the absence of a clear understanding of the mechanics of yeast chromosomes, this chromosomal “stretching” will require new techniques to track individual chromosome kinetochore positions.

If it is found that, as in animal cells, crossing of the sister kinetochores on the spindle axis during metaphase in yeast is rare or never occurs, the sister tension mechanism described in model 2 could be superimposed with the spatial dependency of either the chemical gradient model or the polar ejection force model to predict the observed kinetochore clustering at the quarter spindle (data not shown). So, the modeling does not eliminate the possibility that tension between sister kinetochores plays an important role in spindle dynamics, such as limiting sister kinetochore crossing.

Mechanisms for position sensing

Both the chemical gradient and polar ejection force model require the integration of a position-dependent signal. This may be as simple as a catastrophe promoter binding to the tip of a MT, or as complex as a kinetochore acting as a tensiometer to measure the force felt on a chromatid and mechanically converting this to affect the assembly/disassembly kinetics and thermodynamics of its attached kMT (Murray and Mitchison, 1994; Skibbens and Salmon, 1997).

Spatial chemical gradients that influence MT dynamics have been proposed to be involved in mitotic spindle formation (Dogterom et al., 1996; Carazo-Salas et al., 1999; Heald and Weis, 2000). Stable spatial gradients of Ran-GTP, resulting from localized phosphorylation, have been observed in the mitotic spindle (Kalab et al., 2002; Trieselmann and Wilde, 2002) and stable gradients of other molecules (Op18 for example) are hypothesized to exist (Cassimeris, 2002). Due to the complexities of the FRET imaging system used to visualize Ran-GTP gradients, it is not yet clear if the observed Ran-GTP gradients obey the model assumed here for spatial dependence. The chemical gradient model proposed here could be formulated to have a gradient in the rescue frequency rather than the catastrophe frequency. To fit our model of a spatial dependence in dynamic instability the guanosine nucleotide exchange factor, Rcc1, could be located at the spindle pole bodies in yeast to produce a gradient in Ran-GTP, an MT stabilizer, in which the concentration of Ran-GTP would be highest near the poles. This would require that the counteracting GTPase activating protein, Ran-GAP, be distributed throughout the nucleus. A gradient of an activated catastrophe promoter such as an Op18 or XKCM1 homolog in yeast could also fit our model of a catastrophe frequency gradient resulting in kinetochore clustering at the quarter spindle. Other mechanisms beyond the diffusion and localized reaction model presented here, such as signaling molecules localized on MTs or chromosomes, may also be capable of producing the spatial gradients in MT switching frequencies.

It is still unclear how the mechanism would perform in higher-order organisms with longer spindle lengths relative to sister kinetochore separation (Skibbens et al., 1993; Rieder and Salmon, 1994). For example, in newt lung cells, the separation distance between sister kinetochores is ∼1–2 μm, compared to the pole-to-pole spindle length of ∼50 μm. Both kinetochores would therefore be similarly affected by any concentration gradient and uncoordinated motion would ensue. However, in yeast cells, the sister kinetochore separation distance of ∼0.75 μm is half of the spindle length, enough to straddle the spindle midzone and create differential effects on sister kMTs. A steeper gradient in the switching frequencies, produced by more complicated reaction kinetics, might be required in longer spindles to produce the same effect.

The existence of polar ejection forces in yeast has yet to be confirmed. Polar ejection forces in other organisms have been detected by using a laser to detach chromosome arms from the centromere, after which the detached arms appear to be “pushed” toward the spindle equator (Rieder et al., 1986; Salmon, 1989; Rieder and Salmon, 1994). In yeast, the small size of the spindle and the low level of mitotic chromosome compaction currently prevents this method of detection. The small number of MTs in the yeast spindle (∼40) has suggested that polar ejection forces may not be prominent if steric hindrance is the primary means by which these forces act. However, recent evidence suggesting that molecular motor interaction between chromosome arms and MTs may be the primary mechanism behind ejection forces in vertebrate cells (Antonio et al., 2000; Levesque and Compton, 2001) implies that the steric hindrance of MTs may not be essential. These motors localize to chromosome arms and are capable of binding to adjacent MTs and moving the chromosome arm along the MT toward the spindle equator.

The notion that position sensing is important for chromosome congression in the yeast spindle suggests a conservation of features with higher-level organisms, in which polar ejection forces are directly observed. Further understanding of the yeast spindle and its one-to-one correspondence between kMT and kinetochore should be valuable in deciphering the more complex arrangements of animal spindles. Recently, the spatial dependence of transition frequencies in cytoplasmic MT dynamics was observed in fibroblasts (Komarova et al., 2002). The evidence presented here is the first to support the existence of spatial dependence of kMT dynamic instability in the mitotic spindle of living cells.

Model convolution

By explicitly including image formation in our model, we were able to directly compare simulation predictions to experimentally observed images. An analysis of the predicted kMT length distribution alone would not have allowed discrimination between the various models of kMT dynamics. In this case, model convolution was more effective than image deconvolution because of the blurred and noisy nature of the images; the 32 fluorescent kinetochore markers inside the 1500-nm diameter nucleus cannot be individually resolved using deconvolution (not shown). In general, model convolution offers two advantages over the deconvolution of experimental images: 1), certainty—model convolution predicts a single image, whereas deconvolution of experimental images may converge to a false reconstructed object or an image in which the actual fluorophore locations are still unresolved; and 2), speed—model convolution is executed only once, whereas deconvolution of experimental images is an iterative approach and therefore computationally slow. In general, the model-convolution approach should provide a valuable tool for comparing model predictions to experimental microscope images in cases where subresolution features are of interest.