Comparison of Calculation and Experiment Implicates Significant Electrostatic Contributions to the Binding Stability of Barnase and Barstar

Abstract

The contributions of electrostatic interactions to the binding stability of barnase and barstar were studied by the Poisson-Boltzmann model with three different protocols: a), the dielectric boundary specified as the van der Waals (vdW) surface of the protein along with a protein dielectric constant (ɛ_p) of 4; b), the dielectric boundary specified as the molecular (i.e., solvent-exclusion (SE)) surface along with ɛ_p = 4; and c), “SE + ɛ_p = 20.” The “vdW + ɛ_p = 4” and “SE + ɛ_p = 20” protocols predicted an overall electrostatic stabilization whereas the “SE + ɛ_p = 4” protocol predicted an overall electrostatic destabilization. The “vdW + ɛ_p = 4” protocol was most consistent with experiment. It quantitatively reproduced the observed effects of 17 mutations neutralizing charged residues lining the binding interface and the measured coupling energies of six charge pairs across the interface and reasonably rationalized the experimental ionic strength and pH dependences of the binding constant. In contrast, the “SE + ɛ_p = 4” protocol predicted significantly larger coupling energies of charge pairs whereas the “SE + ɛ_p = 20” protocol did not predict any pH dependence. This study calls for further scrutiny of the different Poisson-Boltzmann protocols and demonstrates potential danger in drawing conclusions on electrostatic contributions based on a particular calculation protocol.

INTRODUCTION

A stereospecific complex of two proteins is likely stabilized by both nonpolar (van der Waals and hydrophobic) and electrostatic interactions. Although the contributions of nonpolar interactions are generally accepted, the roles of electrostatic interactions have been controversial. In the environment of a protein or a complex, the interaction between two charges is relatively strong and long ranged and greatly mediated by the solvent. The formation of a charge pair upon complexation is accompanied by the cost of desolvating the charges. The magnitudes of the desolvation cost estimated by some Poisson-Boltzmann calculations have led to a view that electrostatic interactions destabilize or marginally stabilize protein complexes (Novotny and Sharp, 1992; Elcock et al., 1999; Sheinerman et al., 2000; Lee and Tidor, 2001; Sheinerman and Honig, 2002). In experimental measurements, it is difficult to isolate electrostatic contributions from other factors. Nonetheless there are now accumulating experimental data demonstrating the contributions of electrostatic interactions to the folding stability of proteins and binding stability of protein complexes (Schreiber and Fersht, 1993, 1995; Frisch et al., 1997; Albeck et al., 2000; Sanchez-Ruiz and Makhatadze, 2001; Zhou, unpublished results). In addition, the notion that the higher stability of thermophilic proteins over mesophilic counterparts arise partly from extra polar interactions has become very compelling (Perutz and Raidt, 1975; Perutz, 1978; Vogt and Argos, 1997; Jaenicke and Bohm, 1998; Szilagyi and Zavodszky, 2000; Petsko, 2001; Zhou 2002b; Zhou and Dong, 2003). We have made progress in modeling the contributions of electrostatic interactions to protein folding stability (Vijayakumar and Zhou, 2001; Zhou, 2002a; Dong and Zhou, 2002; Zhou and Dong, 2003). In this article, we study the role of electrostatic interactions in the binding stability of barnase and barstar.

Barnase is an extracellular ribonuclease produced by Bacillus amyloliquefaciens. The active site, consisting of E73, R87, and H102, is located in the middle of a shallow groove running through an entire face of the protein surface. A ring of positive charges (including K27, R59, and R83) interact with the negatively charged RNA substrate (Buckle and Fersht, 1994). The potentially lethal RNase activity is safeguarded by the intracellular inhibitor barstar through rapidly forming a tight complex with the enzyme. Indeed, host cells expressing barnase cannot survive without coexpressing barstar (Jucovic and Hartley, 1996). The interactions between barnase and barstar are dominated by salt bridges and hydrogen bonds, with a cluster of negative charges (Asp-35, Asp-39, Glu-76, and Glu-80) on barstar facing the positive charges across the interface (see Fig. 1; Buckle et al., 1994).

FIGURE 1.

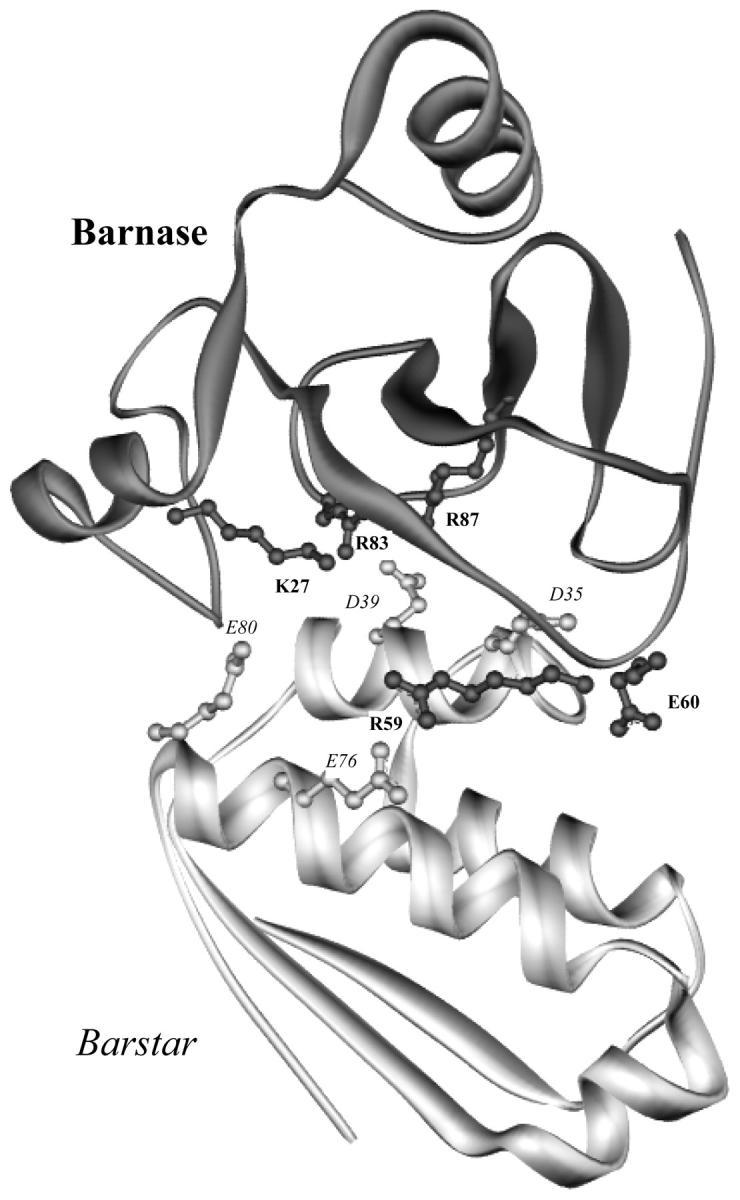
The structure of the complex between barnase (top) and barstar (bottom). Charged residues lining the interface are shown. Barnase side chains are labeled in bold and barstar side chains are labeled in italic.

The association of barnase and barstar is fast (with a rate constant of 6 × 10⁸ M⁻¹ s⁻¹) whereas the dissociation is extremely slow (rate constant = 8 × 10⁻⁶ s⁻¹) (Schreiber and Fersht, 1993). The result is a very high binding constant, K = 0.75 × 10¹⁴ M⁻¹. To elucidate the molecular basis of this tight binding, Fersht and co-workers (Schreiber and Fersht, 1993, 1995; Frisch et al., 1997) studied the effects of a large number of mutations on the binding stability. Neutralizations of charged residues within the interface significantly reduced the binding constant. Here we used the Poisson-Boltzmann model to investigate the roles of these charged residues.

Considerable efforts have been devoted to the parameterization of the Poisson-Boltzmann model. A focus of these efforts is the prediction of pK_a values. The protein-solvent dielectric boundary is commonly defined by the molecular surface (which encloses the protein region excluded to a 1.4-Å solvent probe and will be referred to as the solvent-exclusion (SE) surface). With this specification of the dielectric boundary and a physically reasonable value of 2–4 for the protein dielectric constant ɛ_p, Gilson and co-workers (Antosiewicz et al., 1994, 1996) found that pK_a shifts were consistently overestimated. This indicates an overestimation of the desolvation cost of charges and the strengths of charge-charge interactions. Another study on a salt bridge in barnase also suggested that using the SE surface as the dielectric boundary along with ɛ_p = 4 led to an overestimate of the desolvation cost (Caflisch and Karplus, 1995). To reduce the desolvation cost and weaken the interactions, Gilson and co-workers proposed using a significantly higher value, i.e., 20, for the protein dielectric constant. This high ɛ_p value is now often used in pK_a predictions. However, in all other applications of the Poisson-Boltzmann model, a low ɛ_p value of 2–4 is still routinely used. A physical reason for overestimating the strengths of charge-charge interactions appears to be the neglect of structural relaxations upon changing protonation states and conformational sampling at a given protonation state. For example, inclusion of conformational sampling in Poisson-Boltzmann calculations with ɛ_p = 4 led to pK_a predictions that were as accurate as single-conformation Poisson-Boltzmann calculations with ɛ_p = 20 (Georgescu et al., 2002).

Another simple way to reduce the desolvation cost and strengths of charge-charge interactions is by using the van der Waals (vdW) surface as the dielectric boundary. We have had much success with this approach in rationalizing the effects of charge mutations on protein folding stability (Vijayakumar and Zhou, 2001; Dong and Zhou, 2002; Zhou and Dong, 2003). In this study, we implemented this “vdW + ɛ_p = 4” protocol along with two other protocols: “SE + ɛ_p = 4” and “SE + ɛ_p = 20.” The effects of 17 single and double mutations, ionic strength, and pH on the binding stability of barnase and barstar were calculated.

The “vdW + ɛ_p = 4” and “SE + ɛ_p = 20” results showed qualitative similarities. The electrostatic contribution (ΔG_el) to the binding energy was −11.1 and −4.9 kcal/mol by the two protocols, both indicating an overall stabilization by electrostatic interactions. In contrast, the “SE + ɛ_p = 4” protocol gave ΔG_el = +4.6 kcal/mol, indicating electrostatic destabilization and confirming the earlier calculations of Lee and Tidor (2001) and Sheinerman and Honig (2002). The “vdW + ɛ_p = 4” results for the 17 mutations showed good quantitative agreement with the experimental data of Fersht and co-workers. On the other hand, the “SE + ɛ_p = 4” protocol predicted significantly larger destabilizing effects for the barnase R83Q and R87A mutations and significantly higher strengths of interactions for barnase R83 and R87 with barstar D39. In a rare display of unity, all three protocols yielded nearly identical ionic strength dependence. Only the “vdW + ɛ_p = 4” protocol predicted a pH dependence that is comparable to experimental data.

THEORETICAL METHODS

Electrostatic contribution to binding stability

An outline of the calculation protocol (Vijayakumar et al., 1998; Vijayakumar and Zhou, 2001) is as follows. Hydrogens were added to the barnase/barstar complex (PDB entry 1brs) (Buckle et al., 1994) by the InsightII program (Molecular Simulations, Inc.). The Poisson-Boltzmann equation was solved by the UHBD program (Madura et al., 1995), with the SE and vdW surfaces selected by turning on and off the “nmap 1.5, nsph 500” option. The electrostatic potential φ was calculated first from a 100 × 100 × 100 grid with 1.5-Å spacing centered at the geometric center of the complex. This was followed by a 140 × 140 × 140 grid with 0.5 Å spacing at the same center. A final round of focusing at the N atom of a mutation site was introduced on a 140 × 140 × 140 grid with 0.25-Å spacing. The electrostatic energy of the protein complex (AB) was calculated as

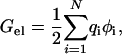(1)

where q_i are the partial charges and N is the total number of atoms of the complex. The same procedure was followed in calculating the electrostatic energy of each of the subunits (A or B), except that the other subunit (B or A) was stripped away. The electrostatic contribution to the binding stability is

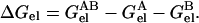(2)

Amber charges and radii (Weiner et al., 1984) were used. The ionic strength was 25, 125, 225, or 325 mM and temperature was 298 K. Protonation states of ionizable groups were those appropriate for pH 7. The solvent dielectric constant was 78. The protein dielectric constant ɛ_p was set to 4 when the vdW surface was used and to 4 or 20 when the SE surface was used. These choices are referred to as “vdW + ɛ_p = 4,” “SE + ɛ_p = 4,” and “SE+ɛ_p = 20.”

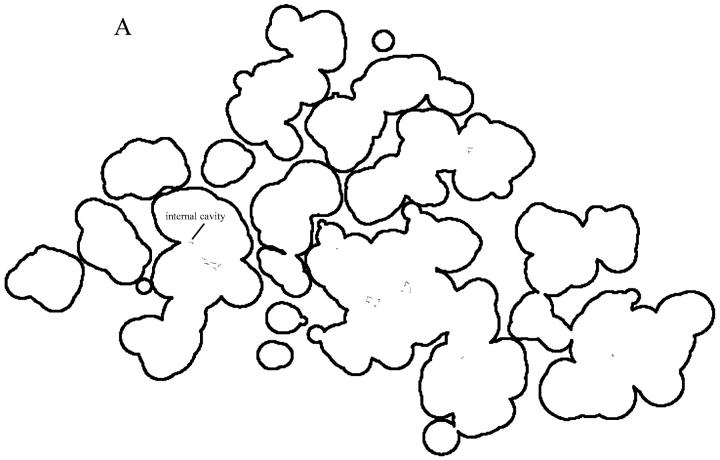
The vdW surface of a protein molecule is surrounded by many small crevices (see Fig. 2). Whether it is physically sound to treat the crevices as part of the solvent dielectric is debatable. Alexov (2003) has argued against such a treatment by noting the fact that x-ray crystallography does not identify many buried waters. However, typically x-ray crystallography only identifies those positions that are visited by water molecules repeatedly, hence positionally disordered water molecules are usually not identified (Ernst et al., 1995; Yu et al., 1999). As noted by Yu et al. (1999), the large body of studies on hydrogen exchange shows that “solvent can penetrate into the deepest recesses of protein molecules” through fluctuating channels or local unfolding. Fitch et al. (2002) has also suggested water penetration in rationalizing experimental pK_a values of buried ionizable residues in the hydrophobic interior of staphylococcal nuclease. The dielectric map generated from the vdW surface (Fig. 2 B) perhaps provides a means to approximately account for the effects of structural fluctuations and transient exposure to solvent when a static structure is used in calculations.

FIGURE 2.

(A) One slice of the vdW surface of barnase. This slice also cut through seven channels leading to the exterior of the protein and one internal cavity. The cross sections of the channels are drawn in dotted lines; the cavity is labeled. (B) The dielectric map on the slice in A generated using the vdW surface as the dielectric boundary with a resolution of 0.5 Å per grid. (C) The dielectric map generated using the SE surface as the dielectric boundary. Protein interior grids with a dielectric constant of 4 are shown in black whereas solvent grids with a dielectric constant of 78 are in white. Dielectric smoothing (Madura et al., 1995) was employed, thus boundary grids had dielectric constant (ɛ) intermediate between 4 and 78. Three gray levels are used to represent grids with 4 < ɛ ≤ 10, 10 < ɛ ≤ 30 and 30 < ɛ < 78.

Eleven charged residues around the interface of the complex were selected for making single and double mutations, resulting in a total of 17 mutants (see Fig. 1). Mutations were modeled in InsightII. Fersht and co-workers (Schreiber and Fersht, 1993, 1995; Frisch et al., 1997) measured the effects of these mutations on the binding constant. They also studied mutations of polar residues and observed consistently smaller effects. We did not investigate the polar mutations. The measured effect of a mutation on the binding free energy is

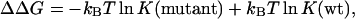(3)

where K(mutant) and K(wt) are the binding constants of the mutant and the wild-type protein, respectively. The change in calculated ΔG_el, ΔΔG_el, by a mutation will be directly compared to the experimental ΔΔG.

Decomposition of ΔΔG_el

Consider a tagged residue in protein A. 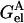can be decomposed into three terms. The first is the solvation term 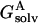, which was calculated by keeping the partial charges on the tagged residue and switching off the partial charges of the rest of the protein. For the second term 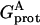, the roles of the tagged residue and the rest of the protein are reversed. The third term 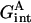represents the interactions between the two parts of the protein. This can be calculated by multiplying the electrostatic potential of the tagged residue (in the protein environment but with the rest of the protein discharged) with the partial charges of the rest of the protein. One may even obtain the contribution from the interaction of the tagged residue with any specified group if only the partial charges of that group are multiplied.

A similar decomposition can be made for the protein complex AB. ΔG_solv, the difference in the first term between AB and A, is the desolvation cost incurred by the tagged residue upon complex formation. The difference in the second term, ΔG_prot, is the desolvation cost for the rest of protein A and for protein B. The different in the third term, ΔG_int, has two contributions: 1), ΔG_int1, the difference in the interaction energy of the tagged residue with the rest of protein A before and after binding protein B; and 2), G_int2, the energy from the new interactions between the tagged residue and protein B formed in the complex. ΔG_int1 arises from the fact that charge pairs in protein A become less exposed to solvent when protein B is bound. Therefore interactions between charges will become stronger because of the diminished screening by the solvent. The change in electrostatic energy by the mere presence of another protein has been noted previously (Zhou, 1993).

When the tagged residue is mutated, ΔΔG_el can be written as

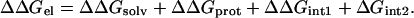(4)

ΔΔG_prot is zero if the mutation does not change the shape of the protein surface. In general, ΔΔG_prot is small because the change in protein shape resulting from a point mutation is small (assuming the rest of the protein is rigid).

Coupling energy

Consider a mutation of a charged residue X on protein A, denoted by “X → 0,” modeled by switching off the partial charges on the residue. In this case ΔΔG_prot(X → 0) = 0 and there are no interactions between the mutated residue and protein B in the complex. Let the interaction energies of X with a charged residue Y on protein B and the rest of protein B be G_X-Y and G_X-B′, respectively. Then we have ΔG_int2(X → 0) = −G_X-Y − G_X-B′ and

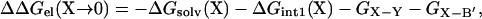(5)

where ΔG_solv(X) is the desolvation cost of charge X and ΔG_int1(X) is the difference in the interaction energy of charge X with the rest of protein A before and after binding protein B. Similarly, when residue Y on protein B undergoes the “Y → 0” mutation, we have

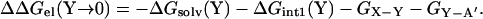(6)

The double mutation “X → 0, Y → 0” can be viewed as a single “Y → 0” mutation on the “X → 0” single mutant. Then

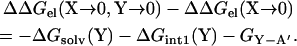(7)

The only difference between the right-hand sides of Eqs. 6 and 7 is the term G_X-Y, which of course is absent when the “X → 0” mutation is made. So

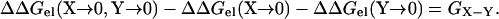(8)

In practice, the fictitious “X → 0” and “Y → 0” mutations can be mimicked by mutating the charged residues X and Y to neutral residues (represented by the generic symbol “O”). The resulting interaction energy G_X-Y corresponds to the coupling energy defined by Fersht and co-workers (Schreiber and Fersht, 1995; Frisch et al., 1997) through a double mutant cycle:

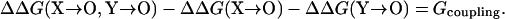(9)

We will compare the calculated electrostatic interaction energy G_X-Y to the experimental coupling energy G_coupling.

Prediction of pK_a

We have developed a simple but robust protocol for calculating pK_a values of selected ionizable residues (Vijayakumar and Zhou, 2001; Dong and Zhou, 2002). If the electrostatic interactions of an ionizable residue with other ionizable groups having similar pK_a values are negligible, then its pK_a can be calculated as

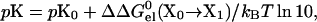(10)

where pK₀ is the pK_a of a model compound, and X₀ and X₁ represent the unprotonated and protonated forms, respectively, of the ionizable residue. Specifically, 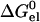represents the change in electrostatic energy when the ionizable residue is brought from the solvent to the protein environment, and 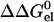(X₀ → X₁) represents the change in 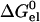upon protonating the residue. The ionizable residue was assigned appropriate partial charges in both the deprotonated and protonated forms.

The three histidines in barnase and barstar (barnase H18 and H102 and barstar H17) fulfill the condition for using Eq. 10. Their pK_a values before and after complex formation were calculated. The ionic strength for these calculations were 110 mM. The model-compound pK_a value for histidine was 6.5.

RESULTS AND DISCUSSION

Effects of charge neutralizations on binding stability

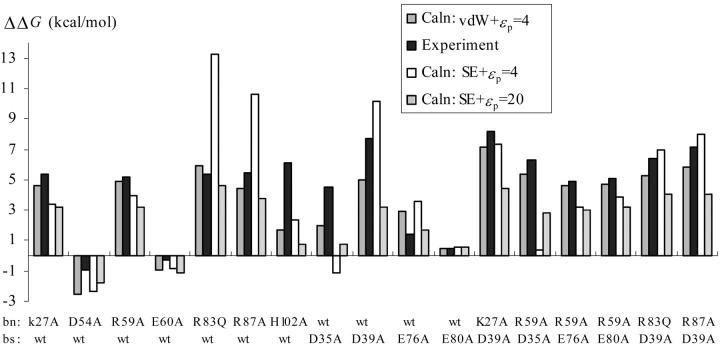
Table 1 lists the calculated effects of the 17 charge mutations on the binding stability of barnase (bn) and barstar (bs) at I = 25 mM. Comparison with experimental results (Schreiber and Fersht, 1993, 1995; Frisch et al., 1997) is shown in Fig. 3. The “vdW + ɛ_p = 4” protocol produced the best agreement with experiment, with a root-mean square deviation (RMSD) of 1.6 kcal/mol, which is 18% of the range of the effects the charge mutations were observed to have on the binding energy.

TABLE 1.

Calculated effects of charge neutralizations on binding stability (in kcal/mol)

Mutation	ASA (Å2)*	ΔΔGel†	ΔΔGsolv†	ΔΔGprot†	ΔΔGint1 + ΔGint2†	Interactions‡
bnK27A	56 → 24	4.65	−0.96	−0.11	5.72	bsD39: 2.5
		3.42	−6.20	−2.92	12.54	bsD35: 1.2
		3.24	−1.06	−0.12	4.42	bnE73: 1.0
						bnR83: −1.0
bnD54A	31 → 31	−2.50	−0.13	−0.33	−2.04	bsD39: −1.0
		−2.35	−0.26	0.03	−2.12
		−1.74	−0.08	0.02	−1.68
bnR59A	214 → 48	4.88	−1.18	−0.56	6.52	bsE76: 3.5
		3.93	−4.07	−3.18	11.18	bsD35: 1.8
		3.21	−0.82	−0.29	4.32
bnE60A	152 → 79	−0.90	−1.04	−0.22	0.36	bsD35: −1.1
		−0.82	−2.53	0.17	1.54	bsL34: 1.0
		−1.09	−0.59	0.04	−0.54
bnR83Q	79 → 12	5.90	−1.32	−0.08	7.10	bsD39: 6.0
		13.27	−4.94	1.05	17.16	bnK27: −1.0
		4.58	−0.70	0.20	5.08	bnR87: −1.0
bnR87A	5 → 0	4.45	−0.83	0.08	5.20	bsD39: 3.7
		10.63	−3.28	1.05	12.86	bnR83: −1.1
		3.73	−0.44	0.21	3.96
bnH102A§	106 → 0	1.67	−0.52	−0.43	2.62	bsD39: 1.7
		2.32	−1.24	−0.94	4.50
		0.76	−0.18	−0.08	1.02
bsD35A	132 → 2	2.02	−2.57	−0.15	4.74	bnR59: 3.0
		−1.09	−10.80	−0.65	10.36	bnK62: 2.0
		0.77	−1.71	−0.04	2.52	bnE73: −1.6
						bnK27: 1.0
bsD39A	90 → 3	5.01	−2.35	−0.82	7.18	bnR83: 6.0
		10.19	−10.16	−0.37	20.72	bnR87: 3.9
		3.20	−1.59	−0.01	4.80	bnK27: 2.4
						bnE73: −2.2
						bnH102: 1.9
						bnD75: −1.8
						bnD54: −1.0
bsE76A	88 → 61	2.90	−0.46	−0.16	3.52	bnR59: 3.7
		3.53	−1.52	−0.41	5.46
		1.70	−0.28	−0.06	2.04
bsE80A	144 → 144	0.50	−0.14	0	0.64
		0.58	−0.24	0.02	0.80
		0.58	−0.11	0.01	0.68
bnK27A/bsD39A		7.19
		7.36
		4.41
bnR59A/bsD35A		5.32
		0.40
		2.79
bnR59A/bsE76A		4.60
		3.20
		2.99
bnR59A/bsE80A		4.73
		3.83
		3.16
bnR83Q/bsD39A		5.23
		6.98
		4.01
bnR87A/bsD39A		5.81
		8.02
		4.01

^*Accessible surface area of wild-type residue before (first number) and after (second number) complex formation.

^†For each mutation, energetic results calculated by three protocols are listed in the order 1), “vdW + ɛ_p = 4;” 2), “SE + ɛ_p = 4;” and 3), “SE + ɛ_p = 20.”

^‡Interaction energies calculated by the “vdW + ɛ_p = 4” protocol are listed. Only those pairs with interaction energies >1 kcal/mol are listed. Positive values indicate favorable interactions in the wild-type complex.

^§bnH102 was unprotonated.

FIGURE 3.

Comparison of calculated and measured effects of neutralizing charged residues lining the binding interface on the binding free energy.

The “SE + ɛ_p = 4” protocol gave significantly larger deviations from experiment. The overall RMSD was 3.4 kcal/mol. This protocol predicted significantly larger destabilizing effects for the bnR83Q and bnR87A single mutations but at the same time predicted a significantly smaller destabilizing effect for the bnR59A/bsD35A double mutation. It also predicted a stabilizing effect for the bsD35A mutation. The “SE + ɛ_p = 20” protocol yielded an intermediate RMSD of 2.7 kcal/mol from experiment. Further comparisons of the three protocols will be given below.

Because of the better performance of the “vdW + ɛ_p = 4” protocol, more emphasis will be placed on this protocol. Unless otherwise noted, calculation results presented and discussed below are from the “vdW + ɛ_p = 4” protocol. Both single mutations and double mutations on barnase Lys-27, Arg-59, Arg-83, and Arg-87 and barstar Asp-35, Asp-39, and Glu-76 were found to substantially weaken the binding stability. The average ΔΔG_el for these seven single mutants was 4.3 kcal/mol. In comparison, the average ΔΔG_el for the six double mutants bnK27A/bsD39A, bnR59A/bsD35A, bnR59A/bsE76A, bnR59A/bsE80A, bnR83Q/bsD39A, and bnR87A/bsD39A was 5.5 kcal/mol. The higher average value for the double mutants is due to the fact many of these charged residues have multiple interactions across the interface. We will return to the interactions later.

The bnD54A and bnE60A mutants provided nice negative controls. Both experiment and calculations with all the three protocols found the neutralization mutations to increase the binding stability. Asp-54 and Glu-60 are located in the periphery of the interface. They perhaps play the role of stabilizing the positive charges clustered around the active site of barnase (Meiering et al., 1992). Asp-54 is only 4.6 Å away from Lys-27. Upon complex formation, Asp-54 and Glu-60 of barnase are placed not far from the cluster of negative charges on barstar. bnE60 is 5.6 Å away from bsD35, whereas bnD54 is 7.2 and 8.0 Å away from bsE80 and bsE39, respectively. The increase in binding stability by the neutralization of bnD54 and bnE60 can therefore be partly attributed to the relief of charge-charge repulsions.

The largest differences between the “vdW + ɛ_p = 4” calculation and experiment occurred in the bnH102A and bsD35A mutants. bnH102 was assumed to be unprotonated (the pK_a values of histidines are discussed below). Both bnH102 and bsD35 are partially exposed before complex formation (with accessible surface areas of 106 and 132 Ų, respectively; see Table 1). They become completely buried in the complex. Mutation to the smaller alanine leads to poorer packing. Thus the bnH102A and bsD35A mutants could lose a considerable hydrophobic and van der Waals contribution to the binding stability. Such a contribution might explain the discrepancy between calculation and experiment for these two mutants. Indeed, our calculation results for ΔΔG_el appeared to be systematically lower than the measured ΔΔG, again pointing to hydrophobic and van der Waals contributions. However, the differences were relatively small (except for bnH102A and bsD35A noted above), suggesting that the dominant contributions of the charged residues to binding stability are electrostatic.

Decomposition of ΔΔG_el

To further elucidate the molecular basis of the electrostatic contributions to binding stability, we have decomposed the calculated ΔΔG_el according to Eq. 4. The results are also given in Table 1. The desolvation cost calculated with the “vdW + ɛ_p = 4” protocol ranged from 0.1 kcal/mol for bnD54 and bsE80, whose solvent exposures are not affected by the complex formation, to 2.6 kcal/mol for bsD35, which, as noted already, becomes buried upon complex formation. This range of desolvation cost is similar to what is calculated for charged residues forming semi-buried salt bridges upon protein folding (Vijayakumar and Zhou, 2001; Dong and Zhou, 2002), despite the fact that some of the cross-interface salt bridges studied here (in particular, the bnR87-bsD39 salt bridge) are much better shielded from solvent than the semi-buried salt bridges near protein surfaces. The explanation lies in the different initial states. In protein folding the charged residues are completely exposed to solvent in the unfolded state. On the other hand, in protein binding the charged residues in the (folded) subunits are already partially shielded from solvent. As expected, ΔΔG_prot is generally quite small.

The charged residues stabilize the protein complex because they form multiple interactions across the interface. Within the interface, charge pairs are shielded from solvent, so the interactions can be very strong. In particular, the interaction energy between bnR83 and bsD39 is −6 kcal/mol. Two different factors work in concert in this case (see Table 2). First, the two charges have a very short distance (the respective distances of bsD39 OD1 from NH2 and NH1 of bnR83 are 2.7 and 3.0 Å). Second, both R83 and D39 are nearly completely shielded from the solvent. The significance of shielding from solvent is well illustrated by the slightly stronger interaction between bnR87 and bsD39 than that between bnR59 and bsE76 (with energies of −3.8 and −3.6 kcal/mol, respectively), despite the fact that the former pair of charges have a considerably longer distance than the latter pair (3.2 vs. 2.6 Å). Both bnR87 and bsD39 are completely buried in the complex but both bnR59 and bsE76 have sizeable exposure to solvent.

TABLE 2.

Calculated and experimental coupling energies of six charge pairs (in kcal/mol)

Charge pair	Distance (Å)	ASA (Å2)*	GX-Y†	Gcoupling‡
K27-D39	4.2	24; 3	−2.5	−4.8
			−6.3
			−2.0
R59-D35	4.4	48; 2	−1.6	−3.4
			−2.4
			−1.2
R59-E76	2.6	48; 61	−3.2	−1.7
			−4.3
			−1.9
R59-E80	6.7	48; 144	−0.7	−0.6
			−0.7
			−0.6
R83-D39	2.7	12; 3	−5.7	−6.7
			−16.5
			−3.8
R87-D39	3.2	0; 3	−3.7	−6.1
			−12.8
			−2.9

^*The two numbers are the accessible surface areas of the two charges in the protein complex.

^†For each charge pair, results calculated by three protocols are listed in the order 1), “vdW + ɛ_p = 4;” 2), “SE + ɛ_p = 4,” and 3), “SE + ɛ_p = 20.”

^‡Schreiber and Fersht (1995).

Note that each energy listed in the last column of Table 1 arises from the interactions of a charged side chain (as the role of the backbone is eliminated by the mutation in the first column) with both the backbone and the side chain of a charged residue across the interface. This explains why the interaction energy between bnR59 and bsD35A is −1.8 kcal/mol when calculated from the bnR59A mutant but −3.0 kcal/mol when calculated from the bsD39A mutant. bsD39 forms a hydrogen bond with the backbone amide of bnR59A. This side chain-backbone hydrogen bond contributes −1.2 kcal/mol. The bsD39A mutant eliminates this contribution along with the side chain-side chain interaction, whereas the bnR59A mutant eliminates only the side chain-side chain interaction, which contributes −1.8 kcal/mol. For all other charge pairs whose two partners have been separately neutralized, there are no strong side chain-backbone interactions across the interface. The interaction energies calculated from neutralizing either charged residue of each pair are in agreement.

Through the decomposition of ΔΔG_el, we identified a charge pair that is not recognized previously for stabilizing the complex. This is between bsD35 and bnK62, having an interaction energy of −2.0 kcal/mol. The two side chains are at a distance of 5.6 Å in the complex. The backbone amide of bnK62 is also oriented favorably toward bsD35, thus the magnitude of the side chain-side chain interaction is somewhat less than 2.0 kcal/mol. It will be interesting to test these results experimentally by neutralizing barnase Lys-62.

The above discussion is directed to ΔG_int2. There were also a number of interactions within barnase that became significantly stronger by the binding of barstar. These included the pairs of Lys-27 and Glu-73, Lys-27 and Arg-83, and Arg-83 and Arg-87. The interactions of the three pairs within the complex were stronger by at least 1 kcal/mol than those in barnase alone.

The decomposition of ΔΔG_el also sheds light on the differences of the three calculation protocols. In general, the desolvation cost and the strengths of charge-charge interactions predicted by the “SE + ɛ_p = 4” protocol were significantly higher than those predicted by the “vdW + ɛ_p = 4” and “SE + ɛ_p = 20” protocols. In some cases (e.g., bnK27A and bnR59A), the two large contributions offset each other so the net effect of the mutation was comparable to those predicted by the other two protocols. However, for bnR83Q, bnR87A, and bsD39A, the large charge-charge interaction energies predicted by the “SE + ɛ_p = 4” protocol were not adequately offset by the desolvation cost, resulting in significantly larger destabilizing effects for these mutations than those predicted by the other two protocols. For bsD35A, the large desolvation cost was more than the charge-charge interaction energy and a stabilizing effect was predicted for the mutation. Relative to the “SE + ɛ_p = 4” protocol, the “vdW + ɛ_p = 4” and “SE + ɛ_p = 20” protocols showed qualitative similarities in the predicted desolvation cost and strengths of charge–charge interactions, with the “SE + ɛ_p = 20” protocol yielding more moderate results. For the two charged residues bnD54 and bsE80 whose solvent exposures are not affected by the complex formation, the three protocols predicted similar desolvation cost and charge-charge interaction energies.

Coupling energies

The interaction energies for six pairs of charges: bnK27 and bsD39, bnR59 and bsD35, bnR59 and bsE76, bnR59 and bsE80, bnR83 and bsD39, and bnR87 and bsD39, were also calculated from a double mutant cycle according to Eq. 8. The results are listed in Table 2. These agreed well from the values obtained from decomposing ΔΔG_el (after eliminating any contribution from side chain-backbone interaction) (see Table 1).

The interaction energies calculated with the “vdW + ɛ_p = 4” protocol compared favorably with the experimental data on the coupling energies. In particular, both experiment and calculation found bnR83-bsD39 to be the strongest interaction pair among the six and bnR59-bsE80 to be the weakest pair. Both the calculated and the experimental results fall in the range of −0.5 to −7.0 kcal/mol. This range is significantly larger than what is found, from −0.5 to −3.5 kcal/mol, for salt bridges formed upon protein folding (Zhou, unpublished results). The reason of course is the better shielding from solvent in the cross-interface salt bridges.

Not surprisingly, the interaction energies calculated with the “SE + ɛ_p = 4” protocol were larger in magnitudes than the “vdW + ɛ_p = 4” results. In particular, relative to the experimental data, the “SE + ɛ_p = 4” results for the bnR83-bsD39 and bnR87-bsD39 interactions, −16.5 and −12.8 kcal/mol, were larger by 7–10 kcal/mol in magnitudes. On the other hand, the “SE + ɛ_p = 20” protocol predicted more moderate interactions than the “vdW + ɛ_p = 4” protocol (and experiment). The double mutant cycle designed to measure the coupling energy minimizes nonelectrostatic contributions. The superior agreement between the “vdW + ɛ_p = 4” calculation and experiment shown in Table 2 further strengthens the case for this protocol.

Ionic strength dependence

We also studied the ionic strength dependence of the binding stability. At an ionic strength of 25 mM, the electrostatic contribution ΔG_el to the binding energy (Eq. 2) of the wild-type complex was −11.1 and −4.9 kcal/mol according to the “vdW + ɛ_p = 4” and “SE + ɛ_p = 20” protocols. Despite the difference in magnitudes, both protocols predicted an overall stabilization by electrostatic interactions. In contrast, the “SE + ɛ_p = 4” protocol predicted ΔG_el = +4.6 kcal/mol, indicating an overall electrostatic destabilization.

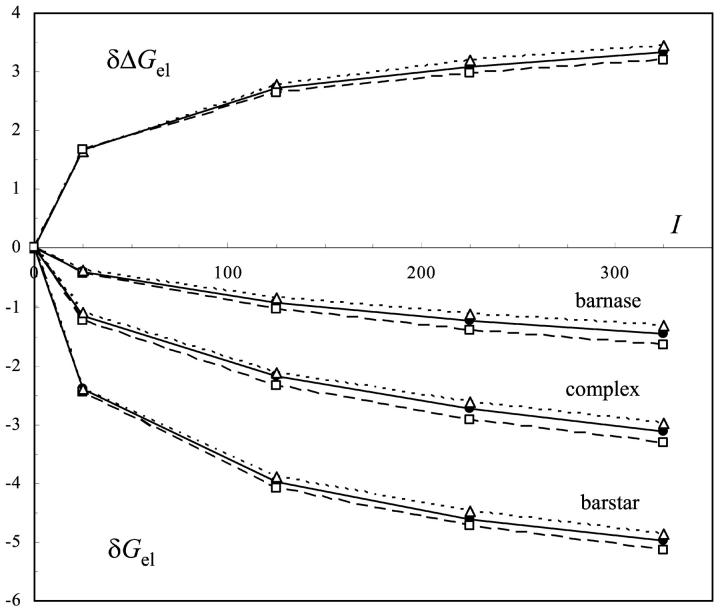
In our previous study of the cold shock protein (Zhou and Dong, 2003), we have noted that the ionic strength dependence of the electrostatic energy of a protein is dominated by the total charge. This finding is confirmed by this study. The net charges of barnase, barstar, and their complex are +2e, −6e, and −4e, respectively. Fig. 4 shows that the electrostatic energies of all the three systems decreased with ionic strength. Barstar showed the steepest decrease, followed by the complex then by barnase. The three calculation protocols gave nearly identical ionic strength dependence.

FIGURE 4.

Ionic strength of the electrostatic energy. Calculated results with the “vdW + ɛ_p = 4,” “SE + ɛ_p = 4,” and “SE + ɛ_p = 20” protocols are shown as filled diamonds connected by solid lines, open squares connected by dotted lines, and open triangles connected by dashed lines, respectively. δG_el represents the difference in the electrostatic energy of a protein between a particular ionic strength and I = 0; δΔG_el = ΔG_el(I) − ΔG_el(I = 0). The experimental ionic strength dependence is shown by filled circles.

The ionic strength dependence of the binding stability as predicted by the change in ΔG_el by ionic strength reasonably reproduced experimental results of Schreiber and Fersht (1993). In particular, ΔG_el calculated by the “vdW + ɛ_p = 4” protocol increased from −11.1 to −10.0, −9.7, and −9.4 kcal/mol when the ionic strength was increased from 25 to 125, 225, and 325 mM, respectively. The increases in ionic strength led to decreases of 1.1, 1.4, and 1.7 kcal/mol in binding stability. In comparison, the measured decreases were 1.4, 2.1, and 2.5 kcal/mol. At higher ionic strengths, the Hofmeister effect may overwhelm the salt screening effect (Baldwin, 1996).

pH Dependence

The calculated pK_a values of bnH18, bnH102, and bsH17 before and after complex formation are listed in Table 3. The results for the histidines in the subunits calculated with the “vdW + ɛ_p = 4” protocol were consistent with available experimental data. Both bnH102 and bsH17 had their pK_a values downshifted, whereas bnH18 had its pK_a upshifted, although the magnitude of the calculated shift was less than measured (Loewenthal et al., 1993). Upon complex formation, the pK_a values of bnH18 and bsH17 changed very little, but the pK_a of bnH102 was downward shifted by 2.4 units. These results can be explained by the fact that bnH18 and bsH17 are away from the binding interface but bnH102 becomes completely buried in the interface. The desolvation cost for creating a buried charge accounts for the large downward shift. Histidine pK_a values in the complex have not been directly measured, but their effects can be inferred from the pH dependence of the binding stability (see below).

TABLE 3.

pK_a values of histidines before and after complex formation

	In subunit		In complex
Residue	Measured	Calculated*	Calculated*
bnH18	7.7†	6.7	6.8
		6.5	6.7
		6.7	6.8
bnH102	5.6‡–6.1§	5.7	3.3
		4.8	−1.0
		5.9	5.9
bsH17	<6¶	5.5	5.7
		1.5	2.2
		6.1	6.4

^*For each histidine, results calculated by three protocols are listed in the order 1), “vdW + ɛ_p = 4,” 2), “SE + ɛ_p = 4,” and 3), “SE + ɛ_p = 20.”

^†Obtained by Loewenthal et al. (1991, 1993) using fluorescence titration.

^‡Obtained by Mossakowska et al. (1989) and Bastyns et al. (1996) from measuring the pH profile of k_cat/K_M for the hydrolysis of GpC.

^§Obtained by Sali et al. (1988) from proton NMR titration in D₂O after correcting for the H/D isotope effect by subtracting 0.2 pKa unit (Loewenthal et al., 1991).

^¶Khurana et al. (1995).

Compared to the “vdW + ɛ_p = 4” predictions, pK_a shifts predicted by the “SE + ɛ_p = 20” protocols were more modest. The most significant difference between the two protocols occurred for bnH102 in the complex, whose pK_a was predicted by the “SE + ɛ_p = 20” protocol to be unaffected by complex formation, a result not compatible with the observed pH dependence of the binding stability (see below). In addition, according to available experimental information (Khurana et al., 1995), the down shift of 0.4 pK_a units for bsH17 before complex formation appeared to be too small. On the other hand, pK_a shifts predicted by the “SE + ɛ_p = 4” protocol appeared to be too excessive. In particular, the down shift of 1.7 pK_a units for bnH102 before complex formation was outside the range of experimental measurements (Sali et al., 1988; Mossakowska et al., 1989; Bastyns et al., 1996).

Assuming that the histidines are the only titrating groups and bnH102 is the only group whose pK_a is appreciably affected by complex formation, the pH dependence of the binding constant is given by

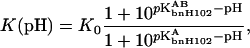(11)

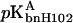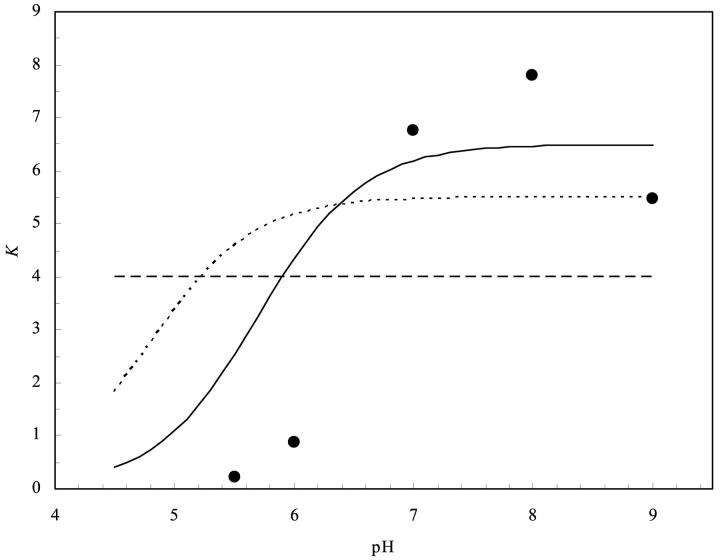
where and 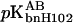are the pK_a values of bnH102 before and after complex formation. In Fig. 5, the predictions of Eq. 11 using the calculated pK_a values listed in Table 3 are compared to the experimental data of Schreiber and Fersht (1993) between pH 5.5 and 9. The “vdW + ɛ_p = 4” result was the closest to experiment, but even it showed appreciable discrepancy. The predicted value for 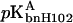appeared too small. The “SE + ɛ_p = 20” protocol did not predict any pH dependence; the transition of the binding constant from low to high pH predicted by the “SE + ɛ_p = 4” protocol occurred far too early.

FIGURE 5.

pH Dependence of the binding constant (in units of 10¹² M⁻¹) at I = 110 mM. The filled circles are experimental data of Schreiber and Fersht (1993). The solid, dotted, and dashed curves are calculated according to Eq. 11 with the pK_a values of bnH102 before and after complex formation set to the “vdW + ɛ_p = 4,” “SE + ɛ_p = 4,” and “SE + ɛ_p = 20” predictions, respectively (see Table 3).

A consequence of Eq. 11 is that the binding constant of the bnH102A mutant with barstar should be independent of pH around pH 6.5. This prediction is consistent with experimental observations between pH 5 and 8 (Schreiber and Fersht, 1993).

Choice of calculation protocol

The “vdW + ɛ_p = 4” protocol produced results on the effects of charge mutations, ionic strength, and pH that were most consistent with experimental data. In comparison, with the “SE + ɛ_p = 4” protocol, the destabilizing effects were significantly larger for the bnR83Q and bn87A single mutations but significantly smaller for the bnR59A/bs35A double mutant and the coupling energies were significantly higher for the bnR83-bsD39 and bnR87-bsD39 charge pairs. The “SE + ɛ_p = 20” protocol showed qualitative similarities to the “vdW + ɛ_p = 4” protocol, but its estimates of desolvation cost and charge-charge interactions appeared to be too modest.

Both the “vdW + ɛ_p = 4” and the “SE + ɛ_p = 20” protocols serve to reduce the apparently excessive desolvation cost and strengths of charge-charge interactions predicted by the “SE + ɛ_p = 4” protocol. The Poisson-Boltzmann model as implemented in this study neglects structural relaxation after a charge mutation and sampling of protein conformations in a given charge state. Such dynamic effects have been shown to effectively increase the protein dielectric constant and thus weaken charge-charge interactions and reduce desolvation cost (Sham et al., 1998; Havranek and Harbury, 1999; Schutz and Warshel, 2001).

A major difference between the vdW and SE surfaces lies in the many small crevices around the interface, which are left as part of the low protein dielectric in the SE specification but treated as part of the high solvent dielectric in the vdW specification. Treating the crevices around the interface as part of the solvent dielectric is arguably in accord with the observed large number of water molecules mediating hydrogen bonds between barnase and barstar in the x-ray structure of the complex (Buckle et al., 1994).

A main goal of this study was to see whether the apparent success of the “vdW + ɛ_p = 4” protocol in rationalizing the effects of charge mutations on protein folding stability (Vijayakumar and Zhou, 2001; Dong and Zhou, 2002; Zhou and Dong, 2003) extends to modeling the roles of electrostatic interactions in the binding stability of protein-protein complexes. The study was not designed to “parameterize” a Poisson-Boltzmann model using the vdW surface. Careful parameterization of Poisson-Boltzmann models have been carried out with the SE surface against experimental hydration free energies of a large number of small molecules (Sitkoff et al., 1994) and with the vdW surface against free energies of the 20 amino acids obtained from molecular dynamics simulations (Nina et al., 1997). However, protein molecules differ from small molecules by strong interactions between different residues and by the fact that most residues are screened from the solvent.

There have been a number of studies using the “SE + ɛ_p = 4” protocol on the barnase-barstar complex (Xu et al., 1997; Roccia et al., 2001; Lee and Tidor, 2001; Sheinerman and Honig, 2002). The results reported in those studies are generally consistent with what we found in this study using the “SE + ɛ_p = 4” protocol. a), Strong interactions between charge pairs and high desolvation cost. Xu et al. (1997) calculated the contributions of the bnR83-bsD39 and bnR59-bsE76 charge pairs. The coupling energies were −19.5 and −6.4 kcal/mol, compared to the “SE + ɛ_p = 4” results of −16.5 and −4.3 kcal/mol listed in Table 2. The small numerical differences between the two calculations appear to stem from the different charge-radius parameters used (CHARMM in Xu et al.'s work whereas Amber in the present work). Xu et al. modeled mutations by switching off charges (the “X → 0” mutation in Eq. 8) whereas we modeled mutations by introducing neutral (Ala or Gln) residues (the “X → O” mutation in Eq. 9), but this technical difference had a rather small effect. For example, the “SE + ɛ_p = 4” coupling energy for the bnR83-bsD39 charge pair changed to −16.1 from −16.5 kcal/mol. The desolvation cost calculated by Xu et al. for the two charge pairs, 34.0 and 15.0 kcal/mol, is apparently much too excessive. For the bnR59-bsE76 charge pair, the calculated charge-charge interactions were not able to offset the large desolvation cost, and a net destabilization of 6.5 kcal/mol was predicted. This prediction obviously is in conflict with experimental observations. b), Overall electrostatic destabilization. Using CHARMM charges and radii, Lee and Tidor (2001) reported ΔG_el = +14.2 kcal/mol for the barnase-barstar complex at I = 145 mM, whereas Sheinerman and Honig (2002) reported ΔG_el = +3.5 kcal/mol for this complex at I = 100 mM. This is to be compared with our “SE + ɛ_p = 4” result of +5.8 kcal/mol at I = 125 mM. In contrast, our “vdW + ɛ_p = 4” result was −10.0 kcal/mol at I = 125 mM. c), Ionic strength dependence. Roccia et al. (2001) reported ionic strength dependence of the electrostatic interaction energy between barnase and barstar. When I increased from 0 to 100, 200, and 300 mM, ΔG_el was found to increase by 1.2, 1.4, and 1.5 kcal/mol, respectively. These increases are more modest than our results predicted by the “SE + ɛ_p = 4” protocol, which increased by 2.8, 3.2, and 3.5 kcal/mol, respectively, as I increased from 0 to 125, 225, and 325 mM. As Fig. 4 shows, the ionic strength dependences of ΔG_el calculated by the “vdW + ɛ_p = 4,” “SE + ɛ_p = 4,” and “SE + ɛ_p = 20” protocols were almost identical. It is not clear what accounts for the discrepancy in ionic strength dependence between our and Roccia et al.'s calculations, but our calculations are in closer agreement with experimental data [note that the 50 mM Tris-HCl buffer used by Schreiber and Fersht (1993) contributes an ionic strength of ∼25 mM, which was not taken into consideration by Roccia et al. (2001)].

Using the “SE + ɛ_p = 2” protocol, Elcock et al. (1999) found ΔG_el = +58 kcal/mol for the acetylcholinesterase-fasciculin complex. On the other hand, Gabdoulline and Wade (2001) recently used the “vdW + ɛ_p = 4” protocol to calculate interaction energies in the association processes of barnase with barstar, acetylcholinesterase with fasciculin, and other protein pairs, because they found that using the SE surface led to “unrealistic” underestimation of association rates.

The same charges affecting the stability of the barnase-barstar complex have also been observed to affect the association rate (Schreiber and Fersht, 1993,1995). Ironically, there is agreement among theoreticians regarding the favorable contributions of electrostatic interactions to the rates of protein-protein association (Gabdoulline and Wade, 1997, 2001; Vijayakumar et al., 1998; Elcock et al., 1999). The transition state for forming a protein complex is solvent separated (Vijayakumar et al., 1998), so the desolvation cost and charge-charge interactions calculated using the SE surface are diminished.

Because opposite conclusions regarding the overall electrostatic contributions to the binding stability are reached by the “vdW + ɛ_p = 4” and “SE + ɛ_p = 20”protocols on the one hand and by the “SE + ɛ_p = 4” protocol on the other, further scrutiny of the three protocols is clearly warranted. A fruitful direction appears to be comparing the different Poisson-Boltzmann protocols against molecular dynamics simulations. At the very least, this study demonstrates that caution is required in drawing conclusions on electrostatic contributions based on a particular Poisson-Boltzmann calculation protocol.