Abstract
The folding thermodynamics of the src-SH3 protein domain were characterized under refolding conditions through biased fully atomic molecular dynamics simulations with explicit solvent. The calculated free energy surfaces along several reaction coordinates revealed two barriers. The first, larger barrier was identified as the transition state barrier for folding, associated with the formation of the first hydrophobic sheet of the protein. φ values calculated from structures residing at the transition state barrier agree well with experimental φ values. The microscopic information obtained from our simulations allowed us to unambiguously assign intermediate φ values as the result of multiple folding pathways. The second, smaller barrier occurs later in the folding process and is associated with the cooperative expulsion of water molecules between the hydrophobic sheets of the protein. This posttransition state desolvation barrier cannot be observed through traditional folding experiments, but is found to be critical to the correct packing of the hydrophobic core in the final stages of folding. Hydrogen exchange and NMR experiments are suggested to probe this barrier.
INTRODUCTION
Our understanding of the process by which proteins reach their biologically active conformation has shifted in the last decade from a pathway specific perspective, to one in which folding proceeds through a multiplicity of pathways (Bryngelson et al., 1995; Dill, 1999; Dobson et al., 1998; Gruebele, 2002; Onuchic et al., 1997).
This new view, based on considerations of energy landscapes, emphasizes the need for a statistical description of the folding process (Bryngelson and Wolynes, 1987, 1990; Plotkin and Onuchic, 2000). Folding is envisioned to proceed on a moderately rough funnel shaped landscape riddled with small local minima that can transiently trap the protein as it descends the funnel (Leopold et al., 1992). For small proteins that fold in a two-state manner, the transition state, or rate limiting step for folding, presents itself in this microscopic picture as a bottleneck in the funnel landscape. Projected onto the traditional macroscopic free energy surface, this bottleneck translates into a free energy barrier arising from the incomplete cancellation of the entropic and enthalpic contributions to folding. An understanding of the folding mechanism of proteins requires a characterization of this transition state ensemble for folding. The identification of transition state structures in protein folding poses a serious challenge, both experimentally and computationally (Crane et al., 2000; Du et al., 1998; Heidary and Jennings, 2002; Krantz and Sosnick, 2001; Lindberg et al., 2002; Nymeyer et al., 2000; Oliveberg, 2001). Experimentally, the nature of the transition state is inferred from φ values (Fersht et al., 1992), which reflect the extent to which the transition state is perturbed upon mutation of a side chain. φ values are defined as:
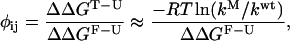 |
(1) |
where ΔΔG is the free energy difference between the wild-type and mutant protein, k is the folding rate and the subscripts U, T, and F correspond to the unfolded, transition, and folded states, respectively. The above expression holds for two-state folders whose kinetics can be described by a Kramers-like expression and assumes that the preexponential factor does not vary upon mutation (Socci and Onuchic, 1995; Socci et al., 1996). When this holds, φ values can simply be calculated from the ratio of folding rates between the mutant and wild-type protein, normalized by the overall change in stability upon mutation (second term on the right hand side of Eq. 1). φ values of 1 correspond to regions of the transition state that are as structured as in the native state, whereas regions with φ values of 0 are unstructured. Intermediate φ values are more ambiguous; they can correspond to partial structure in the transition state, or can be a result of a host of transition state conformations, some of which have structure in the region that is being probed by a mutation, some of which do not. Computations are uniquely poised to decipher the meaning of intermediate φ values, as simulations are effectively single molecule experiments, capable of sorting out information blurred by bulk measurements. Although simulations hold the promise of providing atomistic representations of transition state structures, the realization is hampered by the computational obstacle associated with treating both the protein and solvent in explicit detail. Several research groups have hence turned to simplified (on- (Chan and Dill, 1997; Dinner and Karplus, 1999; Sali et al., 1994) or off-lattice (Borreguero et al., 2002; Ding et al., 2002; Guo and Brooks, 1997; Guo and Thirumalai, 1995; Shea et al., 1998, 1999, 2000; Vekhter and Berry, 1999)) solvent free descriptions of the protein that allow a full characterization of folding events from the denatured to the folded state. More recently, implicit solvent models (Shen and Freed, 2002) combined with atomically detailed proteins models have been used to probe the transition state for folding (Gsponer and Caflisch, 2002). Simulations using explicit solvent models have previously identified transition state structures in proteins well above the melting temperature (Li and Daggett, 1994; Tsai et al., 1999); however, a direct comparison between these high-temperature unfolding transition state structures and the transition state structures obtained under experimental folding conditions remains difficult (Dinner and Karplus, 1999).
In this article, we raise the question of whether identifying the transition state for folding is sufficient to fully understand the folding mechanism of a protein. Standard protein folding experiments, such as stopped-flow fluorescence spectroscopy cannot identify barriers that occur past the rate limiting step for folding. If a dominant barrier is present, the folding process will appear to be two state whether or not small barriers occur posttransition state (Englander, 2000; Sosnick et al., 1996). We stipulate, however, that posttransition state barriers may play a critical role in modulating the final stages of folding. To address the importance of posttransition state barriers, we used importance sampling molecular dynamics simulations to characterize the free energy landscape of the src-SH3 protein domain near its folding transition temperature. This methodology, which employs an atomically detailed protein model with explicit solvent molecules, enables us to identify transition state barriers as well as posttransition state barriers. Our approach circumvents the computational obstacles outlined in the preceding paragraph and provides a microscopic picture of the transition state and mechanism for folding. Experimentally, the src-SH3 protein domain folds as an autonomous unit, with kinetic and thermodynamic signatures of a two-state folder (Grantcharova and Baker, 1997). The protein domain has a 56-residue β-barrel structure (Fig. 1), consisting of two hydrophobic sheets, packed orthogonally to form the hydrophobic core of the protein. The first sheet consists of the three central strands of the protein (β2-β3-β4) and the second sheet of the two terminal strands (β1 and β5) and a portion of the RT loop. Experimental φ values studies have revealed an unusually polarized transition state for src-SH3, in which only the first hydrophobic sheet (β2-β3-β4) is highly structured (high φ values) whereas the rest of the protein appears mostly unstructured (intermediate to low φ values) (Riddle et al., 1999). The transition state of this protein does not resemble an open form of the folded structure, as the second hydrophobic sheet is unformed at the transition state. The formation of the second hydrophobic sheet, along with the packing of the hydrophobic core must occur posttransition state. Recent analytic studies and simulations on simplified hydrophobic clusters suggest that the association of extended hydrophobic surfaces should be accompanied by a dewetting transition, in which the expulsion of water molecules allows the two oily surfaces to interact (Lum et al., 1999). This scenario is reminiscent of the packing of the hydrophobic core of a protein. In the case of src-SH3, the packing of the hydrophobic core occurs after the transition state for folding. A desolvation barrier associated with this type of transition has not been observed in experimental studies of src-SH3 as this posttransition state barrier is not accessible in standard experiments. This barrier however plays a critical role in the folding of the src-SH3 protein.
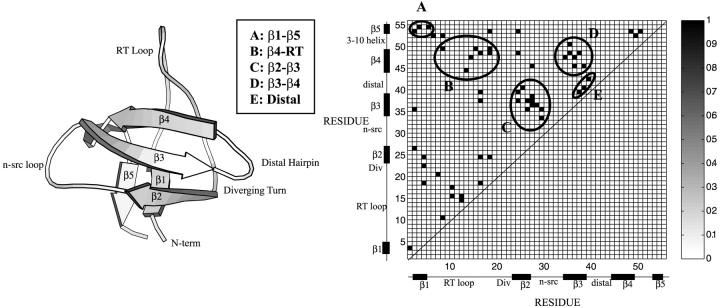
FIGURE 1.
Cartoon diagram of the src-SH3 protein domain and native contact map. A native contact is defined between two residues if the center of geometry of the side chains is <6.5 Å apart. A total of 57 native contacts, listed in Table 1, are obtained in this manner.
In this article, we present an analysis of the free energy landscape for the src-SH3 protein domain near its folding transition temperature. Free energy surfaces at this temperature reveal two barriers, a large one associated with the transition state barrier and a minor one associated with the theorized desolvation of the hydrophobic core. New insights are presented on the nature of the transition state, pathways for folding, and the role of water in mediating the assembly of the hydrophobic core.
METHODS AND MODEL
The protein (pdb code 1SRL) was described in atomic detail using the TOPH19/PARAM19 parameter set and the water was described by the TIP3P model (Jorgensen et al., 1983). The molecular dynamic simulations were performed using the CHARMM software (Brooks et al., 1982). The covalent bonds between hydrogen atoms and the heavy atoms were held fixed using the SHAKE algorithm and a 2-fs time step was used in the Verlet leapfrog integration. All long-range forces were treated using the particle mesh Ewald method. The method and model are described in detail in the articles by Shea and colleagues (Shea and Brooks, 2001; Shea et al., 2002) and are summarized below. In a first step, the native state of the protein is characterized through two 2-ns molecular dynamics simulations at 298 K. Two descriptors of the native state, the number of native contacts and the number of hydrogen bonds, are defined from the native state simulations. A native contact is formed between two nonadjacent residues if the center of geometry of their side chains is within 6.5 Å. A hydrogen bond is formed if the distance between the backbone hydrogen and oxygen of two residues is <2.5 Å. A total of 57 native contacts (listed in Table 1) and 19 native hydrogen bonds were identified. In a second step, three 2-ns high-temperature unfolding simulations (400–500 K) were performed to generate an ensemble of structures spanning the unfolded to the folded state. These structures were clustered after a hierarchical clustering scheme, using the number of native contacts, the number of native hydrogen bonds, and the protein solvation energy in the dissimilarity function. A total of 76 cluster centers were identified in this manner. These clusters centers are then used as the initial conditions structures for the biased sampling at T = 343 K. The third step involves the resolvation of each of the cluster centers, followed by 100–200 ps of equilibration at T = 343 K. Biased sampling, using a harmonic restraint in the fraction of native contacts (ρ), was then performed on each cluster center. The biased sampling was performed for 400–800 ps per structure, using a force constant between 500 and 1000 kcal/mol. In a final step, the sampling data was combined using the weighted histogram analysis method. The density of state as a function of the descriptors (fraction of native contacts, etc.) and temperature were obtained. The density of states was then used to generate free energy surfaces at 343 K as a function of the descriptors. Simulations were performed using the facilities of Argonne National Laboratories.
TABLE 1.
φ values calculated after Eq. 2 from the structures residing at the top of the free energy barrier at ρ = 0.3 (transition state barrier)
| Residue pair | φ | Location | Residue pair | φ | Location | Residue pair | φ | Location |
|---|---|---|---|---|---|---|---|---|
| Thr-1–Val-3 | 0.10 | β1-β2 | Thr-14–Tyr-47 | 0 | RT-distal | Val-27–Ala-37 | 0.18 | β2-β3 |
| Phe-2–Ile-26 | 0.06 | β1-β2 | Asp-15–Pro-49 | 0 | RT-helix | Val-27–His-38 | 0.47 | β2-β3 |
| Phe-2–Trp-35 | 0.01 | β1-β3 | Leu-16–Phe-18 | 0.32 | RT-RT | Val-27–Thr-45 | 0.07 | β2-distal |
| Phe-2–Val-53 | 0.34 | β1-helix | Leu-16–Leu-24 | 0 | RT-β2 | Asn-28–Leu-36 | 0.03 | Nsrc-β3 |
| Val-3–Ala-54 | 0.01 | β1-β5 | Leu-16–Ala-37 | 0 | RT-β3 | Asn-29–Asp-33 | 0 | Nsrc-Nsrc |
| Ala-4–Phe-18 | 0.01 | β1-RT | Leu-16–Ser-39 | 0 | RT-β3 | Asn-29–Trp-35 | 0.17 | Nsrc-β3 |
| Ala-4–Glu-22 | 0.13 | β1-div | Leu-16–Ile-48 | 0 | RT-β4 | Trp-34–Tyr-47 | 0.54 | β3-β4 |
| Ala-4–Leu-24 | 0.15 | β1-β2 | Phe-18–Leu-24 | 0.02 | RT-β2 | Trp-35–Ile-48 | 0.14 | β3-β4 |
| Leu-5–Ala-54 | 0.03 | β1-helix | Phe-18–Ile-48 | 0 | RT-β4 | Trp-35–Ser-50 | 0.34 | β3-helix |
| Tyr-6–Tyr-52 | 0.29 | RT-helix | Phe-18–Pro-49 | 0 | RT-helix | Leu-36–Thr-45 | 0.68 | β3-β4 |
| Asp-7–Lys-20 | 0.41 | RT-div | Phe-18–Trp-35 | 0 | RT-β3 | Leu-36–Tyr-47 | 0.24 | β3-β4 |
| Tyr-8–Ser-10 | 0.01 | RT-RT | Leu-24–Ala-37 | 1.08 | β2-β3 | Ala-37–Ser-39 | 0.58 | β3-β3 |
| Tyr-8–Pro-49 | 0 | RT-helix | Leu-24–Ser-39 | 0.98 | β2-β3 | Ala-37–Ile-48 | 0.40 | β3-β4 |
| Tyr-8–Tyr-52 | 0.13 | RT-helix | Leu-24–Ile-48 | 0.16 | β2-β4 | His-38–Leu-40 | 0.20 | β3-distal |
| Ser-10–Asp-15 | 0.13 | RT-RT | Leu-24–Val-53 | 0.07 | β2-β5 | His-38–Thr-45 | 0.40 | β3-β4 |
| Ser-10–Ser-17 | 0.18 | RT-RT | Gln-25–Leu-40 | 0.68 | β2-distal | Ser-39–Thr-42 | 0.96 | β3-distal |
| Thr-12–Thr-14 | 0 | RT-RT | Ile-26–Trp-35 | 0.55 | β2-β3 | Ile-48–Val-53 | 0.29 | β4-β5 |
| Thr-12–Asp-15 | 0.65 | RT-RT | Ile-26–Ala-37 | 0.68 | β2-β3 | Pro-49–Tyr-52 | 0.46 | helix-helix |
| Glu-13–Gln-44 | 0 | RT-distal | Val-27–Leu-36 | 1.06 | β2-β3 | Ser-50–Val-53 | 0.33 | helix-β5 |
RESULTS AND DISCUSSION
Free energy surfaces and thermodynamics of folding
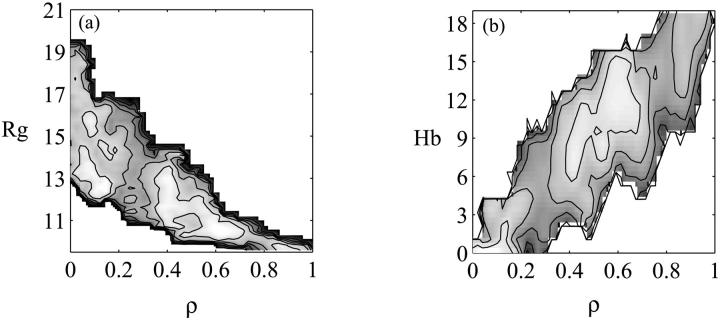
The free energy surface at T = 343 K is plotted as a function of the fraction of native contacts ρ and the radius of gyration Rg in Fig. 2 a and as a function of the fraction of native contacts ρ and the number of native hydrogen bonds Hb in Fig. 2 b. A native contact exists between two residues if the center of geometry of the side chains is <6.5 Å in the folded structure. Similarly, a native hydrogen bond is formed if the distance between the backbone hydrogen and oxygen of two residues is less than 2.5 Å. Two barriers are present in this surface, a major barrier of 2.5 kcal/mol (3.5 kBT) at ρ = 0.3 and a minor one of 1 kcal/mol (1.4 kBT) around ρ = 0.8. The surface is consistent with the experimentally observed single exponential folding kinetics that suggests the presence of a single dominant barrier (without ruling out the presence of smaller, posttransition state barriers).
FIGURE 2.
(a) Free energy surface at T = 343 K as a function of the fraction of native contacts ρ and the radius of gyration Rg. (b) Free energy surface at T = 343 K as a function of the fraction of native contacts ρ and the number of hydrogen bonds Hb. Contour lines are drawn every 1 kcal/mol.
Transition state barrier
Earlier simulations performed at 298 K did not reveal the presence of a barrier in the free energy surface plotted as a function of Rg and ρ (Shea and Brooks, 2001; Shea et al., 2002). At 343 K, however, we see evidence of a significant barrier (3.5 kBT) at ρ = 0.3. This barrier is entropic in origin and can be identified as the transition state barrier for folding. To probe the nature of the transition state structure, we computed the φij values for a contact pair i and j from their probabilities of formation Pij:
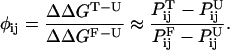 |
(2) |
The subscripts F, U, and T correspond to the folded, unfolded, and transition states, respectively. The transition state structures were defined as all conformations with ρ = 0.3.
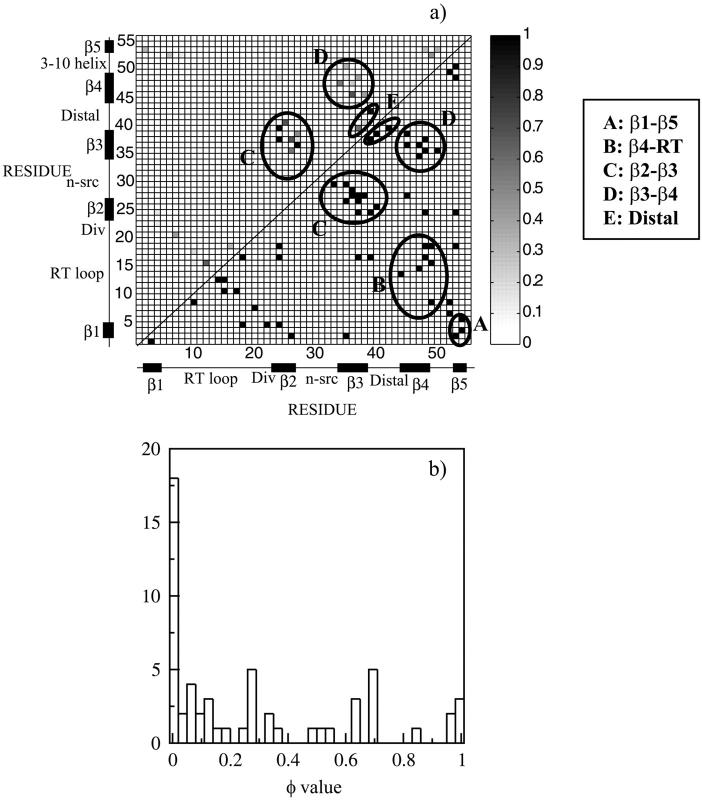
The φ values are represented as a contact map in Fig. 3 a. The distribution is plotted as a histogram in Fig. 3 b. The values are strikingly polarized, displaying φ values near 1 and near 0.
FIGURE 3.
(a) Contact map of the φ values obtained from the structures residing at the free energy barrier of ρ = 0.3 (left hand quadrant). The φ values were calculated according to Eq. 2. Structure is present in the first hydrophobic sheet of the protein consisting of the central β2-β3-β4 strands whereas the rest of the protein is mostly unstructured. The native contact map is shown in the right hand quadrant. (b) Histogram of the φ values. The histogram shows populations at high and low φ values, emphasizing the polarized nature of the transition state.
High φ values: central three stranded β2-β3-β4 region
The highest φ values lie in the central three stranded β2-β3-β4 region, with φ values >0.65 between strands β2 and β3 (Leu-24–Ala-37, Leu-24–Ser-39, Gln-25–Leu-40, Ile-26–Ala-37, Val-27–Leu-36) and in the β3-β4 distal hairpin (Leu-36–Thr-45). The same regions contain φ values ≥0.4: Ile-26–Trp-35, Val-27–His-38 (strands β2-β3) and Trp-34–Tyr-47, Trp-35–Ser-50, Ala-37–Ile-48, His-38–Thr-45 (β3-β4 distal hairpin). Two of the β2-nsrc-β3 φ values are slightly greater than 1, whereas certain contacts in the nsrc loop have φ values of 0 (for instance Asn-29–Asp-33). This implies that the β2-nsrc-β3 region has a different arrangement in the transition state than in the native state. Interestingly, experimental studies by Baker et al. have reported anomalous φ values in this very region (Riddle et al., 1999). Closer examination reveals a number of contacts that are closer together in the transition state than in the native state (for instance Leu-24–Ala-37, Val-27–Leu-36). Our results are consistent with the idea that the β2-nsrc-β3 region has a different core packing in the transition state than in the folded state (Northey et al., 2002; Ventura et al., 2002).
Also of interest is the presence of additional contacts between the distal loop and the diverging turn that are formed in the transition state, but not in the native state (according to our definition of a contact formed if the center of geometry of two side chains are within 6.5 Å of each other), specifically, contact between Glu-22 and Ser-39, Glu-22 and Thr-41, and Glu-22 and Thr-42. Interactions between the distal loop and the diverging turn hence appear to be essential in the rate limiting step for folding.
Low φ values: RT loop and terminal strands
The RT loop is mostly unstructured. The only high φ value involving the RT loop occurs between Thr-12 and Asp-15 (hinge region). The terminal strands are mostly unstructured and do not come in contacts. No contacts are formed between the RT loop and the β3-distal-β4 region.
Hydrogen bonds formation at the transition state barrier
The hydrogen bonds between strands β2 and β3 are highly formed, with contact probabilities PHB of 0.78, 0.84 for pairs Gln-25–His-38 and Leu-36–Val-27. Hydrogen bonds between strands β3 and β4 and in the distal loop are mostly formed (Trp-35–Ile-48: PHB = 0.36), (Ala-37–Gly-46: PHB = 0.60), (Gln-46–Ala-37: PHB = 0.41), (Ser-39–Gly-43: PHB = 0.47), (Ser-39–Gln-44: PHB = 0.28), and (Gln-44–Ser-39: PHB = 0.39). The importance of hairpin formation in establishing the correct topology during folding has been highlighted in recent experimental investigations on both src-SH3 and proteins G and L (McCallister et al., 2000). Similar conclusions were reached in the recent theoretical studies of Thirumalai (Klimov and Thirumalai, 2002).
Hydrogen bonds in the n-src region have low probabilities of contact formation (Asn-28–Leu-36: PHB = 0.10; and Leu-36–Asn-28: PHB = 0.13), suggesting that while the β2-β3-β4 complex is formed, the connecting element (n-src) between β2 and β3 may not be fully structured in the transition state. Hydrogen bonds present in the rest of the protein all have very low contact probabilities indicating that these interactions are still very loosely formed at the transition state. In particular, between RT and β5 (Val-13–Ala-54: PHB = 0.0), RT and β4 (Tyr-14–Tyr-47: PHB = 0.0; Tyr-47–Leu-16: PHB = 0.0), inside the RT-loop (Tyr-8–Phe-18: PHB = 0.0; Phe-18–Tyr-8: PHB = 0.05), β1-β2 (Phe-2–Leu-24: PHB = 0.00; Glu-22–Ala-4: PHB = 0.13), and 310helix-β1 (Tyr-52–Leu-5: PHB = 0.05; Tyr-52–Tyr-6: PHB = 0.09).
The analysis of the probability of hydrogen bond formation confirms the conclusions from the φ value analysis that the transition state at ρ = 0.3 has a structured central β2-β3-β4 sheet although the rest of the protein is still weakly structured. The computationally determined structure of the transition state correlates well with the experimental results of Baker (Riddle et al., 1999), Serrano (Martinez and Serrano, 1999), and Davidson (Northey et al., 2002) on homologous SH3 protein domains.
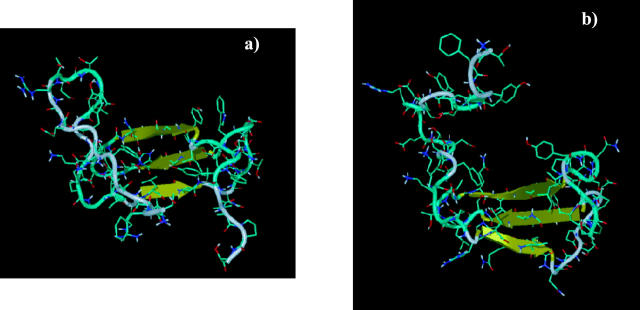
All the structures identified from the maximum in the free energy surface share the characteristic that the central three stranded β2-β3-β4 region is formed, suggesting that this structure is required in the transition state ensemble. The structures differ in the extent to which the other elements of secondary and tertiary structure are formed. Two representative transition state structures are given in Fig. 4. From our simulations, it is clear that the intermediate φ values obtained are the result of the multiple folding pathways accessible to the protein. Indeed on a given pathway, a protein can adopt a conformation in which a native contact (for instance contact Asp-7–Lys-20 in the structure in Fig. 4 a) is formed, whereas on a different pathway, the protein adopts a conformation in which this contact is not made (Fig. 4 b).
FIGURE 4.
Two typical transition state structures are represented in a and b. Structure is present in both cases in the central β2-β3-β4 region. The rest of the protein is mostly unstructured, the degree of structure varying from one transition state conformation to another.
The transition state topology as determined from the contact pair φ values of the structures residing at the top of the free energy barrier is in remarkable agreement with the picture obtained from the experimental residue φ values (listed in Table 4 of Riddle et al., 1999), intimating that generating free energy surfaces through the methodology presented in this article is an efficient and accurate way to characterize the transition state for folding.
Desolvation barrier: a dewetting transition
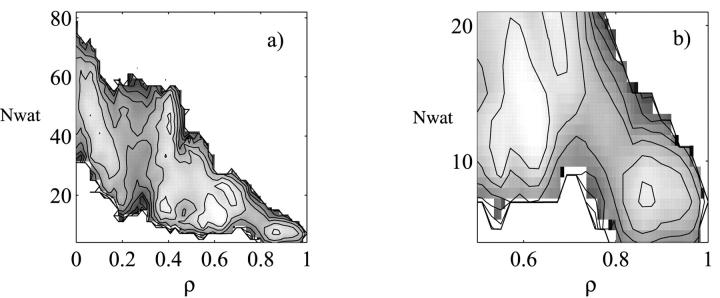
A second, smaller barrier near the folded state (ρ = 0.8) is apparent in the potentials of mean force (pmf) projected onto both the radius of gyration Rg and the fraction of native contacts ρ (Fig. 2 a) as well as onto the number of hydrogen bonds Hb and ρ (Fig. 2 b). To further probe the nature of this barrier, we defined a new reaction coordinate, namely the number of water molecules in the core of the protein (Nwat). The number of water molecules in the core was determined from the number of water molecules residing in an 8-Å sphere centered around the hydrophobic core, as defined by the native protein structure (Shea and Brooks, 2001; Sheinerman and Brooks, 1998). The potential of mean force as a function of ρ and the number of core waters Nwat is represented in Fig. 5 a. A closeup near the barrier is shown in Fig. 5 b.
FIGURE 5.
(a) Free energy surface at T = 343 K as a function of the fraction of native contacts ρ and the number of core water molecules. The core of the protein is defined by an 8-Å radius centered around the hydrophobic core of the protein. The waters residing inside the core are considered core water molecules. (b) Blow up of the free energy in the vicinity of the desolvation barrier. Contour lines are drawn every 1 kBT.
The barrier at ρ = 0.8 is suggestive of a desolvation of the hydrophobic core of the protein in the final stages of folding. In the folded state, the two hydrophobic sheets, which consist of the central strands β2-β3-β4 (sheet 1) and the two terminal strands and the RT loop (sheet 2) are tightly packed, forming the hydrophobic core of the protein. Indeed, structures residing in the folded basin (ρ > 0.8) contain <5 core water molecules. Right before the desolvation barrier, the two hydrophobic sheets are fully formed, but do not yet pack tightly to form the hydrophobic core. The second hydrophobic sheet, which was not formed at the transition state (ρ = 0.3), is now structured. Contact Val-3–Ala-54 (β1-β5), for instance, with a contact probability of 0 at ρ = 0.3, has a formation probability of 0.86 at ρ = 0.75. Indeed, by ρ = 0.8, all of the native contacts hydrogen bonds have high probabilities of formation with the exception of contacts between the two hydrophobic sheets, in particular contacts between the RT loop and the distal hairpin. For instance, both the hydrogen bond between Thr-14 and Gly-46 (RT-distal) and the contact between Thr-14 and Tyr-47 (RT-distal) have low probability of formation (0.34 and 0.39, respectively). Over 10 water molecules reside between the two hydrophobic sheets before the barrier. 6 a represents a structure in the folded basin in which the hydrophobic core is seen to be tightly packed, with no water molecules between the two hydrophobic sheets. The two core water molecules present in this instance lie just outside the actual hydrophobic core (our definition of the hydrophobic core radius of 8 Å allows for some water molecules at the periphery of the hydrophobic core to be included into the count). Fig. 6 b represents a structure with a ρ value of 0.7, (i.e., before the desolvation barrier). The hydrophobic core is open and flooded with water molecules. Interestingly, there is experimental evidence for the presence of disordered water molecules in hydrophobic cavities of proteins (Matthews et al., 1995; Yu et al., 1999). Before the desolvation barrier, the two hydrophobic sheets are connected through a network of water molecules. This is shown in Fig. 7 a, where the backbone donor and acceptor atoms of Tyr-47 and Leu-16 are bridged by a water molecule. In the folded state (Fig. 7 b), Tyr-47 and Leu-16 directly form a hydrogen bond. The water has been expelled from between the sheets enabling the formation of direct interactions leading to the packing the hydrophobic core. The desolvation transition appears to be cooperative in nature. It is interesting to note a distinction between the two types of water molecules present before the desolvation barrier. We observe both waters serving a structural role as backbone hydrogen bond bridges between the residues connecting the hydrophobic sheets as well as water molecules simply residing inside the core. The desolvation barrier separating the structures with open and packed hydrophobic cores is very small, less than 2 kBT, suggesting that the prebarrier, nearly folded solvated structure may be readily accessible under folding conditions. Our results are consistent with observations of penetration and escape of water molecules into the interior of proteins in molecular dynamics simulations of both Cytochrome C (Garcia and Hummer, 2000) and barnase (Caflisch and Karplus, 1994). On a related note, recent studies on staphylococcal nuclease mutants (Dwyer et al., 2000) suggest that water penetration may be responsible for the high apparent dielectric constants of protein interiors. In our simulations, the population of solvated core species at the melting temperature is significant (∼20%), leading to the possibility that NMR studies may be able to identify these structures. We expect that the NMR spectra would reveal an additional peak associated with the different chemical environment felt by the core side chains in the open solvated core conformations. Furthermore, the difference in hydrogen bonding between the native and the open core conformations (nearly a third of the native hydrogen bonds are absent in the open core as illustrated in Fig. 2 b), suggest that infrared spectroscopy and very likely hydrogen exchange experiments would be capable of identifying these species and probing the desolvation barrier. It is interesting to note that NMR studies on drkN-SH3, a homolog of src-SH3 that exists in equilibrium between a folded and unfolded state under nondenaturing conditions, have revealed the presence of a compact, structured unfolded ensemble with a partially solvated hydrophobic core (Mok et al., 1999). We speculate that this solvated core species and in particular the desolvation process of the core may play a role in the functional binding of SH3 to proline-rich ligands. The binding site of SH3 involves residues in both hydrophobic sheets (Feng et al., 1994) and NMR investigations indicate that the binding process involves conformational changes in the core region (Zhang and Forman-Kay, 1997).
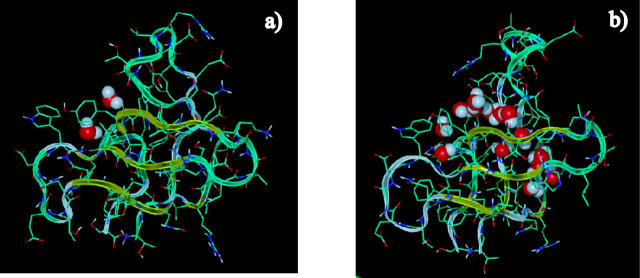
FIGURE 6.
Structures after (a) and before (b) the desolvation barrier. The hydrophobic core is complete after the desolvation barrier, with no waters in the immediate core. Right before the barrier, the two hydrophobic sheets of the protein are fully formed, but are not packed. Water molecules reside in the core.
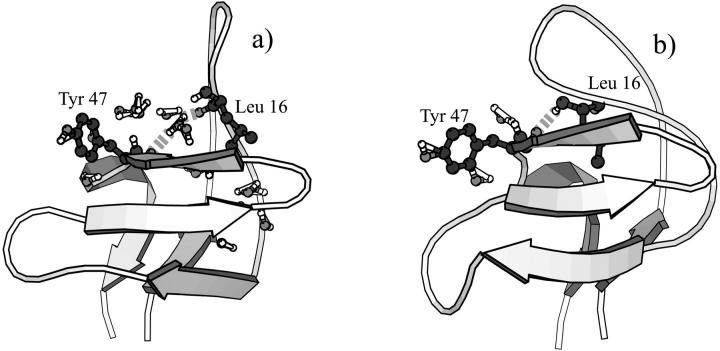
FIGURE 7.
Water molecules before the barrier serve as hydrogen bond bridges between the two core sheets. In Fig. 7 a, a water molecule bridges Leu-16 (RT loop) and Tyr-47 (β4). In Fig. 7 b, postdesolvation, Leu-16 and Tyr-47 form a direct hydrogen bond, closing the hydrophobic core through the RT loop-β4 interaction.
The role of hydrophobic collapse in protein folding has garnered recent theoretical attention (Hummer et al., 2000; Shimizu and Chan, 2002; Sorenson et al., 1999; ten Wolde and Chandler, 2002) and the desolvation barrier observed in our studies may be an important generic feature of all proteins forming a hydrophobic core. Of particular interest are the recent off-lattice simulations by Cheung et al. (2002) in which a Go-model augmented with a desolvation potential was used to characterize the folding of the SH3 domain. Their simplified model reproduces surprisingly well the essential features found in our fully atomic simulations, namely the formation of the transition state before the water expulsion accompanying the formation of the hydrophobic core. It is not clear whether a drying transition, theoretically suggested for protein assemblies (Lum et al., 1999) and computationally observed in nanotubes (Hummer et al., 2001) truly occurs during the packing of the hydrophobic core in protein folding. Despite its name, the hydrophobic core is not comprised uniquely of hydrophobic residues, but rather is interdispersed with polar residues. In addition, the backbone of proteins is polar, allowing for possible hydrogen bonding with water molecules. Finally, the flexibility of the structural elements (sheets) of the protein offer a different environment than the one presented by nanotubes (Hummer et al., 2001) or in the assembly of model rigid hydrophobic cylinders (Lum et al., 1999).
CONCLUSIONS
We presented the first fully atomic simulation of the src-SH3 protein domain with explicit solvent near the folding transition temperature. The free energy landscape for folding was mapped onto a number of representative reaction coordinates using biased sampling methods. Folding is observed to proceed by the formation of the first hydrophobic sheet of the protein (strands β2-β3-β4) followed by the formation of the second sheet, with the packing of the core occurring late in the folding process. The folding of src-SH3 is governed by two barriers, a dominant one early in the folding process (ρ = 0.3) and a minor one at a later stage (ρ = 0.8). The first barrier is an entropic barrier associated with the formation of the transition state for folding (strands β2-β3-β4). Transition state structures identified from this barrier were found to closely resemble experimentally determined transition state structures. The second barrier is a posttransition state desolvation barrier associated with the formation of the hydrophobic core through the expulsion of the water molecules bridging the hydrophobic sheets. This posttransition state barrier, which cannot be observed in traditional folding experiments, is found to play a critical role in the folding of β-barrel proteins.
Acknowledgments
This work was supported by the National Science Foundation Career Award No. 0133504. The authors gratefully acknowledge helpful discussions with Charlie Brooks III, José Onuchic, Tobin Sosnick, Margaret Cheung, and Chinlin Guo.
References
- Borreguero, J. M., N. V. Dokholyan, S. V. Buldyrev, E. I. Shakhnovich, and H. E. Stanley. 2002. Thermodynamics and folding kinetics analysis of the SH3 domain form discrete molecular dynamics. J. Mol. Biol. 318:863–876. [DOI] [PubMed] [Google Scholar]
- Brooks, B. R., R. E. Bruccoleri, B. D. Olafson, D. J. States, D. J. Swaminathan, and M. Karplus. 1982. CHARMM: a program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 4:187–217. [Google Scholar]
- Bryngelson, J. D., J. N. Onuchic, and P. G. Wolynes. 1995. Funnels, pathways and the energy landscape of protein folding: a synthesis. Proteins. 21:167–195. [DOI] [PubMed] [Google Scholar]
- Bryngelson, J. D., and P. G. Wolynes. 1987. Spin glasses and the statistical mechanics of protein folding. Proc. Natl. Acad. Sci. USA. 84:7524–7528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bryngelson, J. D., and P. G. Wolynes. 1990. A simple statistical field theory of heteropolymer collapse with application to protein folding. Biopolymers. 30:177–188. [Google Scholar]
- Caflisch, A., and M. Karplus. 1994. Molecular dynamics simulation of protein denaturation: solvation of the hydrophobic cores and secondary structure of barnase. Proc. Natl. Acad. Sci. USA. 91:1746–1750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan, H. S., and K. A. Dill. 1997. Protein folding kinetics from the perspective of simple models. Proteins. 8:2–33. [Google Scholar]
- Cheung, M. S., A. E. Garcia, and J. N. Onuchic. 2002. Protein folding mediated by solvation: water expulsion and formation of the hydrophobic core occur after the structural collapse. Proc. Natl. Acad. Sci. USA. 99:685–690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crane, J. C., E. K. Koepf, J. W. Kelly, and M. Gruebele. 2000. Mapping the transition state of the WW domain β-sheet. J. Mol. Biol. 298:283–292. [DOI] [PubMed] [Google Scholar]
- Dill, K. A. 1999. Polymer principles and protein folding. Protein Sci. 8:1166–1180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding, F., N. V. Dokholyan, S. V. Buldyrev, H. E. Stanley, and E. I. Shakhnovich. 2002. Direct molecular dynamics observation of protein folding transition state ensemble. Biophys. J. 83:3525–3532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dinner, A. R., and M. Karplus. 1999. Is protein unfolding the reverse of protein folding? A lattice simulation analysis. J. Mol. Biol. 292:403–419. [DOI] [PubMed] [Google Scholar]
- Dobson, C. M., A. Sali, and M. Karplus. 1998. Protein folding: a perspective from theory and experiment. Angew. Chem. Int. Ed. 37:868–893. [DOI] [PubMed] [Google Scholar]
- Du, R., V. S. Pande, A. Y. Grosberg, T. Tanaka, and E. I. Shakhnovich. 1998. On the transition state for protein folding. J. Chem. Phys. 108:334–350. [Google Scholar]
- Dwyer, J. J., A. G. Gittis, D. A. Karp, E. E. Lattman, D. S. Spencer, W. E. Stites, and E. B. Garcia-Moreno. 2000. High apparent dielectric constants in the interior of a protein reflect water penetration. Biophys. J. 79:1610–1620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Englander, S. W. 2000. Protein folding intermediates and pathways studied by hydrogen exchange. Annu. Rev. Biophys. Biochem. 29:213–238. [DOI] [PubMed] [Google Scholar]
- Feng, S. B., J. Chen, H. T. Yu, J. A. Simon, and S. L. Schreiber. 1994. Two binding orientations for peptides to the src Sh3 domain-development of a general model for Sh3-ligand interactions. Science. 266:1241–1247. [DOI] [PubMed] [Google Scholar]
- Fersht, A. R., A. Matouscheck, and L. Serrano. 1992. The folding of an enzyme. I. Theory of protein engineering analysis of stability and pathway of protein folding. J. Mol. Biol. 5:771–782. [DOI] [PubMed] [Google Scholar]
- Garcia, A. E., and G. Hummer. 2000. Water penetration and escape in proteins. Proteins. 38:261–272. [PubMed] [Google Scholar]
- Grantcharova, V. P., and D. Baker. 1997. Folding dynamics of the src SH3 domain. Biochemistry. 36:15685–15692. [DOI] [PubMed] [Google Scholar]
- Gruebele, M. 2002. Protein folding: the free energy surface. Curr. Opin. Struct. Biol. 12:161–168. [DOI] [PubMed] [Google Scholar]
- Gsponer, J., and A. Caflisch. 2002. Molecular dynamics simulations of protein folding from the transition state. Proc. Natl. Acad. Sci. USA. 99:6719–6724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo, Z., and C. L. Brooks III. 1997. Thermodynamics of protein folding: a statistical mechanical study of a small beta protein. Biopolymers. 42:745–757. [DOI] [PubMed] [Google Scholar]
- Guo, Z., and D. Thirumalai. 1995. Kinetics of protein folding: nucleation mechanism, time scales and pathways. Biopolymers. 36:745–757. [Google Scholar]
- Heidary, D. K., and P. A. Jennings. 2002. Three topologically equivalent core residues affect the transition state ensemble in a protein folding reaction. J. Mol. Biol. 316:789–798. [DOI] [PubMed] [Google Scholar]
- Hummer, G., S. Garde, A. E. Garcia, and L. R. Pratt. 2000. New perspectives on hydrophobic effects. Chemical Physics. 258:349–370. [Google Scholar]
- Hummer, G., J. Rasaiah, and J. Noworyta. 2001. Water conduction through the hydrophobic channel of a carbon nanotube. Nature. 414:188–190. [DOI] [PubMed] [Google Scholar]
- Jorgensen, W. L., J. Chandrasekhar, J. Madura, R. W. Impley, and M. L. Klein. 1983. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79:926–935. [Google Scholar]
- Klimov, D., and D. Thirumalai. 2002. Stiffness of the distal loop restricts the structural heterogeneity of the transition state ensemble in SH3 domains. J. Mol. Biol. 315:721–737. [DOI] [PubMed] [Google Scholar]
- Krantz, B. A., and T. R. Sosnick. 2001. Engineered metal binding sites map the heterogeneous folding landscape of a coiled coil. Nat. Struct. Biol. 8:1042–1047. [DOI] [PubMed] [Google Scholar]
- Leopold, P. E., M. Montal, and J. N. Onuchic. 1992. Protein folding funnels: a kinetic approach to the sequence-structure relationship. Proc. Natl. Acad. Sci. USA. 89:8721–8725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, A., and V. Daggett. 1994. Characterization of the transition state of protein unfolding by use of molecular dynamics: chymotrypsin inhibitor 2. Proc. Natl. Acad. Sci. USA. 9:10430–10434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindberg, M., J. Tangrot, and M. Oliveberg. 2002. Complete change of the protein folding transition state upon circular permutation. Nat. Struct. Biol. 9:818–822. [DOI] [PubMed] [Google Scholar]
- Lum, K., D. Chandler, and J. D. Weeks. 1999. Hydrophobicity at small and large length scales. J. Phys. Chem. B. 103:4570. [Google Scholar]
- Martinez, J. C., and L. Serrano. 1999. The folding transition state between SH3 domains is conformationally restricted and evolutionarily conserved. Nat. Struct. Biol. 6:1010–1016. [DOI] [PubMed] [Google Scholar]
- Matthews, B. W., A. G. Morton, F. W. Dahlquist, J. A. Ernst, R. T. Clubb, H.-X. Zhou, A. M. Gronenborn, and G. M. Clore. 1995. Use of NMR to detect water within nonpolar protein cavities. Science. 270:1847–1849. [DOI] [PubMed] [Google Scholar]
- McCallister, E. L., E. Alm, and D. Baker. 2000. Critical role of beta-hairpin formation in protein G folding. Nat. Struct. Biol. 7:669–673. [DOI] [PubMed] [Google Scholar]
- Mok, Y.-K., C. M. Kay, L. E. Kay, and J. D. Forman-Kay. 1999. NOE data demonstrating a compact unfolded state for an SH3 domain under non-denaturing conditions. J. Mol. Biol. 289:619–638. [DOI] [PubMed] [Google Scholar]
- Northey, J. G. B., A. A. Di Nardo, and A. R. Davidson. 2002. Hydrophobic core packing in the SH3 domain folding transition state. J. Mol. Biol. 9:126–130. [DOI] [PubMed] [Google Scholar]
- Nymeyer, H., N. D. Socci, and J. N. Onuchic. 2000. Landscape approaches for determining the ensemble of folding transition states: success and failure hinge on the degree of frustration. Proc. Natl. Acad. Sci. USA. 97:634–639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oliveberg, M. 2001. Characterisation of the transition states for protein folding: towards a new level of mechanistic detail in protein engineering analysis. Curr. Opin. Struct. Biol. 11:94–100. [DOI] [PubMed] [Google Scholar]
- Onuchic, J. N., Z. Luthey-Schulten, and P. G. Wolynes. 1997. Theory of protein folding: the energy landscape perspective. Annu. Rev. Phys. Chem. 48:545–600. [DOI] [PubMed] [Google Scholar]
- Plotkin, S. S., and J. N. Onuchic. 2000. Investigation of the routes and funnels in protein folding by free energy functional methods. Proc. Natl. Acad. Sci. USA. 97:6509–6514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riddle, D. S., V. P. Grantcharova, J. V. Santiago, E. Alm, I. Ruczinski, and D. Baker. 1999. Experiment and theory highlight role of native state topology in SH3 folding. Nat. Struct. Biol. 6:1016–1024. [DOI] [PubMed] [Google Scholar]
- Sali, A., E. I. Shakhnovich, and M. Karplus. 1994. Kinetics of protein folding: a lattice model study of the requirements of folding to the native state. J. Mol. Biol. 235:1614–1636. [DOI] [PubMed] [Google Scholar]
- Shea, J.-E., and C. L. Brooks III. 2001. From folding theories to folding proteins: a review and assessment of simulation studies of protein folding and unfolding. Annu. Rev. Phys. Chem. 52:499–534. [DOI] [PubMed] [Google Scholar]
- Shea, J.-E., Y. D. Nochomovitz, Z. Guo, and C. L. Brooks III. 1998. Exploring the space of protein folding Hamiltonians: the balance of forces in a minimalist beta-barrel model. J. Chem. Phys. 109:2895–2903. [Google Scholar]
- Shea, J.-E., J. N. Onuchic, and C. L. Brooks III. 1999. Exploring the origins of topological frustration: design of a minimally frustrated model of fragment B of protein A. Proc. Natl. Acad. Sci. USA. 96:12512–12517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shea, J.-E., J. N. Onuchic, and C. L. Brooks III. 2000. Energetic frustration and the nature of the transition state in protein folding. J. Chem. Phys. 113:1–9. [Google Scholar]
- Shea, J.-E., J. N. Onuchic, and C. L. Brooks, III. 2002. From the cover: probing the folding free energy landscape of the src-SH3 protein domain. Proc. Natl. Acad. Sci. USA. 99:16064–16068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheinerman, F. B., and C. L. Brooks III. 1998. Calculations on folding of segment B1 of streptococcal protein G. J. Mol. Biol. 278:439–455. [DOI] [PubMed] [Google Scholar]
- Shen, M. Y., and K. F. Freed. 2002. Long time dynamics of met-enkephalin: comparison of explicit and implicit solvent models. Biophys. J. 82:1791–1808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shimizu, S., and H. S. Chan. 2002. Anti-cooperativity and cooperativity in hydrophobic interactions: three-body free energy landscapes and comparison with implicit-solvent potential functions for proteins. Proteins. 48:15–30. [DOI] [PubMed] [Google Scholar]
- Socci, N. D., and J. N. Onuchic. 1995. Kinetic and thermodynamic analysis of proteinlike heteropolymers: Monte Carlo histogram technique. J. Chem. Phys. 103:4732–4744. [Google Scholar]
- Socci, N. D., J. N. Onuchic, and P. G. Wolynes. 1996. Diffusive dynamics of the reaction coordinate for protein folding funnels. J. Chem. Phys. 104:5860–5868. [Google Scholar]
- Sorenson, J., G. Hura, A. Soper, A. Pertsemlidis, and T. Head-Gordon. 1999. Determining the role of hydration forces in protein folding. J. Phys. Chem. 103:5413–5426. [Google Scholar]
- Sosnick, T. R., L. Mayne, and S. W. Englander. 1996. Molecular collapse: the rate limiting step in two-state cytochrome C folding. Proteins. 24:413–426. [DOI] [PubMed] [Google Scholar]
- ten Wolde, P., and D. Chandler. 2002. Drying-induced hydrophobic polymer collapse. Proc. Natl. Acad. Sci. USA. 99:6539–6543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsai, J., M. Levitt, and D. Baker. 1999. Hierarchy of structure loss in MD simulations of src SH3 domain unfolding. J. Mol. Biol. 291:215–225. [DOI] [PubMed] [Google Scholar]
- Vekhter, B., and R. S. Berry. 1999. Simulation of mutation: influence of a “side group” on global minimum structure and dynamics of a protein model. J. Chem. Phys. 111:3753–3760. [Google Scholar]
- Ventura, S., M. C. Vega, E. Lacroix, I. Angrand, L. Spagnolo, and L. Serrano. 2002. Conformational strain in the hydrophobic core and its implications for protein folding and design. Nat. Struct. Biol. 9:485–493. [DOI] [PubMed] [Google Scholar]
- Yu, B., M. Blaber, A. M. Gronenborn, G. M. Clore, and D. L. D. Caspar. 1999. Disordered water within a hydrophobic protein cavity visualized by x-ray crystallography. Proc. Natl. Acad. Sci. USA. 96:103–108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, O., and J. D. Forman-Kay. 1997. NMR studies of unfolded states of an SH3 domain in aqueous solution and denaturing conditions. Biochemistry. 36:3959–3970. [DOI] [PubMed] [Google Scholar]