Entropy Loss in Long-Distance DNA Looping

Abstract

The entropy loss due to the formation of one or multiple loops in circular and linear DNA chains is calculated from a scaling approach in the limit of long chain segments. The analytical results allow us to obtain a fast estimate for the entropy loss for a given configuration. Numerical values obtained for some examples suggest that the entropy loss encountered in loop closure in typical genetic switches may become a relevant factor in comparison to both k_BT and typical bond energies in biopolymers, which has to be overcome by the released bond energy between the looping contact sites.

INTRODUCTION

Gene expression in all organisms comprises the transcription of a certain gene on the DNA into messenger RNA through RNA polymerase starting from the promoter site, and its subsequent translation into a protein. The initiation of the transcription at a specific gene underlies a subtle cooperative scheme of transcription factors, which in turn is determined by a given set of boundary conditions such as the concentration of the transcription factors. Transcription factors often act cooperatively, and they are known to interact with each other over distances of several thousand basepairs (bp). This interaction is effected through DNA looping (Alberts et al., 1994; Blackwood and Kadonaga, 1998; Bolsover et al., 2001; Ptashne and Gunn, 2002; Révet et al., 1999; Snustad and Simmons, 2003), compare Fig. 1.

FIGURE 1.

DNA looping in a circular (left) and linear DNA (right). The rounded boxes indicate the chemical bonds established between the transcription factors through looping at specific contact sites on the DNA double-helix, which are fairly distant from one another in terms of the arc length along the DNA. A telomere loop corresponds to the right configuration with vanishing ℓ₁ [or ℓ₂].

A typical example for DNA looping is found in the genetic switch which determines whether the replication of bacteriophage λ in Escherichia coli follows either the lysogenic or the lytic pathway (Ptashne, 1992; Ptashne and Gunn, 2002; Snustad and Simmons, 2003). A key component of this λ-switch is the λ-repressor which activates the expression of a gene that encodes the production of the λ-repressor itself. λ-repressor can bind to the three operator sites O_R which overlap the two promoter sites of the switch. λ-repressor binds cooperatively as a dimer, and typically under stable lysogenic conditions two such dimers on O_R form a tetramer, the next higher order of cooperativity, which is the main factor for the stability of the λ-switch against noise (Aurell and Sneppen, 2002; Aurell et al., 2002; Metzler, 2001). However, λ-repressor can also bind to the very similar operator O_L, which is located roughly 2300 bp away and not part of the λ-switch. It has been found that the two λ-repressor tetramers at O_L and O_R synergistically form an octamer through DNA looping. This higher-ordered oligomerization enhances the performance of the switch considerably (Amouyal et al., 1998; Bell and Lewis, 2001; Bell et al., 2000; Blackwood and Kadonaga, 1998; Ptashne and Gunn, 2002; Révet et al., 1999; Semsey et al., 2002; Xu and Hoover, 2001). The specific binding along the tetramer-tetramer interface has recently been revealed through crystallographic structure determination (Bell and Lewis, 2001; Bell et al., 2000). Similar realizations of DNA looping also occur in linear DNA, naturally in the form of telomeres or in vitro in engineered DNA (De Bruin et al., 2001; Griffith et al., 1999; Zaman et al., 2002, compare Fig. 1). Multiple looping in large DNA molecules around a locus can be observed in vivo and can be induced in vitro by introducing of specific binding zones on the DNA, which leads to a considerable reduction of the gyration radius of the molecule such that it can be more easily transferred into, for example, mammalian cells (Montigny et al., 2001).

DNA looping often involves large loop sizes of several thousand bp. Therefore, the formation of these loops causes a non-negligible entropy loss which has to be overcome by the binding energy released at the bond formation on loop closure. In the present study, we quantify this entropy loss for such long DNA loops, taking into account self-avoiding effects due to both the monomer-monomer interaction within the loop and the additional effects due to the higher order contact points (vertices) at the loop closure site. The resulting numbers for typical systems suggest that the entropy loss is a relevant factor in the formation of DNA loops in comparison to the thermal energy and typical bond energies found in DNA nucleotides and other biopolymers, and it gives a lower bound for the bond-forming energy required to stabilize the loop.

Entropy loss due to loop formation was studied for the case of disconnected loops by Schellmann (1955), Flory (1956), and Semlyen (1997). In their seminal article, Poland and Scheraga (1965), and Wang and Uhlenbeck (1955), considered coupled Gaussian loops. To our knowledge the full effect of self-avoidance in the DNA looping network has not been considered before. Hereby, the contributions of nontrivial vertices turns out to be a relevant factor, and for multiple looping with a common locus actually become the dominating contribution. The analytical results presented here are derived from a scaling approach for general polymer networks and provide the advantage that, on their basis, estimates for the entropy loss in a given DNA system can be computed in a straightforward manner. It should also be noted that the additional vertex effects studied herein may be crucial in the analytical treatment of the DNA looping dynamics, as the higher-order self-interaction at such vertices poses an additional barrier in the loop closure process (Lee et al., 1976; Merlitz et al., 1998). Our results for long DNA with large loops complement the investigations of the bending and twisting energies in small DNA plasmids (Coleman et al., 2000; Tobias et al., 2000). In the case of intermediate-sized DNA segments, both approaches may be combined.

In what follows, we calculate the scaling results for the entropy loss on looping for the three different cases: 1), looping in a circular DNA; 2), looping in a linear DNA; and 3), multiple looping in a circular DNA. In the Appendix, the general expressions for calculating the system entropy of an arbitrary polymer network are compiled so that the entropy loss for different configurations can be calculated according to the general procedure developed below.

LOOPING IN A CIRCULAR DNA CHAIN

As stated before, we consider the limit in which each segment of the looped DNA, e.g., both subloops created in the circular DNA upon looping, are long in comparison to the persistence length ℓ_p of the double-stranded DNA chain. (It can be assumed that this criterion is fulfilled if the segment contains more than ten persistence lengths.) In this long chain limit, we can neglect energetic effects due to bending or twisting, such that we treat the DNA as a flexible self-avoiding polymer. Therefore, we can employ results for the configuration number of a general polymer network, which we briefly review in the Appendix.

Before looping, the free energy of the circular DNA of total length L is given by

(1)

where H₀ combines all binding enthalpies in the macromolecule and the entropy S_circ = k_B ln ω_circ is determined by the number of configurations (see De Gennes, 1979; see also the Appendix, this article)

(2)

of a simply connected ring polymer of length L in units of the monomer length. The latter can be estimated by the persistence length ℓ_p of the polymer (∼500 Å for double-stranded DNA corresponding to 100 bp; see Marko and Siggia, 1996). In Eq. 2, A_circ is a nonuniversal amplitude, μ is the support dependent connectivity constant, and (Guida and Zinn-Justin, 1998) is the Flory exponent. Thus, S_circ has the form

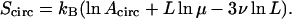(3)

On looping, as sketched in Fig. 1 to the left, the circular DNA is divided into two subloops of lengths ℓ and L − ℓ by creation of a vertex at which four legs of the chain are bound together. For a self-avoiding chain, the number of configurations of the resulting figure-eight shape (Metzler et al., 2002a,b) is not simply the product of the configuration numbers of the two created loops, but has the more complicated form (Duplantier, 1986, 1989; Ohno and Binder, 1988; Schäfer et al., 1992; see also the Appendix, this article),

(4)

In this expression, A₈ is a nonuniversal amplitude, 𝒴₈ is a universal scaling function, and 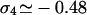is a universal exponent associated with the vertex with four outgoing legs. Note that in the Gaussian chain limit, the exponents σ_N vanish; as we are going to show, the inclusion of the additional effects due to the higher order vertex formation reflected by nonzero values for σ_N are non-negligible. Given the entropy S₈ = k_B ln ω₈ of the figure-eight configuration, the entropy loss suffered from creating this configuration out of the original circular DNA amounts to |S₈ − S_circ|. To proceed, we now evaluate the scaling function 𝒴₈(x) in some special cases, and calculate typical numbers for the required entropy loss compensation. Two limiting cases can be distinguished.

Limiting case 1

If one of the loop sizes is much smaller than the other (ℓ ≪ L − ℓ, say), the big loop of size L − ℓ will essentially behave like a free circular chain so that its contribution to ω₈ will scale like a regular ring polymer, i.e., like (L − ℓ)^−3ν. Consequently, we find the behavior 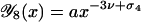for x ≪ 1, where a is a universal amplitude, and therefore (Hanke and Metzler, 2002; Metzler et al., 2002a,b),

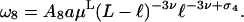(5)

In this case, the free energy difference between the initial circular and the looped states becomes

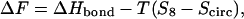(6)

where ΔH_bond is the binding enthalpy at the loop closure site. The formation of the looping bond has to release a higher enthalpy than what is lost in entropy, i.e., ΔH_bond < T(S₈ − S_circ). Collecting the different expressions, we thus find the condition

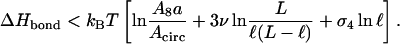(7)

In this expression (and in similar expressions below), the first term in the square brackets is nonuniversal and depends on details of the model (for a Gaussian random walk on a cubic lattice, 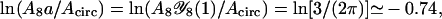is small compared with the other contributions in Eqs. 7 and 9; for the cases discussed below, we give the corresponding numbers in Table 1), whereas the remaining contributions are universal (apart from the fact that L is measured in units of the nonuniversal monomer length).

TABLE 1.

Equation		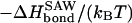	|ΔHNU|/(kBT)
7, 8	7.0	4.7	0.74
9, 10	5.8	3.7	0.74
15, 16	7.0	4.7	0.74
18, 19	8.6	5.7	0.3
22, 23	6.3	4.7	0.74
25, 26	15.8	11.6	0.74
28, 29	67.4	38.8	2.2

Comparison of the calculated minimum bond energies in the fully self-avoiding (SAW) and in the Gaussian (ν = 1/2, γ = 1, and σ_N = 0) cases: the increase due to self-avoiding effects is distinct. We also compare to the (negligible) nonuniversal (NU) contributions (first term in square brackets in the cited equations for ΔH_bond), which are calculated for a Gaussian random walk on a cubic lattice.

To get an estimate for the magnitude of the entropy loss, consider the case of the λ-repressor loop in E. coli. With the size of the entire DNA of ∼3.5 × 10³ kbp and the looping branch of ∼2.3 kbp, the two loops correspond to 3.5 × 10⁴ and 23 monomers, respectively (each monomer corresponds to a persistence length ℓ_p of 100 bp; see above). Neglecting the nonuniversal first term in brackets in Eq. 7, these numbers produce

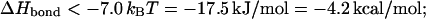(8)

here and in the following examples, we choose T = 300 K and make use of the gas constant, R = 8.31 JK⁻¹ mol⁻¹, and the conversion factor 1 cal = 4.2 J (Abramowitz and Stegun, 1972). Eq. 8 gives a considerable minimal value for the required bond energy between the two looping sites. For comparison, the typical free energy for basepair formation in DNA is 8 kcal/mol for AT pairs and 13 kcal/mol for GC pairs (Breslauer et al., 1986). Thus, even for the relatively small loop of 23 monomers, the required enthalpy release is non-negligible. Note that the relative contribution stemming from the σ₄ term in Eq. 7 amounts to ∼20% of the required enthalpy. In the Conclusion section, we compare the results obtained in the text with the corresponding ones in the Gaussian chain limit, demonstrating the significant increase of |ΔH_bond| if self-avoidance is taken into consideration (see Table 1).

Limiting case 2

If the two created loops are of comparable size, i.e., x = ℓ / (L − ℓ) ≈ 1, the corresponding value of the scaling function 𝒴₈(x) is a finite number. For example, for ℓ = L/2 one finds

(9)

In a modified DNA with two loops of 2.3 kbp each, one finds a bond enthalpy requirement of

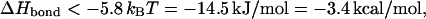(10)

where we again neglect the nonuniversal first term in the square brackets. If both loops are of size 2 × 10³ kbp each, the required bond enthalpy would increase to ΔH_bond < −12.5 kcal/mol.

LOOPING IN A LINEAR DNA CHAIN

A linear chain of length L can assume

(11)

distinct configurations, where A_lin is a nonuniversal amplitude and 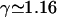is a universal exponent (Caracciolo et al., 1998; Guida and Zinn-Justin, 1998). If looping occurs and produces the A-shape in Fig. 1 to the right, the configuration number is modified to

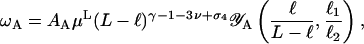(12)

where ℓ is the size of the loop, and ℓ₁ and ℓ₂ are the sizes of the two loose end-segments, respectively.

We distinguish four different cases belonging to two groups: the configuration with ℓ₁ ≈ ℓ₂, and the telomere configuration for which ℓ₁ = 0 (or ℓ₂ = 0).

Case 1

If ℓ₁ = ℓ₂, we find

(13)

where 𝒲_A(x) = 𝒴_A(x,1). If furthermore ℓ ≪ L − ℓ, an analogous reasoning as in the limiting case 1 of the previous section, leads to

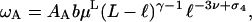(14)

where b is a universal number. The fact that ℓ carries the same exponent as in Eq. 5 is due to the local effect of self-interaction for the small loop; in both cases, the small loop is connected to a 4-vertex.

For the binding enthalpy, we obtain the condition

(15)

To obtain a numerical value, consider the λ-repressor loop of 23 monomers and the E. coli DNA length of 3.5 × 10⁴ monomers, a configuration which can be obtained by cutting the E. coli DNA. Neglecting the (nonuniversal) first term in the square brackets, we find in this case

(16)

where the exact numerical value is slightly smaller than in Eq. 8.

Case 2

Conversely, if ℓ = ℓ₁ = ℓ₂, the simpler expression

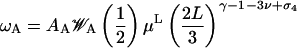(17)

emanates, and the binding enthalpy has to fulfill

(18)

Taking 23 monomers for each segment and neglecting the (nonuniversal) first term in the square brackets yields the condition

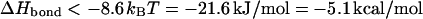(19)

for the binding energy. If the segments are larger by a factor of 100, this value gets modified to ΔH_bond < −11.3 kcal/mol.

Cases 3 and 4

The next two cases belong to the telomere configuration corresponding to Fig. 1 (right) with ℓ₁ = 0 and ℓ₂ = L − ℓ.

Case 3

This case involves a 3-vertex instead of a 4-vertex, and has only one loose end-segment. The number of configurations the telomere configuration can assume is

(20)

where and 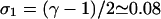(see the Appendix). We note that in Eq. 20, the explicit occurrence of σ₁ is due to the existence of only one loose end. In the two cases (case 1 and case 2, this section) considered above, we encounter two loose ends, and the σ₁ can be incorporated into γ = 1 + 2σ₁.

Let us first calculate the entropy loss in the small loop limit ℓ ≪ L − ℓ. Here, the linear chain part should essentially behave like a simple linear chain, which implies that 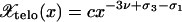for x ≪ 1, and thus

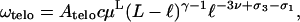(21)

where c is a universal number.

The corresponding condition for the bond enthalpy reads

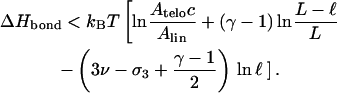(22)

Taking a loop of 2.3 kbp in a chain of length 3500 kbp and neglecting the (nonuniversal) first term in the square brackets gives

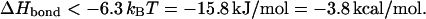(23)

For comparison, if the loop size is 230 kbp, this value is increased to ΔH_bond < −9.3 kcal/mol.

Case 4

If the loop size and the linear chain segment are of equal size, ℓ = L/2, the configuration number becomes

(24)

and we obtain the condition

(25)

Taking a chain length of 460 kbp and neglecting the (nonuniversal) first term in the square brackets we find

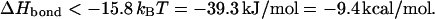(26)

MULTIPLE LOOPING IN A CIRCULAR DNA CHAIN

Assume that m potential connector points are distributed evenly along a circular DNA chain of total length L. If these condense to form a common locus, a number m of loops of equal size are created which are held together at this locus, as sketched in Fig. 2 (Montigny et al., 2001). This creates, in the scaling limit, a high-order vertex where 2m legs are joined. The procedure for the configuration number for this locus configuration yields

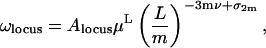(27)

where the universal exponent σ_2m is associated with a vertex with 2m outgoing legs (see the Appendix). It should be noted that this result holds true only if the size of the locus is much smaller than the sizes of the created loops (Metzler et al., 2002a,b).

FIGURE 2.

DNA loop condensation. The circles in the original DNA double-helix denote likely contact points. Formation of bonds between these contacts with one common agglomeration center, as indicated by the dashed lines, result in the locus configuration on the right. Note the reduction in the gyration radius during this process. A higher-order vertex is created at the locus point (Montigny et al., 2001).

Due to the assumption that all m loops are of the same size, we immediately arrive at

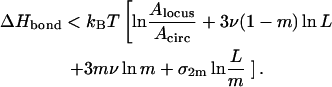(28)

The absolute value of σ_2m increases rapidly with increasing m, and can be determined from Padé or Padé-Borel analysis as shown in Schäfer et al. (1992). We list the topological exponents up to order 8 in the Appendix. Taking a circular chain of 3500 kbp and m = 4, and neglecting the (nonuniversal) first term in the square brackets, we find that the entropy loss is fairly high (using σ₈ = −2.4),

(29)

In this case, the contribution due to the σ₈ term is as large as 50% of the total entropy loss.

CONCLUSIONS

We have presented an analytical method to estimate the entropy loss in different scenarios of DNA looping in the limit of long segments. This approach takes explicitly the self-avoidance and interacting nature of the formed loops and other segments into account, and considers the additional effect of vertex formation, i.e., the effective interaction between different segments at the point where they are joined. This is possible via the scaling theory for arbitrary polymer networks derived by Duplantier. The obtained numbers do not vary much, due to the logarithmic dependence on the segment sizes. However, they are all non-negligible, and therefore have to be compensated by the released bond energy on formation of the DNA loop. We noted that the entropy loss is of the same order or close to the bond melting energy required for splitting an AT or GC bond, i.e., a considerable amount. Moreover, it is to be expected that the vertex effect increases the characteristic bond formation times in analytical approaches which are based on the free energy.

In Table 1 we summarize the obtained estimates for the minimum bond energy ΔH_bond in the present self-avoiding model, and compare them with the corresponding results in the Gaussian limit. The differences are significant, clearly showing the much higher entropy loss in the self-avoiding case. In Table 1 we also show estimates for the corresponding nonuniversal contributions, which we neglected in the explicit calculation of ΔH_bond.

Our calculations are valid in the long chain limit. In units of the monomer size of a typical DNA double-helix persistence length ℓ_p ∼ 100 bp, a minimum number of at least 10 monomers is expected to be required to consider a segment in the final structure flexible. For shorter segments, additional effects due to bending and twisting energy are expected to become relevant. As the mentioned examples document, there are numerous systems, both in vivo and in vitro, in which the flexibility condition is easily fulfilled, and in which our estimation method for the entropy loss becomes fully applicable. The persistence length of single-stranded DNA and RNA is much shorter, typically taken to be of the order ℓ_p ∼ 8 bases. Thus, in single strand looping experiments the expected entropy loss will be considerably larger.

APPENDIX A: CONFIGURATION EXPONENTS FOR A GENERAL POLYMER NETWORK

A general polymer network 𝒢 like the one depicted in Fig. 3 consists of vertices which are joined by 𝒩 chain segments of lengths s₁,…,s_𝒩. Their total length is 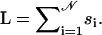In the scaling limit s_i ≫ 1, the number of configurations of such a network is given by Duplantier (1986, 1989), Ohno and Binder (1988), and Schäfer et al. (1992) as

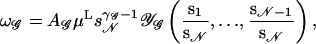(A1)

where A_𝒢 is a nonuniversal amplitude, μ is the effective connectivity constant for self-avoiding walks, and 𝒴_𝒢 is a scaling function. The topology of the network is reflected in the configuration exponent

(A2)

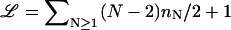is the Euler number of independent loops, n_N is the number of N-vertices, and σ_N is an exponent connected to an N-vertex. Thus, Eq. A1 generalizes the familiar form ω ∼ μ^LL^γ−1 of a linear polymer chain. The numerical values we use in the text are given in Table 2 for the topological exponents σ_N; furthermore, we employ ν = 0.588 and 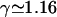(Caracciolo et al., 1998; Guida and Zinn-Justin, 1998). We also make use of the relation γ = 2σ₁ + 1.

FIGURE 3.

Polymer network 𝒢 with vertices (•) of different order (n₁ = 5, n₃ = 4, n₄ = 3, and n₅ = 1).

TABLE 2.

N	σN Padé	σN Padé-Borel	σN Padé-Borel
3	−0.19	−0.19	−0.17
4	−0.48	−0.49	−0.47
5	−0.86	−0.87	−0.84
6	−1.33	−1.29
7	−1.88	−1.75
8	−2.51	−2.23
9	−3.21	−2.71

Topological exponents σ_N for network vertices of order N in three dimensions from various approximate techniques. The columns correspond to the first three columns in Table 1 in Schäfer et al. (1992), where the scaling relation γ_F − 1 = σ_N + Nσ₁, with γ_F from Schäfer et al. (1992) and σ₁ = (γ − 1)/2 with the best available value γ = 1.1575 (Caracciolo et al., 1998) have been used. Note the large discrepancy between the different methods for increasing N.

Note that in this work we consider the entropy of a given polymer network, in which enters the total number of physically distinct configurations. Two configurations are considered distinct if they cannot be superimposed by translation. In particular, the monomers of the chain are distinguishable. For a simple ring of length L this implies that two configurations are distinct even if they have the same trajectory, but differ from each other by a reptation (translation of the chain within the trajectory) by a noninteger multiple of L. The number of configurations of the simple ring is therefore (Duplantier, 1986, 1989),

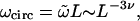(A3)

where 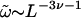is the number of configurations of a ring polymer with indistinguishable monomers. Likewise, ω_circ corresponds to the number of closed random walks of length L which start and end at a given point in space (compare also to Metzler et al., 2002a,b).

The number of configurations of a looped structure (with at least one vertex) is also given by Eq. A1. This is due to the fact that the established looping bond is chemically fixed within the chain, so that the chain cannot reptate within a given trajectory. For the same reason (and in contrast to references Hanke and Metzler, 2002; Metzler et al., 2002a,b), different loops cannot exchange length with each other.