Two Adaptation Processes in Auditory Hair Cells Together Can Provide an Active Amplifier

Abstract

The hair cells of the vertebrate inner ear convert mechanical stimuli to electrical signals. Two adaptation mechanisms are known to modify the ionic current flowing through the transduction channels of the hair bundles: a rapid process involves Ca²⁺ ions binding to the channels; and a slower adaptation is associated with the movement of myosin motors. We present a mathematical model of the hair cell which demonstrates that the combination of these two mechanisms can produce “self-tuned critical oscillations”, i.e., maintain the hair bundle at the threshold of an oscillatory instability. The characteristic frequency depends on the geometry of the bundle and on the Ca²⁺ dynamics, but is independent of channel kinetics. Poised on the verge of vibrating, the hair bundle acts as an active amplifier. However, if the hair cell is sufficiently perturbed, other dynamical regimes can occur. These include slow relaxation oscillations which resemble the hair bundle motion observed in some experimental preparations.

INTRODUCTION

Hair cells of the inner ear detect mechanical stimuli by deflections of the hair bundle, which open tension-gated transduction channels in the cell membrane to admit cations from the endolymph. The current is mostly composed of potassium ions, but also includes a small quantity of calcium ions (Lumpkin et al., 1997). Experiments in which hair bundles are held at a fixed deflection, using a microneedle, have revealed two adaptation processes that modify the transduction current, causing it to decline with time (Howard and Hudspeth, 1987, 1988; Wu et al., 1999; Holt and Corey, 2000; Holt et al., 2002). The first, which can occur on a sub-millisecond timescale, is dependent on the concentration of Ca²⁺ in the endolymph. It is believed to be a consequence of Ca²⁺ entering the hair bundle and binding to the transduction channels, making them more likely to close. The second, which takes up to hundreds of milliseconds, is also dependent on Ca²⁺ concentration, and is thought to be caused by the movement of adaptation motors attached to the transduction channels, which adjusts the tension that gates them.

A number of experiments have demonstrated that hair bundles can generate active oscillations, both in preparations of dissected tissue (Benser et al., 1993; Crawford and Fettiplace, 1985; Martin et al., 2000) and in vivo (Manley et al., 2001). It has been shown on theoretical grounds that the active oscillatory mechanism can provide an explanation for the high sensitivity and sharp frequency selectivity of auditory receptors (Choe et al., 1998; Camalet et al., 2000; Eguiluz et al., 2000; Ospeck et al., 2001) if the system is poised on the verge of spontaneous oscillation. This critical point corresponds to a Hopf bifurcation of the active dynamical system. It has been suggested that a feedback mechanism operates to maintain the system at the critical point where it is most sensitive, leading to the concept of self-tuned critical oscillations. (Camalet et al., 2000).

The purpose of this article is to provide a coherent model for the active amplifier in hair cells, based on the combined action of the two known adaptation mechanisms. In our model the interaction of Ca²⁺ ions with the transduction channels generates an oscillatory instability of the hair bundle. Working on a slower timescale, the adaptation motors act to tune this dynamical system to the critical point, at which it just begins to oscillate. The two adaptation mechanisms together constitute a dynamical system displaying a self-tuned Hopf bifurcation (Camalet et al., 2000). Poised at the oscillatory instability, the hair bundle is especially responsive to faint sounds.

Our model differs from two published models of hair-bundle oscillations. Choe, Magnasco, and Hudspeth (1998) have previously proposed that channel reclosure induced by Ca²⁺ ions can generate a Hopf instability. In their scheme the oscillation frequency is controlled by the kinetics of the transduction channel. In our model the frequency of spontaneous oscillations is governed, instead, by the architecture of the bundle and by the rate at which the calcium concentration equilibrates. This is more consistent with the finding that the rate at which the transduction channel switches is faster than the characteristic frequency, especially in low-frequency hair cells (Corey and Hudspeth, 1983). Camalet et al. (2000) have suggested that the Hopf instability is generated by motor proteins in the kinocilium, and that regulation to the critical point is accomplished by a feedback mechanism involving calcium. Their model is thus the converse of that presented here, but shares the underlying feature of self-tuned criticality. The current model accords better with the observation that some hair bundles lack a kinocilium and others do not change their behavior significantly when the kinocilium is interfered with (Martin et al., 2003).

In addition to demonstrating that the two adaptation processes can combine to provide an active amplifier, we derive expressions that indicate how properties like the characteristic frequency of critical oscillations, and the sensitivity of response to sound waves, depend on parameters like the bundle height and the number of stereocilia. We also investigate how the dynamics can be modified if conditions are perturbed, and show that the bundle can exhibit slow relaxation oscillations which differ in many aspects from critical oscillations, but resemble the active movements recently observed in experiments on hair cells from the frog sacculus (Martin and Hudspeth, 1999).

MODEL

Hair bundle

Hair bundles in different species, or from hair cells with different characteristic frequencies within the same organ of the internal ear of a particular animal, can vary in shape and size, and also in the way that they are coupled to external mechanical vibrations (Hudspeth, 1997). Generally, one can distinguish between free-standing hair bundles (e.g. some reptiles, mammalian inner hair cells) and those whose tips are embedded in an accessory structure (e.g. other reptiles, birds, amphibial saccular hair cells). In experiments on dissected tissue, the accessory structure is usually removed. In this article we will restrict our discussion to the simplest situation of a free-standing hair bundle. A bundle that is directly connected to the tectorial membrane could be described in a similar fashion, but using modified expressions for the stiffness, the friction and the coupling to the external signal.

The hair bundle (see Fig. 1 A) is composed of N stereocilia which slope up against each other, the longest of which has length L. Typically, N and L are inversely related, with the range N = 20–300 (Holt and Corey, 2000) corresponding to L = 30–2 μm. Each stereocilium is joined to the next by an elastic filament – the tip link – which connects to a tension-gated transduction channel in the cell membrane (Corey and Hudspeth, 1983; for a review see Markin and Hudspeth, 1995). The tension in the tip link can be adjusted by a group of myosin motors, which are connected to the transduction channel and move it along the actin filaments inside the stereocilium (Hudspeth and Gillespie, 1994).

FIGURE 1.

(A) Schematic representation of a hair bundle. (B) Three-state model of the transduction channel. Note that Ca²⁺ binds to the channel when it is already in a closed state. The presence of Ca²⁺ therefore does not directly cause channel reclosure, but it does stabilize the closed state and delay reopening.

To set up a coordinate system, we consider first a free-standing bundle. Within a stereocilium, we label the location at which the stereocilium touches its shorter neighbor O. The position of the channel (and the attached motors) relative to O is denoted by l₀ + x_M, where l₀ is the length of a tip link at rest and x_M its extension under tension. When the tip of the bundle is deflected through a lateral displacement X, each stereocilium pivots at its base and adjacent stereocilia are sheared by a displacement γX. The geometric factor γ may be written as γ ≈ b/L, where b ≈ 1 μm is the distance between the roots of neighboring stereocilia (Howard et al., 1988; Howard and Hudspeth, 1988). We label the new location at which the stereocilium touches its shorter neighbor O′. The position of the channel relative to O′ is denoted by l₀ + x. It follows that

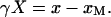(1)

The movement of the bundle is countered by an elastic restoring force, which has two contributions. First, the deformation of the stereocilia at their base provides an effective bundle stiffness K_SP = κN/L², where κ is the pivotal stiffness of a stereocilium. The measured value κ ≈ 1.5 × 10⁻¹⁶ Nm/rad (Crawford and Fettiplace, 1985; Hudspeth et al., 2000) indicates that K_SP varies from 0.01 pN/nm for tall bundles to 10 pN/nm for short ones. The second contribution, which scales in the same way with bundle size and is of similar magnitude, comes from the tension T_TL in the tip links. Movement of the bundle is also resisted by the viscous drag of the surrounding fluid which leads to a friction coefficient ζ ∼ ηL for tall bundles, where η is the viscosity of the endolymph. Thus, when an external force F is applied to the tip of the bundle, its equation of motion is

(2)

(throughout the article we use the convention ). Here, we have written T_TL = T_TL(x, C), anticipating that the tension in the tip links depends on the local intracellular Ca²⁺ concentration C, as well as varying with the position x. For future reference, we note that the mechanical relaxation time of the hair bundle, τ_mech = ζ/K_SP, varies from a few microseconds to tens of milliseconds.

Transduction channel

The mechanically gated transduction channel is the central component of the model, since we postulate that hair bundle oscillations are driven by the force that is generated as the channels change conformation stochastically, as first suggested by (Hudspeth and Howard, 1988). It is generally assumed that transmembrane channel proteins can exist in a number of discrete states, some of which are closed and some open. As indicated in Fig. 1 B, we additionally suppose that the channel protein incorporates a lever arm which amplifies the small structural changes that occur when the channel switches state, and thereby appreciably modifies the tension in the adjoining tip link (Martin et al., 2000). If p_i is the probability that the channel is in state i, and d_i is the position of the lever arm in that state, then the average tension may be written Here, K_TL is the elastic constant of the tip link (or possibly that of a more compliant element in series with it (Kachar et al., 2000)), whose value obtained from micromechanical measurements is K_TL ≈ 0.5 pN/nm (Martin et al., 2000). In the steady state the probabilities 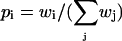are given by the Boltzmann factors 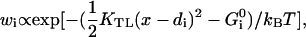where is the free energy of state i. Measurements of the transduction current as a function of bundle displacements in the frog's sacculus are well fitted with a three-state model of the channel (Corey and Hudspeth, 1983), with two closed states (i = C1, C2) and one open state (i = O). The fit indicates that the lever-arm movement is ∼5 times greater for the transition C1 → C2 than for the transition C2 → O, whereas more recent data (Martin et al., 2000) suggests that the total movement is ∼8 nm. We therefore assign the lever arm displacements d_C1 = 0 nm, d_C2 = 7 nm and d_O = 8.5 nm. The free energies 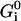depend on the local Ca²⁺ concentration C within the stereocilia (Howard and Hudspeth, 1988), which is strongly influenced by the entry of Ca²⁺ ions through the channel (Lumpkin and Hudspeth, 1995). A higher Ca²⁺ concentration favors closure of the channel, thereby providing a negative feedback. We model this dependence empirically, according to experimental observations (Corey and Hudspeth, 1983), as an effective shift in the channel gating point proportional to the logarithm of the Ca²⁺ concentration

(3)

where the constant D has an empirical value of ∼4 nm in the bullfrog's sacculus (Corey and Hudspeth, 1983) and C₀ is the Ca²⁺ concentration in the free-standing bundle. One possible interpretation of this functional form, indicated in Fig. 1 B, is that Ca²⁺ binds to state C2, causing it to switch to state C1 and thereby stabilizing the closed state. We emphasize that our model does not rely on the channel having three states. A two-state channel (eliminating state C2) would give substantially similar results.

An important aspect of our model is that we assume that the channel kinetics are rapid compared to the bundle oscillations and the calcium dynamics. The evidence for this assumption comes, for instance, from saccular hair cells that detect frequencies up to 150 Hz and have channel opening times around 100 μs (Corey and Hudspeth, 1983). We can therefore consider the different channel states to be thermally equilibrated with one another, and chemically equilibrated with the Ca²⁺ ions. Then we can split the tip link tension T_TL into two components: K_TLx, the passive elastic force that the tip link would contribute in the absence of the transduction channel; and f, the active contribution arising from the channel switching states, also called gating force:

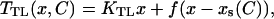(4)

where 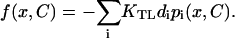A relationship between the gating force and the channel opening probability, which holds in any model with a single open state, reads (van Netten and Kros, 2000).

Calcium dynamics

The dynamics of the calcium concentration in a stereocilium is influenced by a number of processes. As well as the influx of Ca²⁺ through the transduction channel, there is an outflux due to calcium pumps. The ions also diffuse freely, or in association with mobile buffers, and can additionally bind to fixed buffers. A detailed model of this dynamics was developed by (Lumpkin and Hudspeth, 1998), but for our purposes it suffices to use a simplified linearized model in which the Ca²⁺ concentration on the inner side of the channel obeys the equation

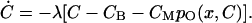(5)

Here C_B is the steady-state concentration which would occur if the channel were blocked, originating from diffusion from other parts of the cell; C_M is the maximal additional contribution from influx through an open transduction channel, and is of order 10 μM. The relaxation rate of calcium concentration fluctuations, λ, is an important parameter in our model. We expect the relaxation time τ_chem = 1/λ to be of the order of milliseconds, corresponding to the measured fast adaptation time (Ricci and Fettiplace, 1997). Note that the slow Ca²⁺ kinetics (along with fast channel switching) is a key difference between our model and that of Choe et al. (1998), where the converse situation is assumed. The slow Ca²⁺ dynamics might seem at odds with the fact that the binding sites on the channel are reached by the incoming ions very quickly. But in our model, the channel is in state C2 when Ca²⁺ binds, i.e., it is closed (Fig. 1 B). It therefore typically senses a concentration which is determined by diffusion within a larger volume, and which also depends on the interaction of Ca²⁺ with fixed and mobile buffers. Because a Ca²⁺ ion binds to one of the buffers in <1 μs (Lumpkin and Hudspeth, 1998), the concentration of free Ca²⁺ equilibrates with that bound to the buffers within a few microseconds of channel closure O → C2. The timescale of Ca²⁺ relaxation is therefore determined by buffering, diffusion to distant parts of the stereocilium and the activity of Ca²⁺ pumps. Indeed, the influence of buffers on the fast adaptation process has been observed experimentally (Ricci and Fettiplace, 1997).

Adaptation motors

Experiments in which a vertebrate hair bundle is suddenly displaced (Howard and Hudspeth, 1987; Wu et al., 1999) show a slow adaptation of the channel current, on the scale of tens of milliseconds. The transduction channel is attached to the actin cortex within a stereocilium by a number of myosin 1C (formerly Iβ) motors. There is strong evidence that these molecular motors mediate slow adapatation (Assad and Corey, 1992; Gillespie and Corey, 1997; Holt et al., 2002), presumably by maintaining the proper tension in the tip link (Hudspeth and Gillespie, 1994). For simplicity, we assume that the motors have a linear force-velocity relation, so that

(6)

where n_M is the number of motors bound to the actin, F_M is the stall force of an individual motor and v_M is its zero-load velocity. We take values typical for a motor protein, F_M ≈ 1 pN and v_M ≈ 0.3 μm/s and suppose that there are N_M ≈ 20 motors per channel (experimental data suggest N_M ≤130 (Gillespie and Hudspeth, 1993)).

Calcium has been shown to influence the action of the adaptation motor (Hacohen et al., 1989; Ricci et al., 1998), possibly by increasing its rate of detachment from actin. The number of bound motors is therefore not constant, but obeys the dynamical equation

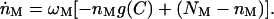(7)

where ω_M ≈ 200 s⁻¹ is the myosin binding rate and g(C) is a function describing the dependence of the detachment rate on the Ca²⁺ concentration.

RESULTS AND DISCUSSION

Linear stability analysis

To examine the dynamical stability of the hair bundle in the absence of a driving force, F = 0, we make use of the fact that the adaptation motors operate on a slower timescale than both the mechanical relaxation of the bundle and the relaxation of the calcium concentration. We can therefore neglect their motion for now, and suppose that x_M is fixed. This leaves two coupled first-order differential equations of motion: Eq. 5 (supplemented with Eq. 3) for the rate of change of Ca²⁺ concentration; and by combining Eqs. 1, 2, and 4, the following equation for the motion of the transduction channels:

(8)

The system has one or more fixed points, given by 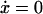and whose stability can be determined from the Jacobian matrix

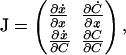(9)

which has trace and determinant

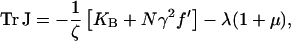(10)

(11)

(throughout the article we use the convention 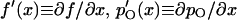and ). Here, K_B = K_SP + Nγ²K_TL is the combined passive elasticity of the bundle due to the stereocilia and the tip links; and μ = C_Mx′_sp′_O is a dimensionless combination of variables which has a value close to unity for the choice of channel parameters specified above (for C_B = 0 it can also be expressed as μ = D(f + K_TLd_O)/k_BT). A fixed point is stable if both eigenvalues of J, evaluated at the fixed point, have a negative real part. This is equivalent (Strogatz, 1994) to the two conditions: det J > 0, and Tr J < 0. The number of fixed points is most readily appreciated by considering the form of Eq. 8 for the velocity as a function of displacement x (see Fig. 2). Two distinct situations can arise depending on the strength of the calcium feedback:

• i. Consider first the case of weak feedback, so that the Ca²⁺ concentration C in the stereocilia is approximately constant. Typically (x,C=const) varies nonmonotonically with x. This is a consequence of a region of effective negative elasticity, caused by the redistribution of the transduction channel states when the bundle is moved (Howard and Hudspeth, 1987; Martin et al., 2000). At large displacements – both positive and negative – the tension T_TL in the tip links is determined by their passive elasticity. But at intermediate displacements, the occupancy of the closed state C1 declines rapidly with increasing x; the resulting force f, caused by the swing of the lever arm, is negative and reduces the tension in the tip links so that T_TL decreases with increasing x. This effect has been termed “gating compliance” by (Howard and Hudspeth, 1987). As indicated in Fig. 2, there will then be either one or three fixed points. According to the index theorem (Strogatz 1994, Sect. 6.8) out of 2n + 1 fixed points, n will be saddle points. Therefore, if the system has three fixed points, the central fixed point is a saddle point and the other two may be either stable or unstable. The number of fixed points depends on the values of the channel parameters, but also on the motor position x_M. Their stability depends additionally on the values of the dynamical model parameters (ζ and λ). A typical example of the location and nature of the fixed points, as a function of the motor position x_M, is shown in Fig. 3 A; in this particular case, the bundle displays a region of bistability. We shall return to this situation later, to discuss the dynamical behavior of the hair bundle in recent in vitro experiments.

• ii. When the calcium feedback is operational, to determine the fixed points it is appropriate to consider the curve (x,C= C(x)), where C(x) is the steady-state Ca²⁺ concentration at fixed x, given by 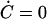in Eq. 5. If the feedback is sufficiently strong, varies monotonically with x (Fig. 2); the readjustment of the channel states caused by the binding of Ca²⁺ ions provides a positive contribution to the active force f, eliminating the region of negative elasticity. The condition for this to occur is that det J > 0 along the curve C(x), or

  (12)

FIGURE 2.

Velocity as a function of displacement x for a fixed location of the motors x_M. If the Ca²⁺ concentration is held constant, (x, C = const) typically has a region of negative slope (solid lines, for three different hypothetical values of C). For a certain range of values of C, the system can then have three fixed points. But if the Ca²⁺ concentration is allowed to adjust, the curve 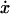(x, C = C(x)), where C(x) is the steady-state solution of Eq. 5, rises monotonically with x (dotted line). There is then a single fixed point. The channel parameters are G_C1⁰ = 0, G_C2⁰ = 60 zJ, G_O⁰ = 70 zJ, d_C1 = 0 nm, d_C2 = 7 nm, d_O = 8.5 nm and D = 4 nm. With these channel parameters K_TLd_O² ≈ 9k_BT (in a simplified two-state channel model neglecting the stereociliary stiffness K_SP the condition for the occurrence of a negative slope is K_TLd_O² > 4k_BT).

FIGURE 3.

Fixed points of the displacement x as a function of the location of the adaptation motors x_M. Trajectories in the plane (x, C) are indicated schematically below. (A) The situation with a weak Ca²⁺ feedback. The system displays a variety of dynamical regimes, including a region of bistability. (B) With strong Ca²⁺ feedback there is a single fixed point, which becomes unstable (and encircled by a stable limit cycle) for an intermediate range of values of x_M. We expect the hair cells to use this regime in vivo.

In this case, there is a single fixed point (Fig. 3 B), which may be either stable (if Tr J < 0) or unstable (if Tr J > 0). In the latter situation, the bundle undergoes limit-cycle oscillations. Significantly, the stability depends on the location of the motors x_M, in addition to the values of the other model parameters. Typically the critical point at which Tr J = 0 is a supercritical Hopf bifurcation, which means that the system is continuously controllable, passing smoothly from the quiescent to the vibrating state as indicated in Fig. 4. Thus by moving along the stereocilia, the motors can determine whether the bundle stays still, or with what amplitude it oscillates spontaneously.

FIGURE 4.

Displacement x as a function of the location of the adaptation motors x_M, for the proposed in vivo situation corresponding to Fig. 3 B. Between the two bifurcation points, x oscillates between a minimum and a maximum value shown by the two curves. The motor-mediated self-tuning mechanism (see text) maintains the system at a working point close to the first Hopf bifurcation. This result was obtained from a stochastic simulation with full channel kinetics, but in the absence of external (thermal) noise. The upper and lower lines show the average maximum and minimum values of the displacement during one period of oscillation. Note that even in the quiescent phase the amplitude is nonzero, due to channel noise. The noisy motion in the quiescent phase has a very different spectrum from the oscillating phase, however.

Frequency of limit-cycle oscillations

We propose that the regime of strong calcium feedback, in which the bundle can oscillate spontaneously, is the regime that is relevant for auditory hair cells in normal physiological conditions. The control parameter that determines the stability of the bundle is

and the Hopf bifurcation occurs at ɛ = 0. It is worth emphasizing that within the scope of a noninertial model with two variables (x and C), in order for the bundle to oscillate spontaneously, it is essential that either the bundle displays a region of negative elasticity at constant Ca²⁺ concentration, or that there is a positive feedback in the Ca²⁺ dynamics. The second option would imply that an increase in the intracellular Ca²⁺ concentration would enhance the Ca²⁺ inflow, which contradicts the present experimental evidence. Our model only allows for the first option and from Eq. 10 it can be seen that the critical condition ɛ = 0 requires that K_B + Nγ²f′ < 0, i.e., the passive bundle stiffness must be more than compensated by the gating compliance. Negative elasticity has been measured in hair cells of the bullfrog sacculus (Martin et al., 2000), and has been interpreted as being due to gating compliance (Howard and Hudspeth, 1987) as discussed above.

For small, positive values of ɛ, the bundle executes small-amplitude limit-cycle oscillations of frequency 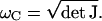From Eq. 11 it follows that the characteristic frequency of the hair bundle scales as

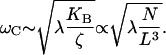(13)

Note that the period of oscillation T_C is approximately given by the geometric mean of the two relaxation times, Little is known about the variability of the calcium relaxation rate λ. If it is constant from cell to cell, the characteristic frequency is determined only by the bundle geometry. For the range of bundle sizes found e.g. in the chick's cochlea (L = 1.5–5.5 μm, N = 300–50 (Tilney and Saunders, 1983)), the frequency of the shortest bundles would then be ∼17 times greater than the frequency of the tallest bundles. This is somewhat lower than the measured frequency range (∼50 Hz–5 kHz, (Manley et al., 1991)). We note, however, that to ensure the existence of an oscillatory instability for all hair cells, ɛ = 0 from Eq. 10 must be fulfilled for each cell. In addition, a strong mismatch between τ_mech and τ_chem would seriously limit the range of amplitudes for which active amplification can be maintained. This suggests that λ may vary with the geometry of the cell; ideally it would scale as λ ∼ K_B/ζ, i.e., τ_chem ∼ τ_mech. Such variation could be achieved by a differential level of expression of calcium pumps or different buffer concentrations. In this case, the range would be enhanced to cover frequencies differing by a factor of 200. In what follows, we shall assume that this scaling (which is equivalent to ) holds. Note that in contrast to the model proposed by Choe, Magnasco, and Hudspeth (1998) no variation of transduction channel kinetics is necessary to achieve a broad range of characteristic frequencies. Instead a simultaneous variation of the hair-bundle geometry and the Ca²⁺ relaxation rate is required.

Critical oscillations

It has been proposed on general theoretical grounds that the frequency selectivity of hair bundles, as well as their sensitivity to weak signals, is conferred by their proximity to a dynamical instability (Camalet et al., 2000; Eguiluz et al., 2000). Poised on the verge of oscillating at a characteristic frequency ω_C, a hair bundle is especially responsive to periodic disturbances at that frequency. To ensure robust operation, a control system is required which maintains the hair bundle close to the critical point at which it just begins to vibrate. The general concept of a self-tuned Hopf bifurcation was therefore introduced (Camalet et al., 2000), whereby an appropriate feedback mechanism automatically tunes the system to the vicinity of the critical point. For the moment, we will assume that this mechanism works effectively, so that each hair cell is poised at a working point very close to its critical point, as indicated in Fig. 4.

In the vicinity of the bifurcation the limit cycle can be described by expanding the equations of motion about the fixed point as a power series, keeping terms up to third order. It is convenient to introduce a complex variable

(14)

where Δx and ΔC measure the difference of x and C from their respective values at the critical point. With the choice

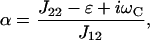(15)

where J₁₂ = λC_Mp′_O and J₂₂ = −λ(1 + μ) (Eq. 9), the equations of motion can be written as

(16)

where 𝒬 represents all quadratic terms and 𝒞 all remaining cubic terms. The expression for the coefficient ℬ is given in the Appendix; for typical parameters, Reℬ is negative, in which case the bifurcation is supercritical and therefore continuously controllable. To leading order, the amplitude of the variable 𝒵 is then given by while all other terms cause only perturbations to the trajectory (Wiggins, 1990). The solution for spontaneous critical oscillations therefore reads

(17)

and the oscillation amplitude of Δx is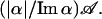

Critical response to sound waves

Sound waves or other vibrations entering the inner ear cause flow in the fluid surrounding the hair bundles. If the (unperturbed) fluid motion at the height of the bundle tip has amplitude A and frequency ω, the force exerted on the bundle tip in Eq. 2 is F = Aωζ_flow cos(ωt). Here, ζ_flow ∼ ηL is the friction coefficient of a stationary bundle in a flowing fluid. Note that ζ_flow is not precisely equal to ζ, which is the friction coefficient of the bundle moving in a stationary flow, because the latter also includes a contribution from shear flow between the stereocilia. This contribution scales as ∼ηL × Nγ² and is negligible for tall bundles but might become significant for short thick bundles. To preserve generality we write ζ_flow/ζ = ν, where ν is a constant of order unity which might vary with bundle geometry.

The external force leads to an additional driving term on the right hand side of Eq. 16, given by

(18)

For sound frequencies close to the characteristic frequency of the bundle, ω ≈ ω_C, and amplitudes larger than the thermal noise, the response of the system is

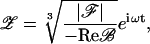(19)

where we have assumed that the bundle is poised precisely at the Hopf bifurcation, ɛ = 0.

Using the estimate Reℬ ∼ −ω_C/d_O² (see Appendix) we obtain

(20)

This is the strongly compressive response characteristic of a Hopf resonance (Camalet et al., 2000; Eguiluz et al., 2000). Displacements of the transduction channel which produce a resolvable response, Δx = 1–10 nm, typically correspond to wave amplitudes A = 1–1000 nm in the fluid.

For weak stimuli, it is important to take the effects of noise into consideration. The buffeting of the hair bundle by the Brownian motion in the surrounding fluid will render the spontaneous critical oscillations noisy. In this regime, signals that yield a response that is smaller than the spontaneous motion can nevertheless be detected, owing to phase locking of the noisy oscillations (Camalet et al., 2000). The ability to detect phase locking in neural signals despite no increase in the firing rate has been experimentally confirmed in a number of species (Narins and Wagner, 1989). In the Appendix we provide an argument for the threshold of detection which suggests that for high frequency bundles containing many stereocilia, the smallest wave amplitude that can be detected may be as small as A ≈ 0.1 nm.

Self-tuning mechanism

To achieve the combination of frequency selectivity, amplification of weak signals and wide dynamic range, the system has to be tuned to the close proximity of the Hopf bifurcation (Tr J = 0 in Eq. 10). We propose that this is accomplished by a feedback control mechanism which is mediated by the adaptation motors. The basic requirement is that when the hair bundle is still, the force exerted by the motors gradually increases so that they advance up the stereocilia (increasing x_M), pushing the system into the unstable regime (see Fig. 4); but when the bundle is oscillating, the motor force gradually declines, so that the motors slip back down the stereocilia, returning the system to the quiescent state. It would appear that some type of high-pass or band-pass filter, which can detect whether or not the bundle is oscillating, must form an integral part of the feedback mechanism that controls the motors.

It has long been known that the hair cells of some vertebrates have, in their cell membranes, a system of potassium channels (BK) and voltage-gated calcium channels that display a resonant response to oscillating input currents (Hudspeth and Lewis, 1988). It has been suggested that their purpose is to sharpen the tuning of the signal passed to the auditory nerve (Crawford and Fettiplace, 1980). It has alternatively been postulated that this system may itself generate self-sustained Hopf oscillations (Ospeck et al., 2001) and could be the basis of active bundle movement. We put forward a further possibility: One role of this system of channels is to detect bundle oscillations and to control the adaptation motors via a flux of calcium ions into the hair bundle (in fact, it is more likely that the motors are regulated by Ca²⁺-controlled secondary messengers diffusing into the hair bundle, rather than by Ca²⁺ directly, but this would not qualitatively alter the following argument).

We model the filtering characteristic of the electrical oscillator by a Lorentzian transmission function

(21)

where V is the receptor potential, R_F is a channel resistance and I_input ∝ p_O is the transduction current. The mechanism operates best if the filter frequency ω_F equals the characteristic frequency ω_C of hair-bundle oscillations, but this matching has to be encoded genetically or achieved by some mechanism beyond the scope of our model. With the value Q ≈ 10 measured experimentally in the bullfrog's sacculus (Hudspeth and Lewis, 1988), the filter distinguishes sufficiently well between the oscillating component of the transduction current and the underlying background level. The voltage-gated calcium channels then provide a Ca²⁺ flux varying (for example) exponentially with the membrane potential, which in turn determines the offset concentration in the stereocilia C_B, which appears in Eq. 5. We model it with the following differential equation

(22)

where the parameters q and V_Ca describe the voltage sensitivity of the K_Ca channels, I_Ca is a measure of these channels' contribution to the Ca²⁺ flux in the region close to the transduction channel, and λ_B is the relaxation rate of the Ca²⁺ current. For the operation of tuning mechanism it is essential that λ_B ≪ ω_C. The contribution of C_B is insignificant when the bundle is quiescent, but grows rapidly if the bundle starts to oscillate.

The Ca²⁺ flowing into the bundle from the cell body regulates the oscillations in two ways. First, it reduces the control parameter of the bifurcation directly, Eq. 10. Second, Ca²⁺ ions binding to the myosin motors enhance their rate of detachment, via the function g(C) in Eq. 7, thereby regulating the total force that the team of motors produces. Here we take g(C) ∝ C³; the precise functional form is not very important.

As shown in Fig. 5, this feedback control mechanism can successfully tune the system to the immediate vicinity of the Hopf bifurcation. In the absence of a sound stimulus, a bundle executes noisy, self-tuned critical oscillations of low amplitude. If a strong stimulus is then applied, the bundle displays the characteristic response given by Eq. 20. The significant flow of Ca²⁺ into the cell elicited by this response detunes the system, so that when the stimulus is cut, the bundle falls still. Gradually, however, the motor-mediated self-tuning mechanism returns the system to its working point, where critical oscillations just set in, and where the hair bundle's sensitivity is maximal.

FIGURE 5.

Self-tuned critical oscillations. In the absence of a stimulus, the bundle performs noisy oscillations with a small amplitude. A strong external stimulus elicits a response that can detune the system for some time. Parameters values: N = 50, K_TL = 0.5 pN/nm, K_SP = 0.15 pN/nm, ζ = ζ_flow = 0.65 pN ms/nm, γ = 0.14 and A = 40 nm (the values of other parameters are listed in the last section of the Appendix).

The hypothesis that the self-tuning mechanism is based on the detection of oscillations in the transduction current could be tested experimentally by disabling the electrical oscillations in the cell body. This could be done by voltage clamping the cell or by specifically blocking, for example, the voltage-gated calcium channels. This would disable the self-tuning mechanism and therefore augment the bundle oscillations. On the other hand, if the electrical resonance is involved in the generation of oscillations, disabling it should eliminate the spontaneous bundle activity.

Slow relaxation oscillations

The self-tuning mechanism described above is sufficiently robust to adjust the hair bundle to the critical point despite the natural variation of conditions that is likely to occur in vivo. Many experimental preparations, however, involve significant perturbation from natural conditions, and this may shift the system into a different dynamical regime. In the following, we consider a particular type of dynamical behavior that can arise when the calcium feedback is weak. In this situation, as previously discussed in Fig. 3 A, the interaction of the transduction channels with the calcium flux can produce a bistable system. If the position x_M of the adaptation motors is fixed, the hair bundle will settle at one or other of the stable positions. However, this state of affairs is upset by the slow calcium feedback acting on the motors (Eq. 7). Suppose, for example, that the bundle is at the fixed point with the higher value of x, for which there is a high probability that the transduction channels are open. The Ca²⁺ ions entering through the channel bind to the motors, causing a fraction of them to detach, and the diminishing force exerted by the motors causes the tension in the tip links T_TL to fall. As indicated in Fig. 6 A, the fixed point vanishes at a critical value of T_TL, and the system then abruptly jumps to the other fixed point. At this lower value of x, the channels are mostly closed. The resulting drop in calcium concentration augments the number of bound motors, increasing the tension in the tip links until the lower fixed point becomes unstable, whereupon the hair bundle jumps back to its initial position.

FIGURE 6.

Slow relaxation oscillator regime. (A) The solid line shows the tension-displacement relation for a channel, the dashed lines the contribution to tension from the passive bundle stiffness (which depends on the position of adaptation motors). In a quasistationary state these two must be equal. For a given position of the adaptation motors, there can be two stable solutions. The motors then move the system from one fixed point to the other. (B) Relaxation oscillations have a lower frequency than and a different shape from the critical oscillations. To achieve this regime the Ca²⁺ concentration outside the bundle was reduced and the self-tuning mechanism was replaced by a constant Ca²⁺ flow from the cell body.

The consequence of this dynamics is a slow relaxation oscillation (Strogatz 1994, Sect. 7.5) of the bundle deflection X, which has a nonsinusoidal form: each abrupt jump in position is followed by an interval of slow motion, as shown in Fig. 6 B. Martin, Mehta, and Hudspeth (2000) have observed oscillations of this type in their preparations of dissected tissue. They attributed the dynamical behavior to precisely the motor-mediated mechanism that we discuss here, and speculated that these oscillations form the basis of mechanical amplification of auditory stimuli. According to our model however, the relaxation oscillations differ in many respects from the Hopf oscillations which provide active amplification. They are considerably slower; their frequency is strongly amplitude dependent; and the frequency does not significantly depend on the viscous relaxation time of the bundle, but is principally governed by the motors' sensitivity to changing calcium levels. In our model, relaxation oscillations are an accidental consequence of the self-tuning mechanism when the system is too far from normal operating conditions.

In the light of our analysis, various interpretations of the experiment of Martin, Mehta and, Hudspeth (2000) are possible. It may be that in saccular hair cells, which are designed to detect low frequency vibrations, slow motor-mediated relaxation oscillators are sufficient to provide a rudimentary amplification of signals. Another possibility is that the observed oscillations can be adjusted to the vicinity of a Hopf bifurcation by some mechanism that we have not considered here, e.g. by alternating the bundle stiffness. A third possibility to bear in mind is that the conditions in preparations of dissected tissue are not precisely the same as those in vivo, and thus the hair bundles may not be operating in the dynamical regime that is physiologically relevant. Careful adjustment might permit the channel adaptation and the motor-mediated self-tuning mechanism to work together as we propose they do in auditory hair cells, in which case more rapid, critical Hopf oscillations might be observed.

CONCLUSION

Our phenomenological model illustrates that the two adaptation processes which have been documented in hair cells can, together, generate a self-tuned Hopf bifurcation. The feedback mechanism that accomplishes the self-tuning requires, in addition, a system to detect bundle oscillations. We have shown that this can be accomplished by the resonant response of the BK and voltage-gated Ca²⁺ channels which has been established experimentally in lower vertebrates. The spontaneous frequency ω_C of a hair cell is specified principally by the architecture of its hair bundle. To ensure robust operation of a hair cell, we expect that both the calcium relaxation rate λ, and the resonant frequency of the electrical oscillator are quite closely matched to the spontaneous oscillation frequency ω_C. The self-tuning mechanism can reliably keep the hair bundle poised on the verge of oscillating in vivo. But the perturbations in conditions which can occur in some experimental preparations may lead to quite different dynamical regimes. Thus, although recent experiments on hair cells of the bullfrog sacculus show promising signs of active amplification (Martin and Hudspeth, 1999, 2001; Martin et al., 2000, 2001), they may well not yet have revealed the full potential of auditory hair cells to detect faint sounds.

APPENDIX

Series expansion

In this section we derive an analytical expression for the third-order coefficient ℬ in the complex equation of motion (Eq. 16). The Taylor expansion of up to third order, with the use of a new variable ξ = Δx − Δx_s(C) can be derived from the equations of motion (Eqs. 5 and 8) and the definition of 𝒵 (Eq. 14):

(23)

Expanding ξ as a Taylor series in Δx and ΔC, expressing the latter in terms of 𝒵 using Eq. 17

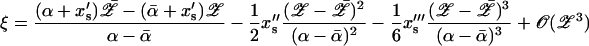(24)

and collecting the real part of the terms containing 𝒵² 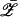yields

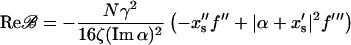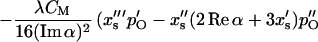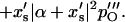(25)

Inserting α = x′_s(−λ(1 + μ) + iω_C)/(λμ) from Eq. 15 gives

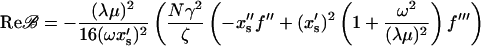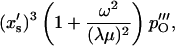(26)

and using the specific form of Δx_s, given by Eq. 3, we finally obtain

(27)

If we assume a matching between the Ca²⁺ relaxation rate and the characteristic bundle frequency, 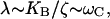the position x of the bifurcation becomes independent of the characteristic frequency and so do the terms p_O, f and all their derivatives, evaluated at the bifurcation. The third-order coefficient then scales as

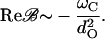(28)

The parameters we use in our simulation give the value Reℬ = −6.7 ω_C/d_O².

Noise

To determine the level of the smallest stimulus that a hair bundle can detect, stochastic fluctuations of the bundle must be taken into account. There are several sources of noise in the system. The most important is the Brownian force that the surrounding fluid exerts on the bundle. The noise resulting from the stochastic opening and closing of channels is less significant, as can be seen by considering a simplified two-state channel model. We denote the lever-arm shift between the two states by d, the average dwell times as τ₀ and τ₁ and the probability of finding the channel in state 1 by p₁. Then the expectation value of the number of channels in state 1 is and the variance is The fluctuation in the total force from all channels is The noise has the spectral density of a dichotomous process

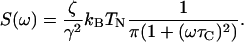(29)

It has the characteristic of a Brownian noise with an effective temperatu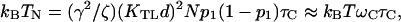re where The second approximation is based on the estimates k_BT ∼ K_TLd_O² (from the condition for the negative stiffness) and ω_C ∼ Nγ²K_TL/ζ (Eq. 13 with λ∼ω_C). Since the channel switching time is shorter than the period of the oscillations, ω_Cτ_C ≪ 1, it follows that the channel noise is negligible compared to the thermal noise. The same can be shown for the influence of stochastic channel opening on the Ca²⁺ concentration inside the stereocilia.

Taking the Brownian force exerted by the fluid into account, the equation of motion for the complex variable 𝒵 becomes

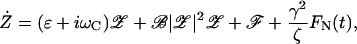(30)

where F_N(t) represents white noise with the autocorrelation function Writing 𝒵′ = 𝒵e^−iωt (and taking the stimulus frequency to be equal to the characteristic frequency), this equation can be transformed to

(31)

(32)

It can be further simplified if we replace the “rotating” noise F_N(t)e^−iωt (which reflects the fact that the noise only acts on the spatial coordinate and not on the Ca²⁺ concentration) with an averaged, homogeneous noise term. The averaged noise then has the temperature and Eq. 32 becomes a Langevin equation for a particle of friction coefficient ζ/γ², moving in a potential U(𝒵′). The equilibrium solution is the Boltzmann distribution 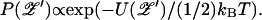For a bundle that is tuned to the critical point (ɛ = 0), the mean-square fluctuation amplitude in the absence of a stimulus (ℱ = 0) is

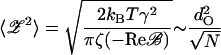(33)

(in the second step we used the estimates Reℬ ∼ −ω/d_O² (Eq. 28) and k_BT ∼ K_TLd_O², the condition for negative stiffness). Using the numerical parameter values we obtain

(34)

Weak stimuli which evoke a response that is smaller than the stochastic fluctuations of the bundle, nevertheless cause phase locking of the spontaneous bundle oscillations (Camalet et al., 2000; Martin and Hudspeth, 2001). The brain might detect such signals through periodicity in the spike train elicited by individual hair cells, or via the synchronicity of spikes from neighboring hair cells, whose characteristic frequencies differ only slightly. In either case, the quantity of interest is the Fourier component of bundle oscillations at the sound frequency. With a finite stimulus force ℱ, the Fourier component is

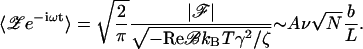(35)

We assume that signals can be detected provided that the signal-to-noise ratio, exceeds a certain threshold value ρ. The smallest detectable amplitude of fluid motion then scales as

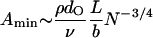(36)

or with our numerical parameter values

(37)

Taking ρ ≈ 0.2, L/b ≈ 3, ν ≈ 1, and N ≈ 200 gives A_min ≈ 0.1 nm for high frequency bundles containing many stereocilia.

Simulation of self-tuned critical oscillations

The model parameters and their values, used in the simulation, are listed in Table 1. The channels were simulated as described in the main text, using a three-state model with parameters G_C1⁰ = 0, G_C2⁰ = 60 zJ, G_O⁰ = 70 zJ, d_C1 = 0 nm, d_C2 = 7 nm, d_O = 8.5 nm and D = 4 nm. The transition rate between the states C1 and C2 and between C2 and O was modeled as , with the free energy in each state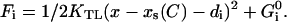

TABLE 1.

Parameter values used in the simulation

Tip-link stiffness	KTL	0.5 pN/nm	Martin et al. (2000)
Channel states	dC2	7 nm
	dO	8.5 nm	Martin et al. (2000)
Channel state energies		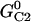60 zJ
		70 zJ
Ca2+ dependent gating point shift	D	4 nm	Corey and Hudspeth (1983)
Switching time	τch	50 μs	Corey and Hudspeth (1983)
Distance between stereociliary roots	b	1 μm	Howard et al. (1988)
Bundle height	L	7 μm	Howard et al. (1988)
Geometric factor	γ	0.14	(Howard et al. (1988)
Pivotal stiffness of a stereocilium	κ	1.5 × 10−16 Nm/rad	Hudspeth et al. (2000)
Number of stereocilia	N	50	Martin et al. (2000)
Viscous friction	ζ	0.65 pN ms/nm
Ca2+ relaxation rate	λ	100 s−1
Channel contribution to the Ca2+ concentration	CM	7 μM	Lumpkin and Hudspeth (1998)
Number of adaptation motors per channel	NM	20
Motor association rate	ωM	200 s−1
Motor speed	vM	0.3 μm/s
Motor stall force	FM	1 pN
Maximum transduction current	IInput/N	500 pA	van Netten and Kros (2000)
Filter resistance	RF	35 mV/nA
Filter Q-factor	Q	10	Hudspeth and Lewis (1988)
Filter frequency	ωF	2π × 50 s−1
Membrane potential	V0	−70 mV
Ca2+ channels gating point	VCa	−65 mV
Ca2+ channels gating charge	q	q/kBT = 0.2 mV−1
Time constant of the slow feedback	λB	1 s−1
Ca2+ gain due to slow feedback	ICa2+	10 μM/s

The resonant filter was simulated using the differential equation corresponding to the filter characteristics given by Eq. 21

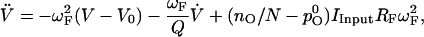(38)

where n_O is the number of open transduction channels and the parameters R_F = 35 mV/nA, I_Input = 0.5 nA, Q = 10, V₀ = −70 mV, p_O⁰ = 0.15 and ω_F = 2π × 50 s⁻¹.

The calcium contribution from the cell body was modeled according to Eq. (22) with I_Ca = 10 μM/s, λ_B = 1 s⁻¹, V_Ca = −65 mV, q/k_BT = 0.2 mV⁻¹.

The adaptation motors were modeled with stochastic attachment at a fixed rate ω_M = 200 s⁻¹ and detachment at a Ca²⁺-dependent rate g(C)ω_M, with g(C) = (0.1 μM⁻³)×C³.

All differential equations were solved using the Euler method. The time step was 1 μs.