Ca²⁺- and Voltage-Dependent Gating of Ca²⁺- and ATP-Sensitive Cationic Channels in Brain Capillary Endothelium

Abstract

Biophysical properties of the Ca²⁺-activated nonselective cation channel expressed in brain capillaries were studied in inside-out patches from primary cultures of rat brain microvascular endothelial cells. At −40 mV membrane potential, open probability (P_o) was activated by cytosolic [Ca²⁺] > 1 μM and was half-maximal at ∼20 μM. Increasing [Ca²⁺] stimulated opening rate with little effect on closing rate. At constant [Ca²⁺], P_o was voltage-dependent, and effective gating charge corresponded to 0.6 ± 0.1 unitary charges. Depolarization accelerated opening and slowed closing, thereby increasing apparent affinity for Ca²⁺. Within ∼1 min of excision, P_o declined to a lower steady state with decreased sensitivity toward activating Ca²⁺ when studied at a fixed voltage, and toward activating voltage when studied at a fixed [Ca²⁺]. Deactivated channels opened ∼5-fold slower and closed ∼10-fold faster. The sulfhydryl-reducing agent dithiotreitol (1 mM) completely reversed acceleration of closing rate but failed to recover opening rate. Single-channel gating was complex; distributions of open and closed dwell times contained at least four and five exponential components, respectively. The longest component of the closed-time distribution was markedly sensitive to both [Ca²⁺] and voltage. We conclude that the biophysical properties of gating of this channel are remarkably similar to those of large-conductance Ca²⁺-activated K⁺ channels.

INTRODUCTION

The blood-brain barrier consists of an intimate anatomical and functional interplay of endothelial and glial cells, and protects the extracellular environment of neurons in the brain from fluctuations of environmental parameters in the blood. Endothelial cells in brain capillaries are specialized in that they are linked by tight junctions to form a layer of high ohmic resistance impermeable to water-soluble molecules. Ion channels on the surface of these endothelial cells control the flow of ions between the blood and the brain (for a review, see Pardridge, 1998).

Only a small number of studies have been published on electrophysiological properties of brain endothelium, most of them limited to reporting the presence of one of the few channel types expressed in these cells, such as amiloride-sensitive (Vigne et al., 1989), stretch-activated (Popp et al., 1992), or Ca²⁺- and ATP-sensitive nonselective cation channels (Popp and Gögelein, 1992).

Ca²⁺-activated nonselective cation channels inhibited by adenine nucleotides have been described in a variety of other cell types including mouse and rat pancreatic acinar (Maruyama and Petersen, 1982a,b, 1984; Suzuki and Petersen, 1988; Gögelein et al., 1990) and ductal cells (Gray and Argent, 1990), rat distal colon cells (Gögelein and Capek, 1990), rat lacrimal glands (Marty et al., 1984), mouse kidney (Teulon et al., 1987; Paulais and Teulon, 1989), rat brown adipose tissue (Koivisto and Nedergaard, 1995; Koivisto et al., 2000), astrocytes (Chen and Simard, 2001), cultured rat cardiac cells (Colquhoun et al., 1981), and various cell lines (Yellen, 1982; Jung et al., 1992; Kamouchi et al., 1999; Suh et al., 2002). Only a few members of this family of channels have been studied in detail, and their properties differ with respect to their apparent affinities for activation by Ca²⁺ (e.g., Colquhoun et al., 1981; Chen and Simard, 2001), their sensitivities to membrane voltage (e.g., Colquhoun et al., 1981; Gray and Argent, 1990) and inhibitory nucleotides (e.g., Paulais and Teulon, 1989; Chen and Simard, 2001) as well as their pharmacological profiles (e.g., Gögelein and Capek, 1990; Popp and Gögelein, 1992). The physiological role of these channels in most of the tissues is still unclear.

Although the presence of a Ca²⁺- and ATP-sensitive nonselective cation channel in endothelial cells of intact brain capillaries has been reported (Popp and Gögelein, 1992), little is known about the characteristics of this channel. Since these cells form the blood-brain barrier, characterization of the brain endothelial channel should contribute to our understanding of blood-brain barrier function.

Several model systems have been developed to study the biology of the blood-brain barrier, including cell lines (Roux et al., 1994) and primary cultures (Abbott et al., 1992). We have previously developed and partially characterized a primary culture of rat brain capillary endothelial (RBCE) cells grown to confluence on a biological matrix (Dömötör et al., 1998, 1999; Sipos et al., 2000), based on the protocol developed by Abbott et al. (1992). The present study, using the excised inside-out configuration of the patch-clamp technique, was aimed at providing a biophysical characterization of gating of the Ca²⁺-activated cation channel in these cells, with a particular focus on regulation by Ca²⁺ and voltage.

MATERIALS AND METHODS

Preparation and culture of rat brain capillary endothelial cells

Primary cultures of rat brain endothelial (RBCE) cells were prepared as described (Dömötör et al., 1998). Briefly, glass coverslips were precoated with a collagen matrix by culturing bovine corneal endothelium on them followed by chemical stripping of the cells, and were stored at −80°C. To obtain brain endothelium, capillaries were isolated from rat brain by gradient centrifugation, digested using collagenase/dispase, and the dissociated cells were plated on the precoated glass coverslips. 48 h later, nonendothelial cells were selectively killed by opsonization with the antibody Thy1.1 followed by incubation for 2 h in a serum containing complement. Endothelial cells were grown to confluence, and recordings were done typically between 5–8 days of culture.

Calibration of Ca²⁺ concentrations

Nominally Ca²⁺-free solution was prepared by adding 1 mM EGTA to a bath solution with no added Ca²⁺. Bath solutions with [Ca²⁺] in the micromolar range were prepared by titrating 1 mM HEDTA (n-(2-Hydroxyethyl)ethylenediamine-n,n′,n′-triacetic acid, K_d(Ca²⁺) = ∼5 μM) with CaCl₂, as calculated using the freeware program Winmaxc. Solutions with [Ca²⁺] > 100 μM were unbuffered. All bath solutions were subjected to ratiometric fluorescent determination of free [Ca²⁺] using 100 nM of the free acid form of FURA-FF, a fluorescent dye with a K_d for Ca²⁺ of ∼5 μM, and little sensitivity to Mg²⁺. Free [Ca²⁺] was measured using the method of Grynkiewicz et al. (1985); i.e., [Ca²⁺]_free = (K_d(R − R_min)/(R_max − R))(S_f380/S_b380), where R is the ratio of the fluorescence emitted at 510 nm when excited at 340 and 380 nm, respectively, and R_min, S_f380, R_max, and S_b380 are the ratios and the emitted intensities at the 380-nm excitation wavelength measured in Ca²⁺-free bath solution (1 mM EGTA added) and with 1 mM Ca²⁺ added to the bath (no EGTA), respectively. To verify the accuracy of this procedure, we used a series of [Ca²⁺] standards ranging from ∼1 μM to 1 mM (Ca²⁺ Calibration Kit #3; Molecular Probes, Eugene, OR) and found that we could verify the free [Ca²⁺] of the standards with relative accuracy. By contrast, we found up to threefold differences between the [Ca²⁺] measured and that predicted by Winmaxc for our bath solutions. Therefore, all [Ca²⁺] reported in this article reflect the values obtained by the direct fluorescent measurements. Without added Ca²⁺ and chelators, our KCl-based bath solution contained 13 μM contaminant Ca²⁺, as determined with FURA-FF. In a series of experiments in which we tested apparent Ca²⁺ affinity of our channels, identical results were obtained using unbuffered solution with 10 μM added Ca²⁺ or a solution in which free [Ca²⁺] was buffered to ∼20 μM using 1 mM HEDTA.

Excised-patch recording

Patch pipettes were pulled from borosilicate glass and fire-polished to resistances of 2–5 MΩ. Pipette solution contained 140 mM NaCl, 2 mM MgCl₂, 1 mM CaCl₂, 10 mM HEPES, and 30 μM benzamil (pH = 7.4 with NaOH). Bath solutions contained 140 mM KCl (substituted in some experiments by NaCl or NMG-Cl, as stated), 2 mM MgCl₂, and 10 mM HEPES (pH = 7.1 with KOH, NaOH, or NMG (N-methyl-D-glucamine), as appropriate). 1 mM EGTA or HEDTA and varying amounts of CaCl₂ were added to obtain bath solutions with various free [Ca²⁺] (see above). Cells were placed into a flow chamber in which the continuously flowing solution bathing the cells could be completely exchanged within 3–5 s after switching electrically controlled valves (HEKA, Lambrecht/Pfalz, Germany). Seal resistances of up to 50 GΩ were routinely obtained and patches in the cell-attached or excised inside-out configuration remained stable for tens of minutes. Recorded currents were amplified using an Axopatch 200B amplifier (Axon Instruments, Foster City, CA), filtered at 500 Hz by an 8-pole Bessel filter (Warner Instrument, Hamden, CT), digitized at a sampling rate of 5 kHz (Digidata 1320, Axon Instruments), and recorded using pCLAMP 8 software (Axon Instruments). All recordings were done at ambient room temperature (∼25°C).

Kinetic analysis

Current records were digitally filtered at 200 Hz using a Gaussian filter, and slow baseline-drifts were corrected using a baseline-update algorithm sensitive to single-channel current transitions (Csanády et al., 2000). Baseline-subtracted currents were idealized by a simple half-amplitude threshold crossing criterion combined with the enforcement of a fixed dead time (t_d) of 1 ms (Csanády, 2000).

For records with multiple (2–10) active channels open probability (P_o) was calculated from the events lists as 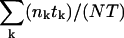, where n_k and t_k denote the number of open channels and the duration, respectively, of the k^th event, N is the number of channels in the patch, and 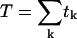is the total duration of the record. Since P_o was close to unity immediately after excision into 1 mM Ca²⁺, the number of channels (N) was taken as the maximum number of simultaneously open channels observed. Mean open time (m.o.t.) and mean closed time (m.c.t.) were calculated using the cycle-time method, i.e., 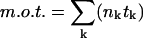/(number of upward transitions), and m.c.t. = (m.o.t.)((1/P_o) − 1).

For single-channel records the distributions of open and closed dwell times were fitted to distributions with one to six exponential components using unbinned maximum likelihood (Colquhoun and Sigworth, 1995), and the Schwarz criterion (Ball and Sansom, 1989; see also Csanády et al., 2000) was used to judge whether the fit was significantly improved by inclusion of each additional component. Errors for the fit parameters (legends to Figs. 7 and 8) represent half-widths of 0.5-unit likelihood intervals. For display, dwell-time histograms were constructed using log-binning (10 bins per decade) and a square-root ordinate (Sigworth and Sine, 1987).

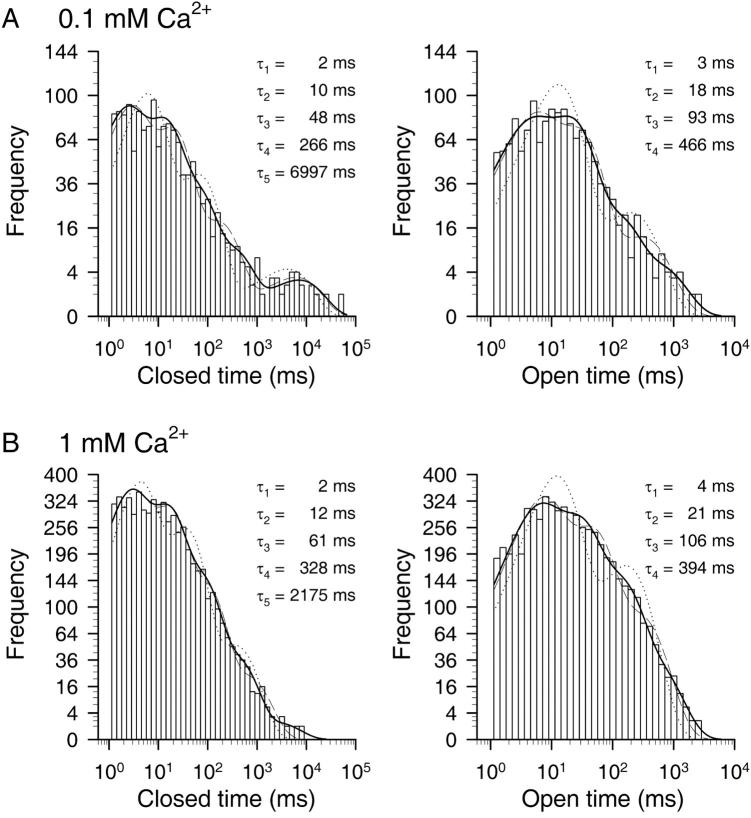
FIGURE 7.

Ca²⁺-dependence of dwell-time distributions. (A and B) Dwell-time histograms of closed (left) and open (right) dwell times of single CA-NSC channels at −40 mV membrane potential in 0.1 mM (A) and 1 mM (B) Ca_i²⁺. Events were binned at 10 bins per decade; ordinate is square-root transformed. Dead time was 1 ms, events were pooled from eight patches, and fitted to distributions with four (open times) or five (closed times) exponential components using maximum likelihood (solid lines; see Methods). Fit parameters were: 0.1 mM Ca²⁺: τ_c1 = 1.7 ± 0.2 ms, τ_c2 = 10 ± 0.7 ms, τ_c3 = 48 ± 4 ms, τ_c4 = 266 ± 37 ms, τ_c5 = 6997 ± 1420 ms, a_c1 = 0.36 ± 0.03, a_c2 = 0.38 ± 0.04, a_c3 = 0.19 ± 0.02, a_c4 = 0.057 ± 0.009, a_c5 = 0.016 ± 0.002, τ_o1 = 2.9 ± 0.4 ms, τ_o2 = 18 ± 1 ms, τ_o3 = 93 ± 11 ms, τ_o4 = 466 ± 68 ms, a_o1 = 0.32 ± 0.03, a_o2 = 0.51 ± 0.05, a_o3 = 0.13 ± 0.02, and a_o4 = 0.040 ± 0.004. 1 mM Ca²⁺: τ_c1 = 2.0 ± 0.1 ms, τ_c2 = 12 ± 0.4 ms, τ_c3 = 61 ± 3 ms, τ_c4 = 328 ± 20 ms, τ_c5 = 2175 ± 613 ms, a_c1 = 0.36 ± 0.02, a_c2 = 0.37 ± 0.02, a_c3 = 0.21 ± 0.01, a_c4 = 0.059 ± 0.004, a_c5 = 0.0025 ± 0.0001, τ_o1 = 4.2 ± 0.2 ms, τ_o2 = 21 ± 0.8 ms, τ_o3 = 106 ± 4 ms, τ_o4 = 394 ± 23 ms, a_o1 = 0.33 ± 0.02, a_o2 = 0.38 ± 0.02, a_o3 = 0.23 ± 0.01, and a_o4 = 0.063 ± 0.003. Also shown are the best fits to closed- and open-time distributions using three or four, and two or three exponential components, respectively (dotted and dashed lines).

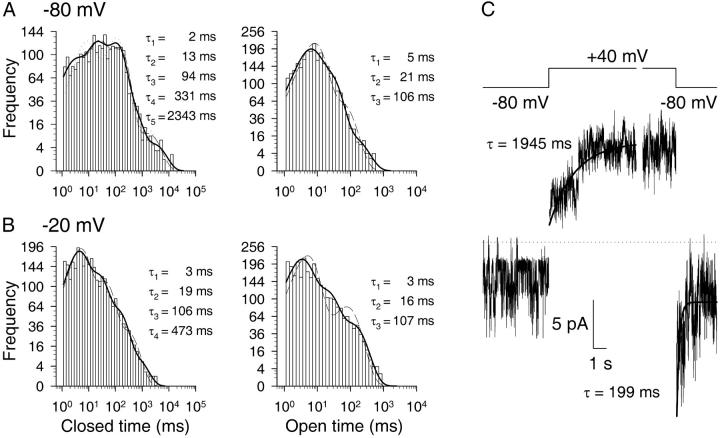
FIGURE 8.

Voltage-dependence of dwell-time distributions and time course of voltage-dependent activation. (A and B) Dwell-time histograms of closed (left) and open (right) dwell times of single CA-NSC channels at −80 (A) and −20 mV (B) membrane potentials in 1 mM Ca_i²⁺. Dead time was 1 ms; events from six patches were pooled. Closed-time distributions at −80 and −20 mV were fit by five and four exponential components, respectively; open times were fit by three components. Fit parameters were: −80 mV: τ_c1 = 1.9 ± 0.2 ms, τ_c2 = 13 ± 1 ms, τ_c3 = 94 ± 4 ms, τ_c4 = 331 ± 29 ms, τ_c5 = 2343 ± 348 ms, a_c1 = 0.19 ± 0.02, a_c2 = 0.29 ± 0.02, a_c3 = 0.39 ± 0.03, a_c4 = 0.11 ± 0.01, a_c5 = 0.020 ± 0.002, τ_o1 = 4.5 ± 0.3 ms, τ_o2 = 21 ± 0.8 ms, τ_o3 = 106 ± 10 ms, a_o1 = 0.50 ± 0.03, a_o2 = 0.45 ± 0.03, and a_o3 = 0.055 ± 0.004. −20 mV: τ_c1 = 3.3 ± 0.2 ms, τ_c2 = 19 ± 1 ms, τ_c3 = 106 ± 6 ms, τ_c4 = 473 ± 56 ms, a_c1 = 0.45 ± 0.03, a_c2 = 0.34 ± 0.03, a_c3 = 0.18 ± 0.01, a_c4 = 0.029 ± 0.002, τ_o1 = 2.7 ± 0.1 ms, τ_o2 = 16 ± 0.8 ms, τ_o3 = 107 ± 5 ms, a_o1 = 0.52 ± 0.03, a_o2 = 0.32 ± 0.02, and a_o3 = 0.16 ± 0.009. Also shown are the best fits to closed-time distributions using three or four exponential components for −80 mV (dotted and dashed lines) and three components for −20 mV (dashed line), as well as the best fits to open-time distributions using two components (dashed lines). (C) Baseline-subtracted, synchronized currents recorded in response to voltage jumps from −80 mV to +40 mV and vice versa were added up from five and nine patches, respectively, containing a total of 14 channels in each case. Ca_i²⁺ was 1 mM. Time courses of activating and inactivating currents were fitted (solid lines) by single exponentials (see Methods). Dotted line shows zero-current level.

Quasimacroscopic current time courses in response to voltage jumps were constructed from single-channel traces after capacitative spikes were subtracted individually using the baseline correction procedure described above. Flat baselines could be obtained for each individual trace for time points >40 ms after the jump. Baseline-subtracted traces were then synchronized around the time point of the jump and added up to provide quasimacroscopic current traces. These traces were fitted with single exponentials after discarding the first 40 ms after the voltage jump, and by constraining the extrapolated value of the fit function at the time point of the jump to i_new(NP_o)_old, where i_new is the single-channel current amplitude observed at the voltage after the jump, and (NP_o)_old is the steady-state NP_o observed before the jump.

Plots of steady-state P_o versus voltage were fitted by the Boltzmann function 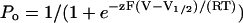to obtain the effective gating charge z and half-maximally activating voltage V_1/2 (T, temperature; V, membrane voltage; F = 96,500 Coulombs/mole; and R = 8.31 Joule(mol K)⁻¹). Plots of opening (r_CO) and closing rates (r_OC) versus voltage were fitted by the functions r_CO(V) = r_CO(0)e^zFV/(2RT), and r_OC(V) = r_OC(0)e^−zFV/(2RT), respectively.

Fitting of macroscopic current relaxations by single exponentials and of various plots by Boltzmann, exponential, Michaelis-Menten, or Hill functions was done by a nonlinear least-squares fitter (SigmaPlot 4.0).

Single-channel conductances

All-points histograms of segments of current recordings, made in the same patch at membrane potentials incremented in 20-mV steps between −80 and +80 mV, were fitted with sums of Gaussians. Distances between adjacent peaks were plotted against voltage, to obtain current-voltage (i/V) plots. For Na⁺/K⁺ or Na⁺/Na⁺ conditions, channel conductances and reversal potentials were obtained from straight-line fits to each plot. For Na⁺/NMG⁺ and Ca²⁺/Na⁺ conditions, i/V plots were fitted to the Goldmann-Hodgkin-Katz (G-H-K) current equation written for two permeant ions,

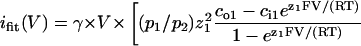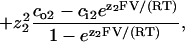to obtain parameters (p₁/p₂) and γ [pS/mM] (p_k and z_k, permeability and valence of k^th ion; and c_ok and c_ik, extra- and intracellular concentration (mM) of k^th ion). Reversal potentials were obtained by solving i_fit(V) = 0 and conductances were defined as the asymptotic slope at very negative or very positive potentials, respectively, of the fits (with Na⁺ assigned k = 2 in the above equation, g₋ = γ [Na⁺]_o and g₊ = γ [Na⁺]_i, respectively, for the Na⁺/NMG⁺ and Ca²⁺/Na⁺ conditions). At least three experiments were made for each ionic condition; conductances and reversal potentials are given as mean ± SE.

Statistics

Student's two-tailed t-test was applied to verify the impact of different experimental conditions on various kinetic parameters, such as apparent pK for activation of P_o by Ca²⁺, half-maximally activating voltage (V_1/2), and the logarithm of the closing rate. For the statistical tests all of these parameters were estimated from individual fits to data obtained from each separate patch, and these individual estimates were verified to be approximately normally distributed with variances that were similar between two compared conditions. The averages of these individual estimates were closely similar in each case to the overall estimate obtained by fitting the pooled data. (The latter estimates are used for the fits shown in Figs. 3, 5, and 6.) One-way ANOVA analysis was applied to test for a correlation between the efficiency of reducing agents to recover P_o and the channel closing rate before the treatment. Results of statistical tests are detailed in the respective figure legends.

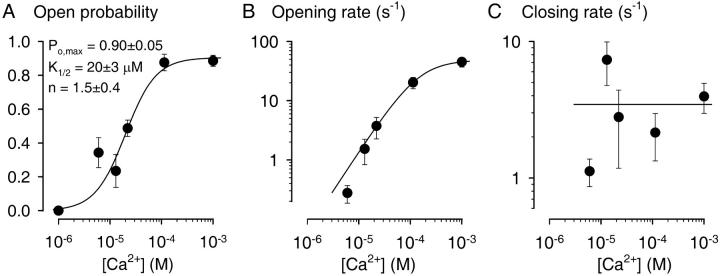
FIGURE 3.

Ca²⁺-dependence of CA-NSC gating immediately after patch excision. Kinetics of channel gating was analyzed for segments of record immediately after excision of patches into bath solutions containing various [Ca²⁺]. Membrane potential was −40 mV. P_o (A), mean opening rate (B), and closing rate (C) as a function of [Ca²⁺]_i. Plots of P_o (A) and opening rate (B) were fitted (solid lines) with the Hill equation and yielded parameters P_o,max = 0.90 ± 0.05, K_1/2 = 20 ± 3 μM, n = 1.5 ± 0.4 for P_o; and r_CO,max = 49 ± 11 s⁻¹, K_1/2 = 145 ± 112 μM, and n = 1.3 ± 0.9 for the opening rate. Plot of mean closing rate (C) was not fitted; instead, average closing rate of 3.5 ± 0.7 s⁻¹ calculated from the data over the whole range of Ca_i²⁺ is shown (solid line). Numbers of experiments: n = 3, 4, 5, 16, 8, and 13, respectively, for [Ca²⁺]_i = 1, 6, 13, 22, 113 μM, and 1 mM.

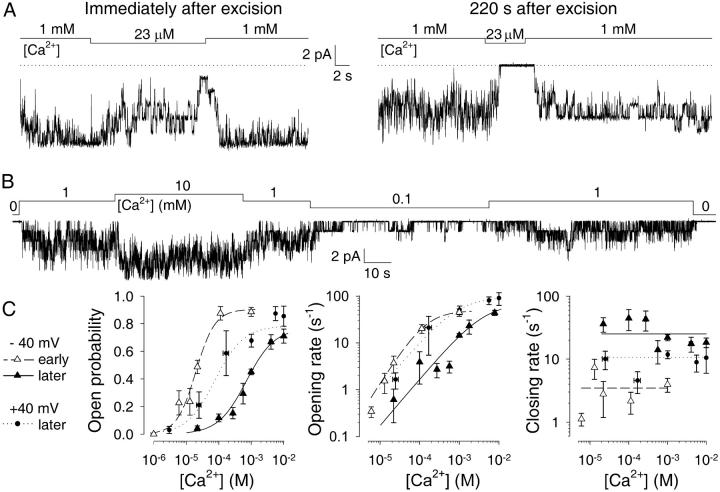
FIGURE 5.

Deactivation decreases the apparent affinity of CA-NSCs for Ca²⁺. (A) Test applications of ∼20 μM Ca²⁺ in the same patch a few seconds (left) and ∼3 min (right) after patch excision. Dotted line marks zero-current level. (B) Current record from a patch with six CA-NSC channels superfused with various [Ca²⁺]. Trace starts ∼4 min after excision. (C) Kinetics of deactivated channels. Plots of P_o (left), opening rate (center), and closing rate (right) as a function of [Ca²⁺]_i assayed at −40 mV (▴) or +40 mV (•) membrane potential. Plots of P_o and opening rate were fitted (solid and dotted lines) with the Michaelis-Menten equation and yielded parameters P_o,max = 0.77 ± 0.06, K_m = 0.71 ± 0.15 mM at −40 mV, P_o,max = 0.78 ± 0.05, and K_m = 79 ± 39 μM at +40 mV for open probability; r_CO,max = 72 ± 10 s⁻¹, K_m = 4.2 ± 1.0 mM at −40 mV; r_CO,max = 97 ± 21 s⁻¹; and K_m = 0.88 ± 0.55 mM at +40 mV for opening rate. Average closing rates over the whole range of [Ca²⁺]_i were 25 ± 2 s⁻¹ at −40 mV, and 11 ± 1 s⁻¹ at +40 mV. For comparison, corresponding plots and fits for freshly excised channels at −40 mV are replotted from Fig. 3, A–C (▵, dashed lines). Numbers of experiments and statistics: n = 11, 17, 13, 9, 129, 20, and 12, respectively, for [Ca²⁺]_i = 22, 100, 270, 560 μM, 1 mM, 4.1 mM, and 10 mM (−40 mV); n = 2, 8, 6, 26, 5, and 4, respectively, for [Ca²⁺]_i = 3, 25, 170 μM, 1 mM, 5.6 mM, and 10 mM (+40 mV). pK_m for stimulation of P_o increased significantly during deactivation (p < 0.00001), decreased significantly upon depolarization to +40 mV (p = 0.00001), but remained significantly higher than immediately after excision (p = 0.04). Average closing rate (log(r_OC)) was significantly accelerated by deactivation (p < 0.00001), significantly slowed by depolarization (p = 0.005), but remained significantly faster than immediately after excision (p = 0.00008).

FIGURE 6.

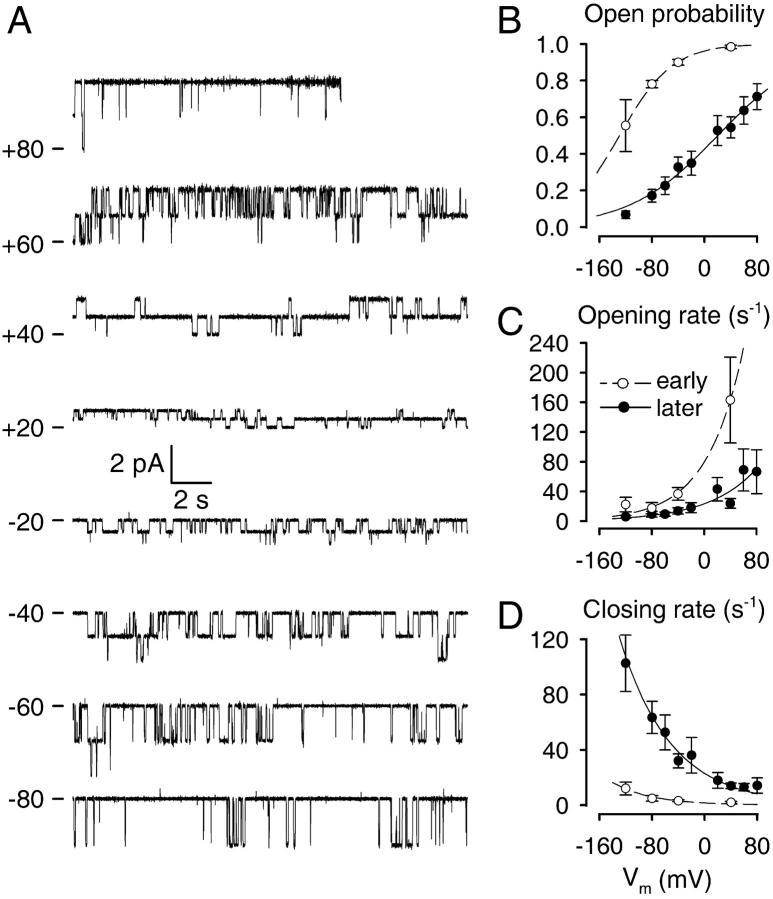
Voltage-dependent gating of CA-NSCs. (A) 20-s current traces of two CA-NSC channels in a patch bathed in symmetrical 140 mM NaCl and 1 mM Ca²⁺ on the cytoplasmic side, at membrane potentials ranging from −80 to +80 mV. Traces start >10 min after patch excision; the seal was lost toward the end of the +80-mV segment. Plots of P_o (B), mean opening rate (C), and mean closing rate (D) as a function of membrane voltage (V_m) in 1 mM Ca_i²⁺ for deactivated channels (•) or early after patch excision (○). P_o plots (B) were fitted with the Boltzmann equation (see Methods) and yielded an effective gating charge z = 0.4 ± 0.1 and half-maximally activating voltage V_1/2 = 20 ± 7 mV for deactivated channels (solid line), and z = 0.6 ± 0.1, V_1/2 = −129 ± 10 mV immediately after excision (dashed line). Plots of mean opening and closing rate (C, D) were fitted with exponentials (see Methods). Fit parameters for opening rate (C) were z = 0.7 ± 0.2, r_CO(0) = 23 ± 7 s⁻¹ for deactivated channels, and z = 0.9 ± 0.2, r_CO(0) = 79 ± 15 s⁻¹ immediately after excision. Fit parameters for closing rate (D) were z = 0.7 ± 0.1, r_OC(0) = 23 ± 4 s⁻¹ for deactivated channels, and z = 0.9 ± 0.3, r_CO(0) = 1.5 ± 0.8 s⁻¹ immediately after excision. Numbers of experiments and statistics: n = 7, 21, 17, 20, 11, 12, 16, 14, and 13, respectively, for V_m = −120, −80, −60, −40, −20, +20, +40, +60, and +80 mV (deactivated channels); and n = 4, 4, 11, and 5, respectively, for V_m = −120, −80, −40, and +40 mV (immediately after excision). The shift in V_1/2 upon deactivation was significant (p < 0.00001).

Chemicals

Tris(2-carboxyethyl)phosphine (TCEP) was purchased from Pierce (Rockford, IL); FURA-FF from Molecular Probes (Eugene, OR); and Thy1.1, complement, and most other reagents were from Sigma (St. Louis, MO).

RESULTS

Nonselective cationic channels in RBCE cells are stimulated by Ca²⁺ and inhibited by ATP and flufenamic acid

Three types of channels were routinely observed in RBCE cells in cell-attached or excised inside-out patches at negative membrane potentials (positive pipette holding potentials) and with a patch pipette filled with NaCl. A cation-selective channel which did not require the presence of cytoplasmic Ca²⁺ for activity could be completely blocked by including 30 μM of the amiloride analog benzamil into the pipette solution (Vigne et al., 1989). Mechanosensitive channels (Popp et al., 1992) became active when negative pressure was applied to the patch pipette after seal formation, but inactivated mostly after patch excision.

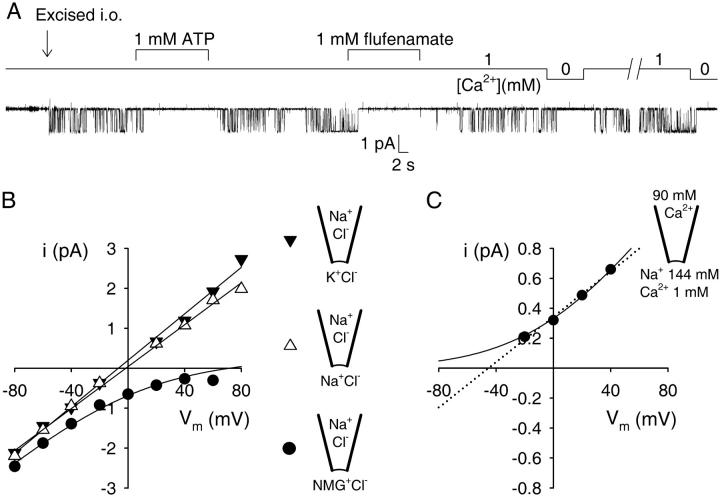
With 30 μM benzamil in the pipette to block amiloride-sensitive channels, and in the absence of mechanical pressure, the only single-channel openings we observed came from a third type of channel, present in >90% of all patches (Fig. 1). These channels were mostly silent when recording from resting cells in the cell-attached mode, but became immediately active when patches were excised into a continuously flowing bath which contained 1 mM Ca²⁺. This activity was completely and reversibly suppressed when the cytosolic face of the excised patch was superfused with 1 mM of either MgATP or the anti-inflammatory drug Na-flufenamate, or when cytosolic Ca²⁺ was washed away by superfusion with a nominally Ca²⁺-free solution (1 mM EGTA, calculated free [Ca²⁺] in the low nanomolar range; see Fig. 1 A).

FIGURE 1.

Defining properties of Ca²⁺ and ATP-sensitive nonselective cation channels (CA-NSCs) in rat brain endothelial cells. (A) A single CA-NSC channel, silent in the cell-attached mode, is activated by excision (arrow) into a high-Ca²⁺ bath solution. The channel is immediately and reversibly shut by superfusion with either Ca²⁺-free solution (1 mM EGTA), or with 1 mM MgATP or Na-flufenamate. (B) Single-channel current-voltage plots and fits under three ionic conditions obtained from a single patch. Pipette solution was NaCl-based (140 mM) in all three cases, while bath solution contained 140 mM KCl (▾), NaCl (▵), or NMG-Cl (•). Straight-line fits to the plots for the KCl-and NaCl-based bath yielded slope-conductances and reversal potentials of 29 ± 1 pS, −7 ± 2 mV, and 26 ± 1 pS, −2 ± 1 mV, respectively. In the case of the NMG-Cl-based bath the plot was fitted with the G-H-K current equation yielding an asymptotic slope conductance of 29 ± 1 pS at very negative voltages (Methods), and a reversal potential of +72 mV. (C) Single-channel current-voltage plot with 90 mM CaCl₂ in the pipette and 144 mM Na⁺ in the bath. A fit to the G-H-K current equation (solid line) assuming zero permeability for Ca²⁺ yielded an asymptotic slope conductance at very positive voltages of 13 ± 0.1 pS (see Methods). A straight-line fit (dotted line) predicted a reversal potential of −45 ± 4 mV.

With NaCl in the pipette and either NaCl or KCl in the bath, single-channel current-voltage plots were linear with a slope conductance of ∼30 pS and reversed at ∼0 mV (Fig. 1 B). Mean conductances were 30 ± 1 pS (n = 4) and 28 ± 1 pS (n = 4) and reversal potentials were −3 ± 2 mV (n = 4) and 4 ± 3 mV (n = 4), respectively, for the NaCl/KCl and NaCl/NaCl conditions. When N-methyl-D-glucamine (NMG⁺) replaced K⁺ on the cytosolic side in the form of NMG-Cl, the asymptotic slope conductance at negative potentials was 32 ± 3 pS (n = 3), but no outward channel openings could be resolved at depolarized potentials (extrapolated reversal potential was +74 ± 10 mV; n = 3; see Methods), indicating that the charge carrier for the intact inward current is Na⁺ and not Cl⁻, and that NMG⁺ does not permeate the channels to any measurable extent (calculated permeability ratio p_Na/p_NMG = 20 ± 8 (n = 3)). The channels are therefore cation-selective, but do not discriminate between Na⁺ and K⁺ (Fig. 1 B).

With 90 mM CaCl₂ in the pipette and NaCl in the bath (1 mM Ca²⁺ was added to the bath to reversibly activate the channels), the slope conductance at positive membrane potentials was 15 ± 1 pS (n = 3), but we were unable to resolve inward channel openings (Fig. 1 C). The lack of data at more negative potentials (channel currents were lost in the noise at −40 mV) precluded the reliable determination of the permeability ratio p_Na/p_Ca by a fit to the Goldmann-Hodgkin-Katz (G-H-K) current equation (the solid line in Fig. 1 C is a G-H-K fit assuming zero permeability for Ca²⁺), but the reversal potential is expected to be more negative than the −45 ± 4 mV predicted by a simple straight-line fit (Fig. 1 C, dotted line). Hence, from the G-H-K current equation (and z = 2 for Ca²⁺), the permeability ratio p_Na/p_Ca is expected to be greater than ∼12. Thus, the channels are little if at all permeable to Ca²⁺.

The obligatory dependence of channel activity on cytosolic Ca²⁺, the observed inhibition by ATP and flufenamic acid, the insensitivity to the extracellularly applied amiloride analog benzamil, as well as the permeation properties are in good agreement with observations of Popp and Gögelein (1992) and Popp et al. (1993), and identify these channels as the Ca²⁺- and ATP-sensitive nonselective cation channels (CA-NSCs) present in intact capillaries of rat brain.

Micromolar cytoplasmic Ca²⁺ is required for stimulation of CA-NSC activity in excised patches

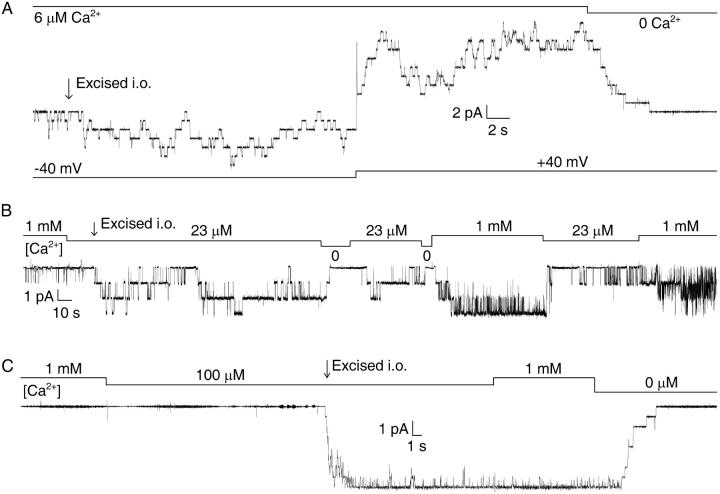
To examine the sensitivity of the channels to internal Ca²⁺, we excised patches into bath solutions with various [Ca²⁺], while holding the pipette potential at +40 mV (membrane potential was −40 mV after excision). Although we did not observe openings of CA-NSCs in patches excised into [Ca²⁺] < 1 μM, we found a dose-dependent activation of channel open probability (P_o) by [Ca²⁺] in the low micromolar range. Excision of patches into a bath containing 6 μM Ca²⁺ resulted in the immediate appearance of channel activity, which was further stimulated approximately twofold when the membrane potential was stepped from −40 mV to +40 mV (Fig. 2 A, patch with ∼25 channels). Excision into a bath with ∼20 μM Ca²⁺ activated channels to an average P_o of ∼0.5 (Fig. 2 B, patch with three channels). Excision into 100 μM Ca²⁺ immediately activated all channels to a P_o of ∼1; subsequent elevation of bath [Ca²⁺] to 1 mM did not have any further stimulating effect, suggesting that an internal [Ca²⁺] ([Ca²⁺]_i) of 100 μM was completely saturating for activation of P_o (Fig. 2 C, patch with eight channels).

FIGURE 2.

Micromolar Ca²⁺ stimulates CA-NSC activity immediately after patch excision. (A) CA-NSC channel activity elicited by excision of a patch into 6 μM Ca²⁺. Note an approximately twofold increase in P_o upon depolarization from −40 to +40 mV. Subsequent application of saturating [Ca²⁺] activated ∼25 channels in this patch. (B) Half-maximal activation of three CA-NSC channels in a patch excised into ∼20 μM Ca²⁺. (C) Maximal activation of eight CA-NSC channels in a patch excised into 100 μM Ca²⁺. Bars indicate changes in bath [Ca²⁺], membrane potential was −40 mV in B and C.

Stimulation by cytoplasmic Ca²⁺ of CA-NSC activity reflects stimulation of opening rate

To characterize Ca²⁺-dependence of gating we analyzed the kinetics of channel current at −40 mV membrane potential within short time windows immediately upon excision into various [Ca²⁺] (compare to Fig. 2). Mean opening and closing rates were extracted from current records of patches with multiple channels as the inverse of the mean closed and open times, respectively (see Methods). The P_o vs. [Ca²⁺]_i plot at −40 mV membrane potential (Fig. 3 A) showed channel activation at [Ca²⁺]_i > 1 μM with a significant P_o at ∼6 μM Ca²⁺, and was best fit by the Hill equation with parameters P_o,max = 0.90 ± 0.05, K_1/2 = 20 ± 3 μM, and a Hill coefficient of 1.5 ± 0.4. Plots of opening and closing rate against [Ca²⁺]_i (Fig. 3, B and C) revealed that activation of P_o by Ca²⁺ was a consequence mainly of increasing opening rate, whereas closing rates were little affected. Indeed, opening rate increased by about two orders of magnitude between 6 μM and 1 mM [Ca²⁺]_i (Fig. 3 B; note logarithmic ordinate). In contrast, closing rates remained within approximately threefold throughout the whole range of [Ca²⁺]_i tested (Fig. 3 C), averaging 3.5 ± 0.7 s⁻¹.

CA-NSC channel activity declines shortly after patch excision

The gating properties illustrated in Fig. 3 are representative of early segments of records immediately after excision (compare to Fig. 2). However, when membrane currents were recorded for prolonged periods after excision, a progressive loss of channel activity was invariably observed. We compared the time courses of this deactivation in various bath [Ca²⁺]. When quasimacroscopic current decay time courses were tentatively fit with single exponentials, ∼30-s time constants were obtained whether bath [Ca²⁺] was ∼20 μM (Fig. 4 A, top), 100 μM (Fig. 4 A, center), or 1 mM (Fig. 4 B), although the delay before observable deactivation seemed proportionally longer at higher [Ca²⁺] (compare Figs. 4 A, top, center, and 4 B; note different timescales). Stability plots, which display P_o, mean open, and mean closed times analyzed over a moving time window, were constructed to analyze the kinetic changes underlying deactivation. Such plots for the bottom trace in Fig. 4 A are shown in Fig. 4, B–D. While P_o in 1 mM Ca²⁺ declined from a value of ∼0.9 just after excision to a relatively steady value of 0.2–0.4 (Fig. 4 B), both a progressive shortening of open times (Fig. 4 C) and a progressive lengthening of closed times (Fig. 4 D) could be observed.

FIGURE 4.

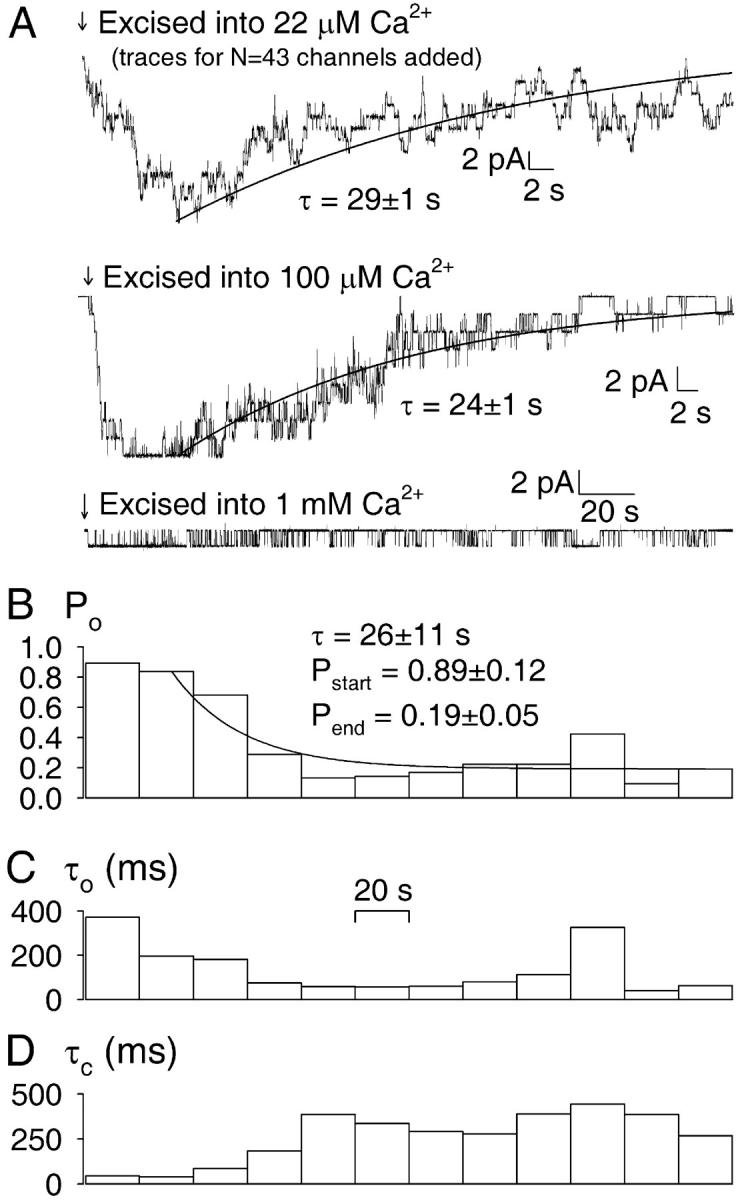
Time courses of deactivation of CA-NSC channels excised into various [Ca²⁺]. (A) (Top) Summed current traces from patches excised into ∼20 μM Ca²⁺, representing a total of 43 channels. Traces were synchronized around the time point of excision (arrow). (Center) Current trace from a patch with nine channels excised (arrow) into 100 μM Ca²⁺. Both decay time courses were fitted with decaying exponentials (solid lines). (Bottom) Current trace of a single CA-NSC channel excised (arrow) into 1 mM Ca²⁺. B, C, D, Stability plots illustrating P_o (B), mean open time (C), and mean closed time (D) analyzed over a moving 20-s time window for the bottom trace shown in A. After exclusion of the first 20-s segment the P_o time course in B was tentatively fit by an exponential relaxing to a new steady state (solid line).

Decline of CA-NSC activity in excised patches reflects loss of apparent affinity for cytoplasmic Ca²⁺

Since the onset of deactivation after excision seemed to occur later when patches were excised into higher [Ca²⁺] (Fig. 4), it seemed possible that the observed decline in channel activity reflects a gradual loss of sensitivity toward activating Ca²⁺. To test this idea, we excised patches into 1 mM Ca²⁺ followed by rapid test applications of low (micromolar) [Ca²⁺] at various times after excision. Whereas the close-to-maximal activity declined only to about half-maximal when bath [Ca²⁺] was lowered to 20 μM a few seconds after excision, a repeated test application of 20 μM Ca²⁺ to the same patch ∼3 min later typically resulted in immediate closure of all channels (Fig. 5 A).

To further characterize the remaining, relatively steady (compare to Fig. 4, B–D) gating of deactivated channels, steady-state activity was observed at several different [Ca²⁺]_i, bracketed by applications of 1 mM Ca²⁺ as a reference (Fig. 5 B). The low P_o of ∼0.3 of these deactivated channels was substantially increased when [Ca²⁺]_i was stepped from 1 mM to 10 mM, and little activity remained at 100 μM [Ca²⁺]_i, indicating that for deactivated channels the apparent affinity for Ca²⁺, as reported by P_o, was shifted to the millimolar range.

The P_o vs. [Ca²⁺]_i plot constructed from such records (Fig. 5 C, left, solid triangles) was reasonably fit by the Michaelis-Menten equation (solid line) yielding an apparent K_1/2 value for activation of P_o by Ca²⁺ of 0.71 ± 0.15 mM. Kinetic analysis revealed overall features similar to those seen before deactivation (compare to Fig. 3, B and C), in that Ca²⁺ mainly stimulated opening rates (Fig. 5 C, center, solid triangles and fit line), whereas closing rates showed little [Ca²⁺]-dependence (Fig. 5 C, right). The almost two orders-of-magnitude lower apparent affinity of these deactivated channels, compared to freshly excised ones (empty triangles and dashed lines, Fig. 5 C, left) for activation of P_o by Ca²⁺ resulted from a lower sensitivity for channel opening by Ca²⁺ (Fig. 5 C, center; compare to Fig. 4 D), as well as from the ∼10-fold faster channel closing rate which averaged 25 ± 2 s⁻¹ for the deactivated channels (Fig. 5 C, right; compare to Fig. 4 C).

For Ca²⁺-activated K⁺-channels it is well-known that the apparent affinity for Ca²⁺ is sensitive to membrane voltage (e.g., Rothberg and Magleby, 2000). Because we found that depolarizing the membrane increased P_o of our CA-NSC channels (Fig. 2 A; compare to Fig. 6 below), we tested whether depolarization affected the apparent affinity for Ca²⁺. The P_o vs. [Ca²⁺]_i plot at +40 mV membrane potential was indeed somewhat shifted to the left, yielding an apparent K_m of ∼80 μM (solid circles and dotted line, Fig. 5 C, left). This partial restoration, at the depolarized potential, of the apparent affinity for Ca²⁺ of deactivated channels was caused both by an increase in the sensitivity of opening rate for Ca²⁺ (solid circles, Fig. 5 C, center), as well as by an overall slowing of the closing rate which averaged 11 ± 1 s⁻¹ at +40 mV (Fig. 5 C, right; see figure legend for detailed statistical analysis).

Gating of CA-NSCs in excised patches is voltage-dependent

Because depolarized membrane potentials activated P_o (Fig. 2 A) by increasing the sensitivity to Ca²⁺ (Fig. 5 C), we systematically examined the influence of membrane voltage on channel gating in inside-out patches exposed to constant [Ca²⁺]. In steady-state records, obtained in 1 mM Ca²⁺ after deactivation, P_o evidently increased with more depolarized membrane potentials (Fig. 6 A). A Boltzmann fit to a plot of steady-state P_o as a function of membrane voltage (Fig. 6 B, solid symbols and line) yielded a half-maximally activating voltage of 20 ± 7 mV, and the slope corresponded to the movement of 0.4 ± 0.1 elementary charges through the entire membrane field. Mean opening and closing rates were both affected by membrane voltage; opening rates (Fig. 6 C) increased, whereas closing rates (Fig. 6 D) decreased exponentially with depolarizing potentials. These tendencies and the resulting fit parameters (legend to Fig. 6) were consistent with the observed overall effect of voltage on channel P_o.

This voltage dependence was not a property acquired only by deactivated channels, because depolarization, even early after excision, increased P_o in all cases (compare to Fig. 2 A). Kinetic parameters (in 1 mM Ca²⁺) were extracted from a limited number of patches in which a relatively late onset of deactivation allowed sampling of early channel gating at −40, +40, −80, −120 mV, and again −40 mV, before a significant decline in channel activity between the two bracketing −40-mV segments was discernible (Fig. 6, B–D, empty symbols). While in these early records P_o was close to unity at −40 mV (average P_o was 0.90 ± 0.02) indicating that 1 mM Ca_i²⁺ was saturating for activation of P_o at this voltage (compare to Figs. 2 C, 3 A, and 4 B), at −80 mV P_o declined to 0.78 ± 0.02, and at −120 mV to 0.55 ± 0.14. A Boltzmann fit to this plot (Fig. 6 B, dashed line) yielded a half-maximally activating voltage of −129 ± 10 mV and an effective gating charge of 0.6 ± 0.1 elementary charges. Thus, deactivation resulted in a shift of the voltage-activation curve by ∼150 mV toward depolarized potentials when studied at a fixed [Ca²⁺], just as it appeared to shift the dose response curve for activation by Ca²⁺ when studied at a fixed voltage (Fig. 5 C).

Complex pattern of CA-NSC single-channel gating

To obtain more information about the mechanism by which Ca²⁺ and voltage regulate gating, we examined how the distributions of dwell times are affected by these two parameters. Since this more detailed dwell-time analysis requires collection of many gating events from long steady-state records, we were restricted to studying records from partially deactivated patches bathed in high [Ca²⁺].

We first compared open- and closed-time distributions at −40 mV membrane potential for 100 μM and for 1 mM Ca_i²⁺, after compiling events from eight single-channel patches in five of which both conditions were tested. Open-time distributions were fit with four exponential components (Fig. 7, A and B, right, solid lines) which gave similar time constants at both [Ca²⁺], although the two longest components seemed somewhat more populated at higher [Ca²⁺] (23 ± 1 and 6 ± 0.3% at 1 mM Ca²⁺ vs. 13 ± 2 and 4 ± 0.4% at 100 μM; see a_o3 and a_o4, legend to Fig. 7) predicting ∼50% longer mean open times at 1 mM Ca²⁺ relative to 100 μM—which is not inconsistent with the observed slight slowing of channel closure by Ca²⁺ (Fig. 5 C, right). Closed time distributions required five components for a good fit (Fig. 7, A and B, left, solid lines). The fifth (longest) component was approximately sixfold more populated, and showed approximately threefold longer lifetime, in 100 μM than in 1 mM Ca²⁺, indicating the presence of a Ca²⁺-sensitive long-lived closed state adequate to explain the observed difference (fourfold) in the mean closed times (Fig. 5 C, center).

Next, we studied the dwell-time distributions at −80 and −20 mV membrane voltages, at a fixed [Ca²⁺]_i of 1 mM (Fig. 8, A and B). Closed-time distributions were fit with five (−80 mV) and four (−20 mV) exponential components (Fig. 8, A and B, left). The voltage-dependent decrease in the fractional amplitude of the three longest components of the closed-time distribution (a_c3, a_c4, and a_c5; see legends to Fig. 8, A and B; Fig. 7 B) was adequate to explain the observed stimulation by depolarization of opening rate (Fig. 6 C); despite its small incidence (2%), the presence of the longest (fifth) component (compare to Fig. 7) alone prolonged the mean closed time at −80 mV almost twofold relative to −20 mV, where this component was not detected (Fig. 8, A and B, left). The depolarization-induced prolongation of mean open times (compare to Fig. 6 D) was caused by a voltage-dependent increase in the fractional amplitude of the longer components of the open-time distribution (see a_o3, legend to Fig. 8; a_o3 and a_o4, legend to Fig. 7 B).

Channel activation elicited by a depolarizing voltage pulse was relatively slow, with ∼10-fold faster deactivation upon repolarization. Time-dependent changes were difficult to quantitate because of the typically small numbers of channels present in a patch. A reconstruction of macroscopic current time courses was attempted by adding up single-channel current traces recorded in response to voltage jumps either from −80 to +40 mV or vice versa (Fig. 8 C). The current relaxations to the new steady states were fit by single exponentials (solid lines) yielding time constants of ∼2 s for activation and of ∼200 ms for the tail current at −80 mV.

Reducing agents partially restore high CA-NSC activity lost after patch excision

Since the rundown observed in excised patches could reflect oxidation of residues at the cytosolic face of the channels, we examined whether dithiothreitol (DTT), a sulfhydryl-reducing agent, would restore activity of CA-NSCs after spontaneous deactivation (Fig. 9 A). Application of 1 mM DTT elicited two effects on CA-NSC activity. A variable increase in P_o was always accompanied by the appearance of fast gating, presumably reflecting flickery block of the channels by DTT. Therefore, the extent of activation attributed to the reducing action of DTT could be fully estimated only immediately after DTT was removed. DTT washoff typically revealed robust reactivation (e.g., of seven out of eight channels, Fig. 9 A), followed by repeated deactivation with a time course similar to that seen initially after excision (Fig. 9 A, solid fit lines).

FIGURE 9.

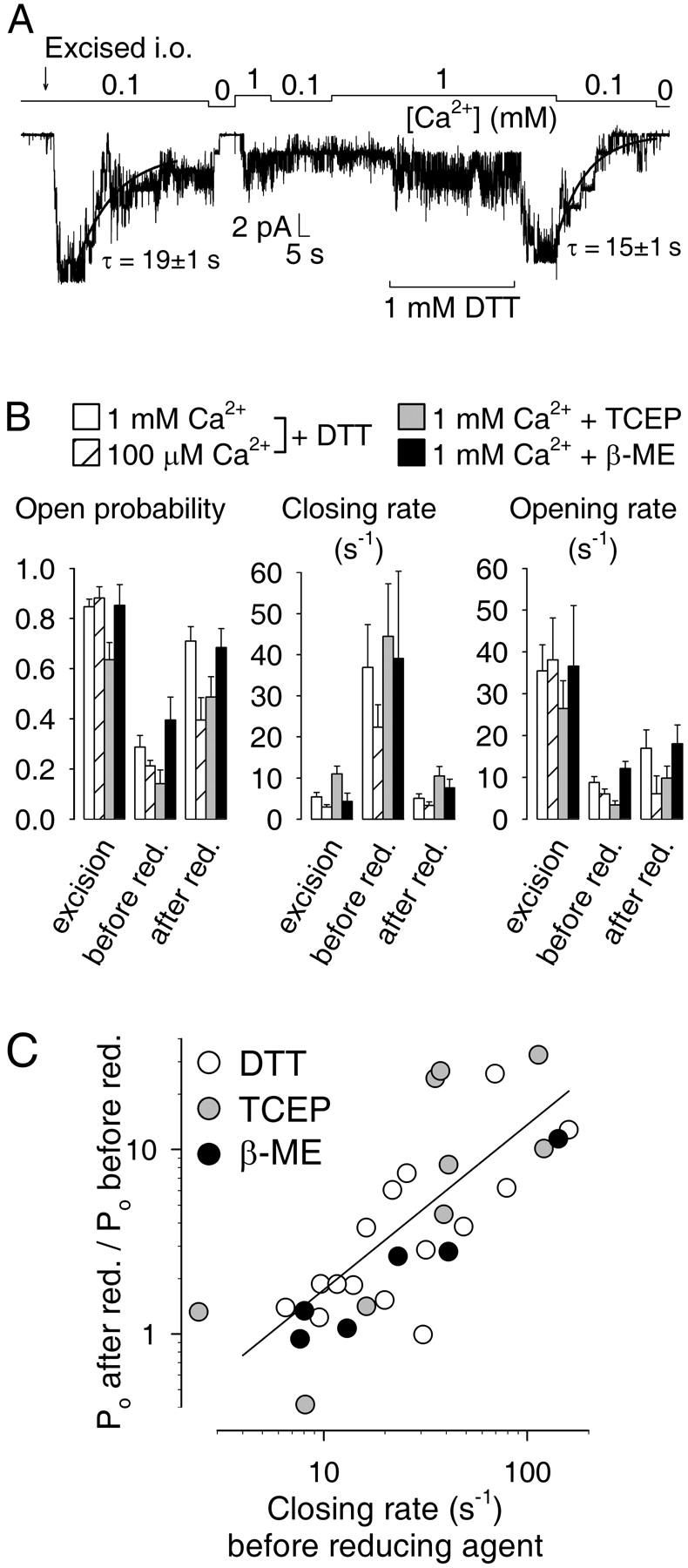
Reducing agents reactivate CA-NSC channels after rundown. (A) Current trace from a patch excised (arrow) into 100 μM Ca²⁺. 1 mM DTT was applied to deactivated channels as indicated (bar). Decay time courses were fitted with single exponentials (solid lines). (B) Comparison of kinetic parameters during deactivation and recovery. Average P_o (left panel) closing rates (center panel) and opening rates (right panel) immediately upon excision, after deactivation, and after treatment with reducing agents (groups of bars at left, center, and right of each panel). The effect of treatment on gating was studied both in 1 mM (□) and 100 μM Ca²⁺ () for DTT, but only in 1 mM Ca²⁺ for TCEP () and β-ME (▪). Reducing agents were applied at 1 mM with 1 mM Ca²⁺ present in all cases. (C) Efficiency of reactivation by reducing agents. Fractional elevation of P_o after treatment plotted against closing rate before exposure to 1 mM DTT (○), TCEP (), or β-ME (•), all in 1 mM Ca²⁺. (Solid line) Linear regression to the log-log plot. Numbers of experiments and statistics: n = 15, 8, 11, and 6, respectively, for DTT (1 mM Ca²⁺), DTT (100 μM Ca²⁺), TCEP, and β-ME. After DTT treatment, P_o increased significantly both in 1 mM Ca²⁺ (p < 0.00001) and in 100 μM Ca²⁺ (p = 0.07), but remained significantly smaller than immediately upon excision (p = 0.04 and p = 0.0004, respectively). Closing rate of deactivated channels, both in 1 mM and 100 μM Ca²⁺, was significantly reduced by DTT (p = 0.005, and p = 0.004) and became indistinguishable from immediate post-excision values (p = 0.83 and p = 0.68). Opening rate of deactivated channels after DTT treatment was somewhat elevated in 1 mM Ca²⁺ (p = 0.08), but not in 100 μM Ca²⁺ (p = 0.997). TCEP or β-ME treatment both significantly stimulated P_o of deactivated channels (p = 0.002 and p = 0.04), and both reduced closing rates to immediate post-excision values (p = 0.88 and p = 0.29).

The extent of the DTT effect was variable; in a total of 23 patches, near-complete reactivation was observed in only 10 cases; smaller increases in P_o in six cases; and in seven cases, no activation occurred at all. To elucidate the reason for this variability, we compared the kinetic parameters of the channels in 1 mM Ca²⁺ right after excision, after deactivation, and after a 30- to 60-s treatment with 1 mM DTT (Fig. 9 B, white bars). DTT treatment of deactivated channels resulted in a substantial elevation of average P_o which, however, remained significantly lower than immediately after excision (white bars, Fig. 9 B, left; see legend to Fig. 9 for detailed statistical analysis). Closing rates, which were accelerated ∼10-fold for deactivated channels (compare to Figs. 4 C and 5 C), were completely restored to immediate post-excision values after DTT treatment (white bars, Fig. 9 B, center). In contrast, opening rates, slowed ∼fourfold by deactivation (compare to Figs. 4 D and 5 C), were only slightly affected by DTT (white bars, Fig. 9 B, right).

Because closing rates showed little dependence on [Ca²⁺] (Fig. 3 C), and deactivation increased closing rate in a Ca²⁺-independent manner (Fig. 5 C, right), we tested the effect of DTT treatment on gating kinetics at lower, 100 μM, Ca²⁺ (Fig. 9 B, striped bars). (During the exposure to DTT 1 mM Ca²⁺ was present in all cases; see also Fig. 9 A). At this lower Ca²⁺ DTT elicited a smaller, but still significant, increase in P_o (Fig. 9 B, left) and restored slow closing rate just as completely as in 1 mM Ca²⁺ (center), but no effect on opening rate was detectable (right).

Alternative sulfhydryl-reducing agents, such as the trialkylphosphine tris(2-carboxyethyl)phosphine (TCEP), a potent and selective reducer of disulfide bridges (e.g., Han and Han, 1994), and β-mercaptoethanol (β-ME) both elicited effects qualitatively similar to that of DTT, in that they both significantly enhanced P_o of deactivated channels (gray and black bars, Fig. 9 B, left); and both exerted their effects mainly by reducing channel closing rate with smaller effects on opening rate (Fig. 9 B, center, right).

Because the reducing agents seemed to influence mainly channel closing rate, which was highly variable for deactivated channels (center group of bars, Fig. 9 B, center panel), we tested whether the variable P_o response of such channels to treatment with various reducing agents correlated with the variability of channel closing rate before the treatment. Assuming that the opening rate (r_CO) is not changed by treatment with reducing agents, the fractional increase in open probability is given by P_o2/P_o1 = (1 + r_OC1/r_CO)/(1 + r_OC2/r_CO), where P_o1, P_o2, r_OC1, and r_OC2 are open probabilities and closing rates before and after the treatment, respectively. Since r_OC2 and r_CO showed relatively little variance, with r_CO ∼ 10 s⁻¹ and r_OC2 < r_CO (Fig. 9 B), the fractional P_o response depends on the largely variable pretreatment closing rate (r_OC1) as P_o2/P_o1 ≈ 1 + (0.1/s⁻¹)r_OC1 or, for r_OC1 > 10s⁻¹, log(P_o2/P_o1) ≈ −1 + log(r_OC1/s⁻¹). Therefore, we fitted a (linear or log-log, Fig. 9 C) plot of P_o2/P_o1 vs. r_OC1 with a straight line and performed one-way ANOVA analysis to determine the significance of the correlation between these two parameters. Both the fit results (fitting the plots with y = a + bx yielded fit parameters a = 2.4, b = 0.11/s⁻¹ for the linear plot, and a = −0.66, b = 0.90 for the log-log plot in Fig. 9 C) and the ANOVA values (p = 0.002 and p < 0.00001) are consistent with the above interpretation. Thus, reducing agents reactivated P_o most efficiently in patches where channel closing rate before the treatment was fast, whereas the nonresponders corresponded to patches in which deactivation had occurred without a marked acceleration of closing rate.

DISCUSSION

The key findings of this work are that 1), CA-NSC channel gating is sensitive to membrane voltage; 2), micromolar Ca²⁺ activates the channels by increasing opening rate; 3), the sensitivities to voltage and Ca²⁺ are interdependent properties; 4), the dwell-time distributions indicate a complex pattern of single-channel gating; and 5), excision of patches into an extracellular environment results in a dramatic decrease in sensitivity toward Ca²⁺ and voltage, a process partially reversed by sulfhydryl-reducing agents.

Molecular identity of the CA-NSC channel

The presence of Ca²⁺- and ATP-sensitive channels selective to monovalent cations has been reported in a variety of tissues including isolated intact capillaries from rat brain (Popp and Gögelein, 1992). The channels we have studied in our primary culture of RBCE cells are identical to the CA-NSCs present in native brain capillaries, based on their identical biophysical properties (Fig. 1).

TrpM4b, a recently identified member of the Trp family of ion channels (reviewed, e.g., in Montell, 2001) is the first cloned channel with biophysical properties similar to those of the native CA-NSCs, in that it is a 25-pS channel selective to monovalent cations and is activated by nanomolar Ca²⁺, although it was not shown to be sensitive to adenine nucleotides (Launay et al., 2002). Most native CA-NSCs require micromolar Ca²⁺ for activation (Colquhoun et al., 1981; Yellen, 1982; Maruyama and Petersen, 1982a; Marty et al., 1984; Gray and Argent, 1990) and are inhibited by adenine nucleotides, although nanomolar Ca²⁺-affinities, comparable to that of TrpM4b, have been reported for nonselective channels in astrocytes (Chen and Simard, 2001) and in an endothelial cell line derived from human umbilical vein (Kamouchi et al., 1999, Suh et al., 2002). It is not clear, at present, whether any of the native CA-NSCs are encoded by the TrpM4b gene (or a splice-variant), and whether the native channels may contain accessory subunits which confer their nucleotide sensitivity (reviewed in Petersen, 2002).

Regulation of CA-NSC channel kinetics by Ca²⁺ and voltage resembles that of large-conductance Ca²⁺-activated K⁺ channels

The original study which reported the presence of CA-NSCs in brain capillaries (Popp and Gögelein, 1992) was conducted in 1 mM cytoplasmic Ca²⁺, and the sensitivity of the channels to [Ca²⁺]_i was not addressed. The present study revealed activation by [Ca²⁺]_i in the low micromolar range ( Fig. 3 A), comparable to CA-NSCs in most native tissues (see above). Analysis of gating kinetics over a range of [Ca²⁺]_i showed that activation by increasing Ca²⁺ reflected a gradual shortening of the mean closed time with little change in the mean open time (Fig. 3, B and C).

Voltage-dependence of gating of CA-NSCs was addressed only by a few of the studies that have examined such channels in various tissues. No pronounced dependence of open probability on membrane potential was reported for nonselective channels in heart muscle (Colquhoun et al., 1981) or neuroblastoma (Yellen, 1982). In contrast, significant voltage-dependence was reported for nonselective cation channels of pancreatic duct cells (Gray and Argent, 1990).

In brain endothelium we have found that CA-NSC channel activity increases when the membrane is depolarized (Fig. 2 A; Fig. 6). The steepness of this voltage-dependence is moderate (effective gating charge z ∼ 1) when compared to that of voltage-gated Na⁺- and K⁺-channels (z ∼ 13; e.g., Islas and Sigworth, 1999) for which depolarization is the primary trigger of channel opening. Still, stimulation by depolarization may have some physiological significance for CA-NSC activation by providing a positive feedback, considering that opening of these channels itself is expected to depolarize the membrane toward a voltage close to 0 mV. When [Ca²⁺] is high compared to the apparent Ca²⁺-affinity of the CA-NSC channel, voltage changes within the physiological range (i.e., between −80 and +80 mV), have little effect on P_o (Fig. 6 B, empty symbols); which might explain why voltage-dependence of gating was not noticed in the original study by Popp and Gögelein (1992). However, significant stimulation of P_o occurs upon depolarization to ∼0 mV from a resting potential of ∼−40 mV (Hoyer et al., 1991) when [Ca²⁺] is limiting (Fig. 6 B, solid symbols).

Although the dwell-time distributions could be studied in detail only for partially deactivated channels, such studies were justified by the qualitatively similar dependence on Ca²⁺ and voltage of the rough gating parameters (P_o, mean opening and closing rate) of such channels and of freshly excised CA-NSCs, differing only in their sensitivities for activating Ca²⁺ and voltage (see Fig. 5 C and Fig. 6, B–D). The pattern of single-channel gating was complex, suggesting the presence of at least four kinetically distinguishable open states as well as of at least five closed states, whose lifetimes and relative occupancies were differentially affected by [Ca²⁺] and voltage (Figs. 7 and 8). The leftward shift in the sensitivity of P_o to [Ca²⁺]_i upon depolarization (Fig. 5 C, left) is consistent with either channel opening being driven by voltage-dependent binding of Ca²⁺ or with any model with (at least) two separate steps involved in channel activation, (at least) one voltage- and (at least) one Ca²⁺-dependent. The many-component dwell-time distributions and their sensitivities to both Ca²⁺ and voltage suggest a complex gating model for CA-NSCs reminiscent of that of large-conductance Ca²⁺-activated K⁺ (BK) channels.

Indeed, there is a remarkable similarity between the gating of CA-NSCs reported in this article, and that of BK channels. BK channels are also activated by voltage and by Ca²⁺. Their voltage dependence is also moderate (z ∼ 2; e.g., Diaz et al., 1998; Rothberg and Magleby, 2000) compared to that of other voltage-dependent K⁺ channels, and their apparent Ca²⁺ affinity is also in the micromolar range; apparent K_1/2 values for activation of BK-channel P_o by Ca²⁺ of 19 μM at −40 mV (Pérez et al., 2001, compare to Fig. 3 A) and of 11 μM at +30 mV (Rothberg and Magleby, 1999) have been reported. Furthermore, apparent Ca²⁺ affinity of the BK channel is shifted by voltage (e.g., Rothberg and Magleby, 2000) much the same way as we find here for the CA-NSC of brain endothelium (Fig. 5 C). Similarly, raising [Ca²⁺]_i shifts the voltage of half-maximal activation (V_1/2) of the BK channel, by as much as 175 mV between extremes of [Ca²⁺]_i, without changing the effective gating charge (Rothberg and Magleby, 2000; compare to Diaz et al., 1998). This is paralleled, in the case of our CA-NSC channels, by a 150-mV shift in V_1/2 during post-excision deactivation (Fig. 6 B), a process which lowers the apparent affinity for Ca²⁺, and thus, the occupancy of the Ca²⁺ binding site(s) at constant [Ca²⁺]_i (Fig. 5 C). Moreover, the way in which BK-channel kinetics is modulated by Ca²⁺ and voltage is mirrored by our CA-NSCs, in that for both channels Ca²⁺ mainly stimulates opening rate, with a much smaller effect on closing rate (10⁴-fold vs. 10-fold over 6 orders of magnitude of [Ca²⁺] for BK channels, Rothberg and Magleby, 2000; compare to Fig. 3, B and C); and for both, depolarization accelerates opening and slows closing (Rothberg and Magleby, 2000; compare to Fig. 6, C and D). Finally, the dwell-time distributions of both BK and CA-NSC channels are complex, indicating multiple closed and open states.

Utilizing the extreme stability of BK single-channel records which allow collection of millions of gating events at steady state, and of macroscopic currents from cloned BK channels overexpressed in Xenopus oocytes, concerted effort from several laboratories over the past 15 years have resulted in multistate allosteric models that explain BK-channel behavior over extreme ranges of Ca²⁺ and voltage (e.g., Stefani et al., 1997; Rothberg and Magleby, 1998, 1999, 2000; Horrigan et al., 1999; Horrigan and Aldrich, 1999). To determine how far the gating of our CA-NSC channels in brain endothelium resembles that of BK channels on this microscopic level will obviously require more detailed analysis of single-channel kinetics over a range of [Ca²⁺]_i and voltage and, once obtainable, of macroscopic ionic and gating currents over a range of voltage.

Deactivation after patch excision

CA-NSCs in excised patches deactivated within 2–3 min (Fig. 4, A and B) due to a gradual shortening of open times and a prolongation of closed times (Fig. 4, C and D), which reflected a desensitization of the channels toward activating Ca²⁺ (Fig. 5) and voltage (Fig. 6). Presumably, the apparent Ca²⁺-affinity starts to decline immediately after excision; the apparent onset of deactivation is delayed in higher [Ca²⁺] (compare the traces in Fig. 4 A) because in high [Ca²⁺] a larger shift in the Ca²⁺-activation curve is required for a substantial decrease in P_o (compare to Fig. 5 C, left). Thus, the perhaps most sensitive condition to measure deactivation rate is to record in 100 μM Ca_i²⁺ where P_o declines from a value close to unity right after excision to near zero within ∼1 min (Fig. 4 A, center trace; and Fig. 5 C, left). Interestingly, inactivation with a similar time course of nonselective cation channels excised from pancreatic acini was noted by Maruyama and Petersen (1984) and was also shown to reflect a loss of sensitivity to Ca²⁺.

Our efforts to understand the molecular events underlying this dramatic loss of Ca²⁺ affinity (and voltage-sensitivity) of CA-NSCs after patch excision remained so far incomplete. One possibility that we considered was that deactivation reflects oxidation of some residues (e.g., cysteines) at the cytosolic face of the channels, once they are exposed to the oxidizing extracellular environment. Such mechanisms have been demonstrated for several ion channels, including BK-channels (DiChiara and Reinhart, 1997; Soto et al., 2002) and nonselective cation channels of brown adipose tissue (Koivisto and Nedergaard, 1995). The dramatic stimulation of deactivated CA-NSCs by sulfhydryl-reducing agents such as DTT, TCEP, and β-ME (Fig. 9, A and B) supports the above hypothesis. However, although these reducing agents were very effective in restoring the slow channel closing rate characteristic of freshly excised channels (Fig. 9 B, center, Fig. 9 C), they had little or no effect on opening rate (Fig. 9 B, right).

Thus, it appears that the two kinetic phenomena which accompany channel deactivation reflect two separate processes. Formation of disulfide bridges may underlie acceleration of closing rate, whereas some other mechanism is responsible for the loss of sensitivity to Ca²⁺ of channel opening rate. Such mechanisms could include dephosphorylation of the CA-NSC channel protein, loss of a diffusible factor or loosely associated auxiliary subunit, or a change in the lipid composition of the membrane, all of which have been observed for different classes of ion channels. It is interesting to note that S-nitrosylation of cysteine side chains has recently been identified as one of the mechanisms by which nitric oxide directly modulates the function of various ion channels (reviewed, e.g., in Ahern et al., 2002). Although the physiological function of the CA-NSC channel in brain capillary endothelium is as yet unknown, the presence of reactive cysteines on the intracellular side suggests that nitric oxide may modulate its behavior, as has been described for nonselective cation channels in macrovascular endothelial cells (Suh et al., 2002).

Physiological implications

Various roles have been proposed for Ca²⁺-activated nonselective cation channels in different tissues, including involvement in cell-volume regulation (Volk et al., 1995) and in fluid secretion (Maruyama and Petersen, 1982b; Marty et al., 1984), and modulation of the driving force for Ca²⁺ entry (Chen and Simard, 2001; Launay et al., 2002). Although the physiological role of the CA-NSC channel in brain endothelium was not addressed by this study, the observed biophysical properties admit some speculation on this subject.

First, the gating machinery of the CA-NSC, which requires micromolar Ca²⁺ for activation, suggests that a local Ca²⁺ source must be responsible for activating these channels; the same way as BK channels are activated by local increases in the concentration of Ca²⁺ ions which enter the cytosol either from the extracellular fluid via active plasma-membrane ion channels (Robitaille et al., 1993; Hoyer et al., 1994), or from intracellular Ca²⁺ stores via ryanodine receptors (e.g., Pérez et al., 2001). In brain capillary endothelium, store-operated Ca²⁺ channels (Dömötör et al., 1998) and a high density of stretch-activated cation channels (Popp et al., 1992) constitute possible Ca²⁺ influx pathways through the plasma membrane, and IP₃ receptors mediate Ca²⁺ release from stores (Dömötör et al., 1998; Sipos et al., 2000; Gerencsér and Adam-Vizi, 2001). In addition to local Ca²⁺, modulation of CA-NSC activity by nucleotides provides a, likely equally important, regulatory mechanism which links channel activity to the metabolic state of the cell.

Second, the lack of discrimination in the CA-NSC pore between Na⁺ and K⁺ (Fig. 1 B) suggests that once activated, opening of the CA-NSCs will result in membrane depolarization, and, possibly, the loading of the cells with Na⁺ (in contrast to BK channels which hyperpolarize the membrane). These consequences of CA-NSC activity are expected to feed back in several different ways onto the mechanisms that regulate Ca²⁺ homeostasis. By reducing the driving force for Ca²⁺, depolarization might limit further Ca²⁺ entry through the plasma membrane (Launay et al., 2002). At the same time, electrogenic Na⁺/Ca²⁺ exchange, a key mechanism in the termination of bulk cytosolic Ca²⁺ transients in RBCE cells (Dömötör et al., 1998), should be slowed both by depolarization and by increased cytosolic [Na⁺]. Such effects may contribute to the shaping of the time course of cytosolic Ca²⁺ signals.

CONCLUSION

We have provided the first quantitative biophysical description of the gating of the Ca²⁺- and ATP-sensitive nonselective cation channel in RBCE cells, with an emphasis on regulation by Ca²⁺ and voltage, and have found a striking similarity to that of large-conductance Ca²⁺-activated K⁺ channels. We have also identified cysteine oxidation as one of the mechanisms responsible for channel deactivation in excised patches. Further studies will need to address the molecular identity, modulation by adenine nucleotides, and the identification of the physiological sources of Ca²⁺ underlying activation of these channels in intact brain capillaries.