Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Jul;85(1):442–450. doi: 10.1016/S0006-3495(03)74489-0

Multichannel Carotenoid Deactivation in Photosynthetic Light Harvesting as Identified by an Evolutionary Target Analysis

Wendel Wohlleben *, Tiago Buckup *, Jennifer L Herek †, Richard J Cogdell ‡, Marcus Motzkus *
PMCID: PMC1303100  PMID: 12829499

Abstract

A new channel of excitation energy deactivation in bacterial light harvesting was recently discovered, which leads to carotenoid triplet population on an ultrafast timescale. Here we show that this mechanism is also active in LH2 of Rhodopseudomonas acidophila through analysis of transient absorption data with an evolutionary target analysis. The algorithm offers flexible testing of kinetic network models with low a priori knowledge requirements. It applies universally to the simultaneous fitting of target state spectra and rate constants to time-wavelength-resolved data. Our best-fit model reproduces correctly the well-known cooling and decay behavior in the S1 band, but necessitates an additional, clearly distinct singlet state that does not exchange with S1, promotes ultrafast triplet population and participates in photosynthetic energy transfer.

INTRODUCTION

Photosynthesis relies on light harvesting (LH) in complexes of pigment molecules that absorb different colors of sunlight and subsequently transfer that energy to a common acceptor state. In purple bacteria, harvested excitation energy from the absorption of blue-green light to the S2 state (1Bu+ in the idealized C2h symmetry) in carotenoids (Car) undergoes ultrafast partitioning between excitation energy transfer (EET) to bacteriochlorophyll (BChl) and relaxation to lower Car states (Sundström et al., 1999). Among the low-lying excited states of Car, the S1 state (Inline graphic) has been studied extensively (Frank, 2001; Polivka et al., 2001; Walla et al., 2000; Zhang et al., 2000a). This state is populated by internal conversion from S2, and undergoes further nonradiative decay to the ground state (S0) and in some LH complexes also EET to BChl (Cogdell and Frank, 1987). Recently a second S2 deactivation channel has been found in LH1 of Rhodospirillum rubrum (Gradinaru et al., 2001) and LH2 of Rhodobacter sphaeroides (Papagiannakis et al., 2002; Zhang et al., 2000b), which leads to triplet population on an ultrafast timescale. In the latter species, that new deactivation channel also plays an important role in the EET to BChl (Papagiannakis et al., 2002).

Despite their biological importance as a protection against oxidation from singlet oxygen, natural Car triplet states are poorly characterized (Christensen, 1999); available information mostly concerns their formation via slow triplet-triplet exchange processes (Bittl et al., 2001). In contrast, the mechanism of ultrafast triplet population can be explained in terms of the electronic structure of a covalent excitation in polyenes, which is made by the spin pairing flip in two of the ethylene units. It can thus be regarded as a simultaneous excitation of two triplets, whose coupling generates an overall singlet state (Tavan and Schulten, 1987). The assembly in the LH complex exerts a lattice distortion on the Car (Freer et al., 1996) that will eventually equal the weak triplet-triplet coupling. This conformational effect explains why fission of the overall singlet state into two localized triplet states (Garavelli et al., 2000; Gradinaru et al., 2001; Tavan and Schulten, 1987) occurs only in the LH complex, but not in solution (Gradinaru et al., 2001; Zhang et al., 2000b).

Here we study the energy flow in LH2 of Rhodopseudomonas acidophila with transient absorption measurements. The structure of this species is known to atomic resolution and comprises nine Car (rhodopin glucoside) and 27 BChl molecules (Mc Dermott et al., 1995). Here, the S1 state transfers only very little (5%) of the energy to BChl, while 50% of the total excitation is transferred directly from S2 (Macpherson et al., 2001). The existence of an alternative decay and transfer channel has not yet been established in this species.

Characterisation of the energy flow network requires a solution of the inverse problem, i.e., to retrieve from the time-resolved absorption spectra (which are composed of overlapping signals from many simultaneously populated states) to the physical target states (each element of that sum, resolved in time and wavelength). Traditional methods to draw mechanistic conclusions (Holzwarth, 1996) may start in the simplest approach from a multitude of independently fitted decay curves, as in the lifetime density method (Croce et al., 2001). Components that overlap in spectrum and/or lifetime will be better resolved if a global analysis of all the data is performed (Beechem et al., 1985), as in singular value decomposition (Chen and Braiman, 1991; Yamaguchi and Hamaguchi, 1998). Those are all purely mathematical fitting procedures, that do not involve a physical model of the dynamics. There is further advantage to be gained with so-called target analysis, where the analysis of multiple experiments is done directly for the final parameters of interest, i.e., for rate constants rather than apparent lifetimes (Beechem et al., 1985). One example of target analysis is compartmental modeling (van Stokkum et al., 1994), which is, likewise the previous methods, a deterministic approach.

Indeterministic evolutionary search algorithms (Goldberg, 1993; Zeidler et al., 2001) have been successfully implemented for the inverse problem of data from highly complex and/or nonlinear systems, among them seismic geology (Nath et al., 2000), pattern recognition (Harvey et al., 2000; Husbands and de Oliveira, 1999; Lavine et al., 2002), Mie light scattering (Li and Wilkinson, 2001), and interferometry (Vazquez-Montiel et al., 2002). Related to our study, in the photosynthesis field, a genetic algorithm has been used to fit a lattice model of Photosystem I to spectroscopic data (Trinkunas and Holzwarth, 1996).

In this article we develop an evolutionary target analysis, a new tool for all time-resolved spectroscopy. Challenging more traditional fitting strategies, our algorithm compares the overall fit of a physical model to the experimental data upon simultaneous changes of all parameters. Based on the numerical integration of many different rate equation models, both the linear parameters (spectra) and nonlinear parameters (conversion rates) are fitted. There are no restrictions regarding sequential/coexisting decays, as with the inherently sequential method of species-associated decay spectra (van Stokkum et al., 1994). Furthermore, there are no restrictions on uniqueness of characteristic timescales, as with singular value decomposition (Yamaguchi and Hamaguchi, 1998) and lifetime density (Croce et al., 2001). The algorithm searches the entire parameter space (exchange rates, spectrum of each target state) for the best global fit. This approach makes the method particularly powerful for the decomposition of regions with many coexisting and overlapping contributions, a common problem with transient absorption detection. The quality of the fit is a measure of the adequacy of a specific model for the energy flow network.

The absorption shape of each target state and the conversion rates between them obtained for the best-fit model are in excellent agreement with literature values for the S1 region (Macpherson et al., 2001). In addition, the analysis reveals ultrafast triplet population from an intermediate, independent singlet state that also transfers energy to the BChl. The evolutionary target analysis favors the same model of ultrafast triplet population as proposed for LH2 from Rb. sphaeroides by the Amsterdam group (Papagiannakis et al., 2002).

MATERIALS AND METHODS

Sample preparation

Cultures of Rps. acidophila strain 10,050 were grown and LH2 extracted as detailed in Macpherson et al. (2001). The stock solution was diluted in a TRIS:HCl buffer (50 mM, pH 8) with 0.3% LDAO detergent to prevent aggregation. The samples had absorption at 490 nm between 0.25 and 0.35 OD, in a 0.2-mm-thick rotating cell.

Ultrafast spectroscopy

A schematic of the conventional setup for the ultrafast transient absorption experiment can be found in the online supporting information. A home-built 1-kHz non-collinear optical parametric amplifier (ncOPA) generated the pump beam, centered at 525 nm, with pulse durations ∼30 fs. This excitation is selective for the Car S2 state. Two types of measurements were performed:

  • For the absorption spectrum measurements, a white-light continuum beam was generated as usual by focusing a weak 800-nm beam in a 6-mm-thick sapphire plate. The probe beam was detected using a photomultiplier in conjunction with a monochromator, with a spectral resolution of 3 nm. The time dispersion in the white light was compensated automatically, after a prior calibration, with a computer-controlled delay line synchronized to the monochromator steps. Every transient absorption spectrum is the average of 20 scans of 100 shots per point.

  • For kinetics measurements in the Car region, a second ncOPA operating at 570 nm, and with a large bandwidth, provided the probe beam. After passing the sample, the beam was split and filtered at 550 and 580 nm, using separate interferometric filters (with 10-nm FWHM). The transmitted light was then detected with amplified photodiodes. For kinetics of B850 we attenuated to pump intensities ∼1014 photons/cm2 and used the white light continuum with detection at 880 nm. Kinetics were measured with delay steps varied between 20 fs around time zero and 5 ps at long delays. Each point is the average of 20 scans of 100 laser shots.

To minimize dispersion and chromatic aberrations, all beams were focused and superimposed in the sample with concave mirrors. The pump was attenuated to pulse energies <80 nJ with a diameter of ∼0.35 mm. The probe beams had diameters ∼0.05 mm such that the probed volume is of homogenous pump intensity. A chopper blocks every other pump pulse so that the absorption signal is defined by S = −log (PpumpON/PpumpOFF) with the transmitted probe intensity P. The use of a reference beam did not result in a significantly better signal-to-noise ratio, probably because the noise from the pump is of the same order. The response function in both types of measurements was much shorter than the fitted decays, i.e., 70 fs when a ncOPA was probe and 110 fs in the case of white light.

Data analysis

All data acquisition and processing software is written in the graphical programming LabView environment (National Instruments, Austin, TX), featuring rich mathematics and visualization libraries. Typical computation times on a 750-MHz Pentium III PC are 2 min for one evolutionary target analysis.

RESULTS

We begin by characterizing the transient absorption kinetics obtained in three spectral windows: 550, 580, and 880 nm. The kinetics at 580-nm-probe wavelength are known to reflect the S1–Sn excited state absorption (ESA; Macpherson et al., 2001). The trace shown in Fig. 1 b has been fitted with a single exponential decay, convoluted with the Gaussian instrument response function. We make no effort to resolve the (sub-100 fs) rise time. The small underlying signal measured at long delay times has been subtracted. It has been assumed to be instantaneous and constant, and is assigned to ESA of BChl. The resulting S1 decay time is 3.7 ± 0.1 ps with only a very small (∼5%) much slower component, in excellent agreement with previous measurements (Macpherson et al., 2001). When probing the red wing of the S1 band we observe an increasingly fast decay, reflecting vibrational cooling of the hot S1 state (Fig. 1 b, inset). Within our resolution of ∼70 fs there are no coherent oscillations visible and the Fourier transform of the residual from the exponential decay is structureless.

FIGURE 1.

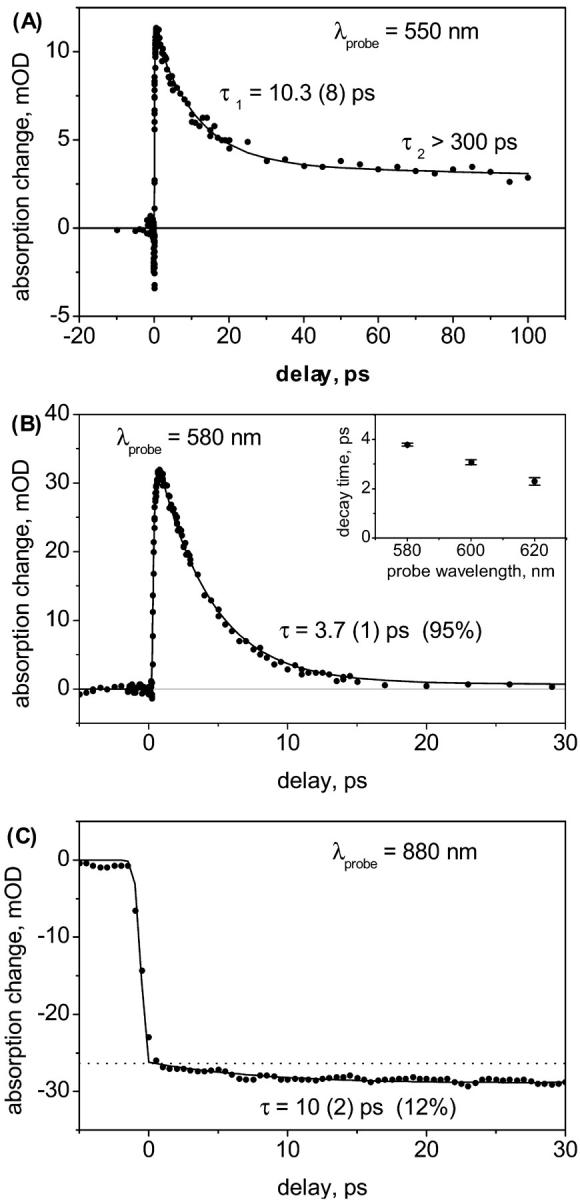
FIGURE 1

Open in a new tab

Kinetics at selected wavelengths. (A) The decay at 550 nm probe wavelength is biexponential with a precursor (S*) that decays within τ = 10.3 ± 0.8 ps into a long-lived state (T) with τ > 300 ps. (B) Kinetics of the S1 state. The decay at 580-nm probe wavelength is 95% monoexponential with τ = 3.7 ± 0.1 ps. The inset shows the increasingly faster decay times at red-shifted probe wavelengths, reflecting vibrational cooling of the S1 state. (C) Kinetics of BChl B850. The dashed horizontal line is a guide to the eye, to show the 12% of population growth from slower components.

The kinetics measured at 550 nm are presented in Fig. 1 a. Here the absorption is weaker but clearly shows a very long-lived component (note the extended delay range as compared to Fig. 1 b). We fit the decay with a double exponential, again convoluted with the instrument response function. The faster decay time is found to be 10.3 ± 0.8 ps. In accordance with previous notation (Gradinaru et al., 2001), we assign this signal to the precursor state S*. The slower decay is much longer than can be determined accurately from the measured delay range, so that we can only give a lower limit of ∼300 ps. This long-lived signal is a strong indication of a carotenoid triplet state T, which is known to have an absorption band in this spectral region between the bleach and the S1 band (Bachilo, 1995). In the fit, we additionally included a negative contribution that decays on the <100 fs timescale. This bleach signal is attributed to stimulated emission from the S2 state at very early times. The delay between the S* ESA and the S2 bleach contributions and the rise time of S* are both fitted to be <100 fs, hinting already at a direct population of S* from the initially excited S2 state.

Fig. 1 c shows kinetics measurements of the BChl stimulated emission from the B850 Qy state (measured at 880 nm) with a double exponential fit. The major component is a fast rise (∼200 fs) and is due to transfer from the initially excited S2 state. Additionally, there is a smaller component (12 ± 2%) of a slow rise, fitted with 10 ± 2 ps. As a comparison, note that the timescale of B800 to B850 transfer is ∼0.9 ps (Macpherson et al., 2001). We identify this 12% of the total EET from Car to BChl as coming from the low-lying singlet states S1 and S*, and since the rise is longer than the S1 lifetime, there must be a contribution from S*. A fit with multiple rise times did not provide unique values, and we rely on the global analysis below to give numbers of relative EET contribution. Previously, a rise contribution to the BChl signal in the same species was observed with a characteristic time of ∼6 ps at 870 nm, but that rise could not be attributed to any source state (Macpherson et al., 2001). We propose that this observation reflected already the EET from the S* channel.

The common belief that the triplet state is located on the Car is further cemented by a saturation experiment: upon scaling up the excitation energy we find identical saturation behavior for the signals at 550 and 580 nm, whereas the BChl B850 signal saturates much earlier due to the close coupling and ensuing annihilation.

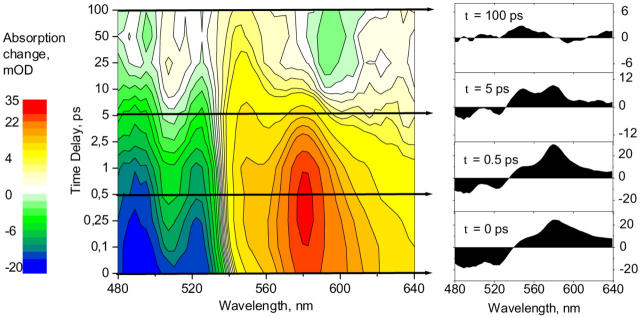
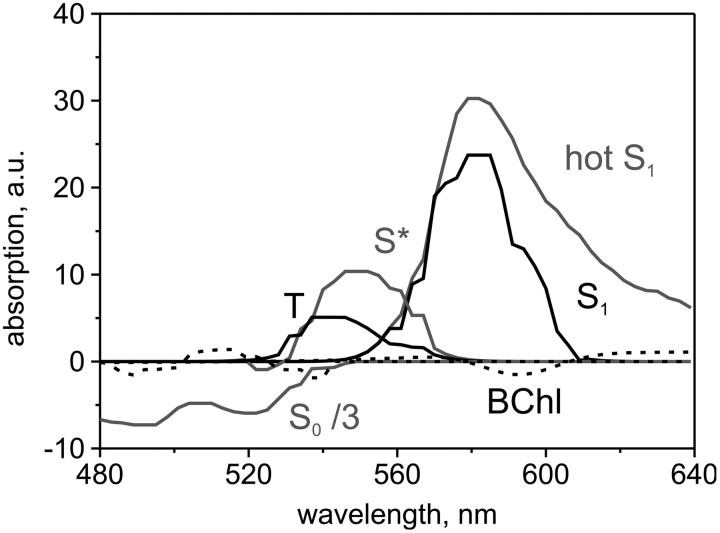
Complementary to kinetics at selected wavelengths are the transient absorption spectra at selected delay times. In the raw data (Fig. 2) we see three major contributions: at 490 and 525 nm, the fast S0–S2 bleach with the 0–1 and 0–0 vibrational bands; at ∼550 nm, the decaying S* and the persistent T absorption; and peaking at 580 nm, the S1 absorption, together with initial vibrational cooling on the red shoulder from 600 to 640 nm. (Coming through a conical intersection from the S2 surface (Fuss et al., 2000) S1 is initially populated in high vibrational levels.) Additionally, at the longest delays, the BChl Qx bleach at 590 nm and the broad Qy ESA are visible.

FIGURE 2.

FIGURE 2

Open in a new tab

Raw data of transient absorption spectra measurements. Wavelengths have been binned to a 3-nm wavelength resolution with better signal-to-noise. Left, two-dimensional contour plot. Zero absorption change is white, positive yellow/red, and negative green/blue. Right, selected delay cuts. At the earliest time, notice the hotS1 absorption >600 nm. Intermediate cuts clearly show the two separate peaks at 550 and 580 nm. At very long delays, a positive signal at 550 nm survives, identified as triplet T absorption.

The raw data shows already the existence of a triplet state, but inspection by eye tells us little about its population characteristics. In the following section we introduce the novel algorithm that globally processes all spectra together. The resulting decomposition of the experimental data into spectra of the individual states and a corresponding kinetics model is presented in the last section.

EVOLUTIONARY TARGET ANALYSIS: ALGORITHM AND RATE EQUATION MODEL

The evolutionary target analysis algorithm solves the classic inverse problem: retrieving from the measured time-wavelength resolved data the physical components (target states) and their respective contributions. In other words, we assume that at any given probe time t and probe wavelength λ, the measured signal Sexp(t,λ) can be described by a sum over all target states i = 1…i with population Pi(t) and spectrum Ai(λ):

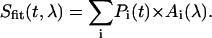graphic file with name M2.gif (1)

We describe the time-dependent populations Pi(t) with a rate equation model that is iterated with a time step Δt according to

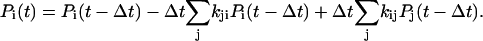graphic file with name M3.gif (2)

Here, kij is the rate of conversion from state j to state i. The first sum describes all decay channels from state i, and the second sum all sources of population from all precursor states j. For N states probed at n wavelengths λ1…λn, the model Sfit(t,λ) = Sfit(t,λ)(Ξ) is defined by the specification of a complete set of parameters Ξ, comprising rate constants kij and amplitudes Ai:

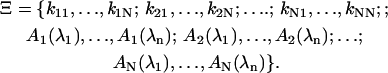graphic file with name M4.gif (3)

Finally, a convolution of the rate equation model with the instrument response function is performed on the matrix Sfit(t,λ).

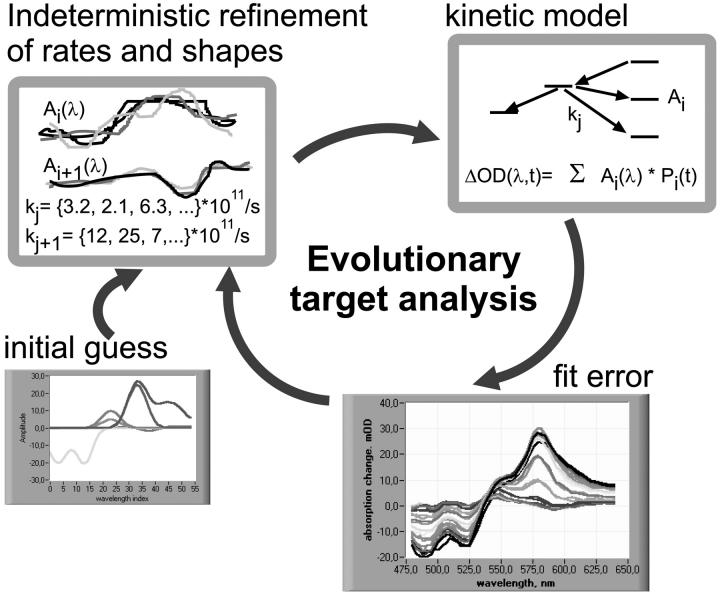
The basic idea of evolutionary target analysis (Fig. 3) is to compare many randomly generated ‘individuals’ Ξ and to optimize the model iteratively, guided by the fitness of each Ξ in Darwinistic meaning. The suitable measure of fitness to achieve the best fit to the experimental data is the quadratic difference

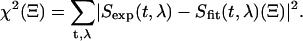graphic file with name M5.gif (4)

The first generation of 48 ‘individuals’ Ξ covers randomly the search space allowed by the parameter boundaries (e.g., maximal or minimal conversion rates). From this set, the eight solutions Ξ with the smallest χ2(Ξ) are taken as ‘parents’ that are recombined and mutated to produce the next generation. In recombination, the parameters of two parents are mixed to create one new individual. With mutation, a number of randomly chosen parameters of a single parent are varied randomly within the preset boundaries (Zeidler et al., 2001). Typically 16 new individuals are produced by recombination, and 32 by mutation to create the next generation. The optimization algorithm implements thus an indeterministic search for the best model within the search space spanned by the several hundred parameters.

FIGURE 3.

FIGURE 3

Open in a new tab

Evolutionary target analysis. The experimenter specifies the energy flow network model to be tested (top right), including reasonably wide intervals for the decay rates and for the target state spectra (top left). An initial guess for the shape of the target spectra (bottom left) is optional. The evolutionary algorithm then optimizes the rates and spectra simultaneously, based on an indeterministic mapping of the entire parameter space within the given intervals. For each set of parameters, the time-dependent spectra are calculated and compared to the experimental data. Only the best sets survive and generate the next generation of parameter sets by mutation and recombination.

A globally better fit of the inverse problem does not require the individual optimization of isolated parameters, but rather the concerted change of several parameters (e.g., the absorption of several states in an overlap region). That is precisely the approach of evolutionary optimization of the entire parameter set described above. An adaptive step length control (Zeidler et al., 2000) decreases the mutation width and thus closes the net around the globally best fit. This analysis applies to the raw experimental data without intermediate processing. No derivatives are needed as, for example, in Levenberg-Marquard nonlinear fitting; only the scalar χ2 has to be calculated. Here, the advantage of evolutionary target analysis becomes obvious: the ease of implementation of rate equation models that have to be numerically integrated. For each individual Ξ, Sfit(t,λ)(Ξ) is calculated on the time-wavelength grid of the experimental data. Initially, the S2 population is set to 1, and the S0 population to −1, since the pump laser excites selectively from the Car S0 to S2 states. All other populations (hotS1, S1, S*, T, and BChl) are set to zero. We treat all EET transfer inclusively as BChl and do not differentiate between transfer to B850 and B800 BChls.

Before the algorithm was applied to the experimental data, it was tested successfully on a computer-generated data set consisting of singly and multipally overlapping Gaussian absorption bands connected with different interconversion rates. We found that for more than approximately five states with complex energy flow and overlapping spectra, one can no longer leave the entire search task to the algorithm. Instead, some physically unlikely ropes of the maximally connected network need to be cut. For example, all rates kij from lower to higher energetic states are fixed at zero, and an initial guess on spectral center positions is required. This input in no way restricts the freedom of the rate equation to account for coexisting and interexchanging channels.

If the input data shows some noise, it is a helpful trick to make use of the inherent multiobjective feedback of evolutionary optimization algorithms: we apply additional genetic pressure on smoothness of target spectra by adding a measure M for smoothness, e.g.,

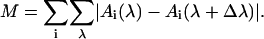graphic file with name M6.gif (5)

The new measure of Darwinistic fitness is χ2 + mM, where the multiplicative factor m is adjusted to give about a quarter relative weight to the smoothness measure. The evolution is now guided by two objectives: low χ2 and smooth target spectra. Another objective might be to place emphasis on a particular range of data. In this case, one would multiply the χ2 from the temporal or spectral window of interest with a factor >1, so that its weight is raised. This approach was used for the BChl rise kinetics within the global data set, to achieve good fitting of the EET contributions.

The percentage Φij of excitation energy deactivation from a source state j into a specific decay channel i = k (as used in Table 1) is calculated from the rates according to 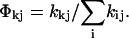Inline graphic The percentage of a cascading deactivation from state j into state l via state k is given by Φlk × Φkj.

TABLE 1.

Rate constants and flow percentages for the best-fit model of carotenoid deactivation in LH2 of Rps. acidophila

Source state Decay channels inverse rates k−1 and percentage of deactivation flow Contribution of source to EET
S2 hotS1 260 fs, 32 ± 5% S* 300 fs, 26 ± 5% BChl 190 fs, 42 ± 7% 42 ± 7%
hotS1 S1 1.5 ± 0.2 ps S*/T > 100 ps, <2%
S1 S0 4.2 ± 0.2 ps S*/T > 60 ps, <5% BChl 35 ± 5 ps, 11 ± 3% 4 ± 1%
S* S0 32 ± 5 ps, 34 ± 6% T 28 ± 5 ps, 39 ± 8% BChl 42 ± 7 ps, 26 ± 6% 7 ± 3%
Open in a new tab

Note that the evolutionary algorithm does not supply error bars on individual parameters, because it always changes the entire parameter set. Instead, we indicate the scatter in the fit results from a few identical fitting runs, that each start with different randomly-generated rate models.

Let us sum up: all parameters that make up the shape of an individual target state (53 points in 3-nm steps from 480 to 640 nm) are glued together by the constraint of having identical time population behavior Pi(t). Several of these constructs become interdependent via the kinetic model that obliges them, for example, to decay from one into the other with kij. The splitting ratio kij/kij′ between channels j and j′ that are populated from the same precursor i is well-defined, if, and only if, the respective decay of j and j′ finally leads again to a common acceptor. Otherwise the lack of knowledge of the relative oscillator strengths of the various transitions used for probing would prevent the determination of population flow. Fortunately, in our case, we have two such final acceptor states—the BChl signal and the bleach recovery of the S2–S0 transition. In that way, a set of several hundred fitting parameters loses independence and becomes a sensible fitting approach.

EVOLUTIONARY TARGET ANALYSIS: RESULTS AND DISCUSSION

To model the excitation energy deactivation in Car, we employ a set of up to seven states with up to 12 transition rates kij that are nonzero. To see if the full complexity is indeed necessary, we also tested various restricted models in which the number of states was reduced and/or the transition rate pattern simplified. Of the global time-wavelength range that determines χ2, these modifications may affect only a very small part, e.g., one state's rise being either instantaneous or delayed. Changes of χ2 with different models are significant whenever they exceed the noise level of the optimal χ2 values in successive fitting runs with an identical model. That noise level is 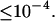Inline graphic

In every scenario, each target spectrum is free to adjust. A bleach component was included in every model; likewise a fixed contribution from BChl ESA and Qx bleach as measured at 100 ps on the red side of the triplet peak. In the more elaborate models an independent, long-lived component in the bleach region was included. The main focus was on the question of existence and interrelation of S*, T, hotS1, and S1 states.

From the quality of the fits with the restricted kinetic models, we can make the following conclusions:

  • Direct population of a long-lived T from S2 without intermediate is excluded, as it raises the optimal χ2 by 4% (compare also the non-single-exponential decay at 550 nm; see Fig. 1 a). There must be an intermediate state.

  • Population of T from S1, is excluded, as in this restriction the optimal χ2 raises by 2%. The early absorption ∼550 nm is not a simple shoulder of S1, but shows independent kinetics, i.e., reflects an independent state S*.

  • Without the hotS1 state, the resulting fitted S1 spectrum only matches the data at intermediate delays, and the shortened fitted S1 lifetime (<3 ps) is not consistent with the bleach recovery, so that the optimal χ2 rises drastically by >50%.

  • A model where hotS1 is independent of S1 but with a faster decay neglects the slight slow rise at the maximum ESA of S1 (see Fig. 2 at 580 nm). The best solution was to make hotS1 a true precursor of S1. Perhaps inclusion of additional intermediate states would better reflect the continuous cooling process, but that was not implemented.

From the fitted conversion rates in the full seven-state model, with branching of S2 into S*/T, hotS1/S1 and BChl, and interconversion between all those states, we conclude:

  • The rate of conversion from S* into S1 is <(150 ps)−1, corresponding to <1.3% of the population. Flow from T is zero to any other state.

  • In the opposite direction, the rate of conversion from hotS1 to either S* or T is <(100 ps)−1, corresponding to less than 0.6% of the population. The upper limit for the conversion rate from S1 to either S* or T is <(60 ps)−1 or <1.6% of the population. The two branches seem to be quite distinct.

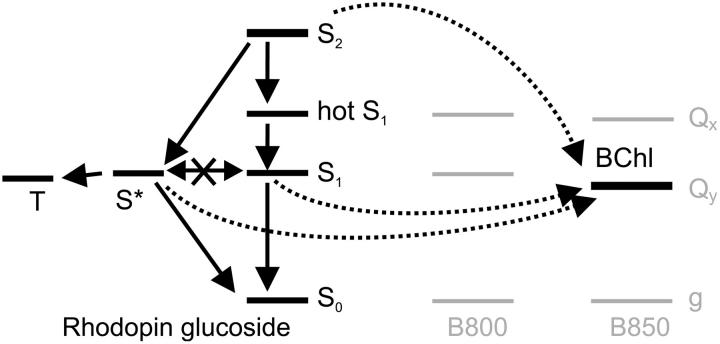
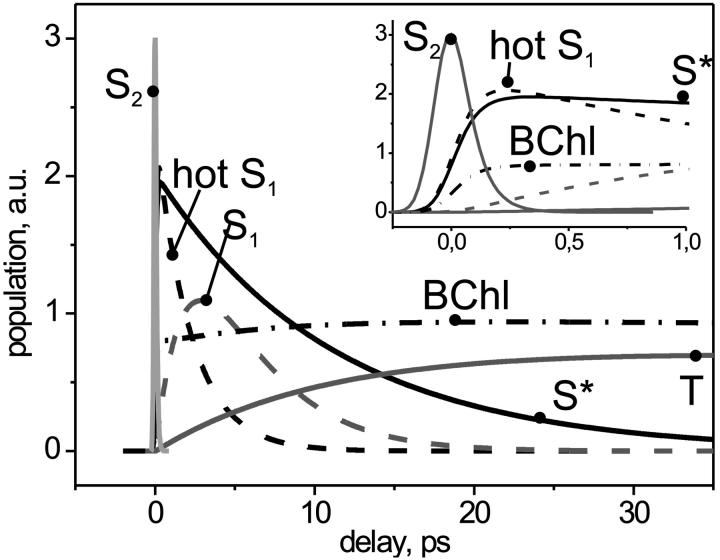
The best-fit results are displayed in Figs. 4–6 and Table 1. The corresponding model of the LH network (Fig. 4) describes S1 and T as two independent deactivation channels from S2 via the two precursors, hotS1 and S*, respectively. There is essentially no transfer between them. The vibrationally cold S1 and T are both blue-shifted of their precursors (Fig. 5). See Fig. 6 for the optimal solution of each state's time-dependent population.

FIGURE 4.

FIGURE 4

Open in a new tab

Model of the LH network. All photosynthetic energy transfer is treated inclusively as a state BChl. HotS1 and S* are both populated directly from S2 and there is no transfer between them. S* undergoes fission into triplet T. Both S1 and S* contribute to energy transfer to BChl.

FIGURE 6.

FIGURE 6

Open in a new tab

Transient populations in the optimal LH network model. The inset shows the first picosecond with the decay of S2 (solid gray) into hotS1 (dashed black), S* (solid black), and BChl (dash-dotted black). The main plot shows how these precursor states populate S1 (dashed gray) and T (solid gray), and let further rise BChl (dash-dotted black).

FIGURE 5.

FIGURE 5

Open in a new tab

Absorption spectra of the best fit model of the excitation energy flow. The vibrationally cold S1 and T are both blue-shifted of their precursors (hotS1 and S*, respectively). The dashed signals from BChl and in the Car S2 region are equally long-lived as the triplet. (S2–S0 bleach is scaled down a factor 3).

These findings give further credence to the triplet population mechanism proposed for Rsp. rubrum (Gradinaru et al., 2001) and Rb. sphaeroides (Papagiannakis et al., 2002), albeit for a different species and with a different approach. Additionally, the analysis provides evidence that the S*/T and S1 channels do not communicate.

The splitting ratio from S2 into hotS1, S*, and EET of 32:26:42%, each ±5, is quite reproducible in successive fitting runs, but the total timescale (inverse sum of all three rates) is not so well-defined due to the limited experimental resolution. The fitted S2 lifetime of 80 fs is thus somewhat longer than previously measured (Macpherson et al., 2001).

Three channels contribute to EET: S2 (42% of total excitation energy), S1 (4%), and S* (7%). The total yield of EET is 53 ± 10%, which compares favorably with the value of 56 ± 1% determined directly in a measurement of the fluorescence efficiency (Macpherson et al., 2001). Transfer from S2 includes both direct transfer to B850 and indirect via B800. If a nonzero rate for transfer from hotS1 is allowed, the fitted rate for coldS1-BChl transfer tends to drop consistently, but the algorithm does not achieve good convergence, such that we cannot exclude an EET contribution from hotS1. Again, the inclusion of intermediate states might help to model the continuous vibrational cooling process and the change of transfer activity during that cooling. The fitted rates of S1 transfer to BChl and decay to the ground state coincide with the values determined in Macpherson et al. (2001). S* splits about equally to fission into triplets, EET, and decay to the ground state with inverse rates ∼30 ps. The resulting lifetime of S* matches the 10-ps scale measured in the kinetics at 550 nm.

The EET from S1 and S* (11% in the evolutionary target analysis) account for the slow rise measured at 880 nm in Fig. 1 c. Since the model does not include the dynamics of transfer from B800 to B850 on the 0.9 ps timescale, it may tend to overestimate a little the slow EET contributions from the low-lying singlet states S1 and S* as compared to the indirect transfer from S2 via B800, because both channels are noninstantaneous and might partially compensate in the kinetics of the fit.

Additional long-lived (>300 ps) signals (dashed line in Fig. 5) make small contributions throughout the Car spectral region. The small oscillatory signal in the region below 550 nm contains both positive and negative spectral features, suggesting it may originate from a bandshift in the S2 absorption (Herek et al., 1998). Alternatively, this signal may be attributed to a ground state bleach contribution from the missing population that is trapped in T, together with a broad positive signal that originates most probably from the blue wing in the T absorption or from BChl ESA. Note that due to their equally long decay times (unresolved in our measurements), the oscillatory and triplet shapes are not well-defined in the region of spectral overlap; only their different rise times make them discernable for the algorithm. At wavelengths longer than 550 nm, the long-lived signal is due to BChl Qx bleach (negative band at 590 nm) and BChl ESA (broad positive signal).

A good indicator of the quality of a model is the successful convergence of the algorithm even without initial guesses on the target spectra and decay times. That is the case for the best-fit model presented above. For a judicious choice of step length adaptation (mutation probability, 0.5; contraction factor, 0.9; and threshold, 0.7, in the notation of our previous study; see Zeidler et al., 2001), convergence is reached after ∼2000 generations to spectra containing low residual noise. These results can then be employed as an ‘initial guess’ in subsequent optimizations. A second fitting run on the same experimental data will then produce nicely smooth spectra as shown in Fig. 5 within few generations (∼500). The decay times obtained by the evolutionary target analysis are consistent with fit results of individual kinetic traces measured at single wavelengths; see Fig. 2, a–c. However, the global analysis values have ∼5× larger uncertainty. A reduction of fit parameter numbers by assuming close-to-Gaussian spectral profiles would improve precision here (Beechem et al., 1985).

The second internal conversion channel of excitation energy deactivation in Car has now been established in three different bacterial species. The fact that the same model of ultrafast energy flow from S2 to T via an independent state S* pops out from two different target analysis approaches confirms the mechanism, and hints at the universality of the triplet channel. It is tempting to speculate about systematic effects already. However, the lifetime of the S* state shows no clear correlation with the conjugation length n of the Car: τS* = 5 ps in Rb. sphaeroides (Papagiannakis et al., 2002) (n = 10), τS* = 10 ps in Rps. acidophila (n = 11), and τS* = 5 ps in R. rubrum (Gradinaru et al., 2001) (n = 13). Instead, symmetry deformations from the protein environment seem to be decisive.

Let us finally address the electronic structure of the triplet precursor band. Perhaps the two-component decay at 550 nm reflects only vibrational cooling of hot triplet that is populated from S2 with an inverse rate of ∼300 fs? Indeed, our model incorporates two red-shifted precursor absorption bands in the S1 and in the T region as totally analogous. However, the triplet precursor band shows EET to singlet BChl and T strictly does not. That is strong evidence for the triplet precursor to be an independent singlet state S*.

Apart from S0 (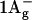Inline graphic) and S1 (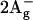Inline graphic), another two states below S2 (1Bu+) are predicted by theory with 1Bu− and 3Ag− symmetry (Tavan and Schulten, 1986). The signature of these states has been found by resonance-Raman excitation experiments (Furuichi et al., 2002): 1Bu− lies below the absorbing state for all N > 5, but 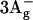Inline graphic lies below the absorbing state only for N > 10. Both have been suggested to be sequential intermediates between S2 and S1 (Fujii et al., 2003). However, a study of beta-carotene in solution with 10-fs time resolution supports the buildup of S1 without intermediates upon S2 decay (Cerullo et al., 2001). Recently, the same group found that carotenoids in solution show a strong spectral evolution on a timescale of 9–50 fs immediately after S2 excitation (Cerullo et al., 2002). They describe their findings with yet another singlet excited state called Sx and identify it with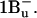 Inline graphic

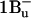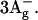Thus, two new spectroscopic signals deserve assignment. S* in LH2 shows an independent EET contribution and has a nonemissive spectrum, consistent with theory for both Inline graphic and Inline graphic Its characteristic ESA shows up in carotenoids with less than 10 conjugated double bonds (Frank et al., 2002), where only 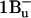Inline graphic is energetically available. Based on these arguments, we are inclined to support Papagiannakis et al. (2002) and identify 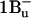Inline graphic with the triplet precursor singlet state S*.

CONCLUSION

In this article we have analyzed the energy flow network upon excitation of the Car in the light-harvesting complex LH2 from Rps. acidophila. We observed ultrafast Car triplet population and provided evidence for photosynthetically relevant energy transfer from a triplet precursor singlet state, S* to BChl. To model this behavior, we developed a new tool for time-resolved spectroscopy, the evolutionary target analysis. Starting from the raw time-resolved spectra, the algorithm extracts the band shapes of the physical target states and their interconversion rates according to a rate equation model of the energy flow network. The algorithm is readily extended to solve the inverse problem also of nonlinear and nonintegrable kinetics. The evolutionary target analysis confirmed the proposed triplet population mechanism via an independent singlet state S*, and provides evidence that S* does not exchange with S1, but participates in EET to BChl. The universality of the S*/T channel in bacterial LH complexes may now be regarded as a working hypothesis.

The precise knowledge of the energy flow network opens the way for control experiments (Herek et al., 2002) that would attempt to induce deviations from the natural network flow via ‘designed’ excitation with shaped fs-pulses. One can imagine to control the competition between the internal conversion channels S* and S1 and thus to silence or selectively prepare only one of several energy transfer channels.

Supplementary Material

[Figure]
biophysj_85_1_442__index.html (1.7KB, html)

Acknowledgments

We are indebted to Prof. K.-L. Kompa for continuous support.

R.J.C. acknowledges funding by Biotechnology and Biological Sciences Research Council.

W. Wohlleben and T. Buckup contributed equally to this work.

References

  1. Bachilo, S. M. 1995. Beta-carotene triplet-state absorption in the near-IR range. J. Photochem. Photobiol. 91:111–115. [Google Scholar]
  2. Beechem, J. M., M. Ameloot, and L. Brandl. 1985. Global and target analysis of complex decay phenomena. Anal. Instrum. 14:379–402. [Google Scholar]
  3. Bittl, R., E. Schlodder, I. Geisenheimer, W. Lubitz, and R. J. Cogdell. 2001. Transient EPR and absorption studies of carotenoid triplet formation in purple bacterial antenna complexes. J. Phys. Chem. B. 105:5525–5535. [Google Scholar]
  4. Cerullo, G., G. Lanzani, M. Zavelani-Rossi, and S. De Silvestri. 2001. Early events of energy relaxation in all-trans-β-carotene following sub-10 fs optical-pulse excitation. Phys. Rev. B. 63:241104. [Google Scholar]
  5. Cerullo, G., D. Polli, G. Lanzani, S. De Silvestri, H. Hashimoto, and R. J. Cogdell. 2002. Photosynthetic light harvesting by carotenoids: detection of an intermediate excited state. Science. 298:2395–2398. [DOI] [PubMed] [Google Scholar]
  6. Chen, W.-G., and M. S. Braiman. 1991. Kinetic-analysis of time-resolved infrared difference spectra of the L-intermediates and M-intermediates of bacteriorhodopsin. Photochem. Photobiol. 54:905–910. [Google Scholar]
  7. Christensen, R. L. 1999. The electronic states of carotenoids. In The Photochemistry of Carotenoids. H. A. Frank, A. J. Young, G. Britton, and R. J. Cogdell, editors. Kluwer Academic Publishers, Dordrecht, The Netherlands. pp.137–157.
  8. Cogdell, R. J., and H. A. Frank. 1987. How carotenoids function in photosynthetic bacteria. Biochim. Biophys. Acta. 815:63–79. [DOI] [PubMed] [Google Scholar]
  9. Croce, R., M. G. Muller, R. Bassi, and A. R. Holzwarth. 2001. Carotenoid-to-chlorophyll energy transfer in recombinant major light-harvesting complex (LHCII) of higher plants. I. Femtosecond transient absorption measurements. Biophys. J. 80:901–915. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Frank, H. A. 2001. Spectroscopic studies of the low-lying singlet excited electronic states and photochemical properties of carotenoids. Arch. Biochem. Biophys. 385:53–60. [DOI] [PubMed] [Google Scholar]
  11. Frank, H. A., J. S. Josue, J. A. Bautista, I. van der Hoef, F. J. Jansen, J. Lugtenburg, G. Wiederrecht, and R. L. Christensen. 2002. Spectroscopic and photochemical properties of open-chain carotenoids. J. Phys. Chem. B. 106:2083–2092. [Google Scholar]
  12. Freer, A. A., S. M. Prince, K. Sauer, M. Z. Papiz, A. M. Hawthornthwaite-Lawless, G. Mc Dermott, R. J. Cogdell, and N. W. Isaacs. 1996. Pigment-pigment interactions and energy transfer in the antenna complex of the photosynthetic bacterium Rhodopseudomonas acidophila. Structure. 4:449–462. [DOI] [PubMed] [Google Scholar]
  13. Fujii, R., T. Inaba, Y. Watanabe, Y. Koyama, and J. P. Zhang. 2003. Two different pathways of internal conversion in carotenoids depending on the length of the conjugated chain. Chem. Phys. Lett. 369:165–172. [Google Scholar]
  14. Furuichi, K., T. Sashima, and Y. Koyama. 2002. The first detection of the 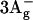Inline graphic state in carotenoids using resonance-Raman excitation profiles. Chem. Phys. Lett. 356:547–555. [Google Scholar]
  15. Fuss, W., Y. Haas, and S. Zilberg. 2000. Twin states and conical intersections in linear polyenes. Chem. Phys. B. 36:273–295. [Google Scholar]
  16. Garavelli, M., B. R. Smith, M. J. Bearpark, F. Bernardi, M. Olivucci, and M. A. Robb. 2000. Relaxation paths and dynamics of photoexcited chains: evidence for creation and annihilation of neutral soliton Pairs. J. Am. Chem. Soc. 122:5568–5581. [Google Scholar]
  17. Goldberg, D. E. 1993. Genetic Algorithms in Search, Optimization, and Machine Learning. Addison-Wesley, Reading, NY.
  18. Gradinaru, C. C., J. T. M. Kennis, E. Papagiannakis, I. H. M. van Stokkum, R. J. Cogdell, G. R. Fleming, R. A. Niederman, and R. van Grondelle. 2001. An unusual pathway of excitation energy deactivation in carotenoids: Singlet-to triplet conversion on an ultrafast timescale in a photosynthetic antenna. Proc. Natl. Acad. Sci. USA. 98:2364–2369. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Harvey, N. R., S. Perkins, S. P. Brumby, J. Theiler, R. B. Porter, A. C. Young, A. K. Varghese, J. J. Szymanski, and J. J. Bloch. 2000. Finding golf courses: the ultra high tech approach. Real-world applications of evolutionary computing. Proceedings. 1803:54–64. [Google Scholar]
  20. Herek, J. L., T. Polivka, T. Pullerits, G. J. S. Fowler, C. N. Hunter, and V. Sundström. 1998. Ultrafast carotenoid band shifts probe structure and dynamics in photosynthetic antenna complexes. Biochemistry. 37:7057–7061. [DOI] [PubMed] [Google Scholar]
  21. Herek, J. L., W. Wohlleben, R. J. Cogdell, D. Zeidler, and M. Motzkus. 2002. Quantum control of the energy flow in light harvesting. Nature. 417:533–535. [DOI] [PubMed] [Google Scholar]
  22. Holzwarth, A. R. 1996. Data analysis of time-resolved measurements. In Biophysical Techniques in Photosynthesis. J. Amesz, and A. J. Hoff, editors. Kluwer, Dordrecht, The Netherlands. pp.75–92.
  23. Husbands, P., and P. P. B. de Oliveira. 1999. An evolutionary approach in quantitative spectroscopy. Lect. Notes Artific. Intell. 1585:268–275. [Google Scholar]
  24. Lavine, B. K., C. E. Davidson, and A. J. Moores. 2002. Genetic algorithms for spectral pattern recognition. Vibr. Spectrosc. 28:83–95. [Google Scholar]
  25. Li, M. Z., and D. Wilkinson. 2001. Particle size distribution determination from spectral extinction using evolutionary programming. Chem. Eng. Sci. 56:3045–3052. [Google Scholar]
  26. Macpherson, A., J. B. Arellano, N. J. Fraser, R. J. Cogdell, and T. Gillbro. 2001. Efficient energy transfer from the carotenoid S2 state in a photosynthetic light-harvesting complex. Biophys. J. 80:923–930. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Mc Dermott, G., S. M. Prince, A. A. Freer, A. M. Hawthornthwaite-Lawless, M. Z. Papiz, R. J. Cogdell, and N. W. Isaacs. 1995. Crystal structure of an integral membrane light-harvesting complex from photosynthetic bacteria. Nature. 374:517–521. [Google Scholar]
  28. Nath, S. K., S. Shahid, and P. Dewangan. 2000. SEISRES—a visual C++ program for the sequential inversion of seismic refraction and geoelectric data. Comput. Geosci. 26:177–200. [Google Scholar]
  29. Papagiannakis, E., J. T. M. Kennis, I. H. M. van Stokkum, R. J. Cogdell, and R. van Grondelle. 2002. An alternative carotenoid-to-bacteriochlorophyll energy transfer pathway in photosynthetic light harvesting. Proc. Natl. Acad. Sci. USA. 99:6017–6022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Polivka, T., D. Zigmantas, H. A. Frank, J. A. Bautista, J. L. Herek, Y. Koyama, R. Fujii, and V. Sundström. 2001. Near-infrared time-resolved study of the S1 state dynamics of the carotenoid spheroidene. J. Phys. Chem. B. 105:1072–1080. [Google Scholar]
  31. Sundström, V., T. Pullerits, and R. van Grondelle. 1999. Photosynthetic light harvesting: reconciling dynamics and structure of purple bacterial LH2 reveals function of photosynthetic unit. J. Phys. Chem. B. 103:2327–2346. [Google Scholar]
  32. Tavan, P., and K. Schulten. 1986. The low-lying electronic excitations in long polyenes: a PPP-MRD-CL study. J. Chem. Phys. 85:6602–6609. [Google Scholar]
  33. Tavan, P., and K. Schulten. 1987. Electronic excitations in finite and infinite polyenes. Phys. Rev. B. 63:4337–4358. [DOI] [PubMed] [Google Scholar]
  34. Trinkunas, G., and A. R. Holzwarth. 1996. Kinetic modeling of exciton migration in photosynthetic systems. 3. Application of genetic algorithms to simulations of excitation dynamics in three-dimensional photosystem core antenna reaction center complexes. Biophys. J. 71:351–364. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. van Stokkum, I. H. M., T. Scherer, A. M. Brouwer, and J. W. Verhoeven. 1994. Conformational dynamics of flexibly and semirigidly bridged electron donor-acceptor systems as revealed by spectrotemporal parametrization of fluorescence. J. Phys. Chem. 98:852–866. [Google Scholar]
  36. Vazquez-Montiel, S., J. J. Sanchez-Escobar, and A. Fuentes. 2002. Obtaining the phase of an interferogram by use of an evolution strategy. Part I. Appl. Optics. 41:3448–3452. [DOI] [PubMed] [Google Scholar]
  37. Walla, P. J., P. A. Linden, C.-P. Hsu, G. D. Scholes, and G. R. Fleming. 2000. Femtosecond dynamics of the forbidden carotenoid S1 state in light-harvesting complexes of purple bacteria observed after two-photon excitation. Proc. Natl. Acad. Sci. USA. 97:10808–10813. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Yamaguchi, S., and H. Hamaguchi. 1998. Femtosecond ultraviolet-visible absorption study of all-trans→13-cis·9-cis photoisomerization of retinal. J. Chem. Phys. 109:1397–1408. [Google Scholar]
  39. Zeidler, D., S. Frey, K.-L. Kompa, and M. Motzkus. 2001. Evolutionary algorithms and their application to optimal control studies. Phys. Rev. A. 64:023420. [Google Scholar]
  40. Zhang, J.-P., R. Fujii, P. Qian, T. Inaba, T. Mizogushi, Y. Koyama, K. Onaka, Y. Watanabe, and H. Nagae. 2000a. Mechanism of the carotenoid-to-bacteriochlorophyll energy transfer via the S1 state in the LH2 complexes from purple bacteria. J. Phys. Chem. B. 104:3683–3691. [Google Scholar]
  41. Zhang, J.-P., T. Inaba, Y. Watanabe, and Y. Koyama. 2000b. Sub-picosecond time-resolved absorption spectroscopy of all-trans-neurosporene in solution and bound to the LH2 complex from Rhodobacter sphaeroides G1C. Chem. Phys. Lett. 331:154–162. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Figure]
biophysj_85_1_442__index.html (1.7KB, html)
biophysj_85_1_442__fig_supporting_info.tif (329.1KB, tif)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES