Abstract
Using molecular dynamics, we study the unbinding of ATP in F1-ATPase from its tight binding state to its weak binding state. The calculations are made feasible through use of interpolated atomic structures from Wang and Oster [Nature 1998, 396: 279–282]. These structures are applied to atoms distant from the catalytic site. The forces from these distant atoms gradually drive a large primary region through a series of sixteen equilibrated steps that trace the hinge bending conformational change in the β-subunit that drives rotation of γ-subunit. As the rotation progresses, we find a sequential weakening and breaking of the hydrogen bonds between the ATP molecule and the α- and β-subunits of the ATPase. This finding agrees with the “binding-zipper” model [Oster and Wang, Biochim. Biophys. Acta 2000, 1458: 482–510.] In this model, the progressive formation of the hydrogen bonds is the energy source driving the rotation of the γ-shaft during hydrolysis. Conversely, the corresponding sequential breaking of these bonds is driven by rotation of the shaft during ATP synthesis. Our results for the energetics during rotation suggest that the nucleotide's coordination with Mg2+ during binding and release is necessary to account for the observed high efficiency of the motor.
INTRODUCTION
This article reports on the use of computer simulations, combined with prior coarse-grained estimates of structure, to examine how ATP is released from the catalyic site of F1-ATPase. Our results shed light on the role of hydrogen bonds and the coordination of Mg2+ in the functioning of this molecular motor. The dynamics we examine take place over timescales much longer than those accessible by straightforward computer simulation. Our method for addressing this timescale issue should be useful in many other contexts.
ATP synthase, also known as F0F1-ATP synthase, is the universal protein that synthesizes ATP from ADP and inorganic phosphate using as its energy source a transmembrane protonmotive force (Mitchell, 1961; Boyer, 1993, 1997; Weber and Senior, 2000). It is located in membranes of mitochondria, chloroplasts and bacteria. ATP synthase consists of two motors: a membrane-spanning portion, F0, and a soluble portion, F1. F0 uses the transmembrane electrochemical gradient to generate a rotary torque to drive ATP synthesis in F1. When driven backward by the torque generated in F1, F0 pumps ions uphill against their transmembrane electrochemical gradient. The rotary torque in F1 is generated by hydrolyzing ATP at its three catalytic sites (Walker, 2000; Elston et al., 1998; Abrahams et al., 1994).
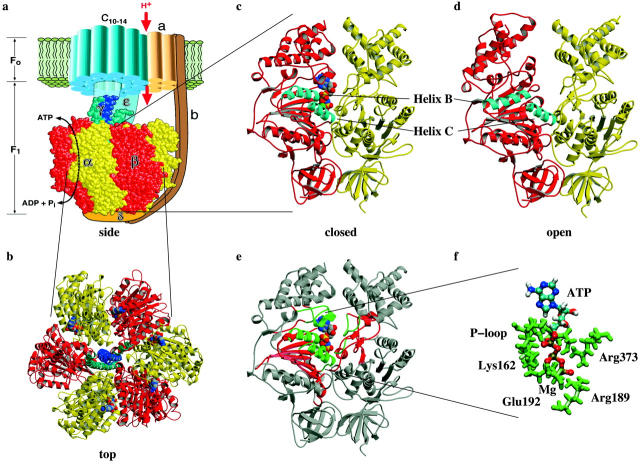
A schematic view of the structure of ATP synthase is shown in Fig. 1 a. The asymmetric membrane-spanning F0 region consists of subunits a and c10–14 (the number of c-subunits varies between species), which contain the proton channels. The soluble F1 region consists of the subunits δ, b2, α, ɛ, β, and the γ-shaft. The three catalytic sites are located in the α3β3 hexamer. The γ-shaft connecting α3β3 to c10–14 is an antiparallel coiled-coil of two α-helices, which penetrates the α3β3 hexamer of alternating α and β-subunits. F1 and F0 are connected to each other by the central γ-shaft and by the peripheral subunits b2 via the δ-subunit on F1 and the a-subunit on F0 (see Fig. 1) (Walker, 2000; Pedersen et al., 2000). Proton flow through the membrane channel at the interface of the c and a-subunits generates a torque that rotates the c ring relative to the a-subunit. Because of the two stalk coupling between F0 and F1, this torque rotates the γ-shaft relative to the α3β3 headpiece. This induces conformational changes in the α3β3 headpiece that drive the release or binding of ATP. Thus the motor can be divided into two counter rotating regions: a “stator” consisting of a, b2, δ, α3β3 and a “rotor” consisting of the γ, ɛ, and the c ring. At each α/β-interface one nucleotide can be bound. However, the sites are not symmetrical: their binding residues lie mainly in one subunit or the other. Only the binding pockets that are mainly in the β-subunits catalyze hydrolysis. During each full rotation of γ, three ATP molecules are sequentially synthesized or hydrolyzed in the three catalytic sites. Therefore the rotation can be divided into three steps per revolution, where each 120° step is associated with the hydrolysis of one ATP (Sun et al., 2003; Yasuda et al., 2001). The asymmetry of the catalytic site contributes to the substeps during rotation. The motor uses the ATP binding free energy to close the binding pocket and to drive the γ-shaft. The energy necessary for one revolution of the γ-subunit is about three times the hydrolysis free energy of ATP. Thus the motor works with a very high efficiency of more than 90% (Kinosita et al., 2000; Yasuda et al., 1998). The conformational changes of neighboring subunits are coupled such that the rates of ATP hydrolysis are accelerated up to five orders of magnitude in multisite catalysis compared with unisite catalysis (Penefsky and Cross, 1991; Senior, 1992; Weber and Senior, 1997, 2000).
FIGURE 1.
(a) Side view of the F0F1-ATPase. (b) Top view of the F1-ATPase, the β-subunits are colored red, the α-subunits yellow, the γ-shaft blue and cyan. ATP and ADP are shown in space-filling mode. (c) Closed and (d) open configurations of the α/β-subunits. (e) Our setup division of the α/β-subunits, the binding pocket region is colored green, its surrounding red and the outer region gray. (f) The three hydrogen binding regions around ATP in the closed state and the location of Mg. The pictures were created with RASMOL (Sayle and Milnerwhite, 1995), VMD (Humphrey et al., 1996), and MOLSCRIPT (Kraulis, 1991).
Due to the F1-ATPase's size (around 50,000 atoms) and due to the timescale of the ATP release or binding (milliseconds), the release or binding of ATP cannot be studied by straightforward molecular dynamics simulations. To circumvent the large system size, we use a setup that focuses on the dynamics of only a fraction of the total system. To surmount the long timescale, we make use of a series of interpolated structures to examine the system's configurations between the tight and the weak binding states of ATP. The interpolated structures constructed by Wang and Oster are based on the x-ray crysallographic structure of Abrahams et al. (Abrahams et al., 1994; Wang and Oster, 1998). A set of 16 equidistant structures were used in our study, starting at the closed and ending at the open ATP binding pocket configuration.
The rationale for these interpolated structures was the demonstration of very tight coupling of the mechanical motions, a tight coordination of the chemical cycle to the mechanical rotation, and especially the generation of a nearly constant torque by the motor (Wang and Oster, 1998; Elston et al., 1998; Oster and Wang, 2000a,b). To generate a constant torque, it is necessary to provide a fairly continuous energy flow from the ATP binding pocket toward the γ-shaft throughout an ATP binding or unbinding event. Due to this high efficiency and tight coupling of the motor, a trajectory is expected to fall close to a smooth curve in configuration space, making interpolated structures useful at a spatially coarse level. On the other hand, one cannot expect this picture to be correct on small length scales characterizing details like the formation of hydrogen bonds. Since the small length-scale details are of interest here, our use of the interpolated structures is confined to atoms that are relatively distant from the nucleotide. In this study, we assumed that the trajectory of the coarse-grained structure in the configuration space is a smooth curve. Under this assumption, the coarse-grained structure in the configuration space can be approximately recovered by a carefully chosen interpolation method. The 16 structures are 16 points on this recovered curve. The index of the interpolated structures does not represent the time, and consequently the sequence of 16 structures does not necessarily represent the real time course. The approach of using the interpolated structures is valid as long as the trajectory of the coarse-grained structure in the configuration space can be well approximated by interpolation. This approach should be used with caution, especially if the two end structures for interpolation are too far apart or if there are large diffusive steps in the trajectory (e.g. myosin).
As illustrated in Fig. 1 e, we divided the α- and β-subunits into three regions centered around the ATP binding pocket. The central region includes the ATP and all residues making direct contact with it. A secondary buffer region surrounding the primary region is used to protect the primary region from possible effects (such as unphysical heating) due to small length-scale errors in the interpolated structure. The remaining atoms surround the secondary region and remain fixed at their interpolated structure positions. The two inner regions include all secondary structure elements in the binding pocket vicinity including the β-sheet of the β-subunit, all α-helices surrounding the ATP, and additional small regions of the α-subunit. With this selection we cover all residues which belong to the common binding motifs found in various nucleotide binding enzymes, e.g. myosin, kinesins, GroEl, etc. (Walker et al., 1982). The movements of the B and C helices reflect the motions taking place in the catalytic site during ATP binding. The role of helices B and C is illustrated in Fig. 1, c and d, which shows the backbone structures of the closed and open configurations of the α- and β-subunits. As the binding pocket opens the relative movement of the two helices with respect to each other increases the gap between the α- and β-subunits through which ATP leaves or enters the binding pocket.
For each interpolated structure, we move the atoms in the primary and secondary regions by molecular dynamics with the external forces arising from the fixed atoms in the tertiary region. The molecular dynamics of the secondary region uses friction and fluctuating forces to control the temperature at 300°K. These dissipative terms allow the secondary region to remove energy from hot spots that may arise at the interface between the secondary and tertiary regions. Thus the secondary region serves to buffer the primary region from small length-scale errors in the interpolated structures used to fix the tertiary region. The molecular dynamics of the primary region follows from the interatomic forces only, with no friction and no random forces. Therefore, our use of distant interpolated structures imposes a natural bias on conformational changes in the binding pocket.
We began our sequence of simulations in the tight binding configuration pocket and drove the primary region toward the open configuration by changing the interpolated coordinates from structure 1 (βTP (Abrahams et al., 1994)) to 16 (βE). We equilibrated the dynamics regions for each interpolated structure of the surrounding tertiary atoms. To begin the molecular dynamics with the nth interpolated structure of the tertiary region (for n > 1), the coordinates of the two inner regions were taken from the (n − 1)th equilibrated simulation step, i.e., the simulation with the (n − 1)th interpolated structure of the tertiary region. This scheme provides sixteen equilibrated structures along the opening pathway of the ATP binding pocket. The use of the equilibrated coordinates of the previous simulation helps to keep the system relatively close to equilibrium throughout the conformational change in the binding pocket region. Only the very first simulation must be initiated differently (see below), and therefore does not benefit from this feature of relatively gentle change. Since each equilibration spans times of the order of 1–10 ns, the computational effort required to study the entire sequence of 16 structures visited by the motor over a period of milliseconds is of the order of that required to create a straightforward trajectory of only ∼100 ns in length.
In a previous molecular dynamics study of the mechanism of F1, the opening of the binding pocket was studied by forcing a 120° rotation of the γ-shaft over a period of about one nanosecond (Böckmann and Grubmüller, 2002). At the end of this fast driven rotation, the system was run for another 3.5 ns in an effort to equilibrate. In our experience, from 1 to 10 ns is required to propagate the reversible effects of 1/16 of that rotation angle. Therefore, the major structural and energetic changes in the binding pocket occur only during the final equilibration period. This behavior is qualitatively different from the mechanism of the F1 motor, in which the rotation of γ and the opening and closing of the binding pocket occur in a nearly reversible manner, influencing each other through continuous propagation of the conformational changes. Our setup moves the system through the same rotation, but through sixteen independently equilibrated steps. We will see that this difference in methodology leads to significant differences in the results.
Another molecular dynamics study of F1 used the method of targeted molecular dynamics to follow the entire 120° rotation of the F1 headpiece and shaft (Ma et al., 2002; Schlitter et al., 1994). The simulation time (500 ps) was even shorter than that of the earlier Böckmann and Grubmüller calculation. As such, small length-scale conformational changes in the binding pocket could not be resolved. Rather, the calculation by Ma et al. (2002) can be viewed as a source of interpolated structures that are strongly biased by the structural difference between the moving structure and the target structure. We cannot tell whether this interpolated structure is consistent with, or relates to, that used in our work. Indeed, Ma et al. (2002) curiously neglect the existence of the prior interpolated structures (Wang and Oster, 1998).
For the analysis of our simulations, we study the energetic and conformational changes in the ATP binding pocket, the changes in the coordination of the Mg2+ cation, and the changes in the hydrogen bond pattern between ATP and the catalytic site. The hydrogen bonds between the ATP molecule and the binding pocket are crucial for the binding process.
The binding process proceeds in two steps, first the diffusion and docking of the ATP molecule into the open binding pocket (weak binding state) and second, the closing of the pocket around the ATP molecule as it anneals into the tightly bound state. The energy transduction takes place during the transition from the weak binding state to the tight binding state, a process we call the “binding transition.” When an ATP docks into the catalytic site, it may not be necessary to strip its hydration waters all at once. Instead, ATP may progressively exchange its hydrogen bonds to hydration waters with bonds to the catalytic site. In its tightly bound state, ATP forms ∼15 to 20 hydrogen bonds with the binding pocket. There are three regions to which ATP is hydrogen bound. First, the so-called Walker or P-loop (residues β-Gly-159-β-Val-164) at the beginning of helix B. Second, the beginning region of helix C, namely β-Arg-189. And third, the residue α-Arg-373 from the α-subunit (see Fig. 1, c–e) (Abrahams et al., 1994). Sequential formation of these 15–20 hydrogen bonds ensures nearly constant force generation throughout the whole duration of the binding transition. This “binding zipper” sequence would lead to the smooth closing motion of the pocket and continuous conformational changes throughout the β-subunit (Oster and Wang, 2000a; Elston et al., 1998; Oster and Wang, 2000b). Thus, the binding zipper sequence would provide the requisite constant torque consistent with the high efficiency of the motor. Due to thermal fluctuations, there must be some deviation from this picture at a molecular level. Although these deviations are apparent in our simulations, we will see that the qualitative truth of the zipper model is also apparent.
METHODS
As noted in the Introduction, we effectively reduce the size of the simulated system by dividing the α and β-subunits into three regions, as shown in Fig. 1 e. The division into these regions was made according to the physical importance of the secondary structure elements for the ATP release and binding (binding pocket region (green in Fig. 1 e): residues α-Ser-335 - α-Asp-347, α-Leu-369 - α-Thr-380, β-Ala-158 - β-Val-173, β-Glu-188 - β-Gly-204, β-Arg-337 - β-Val-348, and β-Gln-416 - β-Lys-430, surrounding region (red in Fig. 1 e): α-Ile-136 - α-Gly-169, α-Ser-320 - α-Val-334, α-Gly-348 - α-Gly-368, β-Lys-151 - β-Gly-157, β-Ala-174 - β-Gly-187, β-Val-205 - β-Gln-221, β-Gln-249 - β-Arg-274, β-Lys-301 - β-Asp-316, β-Asp-330 - β-Ser-336, β-Asp-349 - β-Ile-357, β-Ser-415, and β-Leu-431). In addition, due to our special interest in hydrogen bonding, the two dynamical regions were surrounded by a 30-Å radius sphere of water molecules. The number of water molecules that fit into this volume changes in the interpolated structures. For the first of our 16 simulation steps, the volume contained 1342 waters. At the last step, it contained 1808 waters. The interpolated atomic positions of the outer region of our system are based on the x-ray crystallographic structure of Abraham et.al. (Abrahams et al., 1994) for the closed (starting structure) and open (end structure) states (Wang and Oster, 1998).
For all our simulation steps, we used the CHARMM27 program package (Brooks et al., 1983). Our force field parameters were based on the CHARMM all-atom force field (MacKerell et al., 1998) and for the solvent we used the TIP3P water model (Jorgensen et al., 1990). For the nonbonded interactions the force-switching method was used with a cutoff radius of 14 Å. The interaction energies in Fig. 8 were evaluated without cutoff. The SHAKE algorithm (Ryckaert et al., 1977) was applied for all bonds involving hydrogen atoms, which allowed the use of a 2-fs time step. First, we equilibrated the whole β-subunit and the green and red regions of the α-subunit shown in Fig. 1 e in their closed state (βTP). This region was surrounded by a nonspherical shell of water molecules with a minimum surface distance of 18 Å (9070 water molecules). For the placement of internal water molecules we used the program DOWSER, and the program SOLVATE was used for the placement of the surrounding water molecules (Zhang and Hermans, 1996; Eichinger et al., 2000). To ensure the stability of the volume and shape of our solvent shell, we used a continuously increasing friction coefficient and harmonic constraints for the outermost 6 Å of our solvent shell. The goal was to obtain equilibrated starting coordinates for the two inner regions. We first quenched the system for 10,000 steps and then heated it from 0 to 300 K for 300 ps. Afterwards the system was equilibrated at 300 K for another 1000 ps.
FIGURE 8.
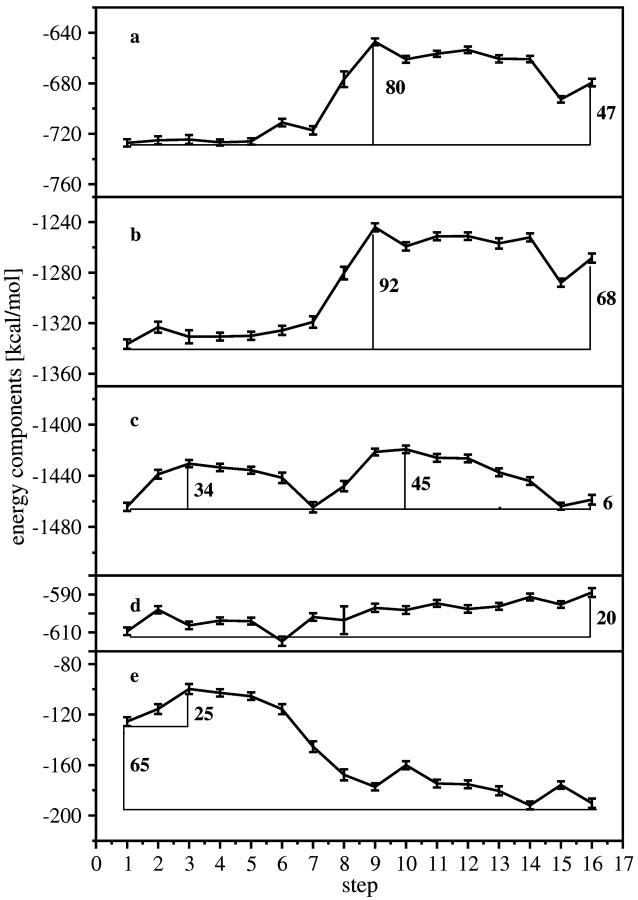
Different components of the interaction energies between ATP, the F1-ATPase, Mg2+, and the solvent. The components were calculated for each step as the sum of the van der Waals and Coulomb interactions between the regions considered. The values were averaged over the last 1 ns of the simulation for the 2nd to 16th steps and over the last 250 ps for the 1st step. (a) Interaction energies between ATP and the F1-ATPase + solvent starting at the closed and ending at the open ATP binding pocket (steps 1–16). (b) Interaction energies between ATP and the F1-ATPase + solvent + Mg. (c) Interaction energies of (ATP with ATPase) + (ATP with solvent) + (ATP with Mg) + (Mg with ATPase) + (Mg with solvent). The interaction energy of ATPase with solvent was not calculated because we did not enclose the entire ATPase with solvent. (d) Interaction energies between ATP and Mg. (e) Interaction energies between Mg and the F1-ATPase + solvent. The energies are therefore added together in the following way: 8(a) + 8(d) = 8(b), 8(b) + 8(e) = 8(c). The error bars were obtained using the blocking method (Jaccucci and Rahman, 1984), within a confidence level of 68.3%.
For the setup of our main simulation, we used the equilibrated coordinates from the above simulation for the inner two regions and a spherical solvent shell with a radius of 14 Å around the ATP molecule. For the outer gray region in Fig. 1 e, we took the interpolated coordinates of the first structure (the tight binding state, βTP) from (Wang and Oster, 1998). The solvent shell was enlarged to a radius of 30 Å, centered on the ATP molecule. This enlargement surrounded the entire dynamics region with solvent. Afterwards, we quenched the dynamic region and the solvent for 1000 steps. To ensure constant volume we used the SBOUND approach for our solvent shell, which applies a soft boundary potential to represent the average influence of the bulk water on the explicit solvent region (Brooks and Karplus, 1983). We applied stochastic forces on the solvent molecules within the outermost 5 Å of the shell, using Langevin dynamics with friction constants up to β = 12 ps−1. For the ATPase region in which we use stochastic dynamics, β = 10 ps−1 was applied. The system was heated from 0 to 300 K for 500 ps and equilibrated for another 1000 ps.
The equilibrated coordinates of this simulation were then used to set up and equilibrate the second simulation step. In this case, the interpolated coordinates of the second structure were used for the outer region. After this simulation was equilibrated, a third was begun with the coordinates of the third interpolated structure for the outer region and the equilibrated coordinates of the second simulation for the inner parts, and so on. Sixteen simulation steps were performed in this way, until the weak binding state (βE) was achieved. The equilibration times for the various structures were usually between 1 and 2 ns. We chose simulation times between 2 and 3 ns from the second to the 11th steps, and extended the run time to 6.5 ns for the 12th to 15th steps, and to 10 ns for the 16th step. To check for equilibration, we monitored the overall root-mean-square deviations in atomic positions from the starting structure (interpolated coordinates for the outer region combined with the coordinates of the n − 1 step for the two inner regions) for the two dynamics regions of our simulated structures during the simulations. We continued the simulations until we had found no significant drift in this quantity as a function of time for ∼1 ns. The final deviations from the starting structures were between 1.4 and 2.2 Å. In addition, we calculated the final root-mean-square deviations in atomic positions between the final structures of our simulations and the interpolated structures for each step, which were between 1.61 and 2.47 Å for the binding pocket (green) region and between 0.92 and 1.44 Å for the surrounding (red) region. The root-mean-square deviations in atomic positions from the closed x-ray structure were 1.58, 1.74, 1.79, 2.25, 2.45, 2.82, 3.35, 3.77, 3.94, 4.41, 4.70, 4.97, 5.64, 5.84, 6.43, and 6.92 Å, respectively, for the binding pocket region of the final structures from the first to the 16th step . The deviations from the open x-ray structure decreased correspondingly from 6.84 to 1.92 Å from the first to the 16th step. In addition, from the behavior of the kinetic energy fluctuations and equipartition, and further from the behavior of potential energy fluctuations, we judge that these simulation times were sufficient to reach equilibrium for each step (Figs. 2 and 3). In our study, equilibrium is the result of relaxation of the interactions among ATP, Mg, ATPase, and solvent near the binding pocket after the region distant from the ATP binding pocket is moved to the next interpolation point. The total simulation time was 65 ns.
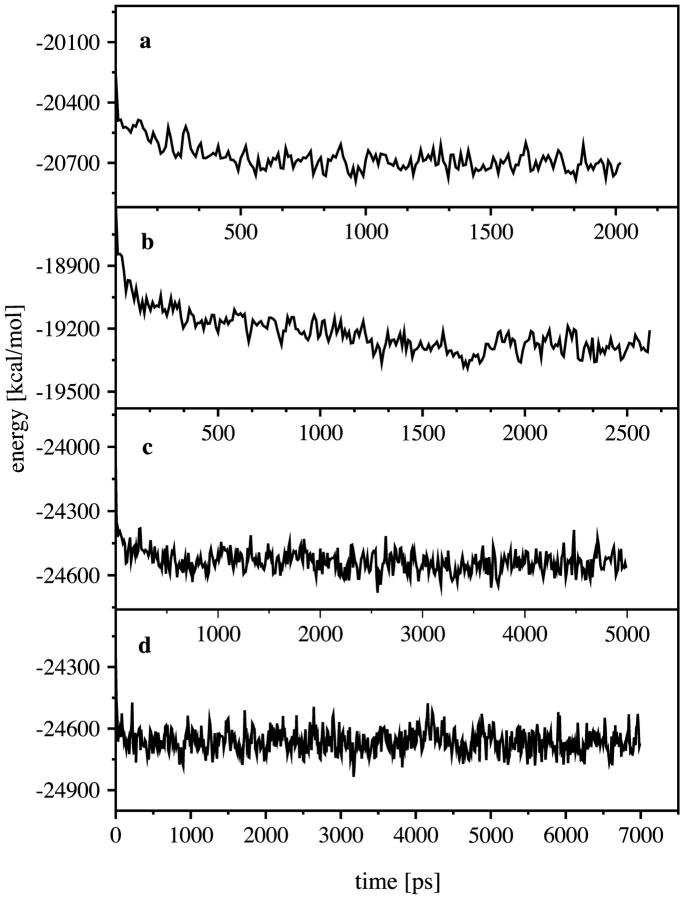
FIGURE 2.
Total potential energy of our system (coarse grained over 10 ps) for the 4th, 8th, 12th, and 16th steps, (a–d) with respect to the simulation time.
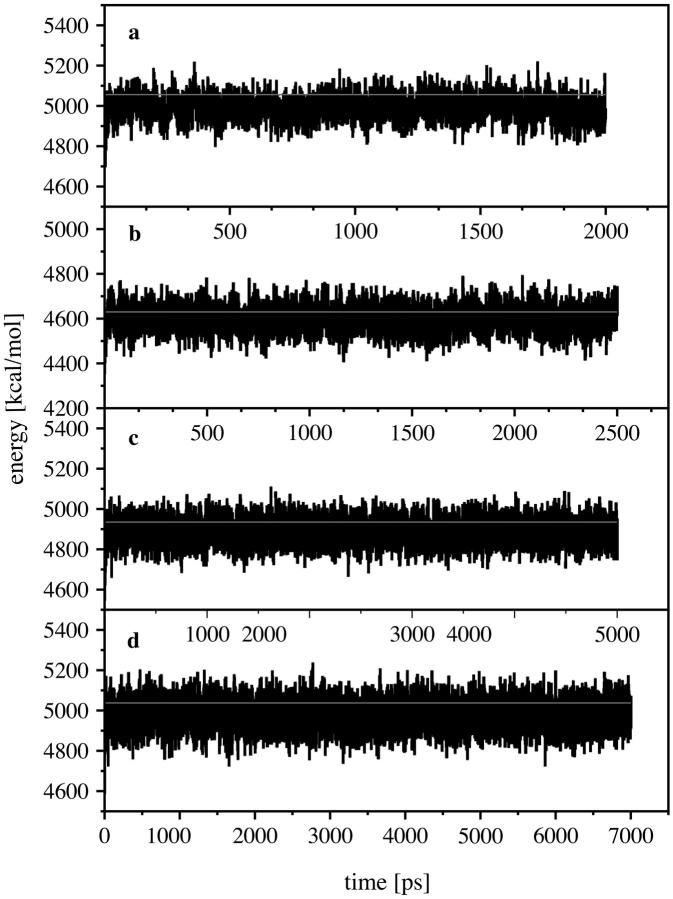
FIGURE 3.
Total kinetic energy of our system for the 4th, 8th, 12th, and 16th steps, (a–d) with respect to the simulation time. The horizontal lines show the expected kinetic energy according to equipartition of the energy.
RESULTS
In this section, we first discuss the overall conformational changes around the binding pocket during ATP release. We then take a closer look at the progression of hydrogen bonds between ATP and its binding pocket during our 16 steps. Third, we consider the coordination of the Mg2+ cation, and finally we discuss the changes in the interaction energies between ATP, Mg2+, protein, and solvent upon unbinding.
Conformational changes of the binding pocket
Fig. 4, a–d provides four representative snapshots of the equilibrated closed and open binding pockets according to our simulations. These show that, in the closed pocket, the ATP molecule is surrounded by all three hydrogen binding regions. By contrast, in the open pocket a space has formed between the P-loop on one side and the helix C and the pocket's α-subunit region on the other side, with a gap between the ATP molecule and the P-loop so that ATP stays close to the α-subunit and helix C regions. An equilibrated intermediate structure where the pocket is half open is shown in Fig. 4 b. In that state the α-phosphate oxygen of ATP is still close to the P-loop, but the distance is already increasing between the β/γ-phosphate oxygens and the P-loop. The phosphate axis has rotated ∼30° and ATP is bridging the pocket. At the end of our simulations (Fig. 4 d), the ATP molecule is located between the two subunits as expected after its primary movement into the binding pocket. In that weak binding state, a newly docked ATP is expected to have contacted the ATPase, but not yet have induced conformational changes. Our simulations are consistent with this expectation. Further, we see that contacts are formed mainly between ATP and Mg2+, and between Mg2+ and the binding pocket.
FIGURE 4.
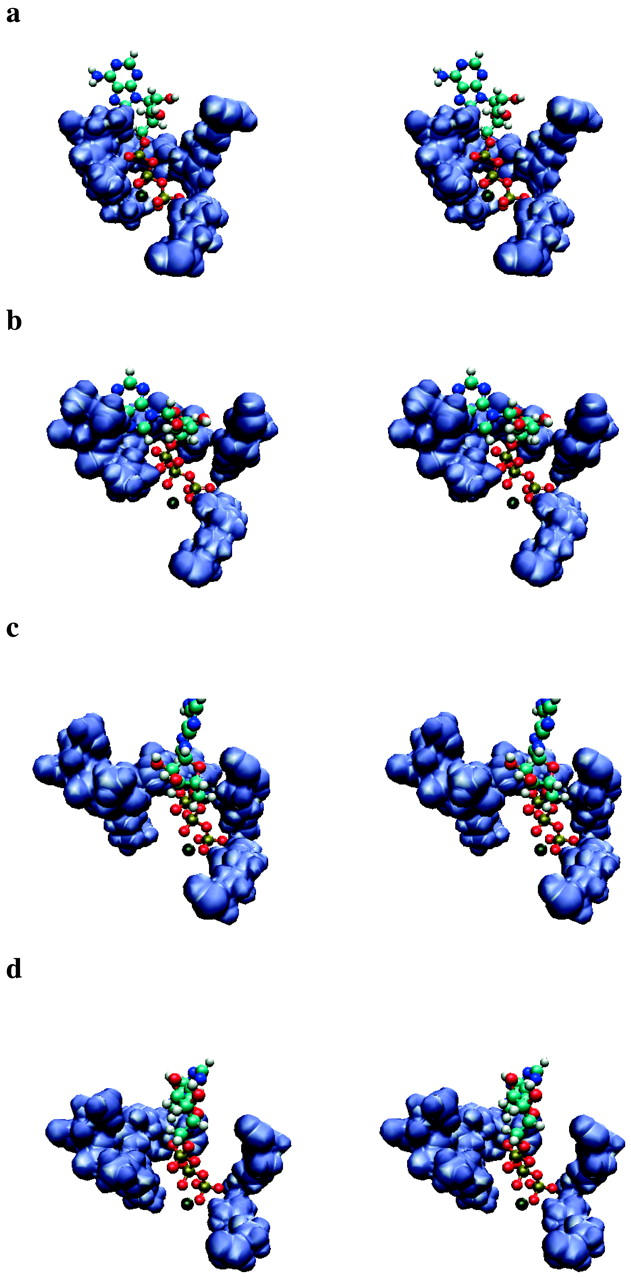
Stereo pictures of the hydrogen binding region and ATP. (a) Closed state, (b) 8th step, (c) 13th step, (d) open state. The orientation is the same as in Fig. 1 f. The pictures were created with VMD (Humphrey et al., 1996).
Hydrogen bonds
According to mutation studies on the affinity of ATP for its binding pocket there are three critical residues for ATP binding to the F1-ATPase: β-Lys-162 on the P-loop, β-Arg-189 on the C-loop, and α-Arg-373 (Futai et al., 2000; Senior et al., 2000; Senior et al., 2002). Due to their strong hydrogen bonds with a γ-phosphate oxygen of ATP, all three residues are thought to play a key role either for the docking of ATP or for multisite catalysis. β-Lys-162 and β-Arg-189 are critical for the binding affinity of ATP (Löbau et al., 1997; Nadanaciva et al., 1999a) and α-Arg-373 was found to be necessary for multisite catalysis (Nadanaciva et al., 1999b; Le et al., 2000). It was suggested that in multisite catalysis the conformational changes due to the binding of ATP to the other catalytic sites lead to changes in the position of α-Arg-373 with respect to the rest of the binding pocket. This allows an optimal positioning of the ATP molecule in the binding pocket through the strong hydrogen bonds formed between the residue and the nucleotide.
Fig. 5 shows the evolution of hydrogen bond populations between the ATP molecule and the binding pocket. At the beginning of our simulations (Fig. 5 a) we can clearly identify the hydrogen bonds formed by β-Lys-162, β-Arg-189, and α-Arg-373 with the γ-phosphate oxygens of ATP. For the tight binding state, hydrogen bonds are observed mainly in the upper left and lower right quadrants. These regions correspond to either (a) the α/β-phosphate oxygens of the ATP molecule, which form mainly hydrogen bonds with the P-loop backbone hydrogens (residues β-Gly-159-β-Val-164, upper left); or (b) to the γ-phosphate oxygens, which are connected to the helix C (β-Arg-189) and the α-subunit (α-Arg-373) (lower right) (see also Fig. 4). Two exceptions are the hydrogen bonds of one γ-phosphate oxygen to the sidechain of β-Lys-162 (on the P-loop), and of one α-phosphate oxygen to α-Arg-373 (α-subunit). Both can be explained by the location of these side chains. The first is close to helix C and the second to the backbone of the P-loop. Those two hydrogen bonds are the only ones outside the upper left and lower right quadrants of Fig. 5 a, and they are the only connections between the “upper part” of ATP (α- and β-phosphate oxygens) and between the α-subunit (see Fig. 2) as well as between the “lower part” (γ-phosphate oxygens) and the P-loop.
FIGURE 5.

Hydrogen bond populations for every other step, starting at the 2nd step (5 a, top left) and ending at the open state (5 h, bottom right). The data are averaged over the last 1 ns of our equilibration runs and show the fraction of the structures in which the specific hydrogen bond is present. Dark spots correspond to high (i.e., the hydrogen bond is present in all structures) and light spots to low populations. A hydrogen bond was defined to exist if its H-A bond length is shorter than 3.0 Å and its D-H-A angle larger than 120°. The Y axis corresponds to the ATP oxygen atoms, starting with the α-phosphate oxygens at the top and ending with the γ-phosphate oxygens at the bottom. Along the X axis the hydrogen bound residues are shown, starting at β-Val-164 and proceeding along the P-loop to β-Arg-189 and α-Arg-373 (see Fig. 4), the last column shows the hydrogen bonds with the solvent.
Following the hydrogen bond patterns from the tight to the weak binding state (Fig. 5, a–h), we observe a continuous trend of weakening and then disappearance of most of the P-loop hydrogen bonds in the upper left rectangle. The hydrogen bonds with helix C and the α-subunit remain intact throughout. Therefore, the first step during the opening of the binding pocket is the movement of helix B away from the α-β interface and the breaking of its hydrogen bonds with the ATP molecule. ATP remains in the interface region, still bound to helix C and the α-subunit.
After the hydrogen bonds with the P-loop are broken, those with β-Arg-189 and α-Arg-373 also start to weaken. In the open pocket the only remaining connections between ATP and the binding pocket are through the coordination of the Mg2+ cation with the β-subunit and three to five weak (or strongly fluctuating) hydrogen bonds. Our convention here is that a “weak” or “strongly fluctuating” hydrogen bond is one whose probability (i.e. population averaged over a simulation run) is below 50%. This result is also consistent with the proposition that binding of ATP is a two-step process. In the first step, the docking into the pocket leads to a weakly bound state in which the majority of the ATP/ATPase hydrogen bonds have yet to form. In the second step, the process of binding is accompanied by the formation of an increasing number of ATP-ATPase hydrogen bonds and a decrease in the ATP-solvent interactions.
During the movement of the P-loop, we observe a migration of the α- and β-phosphate oxygen's hydrogen bonds from β-Thr-163 to β-Gly-159 (Fig. 5, a–d). For example, these bonds move from the beginning of the P-Loop, closest to helix B, to its end. That end is farthest away from helix B and therefore least affected by the helix's movement and at the same time closest to the α-subunit. During this process, the hydrogen bonds with the β-phosphate oxygens are broken first and the ones with the α-phosphate oxygens last. This chronology is consistent with the overall movement of ATP in the pocket (see Fig. 4). The rotation of the ATP phosphate axis of ∼30° with respect to the binding pocket, shown in Fig. 4, can be explained by its tendency to retain the P-loop/α-phosphate hydrogen bonds.
The hydrogen bond between the γ-phosphate oxygen and β-Lys-162, and the hydrogen bond between α-phosphate oxygen and α-Arg-373 remain until the seventh structure. This persistence is longer than that for most of the β-phosphate oxygen hydrogen bonds with the residues β-Val-160 to β-Val-164 and, in the middle of the α-phosphate oxygen's migration, that with β-Gly-159. These hydrogen bonds are clearly important for the overall structure and stability of the pocket in the tight bound state. They may also be important for the closing and opening mechanism: First, the strong α-phosphate oxygen/α-Arg-373 hydrogen bond acts as a retaining force on the ATP molecule during the movement of the P-loop away from the α/β interface. It therefore assists the migration process of the α-phosphate oxygens along the P-loop by holding ATP close to the α-subunit: this might facilitate the opening of the binding pocket and thus contribute to the role of α-Arg-373 in multisite catalysis. Second, longevity retainment of the β-Lys-162/γ-phosphate oxygen hydrogen bond during unbinding, implies that this hydrogen bond also forms early during the ATP binding transition and might thus be important for initiating the process of the ATP binding pocket. This agrees with the experimentally determined importance of this residue for ATP binding (Löbau et al., 1997).
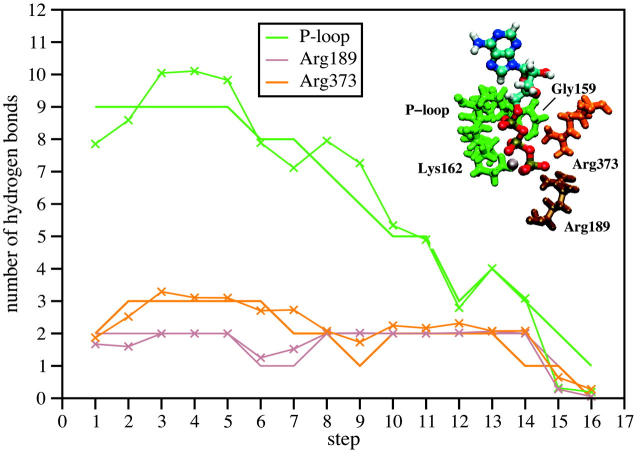
The plot of hydrogen bond numbers in Fig. 6 summarizes these results. It shows a mostly continuous overall decrease in the P-loop hydrogen bonds, starting at the fifth step. The number of hydrogen bonds with the helix C and α-subunit remains constant until the last two steps, when it starts to decrease as well.
FIGURE 6.
Solid line with -X- markers: average number of hydrogen bonds between ATP and its surrounding residues for each step averaged over 1 ns for the 2nd to 16th step (2500 structures) and over 250 ps for the 1st step (625 structures). Solid lines: the total number of hydrogen bonds, which was found for the largest group of analyzed structures for each step, averaged over 25 structures saved every 10 ps for the last 250 ps of the runs. The hydrogen binding sites were divided into three groups: the P-loop (green), α-Arg-373 (yellow) and β-Arg-189 (brown). A hydrogen bond was defined to exist if its H-A bond length is shorter than 3.0 Å and its D-H-A angle larger then 120°.
Coordination of Mg2+
The coordination of ATP to the Mg2+ cation and the cation's coordination with the binding pocket play an important role in ATP's affinity for the pocket and its binding mechanism (Weber et al., 1988; Senior et al., 2000; Frasch, 2000). Without the cation, the affinity of ATP is the same for all three catalytic sites and is much lower than for the ATP/Mg2+ complex. The addition of Mg2+ makes it possible for ATP to proceed to the tight binding state, bending the β through its full range. Since not all three β-subunits can bend completely at the same time without violating steric constraints, there must be an asymmetry in the ATP binding affinities of three catalytic sites. Addition of Mg2+ increases the ATP affinity for the tight binding site up to five orders of magnitude (Weber et al., 1988). EPR studies of the binding of VO2+ as a Mg2+ analog to the F1-ATPase and mutation based kinetic studies, demonstrated the important role of the residues β-Thr-163, β-Glu-192, and the WHB homolog β-Asp-248 for cation binding and coordination (Frasch, 2000). In addition, mutation of β-Glu-188 was found to inhibit ATP hydrolysis, although not the binding of ATP (Weber et al., 1988). In an x-ray crystallographic structure (Abrahams et al., 1994) β-Glu-188 was found in a position which allows the residue to align the water molecule necessary for the hydrolysis step during the reaction. Mutation of β-Glu-192, β-Thr-163, and β-Glu-188 lead to the loss of the motor's capacity for multisite catalysis, indicating a connection between the cation binding and coordination and the conformational changes driving the rotation of γ.
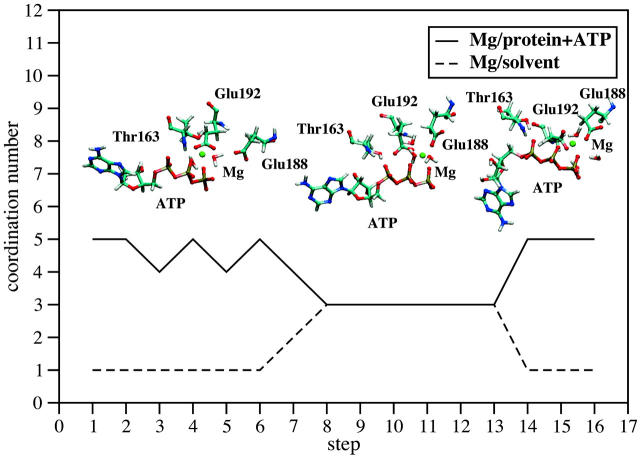
In Fig. 7 we show the coordination of Mg2+ with the ATPase/ATP and solvent. In the tightly bound state (step 1), the cation is mainly coordinated to the protein via the residues β-Thr-163 and β-Glu-192, and to ATP via one β- and one γ-phosphate oxygen. Only one water is found in its coordination sphere. The total coordination number oscillates between five and six throughout the first six simulation steps, indicating an unstable octahedral coordination environment. It was experimentally determined that β-Glu-192, β-Thr-163, and β-Asp-256 are involved in Mg2+ coordination. According to x-ray structural data (Abrahams et al., 1994) and our simulation, β-Asp-256 is hydrogen bonded to the water molecules surrounding the cation, forming only a second sphere coordination. Further, in our simulation, there is no coordination with β-Glu-188 in the tightly bound state. This is consistent with several experimental studies showing that the mutation of this residue inhibits hydrolysis, but not the tight binding of ATP (Weber et al., 1988; Frasch, 2000).
FIGURE 7.
Coordination number of the Mg2+ cation with the F1-ATPase/ATP and the solvent. Atoms are defined to be coordinated if their separation is less than 2.5 Å. The coordination number corresponds to the most often occurring coordination number during the last 250 ps of our equilibration runs, analyzing 25 snapshots, taken every 10ps. The snapshots (left to right) show the first coordination shell around the Mg2+ cation at the 1st, 8th, and 13th step.
After the sixth step in our sequence of simulations, the coordination of Mg2+ with the surrounding solvent molecules increases and the coordination with the binding pocket decreases. From the eighth to the thirteenth steps, the coordination with the residues β-Thr-163 and β-Glu-192 is broken, and the cation assumes coordination with three water molecules, two ATP oxygens and only one amino acid residue (β-Glu-188). After the thirteenth step, the cation reforms its coordination with β-Glu-192 at the cost of its interactions with two water molecules.
Regarding the structures shown in Fig. 4, the cation migrates from β-Thr-163 toward β-Glu-188 as our simulations progress from the tight binding state to the weak binding state. This migration is consistent with the relative movement of the helices B (β-Thr-163) and C (β-Glu-188 and β-Glu-192) with respect to each other. In the tight binding state Mg2+ coordinates with both B and C helices, adding to the overall stability of the binding pocket. The opening of the pocket leads first to an intermediate coordination between Mg2+ and one residue of the two helices, ATP and three water molecules, and subsequently to the formation of a new coordination shell mainly with the ATP molecule and the binding pocket and only one water molecule. However, at this step all coordination residues are located on helix C. At the end of our simulations at the equilibrated sixteenth step, the cation is still attached to the ATPase, forming the weak binding state.
Energy
In order to gain quantitative information on the energetics accompanying the conformational changes, we calculated and averaged the interaction energies between ATP, Mg2+, ATPase, and solvent for each of our simulations. This is shown in Fig. 8.
Fig. 8 a shows the interaction energy between ATP and ATPase/solvent. The overall increase in energy upon unbinding is 47 kcal/mol (∼80 kT). The major changes in the interaction energies coincide with the breaking of the ATP/ATPase hydrogen bonds as shown in Figs. 5 and 6. The energy barrier along our interpolated structures for this process is 80 kcal/mol (∼136 kT).
In Fig. 8 b, interaction energies between ATP and Mg2+ have been added to the data of Fig. 8 a. The ATP/Mg2+ interaction energies are shown separately in Fig. 8 d. They are 20 kcal/mol (34 kT) less favorable in the weak binding state than in the tight binding state. Thus the total energy gain in Fig. 8 b upon tight binding increases to 68 kcal/mol (115 kT), and the energy barrier increases to ∼92 kcal/mol (156 kT).
In Fig. 8 c, the Mg2+ interaction energies with the ATPase and the solvent have been added to the energies in Fig. 8 b, thus showing the total change in the interaction energies of ATP and Mg2+ during the unbinding of ATP. The Mg2+ interaction energies with the ATPase and the solvent are given separately in Fig. 8 e. They are ∼65 kcal/mol (110 kT) less favorable in the tight binding state than in the weak binding state. The difference is due to the overall unfavorable coordination of Mg2+ with the binding pocket and solvent in the tight binding state. The Mg2+ interaction energy drops 52 kcal/mol (88 kT) from the first to the ninth step. Therefore, adding the Mg2+/ATPase + solvent interaction energy to the values in Fig. 8 b leads to qualitative changes in the features of the energy curve. We observe two energetic barriers. The first can be associated with the optimization of the Mg2+ interactions (Fig. 8 e), the second with the breaking of the ATP/ATPase hydrogen bonds (Fig. 8 a). The barrier during the hydrogen bond breaking is lowered by 47 kcal/mol (80 kT) in the ATP release direction, compared with Fig. 8 b.
Regarding the Mg2+ interactions with its surroundings, the large drop in the Mg2+/ATPase + water interactions (Fig. 8 e, 65 kcal/mol (110 kT)) is counterbalanced by the interaction energies between ATP and Mg2+, which become more unfavorable during unbinding, but the overall change of the latter is much lower (20 vs. 65 kcal/mol) and the Mg2+/ATPase + water interactions are the dominant part. The energetic changes at the beginning of our unbinding simulations are mainly related to the Mg2+ interactions with the binding pocket and solvent: the sequential breaking of the hydrogen bonds between ATP and the protein start much later. Therefore, the Mg2+ interactions might facilitate, or even initiate the hydrogen bond breaking and the release of ATP. Experimental observations showed that Mg2+ enhances the binding rates of ATP and the hydrolysis and synthesis reactions of the ATPase and led to the suggestion that the optimization of the coordination shell of Mg2+ shell is important for the binding and release mechanism (Senior et al., 2000). These suggestions are consistent with our results, indicating a catalytic role of Mg2+ by initiating the hydrogen bond breaking between ATP and the binding pocket.
In summary, our simulations suggest that the unbinding process from the tight to the weak bound state proceeds in two major stages. The first involves the change in the coordination of the Mg2+. The second involves the breaking of the ATP/protein hydrogen bonds. The overall energetic changes are 6 kcal/mol from the tight to the weak binding state. The 6 kcal/mol in Fig. 8 c correspond to the change in interaction energy of (ATP with ATPase) + (ATP with solvent) + (ATP with Mg) + (Mg with ATPase) + (Mg with solvent) and are reliable within ±3–5 kcal/mol. These 6 kcal/mol do not correspond to the free energy change of the binding process, which may be dominated by the entropic factors.
DISCUSSION
The results described here provide a microscopic interpretation of the binding zipper model (Wang and Oster, 1998). In the tight binding state ATP forms hydrogen bonds with three regions at the α/β-interface of the ATPase: the P-loop, β-Arg-189, and α-Arg-373. The conformational changes and the corresponding changes in the hydrogen bonding patterns during our simulations can be summarized as follows. During the first steps of ATP release, the P-loop moves from the α/β interface and from the hydrogen bond sites that are located directly at the interface. The P-loop movement leads to a progressive increase in its distance from the other two hydrogen bond sites in going from the tight to the weak binding state. Because ATP is bound to both regions, as the distance between them increases, the hydrogen bonds to the ATP molecule become increasingly strained. Finally, ATP loses its hydrogen bonds with the P-loop, first by the weakening of its β-phosphate oxygen bonds and then by the movement of the α-and β-phosphate oxygens toward the end of the P-loop and the α/β interface. The result is a sequential decrease in the number of hydrogen bonds between ATP and the P-loop as it retracts and slides off the ATP (Figs. 5 and 6).
Our simulation results are consistent with mutation studies that have identified several residues as playing important roles for the binding and release of ATP and for multisite catalysis (Futai et al., 2000; Senior et al., 2000, 2002). The importance of β-Lys-162, β-Arg-189, and α-Arg-373, for example, was connected to their formation of hydrogen bonds with ATP. In our simulations, these residues form the strongest and the last to break hydrogen bonds with the γ-phosphate oxygens. In addition, α-Arg-373 forms a hydrogen bond with one of the α-phosphate oxygens, acting as a restraining force for ATP during the movement of the P-loop and therefore facilitating the migration of the α-phosphate oxygens along the P-loop. β-Lys-162 forms the longest lasting hydrogen bond between the P-loop and a γ-phosphate oxygen. This hydrogen bond is not broken until the end of the movement of the P-loop. Because this hydrogen bond is the only one between the lower part of ATP and the P-loop and remains longer than the P-loop/β-phosphate oxygen hydrogen bonds, its importance might be due to the formation of the first contact between ATP and the P-loop during ATP binding. Therefore, consistent with mutation studies, this residue is critical for the closing mechanism of the binding pocket (Löbau et al., 1997).
As mentioned in the Introduction, another molecular dynamics study was performed on the rotary mechanism of the F1-ATPase (Böckmann and Grubmüller, 2002). In that study, it was found that the hydrogen bonds to the γ-phosphate oxygens break first, contrary to our results. However, for the reasons noted in the Introduction, we suspect that the differences are due to the fact that the simulation does not equilibrate sufficiently to describe the chronology of hydrogen bond breaking reliably.
An interesting aspect of our simulation results concerns the role of the Mg2+ cation. Mutation studies suggest its coordination to β-Glu-192, β-Thr-163, and β-Asp-256 (Frasch, 2000; Weber et al., 1988). All of these residues are necessary for proper ATP binding and multisite catalysis. During our simulations, the coordination of the Mg2+ cation changes considerably. In the tight binding state, it coordinates directly to β-Glu-192 and β-Thr-163, and in the second coordination shell to β-Asp-256. This agrees with the results of the mutation studies and an x-ray crystallographic structure. During unbinding, it loses its coordination with β-Thr-163 due to the movement of the P-loop, and forms one coordination with β-Glu-188. However, this residue was shown experimentally to be unnecessary for ATP binding. Our simulation results suggest that it is involved in the early stages of Mg2+ binding; however, because it contributes only to one coordination site, it might not be crucial for the binding process. The most important residue for Mg2+ coordination is β-Glu-192, because it coordinates to the cation in the weak and tight bound state.
Although we observe significant rearrangement of the ATP hydrogen bonds during the first five steps of our simulations, no sequential breaking of the hydrogen bonds is observed during this period. However, we do observe an optimization of the Mg's coordination and a decrease in its interaction energies with its surrounding during this period. Only after these changes have taken place, do the hydrogen bonds to ATP start to break and the pocket begins to open up. Thus the conformational changes during optimization of the octahedral coordination of the Mg2+ seem to be prerequisite for ATP unbinding from the tightly bound state. This finding could explain the experimental observation that mutation of β-Thr-163 and β-Glu-192 significantly alters the hydrolysis rate of ATP (Frasch, 2000; Weber et al., 1988). The fact that their mutants do not show multisite catalysis demonstrates the importance of proper coordination for the binding mechanism. The crucial geometric requirements on the cation's coordination could also explain the observation that with Ca2+ as a cofactor (which has a different radius than Mg2+), the binding and hydrolysis rates are much lower.
Combining the above statements with our analysis of the interaction energies between ATP, Mg2+, ATPase, and the solvent, we observe that the unfavorable Mg2+ coordination with the ATPase and solvent in the tight binding pocket considerably lowers the energy barrier for ATP release along our interpolated structures. This is due to the energy gain upon better coordination during the unbinding process (Fig. 8 c versus Fig. 8 a). This energetic drop is counterbalanced by an increase of the ATP/ATPase + solvent energy barrier due to the ATP/Mg2+ interactions during unbinding (Fig. 8 b versus Fig. 8 a). However, the total energetic contributions of the latter are much smaller. Therefore inclusion of the Mg2+ interaction energies leads to a decrease of the energy barrier for hydrogen bond breaking of 35 kcal/mol (60 kT), compared with the pure ATP/ATPase+solvent interactions (Fig. 8 c versus Fig. 8 a). However, an additional barrier occurs between the first and the seventh step due to the Mg2+ interactions. During that period the ATP interaction energy remains nearly constant. Therefore, our energy diagram in Fig. 8 c can be divided into two parts: a first energetic barrier, related to the optimization of the Mg2+ coordination, and a second barrier, which is due mainly to the breaking of the ATP/ATPase hydrogen bonds. These changes agree with the experimental observation that the hydrolysis rate increases dramatically in the presence of Mg2+ (Senior et al., 2000). The energetic contribution of the Mg2+ interactions facilitates the release of ATP during the second half of the unbinding process and the Mg2+ interactions are also the major agents for the transition from structure one through seven. This proposition agrees with the fact that multisite catalysis and the formation of the tight binding state depend on the presence of Mg2+ and its coordinating residues β-Thr-163 and β-Glu-192 (Frasch, 2000). Our energetics could explain the lower hydrolysis rate without multisite catalysis and in the absence of the Mg2+ cation. We suggest that early changes during unbinding, or the late changes during binding of ATP (step one to seven), are mainly due to the presence of Mg2+. Therefore, we propose that Mg2+ is necessary to “guide” ATP into the tight binding position; without it the binding might stop around the seventh structure, with an incomplete alignment of the binding pocket and its water for the hydrolysis reaction and thus a lower reaction rate.
It is not possible to compare directly our interaction energies with the experimental binding free energy of 12 kcal/mol (20 kT) (Senior, 1992). We have considered only the first stage in the release of ATP, whereas the biochemical measurements include both the tight binding transition and the docking. In addition, our energetics do not include all of the entropic effects, which have been estimated at around 20 kcal/mol (34 kT) elsewhere (Massova and Kollman, 1999). Possible conformational changes in the more distant regions of the binding pocket, which we have not included in our setup could contribute to that entropy. The entropic aspects of the binding process are important components of the free energy but studying them using molecular dynamics simulations is computationally prohibitive. Nevertheless, it is noteworthy that the experimental binding free energy agrees very well with our overall energetic change of 6 kcal/mol (8.5 kT). Our analysis is consistent with the idea that the continuous hydrogen bond formation/breaking between the ATP molecule and the ATPas are rate determining steps during ATP binding/release and that the correct coordination of Mg2+ is important for the overall process.
Acknowledgments
We thank Sean Sun, Pieter Rein ten Wolde, and Aaron Dinner for helpful discussions.
Financial support of this work was provided to one of us (I.A.) initially from the German Science Foundation and subsequently from the U.S. Department of Energy Basic Energy Sciences Program with DE-FG03-99ER14987. Support for another of us (D.C.) was also provided by the Department of Energy with grant DE-FG03-87ER13793. Computational resources were provided by NERSC at the Lawrence Berkeley National Laboratory, and by an equipment grant supplement to Department of Energy grant DE-FG03-87ER13793. HW was supported by NSF grant DMS-0077971. G.O. was supported by NIH grant GM59875-02.
References
- Abrahams, J. P., A. G. W. Leslie, and J. E. Walker. 1994. Structure at 2.8-angstrom resolution of F1-ATPase from bovine heart-mitochondria. Nature. 370:621–628. [DOI] [PubMed] [Google Scholar]
- Böckmann, R. A., and H. Grubmüller. 2002. Nanoseconds molecular dynamics simulation of primary mechanical energy transfer steps in F1-ATP synthase. Nat. Struct. Biol. 9:198–202. [DOI] [PubMed] [Google Scholar]
- Boyer, P. D. 1993. The binding change mechanism for ATP synthase - some probabilities and possibilities. Biochim. Biophys. Acta. 1140:215–250. [DOI] [PubMed] [Google Scholar]
- Boyer, P. D. 1997. The ATP synthase - A splendid molecular machine. Annu. Rev. Biochem. 66:717–749. [DOI] [PubMed] [Google Scholar]
- Brooks, B. R., R. E. Buccoleri, B. D. Olafson, D. J. States, S. Swaminathan, and M. Karplus. 1983. CHARMM - A program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 4:187–217. [Google Scholar]
- Brooks, C. L., and M. Karplus. 1983. Deformable stochastic boundaries in molecular-dynamics. J. Chem. Phys. 79:6312–6325. [Google Scholar]
- Eichinger, M., H. Heller, and H. Grubmüller. 2000. EGO - An efficient molecular dynamics program and its application to protein dynamics simulation. In Workshop on Molecular Dynamics on Parallel Computers. R. Esser, P. Grassberger, J. Grotendorst, and M. Lewerenz, editors. World Scientific Singapore. 154–174.
- Elston, T., H. Wang, and G. Oster. 1998. Energy transduction in ATP synthase. Nature. 391:510–514. [DOI] [PubMed] [Google Scholar]
- Frasch, W. D. 2000. The participation of metals in the mechanism of the F1-ATPase. Biochim. Biophys. Acta. 1458:310–325. [DOI] [PubMed] [Google Scholar]
- Futai, M., H. Omote, Y. Sambongi, and Y. Wada. 2000. ATP Synthase (H+ ATPase): coupling between catalysis, mechanical work, and proton translocation. Biochim. Biophys. Acta. 1458:276–288. [DOI] [PubMed] [Google Scholar]
- Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD: Visual molecular dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]
- Jaccucci, G., and A. Rahman. 1984. Comparing the efficiency of metropolis Monte-Carlo and molecular-dynamics methods for configuration space sampling. Nuovo Cimento. D4:341–356. [Google Scholar]
- Jorgensen, W. L., R. W. Impey, J. Chandrasekhar, J. D. Madura, and M. L. Klein. 1990. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79:926–935. [Google Scholar]
- Kraulis, P. J. 1991. MolScript: a program to produce both detailed and schematic plots of protein structures. J. Appl. Crystallogr. 24:946–950. [Google Scholar]
- Kinosita, K., R. Yasuda, H. Noji, and K. Adachi. 2000. A rotary molecular motor that can work at near 100% efficiency. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 355:473–490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le, N. P., H. Omote, Y. Wada, M. K. Al-Shawi, R. K. Nakamoto, and M. Futai. 2000. Escherichia coli ATP synthase α-subunit Arg-376: The catalytic site arginine does not participate in the hydrolysis/synthesis reaction but is required for promotion to the steady state. Biochemistry. 39:2778–2783. [DOI] [PubMed] [Google Scholar]
- Löbau, S., J. Weber, S. Wilke-Mounts, and A. E. Senior. 1997. F1ATPase, roles of three catalytic site residues. J. Biol. Chem. 6:3648–3656. [DOI] [PubMed] [Google Scholar]
- Ma, J., T. C. Flynn, Q. Cui, A. G. W. Leslie, J. E. Walker, and M. Karplus. 2002. A dynamic analysis of the rotation mechanism for conformational change in F1-ATPase. Structure. 10:921–931. [DOI] [PubMed] [Google Scholar]
- MacKerell, A. D., D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarth, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin, and M. Karplus. 1998. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Chem. Phys. 102:3586–3616. [DOI] [PubMed] [Google Scholar]
- Massova, M., and P. Kollman. 1999. Computational alanine scanning to probe protein-protein interactions: a novel approach to evaluate binding free energies. J. Am. Chem. Soc. 121:8133–8143. [Google Scholar]
- Mitchell, P. 1961. Coupling of phosphorylation to electron and hydrogen transfer by a chemi-osmotic type of mechanism. Nature. 191:144–148. [DOI] [PubMed] [Google Scholar]
- Nadanaciva, S., J. Weber, and A. Senior. 1999a. The role of β-Arg-182, an essential catalytic site residue in Escherichia coli F1-ATPase. Biochemistry. 38:7670–7677. [DOI] [PubMed] [Google Scholar]
- Nadanaciva, S., J. Weber, S. Wilke-Mounts, and A. Senior. 1999b. Importance of F1-ATPase residue α-Arg-376 for catalytic transition state stabilization. Biochemistry. 38:15493–15499. [DOI] [PubMed] [Google Scholar]
- Oster, G., and H. Wang. 2000a. Reverse engineering a protein: the mechanochemistry of ATP synthase. Biochim. Biophys. Acta. 1458:482–510. [DOI] [PubMed] [Google Scholar]
- Oster, G., and H. Wang. 2000b. Why is the efficiency of F1 ATPase so high? J. Bioenerg. Biomembr. 32:459–469. [DOI] [PubMed] [Google Scholar]
- Pedersen, P., Y. Ko, and S. Hong. 2000. ATP synthases in the year 2000: evolving views about the structures of these remarkable enzyme complexes. J. Bioenerg. Biomembr. 32:325–332. [DOI] [PubMed] [Google Scholar]
- Penefsky, H. S., and R. L. Cross. 1991. Structure and mechanism of F0F1-type ATP synthases and ATPases. Adv. Enzymol. Relat. Areas Mol. Biol. 64:173–214. [DOI] [PubMed] [Google Scholar]
- Ryckaert, J. P., G. Ciccotti, and H. J. C. Berendsen. 1977. Numerical-integration of cartesian equations of motion of a system with constraints - molecular-dynamics of N-Alkanes. J. Comput. Phys. 23:327–341. [Google Scholar]
- Sayle, R. A., and E. J. Milnerwhite. 1995. RASMOL - biomolecular graphics for all. Trends Biochem. Sci. 20:374–376. [DOI] [PubMed] [Google Scholar]
- Schlitter, J., M. Engels, and P. Krüger. 1994. Targeted molecular-dynamics - a new approach for searching pathways of conformational transitions. J. Mol. Graph. 12:84–89. [DOI] [PubMed] [Google Scholar]
- Senior, A. E. 1992. Catalytic sites of Escherichia coli F1-ATPase. J. Bioenerg. Biomembr. 24:479–484. [DOI] [PubMed] [Google Scholar]
- Senior, A. E., S. Nadanaciva, and J. Weber. 2000. Rate acceleration of ATP hydrolysis by F1F0-ATP synthase. J. Exp. Biol. 203:35–40. [DOI] [PubMed] [Google Scholar]
- Senior, A. E., S. Nadanaciva, and J. Weber. 2002. The molecular mechanism of ATP synthesis by F1F0-ATP synthase. Biochim. Biophys. Acta. 1553:188–211. [DOI] [PubMed] [Google Scholar]
- Sun, S., D. Chandler, A. Dinner, and G. Oster. 2003. Elastic energy storage in F1-ATPase. Eur. Biophys. J. In press. [DOI] [PubMed]
- Walker, J. E., M. Saraste, M. J. Runswick, and N. J. Gay. 1982. Distantly related sequences in the α-subunits and β-subunits of ATP synthase, myosin, kinases and other ATP-requiring enzymes and a common nucleotide binding fold. EMBO J. 1:945–951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker, J. editor. 2000. The mechanism of F1F0-ATPase. Biochim. Biophys. Acta. 1458: 221–510.10838039 [Google Scholar]
- Wang, H., and G. Oster. 1998. Energy transduction in the F1 motor of ATP synthase. Nature. 396:279–282. [DOI] [PubMed] [Google Scholar]
- Weber, J., S. T. Hammond, S. Wilke-Mounts, and A. E. Senior. 1988. Mg2+ coordination in catalytic sites of F1-ATPase. Biochemistry. 37:608–614. [DOI] [PubMed] [Google Scholar]
- Weber, J., and A. E. Senior. 1997. Catalytic mechanism of F1-ATPase. Biochim. Biophys. Acta. 1319:19–58. [DOI] [PubMed] [Google Scholar]
- Weber, J., and A. E. Senior. 2000. ATP synthase: what we know about ATP hydrolysis and what we do not know about ATP synthesis. Biochim. Biophys. Acta. 1458:300–309. [DOI] [PubMed] [Google Scholar]
- Yasuda, R., H. Noji, K. Kinosita, and M. Yoshida. 1998. F1-ATPase is a highly efficient molecular motor that rotates with discrete 120° steps. Cell. 93:1117–1124. [DOI] [PubMed] [Google Scholar]
- Yasuda, R., H. Noji, M. Yoshida, K. Kinosita, and H. Itoh. 2001. Resolution of distinct rotational substeps by submillisecond kinetic analysis of F1-ATPase. Nature. 410:989–904. [DOI] [PubMed] [Google Scholar]
- Zhang, L., and J. Hermans. 1996. Hydrophilicity of cavities in proteins. Proteins. 24:433–438. [DOI] [PubMed] [Google Scholar]