Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Aug;85(2):1307–1316. doi: 10.1016/S0006-3495(03)74565-2

Low Dielectric Permittivity of Water at the Membrane Interface: Effect on the Energy Coupling Mechanism in Biological Membranes

Dmitry A Cherepanov *,†, Boris A Feniouk *,‡, Wolfgang Junge *, Armen Y Mulkidjanian *
PMCID: PMC1303247  PMID: 12885673

Abstract

Protonmotive force (the transmembrane difference in electrochemical potential of protons, 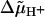Inline graphic) drives ATP synthesis in bacteria, mitochondria, and chloroplasts. It has remained unsettled whether the entropic (chemical) component of 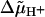Inline graphic relates to the difference in the proton activity between two bulk water phases (ΔpHB) or between two membrane surfaces (ΔpHS). To scrutinize whether ΔpHS can deviate from ΔpHB, we modeled the behavior of protons at the membrane/water interface. We made use of the surprisingly low dielectric permittivity of interfacial water as determined by O. Teschke, G. Ceotto, and E. F. de Souza (O. Teschke, G. Ceotto, and E. F. de Sousa, 2001, Phys. Rev. E. 64:011605). Electrostatic calculations revealed a potential barrier in the water phase some 0.5–1 nm away from the membrane surface. The barrier was higher for monovalent anions moving toward the surface (0.2–0.3 eV) than for monovalent cations (0.1–0.15 eV). By solving the Smoluchowski equation for protons spreading away from proton “pumps” at the surface, we found that the barrier could cause an elevation of the proton concentration at the interface. Taking typical values for the density of proton pumps and for their turnover rate, we calculated that a potential barrier of 0.12 eV yielded a steady-state pHS of ∼6.0; the value of pHS was independent of pH in the bulk water phase under neutral and alkaline conditions. These results provide a rationale to solve the long-lasting problem of the seemingly insufficient protonmotive force in mesophilic and alkaliphilic bacteria.

INTRODUCTION

The transmembrane difference in the electrochemical potential of hydrogen ions (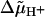Inline graphic) is generated across the coupling membranes of bacteria, chloroplasts and mitochondria by redox- or light-driven proton pumps (Mitchell, 1961, 1966). One of the membrane sides is thereby charged positively (p-side), while the other side charges negatively (n-side). 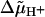Inline graphic is utilized by diverse “consumers” to drive endothermic reactions, primarily the synthesis of ATP from ADP and phosphate by the H+-FOF1-ATP synthase (see reviews by Junge et al., 2001; Boyer, 2002). The protonmotive force (pmf) can be written as

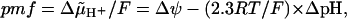graphic file with name M5.gif (1)

where Δψ is the transmembrane electrical potential difference (Mitchell, 1961, 1966). P. Mitchell considered the ΔpH term in Eq. 1 as the pH difference existing between two bulk water phases (p- and n-phases, respectively) separated by the membrane (delocalized, chemiosmotic coupling mechanism). Williams, who argued that in bacteria the p-phase corresponds to the infinitely extended external space, has challenged this notion. He noted that if protons are extruded into this “Pacific ocean,” they would be diluted and the entropic component of the pmf would be lost (Williams, 1978). This argument is particularly important when considering alkaliphilic bacteria, such as Bacillus firmus, which keep their internal pH (the n-phase) ∼3 pH units more acidic than the ambient one (the p-phase; see Krulwich et al., 1996, for a review). As Δψ in these bacteria hardly increases above 200 mV (Guffanti et al., 1984), the straightforward application of Eq. 1 yields a pmf value ∼0, so that it has remained enigmatic how these organisms synthesize ATP.

Deviating from the Mitchell's original bulk-to-bulk concept, several authors have speculated about a surface-to-surface coupling. It has been suggested by Kell that the ejected protons spread at the membrane surface but are somehow prevented from the prompt equilibration with the bulk, so that the local pH at the membrane surface (pHS) might differ from pH in the adjacent bulk (pHB) even at steady state (Kell, 1979). Michel and Oesterhelt came to the same conclusion based on the poor correlation between the ATP yield, as measured in whole cells of halobacteria and the pmf, defined as a sum of Δψ and ΔpHB (Michel and Oesterhelt, 1980). The suggestion that the steady-state pHS at the outer p-surface of cells could stay lower than pHB would lead to a reasonable pmf value even for alkaliphilic bacteria (for comprehensive reviews see Guffanti and Krulwich, 1984; Ferguson, 1985; Kell, 1986).

Evidence for retardation of protonic equilibration between the surface and the bulk has been reported for various biological membranes and membrane enzymes (Drachev et al., 1984; Arata et al., 1987; Jones and Jackson, 1989; Heberle and Dencher, 1992a; Heberle et al., 1994; Haumann and Junge, 1994; Alexiev et al., 1995; Maroti and Wraight, 1997; Gopta et al., 1999) as well as for artificial phospholipid bilayers (Antonenko et al., 1993). Several teams have shown that protons released at the p-side of unsealed bacteriorhodopsin membranes were captured by hydrophilic pH indicators in the bulk at ∼1 ms, one order of magnitude slower than detected by membrane-bound indicators (Drachev et al., 1984; Heberle and Dencher, 1992a; Heberle et al., 1994; Alexiev et al., 1995). The proton movement along the surface of these membranes was fast: the distance of 1 μm was covered in <100 μs (Heberle et al., 1994; Alexiev et al., 1995). In the case of spheroplasts of Rhodobacter sphaeroides (Arata et al., 1987) and whole cells of Rhodobacter capsulatus (Jones and Jackson, 1989), protons appeared at the external p-surface at τ < 5 ms, as detected by the electrochromic shift of carotenoid pigments, which correlates with the absorbance changes of an amphiphilic, membrane-bound pH indicator neutral red (Mulkidjanian and Junge, 1994). On the other hand, hydrophilic pH indicators in the bulk phase responded only at 30–70 ms. Retardation has been also reported for the reaction of proton uptake at the n-side of the photosynthetic reaction centers as studied both in a detergent solution (Maroti and Wraight, 1997) and in the native membrane (Gopta et al., 1999).

The retardation of proton escape from the membrane surface was previously explained by the damping effect of immobile pH buffer at the surface (Junge and Polle, 1986; Junge and McLaughlin, 1987; Jones and Jackson, 1989; Nachliel and Gutman, 1996). However, in this case the rate of proton equilibration had to depend on the concentration of mobile pH buffers or water-soluble pH indicators (see discussion in Junge and McLaughlin, 1987; Gopta et al., 1999; Georgievskii et al., 2002). Contrary to this expectation, the response time of the hydrophilic pH indicator pyranine added to bacteriorhodopsin membranes was independent of its concentration up to 150 μM (Heberle, 1991). In the case of Rb. sphaeroides chromatophore vesicles, the response of another hydrophilic pH indicator (bromcresol purple) started to accelerate only when the dye was added at 500 μM (Gopta et al., 1999). These data indicate retardation in proton exchange between the bulk and the surface by two orders of magnitude as compared to that in a homogenous water phase. As a result, protons/proton vacancies transferred to the surface by proton pumps are compelled first to protonate/deprotonate molecules of neutral water. This mechanism accounts for the high activation energy of proton transfer across the membrane/water interface (∼50 kJ/mol at neutral pH; see Gopta et al., 1999, for more details). The physical nature of the respective potential barrier has remained elusive.

We asked whether the anisotropy in proton transfer was related to specific properties of surface water, the molecular structure of which appears to be altered at a distance of several nanometers from the interface. The most striking evidence of the interfacial water organization has been obtained by the direct measurements of forces between negatively charged mica surfaces. These studies revealed force oscillations with a period of ∼0.25 nm propagating up to 3 nm from the surface (Israelachvili, 1992). Force measurements also exposed the exponentially decaying “hydration” force acting at separations of ≤2 nm. The hydration force was two orders-of-magnitude stronger than repulsion as expected from continuum electrostatics. The origin of this force has remained unclear (Israelachvili, 1992). Similar hydration forces were found by osmotic-stress measurements with various biological objects, such as lipid bilayers, DNA double helices, polysaccharides, and collagen triple helices (Rau and Parsegian, 1992; Leikin et al., 1993; and references therein). These forces were not attributable to the interplay between the electrostatic double-layer and van der Waals interactions alone.

A retardation by a factor of 103–104 of ion transfer across an interface between immiscible liquids, where the buffering effect can be excluded, is well-documented (see Marcus, 2000; Kornyshev et al., 2002 for an extensive coverage of this problem). The retardation might have several reasons, particularly 1), the decreased translational mobility at the surface; 2), the surface tension; and 3), the altered dielectric properties at the surface. The diffusion coefficient of water at the membrane surface is only 5- to 10-fold smaller than the one in the bulk phase (Zhang and Unwin, 2002), so this effect alone cannot be responsible for the experimentally observed retardation. The surface tension effects, as considered by Benjamin (1993), are likely to be negligible in the case of proton transfer because of their expected dependence on the ion size.

This work is devoted to the analysis of dielectric properties of water at the interface. It is argued that the low dielectric permittivity of the surface water leads to a potential barrier for ions, which is high enough to be important for biological energy transduction.

RESULTS

A potential barrier for ions at a membrane surface

It is well-established in electrochemistry that the dielectric permittivity (ɛ) of the first water layer at a surface is one order-of-magnitude smaller than that of the bulk water phase (4–6 vs. 78; see Bockris and Reddy, 1977). The spatial profile of the dielectric permittivity at the interface cannot, however, be inferred from electrochemical data alone. Recently Teschke and co-workers have determined the effective dielectric permittivity of water at a negatively charged mica surface by using the high resolution of atomic force microscopy (AFM). They analyzed how polar silicon nitride tips, either negatively charged as such or neutral when cobalt-coated, were attracted into the low-polar interfacial water layer at distances of 10–20 nm from the surface, where the van der Waals attraction was negligibly small. The dielectric permittivity was found to increase gradually from 4–6 at the interface to 78 at a distance of ∼25 nm from the surface. The data of Teschke and co-workers were obtained on mica. It was worth questioning to what extent they applied to biological membranes. The surface charge density of mica and biological membranes varies in a same range from −0.001 to −0.05 C m−2 (Matsuura et al., 1979; Pashley, 1981; Heinz and Hoh, 1999). The attraction/repulsion profiles similar to those obtained with mica (Teschke et al., 2001) have been measured by AFM for pure 1,2-dipalmitoyl-phosphatidylethanolamine bilayers (Müller and Engel, 1997).

On modeling, we treated the biological membrane as a dielectric layer with a thickness of 3.2 nm and dielectric constant of 4, the dielectric permittivity of water changing from ɛmin = 4 at the surface to ɛmax = 78 in the bulk in accordance with the equation (Teschke et al., 2001),

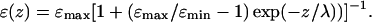graphic file with name M6.gif

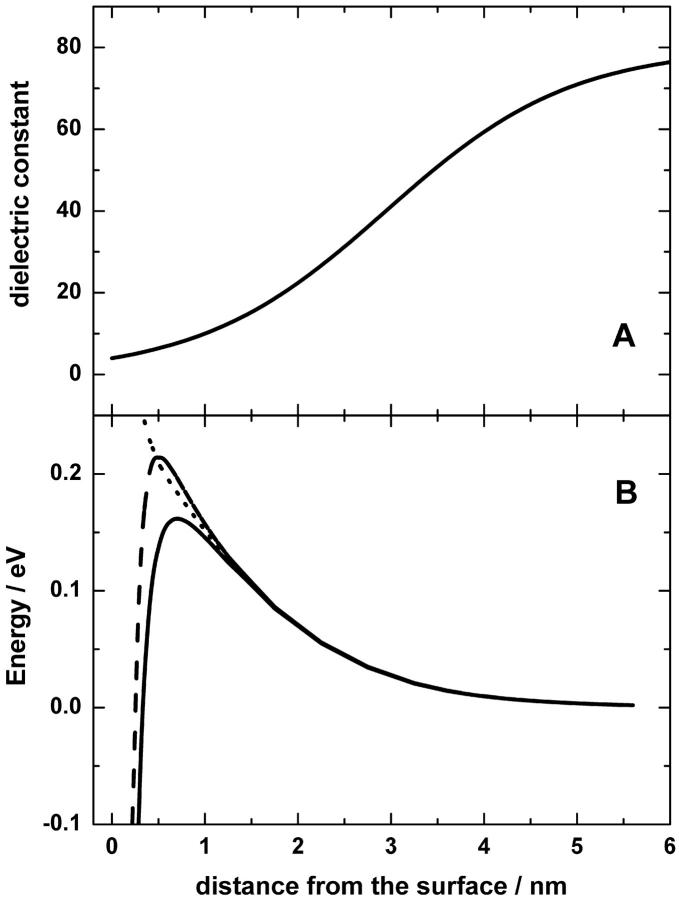
The experiments of Teschke and co-workers were performed at low ionic strength, either in pure water or in the presence of 1 mM of various salts. In the presence of 1 mM monovalent salts, the characteristic length λ was reduced to 10–12 nm, in agreement with the Debye-Hückel theory (Teschke et al., 2001). Because the same characteristic length did not apply to high ionic strength as typical for biological systems, and because there were no experimental AFM data available for high ionic strength, we extrapolated the experimentally obtained ɛ profile to the higher ionic strength of 0.1 M by using the Debye-Hückel theory and took a λ value of 1 nm. This value corresponds roughly to the decay length of hydration forces as measured under high ionic strength conditions with biological surfaces (Israelachvili, 1992; Leikin et al., 1993). The relevant ɛ profile is plotted in Fig. 1 A.

FIGURE 1.

FIGURE 1

Open in a new tab

Dielectric characteristics of the membrane/water interface. (A) The distance dependence of the dielectric permittivity at the mica/water interface. The profile was calculated based on data from Teschke et al. (2001) for an ionic strength of 0.1 M (λ = 1 nm) as described in the text. (B) The potential energy of a cation (solid line) and of an anion (dashed line) and the respective Born solvation energy (dotted line) at the charged membrane/water interface. The calculations by the Poisson-Boltzmann equation were performed for the ionic strength of 0.1 M using the effective radius of probe charges of 0.25 nm. The negative and the positive membrane charges were treated as described in the text.

We analyzed how the decreased ɛ of water at a charged membrane surface would affect the potential energy of an approaching ion. The electrostatic energy of a charged spherical particle with radius a near the membrane/water interface has two main contributions: 1) the electrostatic interaction with discrete charges at the membrane surface (they could be both negative and positive), and 2) the Born solvation energy. Both contributions were calculated by numeric integration of the linearized Poisson-Boltzmann equation

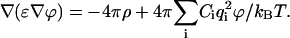graphic file with name M7.gif

The discrete negative and positive charges at the membrane surface were represented by two periodic square lattices with the space intervals of 0.8 and 0.857 nm, respectively. The total charge density of −0.032 C m−2 was assumed equal to the charge density at the surface of chromatophore vesicles from Rb. sphaeroides (Matsuura et al., 1979). Discrete charges were approximated by spheres of radius of 0.25 nm with the uniformly distributed charge density ρ. Numeric integration was performed by the program MUDPACK (Adams, 1993).

We found that the discreteness of the surface charge was notable only at distances of <1 nm from the interface, so the electrostatic potential at long distances (z > 2.4 nm) was calculated by the one-dimensional Poisson-Boltzmann equation using the average surface density (the Gouy-Chapman theory). In the thin layer at the surface (z ≤ 2.4 nm), the electrostatic potential was calculated separately for each lattice by the three-dimensional Poisson-Boltzmann equation. In the latter case, we used the periodic boundary conditions for the x and y coordinates, and nonperiodic boundary conditions for the z coordinate. The boundary conditions in the later case included the Neumann condition ∂ϕ/∂z = 0 in the middle of membrane (z = −1.6 nm) and the Dirichlet condition ϕ = ϕ0 in the bulk water (z = 2.4 nm), where the boundary potential ϕ0 was obtained by the Gouy-Chapman theory. The calculated potentials were superimposed in such a way that the central charge of the negative lattice was placed in the middle of four neighboring charges of the positive lattice. The results of the calculations are presented in Fig. 1 B.

Because the Born solvation energy (or the self-energy) of probing charge did not depend on the charge distribution at the surface, we calculated this term in cylindrical coordinates using the larger lattice (r < 10 nm, −1.2 nm < z < 12 nm). The Born energy was identical for both probe ions (dotted line in Fig. 1 B), whereas the electrostatic potential had opposite sign for anions and cations. Contrary to the Born energy, the electrostatic potential of probe ions was dependent on their position in the x-y plane. We placed the probe cation right above the central charge of the negative lattice and the probe anion above one of the four positive charges, which corresponded to the minimal electrostatic energy of probe ions. The full potential energy of the probe particles (i.e., sum of the Born energy and the electrostatic energy) is shown in Fig. 1 B (solid line for a cation and dashed line for an anion, respectively).

At a distance z > 0.5 nm from the surface, the ions feel the average electrostatic field of the negatively charged membrane (the limit of the continuum surface charge). Fig. 1 B shows that the electrostatic interaction with the surface at these distances (attraction for a cation and repulsion for an anion) is much smaller than the Born solvation penalty. At the distances z < 0.5 nm, the electrostatic attraction to the nearest surface charge dominates over other contributions (the limit of the discrete surface charges). The combined effect results in a potential barrier with a maximum at ∼0.5 nm away from the surface. The barrier height depends on the effective radius and charge of the molecule and on the details of the dielectric permittivity function near the surface. For monovalent cations with the effective radius of 0.25 nm moving toward the surface, the height of the potential barrier can be estimated as 0.1–0.15 eV; for monovalent anions the barrier is higher, at 0.2–0.3 eV (that is, if the potential energy in the bulk phase is taken as the reference value). The difference arises due to the electrostatic effect of negatively charged membrane surface. Considering the movement of particles away from the negatively charged surface, the barrier would be higher for cations than for anions because the former have to overcome the electrostatic attraction to the surface (see Fig. 1 B). The difference in the energetics of cations and anions may be important for interpretation of kinetic experiments where different particles (such as hydroxyl anions, hydroxonium cations, and mobile buffers) can simultaneously participate as proton carriers.

Because the Born energy is the square function of the charge, the barrier height is expected to be four times larger for divalent ions than for monovalent ions, and orders of magnitude greater for polyvalent ions. In the latter case, the energy penalty should impede the approach of polyvalent ions to the surface.

The steady-state proton flux at the membrane/water interface in relation to bioenergetic coupling

In the previous section, we showed that diminished dielectric permittivity of the surface water leads to a potential barrier for cation transport between the surface and the bulk phase. Based on these results, we modeled the stationary proton flux at the membrane/water interface. It has to be emphasized that the presence of fixed pH buffers at the membrane surface does not affect the steady-state proton flux (Junge and Polle, 1986; Junge and McLaughlin, 1987), so that only mobile proton-carrying particles have to be considered. (A model of “pulsed” pH-changes depending on the surface buffering capacity is considered elsewhere; Cherepanov et al., unpublished.)

First, we considered the proton efflux from a single proton pump. The proton consumption by a membrane “sink” can be quantified analogously, just by reversing the sign in the proton flux. It is noteworthy that differently charged water species can serve as dominant proton carriers depending on conditions. Generally, in the absence of mobile pH-buffers, the hydroxonium cation H3O+ is the main proton carrier at pH < 7, whereas at pH > 7 the hydroxyl anion OH− overtakes this function. For simplicity, we use hereafter the term proton, without specifying the chemical nature of the actual carrier.

The stationary proton concentration satisfies the Smoluchowski equation

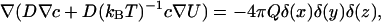graphic file with name M8.gif

where D is the diffusion coefficient, c is the concentration, U is the potential energy of the transferred particles (e.g., H3O+), and Q is the turnover rate of the pump (s−1). The stationary flux reads

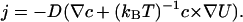graphic file with name M9.gif

In a planar system where the semispace z > 0 represents water and z < 0 the membrane, the boundary condition at z = 0 is jz = 0 (the impermeability of membrane for protons). To obtain an analytical solution, we approximated the potential energy of H3O+ cations near the interface by a steplike function

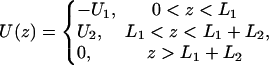graphic file with name M10.gif

where the depth of the potential well at the interface U1 and the height of the potential barrier U2 were taken equal to 0.06 eV and 0.12 eV, respectively, in accordance with the values obtained above (see Fig. 1 B); the thickness of both layers L1 and L2 was taken equal to 0.8 nm. The bulk water was treated as a proton sink/source with a bulk diffusion coefficient D = 10−4 cm2 s−1 and infinite capacity. The diffusion coefficient in both surface layers (z < L1 + L2) was reduced by a factor of 10 in accordance with the experimental data discussed above (DS = 10−5 cm2 s−1). Continuous concentration functions c1(r, z), c2(r, z), and c3(r, z) were defined in the layers 0 < z < L1, L1 < z < L1 + L2, and z > L1 + L2, respectively. 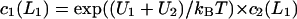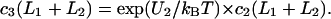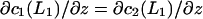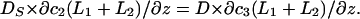The boundary conditions required that Inline graphic and Inline graphic The other two conditions followed from the continuity of the normal component of the flux, giving Inline graphic and Inline graphic Because the normal component of the flux was diminished at the membrane surface (z = 0), we put 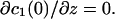Inline graphic The last boundary condition was determined by the properties of the bulk solution. If it did not contain buffers, then c3(∞) = 0 (Model 1). If there was a high concentration of buffer, then c3 = 0 throughout the bulk phase (Model 2).

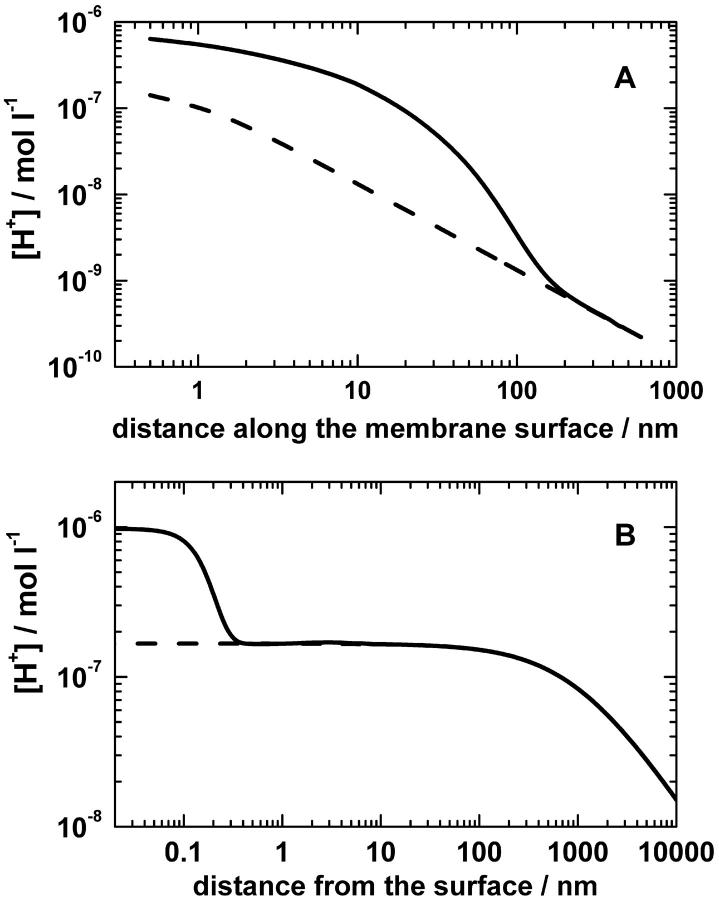
The analytical solution of the models is given in the Appendix. Fig. 2 A illustrates how protons spread over the membrane surface (as calculated by Model 1 for a pump turnover rate of 500 s−1, solid line). Being constrained by the potential barrier, ejected protons initially spread over an area of ∼104 nm2 and only then escaped into the bulk phase. For comparison, the dashed line in Fig. 2 A shows the proton concentration profile in the absence of the potential barrier. Because protons propagated in the bulk solution by orders of magnitude faster than they escaped over the barrier, the concentration of protons in the bulk phase is diminished both in the absence of pH-buffers (Model 1) and in their presence (Model 2).

FIGURE 2.

FIGURE 2

Open in a new tab

Steady-state pH-profiles at the surface of a proton-ejecting membrane. (A) Proton distribution along a planar membrane containing only one proton pump. The cylindrical axis z is perpendicular to the membrane plane, and the axis r is directed along the membrane. The protons ejected by the pump are spread initially along the membrane surface and then escape through the interfacial barrier (no proton sinks in the membrane were considered). The turnover rate of the pump was 5 × 102 s−1, the height of the potential barrier was 0.12 eV, the surface potential was −0.06 V, the bulk diffusion coefficient of protons was 10−4 cm2/s, and the other details of the model are described in the text. (B) Steady-state pH profile at the surface of sealed membrane vesicles with the radius of 1 μm and the surface pump density of 2 × 1011 cm−2. The potential barrier as calculated for the ionic strength of 0.1 M in Fig. 1 B (solid line) was used on modeling. The dashed line shows the proton concentration as calculated without potential barrier.

Turning to the case of several proton pumps, we looked for the steady-state proton distribution around a sealed, proton-ejecting membrane vesicle with a radius R surrounded by an indefinite volume that can serve as a proton sink. We considered a finite spherical model where the pumps are uniformly distributed at the surface. In such a model the total flux across a surface of radius r is

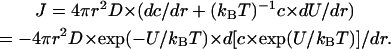graphic file with name M16.gif

Integration yields

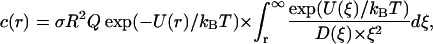graphic file with name M17.gif

where Q is the total rate of proton pumping/consumption at the surface. Taking a typical pump turnover rate of 500 s−1, a surface pump density σ of 2 × 1011 cm−2 (close to the surface density of membrane potential generators in chromatophore vesicles of phototrophic bacteria; see Feniouk et al., 2002), vesicle radius R of 1 μm, and the potential energy profile U(r) as determined in the previous section for the ionic strength of 0.1 M (λ = 1 nm, solid line in Fig. 1 B), we calculated the maximal steady state proton concentration as a function of the distance to the membrane surface (Fig. 2 B, solid line). It came out that the proton concentration rose up to 10−6 M that corresponds to pHS of 6.0. In the absence of potential barrier the proton concentration at the surface was lower, only 10−7 M (Fig. 2 B, dashed line).

As the bulk water phase served just as an infinite sink for the ejected protons, the total concentration of protons in the system was the sum of those present at equilibrium (preexisting protons) and those coming from the pumps. The contribution of protons ejected by the pumps was essential at the surface but decayed at short distance beyond the barrier (see Fig. 2 B). For the following discussion it is important to note that the total concentration of protons in the bulk remained close to their equilibrium concentration. Correspondingly, the total concentration of protons at the surface (10−6 M) substantially deviated from that in the bulk phase if pH of the latter was alkaline or neutral.

As long as protons are consumed at the n-surface, the interfacial proton transfer at this surface is mediated by OH− anions, which originate from the deprotonation of neutral water at the surface proton inlets (at least at pH > 6.0 as shown with chromatophores of Rb. Sphaeroides; see Gopta et al., 1999, for details). Thus the pHS value at the n-surface is determined by the competition of OH− production by proton pumps, OH− consumption (H+ release) by the ATP synthase, and OH− escape into the bulk. The escape of the OH− anions over the potential barrier, in contrast to that of H3O+, is boosted by electrostatic repulsion (see Fig. 1 B). Using the U(r) profile for anions from Fig. 1 B, we calculated that the local alkalinization was negligible at the n-surface at the steady state (not documented).

DISCUSSION

Electrochemists have long claimed that the dielectric permittivity of the first hydrating water layer at a charged surface is on the order of 4–6 (Bockris and Reddy, 1977). The recent AFM experiments of Teschke and co-workers allowed us to quantify the thickness of the low-polarizable layer of surface water from the electrostatic immersion of highly polar silicon nitride and cobalt-coated tips (Teschke et al., 2001). The reason for the decrease might be strong intermolecular correlations in water resulting in the overpolarization of the latter at a charged interface (Kornyshev, 1985; Bopp et al., 1998). It is compatible with this notion that Ishino and co-workers have found that the negatively charged silicon nitride tips were attracted, at small separations, to both the positively and negatively charged Langmuir-Blodgett monolayers (−NH2 and −COOH functional groups) but not to the neutral stearyl amide (−CONH2) and stearyl alcohol (−OH) monolayers (Ishino et al., 1994). This behavior might be caused by the strong positive correlations in the orientations of neighboring water molecules: the dielectric function of liquid water ɛ(k) becomes even negative at the wavelengths of ∼3 Å−1 (see discussion of the over-screening effect by Bopp et al., 1998). The observed dependence of the attraction on the surface charge, which was independent of the sign of the latter, might be caused by ordering of the over-polarized water at the distances of few nanometers from the interface, both on the positively and negatively charged surfaces, leading to dielectric saturation. The extent of such ordering can depend not only on the density of surface charges, but also on the smoothness of the surface and the ionic strength of solution. In the case of a neutral surface, the ordering is likely to be weak and restricted to the first hydration layer.

Here we showed that the low dielectric permittivity of interfacial water leads to a potential barrier for ions moving between the surface and the bulk water phase. Our estimate for the barrier height for cations of 0.1–0.15 eV seems not to be exaggerated. The analysis of the electrochemical data obtained for the neutral interfaces gave an estimate of the potential barrier of 0.15–0.2 eV (Samec et al., 1986; Wandlowski et al., 1989). The molecular dynamics simulations yielded a comparable value of 0.2 eV (Schweighofer and Benjamin, 1995).

By modeling the system where protons spread away from proton “pumps” at the surface, we found that the barrier could cause an elevation of the proton concentration at the interface up to ∼10−6 M.

Implications for energy transduction in biological membranes

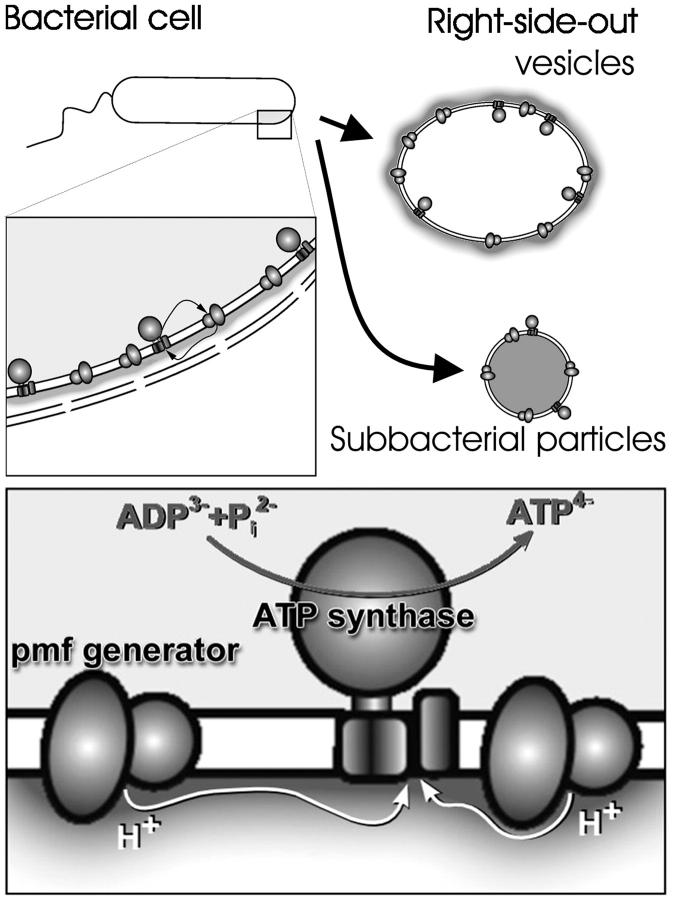
In practice, the relation between ΔpHS and ΔpHB, which is of primary importance for energy transduction, is determined by the size of the p-phase because, as discussed above, the deviation of pHS from pHB is minor from the n-side (see Fig. 3 for the topology of membraneous structures). The rate of the equilibration between pHS and pHB depends on the size of the p-phase. If the p-volume is small, proton pumps would acidify it in seconds. Relevantly, the vast majority of bioenergetic studies were carried out with artificially obtained membrane vesicles such as thylakoids, submitochondrial, and inside-out subbacterial particles with a very small internal p-volume (see Fig. 3). In these cases, the equilibration of the p-phase was expected to be fast (some 10 s), so that the pmf at the steady-state could be approximated by Δψ and by the “bulk” ΔpHB = ΔpHS in agreement with vast amounts of experimental evidence (Cramer and Knaff, 1991; van Walraven et al., 1996; and references cited therein). In these particular cases Mitchell's treatment of the ΔpH term in Eq. 1 is valid.

FIGURE 3.

FIGURE 3

Open in a new tab

Schematic presentation of the topology of different energy-transducing membrane structures. The p-side of coupling membrane is marked by darker color. (Top) A bacterial cell and two types of subbacterial particles. (Bottom) A schematic presentation of a coupling membrane with protons moving along the p-surface from pumps to the ATP synthase.

If the functional volume of the p-phase is very large, pHS could remain more acidic than pHB even at steady state. This might happen in bacterial cells where the periplasmic p-phase faces the “Pacific ocean” (see Fig. 3).

A quantitative evidence for this view comes from membrane transport studies with right-side-out subbacterial vesicles introduced by Kaback and co-worker (Ramos and Kaback, 1977a). These vesicles, which have their p-phase outside (see Fig. 3 for their topology), allow an even more precise control of Δψ and ΔpH than intact bacteria do. It has been shown that energized vesicles of Escherichia coli clamp the inside pH at 7.5 and maintain Δψ at 80 mV (independent of pH outside). On varying the outside pH in the range from 5.5 to 7.5 it was found that the extent of substrate accumulation, although slightly decreasing at higher pH, corresponded to pmf of ∼150–160 mV at pH 7.5 instead of 80 mV as could be expected in the framework of delocalized coupling concept (Ramos and Kaback, 1977b). We suggest the following interpretation of these data: the pHS value at the outer p-surface of these vesicles was 6.2–6.3 at steady state.

Protons that are released by the pumps to the p-surface can either move along the surface to the nearby “pmf consumer”, e.g., an ATP synthase, or escape over the barrier into the bulk phase. The rate of the former, productive reaction is determined by the protonic conductance of the consumer. The rate of the futile proton escape is just proportional to the proton concentration at the surface. In the simplest case, a gradual acidification of the surface would lead to the relative increase in the futile proton escape. It seems more lucrative to block the pumps before the futile proton efflux across the barrier reached remarkable values. In this relation it is noteworthy that the proton-pumping cytochrome bc1 complexes (cytochrome bf complexes in plants), which serve as “hubs” in the vast majority of electron transfer chains, remarkably slow down already at pH <6.5 due to the back-pressure control from the generated pmf (see Kramer et al., 1999, and references therein). This dynamic feedback is likely to prevent the futile proton flux into the bulk by keeping pHS at the p-surface >6.0–6.5.

The considerations presented above point to a coupling mechanism where ATP synthesis is driven by ΔpHS and not by ΔpHB. Under neutral conditions, |ΔpHS| is expected to be >|ΔpHB| by ∼1 pH unit. In mesophilic bacteria, the Δψ value in vivo is 100–150 mV at steady state (Harold, 1986), so that an additional contribution to pmf of 1 pH unit or more might be of a key importance for effective ATP synthesis. As shown in Results, pHS is dependent of pHB and might strongly deviate from the latter under alkaline conditions. This feature could explain the enigmatic bioenergetics of alkaliphilic bacteria.

Although mitochondria and chloroplasts originate from ancient eubacteria (Margulis, 1993), their p-surfaces face the cell interior. On the one hand, the pH of this interior is regulated (clamped), which could favor a difference between pHS and pHB in some cases. On the other hand, the intercellular pH buffers can accelerate the equilibration between pHS and pHB. These points deserve further studies. Anyhow, the potential barrier at the interface is likely to channel proton transfer from pumps to consumers along the surface also in mitochondria and chloroplasts.

Thus, in vivo, the driving force for the ATP synthesis can be better defined as

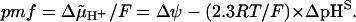graphic file with name M18.gif

One possibility to estimate the values of pHS is to correlate the output (e.g., the ATP yield) with the measured Δψ and ΔpHB. If the output is larger than expected for Δψ − (2.3RT/F) × ΔpHB (see Kell, 1979, 1986, and Ferguson, 1985, for examples), then the value of ΔpHS can be revealed from rather straightforward thermodynamic considerations. Another possibility is to compare the pH dependence of the partial reactions of membrane enzymes as assayed in vitro under pH-controlled conditions with the same reactions in vivo (see Kramer et al., 1999, and references therein). Although with certain limitations, one can compare values of pHB and pHS by using membrane-bound and water-soluble pH indicators, respectively (Krasinskaya et al., 1998).

The outlined coherent picture of electrochemical energy transduction reconciles Mitchell's idea of 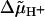Inline graphic as a driving force for the ATP synthesis both with the existence of localized membrane acidic domains as suggested by Williams (1978) and with the anisotropy of proton transfer at the membrane surface (Kell, 1979; Michel and Oesterhelt, 1980; Heberle and Dencher, 1992b; Heberle et al., 1994). Previously, two latter concepts were considered to be at odds with Mitchell's chemiosmotic hypothesis.

Some general implications

The low dielectric permittivity of surface water seems to be a general phenomenon that might manifest itself in different ways. In such a well-characterized system as, for example, the gramicidin A channel, the conductance for K+ ions has been shown to be limited at the applied voltage of ≥200 mV by the ion diffusion in the external water phase (Andersen, 1983). Similar limitation by the events at interface has been revealed when proton conduction by gramicidin was studied (Decker and Levitt, 1988). Quantitative analysis of these data, based on using homogeneous diffusion coefficients for ions, yielded a capture radius for the channel mouth of only ∼0.02 nm (Andersen, 1983; Decker and Levitt, 1988), one order of magnitude smaller than apparent from the crystal structure. A probable reason of this controversy might be the anisotropic character of the ion diffusion coefficient (tensor), with its normal component being 103-fold smaller than the lateral one. Further on, the H+ conductance through the gramicidin A channel has been shown to depend on the proton activity as [H+]0.75 over a range of 5 pH units; this observation remained unexplained (Cukierman, 2000). We suggest that the proton flux to the channel mouth had a considerable surface contribution. In such case the theoretical analysis predicted a flatter dependence of the conductance on the proton concentration as compared to the case of isotropic diffusion in the three-dimensional semispace (Georgievskii et al., 2002).

Another case where the low dielectric permittivity of interfacial water seems to manifest itself is the electrostatic interaction of AFM tips with charged surfaces. The radius of standard SiN tips used in the atomic force microscopy is 2–5 nm, as determined by transmission electron microscopy and by the AFM itself (Schabert and Engel, 1994; Sassaki et al., 1996). This estimate is in good correspondence with the resolution of AFM. However, the calculations of the effective radius from the extent of electrostatic repulsion at the interface yielded an estimate of 100–300 nm for the radii of similar tips (Müller and Engel, 1997). This apparent contradiction can be solved by assuming a lower ɛ-value for the interfacial water on calculations.

Generally, the usage of homogeneous dielectric constant of water can lead to an underestimation of electrostatic forces on modeling the interfacial phenomena. In many cases, however, the application of the classical Poisson-Boltzmann equation allowed to model the experimentally measured surface reactions under assumption of ɛ = 78 at the surface. Such a modeling, however, implied, routinely, several unrestricted parameters. In the simplest case of a lipid membrane, these are the surface charge density, the surface electrostatic potential, the position and thickness of membrane, the dielectric constant of membrane, the effective radii of chargeable groups, and their specific affinity to protons. Because these parameters are roughly independent of each other, one has a considerable degree of freedom on fitting the experimental data. The examples, which we have chosen above and which provide evidence of a lower dielectric permittivity at the surface, represent rare cases where at least some fit parameters can be independently estimated (for example, the size of the gramicidin A channel mouth or the size of an AFM tip).

The kinetic consequences of the potential barrier at the membrane surface might be important for various biological phenomena. As noted above, a strong retardation is expected for divalent ions because the potential barrier height depends on the square of ion charge. In the case of calcium pumps this could lead to the locally elevated concentration of calcium ions at the membrane surface, close to the pump outlets, in agreement with the experimental observations (see Silver, 1999, and references therein).

In the case of anion transporting systems, the electrostatic repulsion of the negatively charged surface could be decreased by patches of the positively charged residues. This expectation is fulfilled in the case of the chloride channel from Salmonella enterica and Escherichia coli, the only anion channel with an available crystal structure: here the chloride “entry” surface indeed carries a cumulative positive charge (Dutzler et al., 2002).

Of special interest are those ions that serve as catalytic substrates of membrane enzymes but are not translocated through the membrane (i.e., nucleotides, phosphate anions, carbonic acids, etc.). These ions usually carry several negative charges, so that potential barrier for them is expected to be very high. In most of the available structures of membrane proteins, the binding/catalytic sites for such ions are located far away from the membrane/water interface (see Fig. 3). In the case of redox enzymes, the peripheral substrate-binding centers are connected with the electron/proton coupling machinery in the membrane core by electron transfer chains formed by numerous redox centers, as it is seen in the structure of the fumarate reductase (Lancaster et al., 1999). In the case of the ATP synthase (Junge et al., 2001) and transhydrogenase (Cotton et al., 2001), rather tricky mechanical gears are used to connect the catalytic sites with the membrane. It is imaginable that the kinetic losses of bringing polyanions into the low-ɛ interfacial water layer are larger than the evolutionary “investments” needed to invent and construct all these transmission gadgets. If so, at least from the enzymes' point of view, the position of these substrate-binding centers at >3 nm away from the membrane/water interface might mark the boundary from which the bulk water phase stretches out.

Acknowledgments

The authors are grateful to M. Y. Galperin, D. B. Kell, and V. P. Skulacher for critical reading of the manuscript and valuable comments.

This work was supported by the Alexander von Humboldt Foundation, the Volkswagen Foundation, the International Association for the promotion of cooperation with scientists from the New Independent States of the former Soviet Union (2001-736), and by grants from the Deutsche Forschungsgemeinschaft (Mu-1285/1, Ju-97/13, SFB 431-P15, 436-RUS-113/210).

APPENDIX

Steady-state proton flux generated by a single proton pump at the membrane/water interface

Here we calculate the proton flux arising due to proton ejection by a point pump in the framework of planar model described in the main text. The stationary Smoluchowski equation in cylindrical coordinates has the form

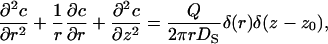graphic file with name M20.gif

where Q is the rate of proton production by the pump. The solution can be obtained as a superposition of the general solution of the homogeneous equation and a partial solution of the inhomogeneous equation. As a partial solution we choose the Green function for diffusion in an infinite space, 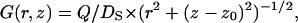Inline graphic normalized in accordance with the source intensity. The general solution of the homogeneous equation can be obtained by separation of the variables. The concentration functions c1(r, z), c2(r, z) and c3(r, z) which are defined in the main text are thereby written as

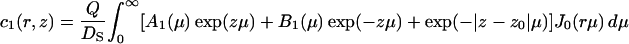graphic file with name M22.gif
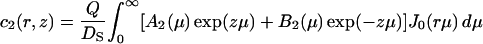graphic file with name M23.gif
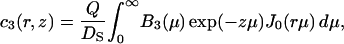graphic file with name M24.gif

where J0 is the Bessel function of the first kind of zero order. The coefficients Ai(μ) and Bi(μ) are determined by the boundary conditions, and for Model 1 they read:

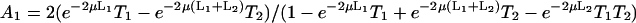graphic file with name M25.gif
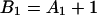graphic file with name M26.gif
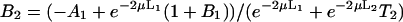graphic file with name M27.gif
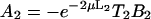graphic file with name M28.gif
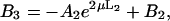graphic file with name M29.gif

where 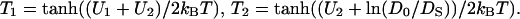Inline graphic The functions c1(r, z), c2(r, z), and c3(r, z) were calculated by numeric integration.

In a similar way we found the solution of Model 2. The latter contains only the functions c1(r, z) and c2(r, z), whereas c3 was zero everywhere in the bulk. The quantitative analysis revealed, however, that protons propagate in the bulk solution by orders of magnitude faster than they cross the potential barrier at the surface. As a result, the solutions of both models were almost identical, so that we quoted only Model 1 in the main text.

References

  1. Adams, J. 1993. MUDPACK-2: multigrid software for elliptic partial differential equations on uniform grids with any resolution. Appl. Math. Comp. 53:235–249. [Google Scholar]
  2. Alexiev, U., R. Mollaaghababa, P. Scherrer, H. G. Khorana, and M. P. Heyn. 1995. Rapid long-range proton diffusion along the surface of the purple membrane and delayed proton transfer into the bulk. Proc. Natl. Acad. Sci. USA. 92:372–376. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Andersen, O. S. 1983. Ion movement through gramicidin A channels. Studies on the diffusion-controlled association step. Biophys. J. 41:147–165. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Antonenko, Y. N., O. N. Kovbasnjuk, and L. S. Yaguzhinsky. 1993. Evidence in favor of the existence of a kinetic barrier for proton transfer from a surface of bilayer phospholipid membrane to bulk water. Biochim. Biophys. Acta. 1150:45–50. [DOI] [PubMed] [Google Scholar]
  5. Arata, H., I. Takenaka, and M. Nishimura. 1987. Flash-induced proton release in Rhodopseudomonas sphaeroides spaeroplasts. J. Biochem. 101:261–265. [DOI] [PubMed] [Google Scholar]
  6. Benjamin, I. 1993. Mechanism and dynamics of ion transfer across a liquid-liquid interface. Science. 261:1558–1560. [DOI] [PubMed] [Google Scholar]
  7. Bockris, J. O., and A. K. N. Reddy. 1977. Modern Electrochemistry. Plenum Press, New York.
  8. Bopp, P. A., A. A. Kornyshev, and G. Sutmann. 1998. Frequency and wave-vector dependent dielectric function of water: collective modes and relaxation spectra. J. Chem. Phys. 109:1939–1959. [Google Scholar]
  9. Boyer, P. D. 2002. A research journey with ATP synthase. J. Biol. Chem. 277:39045–39061. [DOI] [PubMed] [Google Scholar]
  10. Cotton, N. P., S. A. White, S. J. Peake, S. McSweeney, and J. B. Jackson. 2001. The crystal structure of an asymmetric complex of the two nucleotide binding components of proton-translocating transhydrogenase. Structure. 9:165–176. [DOI] [PubMed] [Google Scholar]
  11. Cramer, W. A., and D. B. Knaff. 1991. Energy Transduction in Biological Membranes: A Textbook of Bioenergetics. Springer, New York.
  12. Cukierman, S. 2000. Proton mobilities in water and in different stereoisomers of covalently linked gramicidin A channels. Biophys. J. 78:1825–1834. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Decker, E. R., and D. G. Levitt. 1988. Use of weak acids to determine the bulk diffusion limitation of H+ ion conductance through the gramicidin channel. Biophys. J. 53:25–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Drachev, A. L., A. D. Kaulen, and V. I. Skulachev. 1984. Correlation of photochemical cycle, H+ release and uptake, and electric events in bacteriorhodopsin. FEBS Lett. 178:331–336. [Google Scholar]
  15. Dutzler, R., E. B. Campbell, M. Cadene, B. T. Chait, and R. MacKinnon. 2002. X-ray structure of a ClC chloride channel at 3.0 Å reveals the molecular basis of anion selectivity. Nature. 415:287–294. [DOI] [PubMed] [Google Scholar]
  16. Feniouk, B. A., D. A. Cherepanov, N. E. Voskoboynikova, A. Y. Mulkidjanian, and W. Junge. 2002. Chromatophore vesicles of Rhodobacter capsulatus contain on average one FOF1-ATP synthase each. Biophys. J. 82:1115–1122. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Ferguson, S. J. 1985. Fully delocalised chemiosmotic or localised proton flow pathways in energy coupling? A scrutiny of experimental evidence. Biochim. Biophys. Acta. 811:47–95. [Google Scholar]
  18. Georgievskii, Y., E. S. Medvedev, and A. A. Stuchebrukhov. 2002. Proton transport via the membrane surface. Biophys. J. 82:2833–2846. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Gopta, O. A., D. A. Cherepanov, W. Junge, and A. Y. Mulkidjanian. 1999. Proton transfer from the bulk to the bound ubiquinone QB of the reaction center in chromatophores of Rhodobacter sphaeroides: retarded conveyance by neutral water. Proc. Natl. Acad. Sci. USA. 96:13159–13164. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Guffanti, A. A., and T. A. Krulwich. 1984. Bioenergetic problems of alkalophilic bacteria. Biochem. Soc. Trans. 12:411–412. [DOI] [PubMed] [Google Scholar]
  21. Guffanti, A. A., M. Mann, T. L. Sherman, and T. A. Krulwich. 1984. Patterns of electrochemical proton gradient formation by membrane vesicles from an obligately acidophilic bacterium. J. Bacteriol. 159:448–452. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Harold, F. M. 1986. The Vital Force: A Study of Bioenergetics. W.H. Freeman and Company, New York.
  23. Haumann, M., and W. Junge. 1994. The rates of proton uptake and electron transfer at the reducing side of Photosystem II in thylakoids. FEBS Lett. 347:45–50. [DOI] [PubMed] [Google Scholar]
  24. Heberle, J. 1991. Zeitauflösende Untersuchung der Protonentranslokationsschritte von bakteriorhodopsin mittels chemisch-gekoppelter pH-Indikatoren. Freien Universität Berlin.
  25. Heberle, J., and N. A. Dencher. 1992a. Surface-bound optical probes monitor protein translocation and surface potential changes during the bacteriorhodopsin photocycle. Proc. Natl. Acad. Sci. USA. 89:5996–6000. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Heberle, J., and N. A. Dencher. 1992b. The surface of the purple membrane: a transient pool for protons. In Structures and Functions of Retinal Proteins. J. L. Rigaud, editor. John Libbey Eurotext Ltd. 221–224.
  27. Heberle, J., J. Riesle, G. Thiedemann, D. Oesterhelt, and N. A. Dencher. 1994. Proton migration along the membrane surface and retarded surface to bulk transfer. Nature. 370:379–382. [DOI] [PubMed] [Google Scholar]
  28. Heinz, W. F., and J. H. Hoh. 1999. Relative surface charge density mapping with the atomic force microscope. Biophys. J. 76:528–538. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Ishino, T., H. Hieda, K. Tanaka, and N. Gemma. 1994. Measurements of electrostatic double-layer forces due to charged functional groups on Langmuir-Blodgett films with an atomic force microscope. Jpn. J. Appl. Phys. 33:4718–4722. [Google Scholar]
  30. Israelachvili, J. N. 1992. Intermolecular and Surface Forces. Academic Press, London.
  31. Jones, M. R., and J. B. Jackson. 1989. Proton release by the quinol oxidase site of the cytochrome b/c1 complex following single turnover flash excitation of intact cells of Rhodobacter capsulatus. Biochim. Biophys. Acta. 975:34–43. [Google Scholar]
  32. Junge, W., and S. McLaughlin. 1987. The role of fixed and mobile buffers in the kinetics of proton movement. Biochim. Biophys. Acta. 890:1–5. [DOI] [PubMed] [Google Scholar]
  33. Junge, W., O. Panke, D. A. Cherepanov, K. Gumbiowski, M. Muller, and S. Engelbrecht. 2001. Inter-subunit rotation and elastic power transmission in FOF1-ATPase. FEBS Lett. 504:152–160. [DOI] [PubMed] [Google Scholar]
  34. Junge, W., and A. Polle. 1986. Theory of proton flow along appressed thylakoid membranes under both non-stationary and stationary conditions. Biochim. Biophys. Acta. 848:265–273. [Google Scholar]
  35. Kell, D. B. 1979. On the functional proton current pathway of electron transport phosphorylation. An electrodynamic view. Biochim. Biophys. Acta. 549:55–99. [DOI] [PubMed] [Google Scholar]
  36. Kell, D. B. 1986. Localized protonic coupling: overview and critical evaluation of techniques. Methods Enzymol. 127:538–557. [DOI] [PubMed] [Google Scholar]
  37. Kornyshev, A. A. 1985. Nonlocal electrostatics of solvation. In The Chemical Physics of Solvation. R.R. Dogonadze, E. Kalman, A.A. Kornyshev, and J. Ulstrup, editors. Elsevier, Amsterdam. 77–118.
  38. Kornyshev, A. A., A. M. Kuznetsov, and M. Urbakh. 2002. Coupled ion-interface dynamics and ion transfer across the interface of two immiscible liquids. J. Chem. Phys. 117:6766–6779. [Google Scholar]
  39. Kramer, D. M., C. A. Sacksteder, and J. A. Cruz. 1999. How acidic is the lumen? Photosynth. Res. 60:151–163. [Google Scholar]
  40. Krasinskaya, I. P., M. V. Lapin, and L. S. Yaguzhinsky. 1998. Detection of the local H+ gradients on the internal mitochondrial membrane. FEBS Lett. 440:223–225. [DOI] [PubMed] [Google Scholar]
  41. Krulwich, T. A., M. Ito, R. Gilmour, M. G. Sturr, A. A. Guffanti, and D. B. Hicks. 1996. Energetic problems of extremely alkaliphilic aerobes. Biochim. Biophys. Acta. 1275:21–26. [DOI] [PubMed] [Google Scholar]
  42. Lancaster, C. R., A. Kroger, M. Auer, and H. Michel. 1999. Structure of fumarate reductase from Wolinella succinogenes at 2.2 Å resolution. Nature. 402:377–385. [DOI] [PubMed] [Google Scholar]
  43. Leikin, S., V. A. Parsegian, D. C. Rau, and R. P. Rand. 1993. Hydration forces. Annu. Rev. Phys. Chem. 44:369–395. [DOI] [PubMed] [Google Scholar]
  44. Marcus, R. A. 2000. On the theory of ion transfer rates across the interface of two immiscible liquids. J. Chem. Phys. 113:1618–1629. [Google Scholar]
  45. Margulis, L. 1993. Symbiosis in Cell Evolution. Freeman, New York.
  46. Maroti, P., and C. A. Wraight. 1997. Kinetics of H+ ion binding by the P+ QA− state of bacterial photosynthetic reaction centers: rate limitation within the protein. Biophys. J. 73:367–381. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Matsuura, K., K. Masamoto, S. Itoh, and M. Nishimura. 1979. Effect of surface potential on the intramembrane electrical field measured with carotenoid spectral shift in chromatophores from Rhodopseudomonas sphaeroides. Biochim. Biophys. Acta. 547:91–102. [DOI] [PubMed] [Google Scholar]
  48. Michel, H., and D. Oesterhelt. 1980. Electrochemical proton gradient across the cell membrane of Halobacterium halobium: comparison of the light-induced increase with the increase of intracellular adenosine triphosphate under steady-state illumination. Biochemistry. 19:4615–4619. [DOI] [PubMed] [Google Scholar]
  49. Mitchell, P. 1961. Coupling of photophosphorylation to electron and hydrogen transfer by a chemiosmotic type of mechanism. Nature. 191:144–148. [DOI] [PubMed] [Google Scholar]
  50. Mitchell, P. 1966. Chemiosmotic coupling in oxidative and photosynthetic phosphorylation. Physiol. Rev. 41:445–502. [DOI] [PubMed] [Google Scholar]
  51. Mulkidjanian, A. Y., and W. Junge. 1994. Calibration and time resolution of lumenal pH-transients in chromatophores of Rhodobacter capsulatus following a single turnover flash of light: proton release by the cytochrome bc1-complex is strongly electrogenic. FEBS Lett. 353:189–193. [DOI] [PubMed] [Google Scholar]
  52. Müller, D. J., and A. Engel. 1997. The height of biomolecules measured with the atomic force microscope depends on electrostatic interactions. Biophys. J. 73:1633–1644. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Nachliel, E., and M. Gutman. 1996. Quantitative evaluation of the dynamics of proton transfer from photoactivated bacteriorhodopsin to the bulk. FEBS Lett. 393:221–225. [DOI] [PubMed] [Google Scholar]
  54. Pashley, R. M. 1981. DLVO and hydration forces between mica surfaces in Li, Na, K and Cs electrolyte solutions: a correlation of double-layer and hydration forces with surface cation exchange properties. J. Colloid Interface Sci. 83:531–546. [Google Scholar]
  55. Ramos, S., and H. R. Kaback. 1977a. The electrochemical proton gradient in Escherichia coli membrane vesicles. Biochemistry. 16:848–854. [DOI] [PubMed] [Google Scholar]
  56. Ramos, S., and H. R. Kaback. 1977b. The relationship between the electrochemical proton gradient and active transport in Escherichia coli membrane vesicles. Biochemistry. 16:854–859. [DOI] [PubMed] [Google Scholar]
  57. Rau, D. C., and V. A. Parsegian. 1992. Direct measurement of the intermolecular forces between counterion- condensed DNA double helices. Evidence for long range attractive hydration forces. Biophys. J. 61:246–259. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Samec, Z., Y. I. Kharkats, and Y. Y. Gurevich. 1986. Stochastic approach to the ion transfer kinetics across the interface between two immiscible electrolyte solutions. Comparison with the experimental data. J. Electroanal. Chem. 204:257–266. [Google Scholar]
  59. Sassaki, R. M., R. A. Douglas, M. U. Kleinke, and O. Teschke. 1996. Structure imaging by atomic force microscopy and transmission electron microscopy of different light emitting species of porous silicon. J. Vac. Sci. Technol. B. 14:2432–2437. [Google Scholar]
  60. Schabert, F. A., and A. Engel. 1994. Reproducible acquisition of Escherichia coli porin surface topographs by atomic force microscopy. Biophys. J. 67:2394–2403. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Schweighofer, K. J., and I. Benjamin. 1995. Transfer of small ions across the water/1,2-dichloroethane interface. J. Chem. Phys. 99:9974–9985. [Google Scholar]
  62. Silver, R. B. 1999. Imaging structured space-time patterns of Ca2+ signals: essential information for decisions in cell division. FASEB J. 13(Suppl 2):S209–S215. [DOI] [PubMed] [Google Scholar]
  63. Teschke, O., G. Ceotto, and E. F. de Souza. 2001. Interfacial water dielectric-permittivity-profile measurements using atomic force microscopy. Phys. Rev. E. 64:011605. [DOI] [PubMed] [Google Scholar]
  64. van Walraven, H. S., H. Strotmann, O. Schwarz, and B. Rumberg. 1996. The H+/ATP coupling ratio of the ATP synthase from thiol-modulated chloroplasts and two cyanobacterial strains is four. FEBS Lett. 379:309–313. [DOI] [PubMed] [Google Scholar]
  65. Wandlowski, T., V. Marecek, K. Holub, and Z. Samec. 1989. Ion transfer across liquid-liquid phase boundaries: Electrochemical kinetics by Faradic impedance. J. Phys. Chem. 93:8204–8212. [Google Scholar]
  66. Williams, R. J. P. 1978. The multifarious couplings of energy transduction. Biochim. Biophys. Acta. 505:1–44. [DOI] [PubMed] [Google Scholar]
  67. Zhang, J., and P. R. Unwin. 2002. Proton diffusion at phospholipid assemblies. J. Am. Chem. Soc. 124:2379–2383. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES