On the Mechanism of ATP Hydrolysis in F₁-ATPase

Abstract

Most of the cellular ATP in living organisms is synthesized by the enzyme F₁F_o-ATP synthase. The water soluble F₁ part of the enzyme can also work in reverse and utilize the chemical energy released during ATP hydrolysis to generate mechanical motion. Despite the availability of a large amount of biochemical data and several x-ray crystallographic structures of F₁, there still remains a considerable lack of understanding as to how this protein efficiently converts the chemical energy released during the reaction ATP + H₂O → ADP + P_i into mechanical motion of the stalk. We report here an ab initio QM/MM study of ATP hydrolysis in the β_TP catalytic site of F₁. Our simulations provide an atomic level description of the reaction path, its energetics, and the interaction of the nucleotide with the protein environment during catalysis. The simulations suggest that the reaction path with the lowest potential energy barrier proceeds via nucleophilic attack on the γ-phosphate involving two water molecules. Furthermore, the ATP hydrolysis reaction in β_TP is found to be endothermic, demonstrating that the catalytic site is able to support the synthesis of ATP and does not promote ATP hydrolysis in the particular conformation studied.

INTRODUCTION

Since its discovery in 1929 (Fiske and Subbarow, 1929) much research has been devoted to the molecule adenosine tri-phosphate (ATP) and its role during metabolism in living organisms. This is also true for the protein machine which synthesizes most of this molecule in amounts exceeding a person's own body weight in ATP per day. The enzyme F₁F_o-ATPase that performs this task, resides, e.g., in the membranes of mitochondria, chloroplasts, or bacteria and is probably the most abundant protein in any organism. The F_o part of the enzyme is embedded in the lipid membrane and connected to the solvent-exposed F₁ unit by a central stalk. The synthesis of ATP is ultimately driven by an electrochemical proton gradient across the membrane which is converted into a rotation of the central stalk by the F_o unit. The mechanical rotation of the shaft subsequently leads to conformational changes in the binding pockets located in the F₁ part of ATP synthase, thereby driving synthesis of ATP.

Fig. 1 depicts the F₁ subunit of the mitochondrial enzyme (Gibbons et al., 2000). In its simplest prokaryotic form, the outer part of F₁ consists of a hexamer of α- and β-subunits which are arranged as an (αβ)₃ trimer into the shape of an orange. The remainder of F₁ is made of γ, δ, and ɛ, with γ and ɛ forming the central stalk. The trimeric (αβ)₃ arrangement of F₁ has three catalytic and three noncatalytic sites which are each located at the interface between neighboring α- and β-subunits. Biochemical equilibrium binding studies of F₁-ATPase clearly revealed the presence of three catalytic sites with different binding affinities for ATP, termed tight, loose, and open in Boyer's binding-change mechanism (Boyer, 1993, 2000) or high, medium, and low by Senior and co-workers (Weber et al., 2000b). This was corroborated by the first crystallographic structure of F₁ (Abrahams et al., 1994), which showed all three catalytic sites in different conformations, termed β_TP, β_DP, and β_E. On geometrical grounds Abrahams et al. (1994) suggested that β_DP is the catalytic site of highest ATP binding affinity, but there is still no consensus on how to map binding affinity to structure.

FIGURE 1.

Structure of F₁-ATPase in surface representation. The α-, β-, and γ-subunits are colored in yellow, green, and gray, respectively. The protein subsystem used for the QM/MM simulations is shown in blue and also depicts the water molecules included in the simulations.

F₁F_o-ATPase can also use the energy stored in ATP to drive the reverse process via hydrolysis of the nucleotide, i.e., it can induce the reverse rotation of the central stalk (Noji et al., 1997; Yasuda et al., 2001) and use this to pump protons across the membrane (Weber and Senior, 1997). In fact, the hydrolysis mode of F₁ has been studied much more extensively and is therefore much better understood than the synthesis mode (Weber et al., 2000b; Senior et al., 2002).

Despite extensive research efforts to reveal the molecular mechanism behind ATPase's effectiveness as a recharger of the cell's ATP storage, it was not until two decades ago that scientists started to get a glimpse on how this enzyme performs its task. Boyer's suggestion of a rotational catalytic mechanism—the so-called binding change mechanism (Boyer, 1993)—was confirmed by the first x-ray structure of the water soluble F₁ part of F₁F_o-ATPase published in 1994 (Abrahams et al., 1994). Additional structures have been solved since Walker's seminal publication, revealing, e.g., the complete structure of the γ-subunit (Gibbons et al., 2000) or catalytic sites of F₁ trapped in a transition-state-like conformation (Braig et al., 2000; Menz et al., 2001). The latter can be achieved by the inhibition with transition state analogs such as AlF₃ or AlF₄⁻, but it is unfortunately not clear how closely these structures resemble the actual transition state present during ATP hydrolysis. A more realistic picture of the transition state (TS) conformation is clearly desirable.

The availability of crystal structures also facilitated the interpretation of mutation and deletion studies and much has been revealed with respect to the possible role of specific residues in nucleotide binding, hydrolysis/synthesis, and interaction of the catalytic (αβ)₃ hexamer with the rotating stalk. But whereas the understanding of F₁F_o-ATPase on the biochemical level is quite detailed, there is only limited information on the underlying microscopic processes during the enzyme's working cycle. Very little is known about how the binding pocket efficiently promotes hydrolysis of ATP and about how the small change in chemical structure during the hydrolysis reaction is involved in driving the rotation of the stalk. This is where atomic level computer simulations can be of great use, since they permit a very detailed examination of the protein structure, its energetics, and the interactions between different parts of the system under investigation.

Several computational studies addressing the mechanism of ATP or guanosine tri-phosphate (GTP) hydrolysis in proteins have been carried out for systems other than F₁-ATPase, e.g., for myosin (Okimoto et al., 2001), for p21^ras (Glennon et al., 2000; Langen et al., 1992; Schweins et al., 1994), and Cdc42 (Cavalli and Carloni, 2001). These studies employ different levels of quantum chemical description for the influence of the protein environment on the hydrolysis reaction. The simulations by Okimoto et al. (2001) and Cavalli and Carloni (2001) are both gas phase studies on cluster systems, the latter having met critique by Warshel (2003). The calculations by Glennon et al. (2000), Langen et al. (1992), and Schweins et al. (1994) employ the empirical valence bond (EVB) methodology to examine the GTP hydrolysis reaction in Ras. Furthermore, Warshel and co-workers have thoroughly analyzed the hydrolysis reaction in phosphate esters and characterized the reaction pathways (Florián and Warshel, 1997, 1998).

Since chemical reactions and ATP hydrolysis in particular involve the breaking and formation of chemical bonds, they cannot be studied using molecular dynamics simulations, but rather require quantum chemical methods to model the reactive part of the system. This can be accomplished by selecting a suitable cluster system for the quantum chemical calculations, including the reactive core as well as a number of atoms or residues of the surrounding protein which are believed to sufficiently model the most direct influence of the protein environment. Since quantum chemical calculations are computationally expensive, it is, however, not feasible to include more than a few hundred atoms.

In the present study we employ a quantum mechanical/molecular mechanical (QM/MM) methodology (Warshel and Levitt, 1976; Singh and Kollman, 1986; Field et al., 1990; Stanton et al., 1995; Maseras and Morokuma, 1995; Bakowies and Thiel, 1996; Lyne et al., 1999; Lyne and Walsh, 2001) that permits one to also include, beyond the quantum chemically described core region, a key part of the protein, the latter being treated classically. Due to this separation, QM/MM approaches allow one to treat much larger systems with thousands of atoms in the classical domain (Warshel and Levitt, 1976; Bash et al., 1991; Hartsough and Merz, Jr., 1995; Alhambra et al., 1998; Mulholland et al., 2000; Hayashi and Ohmine, 2000; Warshel, 2003). The present study examines the ATP hydrolysis reaction inside the β_TP catalytic site of F₁-ATPase. We seek to determine the reaction path, its energetics, and the interaction of the protein environment with ATP during hydrolysis. To assess the quality of our QM description, we also performed gas phase calculations of the hydrolysis reaction. Inside the binding pocket we find that a multicenter pathway proceeding via a proton relay exhibits a significantly lower potential energy barrier compared to a conventional single-center reaction. Furthermore, the present study shows that ATP hydrolysis in β_TP is strongly endothermic. β_TP in the particular conformation studied does, therefore, facilitate synthesis of ATP rather than promote its hydrolysis.

METHODS

This section summarizes the computational methods used for the ab initio gas phase study of ATP hydrolysis and for the QM/MM calculations of the same process inside the binding pocket of F₁-ATPase.

Gas phase calculations

For our gas phase study of ATP hydrolysis, we employed an ATP analog (ATPa) consisting of the tri-phosphate moiety of ATP up to the C5′ atom of the ribose subunit. The valency was completed by adding a dummy hydrogen atom to C5′. The initial structures for the ab initio QM calculations on ATPa and on ATPa plus nucleophilic water were constructed and subsequently optimized using a molecular mechanics force field. The resulting structures provided the starting geometries for the ab initio QM optimizations of both systems. For our calculations, we used the quantum chemistry package GAMESS (Schmidt et al., 1993). To study the ATP hydrolysis reaction, we employed the HF/6-31G as well as the HF/6-31G^* level of theory and determined the respective TS and intrinsic reaction coordinate (IRC) pathways. To account for electron correlation effects, we used second-order Møller-Plesset perturbation theory and we refined the single-point energies at the initial, final, and TS geometries.

All TS were characterized by calculating the Hessian matrix to assure the presence of only one eigenmode with imaginary frequency. At both levels of theory we found the nucleophile to be the hydroxide anion in accord with the study by Florián and Warshel (1998) for the methyl-phosphate di-anion. Like Florián and Warshel (1998), we assume that the conformation and the energy of the TS for nucleophilic attack of water on the tetra-anion are similar to the ones for nucleophilic attack of hydroxide on the protonated tri-anion. The optimized reactant state structures at both levels of theory do not deviate significantly from each other. Particularly the hydrogen-bond distances between water and the γ-oxygens remain virtually unchanged, namely 1.90 Å/1.91 Å and 1.88 Å/1.91 Å for the HF/6-31G and HF/6-31G^* levels of theory, respectively. For either basis set the TS structure exhibits a planar, pentacovalent conformation, the major structural difference being a reduction in distance between the nucleophile and the protonated tri-phosphate tri-anion and P_i and the di-phosphate tri-anion by 0.18 Å and 0.23 Å respectively. The TS barrier height at the HF/6-31G (MP2//HF/6-31G) level of theory is 55.51 kcal/mol (48.70 kcal/mol), which is 7.46 kcal/mol (7.39 kcal/mol) lower than the value for HF/6-31G^* (MP2//HF/6-31G^*). Overall, the gas-phase calculations confirm that the HF/6-31G level of theory is sufficient to capture the essential features of the ATP hydrolysis reaction.

QM/MM calculations

The starting configuration for our study of ATP hydrolysis in the β_TP binding pocket of F₁-ATPase was the x-ray crystallographic structure determined by Gibbons et al. (2000) (PDB access code 1E79). The DCCD inhibitor used during crystallization was removed and ADP in β_TP was replaced by ATP. The complete structure was then solvated in a box of water and neutralized with a physiological concentration of Na⁺ and Cl⁻ ions. Particular care was devoted to water molecules inside the binding pockets, and the positions of solvent water molecules close to the nucleotide were confirmed with the program DOWSER (Zhang and Hermans, 1996). A similar approach for placing water molecules was used in other studies, e.g., for the investigation of photo-induced activation in rhodopsin by Saam et al. (2002). The total system contained 327,506 atoms, including 91,901 water molecules. It was then equilibrated for 0.4 ns with the molecular dynamics program NAMD2 (Kalé et al., 1999), using the CHARMM27 force field (Brooks et al., 1983) and the PME method (Darden et al., 1993) to treat the electrostatics. To generate a well-minimized structure as the starting conformation for the QM/MM calculations, the system was then subjected to a simulated annealing protocol: it was cooled down from an initial temperature of 298 K after equilibration to a final temperature of 18 K in steps of 10 K with an equilibration time of 10-ps each. The annealed structure was then extensively minimized using NAMD2. Since the total system with >300,000 atoms was considerably too large to be accessible by our QM/MM methodology, we considered only a subsystem consisting of residues and solvent water molecules with atoms closer than 20 Å to the nucleotide in the β_TP site of F₁-ATPase. Fig. 1 shows the subsystem, which contains a total of 8378 atoms. During all QM/MM simulations, 5702 atoms that were located in a shell between 15 Å and 20 Å around ATP were fixed to preserve the overall shape of the system. This approach is appropriate for studying the ATP hydrolysis pathway and its associated energetics in the particular binding pocket conformation captured by the x-ray structure of Gibbons et al. (2000). The energetics for the full rotational catalytic cycle can then be obtained by considering a series of conformational snapshots taken from the present and other structures of F₁. Furthermore, even though this treatment does not allow one to model the cooperativity between individual subunits of F₁-ATPase, it can nevertheless provide insight into what local structural motions are coupled to larger-scale conformational changes during hydrolysis. The β_TP subsystem was then further minimized using molecular mechanics, employing the AMBER force field (Cornell et al., 1995) for the protein and the TIP3P model (Jorgensen et al., 1983) for the water molecules. The minimization was continued until a RMS gradient <10⁻⁶ Hartree/Bohr was reached.

Our QM/MM method uses an effective charge operator based on restrained electrostatic potential charges (Baily et al., 1993) to construct the QM/MM Hamiltonian and permits one to obtain the optimized geometry of the total QM/MM system. Details and further references with respect to the optimization procedure can be found in Hayashi and Ohmine (2000). Saddle-point searches were carried out in the same fashion as the optimizations. To assure that the trajectory converged toward the TS, the Hessian matrix was recalculated after each QM/MM optimization cycle to ensure proper convergence. The final TS conformation was confirmed by the presence of only one eigenmode with imaginary frequency in the Hessian matrix. Finally, to determine the reaction path connecting the TS to product and reactant states, we performed an IRC search for the QM segment while re-optimizing the MM region after every third IRC point. In addition to the TS between the reactant and the first intermediate state, the system exhibited two further potential energy maxima along the reaction coordinate. Unfortunately, the potential energy landscape in the vicinity of the maxima turned out to be very flat and made a determination of the second and third transition state very difficult. Thus, we characterized the respective maximum energy structures via constrained optimizations using small steps along the reaction coordinate (see Results). The energies of both maxima were estimated to be lower than that of the first TS.

Since the calculations in the present article employ an ab initio QM/MM methodology, all pathways and associated energetics are derived from the ground state potential energy surface and do not include entropic effects or conformational sampling. Hence, we cannot preclude that in the present study, which compares reaction mechanisms involving a different number of water molecules, entropic contributions might lead to quantitative changes in the reaction energetics. However, the main conclusions of our study should be valid, particularly since our approach rests on a comparison between different hydrolysis pathways in β_TP using the same computational technique.

At the interface between the quantum and classical regions we use AMBER parameters to describe the van der Waals interaction. The residue-based cutoff for the van der Waals and electrostatic interactions was chosen to be 12 Å. To satisfy the valencies across bonds at the QM/MM interface, we used the link-atom approach and capped the QM system with hydrogen atoms. The QM/MM code has been implemented in the HONDO (Depuis et al., 1992) and GAMESS (Schmidt et al., 1993) quantum chemistry packages. All QM geometry optimizations were performed using the Hartree-Fock level of theory and the 6-31G basis set (HF/6-31G). Due to the iterative nature of our QM/MM methodology and the size of the quantum-mechanically treated core region, HF/6-31G constituted the largest basis set which we could afford computationally. Our gas phase study (see beginning of Methods) confirmed that the HF/6-31G level of theory is able to properly describe the hydrolysis reaction and that it provides reasonable geometries, but possibly slightly underestimates the reaction barriers. Also, the TS conformation obtained by our QM/MM methodology is in agreement with anticipated features for this type of reaction, e.g., a planar pentacovalent TS structure (Senior et al., 2002), and, hence, provides further confidence in the quality of our description. Since our QM/MM interface is currently not able to perform DFT calculations, we used second-order Møller-Plesset perturbation theory (MP2//HF/6-31G) at selected points along the reaction coordinate to account for electron correlation.

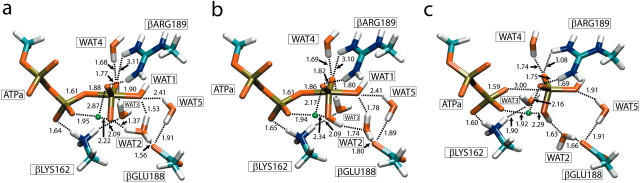
Fig. 2 a shows the QM region chosen in our calculations. It consists of the tri-phosphate part of ATP cut at the C4′-C5′ bond in the ribose subunit (ATPa), the side chain of βLYS162 cut at the C_ɛ-C_δ bond, the side chain of βGLU188 cut at the C_β-C_γ bond, the side chain of βARG189 cut at the C_γ-C_δ bond, a magnesium Mg²⁺, and five water molecules. The protein residues are labeled using the nomenclature for the bovine mitochondrial protein in accord with the initial structure. The water molecules are labeled sequentially from WAT1 to WAT5.

FIGURE 2.

(a) Structure of the QM region in β_TP optimized at the MM level of theory. (b) Structure of the QM region in β_TP optimized via QM/MM simulations. (c) TS structure of the QM region in β_TP for nucleophilic attack of WAT2. The dotted lines indicate hydrogen bonds except for the ones connected to Mg²⁺ located near the center and colored in green. All distances are given in Å. The phosphate atoms are shown in gold, oxygen in red, carbon in light blue, nitrogen in dark blue, and hydrogen atoms in white.

STUDY OF ATP HYDROLYSIS IN THE β_TP CATALYTIC SITE OF F₁-ATPASE

In this section we present the results of our QM/MM study of ATP hydrolysis in the β_TP binding pocket of F₁-ATPase. To initially establish a suitable scheme for dividing the β_TP subsystem into a quantum and a classical segment, we performed a set of QM/MM optimizations employing quantum regions of increasing size and complexity. The final QM region, which was the largest computationally feasible, is described in Methods and is shown in Fig. 2 a. It includes most of the residues in the immediate proximity of the tri-phosphate moiety, all of which have been shown experimentally to be important either for ATP binding or ATP hydrolysis (Boyer, 1997; Abrahams et al., 1994; Gibbons et al., 2000; Weber and Senior, 1997; Weber et al., 2000b; Senior et al., 2002). It should be pointed out that, since the system under investigation is based on the crystal structure by Gibbons et al. (2000), the side chain of αARG373 in β_TP is displaced by >10 Å compared to its position in β_DP. This conformation is different from the arrangement observed in β_TP of other x-ray structures of F₁-ATPase (Abrahams et al., 1994; Braig et al., 2000; Menz et al., 2001). Movement of this residue during the catalytic cycle might, therefore, be important for efficient catalysis.

A comparison of the QM-optimized structures of subsystems for β_TP and β_DP reveals significant differences in the location and relative orientation of important residues other than αARG373. In β_DP, the side chain of βGLU188 approaches the γ-phosphate by 0.33 Å compared to β_TP. The back end of the β_DP binding pocket toward which the hydrolysis product P_i will be released is enlarged compared to β_TP. This is mainly due to residues contributed by the neighboring α-subunit which recede from the γ-phosphate group, e.g., by ∼0.75 Å for αSER344.

MM optimization

After equilibration, simulated annealing, and minimization of the fully solvated F₁ structure, the QM/MM subsystem of the β_TP pocket was prepared as outlined in Methods. Here we report briefly on the final geometry obtained via extensive MM optimization of this subsystem. The reactive core region is shown in Fig. 2 a. The conformation of the nucleoside is C3′-endo for the sugar pucker and anti for the glycosyl rotation between sugar and base. The terminal phosphate group is embedded in a water-filled cavity formed by protein residues and is surrounded by, and hydrogen-bonded to, six solvent water molecules, the positions of some of which can be identified with ones observed in x-ray structures. Five of these six water molecules (WAT1 to WAT5) are included in the QM region. Interestingly, βLYS162 is not hydrogen-bonded to the β- and γ-phosphate group as has been proposed in the literature (Weber and Senior, 1997), but rather to ATP-O_β1 and WAT3. A water molecule, WAT2, which has previously been suggested as the nucleophilic water during hydrolysis (Abrahams et al., 1994; Weber and Senior, 1997), is hydrogen-bonded to ATP-O_γ1 as well as βGLU188-O_ɛ1 and forms a bridge between the two. The carboxyl group of βGLU188 has been proposed to polarize the water molecule in preparation for nucleophilic attack on P_γ or even to serve as a general base (Abrahams et al., 1994). Fig. 2 a indeed shows this group interacting with two water molecules, WAT2 and WAT5. The residue βARG189 forms two strong hydrogen bonds with the oxygens of the γ-phosphate, which suggests a role in mediating conformational changes during product formation. The di-cation Mg²⁺ is chelated to O_β2, O_γ1, and O_γ2, with a distance of ∼1.9 Å in each case. Together with the positively charged side chains of βARG189 and βLYS162, the metal ion Mg²⁺ assists in binding the nucleotide and in screening the localized negative charge which develops in the TS during hydrolysis.

QM/MM optimization

The starting system for the QM/MM optimization was the MM minimized structure described in the previous paragraph. We report here the results of energy optimizations at the HF/6-31G level of theory. Fig. 2 b displays the final QM/MM-optimized structure of the QM segment. The most notable feature compared to the MM-optimized structure (shown in Fig. 2 a) is a drastic rearrangement of water molecule WAT1. In the MM-optimized structure, WAT1 is hydrogen-bonded to ATP-O_γ3 and αSER344-O (not shown). During the QM/MM optimization, WAT1 moves toward WAT2 and hydrogen-bonds to the latter and αSER344-O. This rearrangement brings WAT1 into a near in-line position with respect to ATP-P_γ, suggesting that WAT1 rather than WAT2 is the nucleophilic water during ATP hydrolysis. This change in the hydrogen-bonding network around the γ-phosphate group stems mainly from charge transfer and electronic polarization effects due to the highly charged protein environment, features that are not accounted for by a molecular mechanics force field.

Table 1 compares the bond lengths of ATPa in the QM/MM-optimized structure with the corresponding gas phase values. In the gas phase, the bonds along the phosphate backbone exhibit a pronounced alternation in their lengths. This effect is reduced in the presence of the enzyme and even inverted for the P_α-O_α3 and O_α3-P_β bonds, emphasizing the influence of the protein environment on nucleotide conformation. Of particular importance in this regard are the positively charged residues βLYS162, βARG189, and the metal ion Mg²⁺. The bond lengths in phosphoryl group compounds have been measured spectroscopically (Cheng et al., 2002) and have been found to lie between 1.6 Å and 1.7 Å, in accordance with our values. The residue βLYS162 is strongly hydrogen-bonded to ATP (the βLYS162-N_η to ATP-O_β1 distance being 2.76 Å), but a proton transfer from βLYS162-N_η to ATP as suggested by theoretical studies of hydrolysis in Cdc42 and Ras (Cavalli and Carloni, 2001; Futatsugi et al., 1999) was not observed during the QM/MM optimizations. The coordination of Mg²⁺ observed in the present study closely resembles the one extracted from crystal structure data (Abrahams et al., 1994) and mutational studies (Weber et al., 1998). The metal ion is liganded to three oxygen atoms of ATP (ATP-O_β2, ATP-O_γ1, ATP-O_γ2), βTHR163-O_γ, and two water molecules. One of the latter is coordinated to βGLU192 and βGLU188. It has been shown experimentally (Weber et al., 1998) that βGLU188 is not required for correct positioning of Mg²⁺. Indeed, since Mg²⁺ is stabilized by at least three water molecules and polar or charged residues other than βGLU188, it can bind in this position even in the absence of βGLU188.

TABLE 1.

Comparison of important bond lengths in ATPa obtained via gas phase (HF/6-31G) and QM/MM optimizations

Bond index	Bond length gas phase [Å]	Bond length QM/MM [Å]
Pα–Oα3	1.66	1.73
Oα3–Pβ	1.74	1.63
Pβ–Oβ3	1.65	1.67
Oβ3–Pγ	1.77	1.71
Pγ–Oγ1	1.62	1.61
Pγ–Oγ2	1.62	1.61
Pγ –Oγ3	1.61	1.58

The strong interactions of positively charged groups (βLYS162, βARG189, Mg²⁺) with the negatively charged ATP involve electronic as well as electrostatic contributions. Table 2 lists the Mulliken charges of key moieties in the QM region. It is important to note that whereas an ATP molecule in vacuo has a net charge of −4e, in situ it loses a large amount of electron density (−0.43e) due to charge transfer to the surrounding positively charged groups, namely Mg²⁺ (−0.3e), βLYS162 (−0.09e), and βARG189 (−0.04e). This behavior can be captured only by a QM/MM treatment.

TABLE 2.

Mulliken charges on important groups for the reactant, transition state (TS), first intermediate (IM1), and product conformation derived from HF/6-31G

Group name	Reactant	TS	IM1	Product
ATP*	−3.57	−3.69	−3.53	−3.69
ADP†	−2.41	−2.59	−2.58	−2.73
Pi‡	−1.15	−1.13	−1.01	−0.88
Mg2+	1.70	1.68	1.69	1.71
WAT1	−0.02	–	–	–
WAT2§	−0.01	0.17	−0.04	0.03
H3O+¶	–	0.71	–	–
WAT3	0.00	−0.02	0.00	0.01
WAT4	−0.01	−0.02	−0.01	0.00
WAT5	−0.07	−0.05	−0.05	−0.05
βGLU188	−0.89	−0.85	−0.88	−0.87
βARG189	0.96	0.96	0.96	0.95
βLYS162	0.91	0.89	0.90	0.86

^*ATP refers to the collection of atoms belonging to ATP in the reactant state.

^†ADP refers to the collection of atoms belonging to ADP in the reactant state.

^‡P_i refers to the collection of atoms including P_γ, O_γ1, O_γ2, and O_γ3 of ATP, WAT1-O, WAT1-H₁, and WAT2-H₁.

^§WAT2 in the reactant and transition state consists of the collection of atoms belonging to WAT2 in the reactant state. After the proton transfer, WAT2 in IM1 and the product state consists of WAT1-H₂, WAT2-O, and WAT2-H₂.

^¶H₃O⁺ consists of WAT1-H₂, WAT2-H₁, WAT2-O, and WAT2-H₂.

ATP hydrolysis

The QM/MM-optimized conformation suggests at least two possible mechanisms for the hydrolysis reaction to proceed. In one case, WAT2, which is hydrogen-bonded to and polarized by βGLU188, is the nucleophilic water. This corresponds to a pathway previously proposed based on a water molecule observed in x-ray crystallographic data (Abrahams et al., 1994; Gibbons et al., 2000; Weber and Senior, 1997). The second case involves nucleophilic attack by WAT1 and is suggested by our QM/MM-optimized reactant structure, since WAT1 is already positioned in a near in-line conformation with respect to the γ-phosphate group. Nucleophilic attack by WAT5 might constitute a third mechanism. However, this mechanism was not considered in the present study since WAT5 is >1 Å farther away from the γ-phosphate group than WAT1.

Mechanism involving nucleophilic attack by WAT2

To investigate this pathway, nucleophilic attack was initiated by pushing WAT2 toward P_γ. The reaction proceeded via direct proton transfer from WAT2 to ATP-O_γ1 and subsequent bond formation between WAT2-O and ATP-P_γ. Fig. 2 c shows the TS conformation corresponding to this mechanism. Based on the hydrogen-bond network which is present in the initial conformation of the β_TP subsystem, ATP-O_γ1 is the only viable proton acceptor for WAT2. Direct proton transfer to ATP-O_γ1 was therefore the only such mechanism studied. Similar single-center processes have been investigated theoretically in systems other than F₁ (Glennon et al., 2000; Cavalli and Carloni, 2001; Okimoto et al., 2001) with the assumption that only the nucleotide and a single water molecule are explicitly involved in hydrolysis. We determined the TS for this mechanism and obtained a potential energy barrier height of 50.4 kcal/mol at the MP2//HF/6-31G level of theory. This value is too high to explain the experimentally observed reaction rates even under unisite conditions (Al-Shawi et al., 1989) and suggests that this pathway is likely not the one used by the enzyme. It has to be kept in mind, however, that the activation barriers which follow from our QM/MM methodology reside on the potential energy rather than the free energy surface (see Methods) and, therefore, are not directly related to the experimentally measured reaction rates. We also cannot completely rule out the possibility that the high barrier obtained for the single-center reaction might be due to insufficient equilibration of the QM/MM system. Our QM/MM methodology assumes a unique reactant state structure, and additional conformational sampling might lead to different reactant conformations, which could support proton transfer to oxygen atoms other than ATP-O_γ1 and yield lower reaction barriers. An EVB study by Glennon et al. (2000) for GTP hydrolysis in Ras, which employed a single nucleophilic water molecule, gave energy barriers in agreement with experimental results. These findings, however, do not provide strong evidence for the fact that the same has to hold true in F₁-ATPase.

Mechanism involving nucleophilic attack by WAT1

To determine the reaction path for nucleophilic attack by WAT1, hydrolysis was initiated by pushing WAT1 toward ATP-P_γ. Fig. 3 illustrates the reaction scheme determined by our calculations. Nucleophilic attack proceeds in an S_N2-like manner where the γ-phosphate transiently assumes a pentagonal arrangement of its bound oxygen atoms. The simulations also reveal that the γ-phosphate itself, and not βGLU188, accepts a proton during hydrolysis and, therefore, acts as the general base. Interestingly, a second water molecule, WAT2, explicitly participates in the reaction. The first reaction event is a proton transfer from WAT1 to WAT2, and WAT2 subsequently donates its proton to ATP-O_γ1. This multicenter reaction via a proton relay differs substantially from the single-center process investigated above. Most importantly, we find that the TS barrier for the multicenter pathway is significantly lower than the one encountered in the single-center mechanism, indicating that this pathway establishes the physiologically relevant mechanism.

FIGURE 3.

Schematic representation of the multicenter reaction for ATP hydrolysis, showing the (a) reactant, (b) transition, (c) intermediate, and (d) product state.

Transition state conformation

Fig. 4 a shows the transition state structure determined by a saddle-point search based on the QM/MM Hamiltonian (see Methods). One can clearly discern an H₃O⁺ ion (WAT2) between ATP-O_γ1 and βGLU188. The γ-phosphate and the attacking water molecule WAT1 exhibit a nearly perfect S_N2-like associative conformation. The bond distances between P_γ and O_β3 and the oxygen of WAT1 are 1.88 Å and 1.90 Å, respectively. The dihedral angle of the central PO₃ group is <1° and therefore almost planar. The orientation of the attacking and leaving group oxygen atoms deviates slightly from a perfect in-line arrangement, and the two oxygen atoms form a bond angle of 171° with P_γ. The distances of WAT1's transferring proton to WAT1-O and to WAT2-O are 1.53 Å and 1.01 Å, respectively. The proton, therefore, has already been transferred to WAT2 to form an H₃O⁺ ion. The bond length of WAT2's proton hydrogen-bonded to ATP-O_γ1, on the other hand, is 1.07 Å—i.e., it is longer than a regular O-H bond in a water molecule. The proton has therefore initiated its transfer to ATP-O_γ1. The hydrogen-bond distance between βARG189-N_η2 and ATP-O_γ3 increases from 3.38 to 3.85 Å upon formation of the TS, and the hydrogen bond is, therefore, almost broken. In contrast, the distance between βARG189-N_η1 and ATP-O_γ2 remains unchanged (2.76 Å for both the reactant and the TS), leaving this hydrogen bond intact.

FIGURE 4.

(a) TS structure of the QM region in β_TP. (b) Intermediate state (IM1) structure of the QM region in β_TP. (c) Structure of the QM region for the product conformation of ADP and P_i in β_TP. The dotted lines indicate hydrogen bonds except for the ones connected to Mg²⁺. All distances are given in Å and the color coding is as in Fig. 2.

Intermediate state conformation

To find the state following the formation of the TS along the reaction path, the system was relaxed along the IRC. Interestingly, the system did not proceed toward the product state which is characterized by well-separated ADP and P_i. Rather, it became trapped in an intermediate conformation. This intermediate is denoted as IM1, and Fig. 4 b shows its structure. A similar intermediate state has been proposed earlier, e.g., in a study of GTP hydrolysis in Ras (Glennon et al., 2000). The γ-phosphate moiety remains in the pentacoordinated conformation observed in the TS and the dihedral angle of the central PO₃ group is 3.8°. P_γ and the attacking and leaving group oxygen atoms are almost in-line (170°) and the distance between ADP-O_β3 and P_γ remains nearly constant when compared to the TS structure. The intermediate state exhibits bond formation between the nucleophilic oxygen and P_γ, with a bond length of 1.8 Å, which is 0.1 Å shorter than its value in the TS. This bond formation is accompanied by proton transfer from H₃O⁺ (WAT2) to ATP-O_γ1. Both processes correlate strongly; the formation of the P_γ-WAT1-O bond donates electron density to P_γ and, in turn, facilitates bond formation between ATP-O_γ1 and the proton from WAT2, which involves withdrawal of electron density from ATP-O_γ1 and vice versa.

Product state conformation

To determine the product conformation, we increased the ATP-O_β3-P_γ bond length in steps of 0.1 Å. At each step we fully relaxed the system keeping the ATP-O_β3-P_γ bond fixed. The potential energy along the trajectory was rather flat and the system became trapped in a local minimum after stretching by 1 Å, such that it did not relax back toward the intermediate state upon removal of the constraint. This second intermediate state is denoted as IM2. Furthermore, flipping WAT2 away from P_i, simulated by constrained optimization along the hydrogen bond between WAT2 and P_i in steps of 0.05 Å, led to the formation of the product state in which the ADP and P_i moieties are even further separated. Thorough QM/MM optimization of this arrangement resulted in a fully hydrolyzed product conformation of ADP and P_i. Hence, in addition to the TS, we find two additional energy barriers along the reaction coordinate, corresponding to pulling along ATP-O_β3-P_γ (denoted by B1) and flipping of WAT2 (denoted by B2), respectively.

The constrained optimizations gave upper limits for the two energy barriers. The estimates for both were lower than the energy barrier of the first TS, confirming that the latter controls the rate-limiting step for ATP hydrolysis. Fig. 4 c displays the final product conformation inside the binding pocket. One can clearly discern that the chemical bond between P_γ and ADP-O_β3 is completely broken, as indicated by a bond length of 3.0 Å. The phosphate group P_i assumes a tetrahedral conformation. ADP and P_i do not, however, separate further due to the tight confinement by amino-acid residues of the binding pocket, particularly by the side chains of βGLU188, βARG260, and βMET222 and the backbone of αSER344, which are all located at the end of the binding pocket facing P_i. Water molecules also contribute to forming the constrained conformation. WAT5 is being pushed toward βMET222 and toward the backbone amide group of βARG189 to which it is hydrogen-bonded at a distance of 2.93 Å. WAT2 is being pushed toward the guanidinium group of βARG260 at a hydrogen-bonding distance of 3.05 Å with WAT2-O.

Energetics of hydrolysis

Based on the optimized structures described above, the energetics of the hydrolysis reaction was determined at the MP2//HF/6-31G level of theory. The left-hand panel of Fig. 5 shows the relative energies of the TS, the intermediate (IM1 and IM2), and the product conformations, as well as the two barriers B1 and B2 with respect to the reactant state. To investigate the effect of the protein environment in the β_TP binding site on the energetics of the reaction, we also calculated the energy of ATP hydrolysis in vacuo. The TS and the product state energies relative to the reactant state in vacuo for the HF/6-31G level of theory are shown in the right-hand panel of Fig. 5. The gas phase calculations are not intended to provide quantitative estimates for the rate enhancement by the enzyme, which would require studies of ATP hydrolysis in solution. They are rather intended to serve as a qualitative probe of the shape of the reaction energy profile. One can clearly see that the reaction energy profile inside the binding pocket is markedly different from that found in vacuo. First, the hydrolysis reaction in β_TP is strongly endothermic (21.9 kcal/mol), whereas it is exothermic (−15.2 kcal/mol) in vacuo. This indicates that β_TP has the capacity to catalyze the synthesis of ATP from ADP and P_i, which is evidently essential for the protein's function.

FIGURE 5.

Energetics of ATP hydrolysis. (Left) Energies along the reaction coordinate for ATP hydrolysis inside β_TP determined via QM/MM (TS, transition state; IM1, first intermediate; B1, barrier 1; IM2, second intermediate; and B2, barrier 2). (Right) HF/6-31G gas phase energies for nucleophilic attack of water on ATPa. Also shown is the MP2 energy at a P_γ-O_β3 separation of 3.0 Å, which corresponds to the final separation of products ADP and P_i inside the protein environment.

The endothermic reaction energy profile is caused by the strong stabilization of the reactant ATP and the destabilization of the products ADP and P_i due to the tight confinement by the binding pocket. The strong association of βARG189 with the γ-phosphate in the reactant state (see Fig. 2 b) contributes to the stabilization. As shown experimentally, βARG189 is one of the residues involved in ATP binding (Nadanaciva et al., 1999b). Since the γ-phosphate loses negative charge in the course of the hydrolysis reaction, as schematically shown in Fig. 3, the stabilization by βARG189 in the product state is weaker than in the reactant conformation, thereby contributing to the endothermic reaction energy. In fact, a detailed Mulliken population analysis, which is summarized in Table 2, indicates that P_i loses −0.27e of electron charge during the hydrolysis reaction. The charge is transferred to ADP which itself gains −0.32e.

The electrostatic repulsion between ADP and P_i further contributes to the destabilization of the product state. Even though the chemical bond between them is broken in the product state, the binding pocket forces the product species, which are both negatively charged, to remain close to each other. This destabilizing interaction between ADP and P_i was confirmed by our gas phase calculations (see Fig. 5) which showed that the energy in vacuo at a distance equivalent to the one found in the product state in situ (3.0 Å) is 31.2 kcal/mol higher relative to the reactant state.

The barrier heights for hydrolysis (28.2 kcal/mol) and synthesis (6.3 kcal/mol) were calculated at the MP2//HF/6-31G level of theory and were found to be significantly lower inside the binding pocket than in vacuo (48.7 kcal/mol and 63.9 kcal/mol, respectively). The rather moderate barrier in the reverse direction is a prerequisite for efficient synthesis of ADP and P_i toward ATP. As mentioned before, one remarkable feature of TS formation is the involvement of a second water molecule (WAT2) in addition to ATP and the nucleophilic water WAT1. The TS barrier encountered during this multicenter process (28.2 kcal/mol) is >20 kcal/mol lower than the one found for a conventional single-center reaction (50.4 kcal/mol).

After passing the TS, the hydrolysis reaction proceeds toward the formation of IM1 (Fig. 4 b). The energy of the intermediate state is 23.4 kcal/mol at the MP2//HF/6-31G level of theory, i.e., 4.8 kcal/mol lower than the TS as shown in Fig. 5. The second intermediate (IM2) evolves from IM1 upon further dissociation of the ATP-O_β3-P_γ bond. This process exhibits a second energy barrier (B1) and a rather flat overall potential energy profile. The third and last barrier (B2) along the reaction path between IM2 and the product state is due to flipping of WAT2. Since the height of both B1 and B2 (27.1 kcal/mol and 27.2 kcal/mol, see Fig. 5) was estimated to be lower than the energy barrier in the TS, the rate-determining step of the hydrolysis/synthesis reaction is the barrier crossing at the TS. Fig. 5 also includes the potential energies of the hydrolysis reaction computed at the HF level of theory, which neglects dynamic electronic correlation effects. Although there is no qualitative change in the reaction profile at the HF level, the potential energy barriers are largely overestimated (i.e., by 4.5 kcal/mol and 6.8 kcal/mol in situ and in vacuo, respectively), revealing the importance of electron correlation effects in the TS.

Interactions between catalytic core and protein matrix

To identify the role of the protein matrix for catalysis along the multicenter pathway, we analyzed the interaction between the reactive core and the protein in terms of the contributions from individual amino-acid residues. For this purpose we used a reduced QM/MM system in which the reactive core consisted of only ATP, Mg²⁺, and WAT1 to WAT5. The remainder of the protein environment was treated by MM methods. The small system was introduced to avoid the quantum mechanical calculation of electronic interactions, which is computationally expensive, and to rather use restrained electrostatic potential charges for an estimate of the relevant electrostatic interactions.

The left-hand panel of Fig. 6 shows the electrostatic interaction energies between reactant and protein decomposed into contributions from individual amino-acid residues. Since the reactive system has two negative charges, positively (negatively) charged residues of the binding pocket provide a large electrostatic stabilization (destabilization). The right-hand panel of Fig. 6 displays changes in the electrostatic interaction energies upon formation of the TS. The major contributions are provided by three of the charged residues, namely, βLYS162, βGLU188, and βARG260. One can clearly see that βGLU188 substantially stabilizes (−31.4 kcal/mol) the TS. As discussed above, WAT2, which is hydrogen-bonded to the carboxylate of βGLU188, accepts a proton from WAT1 and becomes H₃O⁺ in the TS. The negatively charged carboxylate thus interacts favorably with the H₃O⁺ moiety and in turn stabilizes the TS. This stabilization is partially compensated by the positively charged guanidinium group of βARG260 (17.3 kcal/mol), which is also close to H₃O⁺.

FIGURE 6.

Interaction energies between the QM system consisting of ATP, Mg²⁺, and WAT1–WAT5 and the protein environment. The bottom of both figures indicates the location of individual residues within different subunits of F₁. (Left) Coulomb interaction between the QM segment and protein residues in the reactant state. (Right) Difference in Coulomb interaction between the TS and the reactant state.

A stabilizing contribution is also provided by βLYS162. As discussed above, the hydrolysis reaction involves movement of electron density away from the γ-phosphate toward ADP. The Mulliken population analysis presented in Table 2 shows that ADP gains −0.18e in electron charge upon formation of the TS. Since βLYS162 is hydrogen-bonded to ADP-O_β1 (compare Figs. 2b, 4a, and 4c), their mutual interaction becomes stronger. This increase manifests itself in a decrease in the distance between βLYS162-N_η and ADP-O_β1 upon going from the reactant state (2.76 Å) to the TS (2.69 Å) and final state (2.63 Å).

DISCUSSION

We have used QM/MM simulations to examine the hydrolysis reaction of ATP in the β_TP catalytic site of F₁-ATPase. Our QM/MM approach combined an ab initio quantum mechanical description of the reactive core with a classical molecular mechanical treatment of the protein environment. This allowed us to examine the catalytic effect which is exerted by the protein in atomic and electronic level detail. Our simulations show that the hydrolysis reaction in the β_TP binding pocket is strongly endothermic. Specific interactions between the nucleotide and the enzyme are therefore responsible for the inversion of the reaction energetics present in solution and, thereby, favor the presence of ATP over the hydrolysis products ADP and P_i in the particular conformation studied. We also found that an efficient pathway for hydrolysis proceeds via a multicenter reaction involving a proton relay mechanism. The corresponding potential energy barrier height is significantly lower than the one for a conventional single-center pathway. Both the inverted reaction energetics and the reduced barrier height are a prerequisite for the ability of F₁F_o-ATPase to synthesize ATP.

Mechanism for conversion of chemical into mechanical energy

One of the central questions pertaining to ATP hydrolysis inside F₁-ATPase is the way in which chemical energy provided by ATP hydrolysis is converted into rotation of the γ-subunit. Two popular proposals address the mechanism of force generation during ATP hydrolysis. The first one asserts that the hydrolysis reaction itself initiates mechanical conformational changes at the α/β subunit interface (i.e., hydrolysis is energy-linked) which eventually lead to rotation of the γ-stalk. This mechanism is supported by biochemical mutation studies (Weber et al., 2000a; Weber and Senior, 2003). Single molecule studies (Kinosita et al., 2000; Yasuda et al., 2001) point to a second and quite different scenario. Here, the main driving force behind rotation of the γ-subunit is either ATP binding, or ADP and P_i unbinding, or both. The actual hydrolysis reaction serves as a switch mechanism and resets the ATPase cycle by facilitating dissociation of the products ADP and P_i from the binding pocket.

The results of our simulations support the latter mechanism. Due to the endothermic reaction profile in β_TP, hydrolysis of ATP does not readily take place and the final product energy of 21.9 kcal/mol virtually prevents the presence of products. If ATP hydrolysis were energy-linked and, hence, provided the force-generating step for stalk rotation, one would expect a considerably less endothermic or even exothermic reaction profile. The large endothermicity of the reaction energy profile is consistent with experimental data, which suggests that the equilibrium constant for ATP hydrolysis/synthesis is close to one, K ∼ 1, corresponding to almost equi-energetic reactant and product energy levels (Senior et al., 2002). The reason being that the hydrolysis process probed by the experimental determination of K likely involves larger-scale conformational motions, which our QM/MM methodology is not able to describe. Rather, our simulations explore conformations and their associated energetics close to the one captured in the x-ray crystal structure, allowing for local structural changes only. In addition, Weber and Senior (2003) have pointed out that the experimental evidence for K ∼ 1, obtained via unisite and O¹⁸ exchange experiments, may not apply to steady-state catalysis.

Even though the multicenter reaction has a considerably lower reaction barrier (28.2 kcal/mol) than the single-center one (50.4 kcal/mol), the barrier is still too high to achieve ATP hydrolysis in accord with the experimentally determined turnover rate of F₁-ATPase. Using the well-known relation between barrier height and reaction rate in the framework of transition state theory (Warshel, 1989), and assuming that the potential energy barriers are similar to the free energy values, one can estimate that a barrier of 28.2 kcal/mol corresponds to a turnover rate of 1.2 × 10⁻⁸ s⁻¹, which is orders-of-magnitude smaller than the experimentally observed value. Even though the rate obtained from the true free energy barrier will be somewhat different, one can conclude that the β_TP site has to undergo further conformational changes to reduce the TS barrier and to lower the product state energy to enhance the hydrolysis reaction. Such a conformational change can be enforced via binding of ATP to a neighboring site and subsequent rotation of the γ-stalk (Yasuda et al., 2001). This transforms β_TP into a β_DP-like configuration where efficient ATP hydrolysis could then take place. The hydrolysis reaction, in fact, has been suggested to take place after a 90° rotation of the γ-stalk (Yasuda et al., 2001). A mechanism which couples nucleotide binding and unbinding to conformational changes also accommodates nicely the cooperativity which is observed in F₁-ATPase. Binding of ATP to multiple sites significantly increases the hydrolysis rate by ∼10²-fold compared to the rate under unisite conditions (Weber and Senior, 1997; Weber et al., 2000b; Al-Shawi et al., 1990). Our results suggest that under unisite conditions the hydrolysis reaction is arrested at β_TP, which likely is the site of highest ATP affinity. For the reaction to proceed, the binding site has to rely on spontaneous conformational fluctuations that alter the reaction energetics accordingly.

Role of catalytic residues

Our computational study clarifies the role of several residues in the β_TP binding pocket for catalysis whose importance has been stressed by many mutation studies. The carboxyl group of βGLU188 has been suggested to be involved in activating and aligning the nucleophilic water, or even to act as a general base during the hydrolysis reaction. The mutation βE181Q in the Escherichia coli enzyme (corresponding to βGLU188 in the mitochondrial system) failed to bind the transition state analog MgADP.AlF_x (Nadanaciva et al., 1999a) and showed a reduction in the unisite equilibrium constant for hydrolysis by two orders of magnitude (Senior and Al-Shawi, 1992; Amano et al., 1994), highlighting the residue's importance for transition state stabilization. The fact that the mutations βE190D and βE190DCax in F₁ of Bacillus PS3 (corresponding to βGLU188 in the mitochondrial system) severely impair catalysis (Amano et al., 1994) proves that efficient hydrolysis requires exquisite positioning of the carboxyl group in addition to the presence of a negative charge.

Our results show that βGLU188 does not directly align the nucleophilic water, but rather positions and activates a second water molecule WAT2 which participates in the proposed multicenter reaction pathway. The correct arrangement of WAT2 by βGLU188 is crucial for the proton relay mechanism to proceed and, consequently, for efficient hydrolysis. An aspartate residue at the same position could certainly not provide an equivalent alignment. The analysis of the interaction energies between the reactive part and the protein environment also revealed that the negative charge on the carboxyl group does play a major role in stabilizing the positive charge which develops in the TS on the H₃O⁺ ion.

Mutation of the residues βARG246 and βMET209 in E. coli (corresponding to βARG260 and βMET222 in the mitochondrial enzyme) has been shown to impair uni- and multisite catalysis (Al-Shawi et al., 1989, 1990; Wilke-Mounts et al., 1995; Noumi et al., 1986) and a role for βARG260 in signal transmission has been suggested (Al-Shawi et al., 1990). The simulated β_TP subsystem contains a strong salt bridge between βGLU188 and βARG260 which persists over the course of all simulations. A similar salt bridge is also present in β_DP, but absent in the β_E site of the same structure (Gibbons et al., 2000) and, therefore, might play a role in the propagation of conformational changes, e.g., through a switch mechanism similar to that found in kinesin (Kikkawa et al., 2001).

The QM/MM-optimized structure of the final state shows that P_i and several associated water molecules are pushed toward the end of the binding pocket formed by βGLU188, βARG260, and βMET222. The water molecule WAT2, which is hydrogen-bonded to an oxygen atom of P_i, is squeezed between βGLU188 and βARG260 (the WAT2-O-βGLU188-O_ɛ1 and WAT2-O-βARG260-N_η2 distances are 2.63 Å and 3.05 Å, respectively). WAT2, therefore, has the capability to weaken or even break the salt bridge during further progression of the hydrolysis reaction.

Mutations in the residues βLYS155 and βARG182 of the E. coli enzyme (βLYS162 and βARG189 in the mitochondrial enzyme) have shown the importance of their positive charge for binding of substrate MgATP and for transition state stabilization (Nadanaciva et al., 1999a,b). Our simulations reveal that the positive charge of βLYS162 contributes to stabilizing the transition state and interacts favorably with the developing negative charge. Contrary to earlier suggestions, βLYS162 in our simulations is only hydrogen-bonded to the β-phosphate group and interacts with the γ-phosphate moiety only via the intervening water molecule WAT3. This will facilitate departure of P_i from ADP after hydrolysis has taken place.

Theoretical studies of G-proteins (Cavalli and Carloni, 2001; Futatsugi et al., 1999) have suggested that proton transfer from a lysine residue (corresponding to βLYS162 of the present system) to the phosphate oxygen atoms of GTP takes place during hydrolysis. No such proton transfer was observed during the present simulations. Despite a strong hydrogen bond between βLYS162-N_η and ATP-O_β1 (see Fig. 2 b) and transfer of ∼−0.1e of electron density from ATP to βLYS162, no drastic changes in distance and electronic population as expected for proton transfer were observed. The QM calculations by Futatsugi et al. (1999) and Cavalli and Carloni (2001) were carried out for cluster systems of the binding pockets and, therefore, omitted most of the protein environment surrounding the binding pocket. For this reason, it has been argued that the observed proton transfer to βLYS162 is an artifact due to an improper treatment of the protein environment (Gibbons et al., 2000; Warshel, 2003). The present study, on the other hand, takes into account the electrostatic field of a large part of the protein surrounding the catalytic site. The positively charged residue βLYS162 is thus properly stabilized by the environment and proton transfer is prevented by an increase in pK_a. Neglecting this stabilization, as was the case in the above-mentioned QM studies of G-proteins, likely lowers the pK_a of lysine artificially and may thus induce proton transfer.

An involvement of βARG189 in the transmission of conformational changes to the α-subunit to promote multisite catalysis and rotation of the γ-stalk has been suggested earlier (Weber et al., 2000a). The guanidinium group of βARG189 retains a strong hydrogen bond to ATP-O_γ2 over the full course of the simulations. This residue, therefore, is able to transmit conformational changes correlated with separation of product ADP and P_i. This is further amplified by the water molecule WAT5, which is being pushed toward the backbone nitrogen of βARG189 (to which it is hydrogen-bonded at a distance of 2.93 Å in the final state). Since βARG189 adjoins βGLU188, the forced movement of the former during hydrolysis can assist in breaking the salt bridge between βGLU188 and βARG260 or cause conformational changes in the neighboring α-subunit.

Overall, our simulations support the view that the residues at the end of the binding pocket are involved in mechanical transmission to relay successful ATP hydrolysis to the neighboring catalytic sites and to prepare the binding pocket for release of P_i and ADP.

One residue which is particularly important for the proposed hydrolysis mechanism is αSER344. It hydrogen-bonds to the nucleophilic water, WAT1, and is responsible for the correct positioning of the latter. The significance of αSER344 is further stressed by the fact that this residue is part of a highly conserved region with amino-acid sequence VISIT in the α-subunits of F₁-ATPases. The importance of this region has also been confirmed by mutation studies (Maggio et al., 1987; Wise et al., 1984). αSER344 is part of an α-helix connected to a loop region that, by itself, is in close contact with the γ-subunit of the stalk. It is conceivable, therefore, that movement of the α-helical region containing αSER344 by 2–3 Å due to rotation of the stalk causes the displacement of WAT1 toward ATP and thereby initiates the hydrolysis reaction. Candidate residues on the γ-subunit that might participate in such a mechanism are γ4–8 and γ248–255 on geometrical grounds (bovine mitochondrial F₁-ATPase nomenclature). This is in accord with mutation studies, which suggested the importance of particular stalk residues for efficient energy coupling of F₁F_o-ATPase (Nakamoto et al., 1993; Nakamoto and Al-Shawi, 1995) and is also consistent with a recent publication, which found the C-terminal part of the γ-subunit to not be required for ATP hydrolysis-driven rotation (Müller et al., 2002).

Comparison of the QM/MM-optimized structure with the conformation of β_TP in the crystal structure by Abrahams et al. (1994) reveals a striking similarity in the location of WAT1 and the position of electron density for the proposed nucleophilic water in the x-ray data. The distances between αSER344-O and WAT1-O are 2.4 Å and 2.7 Å, and the distances between ATP-P_γ and WAT1-O are 4.0 Å and 4.2 Å for the x-ray structure and the QM/MM-optimized system, respectively. In contrast to the structure by Abrahams et al., WAT1 is not hydrogen-bonded to βGLU188 but rather to WAT2 and WAT5, this being the key to the proposed proton relay mechanism. The QM/MM-optimized structure also shows that the nucleotide is not only tightly bound to the β-subunit, e.g., via the P-loop, but also to the α-subunit, mainly via three intervening water molecules, WAT1, WAT3, and WAT4. The α-subunit has, therefore, considerable catalytic control, particularly since it binds the proposed nucleophilic water through αSER344. Our simulations stress the fact that a deeper understanding of the catalytic mechanism in F₁-ATPase cannot be reduced to the effect of protein residues on the nucleotide alone, but has to take into account their complex influence on the solvent molecules and the interplay between all three entities: nucleotide, solvent, and protein.

Multicenter proton relay mechanism

As mentioned earlier, hydrolysis reaction processes of nucleoside-phosphates have also been investigated in other proteins, e.g., myosin and G-proteins (Glennon et al., 2000; Cavalli and Carloni, 2001; Futatsugi et al., 1999; Okimoto et al., 2001). These studies greatly differ in the way they treat the influence of the protein environment on the chemical reaction and range from ab initio studies of relatively small cluster systems to QM/MM studies based on the EVB methodology. Due to its empirical nature, the ability to calculate free energies and the capability to perform proper configurational averaging, the latter approach has been shown to provide a faithful description of reaction pathways and their associated free energy profiles (Warshel, 2003). The reaction barrier heights for nucleotide hydrolysis computed by ab initio QM calculations on cluster systems of Ras and myosin are ∼42 kcal/mol (Futatsugi et al., 1999; Okimoto et al., 2001). The corresponding rate constants calculated via transition state theory are more than 18 orders-of-magnitude larger than physiological timescales suggest, which are on the order of seconds. The EVB studies of Ras by Warshel and co-workers (Glennon et al., 2000; Langen et al., 1992; Schweins et al., 1994), on the other hand, provide reaction pathways and barriers in agreement with experiments and allow one to quantify the energetic contributions of specific residues to the overall reaction mechanism. All of the above mentioned theoretical studies assumed that hydrolysis proceeds via a direct one-center reaction involving a single water molecule. Our present study, however, suggests, that in the β_TP binding pocket of F₁-ATPase, the reaction barrier on the potential energy surface is significantly reduced when hydrolysis takes place via a multicenter proton relay. It needs to be further investigated if this picture does not change qualitatively when considering the reaction free energy. The reduction in barrier height nevertheless suggests that the catalytic sites of F₁-ATPase might take advantage of a pre-oriented solvent environment to lower reaction barriers.

Endothermicity of reaction profile

Recently, Yang et al. (2003) carried out classical free energy calculations to obtain the reaction free energies of hydrolysis in all catalytic sites of F₁-ATPase via thermodynamic integration. The authors estimated the hydrolysis reaction free energy in the β_TP binding site to be slightly endothermic (1.4 kcal/mol). Even though the endothermic reaction energy profile is in accord with the present study, the magnitude differs largely (21.9 kcal/mol). This discrepancy may be due to a variety of reasons. First, the two studies are based on different x-ray structures: Yang and co-workers used the structures by Braig et al. (2000) and Menz et al. (2001), whereas the present study is based on the structure by Gibbons et al. (2000). A major conformational difference lies in the position of the side chain of αARG373 in β_TP. In the first two structures, the guanidinium group is close to the terminal phosphate moiety, whereas it is bent away from the phosphate in the third one. Since this arginine is known to play a role during hydrolysis (Nadanaciva et al., 1999c), the structural difference may account for the discrepancy in the reaction energy. Furthermore, the methodologies used in each study are quite different and have their individual merits and shortcomings. The simulations by Yang et al. (2003) take into account thermal fluctuations, and hence, entropic contributions of the protein environment. Fluctuations are missing in the present QM/MM treatment and the final reaction energy might therefore be overestimated due to insufficient product relaxation. On the other hand, the treatment of the interaction of ATP with the protein environment in the classical simulations by Yang et al. (2003) can be poor due to the extremely polar nature of the binding pocket. As discussed in Results, the present QM/MM study clearly indicates that the interaction of the nucleotide with the nearby positively charged residues largely involves electronic polarization and charge transfer, which are neglected in the classical treatment. To obtain a more comprehensive picture of the reaction profile, a more extensive study should be performed in the future.

CONCLUSION

This study investigated the hydrolysis reaction of ATP in the β_TP binding pocket of F₁-ATPase. Efficient hydrolysis is found to proceed via a multicenter proton pathway involving specific interactions of ATP with the protein and solvent environment. This conclusion is derived from the finding that our simulations give a much reduced potential energy barrier for this pathway compared to conventional attack by a single water molecule.

Overall, the hydrolysis reaction in β_TP is strongly endothermic, reflecting the essential role of protein-ATP interactions for ATP synthase activity. The binding pocket conformation studied does not support ATP hydrolysis and structural changes induced by rotation of the stalk are required to bring β_TP into a hydrolysis-promoting geometry. To elucidate the dependence of the reaction energetics on binding site conformation, one should study the ATP hydrolysis reaction profile in the β_DP site using the same approach as for β_TP. β_DP captures a structural snapshot at a later stage along the catalytic cycle of ATP hydrolysis and is expected to exhibit an energetically more favorable environment for the hydrolysis products ADP and P_i. In fact, structural differences between the β_TP and β_DP catalytic sites, such as displacement of αARG373, have been observed in the x-ray structure (Gibbons et al., 2000) as well as in the derived QM/MM subsystems for β_TP and β_DP.