Computational Modeling of Cell Adhesion and Movement Using a Continuum-Kinetics Approach

Abstract

Adhesion of leukocytes to substrate involves the coupling of disparate length and timescales between molecular mechanics and macroscopic transport, and existing models of cell adhesion do not use full cellular information. To address these challenges, a multiscale computational approach for studying the adhesion of a cell on a substrate is developed and assessed. The cellular level model consists of a continuum representation of the field equations and a moving boundary tracking capability to allow the cell to change its shape continuously. At the receptor-ligand level, a bond molecule is mechanically represented by a spring. Communication between the macro/micro- and nanoscale models is facilitated interactively during the computation. The computational model is assessed using an adherent cell, rolling and deforming along the vessel wall under imposed shear flows. Using this approach, we first confirm existing numerical and experimental results. In this study, the intracellular viscosity and interfacial tension are found to directly affect the rolling of a cell. Our results also show that the presence of a nucleus increases the bond lifetime, and decreases the cell rolling velocity. Furthermore, it is found that a cell with a larger diameter rolls faster, and decreases the bond lifetime. This study shows that cell rheological properties have significant effects on the adhesion process contrary to what has been hypothesized in most literature.

INTRODUCTION

The study of leukocyte adhesion on blood flow in microvessels is important for understanding the resistance changes in microcirculation (Skalak, 1972; Weiss, 1990). The models proposed previously in the literature, e.g., (Bell, 1978; Dembo et al., 1988) do not take into account the rheological properties of the cell, which can substantially limit the predictive capability of these models. Evans et al. (1991) introduced a different model in which the reverse reaction rate (or off rate) followed a power law at low forces to capture variations in rupture behavior from ductile to brittle. Later, using the Brownian dynamics approach, Evans and Ritchie (1997) derived a more general reverse reaction rate expression that depends on the deformation of the energy landscape caused by the external force and the spatial variation of frictional interactions between molecules. In this study, we will use the model proposed by Dembo because it allows both the reverse and forward reaction rates to vary.

Adhesion to vascular endothelium is a prerequisite for the circulating leukocytes to migrate into tissues. This event involves a multistep process that includes: i), rolling of the cell along the blood vessel wall; ii), margination (firm adherence of the cell to the blood vessel wall); and finally iii), diapedesis or emigration (cell squeezes through the capillary wall). This three-step stage is mediated by a series of different endothelial cell-leukocyte adhesion molecules (Long, 1995). Hydrodynamic flow surrounding the cell exerts forces on the adhesion bonds, which can shorten their lifetime or even extract the receptor molecule from the cell surface (Alon et al., 1997, 1998; Evans, 1999). Evans (1999) showed that, under an external force, bond lifetime and rupture strength are intimately tied together by thermally activated kinetics in a way that depends on how the force is applied over time.

Significant progress has been made toward understanding the receptor-mediated cell adhesion process (Lauffenburger and Linderman, 1993). Detailed experimental studies of the adhesive bonds have suggested that adhesion molecules of the selectin family are involved in maintaining the initial rolling of the leukocytes on the endothelium, whereas the integrin bonds are responsible for the firm and prolonged attachment of the cells to the endothelium. Hammer and Tirrell (1996) have presented a comprehensive review of the fundamental parameters that characterize biomolecule function in cell adhesion.

Mathematical models proposed so far to describe different events in cell adhesion are based on either the equilibrium concept (Bell et al., 1984; Evans, 1985a,b) or the kinetics concept (Dembo et al., 1988; Hammer and Lauffenburger, 1987; Dong et al., 1999). Here we follow the kinetics model because it is designed to handle the dynamics of the cell adhesion process. In the kinetics approach, both bond association and dissociation occur according to the forward reaction rate, k_f, and reverse reaction rate, k_r, respectively. The merits of this approach have been reviewed in Shyy et al. (2001). For a review on cell adhesion simulations using probabilistic and Monte Carlo approaches, the reader is referred to Zhu (2000).

One flaw with all these models is that they do not take into consideration the deformation of the cell. Dong et al. (1999) and Dong and Lei (2000) attempted to address this issue by assuming the cell membrane to be a two-dimensional (2-D) elastic ring. They show that the intracellular viscosity and cell membrane bending stiffness have profound effects on adhesion. However, their model does not accurately describe the rheological behavior of the leukocyte because in their study only a small portion of the adhesion length is allowed to peel away from the vessel wall. This constraint is not physical so a more comprehensive model is presented here.

A major computational challenge for the adhesion studies is the presence of the disparate length scales between a cell, on the order of μm, and the adhesion bonds, on the order of nm. Although the physical phenomena within the μm range can be well represented by a continuum mechanics model, molecular effects become significant within the nm range.

The objectives of this work are to develop a computational strategy for multiscale problems, and to investigate the effects of some key adhesion parameters and rheological properties on the rolling and displacement of a white blood cell in contact with a substrate. The cell is modeled first as a simple liquid drop to show the essence of the computational approach, and then as a compound drop to highlight the role of the nucleus in the cell behavior. The adhesion mechanism is modeled based on the kinetics concept. The cellular level model consists of a continuum representation of the field equations for momentum transfer and mass continuity, and an interfacial tracking capability to allow the cell to change its shape continuously. The various aspects of the modeling are described below.

COMPUTATIONAL METHODS

Development of the multiscale model

To form a comprehensive modeling framework to treat the disparate scales between cell deformation (μm) and bond length (nm), a multiscale model to account for both macro/micro (continuum) and nano (ligand-receptor) levels of phenomena is needed (Fig. 1). In our multiscale model, the macro/micro component deals with the deformation of the cell, the nano part takes care of the adhesion aspect, and a numerical procedure is used to transfer information between the two components. To outline the proposed method, a 2-D representation of a cell modeled as either a simple or a compound drop is studied in a planar channel under an imposed flow (Fig. 2). The flow is assumed to be uniform at the entrance of the channel, as is the case when a flow enters the orifice of a parallel plate chamber. This is done to generalize the problem so that no assumption has to be made concerning the velocity profile of the flow as it approaches the cell. The cell is attached to one side of the channel wall with adhesive bonds governed by the kinetics model proposed by Dembo et al. (1988).

FIGURE 1.

Macro/Micro- and Nanomodel. The cellular model is shown on the left (μm scale), whereas the enlarged area on the right shows the nanodomain for the receptor model (nm scale).

FIGURE 2.

Schematic of the problem statement. (a) Simple liquid drop. (b) Compound drop model. In both cases, the inlet flow is uniform. The uniform inlet flow is selected to simulate the entrance of a flow into a 2-D parallel plate chamber. This imposed uniform inlet flow is more general than assuming a simple shear flow or parabolic velocity profile. It allows us to investigate entrance effects if needed. In the studied case, the cell is located far enough from the entrance so that the flow is parabolic.

Macro/micro scale model

A detailed description of the method used to treat the deformation of the cell can be found in the literature (Udaykumar et al., 1997; Shyy et al., 2001). Briefly, the deformation of the cell due to an external fluid is governed by the incompressible Navier-Stokes equations given below.

Governing field equations:

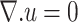(1)

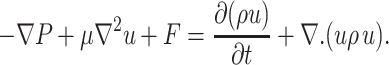(2)

In these expressions, u is the fluid velocity, P the pressure, F the body force, μ the dynamic viscosity of the fluid, ρ the density of the fluid, and t time. Constant properties are considered in each medium (such as cytoplasm), whereas property variations are allowed between media (like cytoplasm and nucleus, or inside and outside of the cell). In the problems to be treated here, inertial effects are negligible so the inertia term in Eq. 2 can be omitted. However, for generality, we will keep all the terms.

Interfacial treatment

The interfacial conditions adopted in the cellular model are based on the mass flux and force balances, namely,

Continuity condition:

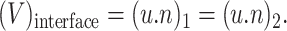(3)

Balance of normal stresses—the dynamic Young-Laplace equation:

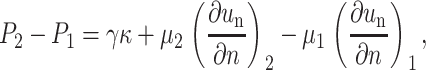(4)

where κ is the curvature for two-dimensional flows and twice the mean curvature for three-dimensional flows, γ is the interfacial tension, and n is the normal vector at the interface. The subscripts 1 and 2 represent the fluid outside and inside the cell, respectively.

In this approach, the interfacial force is converted into the source term, via local integration, in the momentum equation as follows:

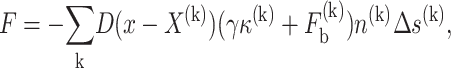(5)

where D is the delta function, γ the interfacial tension, κ the curvature, Δs is the arc length (for 2-D problems), n is the normal direction vector, and F_b is the bond stress that is defined by the nanoscale model.

The macroscopic model has been assessed by investigating the effects of capillary number, Ca = μU/γ, Reynolds number, Re = (ρUd/μ), as documented in N'Dri et al. (2000) and Shyy et al. (2001).

This macroscopic model provides information about the cell shape, and velocity and pressure in the entire field. Information about the instantaneous membrane shape and local hydrodynamic force obtained from the macroscopic model is transmitted to the nanoscale model.

Nanoscale model

The interaction between the cell and substrate surface at the microscopic level is analyzed with the model proposed by Dembo et al. (1988). This model treats a bond as a spring, and the force of a bond, f_b, is given by:

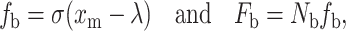(6)

where σ is the spring constant, x_m and λ are the current and the equilibrium lengths of a bond, F_b is the total bond force, and N_b is the bond density.

Calculation of the bond density, N_b

The balance equation for the formation and dissociation of bonds is given by a simple kinetic relationship:

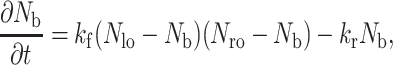(7)

where N_b is the bond density, k_r and k_f are the reverse and forward reaction rate coefficients, respectively, N_lo is the initial ligand density on the surface, and N_ro is the initial density of receptors on the cell membrane.

The reverse and forward reaction rate coefficients are, respectively, given by:

(8)

and

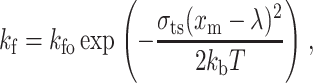(9)

where k_ro and k_fo are, respectively, the initial reverse and forward equilibrium reaction rates, σ the spring constant, σ_ts is the transition spring constant, x_m the actual length of a bond, λ the equilibrium bond length, k_b the Boltzmann constant, and T is the temperature.

The kinetics equation is solved using a fourth-order Runge-Kutta method where the initial bond density, N_bo, is obtained by solving the following equilibrium equation:

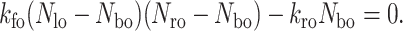(10)

The macro/micro model has been used to offer preliminary analysis of a membrane being pulled away from a surface at a constant velocity (Shyy et al., 2001; N'Dri et al., 2000). The effects of reaction rates, ligand density, and other parameters on the adhesion process have been reported.

Macro/micro- and nano communication

The transfer of information between the macroscopic and microscopic scales is done as follows. First, an initial membrane shape given by the macroscopic model is used as the input for the microscopic model. At time zero, the bond force is initialized (here, it is set to zero), and the macroscopic model provides the pressure and velocity around the cell. This information along with the shape of the cell is then transferred to the microscopic model to calculate the bond density and bond force. The macroscopic model uses the latter data to determine the new shape and position of the cell. Such two-way procedures continue throughout the entire computation. Fig. 3 shows a flowchart illustrating the multiscale model.

FIGURE 3.

Flow chart showing the interaction between the nanomodel (receptor scale) and the macro/micromodel (vessel/cellular scale).

Computational procedures

The computational procedures for the above-described cell adhesion problem consist of the following key elements: i), field equation solvers for mass and momentum conservation, ii), interfacial movement in response to cell and surrounding fluid interactions, and iii), communication between the field equation solvers and the interfacial treatment. In this approach, the field equations are solved using fixed Cartesian grid, while the interface moves through the mesh based on discrete, massless markers. This approach forms the so-called Eulerian-Lagrangian technique (Shyy et al., 2001). The advantage of the fixed-grid approach is that grid topology remains simple while large distortions of the interface take place. However, because the interface assumes irregular shapes and moves continuously in time, proper accounts of the interfacial conditions and capabilities for handling irregular geometries in different materials are critical steps. Different approaches can be used in this regard. An effective approach is the immersed boundary technique (IBT) originally used by Peskin (1977) and later extended by various researchers for different problems involving free and moving boundaries (Fauci and Peskin, 1988; Juric and Tryggvason, 1996; Kan et al., 1998; Udaykumar et al., 1997; Unverdi and Tryggvason, 1992). The other approach is the sharp interface method (Kwak and Pozrikidis, 1998; Shyy et al., 1996; Ye et al., 1999, 2001). For a review of alternative approaches, we refer to Shyy et al. (2001), and the references cited therein. In this article, we have adopted the IBT. A summary of this method is given below.

Immersed boundary technique

The IBT approach incorporates the interfacial condition into the field equation without explicitly tracking the interface. As detailed in Udaykumar et al. (1997), the interface can be handled by using marker points.

Interface information

The immersed interface is denoted by C(t), the interface is either a curve for a 2-D problem or a surface for a 3-D problem. The interface is represented by K marker points of coordinates with k = 1,….,K and s is the arc length. Fig. 4 shows the interface numbering and representation. The marker points are regularly separated 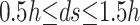where h is the grid size. The interface is parameterized as a function of the arc length s by fitting quadratic polynomials through three consecutive marker points of coordinates 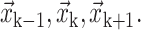Once the position of the interface is known, the normal and the curvature are evaluated. The convention adopted is that the unit normal point form Fluid 2 to Fluid 1. In 2D, the normal is given by:

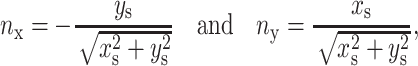(11)

where the subscript s denote d/ds. The curvature is then obtained by taking the divergence of the normal vector

(12)

FIGURE 4.

Interface representation and numbering.

Material property assignment

With the known interface position, the material properties are assigned using a Heaviside step function.

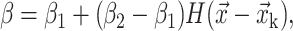(13)

where β is any material property such as density ρ or dynamic viscosity μ. The subscripts 1 and 2 denote Fluid 1 and Fluid 2, respectively, as shown in Fig. 4, and is the discrete Heaviside step function defined as follows:

(14)

where dim is the spatial dimension, d = 2h with h the grid size, is the grid coordinate, and 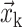is the interfacial point coordinates. Fig. 5 provides an illustration of the Heaviside function.

FIGURE 5.

Heaviside function definition illustration.

The next step is to communicate the force stored at the interface to the nearby grid points.

Source term computation

The surface tension, while exerted on the interface only, can be accounted for in the IBT via modeled source terms in the momentum equation by means of integral source terms. Specifically, it is lumped into the source term 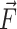in Eq. 2. Here we show this force only on the discretized form:

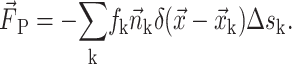(15)

The force at the grip point P is computed based on the sum of the interfacial force f_k of the marker point located inside a circle of radius 2h weighted by the Delta function as shown in Fig. 6. The delta function spreads over 4h and is the derivative of the Heaviside step function. It is computed as follows:

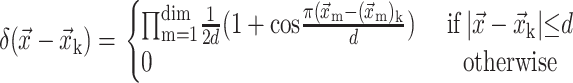(16)

FIGURE 6.

Source term computation at the grid point P. Marker points contributing to the computation are also shown.

Once the interfacial position is known, the material properties can be assigned properly then the interfacial force is spread to nearby grid points and finally the flow field equation can be solved. The next step is to compute the interfacial point velocity.

The projection method for field equation solutions

Equations 1–4 are solved using the projection method on a fixed Cartesian collocated grid. The projection method or fractional steps is divided into three fractional steps:

Fractions step 1: solve momentum without pressure

The convection terms are explicitly treated using the Adams-Bashforth scheme, whereas the diffusion terms are treated implicitly using the Crank-Nicholson schemes. Both schemes are second-order accurate. Fig. 7 shows the location of the velocity component and the pressure on a grid cell.

FIGURE 7.

Velocity and pressure location on a given grid cell.

Evaluation of the intermediate velocity and for a 2-D problem

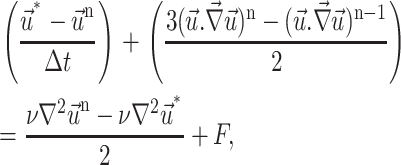(17)

where n is the time step level and F the source term

The pressure equation is derived by assuming that the velocity satisfies the continuity equation at n + 1 time step level.

Fractional step 2: solve for the pressure.

(18)

Fractional step 3: combination of velocity with pressure

Finally, the correction step is done as follows.

At the cell center:

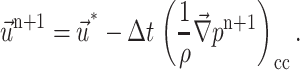(19)

At the cell face:

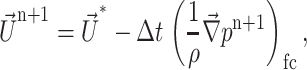(20)

where the subscript cc stands for cell center and fc stands for face cell.

Interfacial velocity computation

The velocity at the marker point is denoted by V_k and should satisfy the continuity condition, so in discretized form the interfacial velocity is:

(21)

where h is the grid size, i and j are the grid location indices, and is the fluid velocity. The computation of the interfacial velocity is illustrated in Fig. 8. The velocity is computed by taking the sum of all the grid points located inside a circle of radius 2h.

FIGURE 8.

Interfacial point velocity computation. Grids contributing to the computation are also shown.

The last step is the advection of the interface and this is done using the following equation:

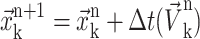(22)

RESULTS AND DISCUSSION

All the results presented below are based on the nondimensional parametric variations normalized by the reference scales given in Table 1. In all computation, the outer viscosity (plasma) is kept constant.

TABLE 1.

Reference values

Length	Viscosity
L = 30 μm	μ = 1 dyne s/cm2
Velocity	Density
U = 600 μm/s	ρ = 1.0 g/cm3
Spring constant	Bond density
σ = 5.0 dyne/cm	Nb = 5.1010 cm−2
Reverse reaction rate	Interfacial tension
kro = 0.1 s−1	γ = 0.1 dyne/cm

This is a list of the scaling parameters and values used in the study.

Simple drop model

In this problem, a two-dimensional cell attached to a vessel wall is subjected to a uniform flow imposed at the inlet of the channel (Fig. 2 a). Tables 2 and 3 give, respectively, the values of the macro/micro- and nanoparameters used in the study. The cell is first modeled as a liquid drop with a constant viscosity and surface tension. This is the simplest model one can use to describe qualitatively certain rheological behaviors of leukocytes (Evans and Yeung, 1989; Tran-Son-Tay et al., 1991; Kan et al., 1999). In all the computations, unless specified otherwise, the values used for k_ro, σ, and σ_ts are taken equal to 0.1 s⁻¹, 5 dyne/cm, and 4.5 dyne/cm, respectively. Using these parameters, the effects of the reverse reaction rate, the wall, and the spring constant σ on the rolling/displacement of the cell along the endothelium are evaluated.

TABLE 2.

The macroscopic-model parameters

Tube diameter	Cell viscosity
30 μm	10–1000 dyne s/cm2
Cell diameter	Plasma viscosity
6–8 μm	1.0 dyne s/cm2
Tube length	Plasma density
120 μm	1.0 g/cm3
Inlet velocity	Interfacial tension
50–600 μm/s	10−3–8.0 dyne/cm

Shown is the range of values used in the computational work.

TABLE 3.

Values used in the microscopic model

Nr = 2.0–5.0 1010 cm−2 (Bell et al., 1984)	kb = 1.38 10−16 dyne cm/K (Boltzman constant)
kfo = 10−14 cm2/s (Hammer and Lauffenburger, 1987)	λ = 5.0 10−6 cm (Bell et al., 1984)
kro = 10−11–10 s−1 (Bell, 1978)	rc = 4.0 10−4 cm (Schmid-Schonbein et al., 1980)
σ = 0.5–10 dyne/cm) (Dembo et al., 1988)	Fσ = (σ − σts) / σ = 0.1
σts = 0.48–9.5 dyne/cm (Dembo et al.,1988)	Nl = 2.0–5.0 1010 cm−2 (Lawrence and Springer, 1991)

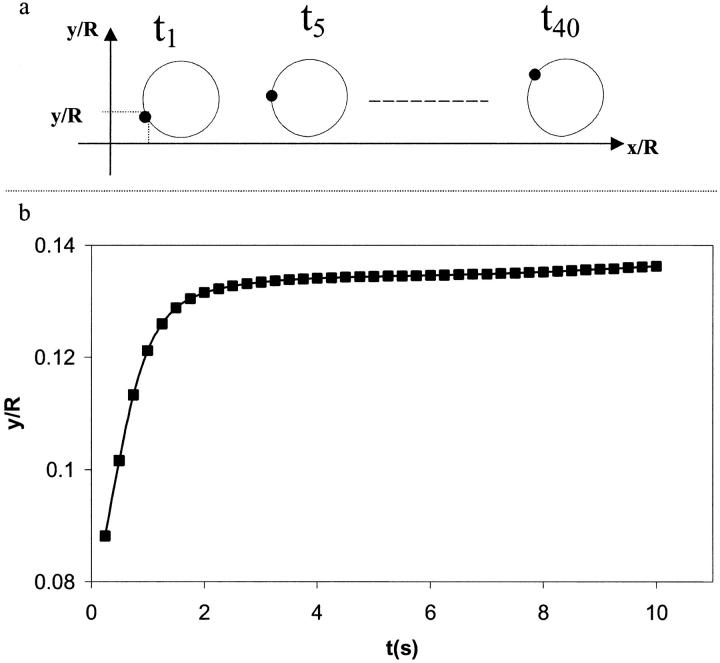
Fig. 9 a shows the instantaneous position of an interfacial point on the cell surface for a given k_ro. It is found that the cell translates along the wall and rotates at the same time. The combination of these two movements leads to the rolling of the cell along the wall. The cell initially rolls along the wall and starts to slide along the vessel wall when the bonds offer no more resistance as shown by the plateau observed in Fig. 9 b.

FIGURE 9.

Instantaneous location of an interfacial point on the cell as a function of position and time for a simple drop model (k_ro = 1.0 and 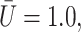μ = 100, γ = 1.0). (a) Schematic showing the position of an interfacial point on the cell to demonstrate cell rolling. (b) Vertical distance between a specific interfacial point and the surface wall as a function of time. y is the ordinate of the interfacial point shown in Fig. 4 a and R is the tube radius. The points shown correspond to the simulation data.

In what follows, a cell is considered peeled away from the surface when the cell travels more than two cell radii. Beyond this distance, our simulation shows that the shape of the cell becomes nonphysical. Kuo et al. (1997) have made similar assumptions in their study in which the leukocyte is modeled as a solid body. They assume that bonds are broken if the cell travels 10 cell radii.

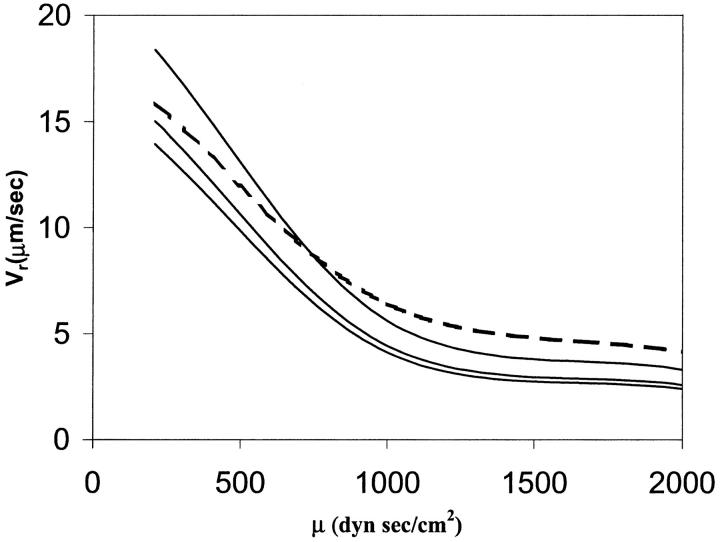
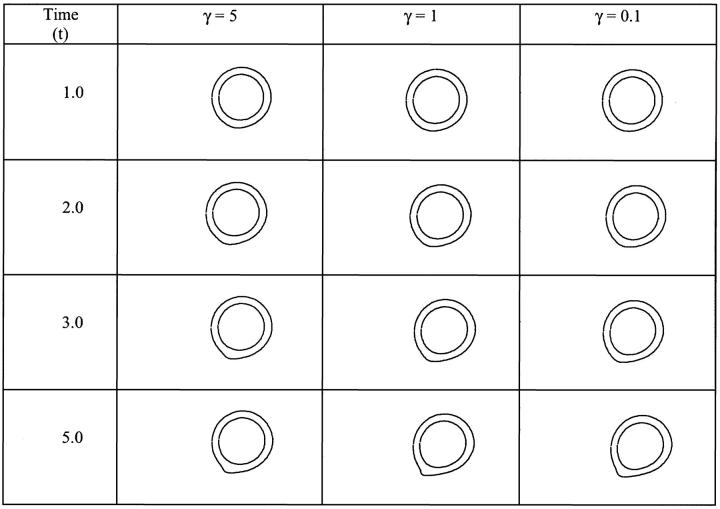
Dong et al. (1999) and Dong and Lei (2000) have modeled the cell as a liquid drop enclosed in an elastic ring. In their approach, the initial shape of the elastic ring is the one taken from the picture of an experiment of a cell adhering on a surface under a known shear rate. They assume that only a small portion of the adhesion contact can be peeled away from the wall (that length is not specified in their work). This assumption allows them to use an energy approach to calculate the cell rolling velocity. In this model, we do not make that assumption. We solve the full flow field and fluid-interface interactions, and let the flow dictate the contact area. The adhesion parameters and cell viscosity used in this study are the same as those in Dong and Lei (2000). The only unknown parameters in their study are the cell surface tension, the contact length and the number of bonds. In Fig. 10, a comparison between Dong and Lei's (2000) numerical study and our results is shown for 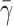= 4.0, 5.0, and 10 by keeping the contact length and the number of bonds constant. A high value of the surface tension 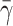= 10 gives a good overall agreement between our result and that of Dong and Lei (2000). This is expected, because as the surface tension increases, the liquid drop model should provide results similar to the 2-D elastic model. However, because our approach is more general, additional information can be found. For example, we do not constrain the cell to a peeling motion only; we allow the cell to be lifted away from the surface.

FIGURE 10.

Effects of cytoplasm viscosity and surface tension on the cell rolling speed: simple drop model. The dashed line corresponds to the numerical results of Dong and Lei (2000), and the solid lines to this study. In all cases, 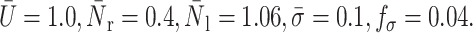The three solid curves correspond to 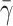= 4.0, 5.0, and 10, from bottom to top respectively.

A comparison of the bond lifetimes computed in our study and the experimental results obtained by Schmidtke and Diamond (2000) for one bond is shown in Fig. 11. Although no information about the reaction rates and spring constant is given, we have found that for the adhesion parameters considered, these values do not significantly affect the rolling and displacement of the cell along the vessel wall. The key parameters are the cell rheological properties, the receptor density and the ligand density. In this comparison, the cell surface tension is taken to be 1.2 and the viscosity is varying from 50 to 300. The top line in Fig. 11 corresponds to the highest viscosity value. Good agreement is seen for a surface tension of 1.2 and a viscosity of 200, even though a viscosity value of 300 provides a better fit for shear rate values below 200 s⁻¹.

FIGURE 11.

Effects of cytoplasm viscosity and shear rates on the bond lifetime: simple drop model. The squares correspond to the experimental results of Schmidtke and Diamond (2000), and the lines to our study.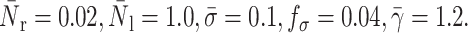

Compound drop model

The case of the compound drop model is illustrated in Fig. 2 b. In the model, the nucleus occupies 44% of the volume of the cell (Schmid-Schonbein et al., 1980), and the rheological properties (viscosity and surface tension) of the nucleus are taken to be 10 times that of the cytoplasm and cellular membrane (Table 2). The kinetics parameters used are the same as in the simple drop model. The problem to be solved is the same as before: a cell is attached to a vessel wall, with a uniform flow imposed at the inlet of the vessel tube.

It should be noted that the nucleus of a neutrophil is small and segmented. Its contribution may not be as large as the one predicted by this model but it is difficult to assess this at the present time. A neutrophil nucleus is asymmetric and it has been shown by Kan et al. (1999) that nucleus eccentricity affects the instantaneous shapes of the cell during recovery. In addition, Kan et al. (1998, 1999) have shown that the presence of a nucleus, although small in size, is needed to reconcile the various leukocyte rheological data published in the literature. Therefore, this compound drop model describes better the structure of a lymphocyte, but is nevertheless a good model for evaluating the effect of key parameters on the rheology and adhesion of leukocytes in general.

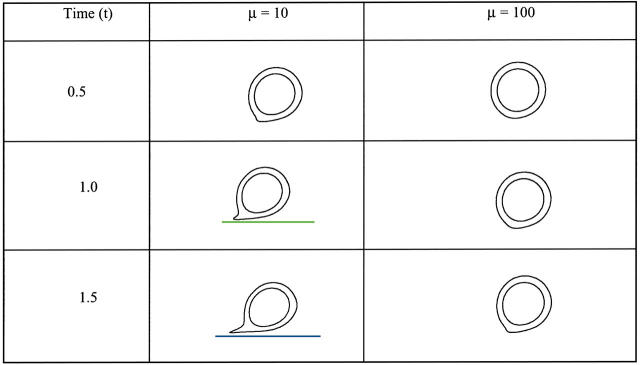
Fig. 12 shows cell shapes at different time instants and inlet velocities. We observe that an increase of the inlet velocity accelerates the movement of the cell along the vessel wall, and causes the bonds to break at a distance closer to the wall surface. This is due to the fact that when the inlet velocity is increased, the cell is pushed by a higher hydrodynamic force.

FIGURE 12.

Instantaneous cell shapes for different values of inlet velocities: compound drop model. The horizontal line corresponds to the bottom channel wall.

The viscosity ratios between the plasma, cytoplasm, and nucleus are defined as follows:

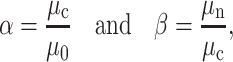(23)

where μ₀ is the plasma viscosity, μ_c is the cytoplasm viscosity, and μ_n is the nucleus viscosity.

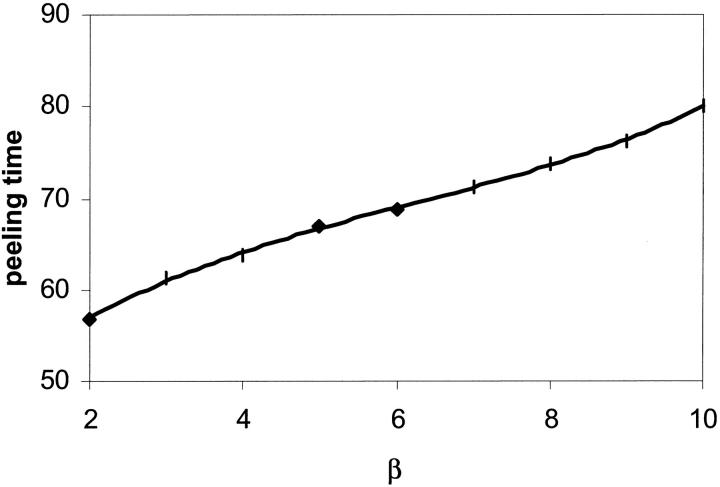
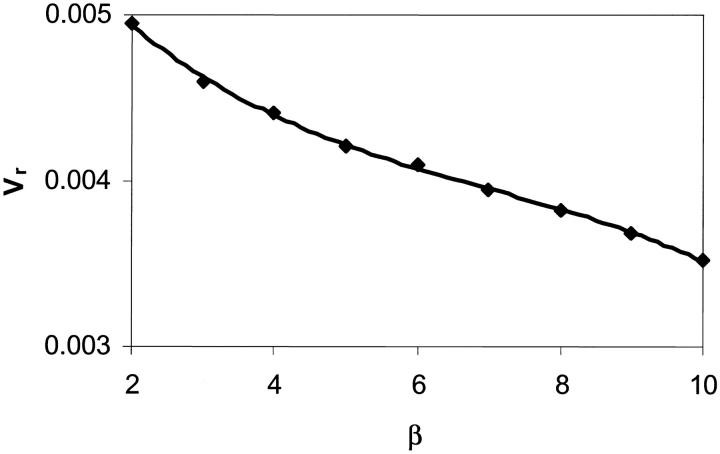
The effects of β on the peeling time and rolling velocity are shown in Figs. 13 and 14, respectively. A higher value of β increases the bond lifetime and decreases the rolling velocity. The effects of α and β on the bond lifetime as a function of shear rate are shown in Fig. 15 and compare well with the experimental measurements made by Schmidtke and Diamond (2000), especially for shear rates less than 200 s⁻¹. In our computation, the surface tension of the cell is kept fixed whereas the viscosity ratios are varied. It is seen that a decrease in the cytoplasm/plasma or nucleus/cytoplasm viscosity ratio lowers the bond lifetime. Overall, our simple and compound drop models both produce results in agreement with published experimental data. The presence of a nucleus is found to increase the bond lifetime and to decrease the cell rolling velocity.

FIGURE 13.

Effect of the nucleus to cytoplasm viscosity ratio, β, on the peeling time: compound drop model. α = 100, The points shown correspond to the simulation data.

FIGURE 14.

Effect of the nucleus to cytoplasm viscosity ratio, β, on the rolling velocity: compound drop model. α = 100, The points shown correspond to the simulation data.

FIGURE 15.

Effects of intracellular viscosity and shear rate on the bond lifetime: compound drop model. The squares correspond to the experimental results of Schmidtke and Diamond (2000), and the lines to this study. 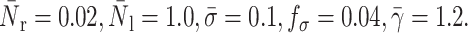For a surface tension value of 0.12 dyne/cm, the best fit to the experimental data is given for a cytoplasm and nucleus viscosity value of 200 dyne s/cm² and 1000 dyne s/cm², respectively. Cytoplasm and nucleus viscosity values of 100 dyne s/cm² and 1000 dyne s/cm², respectively, also form a reasonable set. All these values are within the range of the values reported in the literature (see Table 2).

The effects of surface tension on the bond lifetime are shown in Fig. 16. A lower surface tension allows the cell to maintain a larger curvature, which enables the cell to remain attached with a smaller contact area, as shown in Fig. 17. Consequently, the cell can remain attached with a smaller and sharper curved contact area and delay the lifting of the cell from the wall. For the parameter values used, the cell with the highest surface tension describes best the experimental results of Schmidtke and Diamond (2000). It is also shown that a cell with a lower cytoplasmic viscosity deforms more, remains closer to the surface, and rolls faster, as shown in Fig. 18, causing a decrease in bond lifetime.

FIGURE 16.

Effects of surface tension and shear rate on the bond lifetime: compound drop model. The squares correspond to the experimental results of Schmidtke and Diamond (2000), and the lines to this study. 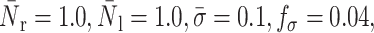α = 100, and β = 10. For cytoplasm and nucleus viscosity values of, respectively, 100 and 1000 dyne s/cm², a surface tension of 0.3 dyne/cm gives the best fit to the experimental data. A surface tension value of 0.12 dyne/cm also provides a good fit. All these values are within the range of the values reported in the literature (see Table 2).

FIGURE 17.

Instantaneous cell shapes for different values of interfacial tension, γ. 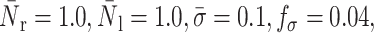α = 100, and β = 10, The horizontal line corresponds to the bottom channel wall.

FIGURE 18.

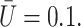Effect of viscosity on the cell shape as a function of time. β = 10, The horizontal line corresponds to the bottom channel wall.

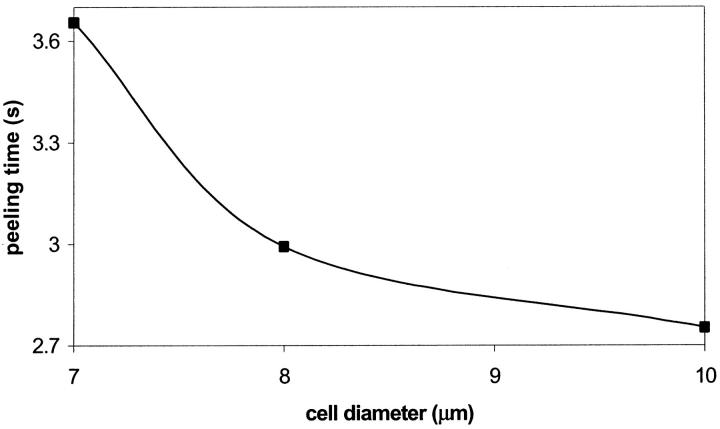
The effect of cell diameters on the peeling time is shown in Fig. 19. Three cell diameters of 7 μm, 8 μm, and 10 μm corresponding, respectively, to the average size of lymphocytes, neutrophils, and monocytes are selected. It is seen that a larger diameter cell decreases the peeling time and increases the cell rolling velocity. This result is consistent with the simulation of Tees et al. (2002) and experiments of Shinde Patil et al. (2001). A larger cell causes a greater blockage of the vessel, which results in larger local hydrodynamic forces.

FIGURE 19.

Effect of cell diameter on the dimensional peeling time: compound drop model. α = 100, The points shown correspond to the simulation data.

Changing the values of the spring constant (σ) by a factor of two or less has little impact on cell rolling, as observed by Chang et al., (2000). The results are not shown for conciseness, but the nucleus tends to delay the rolling of the cell along the vessel wall.

In summary, we have shown that the rheological properties of a cell have significant effects on the adhesion process contrary to what has been hypothesized in the literature (Hammer and Lauffenburger, 1987; Tees et al., 2002).

SUMMARY AND CONCLUSIONS

In this study, a multiscale computational approach for studying the adhesion kinetics, the deformation, and the movement of a cell on a substrate is presented. This method breaks the computational work into two separate but interrelated domains. At the cellular level, a continuum model satisfying the field equations for momentum transfer and mass continuity is adopted. At the receptor-ligand, or molecular, level, a bond molecule is mechanically represented by a spring. A reversible two-body kinetic model characterizes the association and dissociation of a bond. Communication between the macroscopic and microscopic scale models is facilitated interactively in the course of computation.

The computational model is assessed using an adherent cell, allowed to roll along the vessel wall under imposed shear flows. The cell is first modeled as a liquid drop to illustrate the computational approach, and then as a compound drop to evaluate the effect of the nucleus. The results compare very well with those obtained computationally (Dong et al., 1999; Dong and Lei, 2000; Chang et al., 2000; Tees et al., 2002) and experimentally (Schmidtke and Diamond, 2000; Shinde Patil et al., 2001). With these key validations, this approach is now ready to be extended to address various issues associated with cell adhesion. Shao et al. (1998) have found that after the microvillus reaches its natural length, it will extend under a small pulling force or form a tether under a high pulling force. In our computation, we observed that a tether is formed for high inlet velocity, thus for high pulling force as shown in Fig. 12. In addition, we have observed a lifting of the cell from the vessel wall leading to its peeling as shown in Fig. 9. Similar observations were made by Sukumaran and Seifert (2001) who studied the influence of the shear flow on vesicles near a wall and by Hodges and Jensen (2002) in their numerical study. In the latter study, the cell is modeled as a liquid drop adhering to a flat surface subjected to a simple shear flow. They found that the distance of the cell above the plane surface increases rapidly with time, then reaches a plateau as observed in Fig. 9 of this study. In addition, Hodges and Jensen (2002) reported that changing the suspending fluid viscosity value (the inside fluid is inviscid) does not affect the cell rolling velocity. However, they did not investigate the effects of the nucleus and cytoplasmic viscosities. In this study, it is shown that varying the cytoplasmic and/or nucleus viscosities influences the rolling velocity of the cell, indicating that hydrodynamics has an effect on cell adhesion.

In our study, bond formation is not considered per se due to the numerical resolution. We consider that a bond is formed when the distance between a receptor and ligand is less than a bond length, taken as 5 × 10⁻⁶ cm. Although in this study mesh resolution does not allow bond formation to be directly simulated, we can deduce from Fig. 13 that an increase of the shear stress keeps the cell closer to wall, and increases the contact area. This is consistent with published results (Alon et al., 1997, 1998) that a higher shear stress can enhance bond formation. How this phenomenon occurs is not clear. Does an increase of the shear stress increase first the diffusion and convection of bond molecule toward the contact area, or does an increase of the shear stress lead to an increase of the contact area due to cell deformation?

Although the proposed approach is able to describe key features of cell adhesion, several issues still need to be addressed. For example, experimental results have shown that there is a threshold stress above which cell rolling occurs (Shao et al., 1998). However, the models proposed in the literature cannot capture this feature, indicating that the straightforward analogy between a bond molecule and a spring model is incomplete. A bond model with a yield force can be used to help resolve this deficiency. Another issue is the characterization of the association and dissociation of bonds and the bond length before rupture because of the required computational time.

In this work, we have neglected membrane roughness (microvilli) and the effect of nonspecific forces in the bond force computation. In addition, we have assumed that the bond molecules are fixed on the membrane surface, which is not the case because bond molecules have shown to diffuse laterally to the contact area (Bell et al., 1984). The model is also limited by the fact that the only stresses acting on the membrane are those coming from the bond molecules, as made by Dembo et al. (1988) in the derivation of the reverse reaction rate constant. Furthermore, although the compound liquid drop model can capture most of the features of cell recovery and explain the reasons for the different published values for leukocyte viscosity, it does not include elastic effects that may be needed to fully describe leukocyte rheology (Tran-Son-Tay et al., 1994, 1998; Drury and Dembo, 1999, 2001; Kan et al., 1998, 1999). Another important issue is the use of a 2-D cell model because some of the present results may not hold in a 3-D world.

Nevertheless, this effort has offered a comprehensive framework to couple the cellular and the receptor-ligand dynamics and has shown that cell rheological properties have an effect on adhesion process. In the future, we will exploit the capabilities of large-scale parallel molecular dynamics computation to explicitly track the formation and dissociation of a bond, which has a timescale too small, of the order of 1 ns or less, to be accurately determined by the existing numerical technique.