When Translocation Dynamics Becomes Anomalous

Recent single molecule experiments probing the passage process of a short single-stranded DNA (ssDNA) through a membrane channel (translocation) allow us to measure the passage time distribution. Building on a recent modeling approach, (Lubensky and Nelson, 1999), which has been demonstrated to be valid for chains of up to ≃300 nucleotides and therefore well applies to the system we have in mind, we discuss the consequences if the associated dynamics is not of Markov origin, but if strong memory effects prevail during the translocation. Motivation is drawn from recent results indicating that the distribution of translocation times is broader than predicted by simple Markovian models based on Brownian motion.

The translocation of biomolecules through membrane pores (channels) is one of the most vital processes within or across biological cells, serving both delivery and signaling purposes (Alberts et al., 1994). In (bio)chemistry, forced translocation is used in selection/purification of larger molecules, and in medicine, it plays an important role in drug delivery. Whereas the translocation of short, inflexible molecules is primarily determined by the properties of the pore (energy-driven transport, sticking events within the pore, etc.) and the difference of the chemical potential between the cis and trans sides of the pore, semiflexible and flexible molecules, in addition, have to cross an entropy barrier while being (partially) confined within the channel (Lubensky and Nelson, 1999; Muthukumar, 2001, 1999; Slonkina and Kolomeisky, 2003; Sung and Park, 1996). In the presence of a high external bias and for the rather short chains used in typical experiments, the entropic slowdown as well as the other interactions between chain and channel wall become negligible, the passage being dominated by the applied drift (Lubensky and Nelson, 1999). In what follows, we develop a scenario according to which the translocation dynamics is governed by slowly decaying memory effects, leading to a different behavior in the distribution of passage times which we believe can be measured experimentally.

Experimentally, the translocation of ssDNA can be observed on a single molecular level, both voltage driven (Akeson et al., 1999; Kasianowicz et al., 1996; Meller et al., 2001) and in the absence of an external electric field (Bates et al., 2003). In such single-molecule translocation assays, fairly short chains are used, with some 60 bases corresponding to ∼12 persistence lengths, or six Kuhn lengths (Frank-Kamenetskii, 1997). The width (≃50 Å) of the membrane amounts to about one persistence length (≃40 Å) of the ssDNA. A good measure for the translocation process is the distribution of passage times, i.e., the statistics of time spans the chain needs to cross from the entry (cis) side to the exit (trans) side of the pore. In the results, one observes two (or three) different timescales: the shortest corresponds to chains that retract from the pore back to the cis side, before completing the passage through the pore; the other (one or two) correspond(s) to real passage times (if there are two peaks, this can be explained by different orientations of the chain in respect to the passage direction (Lubensky and Nelson, 1999)).

In a recent experiment (Bates et al., 2003), it was noted that the first passage time distribution contains nonnegligible contributions over a large time range even in the presence of a low driving voltage, a case in which a Markovian model would predict exponentially fast decay. This may well indicate that additional mechanisms, so far neglected, play a role in the translocation dynamics, which might effect long-tailed first passage time distributions, and therefore imply a possible modeling by assuming a non-Markovian behavior of the system. In this note, we construct a framework in the limit of strong non-Markovian effects, taking into account anomalous translocation dynamics through long-tailed memory effects. Given the accuracy of the newly reported experiments in Bates et al. (2003), it might well be possible to resolve such effects in log-log analyses of the presently available, or future data. We collect a number of possible sources for such anomalous dynamics.

In the presence of a bias field and for chains with≲300 nucleotides, the translocation dynamics in the Markov limit has been shown to follow the Smoluchowski-type equation (Lubensky and Nelson, 1999)

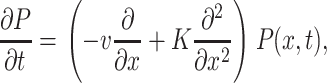(1)

where P(x, t) is the probability density function (pdf) to find the chain at position x at time t, and v and K are the associated drift and diffusion constants, which may be determined from more microscopic models (Lubensky and Nelson, 1999). The translocation process without retraction from the pore can thus be described by the first passage time distribution F(t) from the point x = L to x = 0. In the presence of the external drift, this leads to the result (see, for instance, Redner (2001))

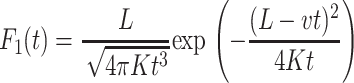(2)

Note the sharp exponential decay for longer passage times. In this picture of Markov advection-diffusion, the mean first passage time from the origin to an absorbing boundary a distance L away is given by 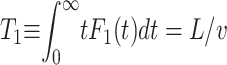, i.e., the statistical mean corresponds exactly to a classical linear motion with the drift velocity v. Thus, the influence of the diffusivity in this average becomes negligible and the motion can be characterized by the mean 〈x〉 = vt.

This picture dramatically changes in the presence of long-tailed memory, effected by a waiting time distribution

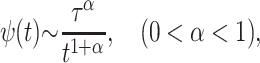(3)

according to which interruption times of the transport process in a multiple trapping model are distributed (Metzler and Klafter, 2000a), i.e., the transport process is being stalled successively, and the sticking intervals follow Eq. 3. In this situation, the relation for the mean gets modified to 〈x〉 = v_αt^α, where v_α is an appropriately generalized velocity, and the corresponding generalization of Eq. 1 is the fractional Fokker-Planck-Smoluchowski equation (Metzler and Klafter, 2000a)

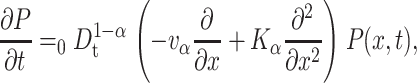(4)

with K_α = Kv_α/v, and the fractional Riemann-Liouville operator

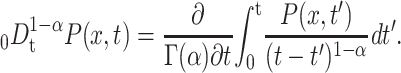The waiting time in the expression Eq. 3 is scaled to the internal timescale τ (Metzler and Klafter, 2000). A typical feature in this anomalous case is that the maximum of the pdf due to the strong persistence of the initial condition (i.e., the probability of not moving), remains at the initial location x = 0, and the mean first passage time diverges: 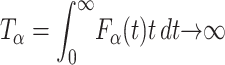. The associated first passage time distribution in the presence of Eq. 3 can be determined from the classical result Eq. 2. Recalling the scaling relation for the pdf P(x, u) in Laplace space (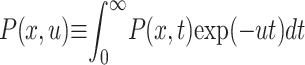) between the solutions of Eqs. 1 and 4 (Metzler and Klafter, 2000), the following scaling holds between the Markov survival probability and its non-Markov analog,

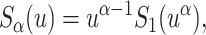(5)

in rescaled variables. This scaling relation can be rewritten in terms of the generalized Laplace transformation

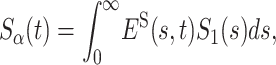(6)

where the Laplace transform of the kernel E^S(s, u) is given by the modified one-sided Lévy distribution , and therefore (Metzler and Klafter, 2000)

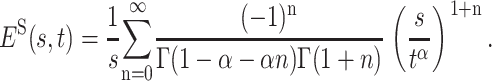(7)

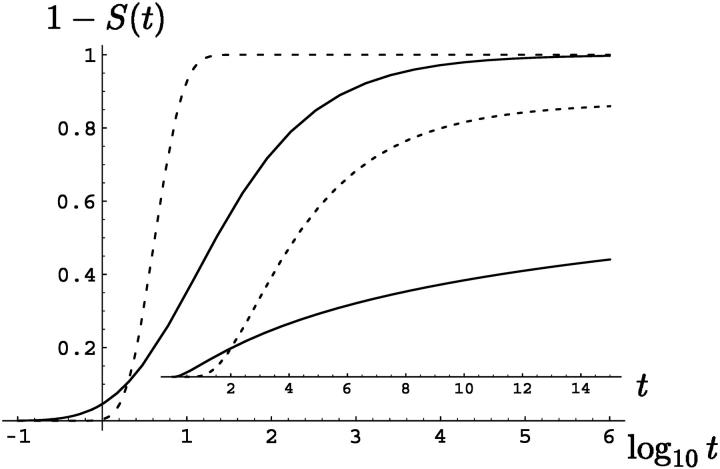
In particular, for α = 1/2, one obtains 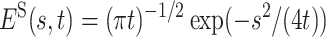. The pronounced difference between the Markov result and its non-Markov analog in the presence of the long-tailed distribution Eq. 3 for the experimentally measured quantity 1 − S(t), i.e., the translocation probability, is displayed in Fig. 1.

FIGURE 1.

Translocation probability 1 − S(t) for long-tailed waiting time with index α = 1/2 (solid line), in comparison to the Markov counterpart (dashed line) on a log-lin plot. In the inset (lin-lin plot), the much slower increase of 1 − S(t) in the non-Markovian result is even more distinct. In the plot, the dimensionless quantities, L = 5, and v = 1 were chosen.

It is straightforward to show that there exists a similar scaling relation for the first passage time density:

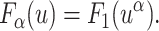(8)

From this relation, and the small-u expansion , one can by Tauberian theorems (Feller, 1968) deduce the longtime behavior of the first passage time density (Scher and Montroll, 1975; Scher et al., 2002; Barkai, 2001),

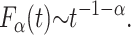(9)

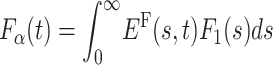Thus, in contrast to the Markov case, in the presence of long-tailed waiting times, the density F_α itself exhibits a long tail, and the mean first passage time diverges. In this case, in analogy to Eqs. 5 and 6, the transformation from F₁ to F_α, , can be rewritten as , with

(10)

For α = 1/2, one infers 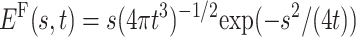. Note that in the case discussed here no turnover between two power laws, from t^α−1 to t^−α−1 results, in contrast to the properties of the cases discussed in Scher and Montroll (1975) and Scher et al. (2002). In Fig. 2, we depict the functional behavior of the first passage time distribution for an external bias, in comparison to the Markov case, revealing the distinct inverse power-law tails in the presence of Eq. 3.

FIGURE 2.

First passage time density F_α(t) for α = 1/2 (solid line: v = 10 (upper curve) and v = 5) and Markov case (dashed line: v = 10). Note the higher peak in the Markov case, indicating that the tail falls off faster than in the case with long-tailed waiting times. The inset shows the double-logarithmic plot with the −3/2 power-law asymptotics, for v = 10, 5, and 2.5.

Conversely, in the absence of a drift, the reflecting boundary at x = 0 cannot be a priori neglected (the retraction of the chain toward the cis side is no longer suppressed by the bias; compare Lubensky and Nelson, (1999)), and the corresponding first passage time distribution follows from the eigenvalue problem, such that the survival probability in the anomalous case is given by a sum over Mittag-Leffler decays:

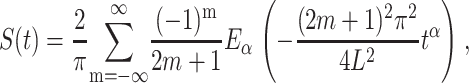which in the Markov limit α = 1 reduce to the exponential function, and therefore a considerably faster decay (Metzler and Klafter, 2000b)). The Mittag-Leffler function 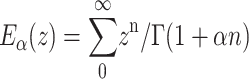is the “natural generalization” of the exponential function e^z ≡ E₁(z). E_α(−ct^α) interpolates between an initial stretched exponential and a final inverse power law ∼t^−α (Metzler and Klafter, 2000).

In particular, the longtime behavior of the first passage distribution F(t) ∼ t^−1−α ensues, i.e., the asymptotic behavior is analogous to the one derived from the case with drift (in contrast to the drift-free case without the reflecting barrier, in which F(t) ∼ t^−α/2−1) (Metzler and Klafter, 2000, 2000b; Barkai, 2001).

In both cases with and without drift, the first passage time distributions in the generalized case with long-tailed memory based on the waiting time form (Eq. 3), the corresponding F(t) exhibits a distinct maximum, its functional form being rather similar to the corresponding Markov limit, when viewed on a linear scale. On a double-logarithmic scale, the power law F(t) ∼ t^−1−α differs from the much faster, exponential decay in the Markov limit. In particular, for both cases drift-free and with drift, the same power-law behavior is expected, an additional consistency check in experiments. The latter statement, however, only holds if the mechanism affecting the broad form (Eq. 3), and the value of α in particular, is not affected by the magnitude of the external field. There are indications from the recent studies (Bates et al., 2003) that this may actually be the case: if the external drift is increased, the stalling events become less pronounced. This can influence α, but it could also introduce a cutoff at some time t_c in the waiting time distribution ψ(t), and therefore cause a system response that is closer to the Markov case than in the absence of the drift. We stress that in the presence of long-tailed first passage time distributions, the most probable passage time corresponding to the value at which F(t) peaks, becomes a rather meaningless quantity, as the mean first passage time diverges. We also note that the fit in reference Bates et al. (2003) of the passage time distribution by two exponentials with significantly different timescales in our approach becomes replaced by a continuum distribution of relaxation times.

Let us now list a number of potential sources for the waiting time distribution ψ(t):

• i. During the passage, sticking events caused by pore-chain interactions may occur. As these events would be expected to be correlated with the cooperative motion of the pore molecules, and possibly the translocating chain itself, a good guess would be that this causes power laws of the form Eq. 3, e.g., as observed in ligand rebinding in proteins (Glöckle and Nonnenmacher, 1995).

• ii. It is known from patch clamp measurements on single fast chloride channels (Blatz and Magleby, 1986), that ion channels open and close repeatedly. For the distribution g(t) of duration times of such channel gating events, it was typically found that it follows a modulated power-law trend, g(t) = A(t)t^−β, β > 0, where the modulation factor A can follow logarithmic oscillations before eventually being cut off by an exponential (Nonnenmacher and Nonnenmacher, 1989), or be constant (Millhauser et al., 1988). Within a finite time window, both are indistinguishable. It is therefore fair to say that gating events in a given time window in single ion channels follow power-law statistics, and typical values for β are ∼1.6. The distribution g translates into our waiting time distribution ψ(t) from Eq. 3 with α = β − 1.

• iii. For longer chains, Chuang et al. (2001) argued that the diffusion of the chain becomes anomalous. Naively viewing the translocation as a waiting time process during which the monomers in the pore channel have to wait until they are given way by the vicinal monomers, and so on, creating a non-Markov process which, on some coarse-grained level, may well be described by Eq. 3; compare also Douglas (2000).

This list of scenarios is not meant to be complete. However, one might suspect that the sticking scenario (i) is most liable to be affected by the strength of the external bias, producing an effect similar to the recent experiments reported by Bates et al. (2003), in which the dynamics exhibits the abovementioned turnover from broad to Brownian motion-type statistics on increase of the external bias field.

In some translocation experiments, apart from the sharp initial peak in the first passage time density stemming from immediately retracting chains back to the cis side, there occurs another hump similar to the one of the translocated chains discussed above. It has been argued that this is due to the existence of second characteristic passage time, depending on the orientation of the chain to the membrane channel in respect to the cis-trans direction (“head or tail first”) (Lubensky and Nelson, 1999). The same effect is expected in the case with long-tailed statistics following Eq. 3. However, it might well be that the associated power-law exponent α is different for the two orientations, as the nature of the effective interactions giving rise to the long-tailed waiting times may depend on this head-tail difference.

One might speculate about the biological relevance of anomalous translocation dynamics. On the one hand, it might be the outcome of a tradeoff between lack of specificity, if the passage is too free and a large variety of molecules could pass the membrane, and too high suppression, which would require active transport through the pore, implying a fairly large energy cost for long molecules. On the other hand, it might be advantageous to have a large variation in the arrival times of translocated molecules on the trans side (and thereby very efficient retention of untranslocated molecules on the cis side).

We have discussed possible changes arising in the distribution of first passage times in biopolymer translocation through a membrane channel, and listed a number of reasons that might give rise to such anomalous behavior. It should be possible to determine the quantity F(t) from experiments to sufficient accuracy, to be able to distinguish the normal (Brownian) dynamics result from its anomalous counterpart in both the presence and absence of an external drift. The large qualitative difference between exponential and power-law forms should be easily discernible on a double-logarithmic scale. It should, however, be stressed that the onset of the power-law trend depends on the strength of the drift, and might occur for fairly large times if the drift is weak. We finally mention that the proposed long-tailed effects may also pertain in other systems, like during the ejection of the DNA of bacteriophages from the capsid through a long pipe-like channel into the host cell (Alberts et al., 1994; Muthukumar, 2001).