DNA Basepair Step Deformability Inferred from Molecular Dynamics Simulations

Abstract

The sequence-dependent DNA deformability at the basepair step level was investigated using large-scale atomic resolution molecular dynamics simulation of two 18-bp DNA oligomers: d(GCCTATAAACGCCTATAA) and d(CTAGGTGGATGACTCATT). From an analysis of the structural fluctuations, the harmonic potential energy functions for all 10 unique steps with respect to the six step parameters have been evaluated. In the case of roll, three distinct groups of steps have been identified: the flexible pyrimidine-purine (YR) steps, intermediate purine-purine (RR), and stiff purine-pyrimidine (RY). The YR steps appear to be the most flexible in tilt and partially in twist. Increasing stiffness from YR through RR to RY was observed for rise, whereas shift and slide lack simple trends. A proposed measure of the relative importance of couplings identifies the slide-rise, twist-roll, and twist-slide couplings to play a major role. The force constants obtained are of similar magnitudes to those based on a crystallographic ensemble. However, the current data have a less complicated and less pronounced sequence dependence. A correlation analysis reveals concerted motions of neighboring steps and thus exposes limitations in the dinucleotide model. The comparison of DNA deformability from this and other studies with recent quantum-chemical stacking energy calculations suggests poor correlation between the stacking and flexibility.

INTRODUCTION

The mechanical deformability of DNA plays an important role in various biological processes, including protein-DNA interactions, DNA packing in viruses, the formation of chromosomes, and higher-order organization of the genetic material in a cell nucleus. Many of these phenomena occur within the framework of linear elasticity, where the magnitude of deformation is proportional to the applied force (Hooke's law). In such a “harmonic regime”, the energy of deformation may be expressed as a quadratic function of suitable structural variables. What remains to be established are the constant coefficients in such a function, i.e., the “elastic constants” (or “force constants”) describing the linear elastic properties of the system under study. As an example, one can consider a long piece of DNA as a flexible rod and characterize its properties by such elastic constants as the bending rigidity (or dynamic bending persistence length), stretch modulus, and twist rigidity (Munteanu et al., 1998; Olson, 1996; Olson and Zhurkin, 2000; Schlick, 1995; Tobias et al., 2000). Beyond these macroscale features of DNA, there is also considerable biological interest in the mechanical properties of DNA on much shorter length scales, namely at the level of one or several basepair steps, in which case the sequence-dependent differences in DNA structure and deformability may influence the binding of proteins (the so-called indirect readout).

Several experimental and theoretical studies have already been performed in an attempt to establish DNA sequence-dependent mechanical properties at the level of basepair steps. In an extensive and related study, Olson and co-workers (Olson et al., 1998) analyzed an ensemble of protein-DNA crystal structures to obtain harmonic deformation potentials for six helicoidal parameters (twist, tilt, roll, shift, slide, rise) of all 10 unique basepair steps including all the coupling terms. This gives a complete description of DNA basepair step deformability in the harmonic approximation. Their method is based on the assumption that external perturbations due to protein binding, neighboring basepairs, and/or crystal environments all impose forces on the dinucleotide step under study, and that this results in deformation of the DNA with respect to the equilibrium state. Further, if many independent perturbations occur, the resulting distortions will have a Gaussian distribution, a consequence of the central limit theorem of statistics. One can then use the known relation between correlations of quantities with a multidimensional Gaussian distribution and the stiffness matrix (Landau and Lifshitz, 1980) to obtain the desired force constants. These constants, however, are only relative ones, expressed in units of kT, where k is the Boltzmann constant and T is an unknown factor, the effective temperature of the ensemble. Thus, to interpret the values, some effective temperature must be chosen and this is accomplished by calibrating the force constants to some known property. Recently, Matsumoto and Olson (2002) performed a normal mode analysis of model DNA fragments based on the above-mentioned perturbed crystal structures force field, which they calibrated against elastic constants of a generic DNA.

A completely different approach to estimate the sequence-dependent deformability of DNA basepair steps has been adopted by Anselmi et al. (2000, 2002). They assume that bending and torsional rigidity of various dinucleotide steps are modulated according to the differences in their melting temperatures. They argue that the maximum amplitude of thermal fluctuations that a dinucleotide step can withstand before it melts is approximately the same for all steps, and that a harmonic deformation potential is valid up to temperatures close to the melting one. The maximum basepair step-independent squared fluctuation amplitude is then equal to kT_m/C (where T_m is the melting temperature and C a force constant), thus C is proportional to T_m. This force field is also relative and effectively describes the sequence-dependent modulation of a generic bending and twisting stiffness.

To obtain sequence-dependent DNA deformability data, other experimental methods have recently been used as well. The submicrosecond bending dynamics of duplex DNA were investigated by Okonogi et al. (2000) using an electron paramagnetic resonance technique; they studied the effect of insertion of a tract of alternating A and T (the AT tract) into a DNA fragment and concluded that the AT tract should be 20% more flexible than the control sequence. Roychoudhury et al. (2000) have studied mechanical properties of a nucleosome positioning motif by the method of cyclization kinetics and found out that this motif is much more flexible than the control sequence. More recent high-throughput cyclization experiments by this group further suggest enhanced flexibility of AT repeat sequences (Zhang and Crothers, 2003). Pedone et al. (2001) measured the torsional elastic constants of 10 different 27-mer DNA oligomers by fluorescence polarization anisotropy. The common feature of these studies is that they generally establish the average mechanical properties of specific sequences longer than one or several basepair steps.

Nevertheless, detailed crystallographic studies aimed at understanding the deformabilities of dinucleotide steps under various conditions have been accumulating. Chen et al. (2001a,b) studied the indirect readout in the CAP-DNA complex that contains an extremely deformed primary kink, and Mack et al. (2001) investigated the intrinsic bending and deformability of the TA step, in contrast to the AT step.

Besides the experimental investigations, various computational approaches have been applied to tackle the problem. In general, one tries to obtain an effective force field on a larger scale (e.g., elastic constants of a flexible rod) from simulations with small-scale force fields such as interatomic potentials. The range of methods includes normal mode analysis (Matsumoto and Go, 1999; Matsumoto and Olson, 2002), energy minimization or molecular dynamics (MD) of structures deformed by imposed restraints (Banavali and MacKerell, 2002; Cluzel et al., 1996; Konrad and Bolonick, 1996; Lavery and Hartmann, 1994; Packer and Hunter, 2001; Varnai and Lavery, 2002), and the analysis of fluctuations from unrestrained molecular dynamics.

This last method, restricted to the harmonic (linear) elasticity regime, does not require any external perturbations imposed on the system. One has to choose appropriate structural variables to describe the deformation of the system (such as the six helicoidal parameters in the case of a basepair step) and calculate their mutual correlations based on their time courses obtained from molecular dynamics. The inversion of the correlation matrix then gives the stiffness matrix, i.e., the elastic constants, as noted above (Landau and Lifshitz, 1980).

Unrestrained molecular dynamics of DNA with explicit inclusion of water and ions and with accurate treatment of the long-range electrostatic interactions has come of age and has been successfully applied to a range of problems—see recent reviews (Beveridge and McConnell, 2000; Cheatham and Kollman, 2000; Cheatham and Young, 2001) and references therein. It is now becoming clear that it can be used to study not only DNA “average” properties like the structure and conformational preferences, but also dynamical events connected with thermodynamic fluctuations in the system at nonzero temperature. Since one can see each and every atom in its motion, a microscopic picture of various phenomena can be obtained, as far as the limitations in the force field and trajectory length permit. An interesting example is recent studies on the relationship between dynamic cation positions and the structure of the minor groove (Hamelberg et al., 2000, 2001). In an early attempt to calculate DNA elastic properties from unrestrained molecular dynamics, Bruant et al. (1999) applied the method of fluctuations in a simplified form to 1-ns molecular dynamics of two 15-bp oligonucleotides. In our previous work (Lankas et al., 2000) we calculated harmonic elastic constants of 3–11 bp duplex DNA fragments using four 5-ns unrestrained MD trajectories of 17-bp duplexes. Our description of the fragment deformation was “global”: we measured the total fragment length, total twist, and two angles defining the fragment bending into the grooves of the central basepair and into the perpendicular direction—DNA was thus considered as an unshearable, anisotropic flexible rod. We obtained the stretch modulus, twist rigidity, and anisotropic bending rigidities as well as all the coupling terms. The calculated values were in very good overall agreement with experimental results for generic DNA; however, the atomic resolution approach exposed the pronounced sequence dependence of the DNA elasticity. We further applied the method to polypurine tracts containing modified bases (Lankas et al., 2002) showing that the presence or absence of the N2 amino group is a primary factor to determine structures and elasticities of polypurine tracts.

Molecular dynamics simulations can also be used to study DNA deformability at the basepair step level. McConnell and Beveridge (McConnell and Beveridge, 2001) assigned a specific flexibility to each of the 10 dinucleotide steps based on the area of their roll-tilt plots enclosing 98% of the MD data points. This can be compared directly with the “volume of conformation space” proposed by Olson et al. (1998). Recently, Thayer and Beveridge (2002) divided the roll-tilt plots into quadrants and 10 concentric rings, thus providing more detailed information about the distribution of MD data for use in their Hidden Markov Model to describe DNA-protein interaction.

These approaches already give a certain idea about the relative deformabilities in roll and tilt of the dinucleotide steps and are independent on any assumption about the harmonic nature of the deformation potential. The aim of the present work, however, is to obtain a description of DNA mechanical properties on the basepair step level by calculating harmonic potential energy functions of the 10 unique basepair steps. The energy is expressed in terms of the six helicoidal parameters: twist, tilt, roll, shift, slide, and rise. The calculations are based on atomic-resolution molecular dynamics simulations of two DNA oligomers using a reliable simulation protocol. The method of fluctuations is used to calculate the complete stiffness matrix, including all the couplings. This allows a direct comparison with the force constant estimates from x-ray data by Olson et al. (1998) and with other experimental results. Further, a relationship between DNA sequence-dependent deformability and stacking energy is discussed. Finally, we demonstrate the limitations of the model related to the coupling between different basepair steps in a DNA sequence. A thorough theoretical treatment of the problem has recently been provided by an independent study (Gonzalez and Maddocks, 2001).

METHODS

The effective temperature

Matsumoto and Olson (2002) obtained the effective temperature by performing a normal mode analysis of a model homopolymer with simplified, generic basepair step interactions derived from the x-ray data. The temperature was chosen in such a way that the normal modes of the homopolymer corresponded to those of an elastic rod with a bending persistence length of 550 Å, twist persistence length of 360 Å, and stretch modulus of 1900 pN, values comparable to the elastic constants of generic DNA. Although Matsumoto and Olson do not report the effective temperature directly, it can be estimated from other data in their study. The six-step parameters in their generic homopolymer have certain mean values and standard deviations but are uncoupled to each other. Starting with twist, we assume that the twist rigidity of the whole polymer is due to pure twisting of the individual steps. Since the steps are identical, isolated units in the model, the twist rigidity of the polymer is equal to that of a single step. Denoting the root mean-square deviation (rmsd) of the twist by rmsd(Tw), the distance between basepairs in the step (taken as (Shift² + Slide² + Rise²) ^1/2) by l, and assuming that the average twisting energy is equal to (1/2)kT (the equipartition principle), we have T_eff = (C/kl).(rmsd(Tw))². Substituting for rmsd(Tw) the value of 5.5° (i.e., 0.096 rad) reported in the study, we obtain T_eff = 295 K. As a backward check, we assumed that T_eff = 295 K, calculated the force constants with respect to tilt and roll (based on the rmsd values in the study), and then computed their harmonic average. In this case, it should approximate the isotropic bending persistence length of the whole polymer (Lankas et al., 2000). The result is 550 Å, exactly as reported by Matsumoto and Olson. We thus suppose that the effective temperature of the x-ray ensemble of Olson et al. is 295 K and use this value throughout our study.

Molecular dynamics simulations

Two different DNA duplexes were built from Arnott B-DNA models (Arnott et al., 1980, 1983) using the nucgen module of AMBER6 (Pearlman et al., 1995). These were the DNA sequences d[GCCTATAAACGCCTATAA] and d[CTAGGTGGATGACTCATT]. The Cornell et al. (1995) force field was used for all the simulations discussed. The initial in vacuo models were minimized for 500 steps (250 steps steepest descent followed by 250 steps of conjugate gradient minimization) with no cutoff and use of the generalized Born implicit solvent model implemented in AMBER6/7 with the default radii. The minimized duplex structure was then solvated with TIP3P waters (Jorgensen et al., 1983) with at least a 9 Å buffer of water in each direction in a truncated octahedral unit cell. Net-neutralizing Na⁺ ions were added at favorable electrostatic positions and then an additional set of 20 Na⁺ and 20 Cl⁻ ions were added (also at favorable electrostatic positions). Assuming an ∼75 Å truncated octahedral box, the addition of 20 extra ions corresponds to ∼100 mM added salt. To avoid initial bias due to the positioning of the ions (Cheatham and Young, 2001), the initial ion positions were randomized by random swaps with water molecules such that no ion was closer than 5 Å to the DNA or 3.5 Å to any other ion.

Initial minimization was performed with the coordinates of the DNA held fixed allowing only the water and ions to move. This first involved minimization for 500 steps of steepest descent and 500 steps of conjugate gradient minimization using the particle mesh Ewald method (Essmann et al., 1995; Sagui and Darden, 1999) (and an 80 × 80 × 80 charge grid, an 8 Å cutoff, 1 × 10⁻⁵ direct space tolerance, fourth order B-spline interpolation, and an Ewald coefficient of ∼0.35). SHAKE (Ryckaert et al., 1977) was disabled for the minimization. An 8 Å cutoff was used for the van der Waals interactions and the pair list was updated every 25 steps. After the minimization, 150 ps of molecular dynamics were performed (with a 2 fs time step and SHAKE on the hydrogens with a tolerance of 10⁻⁸) applying constant pressure and temperature with Berendsen temperature coupling (Berendsen et al., 1984) with relaxation constants of 1.0. The cutoff for pair interactions was set at 9 Å, and a 1.0 Å buffer was built for the pair interaction list that was updated heuristically to avoid omission of pair interactions. A long-range bulk density van der Waals correction was applied. Particle mesh Ewald was applied as before, except that the cutoff was 9 Å leading to an Ewald coefficient of ∼0.31. At least 20 ns production simulations were initiated after the brief equilibration with no restraints applied. The only change in runtime parameters for the production simulations was that the center of mass translation was removed periodically (every 5000 steps) (Chiu et al., 2000; Harvey et al., 1998) and the pressure/temperature coupling times were increased to 5.0.

ANALYSIS

Trajectory snapshots were saved every picosecond. The time courses of the basepair step helicoidal variables (twist, tilt, roll, shift, slide. rise) were obtained by analyzing the DNA structure in each snapshot using the 3DNA code (Lu et al., 2000). The first nanosecond was excluded from the analysis. Assuming that the probability of a fluctuation, w, is an exponential function of the corresponding free-energy change E, 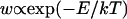(Einstein's formula), it can be shown that the correlation matrix of the structural variables is proportional to the inverse of the stiffness matrix (Landau and Lifshitz, 1980). Let 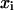and 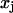be two helicoidal variables, 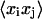their correlation, F the stiffness matrix, and 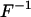its inverse. Then 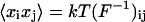. We substituted to the left-hand side the time correlations obtained from the simulation trajectory and inverted the relation to compute the elements of the stiffness matrix, i.e., the desired elastic constants.

The square of the “accessible conformational volume” is defined as the determinant of the correlation matrix (the last equation shows that it can also be calculated as the reciprocal value of the determinant of F, multiplied by kT). This is a direct analogy with the one-dimensional case where the dispersion, 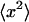, gives the square length of the interval where the variable x spends most of the time. The computer code for obtaining DNA basepair step deformabilities from molecular dynamics simulations is available upon request from the authors.

RESULTS AND DISCUSSION

We performed unrestrained molecular dynamics simulations of two 18-bp DNA duplex oligonucleotides in NPT ensemble with explicit representation of water and ions. The trajectory length is 20 ns in both cases. A truncated octahedral box with periodic boundary conditions was used, which lead to a relatively large system of ∼40,000 atoms. The AMBER 6 simulation package (Pearlman et al., 1995) with the Cornell et al. (1995) force field was used. The following DNA oligomers were simulated: d(GCCTATAAACGCCTATAA) and d(CTAGGTGGATGACTCATT). The first one contains the TATAAACGCC decamer, a strong nucleosome positioning motif (Widlund et al., 1997, 1999) whose elastic properties have recently been investigated by Roychoudhury et al. (2000). Using the method of cyclization kinetics, they found that a 30-bp construct containing three repeats of the motif exhibits a nearly twofold decrease in the bending rigidity and a twist modulus smaller by 35% with respect to generic DNA. We can thus expect that our first sequence as a whole will have unique elastic properties. The second sequence, in contrast, was used by Roychoudhury et al. as a control and was found to behave quite normally. Although it is not a purpose of this study to calculate the elastic properties of these sequences as a whole, i.e., the global flexibilities (work in progress), we could assume that the differences in global behavior are reflected on the local, basepair step level. It is possible that the deformability of at least some basepairs is context-dependent, as was recently demonstrated (Mack et al., 2001). Thus choosing two sequences with dramatically different elastic properties would enable us to cover a wide range of the basepair step behavior including its context dependence. Note that all 10 unique steps are represented at least once in our systems, most of them 2–3 times.

To compare our results with the crystallographic data of Olson et al. (1998), one has to calibrate the latter to obtain absolute values of the force constants. In other words, it is necessary to establish the effective temperature of the crystallographic ensemble (which is a purely statistical property and has nothing to do with the real, physical temperature of the crystals). We have done this as explained in the Methods section. The resulting value, 295 K, is used throughout our study.

Diagonal force constants

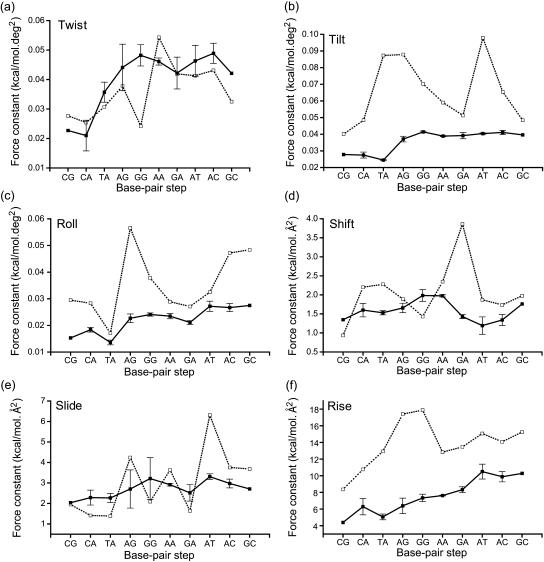
Table 1 shows the full list of the force constants for the 10 unique basepair steps calculated form the simulations. Fig. 1 summarizes the sequence dependence of the diagonal force constants. The numbers are calculated as averages of the corresponding force constants of all identical basepair steps in the simulated sequences with the error bars indicating the range of calculated values. The two dinucleotide steps at each end of the oligomers were excluded from the analysis since they may be subject to end-effects. Note that the first three steps on the x axes are of the YR type (pyrimidine-purine), the last three are RY (purine-pyrimidine), and the four in the middle are RR (purine-purine). For comparison, the figures also present the data by Olson et al. (1998). The larger the force constant, the stiffer the degree of freedom is.

TABLE 1.

Force constants in harmonic potential energy functions describing the deformation of individual basepair steps

	CG	CA	TA	AG	GG	AA	GA	AT	AC	GC
Twist-twist	0.0227	0.0210	0.0357	0.0441	0.0482	0.0461	0.0422	0.0463	0.0489	0.0421
Tilt-tilt	0.0278	0.0275	0.0245	0.0371	0.0414	0.0389	0.0392	0.0404	0.0411	0.0396
Roll-roll	0.0153	0.0184	0.0136	0.0227	0.0241	0.0235	0.0211	0.0272	0.0267	0.0275
Twist-tilt*	0.0014	−0.0005	−0.0008	−0.0027	−0.0004	0.0060	0.0005	−0.0003	0.0007	0.0002
Twist-roll	0.0031	0.0049	0.0084	0.0057	0.0044	0.0083	0.0086	0.0081	0.0076	0.0070
Tilt-roll*	0.0011	0.0009	−0.0001	−0.0027	−0.0009	0.0033	−0.0002	0.0007	0.0029	−0.0010
Shift-shift	1.3464	1.6003	1.5294	1.6568	1.9839	1.9748	1.4302	1.1932	1.3410	1.7614
Slide-slide	2.0342	2.2856	2.2691	2.7056	3.2154	2.9137	2.5179	3.3095	2.9739	2.7084
Rise-rise	4.3896	6.2903	5.0546	6.3875	7.3347	7.6206	8.3295	10.4992	9.8821	10.2808
Shift-slide*	−0.1867	−0.2832	0.0516	−0.0263	0.0572	0.1711	0.0259	−0.0965	−0.1574	0.3178
Shift-rise*	−0.0411	−0.0651	−0.0330	−0.0318	0.2151	0.1922	0.0250	−0.0231	−0.0059	0.1312
Slide-rise	1.4671	0.8160	0.9130	1.3204	1.1959	1.3815	1.1528	2.4811	2.5929	2.5578
Twist-shift*	0.0226	−0.0102	−0.0058	−0.0311	0.0238	0.0568	−0.0011	−0.0082	0.0051	−0.0012
Twist-slide	−0.0855	−0.0170	−0.0926	−0.1764	−0.2250	−0.2180	−0.2056	−0.1157	−0.2007	−0.1929
Twist-rise	−0.1243	−0.1259	−0.0932	−0.1437	−0.1142	−0.1587	−0.1276	−0.0891	−0.1600	−0.1603
Tilt-shift	−0.0516	0.0040	0.0233	−0.0194	−0.0653	0.0015	−0.0262	0.0241	−0.0049	−0.0478
Tilt-slide*	0.0103	−0.0021	0.0052	0.0078	0.0050	−0.0075	−0.0023	−0.0097	−0.0129	−0.0183
Tilt-rise*	0.0047	−0.0158	−0.0032	0.0498	−0.0838	−0.2054	−0.0829	0.0063	0.0439	−0.0632
Roll-shift*	0.0106	−0.0024	−0.0097	−0.0143	−0.0042	0.0158	0.0112	0.0090	0.0141	−0.0015
Roll-slide	−0.0205	0.0093	−0.0078	−0.0291	−0.0070	−0.0220	−0.0006	−0.0499	−0.0022	0.0055
Roll-rise	−0.0199	−0.0865	−0.0370	−0.0010	0.0044	−0.0541	−0.0121	0.0927	0.1089	0.1257

Force constants are in units of kcal/mol·deg², kcal/mol·Å², or kcal/mol·deg·Å for angular, translational, or mixed deformations, respectively.

^*These coupling constants should be zero for self-complementary steps (CG, GC, AT, TA) since tilt and shift change sign upon changing the direction in which a DNA sequence is followed, and energy must not depend on this direction. Due to the influence of sequence context and/or limited sampling, the constants calculated from our simulations are nonzero. However, none of them ranks among the most important couplings for self-complementary steps (see Fig. 2 a).

FIGURE 1.

Diagonal force constants in basepair step harmonic deformation potentials obtained from molecular dynamics simulations (solid line) as compared with those from the x-ray study of Olson et al. (1998) (dotted line). Error bars in the simulation data indicate the range of values observed. These constants describe the energetics of a deformation in which only one helicoidal parameter is changed whereas the others retain their equilibrium values. See Table 1 for a complete list of all constants, including the coupling terms.

Considering the twist rigidity, the simulations suggest that the CG and CA steps are by far the most flexible; the value of the TA step is distinctively higher, and the remaining steps have on average still higher twist rigidities that are comparable to each other. This confirms the exceptional softness of the YR steps; however, TA seems to be slightly stiffer than CG and CA. The relatively large error bars in the simulation data indicate significant differences for the twist rigidities for different instances of the same basepair step. This might indicate a high sensitivity of the twist stiffness to the sequence context; it may be, however, also related to limited sampling on the present simulation timescale. Overall, the x-ray data show similar trends and are quantitatively comparable with the simulation results. The important exception is GG, which in the x-ray data stands out of the general trend and is suggested to be the most flexible of all steps, even more than CA.

Turning to tilt, the simulations show a simple picture: the YR basepair steps are flexible whereas the other steps are stiffer, and within each group the values of the force constants are directly comparable. The crystallographic data, by contrast, suggest a more complex dependence: CG is the most flexible step but the values of CA, GA, and GC are comparable, and the YR step TA in fact ranks among the stiffest.

The stiffness with respect to roll is of particular interest since roll is more flexible than tilt and thus preferentially involved in spontaneous bending. The simulation data suggest three distinct groups of steps: the YR basepair steps are the most flexible, the RR show intermediate flexibility, and the stiffest are RY. The observed higher flexibility of YR steps toward basepair roll is likely related to different balance of intrastrand and interstrand van der Waals contributions to stacking in these steps. The roll perturbs coplanarity of bases within one strand and thus reduces the van der Waals (overlap) component of intrastrand stacking (due to a nonuniform vertical distance of the bases). It is especially pronounced for rolls compressing the major groove, as the consecutive bases are somewhat noncoplanar (open toward the minor groove) for roll = 0. It is a result of a concerted effect of propeller twisting and right-handed helical twisting. Among the basepair steps, the YR ones show the lowest intrastrand overlap of bases whereas they have extensive interstrand stacking involving noncoplanar bases due to propeller twisting. In contrast to the intrastrand stacking the interstrand stacking improves with roll motion compressing the major groove, as it alleviates the interstrand clash of bases in the minor groove and improves their coplanarity. The opposite effect of roll on intra- and interstrand stacking in YR steps contributes to the roll flexibility. The crystallographic data for roll once again show a rather complex dependence: TA is the most flexible, the values for CG, CA, AA, and GA are comparable, and there is a peak at AG.

In the case of shift, neither x-ray nor simulations shows any clear sequence specific tendency. Note that x-ray data suggest CG as the most flexible, followed by GG, and predict a sharp stiff peak for GA, which is not observed in simulation. In both simulation and analysis of the x-ray data, the slide stiffness shows a slight increasing tendency from YR over RR to RY; however, large oscillations are observed in the analysis based on the crystal structures. Interestingly, large oscillations at AG and GG in the x-ray data correspond to large variances in the simulation data. The small increasing trend observed with shift is quite pronounced in the case of rise. Only AG and GG in the x-ray data exhibit apparently higher rise rigidity.

It is interesting to compare these data with the dinucleotide flexibilities obtained by Anselmi et al. (2002) from melting temperatures. This force field is shown to have predictive power in the case of sequence-dependent differences in nucleosome binding free energies, as well as in other problems (Anselmi et al., 2000, 2002). Anselmi et al. suggest that the isotropic bending rigidity and the twist rigidity is modulated in the same way, depending on the melting temperature of the step. The modulating factors span a rather narrow range, from 0.894 for TA (the most flexible) to 1.180 for the most rigid GC step. The CG step is found to be the most “generic” with the scaling factor close to 1. The other steps fall into two categories: the more flexible with factors ∼0.95 (CA, AG, AA, AT) and the more rigid with the values ∼1.04–1.07 (GG, GA, AC).

The coupling terms

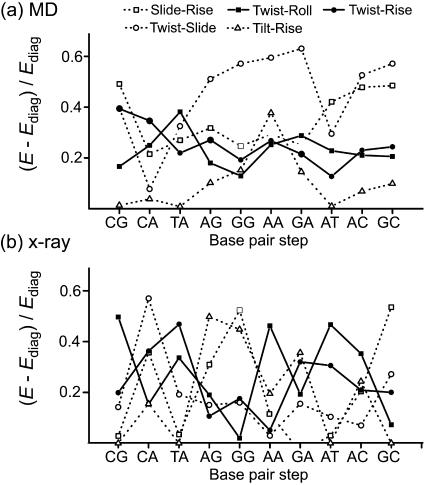
To obtain a complete picture of the basepair step deformability, one has to take into account the nondiagonal elements of the stiffness matrix (the “coupling terms”) as well. One way to do this is to calculate the volume of the conformational space in which the basepair spends most of the time (Olson et al., 1998). The square of the volume can be estimated as the determinant of the covariance matrix or, equivalently, as the reciprocal of the determinant of the stiffness matrix, multiplied by kT. Note that due to the invariance of the determinant with respect to the coordinate system rotation, its value is equal to the product of the eigenvalues of the matrix.

We calculated the conformational volume for all 10 steps. The volume for CG was the largest and thus this step stands out as the most flexible. The other YR steps, CA and TA, have comparable values of ∼60% of the CG one. The remaining steps occupy a range of 30% (GA) to 20% (AT) of the CG value. Thus, AT seems to be the stiffest step. The x-ray values reported by Olson et al. show similar trends, with CG the most and AT the least flexible; however, their values for TA and GG are quite close to each other. In any case, one should keep in mind that the conformational volume gives only a very broad idea about the step flexibility. The energetics of any specific deformation can be fully understood only by considering the force constants themselves.

A natural question might arise: how big an error is introduced if one neglects the couplings? Obviously, the magnitude of the coupling terms themselves is not of much help since their relative effect depends also on the corresponding diagonal terms. Here we propose a quantitative criterion enabling us to judge the relative importance of couplings. Assume a deformation involving just two helicoidal variables whereas all the others remain at equilibrium. Denote by x and y the deviations of these two variables from their equilibrium values. Then the energy of deformation is expressed as 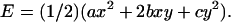Let E_diag be the energy computed from the above formula but without couplings (b is set to zero). A simple calculation shows that the maximum relative error (in absolute value) due to ignoring the coupling term is equal to the absolute value of b, divided by the harmonic average of a and c: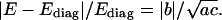

The largest relative error is connected with the twist-roll, slide-rise, twist-slide, and twist-rise couplings (see Fig. 2 a). However, in the case of RY steps, the values of the roll-rise are very close to those of twist-roll. The values for other couplings are in general small. An exception is the tilt-rise coupling that has a peak at the AA step. Other couplings are in general small and form a narrow belt near zero (not shown in the figure). Note that the largest relative error in energy due to neglecting the couplings can be as high as 60%.

FIGURE 2.

Comparison of the relative importance of various coupling terms. The values indicate the relative error caused by neglecting the coupling term in a deformation where only two different variables are involved. See text for details. (a) Results from simulations. (b) Crystallographic data from Olson et al. (1998). In simulations, the other couplings not shown in the figures form a narrow belt near the zero value; in crystallographic data, however, they uniformly fill the space between zero and the uppermost curves.

The corresponding values for the crystallographic data (Fig. 2 b) again suggest the twist-roll, slide-rise, twist-slide, twist-rise, and tilt-rise to bound the data, with values up to 55%. However, tilt-shift is close to tilt-rise for RR steps and reaches a value of 40% for CG and GC. The other coupling errors almost uniformly fill the space between zero and the above-mentioned “envelopes”, rather than forming any kind of a narrow belt around the zero value. Thus, contrary to the simulations, the x-ray data suggest no simple trend as far as the importance of the coupling terms is concerned.

Methodological issues

A very important question concerns the sensitivity of the calculated data to the helicoidal analysis algorithm used. The problem was extensively studied by Lu and Olson (1999) with the conclusion that the helicoidal parameters depend significantly on the choice of the basepair reference frame but are much less sensitive to the specific mathematical procedure used. In the present case, the x-ray data by Olson et al. (1998) are based on the CompDNA analyzer (Gorin et al., 1995) whereas our calculations were performed using the 3DNA program (Lu et al., 2000), which conforms to the recently established “Tsukuba convention” (Olson et al., 2001). To check for possible discrepancies between results produced by the two algorithms, we calculated ensemble averages and standard deviations of a number of basepair steps using both programs. The angular parameters were found to be consistent within 0.1° (twist) to 0.2° (tilt and roll), resulting in <5% differences in standard deviations. The averages of shift differed by no more than 0.05 Å, those of slide and rise by <0.01 Å, whereas the differences in standard deviations were ∼3% (0.01 Å) in rise and <1% in shift and slide. Since the force constants are, broadly speaking, dependent on the square of the standard deviation of the helicoidal parameters, we conclude that our use of the 3DNA program may introduce a difference in force constants of <10% and cannot alter any general trends in the data.

Our calculations are based on a simple equation stating that the covariance matrix is equal to the inverse of the stiffness matrix, multiplied by kT. The same relationship was also used by Olson et al. (1998) and in our previous studies (Lankas et al., 2002, 2000). It is a mathematical consequence of the fundamental assumption that the probability of a fluctuation is an exponential function of the corresponding free-energy change (Einstein's formula) and that the free energy is quadratic in structural variables (Landau and Lifshitz, 1980). However, the basepair step is a small system and such “macroscopic” reasoning may be outside its limits of validity. Recently, Gonzalez and Maddocks (2001) performed a detailed theoretical analysis of the problem from the microscopic point of view where the probability measure is an exponential function of the Hamiltonian. They showed that due to the non-Cartesian nature of the angular variables (twist, tilt, roll), a Jacobian must be included in the above-mentioned relation between the covariance and stiffness matrices. The Jacobian appears due to the change of variables from angular to canonical ones and its form depends on the precise definition of the helicoidal parameters. Nevertheless, the relation reduces to the simple one used here if the Jacobian is constant. To clarify the situation, we performed an analytical calculation of the Jacobian for the case of the 3DNA algorithm used here and found that it is equal to 1, on condition that Roll² + Tilt² ≪ 1 (in radians). This is satisfied for all but the most distorted structures; for example, if Roll = 20° and Tilt = 10°, their sum of squares is still only 0.15 rad².

An important point concerns the choice of the all-atom force field to be used in simulations. The Cornell et al. (1995) force field is known to be relatively soft. This is demonstrated by its facility for A-DNA to B-DNA transitions as well as B-DNA to A-DNA transitions (under the appropriate conditions) and also by its bending properties that have been shown to be consistent with experiment. It is not as evident that these subtle properties will be reproduced by other available nucleic acid force fields, including the Cheatham et al. (parm98/99) (Cheatham et al., 1999; Wang et al., 2000), Langley BMS (Langley, 1998), and MacKerell all27 (Foloppe and MacKerell, 2000) force fields. Part of the enhanced flexibility of the Cornell et al. force field relates to its relatively faster sugar repuckering compared to the other force fields (Cheatham et al., 1999; Cheatham and Young, 2001). In our experience, despite the known deficiencies of lower than expected helical twist, sugar pucker, and backbone χ-angle values, the Cornell et al. force field has been shown to perform very well not only for structure, but also its elastic properties (Lankas et al., 2002, 2000). In contrast, the newer parm99 force field, which supposedly fixes up the known deficiencies, does not seem to show proper A-B DNA equilibria (Cheatham et al., 1999) or DNA bending and dynamics (data not shown).

The hypothesis that stacking energy may have a determining influence on DNA deformability was proposed by Hagerman (1988) and briefly discussed by Anselmi et al. (2002) and Pedone et al. (2001) in connection with their suggested sequence-dependence of DNA stiffness. The issue is also addressed in our previous works on simulating DNA deformability (Lankas et al., 2002, 2000). Anselmi et al. compared the relative rigidities for each dinucleotide step obtained from the melting temperatures (Gotoh and Tagashira, 1981) with relative stacking energies based on an early theoretical work (Ornstein et al., 1978) and reported a correlation coefficient of 0.96 between the two scales. However, the order of stability of the 10 basepair steps suggested by these old semiempirical calculations differs significantly from that predicted by recent ab initio computations (Hobza and Sponer, 2002; Sponer et al., 2000, 1997). Modern electron correlation calculations represent almost converged estimates of stacking energies and provide their reliable relative order (Hobza and Sponer, 2002). Recently evaluated sequence-dependent stacking energies (Sponer et al., 2000, 1997) predict very similar high stability of both GC and CG, somehow lower stability for CA, AC, and AA, and the least stable GG. These trends are followed neither by the thermal stability data used by Anselmi et al. (correlation coefficient 0.3) nor by the crystallographic data of Olson et al. (1998). They are not followed by our MD results either, although modern empirical force fields like the one used here have been shown to reproduce well the contemporary quantum chemical data (Sponer et al., 2000, 1997). Thus, we suggest that neither DNA stiffness nor its thermal stability is determined simply by the magnitude of base stacking: a complex interplay of contributions such as potential energy profiles and hydration effects seems to play a role.

Beyond the dinucleotide model

Both the model of Olson et al. (1998) and our simulation approach presented here so far are based on the assumption that individual basepair steps can be treated as independent units. Anselmi et al. (2002) also report the rigidities decomposed into individual step contributions. However, since increasing evidence is accumulating that points to the influence of the larger sequence context on structure and deformability of DNA basepairs, it is prudent to question this underlying assumption. Recently, a thorough crystallographic analysis (Mack et al., 2001) demonstrated that the AT steps within an alternating AT context behave differently from those in an A-tract. Similarly, this crystal data suggest sequence and crystal packing effects on TA step structure and dynamics. However, NMR data provide somewhat conflicting evidence indicating that TA step dynamics are largely independent of sequence context (McAteer et al., 1995; McAteer and Kennedy, 2000). Despite this, sequence context is likely important for both structure and dynamics. For example, the progressive narrowing of the minor groove in the A-tract seems to be saturated only at the sixth AA step (Lankas et al., 2002). Similarly, a solution study of G-tracts by Fourier transform infrared and circular dichroism spectroscopy (Lindqvist and Graslund, 2001) revealed that the base-stacking pattern of a G-tract up to 8 bp long (G₄C₄) is largely affected by the group of bases flanking its 5′ end. Analysis of crystal structures also suggests that the conformations of CG, GC, and GG steps are all strongly context dependent (Packer et al., 2000).

To understand the importance of nearby neighbor influences, one may assume that a basepair step is embedded in an “external field” defined by its sequence environment and that different contexts produce different fields and thus influence the step behavior. The problem is well defined if the field is constant (or slowly changing), acting as an external parameter in the thermodynamic treatment of the system (Landau and Lifshitz, 1980). However, the basepairs in all steps probably move on a comparable timescale, meaning that this field would change as rapidly as the spontaneous conformational fluctuations of the step itself. It is thus more natural to suppose that some coupling between different basepair steps in a sequence exists.

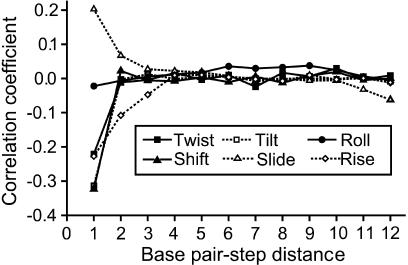
Here we address the problem by investigating possible correlations of motions in different dinucleotide steps of our oligomers. Time series of helicoidal parameters of different steps obtained from the simulations were correlated in a pairwise manner. For example, the time course of twist of a particular step was correlated with twist time courses of all other steps; the same was done for the other parameters. The correlation coefficients, averaged over all equidistant steps in both oligomers, are shown in Fig. 3. The x axis indicates the separation between the steps. The value for “distance 0”, i.e., the correlation coefficient for a step with itself, is by definition 1 and is not shown in the figure. Thus, “distance 1” indicates the correlations of helicoidal parameters in two neighboring basepair steps. Note that this correlation is by far the most important. Shift and tilt are most negatively correlated, twist and rise slightly less. By contrast, slide is the only parameter found to be positively correlated in the neighboring steps. The correlation of roll is very small already between the nearest neighbors. Although the correlations of twist, tilt, and shift almost cease beyond the nearest neighbor, those of slide and especially rise persist at least up to the next-nearest neighbor. We also calculated these data for the two oligomers separately, but the results are very similar.

FIGURE 3.

Correlation coefficients describing pairwise correlations of fluctuations of helicoidal parameters in different basepairs along a sequence. The numbers on the x axis indicate the distance between the basepairs. Thus, the value at x = 0 expresses a correlation of movements of a basepair with itself; it is 1 by definition and is not shown in the figure. The value at x = 1 is a correlation coefficient for the nearest-neighboring basepair steps, x = 2 indicates the next-nearest neighbors, etc. The data are averages over all equidistant steps in both simulated sequences. Note that most of the correlations fade away beyond the nearest neighbor; however, slide and twist persist to a longer distance, and roll is almost uncorrelated.

One could pursue this type of analysis further and compute, for example, the correlations between two different helicoidal parameters in different steps, etc. This is not a purpose of this study, but the present data already indicate that to obtain a more realistic description of DNA properties, one has to take the coupling between different basepair steps into account.

CONCLUSIONS AND PERSPECTIVES

The aim of this work is to describe the free-energy changes upon deforming a basepair step in DNA. Our approach, based on the analysis of helicoidal parameter fluctuations in atomic-resolution molecular dynamics simulations, allows us to construct sequence-dependent deformation potentials for the 10 unique dinucleotide steps. The method, limited to the linear (harmonic) elasticity regime, provides absolute quantities and requires no additional calibration.

Our data exhibit relatively simple trends. The exceptional flexibility of the YR steps has been observed in the case of angular parameters (twist, tilt, roll), although in the case of twist the TA step seems to be somehow stiffer than CG or CA. The stiffness in roll shows a particularly unambiguous behavior, with three distinct groups of steps: the flexible YR, intermediate RR, and stiff RY. Note also that the variance of values for different instances of identical steps in the sequences (indicated by error bars in Fig. 1 c) is particularly narrow. Among the translational parameters, rise shows generally increasing stiffness from YR through RR to RY, whereas no simple dependence has been observed in the case of shift and slide.

However, it should be stressed that a complete description of the basepair step deformability could be achieved only by taking into account the couplings between changes of different parameters. We propose a quantitative criterion to evaluate the relative error in deformation free energy upon neglecting a coupling term. The results suggest that slide-rise, twist-roll, and twist-slide couplings are the most important.

We extensively compared our data with published basepair step deformation potentials deduced from an ensemble of crystal structures (Olson et al., 1998). The crystallographic data generally exhibit more complicated sequence dependence and occasionally larger variations between different dinucleotide steps.

During the final preparation of our manuscript, a closely related experimental study appeared (Okonogi et al., 2002). The authors investigated a set of 50-bp sequences at the submicrosecond timescale using the electron paramagnetic resonance technique and determined sequence-dependent harmonic deformabilities of the 10 unique steps. They assumed the bending potential to be isotropic, i.e., the force constants for roll and tilt are supposed to be the same. Other degrees of freedom were not explicitly taken into account. Although our results cannot be directly compared with these data because of the different number of degrees of freedom, an approximate comparison is possible. We first estimate the isotropic bending constant κ_i of a particular step i by the harmonic average of the corresponding values for tilt and roll, and then establish the “generic” bending constant κ by the harmonic average of κ_i values for the 10 steps. This enables us to calculate the inverse relative bending rigidity r⁻¹ = κ/κ_i, tabulated also in the study of Okonogi and co-workers (Okonogi et al., 2002, Table 6). The general picture emerging from both studies is much the same: the YR steps stand out as the most flexible, followed by intermediate RR and more rigid RY (although the experimental value for AT is close to that for GG). This agreement of two completely different approaches supports the validity of the explicit-solvent molecular dynamics simulations. Our range of values is narrower than in the study of Okonogi et al. (their ratio of highest to lowest bending constant is ∼4, compared to 1.65 in our case). This may be partially caused by the fact that our timescale (20 ns) is shorter than in the experiment (1 μs). On the other hand, the inclusion of more degrees of freedom enables us to suggest a more detailed picture: the YR steps seem to be the most flexible both in roll and tilt, whereas RR and RY steps differ only in roll, their tilt force constants being very similar to each other.

Anselmi et al. (2000, 2002) proposed a set of sequence-dependent deformabilities based on DNA thermal stability data. A comparison with recent quantum-chemical stacking energy calculations demonstrates that the correlation between the thermal stability scale used by Anselmi et al. and the corresponding values of stacking energies from modern calculations is actually rather poor. It is difficult to quantitatively correlate these energies with our results or the x-ray data since the full harmonic basepair step potential comprises 21 force constants and not just one value. However, the general trend suggesting exceptional flexibility of the YR steps is by no means followed by the stacking energy values. Thus, it seems that DNA deformability and possibly also thermal stability cannot be explained as a simple consequence of the sequence-dependent stacking energy differences, and more complex approach will be necessary.

The correlation analysis of simultaneous structural fluctuations in different basepair steps of a fragment reveals a pronounced correlation of DNA motions up to the distance of 2–3 basepair steps. This emphasizes the fact that basepair steps do not behave as isolated units and that nonlocal deformability models would be necessary to more realistically describe the elastic properties of DNA.

Overall, this work once again suggests that modern atomic-resolution molecular dynamics simulations based on reliable force fields are capable to capture not only static features of DNA, but also its dynamic and coarse-grained properties. This experience paves the way to studying other aspects of large-scale behavior of nucleic acids by atomistic simulations.