Effect of Detergents on the Association of the Glycophorin A Transmembrane Helix

Abstract

We have examined the role of the environment on the interactions between transmembrane helices using, as a model system, the dimerization of the glycophorin A transmembrane helix. In this study we have focused on micellar environments and have examined a series of detergents that include a range of alkyl chain lengths, combined with ionic, zwitterionic, and nonionic headgroups. For each we have measured how the apparent equilibrium constant depends on the detergent concentration. In two detergents we also measured the thermal sensitivity of the equilibrium constant, from which we derive the van't Hoff enthalpy and entropy. We show that several simple models are inadequate for explaining our results; however, models that include the effect of detergent concentration on detergent binding are able to account for our measurements. Our analysis suggests that the effects of detergents on helix association are due to a pair of opposing effects: an enthalpic effect, which drives association as the detergent concentration is increased and which is sensitive to the chemical nature of the detergent headgroup, opposed by an entropic effect, which drives peptide dissociation as the detergent concentration is raised. Our results also indicate that the monomer-monomer interface is relatively hydrophilic and that association within detergent micelles is driven by the enthalpy change. The wide variations in glycophorin a dimmer, stability with the detergent used, together with the realization that this results from the balance between two opposing effects, suggests that detergents might be selected that drive association rather than dissociation of peptide dimers.

INTRODUCTION

The folding and association of proteins depend on the precise balance between protein-protein and protein-solvent interactions; for soluble proteins, the hydrophobic effect is of paramount importance (Tanford, 1973). There is no single principle corresponding to the hydrophobic effect by which to describe the interactions between a membrane protein and its various solvents. Different regions of the polypeptide chain contact surface water, the lipid headgroups, and the hydrophobic acyl chains of the membrane (White et al., 2001; de Planque et al., 2002; Glover et al., 2002). For the hydrophobic parts of membrane proteins, which often traverse the membrane as α-helices, it is the balance between protein-protein and protein-lipid interactions that are important. Thus membrane protein folding and stability depend on a complex series of interactions with a spatially heterogeneous solvent. It is this complexity coupled with solubility requirements that limits studies of membrane protein folding, stability, and structure in vitro (Booth et al., 2001; Rosenbusch, 2001).

These numerous challenges posed for the study of integral membrane proteins are, however, being met, yielding new insight into specific amino acid sequences that are important for the folding, structure, and function of membrane proteins (Dawson et al., 2002; Fleming and Engelman, 2001; Senes et al., 2000; Popot and Engelman, 2000). Several novel classes of membrane protein structures have been solved, in which new kinds of interactions between transmembrane helices have been observed (Fu et al., 2000; Sui et al., 2001; Chang and Roth, 2001; Locher et al., 2002). These studies have highlighted the importance of small amino acids in mediating tight interactions between helices (Fu et al., 2000; Sui et al., 2001; Eilers et al., 2000). The high-resolution structures also describe several well-ordered lipids bound to the protein surfaces through bridging waters, as well as electrostatic, hydrogen bonding, and van der Waals interactions (Luecke et al., 1999; McAuley et al., 1999). For example, it appears that the bacteriorhodopsin lattice in purple membrane involves approximately as much protein-lipid surface area as it does protein-protein surface area (Luecke et al., 1999). It has long been known that specific lipids can affect protein stability and function. Successful cocrystallization experiments, such as these, reveal in atomic detail the ways that lipids can serve a structural role and thus modify protein function or mediate assembly into large arrays.

In striking contrast to our growing knowledge of integral membrane protein sequences and structures, our current understanding of a thermodynamic basis for their structure and stability remains rudimentary. Two principles of fluid lipid membranes have been proposed to be of particular importance: the hydrophobic mismatch (de Planque et al., 2002; Mouritsen and Bloom, 1993), and headgroup interactions (Killian and von Heijne, 2000). The first refers to the extent to which the hydrophobic region of a membrane protein matches the thickness of the membrane in which it resides. The second refers to the interactions of lipid headgroups with each other and with specific side chains. Though both of these aspects have been suggested to be important, there is little quantitative experimental information on their role. Our limited information on protein-lipid interactions hampers any comprehension of the fine balance of forces that modulate the interactions between transmembrane helices. It is therefore important to examine this type of interaction to understand the balance of forces that drives the associations between transmembrane helices in membrane proteins, and thus determines their structure, stability, and activity.

It has long been necessary to empirically screen detergents and lipids to find conditions that preserve activity and allow crystallization (Rosenbusch, 2001). Indeed, the ability of lipids to modulate protein quaternary structure was dramatically illustrated recently when bacteriorhodopsin was crystallized from mixed long-chain/short-chain lipids that can form bilayer disks known as bicelles. In contrast to previous methods (Grigorieff et al., 1996; Pebay-Peyroula et al., 1997), which crystallized bacteriorhodopsin trimers, this new approach yielded bacteriorhodopsin to be crystallized as a monomer (Faham and Bowie, 2002). We do not yet have sufficient information to understand which lipid properties are most important for stabilizing the bacteriorhodopsin monomer, and determining the crystallization form. The possibilities including bicelle thickness, loss of the phytanoyl chain that packs alongside helix D, and headgroup interactions.

For many years, the dimerization of the glycophorin A (GpA) transmembrane helix has been used as an example of transmembrane helix association (Bormann et al., 1989; Lemmon et al., 1992a,b; Langosch et al., 1996; Fleming et al., 1997; Russ and Engelman, 1999). On the basis of site-directed mutation analysis, the sodium dodecyl sulfate (SDS) stable dimerization was found to be strongly dependent on a seven-residue motif (LIxxGVxxGVxxT) (Lemmon et al., 1992a,b). This sequence motif was used as the basis for predicting the dimer structure from molecular dynamics calculations (Treutlein et al., 1992), a structure that has been largely confirmed by solution NMR (MacKenzie et al., 1997). The knowledge of the structure and a wealth of information on the sequence requirements for the observation of dimers in SDS gels have made this system ideal for more detailed examinations of transmembrane helix interactions. More detailed examination of the sequence dependence using either quantitative SDS PAGE analysis (Mingarro et al., 1996) or a genetic reporter system (Brosig and Langosch, 1998) has called into question the sequence specificity of this interface and the precise role of the sequence in driving assembly. Many substitutions in the dimerization motif appear to be allowed and not to completely prevent dimerization (Lemmon et al., 1992b; Mingarro et al., 1996; Brosig and Langosch, 1998, Mingarro et al., 1997). Interestingly, this approach has also shown the importance of sequences adjacent to the transmembrane region in permitting dimerization in SDS micelles (Orzaez et al., 2000).

Various developments have been made to try and quantify the monomer-dimer equilibrium. Russ and Engelman have developed a genetic approach based on the ToxR transcriptional activator (Russ and Engelman, 1999). This system seems to provide reasonable relative levels of association and is well adapted to genetic screening, though it is difficult to quantify the degree of interaction and not yet possible to determine the oligomeric state. In addition, three biophysical approaches have been developed to measure transmembrane helix association. Analytical ultracentrifugation in the neutrally buoyant detergent octyl-pentaoxyethylene (C8E5) has been used to determine the relative effect of sequence perturbations on GpA association (Fleming et al., 1997, Fleming and Engelman, 2001). These studies were unfortunately slightly hampered by the presence of tetramers, and due to the necessity of using a particular detergent, are ill-adapted to systematically investigating the effects of environment. Small angle x-ray scattering measurements have been performed in dodecyl-dimethyl-aminobenzoate and β-octyl glucoside using sucrose to match the buffer and detergent micelle electron density (Bu and Engelman, 1999). These measurements allowed the determination of a dissociation constant for a GpA transmembrane helix mutant. Although such measurements are reasonably well adapted to investigations of environmental effects, the range of dissociation constants accessible is relatively restricted due to the need for relatively high concentrations of material.

We have developed a fluorescence resonance energy transfer (FRET) method well adapted for investigating the effects of environment on the dissociation constant of the GpA transmembrane helix (Fisher et al., 1999). This assay uses synthetically labeled peptides and measures the sensitized fluorescence of the acceptor (a coumarin derivative) by the donor (pyrene). Our approach allows studies over a wide range of peptide concentrations and thus the determination of dissociation constants between micromolar and picomolar. Furthermore the use of a fluorescence method permits studies in a wide range of different environments, allowing extensive variation of the solvent composition. Notably, for the study reported here, the range includes diverse detergents at a wide range of concentrations and temperatures. In our previous study, we showed that the detergent dramatically influences the kinetics and thermodynamics of GpA helix association without altering the secondary structure. Thus direct thermodynamic comparison of GpA equilibrium constants in different detergents is justified since the thermodynamics of helix association appears to be uncoupled from the secondary structure formation, as supposed by the two-stage model (Popot and Engelman, 1990, 2000). It should be remembered, however, that the method does depend on the presence of an extrinsic probe, the fluorophore. This study builds on our previous work, and our measurements are examined in an effort to produce a robust thermodynamic model for helix-helix interactions in detergent solutions and to further our understanding of the role of the hydrophobic environment in such interactions.

MATERIALS AND METHODS

Peptides corresponding to the sequence of the human glycophorin A transmembrane domain (residues 69–101) were synthesized and purified as described. The peptides were labeled with a donor (pyrene) or with an acceptor 7-(N,N-dimethylamino)-coumarin at the amino terminus (Fisher et al., 1999; Fisher and Engelman, 2001). The identity and purity of the peptides were confirmed by mass spectroscopy, amino acid analysis, and HPLC. Lyophilized peptides were reconstituted in 25 mM Na phosphate buffer pH 7.4, 0.2 M NaCl, with the appropriate detergent at the specified concentrations.

Detergents and amphiphiles were of the highest available quality: C₁₂Sulfate Na salt (Sigma, St. Louis, MO), C₁₂DAO and other alkyl-dimethyl-amine-N-oxides (Fluka, Buchs, Switzerland), C₁₂DMAB (Boehringer Mannheim, Meylan, France), and C₁₀ and C₁₂ Maltosides (Calbiochem, LaJolla, CA). Where necessary, contaminants that absorb in the 250–400 nm spectral range were removed by recrystallization. Stock detergent solutions were prepared gravimetrically from desiccated detergents and dissolved in phosphate NaCl buffer and aliquoted before storage at −20°C. All measurements, including the critical micelle concentration (CMC) determinations, were made using the same stock solutions. Final detergent concentrations were calculated volumetrically—estimates of the precision of the dilutions using infrared absorption spectroscopy suggest that these are between 1% and 2%.

The CMC of each detergent was measured by ANS fluorescence (de Vendittis et al., 1981). A solution of 2–5 μM ANS in the buffer for dimerization measurements was titrated with detergent and the fluorescence intensity was measured (380 nm excitation, 490 nm emission). A graph of the fluorescence intensity as a function of detergent concentration exhibits a discontinuity at the detergent concentration where micelles form, corresponding to the CMC (data not shown). The measured CMCs are given in Table 1.

TABLE 1.

Summary of the sensitivity of the GpA association to several detergents

Detergent	CMC (mM)	Nagg	ΔG° 1 M detergent (kJ mol−1)	dΔG°/dLog([Det]micellar) (kJ mol−1)	Detergent released
C12Sulfate	1.0	81	23.99 ± 0.73	−3.52 ± 0.31	48
C12DMAB	4.5	47	15.80 ± 0.46	−3.59 ± 0.22	29
C12Maltoside	0.2	85	31.51 ± 0.57	−3.72 ± 0.27	55
C10Maltoside	1.5	69	27.54 ± 0.74	−7.54 ± 0.44	91
C12DAO	1.1	76	24.86 ± 0.31	−6.94 ± 0.18	92
C11DAO	7.1		15.52 ± 0.50	−6.50 ± 0.27
C10DAO	14.5		17.13 ± 1.04	−5.05 ± 0.55

For each of the detergents examined, the CMC was measured experimentally by ANS fluorescence, as described in Materials and Methods. The values of ΔG° at 1M detergent and its sensitivity to the detergent concentration were estimated by nonlinear fitting to the original FRET data, as in Fig. 1 C. The aggregation numbers were obtained from Anatrace literature (www.anatrace.com) except for C₁₂DMAB (Chevalier et al., 1996). The amount of released detergent obtained using the protein detergent complex model (Josse et al., 2002) described in the text were obtained from the detergent sensitivities of apparent ΔG° and the detergent aggregation numbers (Detergent released = (N_agg dΔG°/dLog([Det]_mic))/−5.74).

All fluorescence spectra were recorded on a Fluorolog 3-21 photon counting spectrofluorimeter (Spex, Longjumeau, France) equipped with a 450W xenon source, an additive double excitation monochromator, a single emission monochromator, and a cooled photomultiplier.

FRET between pyrene- and coumarin-labeled GpA peptides was measured as previously described (Fisher et al., 1999). Briefly, the assay was developed to provide a sensitive measure of transmembrane peptide association that is relatively insensitive to the details of the peptide-detergent complex. Fluorescence excitation spectra were recorded and corrected for the direct emission of the fluorophores. The relative contribution of pyrene and coumarin to the fluorescence emission at 500 nm was calculated, and it is this ratio that provides a sensitive measure of the degree of dimerization in diverse environments. The signal can readily be measured at peptide concentrations ranging from micromolar to several picomolar. The dissociation constant was determined from the dependence of the FRET signal on the peptide concentration. In each titration, the detergent concentration remained constant. The use of an entire titration curve allowed us to observe any departure from a simple dimerization reaction, and in particular to avoid conditions in which higher order oligomers form.

The experimental protocol allows the accurate measurement of pyrene-coumarin energy transfer, and a measurement precision of ∼2% in the pyrene/coumarin intensity ratio is typical. For dissociation constants in the nanomolar range, precision is limited by dilution and measurement errors to ±5%; this precision falls for dissociation constants outside this range due to the difficulty of observing the entire titration curve, and the dissociation constant precision can be estimated at ∼±15% for values of 10 pM or 100 μM. The largest errors in our analysis are probably associated with the determination of the CMC where the errors are ∼±10%. This error effectively limits the utility of measurements at detergent concentrations close to the CMC, especially for detergents with a high CMC. It should be noted that we have not taken into account the modification of the free detergent concentration due to peptide binding. This simplification we justify for two reasons: first the peptide concentrations are in the nanomolar range, whereas the detergent concentrations are in the millimolar range; and second, no dependence of the dissociation constant on peptide concentration was observed.

Determination of dissociation constants, extraction of model parameters, and nonlinear least-squares fitting were performed using the solver integrated in Excel (Microsoft, Redmond, WA). In each case, spreadsheets were set up to calculate the root mean-square error between the observed values and those predicted by the model, and this difference was minimized by adjusting the model parameters.

RESULTS

In our previous work, we observed that both the kinetics and thermodynamics of the GpA equilibrium were dramatically affected by the detergent in which the peptides were dissolved (Fisher et al., 1999). In contrast, the secondary structure of the GpA transmembrane domain was insensitive to the details of the detergent as well as to changes in the oligomeric state. Thus the observed GpA equilibrium corresponds to a change in quaternary structure that includes peptide-peptide interactions as well as peptide-detergent interactions, without coupling to changes in helical content. Here we examine more closely the effects of detergent concentration and the nature of the detergent on the apparent GpA dissociation constant using the FRET technique developed previously. A series of seven detergents were chosen to offer a range of alkyl chain lengths, as well as ionic, zwitterionic, and nonionic headgroups. In addition, the surface activity of the series, as reflected in the critical micelle concentration, spans two orders of magnitude. More practically, since the ultraviolet absorption of detergent impurities determines the lower limit at which measurements can be made, the detergents were selected because they were commercially available in analytical grade.

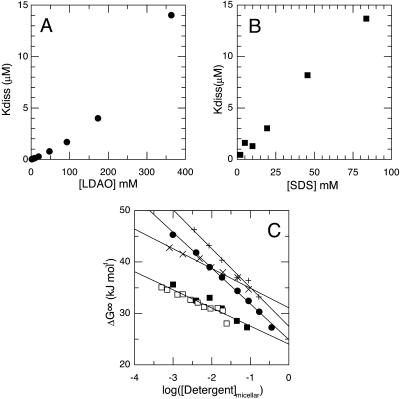
To gain insight into the thermodynamic effects of different detergents, the effect of detergent concentration on the monomer-dimer equilibrium was measured over a wide range of detergent concentrations. In Fig. 1, A and B, we show the effect of varying the detergent concentration of two of the detergents chosen, SDS (C₁₂Sulfate) and dodecylamine-N,N-dimethyl-N-oxide (C₁₂DAO), on the observed dimer dissociation constant. As expected, we find that the peptide dimer is much less stable in C₁₂Sulfate than in C₁₂DAO. Interestingly, as can be appreciated from the figures, the two detergents behave in qualitatively different ways. Whereas the C₁₂Sulfate data give a slightly concave series of points, with successive increases in detergent concentration having diminishing effects, the C₁₂DAO data give a convex set of points with successive increases in concentration having augmenting effects. This observation is very surprising and illustrates that there are very large differences in how specific detergents affect transmembrane helix association. The other detergents showed behaviors qualitatively similar to C₁₂Sulfate or C₁₂DAO.

FIGURE 1.

Effect of detergent concentration on the GpA equilibrium in detergent micelles. A and B shows the effect of the detergent concentration on the apparent GpA dimer dissociation constant. Results with two representative detergents are shown: C₁₂DAO (A) and C₁₂Sulfate (B). C shows the typical quasilinear relationships obtained for plots of apparent dissociation free energy (ΔG°) as a function of the logarithm of the micellar detergent concentration. The micellar detergent concentration is calculated by subtracting the CMC from the total detergent concentration. Data for four typical detergents are shown: C₁₂Sulfate (▪), C₁₂DAO (•), C₁₀Maltoside (+), and C₁₂Maltoside (×). Two sets of data obtained with different lots of C₁₂Sulfate are shown as solid and open symbols. The points represent best-fit values obtained by nonlinear fitting of the FRET titration data at each detergent concentration. The lines represent best fit values obtained by fitting the complete set of FRET titration data in a given detergent. The measured CMC of each detergent studied is listed in Table 1.

Despite the qualitatively different behavior of the detergents investigated over a wide range of detergent concentrations, their behavior at concentrations close to the CMC was very similar. The reconstituted peptide-detergent solutions were diluted with detergent or buffer such that the final detergent concentration was either above or below the CMC (listed in Table 1). For all seven detergents, dilution with buffer containing detergent above the CMC decreased peptide association, whereas dilution with buffer containing detergent below the CMC increased the extent of peptide association (data not shown). Furthermore, as the detergent concentration approached the CMC, there was often evidence for peptide association into higher-order oligomers. Such evidence includes increased cooperativity of the titration curves, a substantial increase in pyrene-sensitized emission, and occasionally an apparent reduction in coumarin absorption. These observations suggest that when the detergent concentration was close to the CMC, there was sufficient detergent to prevent precipitation of the peptides but insufficient detergent to fully dissolve them.

For each of the detergents examined, the extent of the micellar phase can be estimated by accounting for variations in the solubility of the detergent monomers, which is reflected in the CMC. In Fig. 1 C, the apparent dissociation free energy is plotted as a function of the increasing detergent concentration in the micellar phase. In all cases, the log-log representation shows an approximately linear relationship between the standard dissociation free energy and the logarithm of the estimated micellar detergent concentration. It should be noted that for several detergents, there are significant deviations from a linear relationship in the log-log plots, for example C₁₂DAO and C₁₂Maltoside in Fig. 1 C.

The details of the different quasilinear relationships found for the seven detergents that we investigated are shown in Table 1. Our results show some surprising trends, for example a number of detergents have slopes much greater than C₁₂Sulfate and thus, by extrapolation, at very high concentration would be more effective than C₁₂Sulfate at dissociating the GpA dimer. It is also clear that the effects of aliphatic chain length are complex. Whereas for the N,N-dimethyl-N-oxides (C₁₂DAO, C₁₁DAO, and C₁₀DAO—see Table 1) decreasing chain length decreases the slope, for the alkyl-maltosides (C₁₂Maltoside and C₁₀Maltoside) decreasing the chain length increases the slope. Equally there is no obvious relationship between the detergent CMC and the detergent sensitivity of the GpA dimerization.

The simplest explanation for the effect of detergent concentration on the dissociation constant would be that raising the detergent concentration simply dilutes the peptides in a micellar phase and so drives dissociation entropically. This simple model predicts a slope of −5.71 kJ mol⁻¹ (2.303 × 8.314 J mol⁻¹ K⁻¹ × 298 K) for the linear relationship between the apparent standard free energy of dissociation and the logarithm of the micellar detergent concentration. In contrast with this prediction, the results in Table 1 show slopes varying between −3.52 kJ mol⁻¹ and −7.54 kJ mol⁻¹, suggesting that a more complex model is necessary.

Recently two other models have been discussed to account for the observed dependence of the apparent equilibrium constant of association in detergent solutions on the detergent concentration and to explain deviations from the expected slope of –5.71 kJ mol⁻¹ (Fleming, 2002; Josse et al., 2002).

In the second simple model proposed by Fleming (2002), association is considered essentially in the context of the simple two-phase model above, and the reduced slope that we had previously observed in SDS (Fisher et al., 1999) is attributed to an activity coefficient less than unity. Unfortunately, this view is unable to explain the slopes more negative than −5.71 kJ mol⁻¹ that we observe. In the model of Josse et al. (2002), derived from Wyman's treatment of ligand binding (Wyman, 1964), release of detergent monomers during association results in the creation of a certain number of additional micelles, and that there is no reason that a single micelle should be formed and thus the slope need not be −5.71 kJ mol⁻¹ but that any slope is possible. In agreement with this model, we observe approximately linear relationships between the apparent free-energy change and the logarithm of detergent concentration. In Table 1, we list the predicted number of detergent molecules released based on the observed slopes and published aggregation numbers. As can be appreciated, in the context of this model, the number of released detergent molecules varies greatly from detergent to detergent (a factor of 3 between C₁₂DMAB and C₁₂DAO), which would appear hard to reconcile with structural considerations. In the simple case considered by Josse et al. (2002) with fixed detergent binding the model is again entirely entropic. However, in the more general case of ligand binding polynomials considered by Wyman (1964), entropic and enthalpic contributions are to be expected.

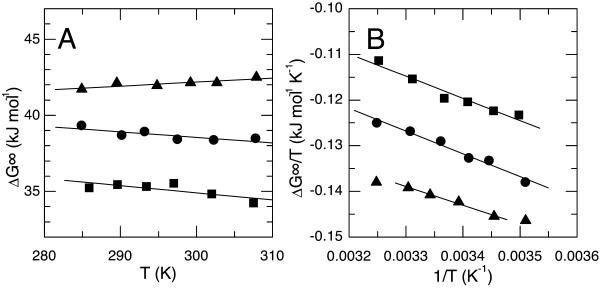
Detailed thermodynamic measurements of soluble proteins have established that the free energy of a protein folding reaction typically results from opposing enthalpic and entropic terms. To better understand how the detergent modulates GpA dissociation, we investigated the entropic and enthalpic contributions to the apparent free energy. In two detergents, C₁₂DAO and C₁₂Sulfate, we measured the temperature sensitivity of the dissociation constant at detergent concentrations spanning two orders of magnitude. Shown in Fig. 2, A and B, are the van't Hoff plots used to determine the standard enthalpy and entropy changes at three C₁₂DAO concentrations. The results for C₁₂Sulfate were essentially as we have previously published (Fisher et al., 1999). As in C₁₂Sulfate, the van't Hoff plots in C₁₂DAO are approximately linear, indicating little if any change in the heat capacity (C_P = dΔH/dT). It is also gratifying to note that in all cases, the apparent enthalpy and entropy changes obtained from van't Hoff plots give the observed apparent free-energy change (ΔG° = ΔH° − TΔS°), suggesting that our treatment of the process as a monomer-dimer equilibrium is justified.

FIGURE 2.

Effect of temperature on the thermodynamics of GpA dimerization. A and B show van't Hoff plots at three different detergent concentrations spanning two orders of magnitude: 2 mM (▴) 20 mM (•), and 91 mM (▪). The data illustrated were obtained with the detergent C₁₂DAO. At each detergent concentration, the slopes obtained from these graphs were used to determine the standard enthalpy (ΔH°) and entropy (ΔS°) changes of dissociation.

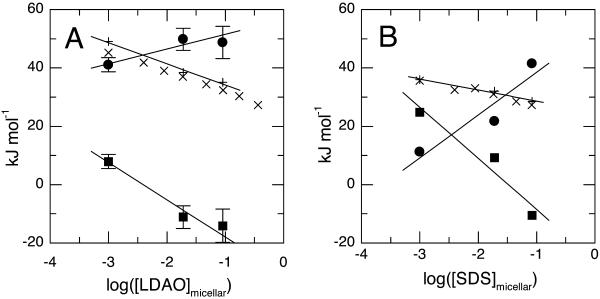
The free energy, enthalpic, and entropic terms are plotted in Fig. 3, A (C₁₂DAO) and B (C₁₂Sulfate), as a function of the logarithm of the micellar detergent concentration. It is clear that the three thermodynamic parameters, ΔG°, ΔH°, and ΔS°, behave differently with changing detergent concentration. Thus for C₁₂DAO at low detergent concentrations, both enthalpy and entropy drive association. As the detergent concentration rises, the enthalpy changes become slowly more favorable for association while the entropy change rapidly starts to drive dissociation (−TΔS becomes negative). The results obtained for C₁₂Sulfate (Fig. 3 B) are qualitatively similar to those just described, though the detergent concentration dependencies of the enthalpy and entropy are more marked but also more nearly cancel each other. These values are tabulated in Table 2.

FIGURE 3.

Effect of detergent concentration on thermodynamic parameters for dimerization. Data are shown for two detergents: C₁₂DAO (A) and C₁₂Sulfate (B). In each panel, circles represent standard enthalpy changes (ΔH°); squares, the contribution of the standard entropy changes to the standard free energy change (−TΔS°) at 25°C, and crosses (+) standard free energy changes (ΔG°) calculated as ΔH°−TΔS°. The second group of crosses (×) show the standard free energy changes calculated from the observed equilibrium constants at 25°C.

TABLE 2.

Detergent concentration sensitivity of different thermodynamic parameters

Detergent	dΔG° (kJ mol−1) dLog([Detergent]micellar)	dΔH° (kJ mol−1) dLog([Detergent]micellar)	−dTΔS° (kJ mol−1) dLog([Detergent]micellar)
C12Sulfate	−3.79 ± 0.57	13.7 ± 4.0	−17.5 ± 4.5
C12DAO	−7.27 ± 0.86	5.1 ± 1.8	−12.8 ± 2.2
Simple model	−5.74	0.0	−5.74

The sensitivity of the various parameters to the logarithm of the micellar detergent concentration was determined from the slopes of the different lines shown in Fig. 3. The simple model, described in the text, represents the values expected for a detergent that is able to form an ideal solution dissolving the peptide monomers and dimers entirely and exclusively in the micellar phase; this is fixed as –5.74 kJ mol and entirely entropic.

Importantly the observed effects of detergent concentration show that both the entropy and enthalpy of dissociation are sensitive to this parameter and that the resulting dependence of free energy on detergent concentration derives from the balance between opposing effects on enthalpy and entropy. Furthermore, the entropic effects are much larger than can be accounted for by the simplest model introduced above of peptide dilution in a hydrophobic phase (Table 2). It thus seems that none of the simple models introduced above are able to explain the effects of detergent concentration that we observe, either qualitatively or quantitatively.

DISCUSSION

Our experimental results provide evidence for diverse behavior of a peptide monomer-dimer equilibrium in a variety of different detergents. The observed free energy of dimerization, in all the examined cases, depends strongly on the micellar detergent concentration. However, whereas in some detergents such as C₁₂Sulfate there is a saturation phenomenon, as we had initially suspected in our earlier article, in several other detergents the dissociation is catastrophic with successive detergent additions having progressively larger effects. Closer examination of these effects in terms of enthalpy and entropy changes for two specific detergents (C₁₂Sulfate and C₁₂DAO) shows that the observed effects of detergent concentration on free energy are the result of opposing effects of the detergent concentration on the enthalpy and entropy of dissociation. The dissection of the effects of varying detergent concentration in terms of headgroup chemistry and alkyl-chain length are far from obvious. Chain length variations have effects that depend on headgroup chemistry, and there is little obvious coherence between the quantitative effects of detergent concentration on peptide dimerization and detergent chemistry.

The observation that different detergents can show different dependencies of dissociation free energy on the logarithm of micellar detergent concentration, coupled with the observation that this dependency results from a balance of enthalpic and entropic effects, suggests that detergents might be selected in which the dissociation is independent of detergent concentration or even that adding detergent could drive association rather than dissociation. Understanding the molecular origins of the competing enthalpic and entropic effects may help us find or define such detergents that would potentially be extremely useful for membrane protein purification and crystallization. It is necessary to explain the different phenomena we describe to better understand the effects of detergent concentration and understand the interactions between polypeptides and amphiphiles.

As we commented above, the simple models that have been proposed in the literature are unable to explain this balance between enthalpic and entropic effects. Indeed, to explain the presence of enthalpic effects, the detergent must play a more active role than a simple diluent. To analyze these effects in the complex peptide-detergent-water system, two different approaches can be adopted. First, the detergent and peptides can be considered as cosolutes in an aqueous solvent, or alternatively the peptides can be considered as solutes in a binary detergent-water solvent.

The first approach follows the development of Josse et al. (2002) based on the insights of Wyman (1964) as to the effects of ligands on linked equilibria. Unfortunately this development is rather difficult since ΔN (the number of detergent molecules released on dimerization) and N_agg (the aggregation number of the detergent) are not constant. For example, in the case of SDS it is known that the aggregation number varies considerably with detergent concentration following an [SDS]^0.25 power law (Quina et al., 1995). Thus, over the range of concentrations we have studied, it is unreasonable to consider N_agg as constant and so equate the detergent activity with the micellar concentration calculated as ([Detergent] − CMC)/N_agg. It is equally reasonable to suppose that ΔN changes, the observed quasilinear relationships observed both by us and Josse et al. (2002) thus reflects a balance between three separate and variable factors: the detergent aggregation number, the number of detergent molecules bound to monomers, and the number bound to dimers. These three factors all vary with detergent concentration in a poorly parametrized manner.

The second approach considers that the observed behavior results from the product of the dimerization in the absence of solvent and the differences in solvation of the monomers and dimers. Furthermore, the solvation being a property of the molecular surface, the difference in solvation of monomers and dimers is equivalent to the solvation of the interfacial region in the monomers, which becomes buried in the peptide dimers. The difficulty with this approach is that the solvent is a complex mixture of detergent and water; thus detailed analysis requires understanding of the solvent structure and solvation of hydrophobic peptides by detergents. This understanding is not currently available, though the first results of molecular dynamic calculations are becoming available (Bond and Sansom, 2003). Nevertheless some interesting insights can be obtained from this analysis even in the absence of a molecular understanding of the solvation, since the observed changes resulting from either alterations in the detergent chemistry or concentration can be attributed to changing interactions of the solvent with the interface region of the peptides.

The increasingly unfavorable enthalpy of dissociation at higher detergent concentrations implies that detergent binding to the interface is increasingly endothermic. The endothermic nature of the detergent-interface interactions would appear to suggest that solvent-peptide interactions are not particularly favorable and thus that the interface region is relatively hydrophilic, preferring to interact with a solvent poor in detergent rather than one rich in detergent. Furthermore, this effect appears to be particularly sensitive to the nature of the detergent headgroup. This sensitivity of the enthalpy to headgroup chemistry is indeed expected since specific enthalpic hydrogen bonding and ionic interactions are dependent on this part of the detergent molecules. Indeed, in the simulations of Bond and Sansom (2003), numerous H-bonds are observed between the detergent headgroups and the solubilized protein, though the effect of detergent concentration on these remains unknown.

All the models discussed consider that the hydrophobic volume available to dissolve the peptides is an important entropic parameter. For the two detergents examined in detail, the sensitivity of the entropy of dissociation to detergent concentration is even greater than anticipated. This might suggest that this entropic contribution is not entirely associated with the hydrophobic volume, but that more specific entropic effects are also involved. Despite this, we do observe that the sensitivity of the entropy to detergent concentration appears to be rather insensitive to the nature of the detergent headgroup.

Thus a picture emerges for the detergent sensitivity of the monomer dimer equilibrium resulting from two opposing effects: first; an entropic effect that is strongly dissociative, sensitive to detergent concentration, and relatively insensitive to headgroup chemistry. This is counterbalanced by a second associative enthalpic effect modulated both by headgroup chemistry and detergent concentration. It is, however, unclear from our data how alkyl chain length plays on these parameters. The image of two opposing effects modulated differently by detergent chemistry and concentration suggests that it might be possible to define detergents able to drive association of transmembrane helices rather than dissociation.

If an approach considering a complex detergent-water solvent does allow some conclusions to be drawn for the different detergent sensitivities, the same cannot be said for the absolute values of the apparent dimerization energy as a function of detergent chemistry. This is because it is impossible to define a “sensible” reference state for such a complex solvent where we can measure dimerization or to which we can reasonably extrapolate energies. Defining such a reference state depends on a better understanding of the chemistry behind peptide solvation by detergents.

Lillian E. Fisher's present address is Cellular Biophysics and Biochemistry Program, Memorial Sloan Kettering Cancer Center, 1275 York Ave., Box 251, New York, NY 10021 USA.