Pathway Shifts and Thermal Softening in Temperature-Coupled Forced Unfolding of Spectrin Domains

Abstract

Pathways of unfolding a protein depend in principle on the perturbation—whether it is temperature, denaturant, or even forced extension. Widely-shared, helical-bundle spectrin repeats are known to melt at temperatures as low as 40–45°C and are also known to unfold via multiple pathways as single molecules in atomic force microscopy. Given the varied roles of spectrin family proteins in cell deformability, we sought to determine the coupled effects of temperature on forced unfolding. Bimodal distributions of unfolding intervals are seen at all temperatures for the four-repeat β_1–4 spectrin—an α-actinin homolog. The major unfolding length corresponds to unfolding of a single repeat, and a minor peak at twice the length corresponds to tandem repeats. Increasing temperature shows fewer tandem events but has no effect on unfolding intervals. As T approaches T_m, however, mean unfolding forces in atomic force microscopy also decrease; and circular dichroism studies demonstrate a nearly proportional decrease of helical content in solution. The results imply a thermal softening of a helical linker between repeats which otherwise propagates a helix-to-coil transition to adjacent repeats. In sum, structural changes with temperature correlate with both single-molecule unfolding forces and shifts in unfolding pathways.

INTRODUCTION

Forced unfolding has been demonstrated in vitro for a wide range of multidomain cytoskeletal proteins (Rief et al., 1997, 1999; Furuike et al., 2001) and adhesion proteins (Oberhauser et al., 1998, 2000; Carl et al., 2001). Such unfolding increasingly explains cell-scale phenomena ranging from stress-facilitated attachment (Krammer et al., 2002) to viscoelasticity (Minajeva et al., 2001; Lee and Discher, 2001). Extensible unfolding of single proteins by atomic force microscopy (AFM) was initially reported to yield similar kinetic parameters to solution unfolding by denaturants (Carrion-Vazquez et al., 1999), but subsequent mutagenesis studies established different pathways, hence different kinetics (Fowler et al., 2002). Distinct pathways versus thermal unfolding have also been simulated by implicit-solvent molecular dynamics (Paci and Karplus, 2000): α-helical proteins such as spectrin show helical fraying and fragmented unfolding at high temperature in contrast to forced stretching where helix unwinding is described as cooperative in its propagation. A major qualification on such simulation predictions is that they lack any collective hydrodynamics and are performed at rates, and therefore forces, that are orders-of-magnitude greater than experimental rates of heating or extension (Evans, 2001).

How forced unfolding is influenced by temperature, especially as the transition temperature of a protein is approached, is the focus of the AFM studies here on β-spectrin. We show that cooperativity indeed decreases with temperature as pathways of unfolding shift for the first four i.e., β1–4, (of 17) tandem repeats studied here. We also show that unfolding forces decrease in almost direct proportion to loss of helix in the folded state of each three-helix repeat at a given temperature. Similar temperature studies of DNA stretching have already shown that the force needed to alter interstrand interactions and drive a transition from B-DNA to S-DNA (S for stretched) decreases nonlinearly with temperature (Clausen-Schaumann et al., 2000; Williams et al., 2001). Moreover, the transition force F is most simply approximated by the known temperature-dependent basepairing ΔG(T) divided by the molecular-scale gain in length per basepair (x = 0.24 nm) during the DNA transition, i.e., F(T) ≈ ΔG(T)/x. Whether simple relations between rupture forces and energy increments also apply to forced unfolding of a protein domain is one motivation for the work here.

Among protein, spectrin is highly suited for temperature studies because its three-helix repeats display relatively low and accessible (by AFM) midtransition or “melting” (MacDonald and Pozharski, 2001) temperatures, T_m. With intact erythrocyte spectrin composed of both α- and β- chains, transitions have been reported at temperatures close to 40°C (Minetti et al., 1986; Grimaldi et al., 1989), whereas the T_m of various short constructs of α-spectrin have been reported to be near 50°C (DeSilva et al., 1997; Menhart et al., 1996; MacDonald and Pozharski, 2001). Melting is thus close to 37°C and therefore potentially relevant to spectrin pathophysiology (Zhang et al., 2001).

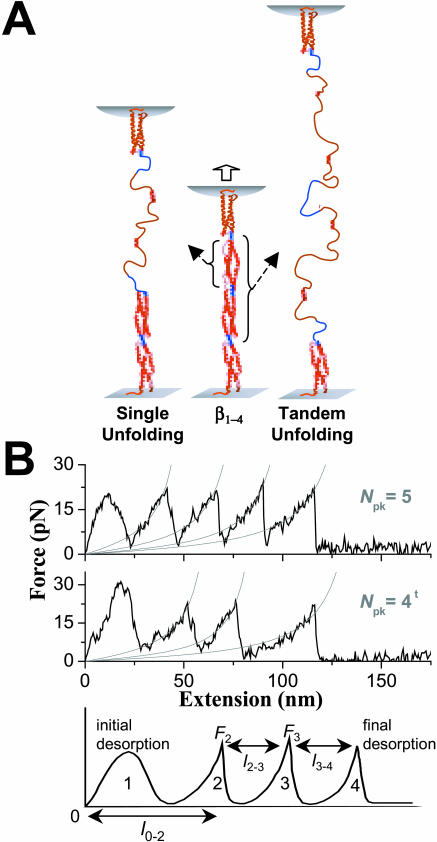
Forced extension of various native spectrin family proteins off various substrates has already shown that the characteristic three-helix repeats can unfold independently and at much lower forces compared to most β-sheet proteins studied at similar extension rates (Rief et al., 1999). Tandem repeat unfolding (Fig. 1 A) occurs frequently with the four-repeat erythroid β-spectrin construct here as well as with β1–3 and β1–2 truncations (Law et al., 2003). Perhaps surprising, these tandem repeat unfolding events occur at the same level of average force as the single repeat unfolding events. Partial unfolding events shorter than a single repeat have also been reported to occur with a flexibly linked concatemer of a chicken brain α-spectrin repeat (Lenne et al., 2000; Altmann et al., 2002) upon initial extension—where proximity to the substrate can complicate analyses. Partial unfolding is not seen with the present erythroid β1–4 protein in thorough ensemble-scale studies (Law et al., 2003). Tandem events that do occur with β1–2 spectrin constructs in the latter work have suggested, in particular, that cooperative propagation of tandem unfolding occurs via a helix-to-coil transition through inter-repeat helical linkers. Inter-repeat helices are indeed believed to be present a significant fraction of the time in these β-spectrin constructs due to their high homology (Ursitti et al., 1996) to α-actinin, for which a crystal structure shows four repeats interconnected by three contiguous helical linkers (Ylanne et al., 2001). A helical linker is also seen in crystal structures of a tandem repeat of chicken brain α-spectrin (Grum et al., 1999). However, nuclear magnetic resonance studies of at least one erythroid α-spectrin construct in solution (Park et al., 2000) also offer some evidence that the inter-repeat linker can be disordered. Whereas AFM results for the flexibly linked concatemers of Lenne et al. (2000) reportedly show no evidence of tandem repeat unfolding, a roughly similar proportion of single and tandem unfolding events were reported for β1–4 in Law et al. (2003). This suggests that the linker between repeats is sometimes helical and sometimes unstructured at room temperature.

FIGURE 1.

Forced extension schematic and AFM force spectrograms for β_1–4 spectrin. (A) Unfolding of either single or tandem repeats. Blue linker regions are shown between the four red repeats. (B) Force-extension curves show the number of peaks (N_pk) for both single and tandem unfolding processes. Curves with the latter are characterized by at least one peak-to-peak length that is twice those of single repeat unfolding events, and such curves are denoted with a superscript t on the N_pk. Force peaks after the first are less symmetric and are fit, for simplicity, by the WLC model F(x) = (k_BT/p) [(x/L_C) + 0.25/(1 − x/L_C)² − 0.25] where x is chain extension and L_C is the contour length appropriate to the number of unfolded repeats. The fitted persistence length, p, that characterizes the minimal flexible length of an unfolded domain, averaged 0.5 nm at 23°C, consistent with prior reports (Law et al., 2003; Rief et al., 1999). The last spectrogram illustrates how a four-peak spectrogram is analyzed and how l_0–2 is measured. Force spectrograms with three or more peaks correspond to unfolding, but spectrograms with 0–2 peaks accounted for most of the data.

Helix-to-coil transitions (Cantor and Schimmel, 1980) are known for their sensitivity to small environmental changes such as temperature. Our results here will show that the helical repeats of spectrin become disproportionately easier to unfold as T approaches T_m. Our results will also suggest that the inter-repeat helix in spectrin softens with temperature, shifting pathways of frequent tandem repeat unfolding to predominantly single repeat unfolding processes. More generally, perhaps, temperature-coupled forced unfolding is expected to offer new opportunities for probing key protein folding interactions such as hydrogen bonding and hydrophobicity.

MATERIALS AND METHODS

Protein preparation

The four N-terminal repeats of the 17-repeat erythroid βI-spectrin (β1–4; Table 1), which encompasses residues 293–743, were expressed recombinantly as described previously (Ursitti et al., 1996). Stable monomer was purified by gel permeation chromatography in phosphate-buffered saline (PBS) and kept on ice for AFM studies. Immediately before use, any protein aggregates were removed by centrifugation at 166,000 g at 2°C for 1 h; and monodispersity was verified by dynamic light scattering.

TABLE 1.

Primary structure properties of spectrin constructs (aa = amino acids)

Domain	Number of aa	Contour, lc (nm)
β1	120	44.3
β2	114	42.1
β3	109	40.2
β4	106	39.1
extra	2	0.7
Total, Lc		166.4
Average		41.6

Domain and total contour lengths, l_c and L_c, respectively, have been calculated with a peptide length of 0.37 nm.

An AFM experiment was begun by adsorbing 100 μl of 0.03–0.1 mg/ml protein for 15 min at room temperature onto either freshly cleaved mica or amino-silanized glass coverslips. The surface was then lightly rinsed with PBS and placed without drying, under the head of the AFM; all measurements were carried out in PBS. Lower protein concentrations generated minimal AFM results; higher protein concentrations showed higher unfolding forces, proving consistent with the results below indicating that domains in multiple, parallel chains are forced to unfold all at once. Fluorescence imaging of labeled protein demonstrated homogeneous adsorption, and AFM imaging after scratching the surface showed no more than a monolayer of molecules covered the substrate (Carl et al., 2001).

Dynamic force spectroscopy

Two AFMs were used with similar results: 1), a Nanoscope IIIa Multimode AFM (Digital Instruments, Santa Barbara, CA) equipped with a liquid cell; and 2), an Epi-Force Probe (Asylum Research, Santa Barbara, CA). Sharpened silicon nitride (Si₃N₄) cantilevers (Park Scientific, Sunnyvale, CA) of nominal spring constant k_C = 10 pN/nm were commonly used, with equivalent results obtained using 30-pN/nm cantilevers. k_C was measured for each cantilever using the manufacturer's directions at each temperature, and additional calibrations were performed as described previously (Carl et al., 2001). Temperatures in the range used seemed to have little effect on the k_C and this was confirmed with the Digital Instruments equipment. Experiments were done at imposed displacement rates of 1 nm/ms. For the high temperature experiments, samples were first studied at 23°C, and the temperature was then raised. These experiments were challenging due to the propensity of the bilayered (gold and silicon nitride) cantilever to bend. The laser had to be realigned each time after raising the temperature to 37 and 42°C, and only the rare cantilever that yielded a high laser sum and low data noise was used. Temperatures >42°C caused the cantilever to bend so much that the laser would not deflect off the tip. Low temperature experiments (10°C) were done inside a cold room. The desired temperatures for both high and low temperature studies were controlled and monitored using the Nanoscope Heater Controller (Digital Instruments). For any one temperature, thousands of surface-to-tip contacts were collected and later analyzed with the aid of a semiautomated, visual analysis program custom-written in C++. Since protein unfolding events are stochastic and the experiment intrinsically random in many ways, collecting and analyzing thousands of peaks is necessary to provide an accurate statistical survey of the unfolding possibilities. Initial results at the beginning of an experiment lasting many hours were similar to those obtained at the end of the experiment. Nearly all of the data was thus analyzed.

Circular dichroism measurements

Circular dichroism spectra were measured at a number of temperatures using a 1-mm pathlength cell on a J715 spectropolarimeter (Jasco, Easton, MD) in the same buffer (PBS, pH 7.4) as that used in AFM experiments. The instrument was calibrated with d-10-camphorsulfonic acid. Samples were equilibrated at each temperature for 20 min before taking measurements.

RESULTS AND DISCUSSION

Accurate descriptions of energy landscapes that govern multiple transition pathways should rely on an unbiased collection and analysis of many single molecule experiments. For all temperatures studied here, a fixed set of 5000 tip-to-surface contacts were made after adsorbing the spectrin construct to the surface, and a small fraction—consistent with one or two molecules (Law et al., 2003)—of tip retractions show clear sawtooth patterns in force (Fig. 1 B). At each temperature, a number of the AFM-imposed extensions also show some sawtooths with peak-to-peak separations that prove longer than most by a factor of ∼2. These correspond to tandem repeat unfolding as events elaborated further below. Regardless, the maximum number of peaks per force-extension curve for this four-repeat spectrin construct is no more than six, as reported earlier for our room temperature studies (Law et al., 2003). Two extra peaks are consistent with our prior conclusions from 2-, 3-, and 4-repeat spectrin constructs that show the first and last peaks reflect surface and tip desorption processes and that each repeat contributes no more than one peak. Partial unfolding of a repeat as a mechanism of force relaxation is thus ruled out here, although two repeats yielding one peak will be clearly shown below and most prominently at low temperature.

The exponentially increasing portions of the asymmetric force-extension curves are fit well by the wormlike chain (WLC) model for entropic elasticity and correspond, as is typical in such experiments, to extension of an unfolded domain up to the point where another (hitherto folded) domain in the chain unfolds. The last spectrogram in Fig. 1 B illustrates how a four-peak spectrogram is analyzed. The first peak and the height of the last peak are ignored in the analyses as desorption events, and peak forces and peak-to-peak (l_pk−pk) lengths were analyzed as illustrated. The total unfolding length is the sum of all the l_pk−pk values, and this sum is found to never exceed the molecule's total contour length (Table 1).

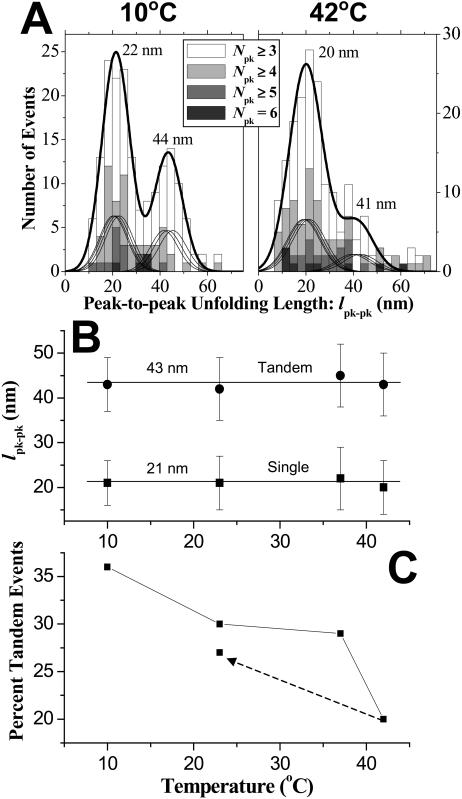
Tandem repeat unfolding events are cumulated in the l_pk−pk histograms of Fig. 2 A for the extremes in temperature studied, 10°C and 42°C. Both histograms appear bimodal with principal means differing by a factor of 2.0 (within 5%) per earlier measurements at 23°C (Law et al., 2003). The major peaks in the distributions are fit with sums of Gaussians that reflect proportional contour lengths for each repeat as listed in Table 1; the minor peaks are likewise fit but with contour lengths of tandem repeats. The 10°C distribution clearly shows a more distinct and prominent tandem repeat peak at 41–44 nm compared to that for 42°C or any of the other intermediate temperatures studied. This indicates that tandem unfolding events are more frequent and energetically favored at lower temperatures.

FIGURE 2.

Temperature effects on unfolding length and percentage of tandem events. (A) Peak-to-peak unfolding length from ensembles of extension curves at 10°C and 42°C. The unfolding distributions for both temperatures were fitted with sums of Gaussians that reflect proportional contour lengths for single repeats. The minor peaks were likewise fitted but with proportional contour lengths of tandem repeats. The overall sum of all the Gaussians is indicated by the heavy black line. (B) A factor of nearly two between the major (single repeat) and minor (tandem repeats) peaks is apparent for temperatures from 10 to 42°C. (C) The percentage of tandem repeat unfolding events decreases with temperature. The dotted arrow indicates that in cooling from 42°C to 23°C, the percentage of tandem repeat unfolding events returns to within 90% of the initial value.

Independent of temperature, single repeat l_pk−pk values are centered at 20–22 nm, and tandem repeat l_pk−pk values are centered at 41–44 nm (Fig. 2 B). The narrow ranges make the identification of peaks very clear. To determine the relative frequency of tandem events, a scatterplot is first made of length versus force (Law et al., 2003), and one-molecule events at low force are separated from higher force events typical of a less frequent two-molecule event or else loop extension (as clarified below). The percentage of tandem events at each temperature (Fig. 2 C) shows that the tandem event percentages decrease nonlinearly from nearly 40% frequency at 10°C to ∼20% at 42°C. The dashed line in this same figure illustrates the reversible effect of cooling the sample back down to 23°C from 42°C and repeating the collection of unfolding spectrograms. The result demonstrates the reversible reproducibility of temperature effects in AFM.

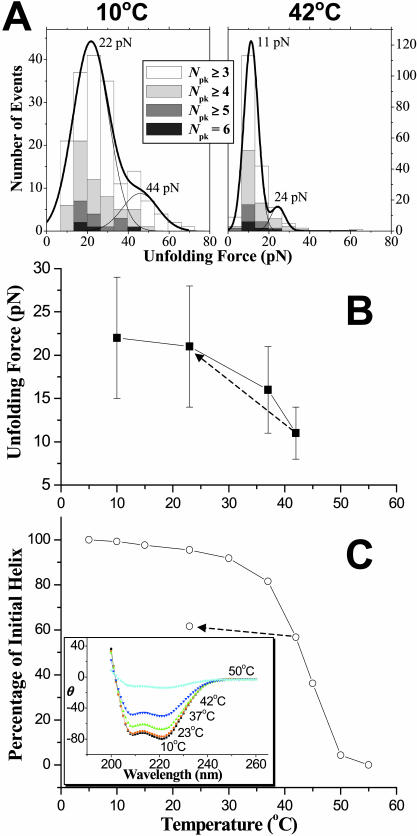
Although temperature has no significant effect on the unfolding lengths (Fig. 2 B), it does have a dramatic effect on the unfolding forces as T approaches T_m. Unfolding force histograms were fitted with two Gaussians of the same width (Fig. 3 A), where the second, minor Gaussian at nearly twice the force reflects the extension of two molecules or a loop (Law et al., 2003). Mean forces for the major peaks (and their variances) at 10°C and 23°C are statistically the same 21–22 pN (Fig. 3 B), which is in close agreement with previous measurements on this and related spectrin constructs (Rief et al., 1999; Law et al., 2003). However, the average force is seen to decrease significantly and nonlinearly with temperature to 16 pN at 37°C and to 11 pN at 42°C. The force that drives DNA's B-S transition is also found to decrease nonlinearly with temperature (Clausen-Schaumann et al., 2000; Williams et al., 2001), although the approach to T_m seems far less sharp compared to here. The change in force is nonetheless reversible (Fig. 3 B, dashed line) as reported above (Fig. 2 C) for the tandem event frequency.

FIGURE 3.

Nonlinear temperature dependence of both unfolding force and percentage of initial helix for β_1–4 spectrin. (A) Force distributions from ensembles of extension curves at 10°C and 42°C. Force distributions were fitted with two Gaussians. The major Gaussian indicates the force to unfold a single protein chain and the minor Gaussian, at about twice the force, represents unfolding of two independent chains. (B) Unfolding forces of single molecules show that the average unfolding forces decrease by half from 10°C (22 pN) to 42°C (11 pN). The dotted arrow indicates that when the sample was cooled to 23°C from 42°C, the unfolding force returns to 21 pN. (C) Percentage of initial helix versus temperature from circular dichroism. At 42°C, the percentage of initial helix is 56%. The dotted arrow indicates the effect of cooling the sample from 42°C to 23°C: the percentage of initial helix increases <10%. The unfolding forces and percentage of initial helix, nonetheless, follow the same nonlinear decrease with temperature. The inset shows CD spectra up to 55°C, where β_1–4 is completely unfolded.

The decrease in AFM-detected unfolding force clearly reflects T approaching T_m, since circular dichroism (CD) shows the characteristic double-well spectrum of α-helical structure is halfway to baseline at T_m ∼ 43°C (Fig. 3 C). By 50°C, CD shows β_1–4 spectrin has lost most of its helix content in a complete helix-to-coil transition. Such nonlinear changes are consistent with results of others near 40°C or slightly higher (Minetti et al., 1986; Grimaldi et al., 1989; DeSilva et al., 1997; Menhart et al., 1996; MacDonald and Pozharski, 2001). Even though the AFM force results follow the same trend as CD measurements, the CD does not show the same reversibility. Cooling the spectrin solution in CD back to 23°C from 42°C increases the percentage of helix only by ∼9% (dotted line in Fig. 3 C). This is probably because aggregation of thermally unfolded protein in solution inhibits proper refolding. In contrast, the AFM experiments are performed on surface immobilized proteins that clearly limit diffusion and aggregation. With AFM, however, higher temperatures are not easily attained due to severe bending of the soft cantilevers needed.

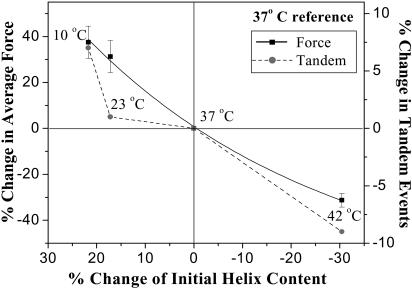
The AFM and CD measurements here show that increasing temperature yields nonlinear reductions in the respective force and percentage of initial helix. Fig. 4 shows that the relationship between normalized changes in average force versus helix content deviates only slightly from a line (using physiological 37°C as a reference temperature). Fig. 4 also plots the percentage change in tandem events versus the percentage of initial helix, and indicates a similar correlation as the force except at low temperature: from 10°C to 23°C, a few-percent helix is lost in heating but the frequency of tandem events decreases substantially more. This indicates, we propose, that a small helical linker (∼10–15 residues) seen in various crystal structures of related spectrin family proteins (e.g., Grum et al., 1999) is melting earliest, and its loss buffers against helix-to-coil transitions that cooperatively propagate unfolding from a single repeat to a tandem pair. A helical linker here is also implicated by the fact that AFM results for flexibly linked concatemers of spectrin repeats (Lenne et al., 2000) show no evidence of tandem repeat unfolding. The high frequency of either tandem or single repeat pathway being taken here (e.g., 37% tandem events at 10°C; Fig. 2 C) further implies that the putative linking helix is intact only for a finite fraction of the time to propagate unfolding. This softness of the linker at all temperatures may explain why no βI-spectrin crystal structures have yet been reported, whereas several other spectrin family tandem repeat structures are published.

FIGURE 4.

Percentage change in both mean unfolding force and tandem events versus percentage change in helix content using 37°C as the reference temperature. The weakly nonlinear relationship for change in force is fitted with a second-order polynomial function.

In contrast to disruption of the linker, an increase in temperature is seen to only weaken the spectrin repeats' coiled-coil triple helical structure. Importantly, the variance in unfolding force does not grow with temperature, which might otherwise have suggested some repeats unfold and others are unaffected. With double-stranded DNA, both Clausen-Schaumann et al. (2000) and Williams et al. (2001) showed that temperature melts and softens the bonds between the strands. A helical linker between spectrin repeats is qualitatively different from the repeats themselves in that the linker lacks any adjacent helices to interact with. Intramolecular hydrogen-bonding studies by Ragone (2001) indeed provide evidence that side-chain-to-side-chain interactions provide stabilizing contributions to helical structures. In a study of ionic strength effects on the thermal unfolding of spectrin peptides, Lusitani et al. (1998) also suggested that inter-repeat regions are less stable and more vulnerable to ionic strength effects which account for strong conformational changes under different ionic strengths.

If the linkers are indeed weaker and unfolded at elevated temperatures, the protein should have a longer unfolded length before unfolding with the AFM. We therefore analyzed the l_0–2 length (defined in Fig. 1 B) for the longest extension curves with five or more peaks. The l_0–2 length at 10°C is close to the estimated folded length of 26 nm for a four-repeat spectrin (based on α-actinin's structure; Ylanne et al., 2002), and this length increases gradually to ∼1.5× that value at 42°C. This increase includes contributions from extension due to initial desorption, stretching of any unfolded structure, and also unfolding of weakened and disrupted regions of the protein. Per each of the three linkers, the measured increase in length l_0–2 corresponds to the contour length of ∼12 amino acids or, if folded, an ∼2-nm helical linker between repeats.

Energetic considerations

In addition to cited temperature studies of forced transitions in double-stranded DNA, a recent temperature-dependent study of biotin-avidin bond rupture forces by Lo et al. (2002) concluded that temperature has a significant cooperative effect on the rupture forces. At higher T, it takes less time for thermal fluctuations to induce rupture under an applied bias force. The argument should, in principle, extend to fold-stabilizing interactions and protein unfolding. However, contrasting with the linear dependence of rupture force F vs. T shown by Lo and co-workers, we find here that unfolding force is increasingly nonlinear as T approaches T_m (Fig. 3 B). A hybrid kinetic-thermodynamic theory of Lo and co-workers predicts F^b = c₁ − c₂ T (T in Kelvin), where b = 2 for Hookean-type models of cantilever and bond elasticity, and the c_i values are constants related, among other factors, to the activation energy ΔG^* governing kinetics. Fitting Lo and co-workers' most general form to our force-versus-temperature results of Fig. 3 B yields a very different exponent of b = 6.64 (as well as c₁ = 73 × 10⁸, c₂ = 0.23 × 10⁸; fit R = 0.95). The Hookean-type model of Lo and co-workers clearly does not fit here. Although different models for elasticity may prove predictive one day, the notion of integrating or comparing equilibrium results (from CD) with kinetics (from AFM) does prove useful below in a simpler analysis of our spectrin measurements.

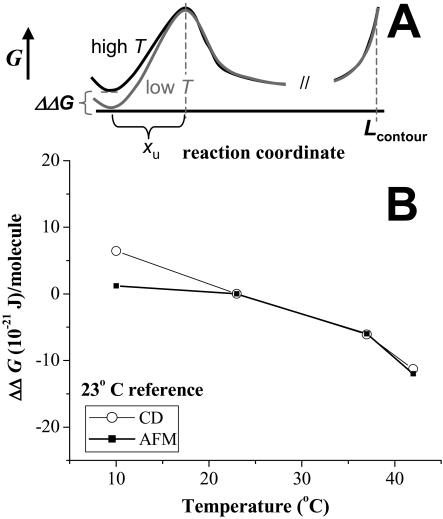
An equilibrium difference in free energy between folded and unfolded states, ΔG_eq(T), is provided by our CD measurements. In particular, the CD experiments were performed over a period of hours, allowing the protein solution to equilibrate at each temperature. In contrast, the subsecond unfolding times forced on a protein in the AFM experiments imply a well-known rate dependence to the unfolding force and also that AFM provides insight into the free energy difference, ΔG^*(T), between folded and transition states (Rief et al., 1998; Evans, 2001). Given this distinction in measurements, suppose that both the unfolded state and the transition state are invariant, but that the free energy of the folded state increases with temperature. Fig. 5 A provides a sketch of relevant energy landscapes for both low T and high T. For the two different temperatures, the difference in equilibrium free energies is given by ΔΔG_eq = ΔG_eq(T₂) − ΔG_eq(T₁). Likewise, the difference in free energies from the folded states to the common transition state is ΔΔG^* = ΔG^*(T₂) − ΔG^*(T₁). Clearly, in the case, it is supposed to be ΔΔG_eq = ΔΔG^* (see Fig. 5 A). We show that this relation holds approximately for the temperature results here.

FIGURE 5.

Energetic comparison between AFM and CD. (A) Low and high temperature free energy landscapes for protein unfolding, with the unfolded state free energy used as a reference. (B) The temperature-dependent change in folding-unfolding free energy difference (ΔΔG) for both CD and AFM. 23°C is used as reference. Both calculations clearly show decreases in ΔΔG with temperature, emphasizing the increased tendency to unfold at higher temperature.

For CD measurements, we neglect irreversibility and determine ΔG_eq(T) (Cantor and Schimmel, 1980; MacDonald and Pozharski, 2001) from equilibrium between just two states. Fig. 3 C gives the fraction unfolded at a given temperature X_u(T) and therefore the fraction folded as (1 − X_u(T)).

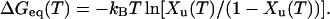(1)

Importantly, because the variance in AFM unfolding force stays narrow with temperature, an equal fraction of helical content is lost in all repeats upon heating. We thus conclude that Eq. 1 applies to each single repeat. The difference in unfolding free energy per molecule,

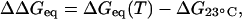(2)

is shown in Fig. 5 B, where a reference T = 23°C is used. ΔΔG_eq clearly becomes more negative with increasing T.

In calculating ΔΔG^*, we exploit prior demonstrations (Carl et al., 2001) that show the linear approximation of Bell (Bell, 1978; Evans and Ritchie, 1999; Rief et al., 1998) for work done by a force leads to

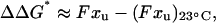(3)

where the average force F as a function of T is extracted from Fig. 3 B, and x_u is a known transition state length of x_u ≈ 1.2 nm at 23°C (Law et al., 2003). As others have shown before (Rief et al., 1997; Evans, 2001), x_u is obtained from the extension rate dependence of F. Compared to the ∼5-nm length of the three-helix repeat, x_u ≈ 1.2 nm suggests significant helix displacement before unfolding. Preliminary results imply a similarly weak dependence of F on extension rate at 37°C, which is consistent with a single transition state at x_u ≈ 1.2 nm as sketched in Fig. 5 A (see Carl et al., 2001). Both Carl and co-workers and Best and co-workers (Best, et al., 2002) establish Eq. 3 as a good approximation when x_u is essentially constant. Calculating ΔΔG^*(T) per Eq. 3, Fig. 5 B shows that ΔΔG_eq ≈ ΔΔG^*, suggesting consistency between CD and AFM measurements. The principal discrepancy is the 10°C result, but this would fit well within uncertainties given the error bars for the unfolding force (see Fig. 3 B).

Relation to thermal softening of red cell shear elasticity

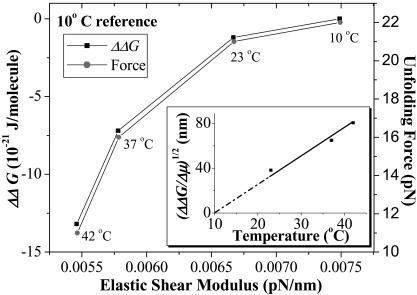
The decrease in both unfolding force F and ΔΔG with temperature provide a basis for better understanding the long-established temperature-dependent deformability of the red cell membrane. Using a shear flow to distort red blood cells, Rakow and Hochmuth (1975) showed an irreversible transition in red cell deformability at 46–50°C. Waugh and Evans (1979) subsequently showed, using a micropipette to aspirate individual red cells, that the shear elastic modulus, μ, decreases linearly with temperature up to at least 42°C. The latter study concluded that the entropy of the spectrin network in extension increases at higher temperatures, i.e., spectrin becomes more disordered by stretching. As recognized by Waugh and Evans, this is not consistent with the widely presumed entropic chain elasticity such as WLC elasticity where F simply scales as T. The cell measurements are consistent, however, with processes such as protein unfolding. The thermal elasticity data is seen to correlate nonlinearly with the temperature-dependent unfolding force as well as ΔΔG (Fig. 6). Just as the membrane becomes softer with temperature, both the free energy differences for spectrin unfolding and the unfolding force itself decreases. The inset to Fig. 6 shows a relative elastic length, (ΔΔG/Δμ)^1/2, for the red cell membrane; this is seen to increase above the 10°C reference. At 37°C, for example, an incremental length of ∼65 nm approximates the length of three unfolded spectrin repeats (see Fig. 1 B). Thermal softening in red cell membrane elasticity may thus be due to spectrin unfolding.

FIGURE 6.

Nonlinear correlations between the red cell's shear elastic modulus and both ΔΔG and unfolding force, F. The elastic modulus, μ, data is extracted from Waugh and Evans (1979) and plotted against ΔΔG and unfolding forces from these AFM results. The reference temperature for ΔΔG is 10°C. Each data point is labeled with the temperature at which the data was extracted. The inset shows that, with increasing temperature, the relative length (ΔΔG/Δμ)^1/2 also increases, representing increased unfolding of spectrin repeats in the heated cell membrane.

CONCLUSION

Structural changes in spectrin with temperature correlate well with both single molecule unfolding forces and shifts in unfolding pathways. For all temperatures studied, the unfolding process appears bimodal and reveals both tandem repeat unfolding and single repeat unfolding. Increasing the temperature shifts the unfolding pathway from tandem repeat processes toward single repeat processes. The likely explanation is that the inter-repeat linker, which is frequently helical at low temperature, becomes an unfolded coil at higher temperature. This partial melting would tend to limit highly cooperative helix-to-coil transitions that propagate unfolding from one repeat to the next. As temperature approaches the melting temperature of spectrin, the mean unfolding force decreases substantially, and it does so in near proportion to the loss of helix. Based on the respective timescales of the measurements, CD and AFM might be considered to access equilibrium and nonequilibrium pathways of unfolding, but only heating and cooling in AFM proves reversible. The results do not directly address whether the unfolding pathways are otherwise the same, but they do suggest a mechanism of thermal unfolding by which thermal softening of the cytoskeleton will occur as seen in cell-scale measurements. Quantitation of the decrease in tandem events together with the decrease in unfolding force and correlation with decreased helical content should provide new opportunities to develop temperature-dependent interaction potentials in molecular dynamics and related simulation methods for protein unfolding and folding.