Theoretical Investigation of Infrared Spectra and Pocket Dynamics of Photodissociated Carbonmonoxy Myoglobin

Abstract

Molecular dynamics simulations of the photodissociated state of carbonmonoxy myoglobin (MbCO) are presented using a fluctuating charge model for CO. A new three-point charge model is fitted to high-level ab initio calculations of the dipole and quadrupole moment functions taken from the literature. The infrared spectrum of the CO molecule in the heme pocket is calculated using the dipole moment time autocorrelation function and shows good agreement with experiment. In particular, the new model reproduces the experimentally observed splitting of the CO absorption spectrum. The splitting of 3–7 cm⁻¹ (compared to the experimental value of 10 cm⁻¹) can be directly attributed to the two possible orientations of CO within the docking site at the edge of the distal heme pocket (the B states), as previously suggested on the basis of experimental femtosecond time-resolved infrared studies. Further information on the time evolution of the position and orientation of the CO molecule is obtained and analyzed. The calculated difference in the free energy between the two possible orientations (Fe···CO and Fe···OC) is 0.3 kcal mol⁻¹ and agrees well with the experimentally estimated value of 0.29 kcal mol⁻¹. A comparison of the new fluctuating charge model with an established fixed charge model reveals some differences that may be critical for the correct prediction of the infrared spectrum and energy barriers. The photodissociation of CO from the myoglobin mutant L29F using the new model shows rapid escape of CO from the distal heme pocket, in good agreement with recent experimental data. The effect of the protein environment on the multipole moments of the CO ligand is investigated and taken into account in a refined model. Molecular dynamics simulations with this refined model are in agreement with the calculations based on the gas-phase model. However, it is demonstrated that even small changes in the electrostatics of CO alter the details of the dynamics.

INTRODUCTION

The literature on the binding, photodissociation, and rebinding of small ligands such as O₂, NO, and CO with myoglobin (Mb) is extensive (Brunori, 2000; Frauenfelder et al., 2002). This is due to the importance of myoglobin as both a protein in its own right and as a model system for the study of the function of proteins in general, in particular the protein control of ligand binding and discrimination. In addition, the small size of myoglobin (153 residues) and apparently simple reaction (reversible binding of small ligands) make it an ideal subject for theoretical studies.

Despite the wealth of information available from numerous experimental and theoretical studies, a microscopic description of ligand binding remains elusive, and fundamental questions still remain unanswered. Where does the free ligand go in the moments after photodissociation (Nienhaus and Nienhaus, 2002)? What are the timescales involved in the ligand motion? How and when does the ligand rebind to the heme (McMahon et al., 2000)? What are the energy barriers involved (Harvey, 2000)? What is the origin of such energy barriers (Meuwly et al., 2002)? Some of these questions are only now starting to be answered.

Experimentally, agreement seems to have been reached on the events after photodissociation of CO from Mb (Frauenfelder et al., 2001; Nienhaus et al., 2002; Ostermann et al., 2000). Lim et al. (1993; 1995a,b; 1997) have presented strong evidence for the presence of a docking site within the protein, adjacent to the heme at the edge of the distal heme pocket, which reversibly binds CO. Through a series of time-resolved infrared studies, evidence supporting the docking process has been observed (Lim et al., 1995b) and the timescale of the process from photodissociation to docking was estimated to be 0.5 ps (Lim et al., 1997). The docking process and the timescales involved can be dramatically altered by making mutations in the region of the docking site. Recently, Schotte et al. (2003) showed that in the mutant L29F, in which Leu²⁹ is replaced by a Phe, the nature of the docking site in the distal heme pocket is changed and, instead of remaining in the docking site for nanoseconds, the photodissociated CO ligand rapidly moves from the distal heme pocket to other regions of the protein.

Further important details concerning wild-type myoglobin were obtained from the polarized infrared spectroscopy study of Lim et al. (1997). Because of the inhomogeneous electric field inside the heme pocket, the center frequency of the absorption band of CO will be both position and orientation dependent. Thus, the time-resolved polarized infrared spectrum of photodissociated CO allows the dissociation trajectories to be probed directly. From this study, the observed splitting of 10 cm⁻¹ in the infrared spectrum of the photodissociated CO (Lim et al., 1995b) was assigned to two possible orientations of the CO within the docking site, named B₁ and B₂.

Although molecular dynamics simulations support the notion of a docking site at the edge of the distal heme pocket (Ma et al., 1997; Meller and Elber, 1998; Vitkup et al., 1997), they have, for example, not yet reproduced the experimentally observed splitting (Ma et al., 1997). There could be several reasons for this. First, although the length of the simulations corresponds to the timescale of the docking process, the data collected may not be sufficiently complete to enable reproduction of the splitting. Specifically, the experiments probe a (largely unknown) distribution of CO positions and orientations within the active site. Alternatively, the models used to describe the CO ligand in the simulations may not be of sufficient accuracy. In addition, free-energy barriers have not been calculated.

In this article, we present the results of molecular dynamics (MD) simulations using a fluctuating charge model for the CO ligand, fitted to high-level ab initio calculations of the dipole and quadrupole moment functions taken from the literature (Maroulis, 1996; 2001). Infrared spectra of the photodissociated CO ligand are calculated from the trajectories using a time-correlation function approach (McQuarrie, 1976). The results obtained reproduce the experimentally observed splitting of the infrared spectrum, and almost quantitatively predict the magnitude of the splitting and the position of the adsorption band. Furthermore, the 1 ns trajectories permit observations of behavior not seen in shorter trajectories. We compare the results from our fluctuating charge model with those from the original three-point charge model of Straub and Karplus (1991) and investigate the effects of the Leu²⁹ 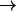Phe mutation (Schotte et al., 2003).

The rest of this article is organized as follows. In the next section, we describe the theoretical methods used, including the development of the new fluctuating charge model and the time-correlation methods for the calculation of infrared spectra. The results obtained with this model are described in the “Results” section, along with details concerning the reparametrization of the charge model that takes the protein environment into account. In the final section, “Conclusions”, we discuss the results obtained and make some conclusions.

THEORETICAL METHODS

Details of the molecular dynamics simulations

All MD simulations were carried out with the CHARMM program (Brooks et al., 1983) and the CHARMM 22 force field (MacKerell et al., 1998). Other parameters required to describe the heme-ligand interactions were taken from Kuczera et al. (1990) and Meuwly et al. (2002).

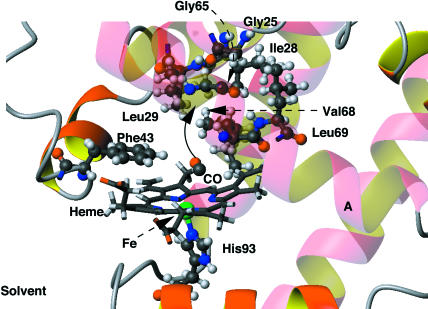
The computational setup follows a similar procedure to previous studies of the photodissociation of MbNO and MbCO (Meuwly et al., 2002; Straub and Karplus, 1991). A summary of the principal features is given here for completeness. The initial MbCO structure was taken from the x-ray study of Kuriyan et al. (1986), to which hydrogen atoms were added. A detailed view of the active site region is shown in Fig. 1. Since the simulation is focused on the region surrounding the heme group, the stochastic boundary method was used to increase computational efficiency (Brooks and Karplus, 1983). The heme pocket was solvated by three sequential overlays of a 16 Å sphere of equilibrated water molecules, centered on the heme, and a solvent boundary potential with radius 16 Å was applied to constrain the water molecules. A “reaction region” of radius 12 Å centered on the heme was defined, inside which the system was propagated with Newtonian dynamics. The dynamics of the buffer region between 12 and 16 Å from the center was described using Langevin dynamics. The system contained a total of 2532 heme protein atoms, the CO ligand, and 167 water molecules, which were represented by a modified TIP3P potential (where the van der Waals interactions are shared between the H and O sites) (Jorgensen et al., 1983). The nonbonded interactions were truncated at a distance of 9 Å using a shift function for the electrostatic terms and a switch algorithm for the Van der Waals terms. Friction coefficients of 62 ps⁻¹ and 250 ps⁻¹ were applied to the oxygen site of water and the remaining nonhydrogen atoms, respectively. The entire system was equilibrated for 90 ps at 300 K. Initial geometries for the photodissociation were taken from the equilibration at 80, 85, and 90 ps.

FIGURE 1.

The active site region of MbCO. The residues involved in forming the docking site at the edge of the distal heme pocket and the xenon 4 pocket are shown in a ball-and-stick representation. The heme unit is drawn in a line representation. Helix A is in the foreground and all helices are shown transparent for clarity. The solid arrow points toward the entrance of the xenon 4 pocket.

A similar procedure was followed for the L29F mutant. The protein structure was taken from the x-ray structure of Brucker et al. (1998) at 1.9 Å resolution (Protein Data Bank reference 1JDO), to which hydrogen atoms were added. The methionine initiator and D122N mutation were removed, leaving the L29F mutant, which was solvated and equilibrated as described above.

The photodissociation event was modeled by the “sudden” approximation, as used by Meuwly et al. (2002). The Fe-C bond is deleted and the potential parameters for the bound state are replaced by those for the dissociated state. A repulsive term of the form r⁻¹² was added and all nonbonded interactions between the CO and the heme “gate” were switched off. After 0.1 ps of dynamics, by which time the Fe-C bond is fully dissociated, the repulsive term was switched off and the nonbonded interactions were reintroduced. Subsequently, three 1 ns trajectories of photodissociated MbCO were calculated at 300 K. These trajectories were analyzed and properties such as the CO infrared spectrum were calculated.

The infrared spectrum can be calculated from the time dependence of the dipole moment of the dissociated CO molecule, μ(t). For this, the real-time dipole-dipole autocorrelation function, C(t), is constructed. The infrared spectrum, C(ω), is then calculated from the Fourier transform of C(t) (McQuarrie, 1976). The time correlation function is accumulated over 2ⁿ time origins, where n is an integer such that 2ⁿ corresponds to between ∼1/3 and 1/2 of the trajectory, with the time origins separated by 1 fs. This function can then be transformed using a fast Fourier transform with a Blackman filter to minimize noise (Allen and Tildesley, 1989). The final infrared adsorption spectrum is then calculated by evaluating

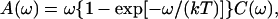(1)

where k is the Boltzmann constant and T is the temperature in Kelvin.

Charge models for CO

A range of models for representing CO molecules are available in the literature (Berne and Harp, 1970; Elber and Karplus, 1990; Fracassi and Della Valle, 1984; Straub and Karplus, 1991). These range from Stockmayer models (Lennard-Jones spheres with embedded dipole and quadrupole moments) (Berne and Harp, 1970) to diatomic models that neglect the quadrupole moment (Elber and Karplus, 1990), and a more complicated five-site model used in lattice dynamics simulations of solid CO (Fracassi and Della Valle, 1984). More recently, a three-site model for CO was developed by Straub and Karplus (1991), which has subsequently been used in a number of simulations of CO in myoglobin (Ma et al., 1997; Meller and Elber, 1998; Sagnella and Straub, 1999; Vitkup et al., 1997). It consists of charges and Lennard-Jones interaction sites on the C and O atoms, and a further charge site at the center of mass. This three-site model approximately reproduces the experimentally observable dipole and quadrupole moments and a range of other properties such as ab initio interaction energies with various molecules and the lattice constant of solid CO. The interatomic CO potential is derived from an anharmonic rotational Rydberg-Klein-Rees (RRKR) model (Huffaker, 1976a,b), which quantitatively reproduces the vibrational frequencies of CO. For the calculation of infrared spectra, this model can be improved in several ways. First, the dipole and quadrupole moments of the CO molecule are not in exact agreement with experiment or theory (Maroulis, 1996, 2001; Muenter, 1975; Roco et al., 1995). This is due to the fact that the model was parametrized to reproduce interaction energies. Second, the model is unable to reproduce the experimentally observed dipole moment function—the dipole moment derivative is an order of magnitude too small (Luis et al., 1995; Maroulis, 1996).

In the following we present an electrostatic model of CO that is based on fluctuating charges, although retaining the three-site character of the original model of Straub and Karplus (1991) (SK model). The present model (NM model) is designed to correctly describe the dipole μ(r) and quadrupole moment functions Θ(r) as a function of the CO bond length r.

We have taken the three-point charge model of Straub and Karplus (1991), with charges on the C and O atoms and an additional charge site at the center of mass, and allowed the charges to fluctuate. To fit such a fluctuating charge model, the multipole moment functions need to be known. To our knowledge, no experimental determination of the quadrupole moment function of CO is available in the literature. Semi-empirical dipole moment functions (where experimental data are included in a theoretical model) are available from work by Chackerian and Tipping (1983), for example. For consistency and values that are as accurate as possible, results from ab initio calculations were used for both moment functions. Self-consistent field calculations predict the C⁺O⁻ polarity (Szabo and Ostlund, 1989), rather than the counterintuitive but experimentally verifiable C⁻O⁺ polarity (Meerts et al., 1977; Muenter, 1975). However, the polarity is correctly predicted by higher-level ab initio calculations. Here, we used the ab initio dipole and quadrupole moment functions of Maroulis (1996, 2001) calculated at the CCSD(T) level with a [6s4p4d2f] basis set designed for the calculation of electronic properties. The importance of allowing the dipole moment to vary becomes clear when one notes that the CCSD(T) dipole moment changes sign (i.e., the dipole reverses polarity) upon an increase in the bond length from equilibrium of 0.05 Å. In the following, a positive dipole moment indicates the polarity C⁻O⁺.

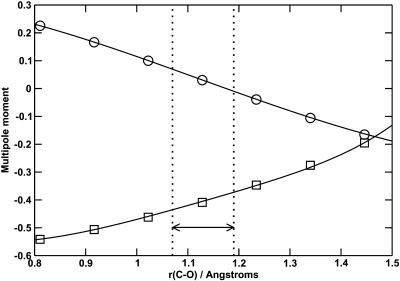
Fitting both moment functions simultaneously leads to a unique description of the site charges. The charge variations at the C and O sites were fitted to cubic functions, q = a₀ + a₁r + a₂r² + a₃r³, where q is the charge in |e|, a₀ to a₃ are constants of the fit, and r is the CO bond length in Å. The charge at the center of mass was defined as the magnitude of the sum of the charges on C and O. The parameters of the fit are given in Table 1 and the fitted multipole moments are shown in Fig. 2. The quadrupole moment was evaluated at the center of mass, not at the bond center as was the case in the original potential (Straub and Karplus, 1991). For the C-O stretching potential, the RRKR model from the original potential was retained (Straub and Karplus, 1991) and the Lennard-Jones parameters for C and O are given in Table 2.

TABLE 1.

Parameters of the fits of the charges

Site	a0/e	a1/(e/Å)	a2/(e/Å2)	a3/(e/Å3)
NM model
C	−11.0	20.2	−13.1	3.1
O	−11.3	22.3	−16.0	4.0
Refitted NM model
C	−10.5	19.1	−12.3	2.9
O	−9.8	18.9	−13.4	3.4

Parameters of the fits of the charges on the C and O atoms. The charges are fit to a function of the form q = a₀ + a₁r + a₂r² + a₃r³, where the charge is in units of |e| and the CO bond length, r, has units of Å. The charge at the center of mass site is defined as |q_C + q_O|.

FIGURE 2.

Variation of the dipole (circles) and quadrupole (squares) moments of CO with bond length. The theoretical values from Maroulis (1996, 2001) are given by the symbols, with the fits given by the lines. The units of dipole and quadrupole moment are eŠand eŲ, respectively. The region between the two vertical lines indicates the typical range of bond lengths sampled during molecular dynamics simulations.

TABLE 2.

Nonbonded parameters for C and O

Site	ɛ/kcal mol−1	σ/Å
C	−0.0262*	2.15†
O	−0.1591*	1.75†

^*Straub and Karplus (1991).

^†L. S. D. Caves (unpublished results).

RESULTS

Infrared spectrum of free CO

To investigate the performance of the C-O stretching potential and validate the methodology described above for calculating infrared spectra, we first calculated the infrared spectrum of a free CO molecule in vacuum. Infrared spectra at 10, 50, and 300 K were calculated from three 1 ns MD simulations.

At 300 K, there is a single strong absorption occurring at ∼2183 cm⁻¹. The effect of temperature is small, with the absorption shifting by 2 and 2.5 cm⁻¹ to the blue at 50 and 10 K, respectively. The full width at half-maximum is 0.3 cm⁻¹ at 300 K, and in all simulations a single, unsplit signal is observed. The absorption differs by ∼40 cm⁻¹ from the experimentally observed value of 2143.3 cm⁻¹ for gas phase ¹²CO (Ewing, 1962).

An accurate fundamental excitation energy was calculated by solving the radial Schrödinger equation for the one-dimensional RRKR potential using the program LEVEL (Le Roy, 1996). The lowest energy levels were found to be 1082.4 (ν = 0, J = 0) and 3227.0 (ν = 1, J = 0) cm⁻¹ above the minimum of the potential energy curve, leading to an energy difference of 2144.6 cm⁻¹. This is in almost perfect agreement with experiment. Thus the observed shift of 40 cm⁻¹ with respect to experiment is due to the use of the dipole-dipole autocorrelation function to calculate the stretching frequency.

Calculations of the infrared spectrum of CO in photodissociated MbCO

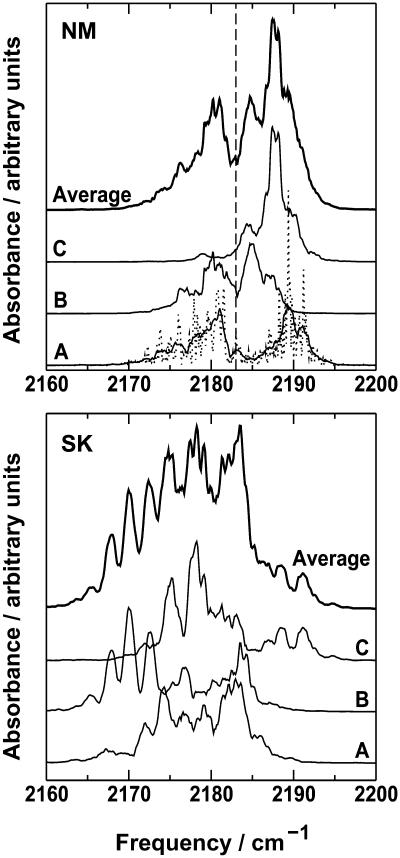
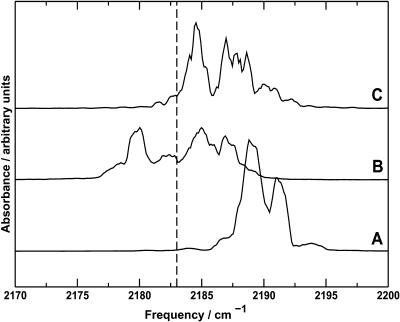
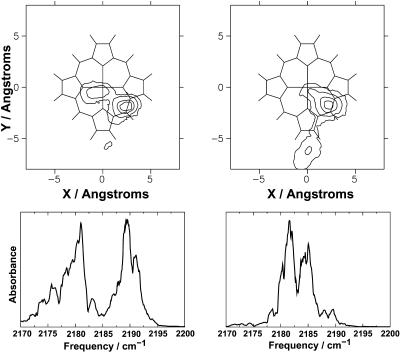
The infrared spectrum of the photodissociated CO molecule was calculated using the dipole moment time series from the trajectories. Each spectrum was slightly different, reflecting the different distributions of the CO position. The infrared spectra obtained from the three trajectories and the average spectrum are shown in Fig. 3. A number of peaks can be seen at different positions between 2170 and 2200 cm⁻¹.

FIGURE 3.

Top (NM): Infrared spectra of CO in Mb calculated over 1 ns from trajectories A, B, and C at 300 K using the new three-point fluctuating charge model. The raw and smoothed spectra are shown for trajectory A, and the smoothed spectra from trajectories B and C have been displaced vertically for clarity. The vertical dashed line indicates the calculated position of the absorbance of a free CO from the Fourier transform of 〈μ(0)μ(t)〉 at T = 300 K. The average spectrum is also shown. Bottom (SK): Infrared spectra of CO in Mb calculated from three 1 ns trajectories at 300 K using the three-point fixed charge model of Straub and Karplus (1991). The average spectrum is also shown.

One particular advantage of using the dipole autocorrelation function to calculate infrared spectra is that one can use segments of the autocorrelation function corresponding to parts of the trajectory that are of interest. Such parts can be identified from time series accumulated during the simulations. The resolution of the spectrum will depend on the length of the section of the simulation taken into account. For example, a resolution of 1 cm⁻¹ or better is only possible if a minimum of 66 ps of data from the trajectory is used.

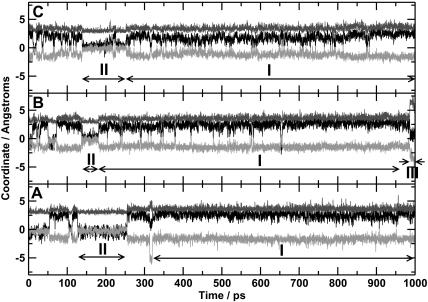
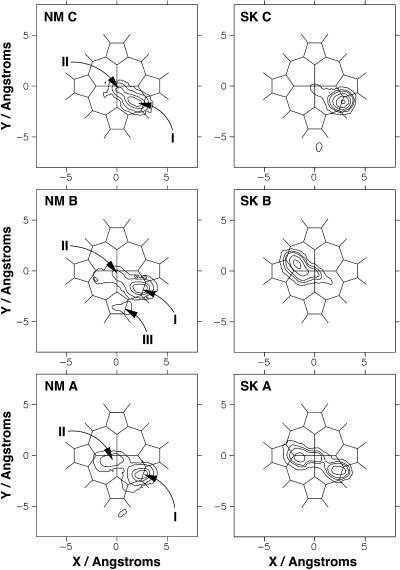
The time evolution of the x, y, and z coordinates of the center of mass of the CO molecule is shown in Fig. 4 for the three trajectories, labeled A, B, and C. From this, the probability distribution of the center of mass of the CO molecule over the xy plane can be calculated. It is shown in Fig. 5 for the three trajectories. To construct the probability distribution, the entire protein was reoriented so that the least-squares plane containing the four nitrogen “gate” atoms lies in the xy plane, with the center of mass of the four nitrogen atoms placed at the origin. The orientation of the protein in the global reference frame is kept the same. Various features are marked by Roman numerals and will be described in more detail below.

FIGURE 4.

Time series for the x (black), y (light gray), and z (dark gray) coordinates of the center of mass of the CO calculated in the three trajectories. Bottom: trajectory A; middle: trajectory B; and top: trajectory C. Features I–III are discussed in the text.

FIGURE 5.

Contour plots indicating the probability distribution of the center of mass of the CO molecule during the three trajectories A, B, and C for the three-point fluctuating charge model (left, NM) and the three-point fixed charge model of Straub and Karplus (1991) (right, SK). Features I–III are discussed in the text.

The calculated spectra correspond to the signal from a single molecule and are therefore sensitive to the precise position and orientation of the CO molecule, as well as to the surrounding protein environment that is continually changing. In experiments, the spectra recorded correspond to many CO molecules in different environments and therefore give an average picture of the CO environment. Compared to the “single molecule spectra” calculated here, some features will move, some will change in magnitude, and some will even appear or disappear as the signal is averaged over an ensemble of molecules.

It is also of interest to assess the convergence of the simulation results. In general, for long enough simulations, certain observables should become stationary. However, the behavior of individual infrared spectra is slightly different. If a peak in the infrared spectrum arises from a specific section of the trajectory, the feature will persist even when the trajectory is exploring additional parts of phase space, which may have a different characteristic spectrum. To investigate convergence, it is therefore useful to take the average of several infrared spectra. The average spectrum over the 1 ns trajectories (Fig. 3) shows two principal bands separated by ∼8 cm⁻¹ with intensities approximately in the ratio 2:1. This is in good qualitative agreement with the experimental spectra of Lim et al. (1995b, 1997) and gives some confidence in the methods used. In the present case, the time range over which the average is taken is also important, since there are several processes occurring after the photodissociation of CO from Mb: docking, diffusion through the protein, and loss of the CO to the solvent. Only the first process is important during the 1 ns trajectories presented here, but if the trajectories are extended, diffusion through the protein environment may become important, which changes the nature of the infrared spectra. To understand the details of the spectra, we need to consider more closely the individual parts together with the detailed information available from the simulations.

Feature I: The docking site at the edge of the distal heme pocket

Feature I in Figs. 4 and 5 can be associated with CO sampling a position corresponding to the proposed docking site (Lim et al., 1995b), a region between the heme plane and residues Leu²⁹, Phe⁴³, Val⁶⁸, and Ile¹⁰⁷ at the edge of the distal heme pocket. The time taken for the CO to reach this docking site after photodissociation varies considerably. CO is observed at this site 54, 10, and 0.5 ps after photodissociation for trajectories A, B, and C, respectively. This can be compared to the results from time-resolved infrared experiments, where the signal corresponding to CO in the docking site is first observed 0.2 ps after photodissociation. Evolution in the position and shape of the experimental peaks continues to occur over the first 10 ps after photodissociation. The data from our simulations are therefore consistent with the observed timescales.

In the simulations, the docking site occupies a region ∼2.9 Å from the heme normal and 3.5 Å from the heme plane, adjacent to the porphyrin c ring. This is slightly farther from the heme normal than was found in the x-ray studies of Schlichting et al. (1994) (a distance of 1.9 Å) and Hartmann et al. (1996), and significantly farther away than that found by Teng, Šrajer, and co-workers (Šrajer et al., 1996; Teng et al., 1994) (who found a distance of 1.2 Å). The distance from the heme plane is in closer agreement with the x-ray structures, where the average distance was found to be between 2.8 and 3.1 Å. The MD simulations of Vitkup et al. (1997) and of Meller and Elber (1998) agree qualitatively with the x-ray studies, but a detailed comparison is difficult due to the different temperatures and timescales used.

Our results are consistent with these observations, since the observed peak in the probability distribution is large (the maximum probability occupies a circle of ≈1 Å radius). The probability distributions from our simulations are considerably broader than the distributions presented by Vitkup et al. (1997) and more extended than the distributions from the calculations of Meller and Elber (1998). This is probably a consequence of using longer simulations. In addition, it can be seen from the time series presented in Fig. 4, as well as in the contour plots in Fig. 5, that the docking site can be more or less localized. In trajectory A, the CO is very localized (little variation in x, y, and z coordinates over significant time), whereas in trajectory C it is much more diffuse. The more delocalized CO position from trajectory C will give a mean CO position closer to the heme normal than the more localized position. How localized the CO is within the docking site will primarily depend on motions of the protein environment and will only become apparent from long simulations.

The infrared spectra of the CO molecule in the docking site were calculated from the dipole moment time series over the sections of the trajectory labeled I in Fig. 4 and are presented in Fig. 6. Each spectrum is slightly different, reflecting the different distributions of the CO position observed and described above. Two clear features can be observed in each spectrum, with a splitting of 3–7 cm⁻¹. This is slightly smaller than the splitting of 10 cm⁻¹ observed experimentally, but is of the correct order of magnitude. In the spectra calculated from trajectories B and C (where the docking site was observed to be slightly more diffuse), there is some evidence for a third peak; however, we will restrict our discussion to the two main peaks observed.

FIGURE 6.

Smoothed infrared spectra calculated for CO in the docking site (feature I) from trajectories A (bottom), B (middle), and C (top). The vertical dashed line indicates the calculated position of the absorbance of free CO. The spectra have been displaced vertically for clarity.

It is useful to compare the spectra in Fig. 6 with those presented in Fig. 3 from the full trajectory. The most striking change is the disappearance of the broad feature between 2170 and 2182 cm⁻¹ from trajectory A, which is observed in the full spectrum but not in the spectrum of CO in the docking site. This is clearly associated with CO in a position away from the docking site. More subtle changes are observed in, for example, the spectra from trajectory C. In Fig. 3, the spectrum is dominated by a single feature at 2187–2188 cm⁻¹, whereas in the spectrum due to CO in the docking site, two separate and approximately equal bands are observed.

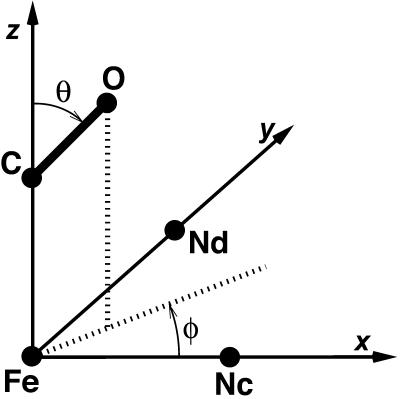
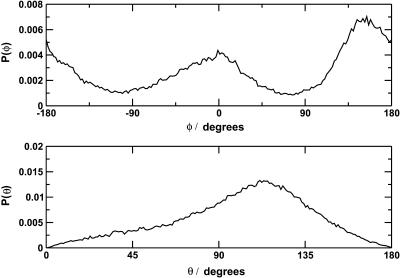
To test the hypothesis that the splitting of the infrared spectrum is due to two different orientations of the CO molecule within the binding site, the orientation of the CO molecule within the heme pocket was investigated. The orientation of the CO molecule can be described by the polar angles θ and φ as shown in Fig. 7. Fig. 8 illustrates the calculated probability distribution of θ and φ over region I from trajectory C (Fig. 4), corresponding to CO in the docking site at the edge of the distal heme pocket. The distribution in θ is broad and slightly asymmetric, with a maximum at ∼110°. This corresponds to a CO molecule oriented almost parallel to the heme plane, in agreement with experimental results (Lim et al., 1995b).

FIGURE 7.

Definition of the polar angles θ and φ used to describe the orientation of the CO molecule with respect to the heme plane.

FIGURE 8.

Calculated probability distributions for the orientational angles θ and φ (see Fig. 7) calculated over feature I of trajectory C with the fluctuating charge model.

The distribution of φ values is clearly bimodal, with maxima at ∼0 and 155° and minima at ∼±90°. The maxima correspond to a CO molecule lying approximately parallel to the x axis, with either the C or O atom toward the origin. The magnitude of the peak at ±180° is slightly greater than the magnitude at 0°, and this suggests a slight preference for the orientation with O toward the center of the heme. The free-energy profile, G(q), for a progression coordinate q (in this case q = φ), can be estimated from a probability distribution P(q) using the relationship G(q) = −RT ln(P(q)) + G₀, where R is the ideal gas constant, T is the temperature, and G₀ is a constant (McQuarrie, 1976). From G(q), the free-energy barriers can be estimated. For the probability distribution P(φ) shown in Fig. 8, the free-energy barrier to rotation of CO parallel to the heme plane was found to be ∼0.9 kcal mol⁻¹ for the transition 0° → 155° and 1.2 kcal mol⁻¹ for the reverse transition. The difference in free energy between the two orientations is ∼0.3 kcal mol⁻¹, with the orientation φ = 155° lower in free energy. This is in quantitative agreement with the experimental results of Lim et al. (1997), who found a free-energy difference of 0.29 kcal mol⁻¹ between the two orientations, with the orientation with the O atom closer to the center of the heme being lower in free energy.

Feature II: The central site

Feature II in Figs. 4 and 5 indicate that significant probability density occurs in a region ∼3 Å above the center of the heme. The CO occupies this central site for between 50 and 150 ps in each of the trajectories, with the CO molecule lying approximately parallel to the heme plane. It seems reasonable to suggest that rebinding of CO would occur from this site, were this possible in the current simulations.

The infrared spectrum of the CO molecule above the center of the heme was calculated using the dipole moment time series from region II in trajectory A (Fig. 4). Due to the rather short time interval available (100 ps), the resolution was quite poor (≈0.66 cm⁻¹) and a broad peak (full width at half-maximum ≈4 cm⁻¹) centered at ∼2177 cm⁻¹ was found (spectrum not shown).

The normalized probability distribution, P(x), of the x coordinate of the center of mass of CO was calculated from trajectory B by binning the time series x(t) from the entire trajectory as done for θ and φ in Fig. 7 (see above). The resulting probability distributions (not shown) exhibit two peaks, corresponding to the docking site and the site above the center of the heme. Using the relationship as before, the free-energy barrier to motion along the x axis between the two sites was estimated to be 5.7 kcal mol⁻¹ for the movement of the CO from the docking site to the central site and 1.3 kcal mol⁻¹ for the reverse process. This energy barrier is in addition to any barrier that would eventually be present for the rebinding process, such as the movement of the iron atom toward the heme plane, and to barriers corresponding to motion in the y and z directions.

Feature III: Excursions of CO away from the central and docking sites

One other feature of note can be observed at the end of trajectory B, labeled III in Fig. 4. The distance between the CO and the heme plane increases significantly, to up to 6–7 Å, and the CO molecule leaves the docking site at the edge of the distal heme pocket. This corresponds to the CO entering the “xenon 4” cavity (see the solid arrow in Fig. 1), as has been observed by Ostermann et al. (2000) and Scott et al. (2001). The xenon 4 cavity is a hydrophobic pocket adjacent to the heme binding pocket, lined by the residues Gly²⁵, Ile²⁸, Leu²⁹, Gly⁶⁵, Val⁶⁸, Leu⁶⁹, Leu⁷², Ile¹⁰⁷, and Ile¹¹¹, which was found to bind Xe atoms (Tilton et al., 1984). The CO is then observed to return to the docking site. This only occurs once in all three trajectories, an observation consistent with the results of Elber and Karplus (1990), who found that the transitions of CO between cavities (heme pocket, xenon cavities) are rare events that are rapid and involve the crossing of barriers. The kinetic data of Ostermann et al. (2000) suggests a rate constant of the order of milliseconds and barriers of between 2.7 and 5.4 kcal mol⁻¹ for motion to and from this pocket in the mutant L29W. Further simulations would be required to investigate this behavior more fully. This also suggests that even longer simulations may reveal behavior that is not observable on the nanosecond timescale.

Comparison of the fluctuating charge model with the original fixed charge model

Three 1 ns trajectories using the initial Straub and Karplus model were calculated using identical initial conditions as for the trajectories presented above (see previous section) and the corresponding infrared spectra were obtained. Since the dipole moment time series is not directly available in simulations using this model, the infrared spectra were calculated from the C-O bond-length time series. Within this approach only the positions of the peaks are significant.

Infrared spectra from these simulations and the corresponding contour plots showing the distribution of the center of mass of the CO ligand are presented in Figs. 3 and 5. It can be seen from the contour plots that the behavior of the CO ligand is similar to that observed in the simulations using the three-point fluctuating charge model. The CO ligand is found to spend time in the center of the distal heme pocket (trajectories A and B), in the docking site at the side of the distal heme pocket (trajectories A and C), and also make a single short excursion toward the xenon 4 pocket (trajectory C). In this respect, the two charge models give similar results. However, the infrared spectra reveal differences. First, the infrared spectra calculated from the C-O bond time series span a wider range of frequencies (2165–2195 cm⁻¹). The peaks are broad and coarse. In particular, the average spectrum is broad with many peaks, showing no clear splitting as was found with the three-point fluctuating charge model.

Further differences concern the orientation of the CO ligand within the docking site. The orientational angles θ and φ were calculated from trajectory C, where the CO was found to remain almost exclusively in the docking site at the edge of the distal heme pocket. The probability distribution of the angle θ has a maximum at ∼120°, corresponding to a CO molecule that is not parallel to the heme plane. This is similar to the structure found in the x-ray structure of Teng et al.(1994) and to one of the structures found in the MD simulations of Vitkup et al. (1997), who used a slightly different model for the CO ligand. The distribution function of the angle φ shows weak maxima at 0° and 150°, but is quite flat when compared to the corresponding distribution function from the three-point fluctuating charge model. Using the relationship G(q) = −RT ln(P(q)) + G₀ as before yields a free-energy difference between the two favored orientations of ∼0.3 kcal mol⁻¹, in good agreement with experiment and with the result from the simulations presented above. However, the energy barriers between these orientations are much smaller, 0.14 and 0.45 kcal mol⁻¹ for the 0° → 150° and 150° → 0° transitions, respectively. These are reductions of 85% and 60% compared to the values obtained from the fluctuating charge model. This may contribute to the fact that no obvious splitting of the infrared spectrum is found with the Straub–Karplus model.

Effect of the L29F mutation

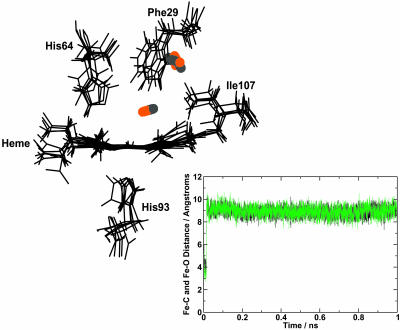
A 1 ns trajectory was calculated using the L29F mutant and the three-point fluctuating charge model. Five snapshots showing the configuration of the residues around the distal heme pocket during the nanosecond and the Fe-C and Fe-O distance time series are presented in Fig. 9. After dissociation, the CO molecule moves rapidly away from the distal heme pocket (within 20 ps) into a region corresponding to the xenon 4 pocket and remains there. This differs dramatically from the behavior in the native protein where the CO remains almost exclusively in the distal pocket, either in the docking site at the edge of the distal heme pocket or in the center of the pocket. The rapid escape of the CO after photodissociation agrees with the findings of recent experiments by Schotte et al. (2003) and gives confidence in both the methods and the model used. More detailed studies of the processes after dissociation and the subsequent dynamics on an even longer timescale may give further insight into effects of mutations on the dynamics of CO.

FIGURE 9.

Configurations at 5, 205, 405, 605, and 805 ps after photodissociation of the L29F mutant, showing the movement of the CO from the distal heme pocket to the xenon 4 pocket, which lies in front of the plane of the figure. Various residues around the heme unit are shown and labeled. The five frames are fit to the first frame. (Inset) Variation of the Fe-C (dark line) and Fe-O (light line) distances over a 1 ns trajectory for the L29F mutant. The CO leaves the distal heme pocket within 20 ps after dissociation.

Effect of the protein environment on the CO molecule

The CO model described above was parametrized using gas-phase data. Since the interior of the protein may be different from the gas phase due to the surrounding residues and charges, it is of interest to consider the effect of the protein environment on the dipole and quadrupole moments of the CO molecule. For this, 51 snapshots were taken from each of the 1 ns trajectories such that all of the main features were sampled, giving a total of 153 different configurations. For each configuration the potential energy curve and molecular properties (dipole and quadrupole moment) were calculated using a mixed quantum mechanical/molecular mechanical (QM/MM) method (Field et al., 1990). The system was partitioned into a QM part (the CO molecule) and an MM part (the protein). Using the QM code CADPAC (Amos, 1995) interfaced with CHARMM (Lyne et al., 1999), the energy and multipole moments of CO were calculated at the MP2/cc-pVTZ level for each configuration. To investigate the potential energy curve and the multipole moment functions, the CO bond length was varied between 1.08 Å and 1.20 Å in steps of 0.01 Å, keeping the center of mass and the orientation of the CO molecule fixed in space. This range of distances was selected since it corresponds to the range of CO bond distances observed in the trajectories.

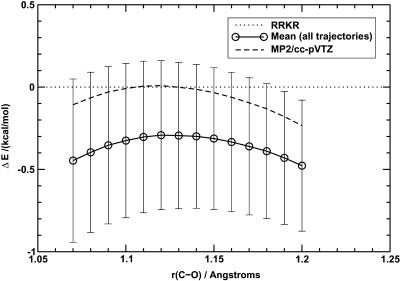
The mean potential energy curve for each series of configurations was calculated, together with the mean and standard deviation over all 153 configurations. The energy of the CO within the protein varies considerably, with the mean energy at each C-O distance having a standard deviation of the order of 0.4 kcal mol⁻¹ over the entire range of C-O bond distances. However, the mean potential energy curves from the individual trajectories are remarkably similar.

In Fig. 10, the shapes of the RRKR and the average MP2/cc-pVTZ potential energy curves are compared. For this, the positions of the minima of the two curves are superimposed (the minima are at r(C-0) = 1.128 Å and r(C-O) = 1.134 Å for the RRKR and the MP2/cc-pVTZ potentials, respectively). It can be seen that the MP2/cc-pVTZ potential energy curve agrees satisfactorily with the data from the RRKR potential although the deviation becomes greater at longer C-O bond lengths. This deviation significantly affects the vibrational energy levels, with the splitting between ν = 0 and ν = 1 calculated to be 2110 cm⁻¹ for the MP2/cc-pVTZ potential energy curve, compared to 2144.6 cm⁻¹ for the RRKR potential, using the LEVEL program as previously. The MP2/cc-pVTZ potential energy curve was, however, not used in calculations of the infrared spectrum. It can also be seen that, in general, the total energy of the CO molecule from the ab initio calculations is increased in magnitude by 0.3–0.5 kcal mol⁻¹ upon moving from vacuum to the protein interior (see Fig. 10).

FIGURE 10.

Deviation of the QM energies of CO from the RRKR model for free CO and for CO inside the protein matrix. The error bars correspond to ±1 SD. The energies from the RRKR model have been translated so that the minimum of the RRKR potential energy curve occurs at 1.134 Å, the optimized C-O bond length at the MP2/cc-pVTZ level of theory.

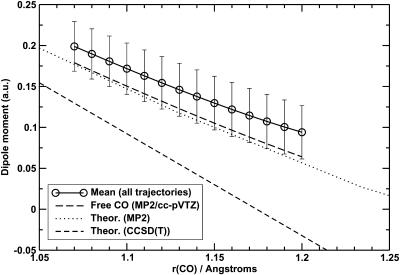
Similar effects are observed for the dipole and quadrupole moments of CO inside the protein if μ and Θ are calculated by QM/MM. The mean dipole moment of CO in the protein is enhanced by 0.04 a.u. over the free CO, with a considerable standard deviation (0.033 a.u.). This is shown in Fig. 11. The quadrupole moment is also enhanced, with a significant standard deviation. Thus, multipole moments of gas-phase CO are smaller than the corresponding values in the protein environment.

FIGURE 11.

Comparison of the dipole moment of free CO at the MP2/cc-pVTZ, MP2/6s4p4d2f, and CCSD(T)/6s4p4d2f levels with μ of CO inside the protein matrix at the MP2/cc-pVTZ level. The error bars correspond to ±1 SD. The MP2 and CCSD(T) values with the large basis were taken from Maroulis (1996, 2001).

To take the effects of the protein environment into account in the MD simulations, the fluctuating charge model was refitted. This was done by first determining empirical shift functions, which transform the gas-phase MP2/cc-pVTZ values for the μ and Θ for the free CO into the CCSD(T)/6s4p4d2f values. The shift functions were quartic and quadratic functions for the dipole and quadrupole moments, respectively. They were applied to the curves describing the mean dipole and quadrupole moments of CO inside the protein. The resulting moment functions should then describe the mean CCSD(T) moments of a CO molecule inside the protein. The coefficients of the revised fit are given in Table 1.

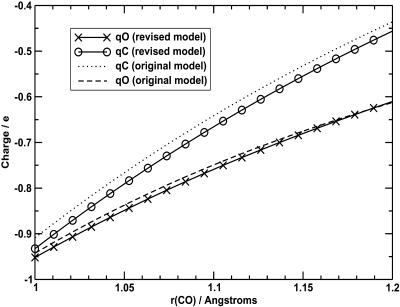
The original and revised charges are plotted in Fig. 12 as a function of bond distance. It can be seen that they are slightly different from the initial charges. The charge at the C atom is almost uniformly reduced in magnitude by 0.025|e| over the range fitted. The charge at the oxygen site is slightly reduced at short bond lengths, with virtually no change at longer bond lengths.

FIGURE 12.

Variation of the refitted charges with C-O bond length (symbols and solid lines). The fit for the original model is shown for comparison (dotted and dashed lines).

The three 1 ns trajectories described above were recalculated using the refitted charge model and were found to be significantly different, despite the identical initial conditions. Due to the slightly different charges at the C, O, and center of mass sites (as shown in Fig. 12), the trajectories diverge rapidly. To illustrate this, contour plots showing the cumulative distribution of the center of mass of the CO molecule during trajectory A with the original and revised charge models are shown in Fig. 13, along with the associated infrared spectra calculated over the entire trajectories. These show that the charge model used for the CO molecule can significantly affect the dynamics. However, features I–III found for the original fluctuating charge model are still observed in the trajectories using the refitted model. Thus, even if details of trajectories vary depending on the charge model, average quantities (such as splittings in the infrared spectra or barriers to rotation) are still comparable.

FIGURE 13.

Contour plots of the probability distribution of the center of mass of CO (top) and associated infrared spectra (bottom) calculated with the original fluctuating charge model (left) and the refitted fluctuating charge model (right). Significant differences in the details of the dynamics can be observed. However, the overall behavior is similar.

CONCLUSIONS

A new fluctuating charge model for CO has been developed from which the dipole moment time series, μ(t), of CO is obtained directly from the molecular dynamics simulations. The charge model was fitted to high-level ab initio calculations of the dipole and quadrupole moment functions taken from the literature. In addition, the sensitivity of the charge model was investigated by taking the protein environment into account. From this charge model the CO infrared spectrum was calculated via the dipole-dipole autocorrelation function.

Three 1 ns molecular dynamics simulations of photodissociated MbCO were carried out using both the fluctuating charge model and the refitted charge model, and the results were analyzed. Three main features common to both models were observed:

1. The CO was found to spend significant periods of time in the region at the edge of the distal heme pocket, commonly referred to as the docking site, in agreement with previous experimental and theoretical results (Lim et al., 1995b, 1997; Meller and Elber, 1998; Vitkup et al., 1997). For the first time, the infrared spectrum of the dissociated CO molecule calculated from the trajectories reproduces the experimentally observed splitting of the peak corresponding to CO in the docking site. From the time series of the coordinates, the origin of the splitting can be attributed to the two possible orientations of the CO molecule within the docking site, with the splitting in almost quantitative agreement with experiment.

2. A second region of high probability density for the CO was found to occur above the center of the heme. The infrared spectrum of the CO in this central site was calculated to give one broad peak at ∼2177 cm⁻¹, shifted ∼6 cm⁻¹ to the red of the free CO.

3. The CO is observed to briefly leave the heme pocket before returning. This corresponds to the CO entering the xenon 4 pocket. This phenomenon has also been observed experimentally (Ostermann et al., 2000; Scott et al., 2001) but it appears to be a rare event, occurring only once in the three simulations presented here. This behavior is different to the dynamics of CO in the L29F mutant, where the CO is observed to move rapidly from the distal heme pocket to the xenon 4 pocket.

Comparison of the new three-point fluctuating charge model with the fixed charge model of Straub and Karplus (1991) reveals both similarities and differences. Although the general observations remain unchanged compared to simulations with the fluctuating charge models, there are differences in the details. The barrier between the two possible orientations of the CO molecule within the docking site at the edge of the distal heme pocket is considerably smaller with the Straub-Karplus model than with the new fluctuating charge model. This is probably due to the different description of the electrostatics, which is important for describing the interactions of CO with the polar interior of the protein, and may be responsible for the lack of splitting in the CO infrared spectrum. The smaller forward (0.14 vs. 0.9 kcal/mol) and reverse (0.45 vs. 1.2 kcal/mol) barriers in the estimated free-energy profile G(q) give a flatter free-energy curve and allow for an almost unhindered rotation of the CO molecule. This is in contrast to the fluctuating charge model where the rotation of the CO is more strongly hindered (see Fig. 8). The present results suggest that this difference plays a role for the splitting of the infrared bands as the two bands originate from two orientations (Fe···CO and Fe···OC) of the CO molecule with respect to the Fe atom. Also, the fluctuating charge model allows for a coherent calculation of the infrared spectrum as the charge distributions used to describe the dynamics of the CO is the same as the dipole moment function from which the dipole time series is calculated. The Straub-Karplus model is a useful model for the investigation of the dissociation and the pocket dynamics. However, the present work suggests that for investigations of infrared spectra and other properties that depend sensitively on electrostatic interactions, a more detailed model (such as the three-point fluctuating charge model presented here) is preferred.

Environmental effects of the protein on the CO molecule were quantitatively assessed by static mixed QM/MM calculations. The shape of the CO stretching potential is somewhat altered around the minimum of the potential and the energetics vary by up to 1 kcal mol⁻¹ while largely preserving its shape. Also, the dipole moment of CO is enhanced by ∼10% compared to the gas phase value whereas the functional form of μ(r) is essentially unchanged. Simulations with an accordingly modified fluctuating point charge model reveal some differences in the actual dynamics although on average the results of the two fluctuating charge models are comparable. The major remaining differences between the empirical and a fully quantum description of the interactions between CO and myoglobin are in the intermolecular CO potential. Because the CO potential does not change its shape appreciably, the associated forces remain mostly unchanged. Although the dynamics could be influenced by quantum effects, their magnitude is not large and lie within the intrinsic accuracy of ab initio methods (≈1 kcal/mol).

The results show that an accurate description of the molecular charge distribution, together with long timescale MD simulations, give results in good agreement with experiment. In particular, the splitting of the infrared spectrum and the free-energy difference between the Fe···CO and Fe···OC conformations are correctly reproduced. Together with the detailed experimental results, this gives a consistent picture of CO dynamics within the primary binding site of Mb. Furthermore, preliminary investigations of the L29F mutant show that CO escapes the binding pocket on a picosecond timescale as was recently found in experiments.